Abstract
Boiling of mixtures in channels is involved in many chemical processes, and refrigerant mixtures are finding a rapidly increasing use in the refrigeration industries. Hence, reliable prediction of CHF (critical heat flux) is needed. There is no published method that has been verified over a wide range of parameters. In this study, available data for CHF in tubes and annuli were compared to general correlations for tubes and annuli, which are well-verified for single-component fluids. This paper presents the results of this comparison. It was found that general correlations for single-component fluids were in satisfactory agreement with data for mixtures. The data included mixtures of refrigerants and chemicals, reduced pressure 0.02 to 0.8597, mass flux 200 to 3798 kgm−2s−1, temperature glide 2.1 to 21.9 K, and critical quality −0.46 to 0.99. The data for annuli were predicted with a MAD (mean absolute deviation) of 13.6%, and the data for tubes had a MAD of 13.9% when compared to the Shah correlations for single-component fluids. Based on the results of the present data analysis and results of research on pool boiling, a range is identified in which pure fluid correlations can be used for mixtures. This will be useful in the design of heat exchangers involving the boiling of mixtures in channels.
1. Introduction
Many applications involve the boiling of mixtures inside tubes. These include chemical processes and refrigeration where mixtures are being increasingly used to replace the refrigerants that cause damage to the environment. Methods to accurately predict CHF (critical heat flux) are therefore needed for designing such heat exchangers. A literature survey showed that no well-verified prediction method is available. Development of such a prediction method is therefore desirable. In order to develop one, it was decided to first compare available data with correlations that have been found reliable for single-component fluids. Data for only those mixtures could be analyzed, which are supported by REFPROP [1]. This comparison showed that data for tubes and annuli were in satisfactory agreement with proven correlations for single-component fluids using mixture properties. The data included mixtures of refrigerants (R-407C, R-12, R-114) and chemicals (benzene, acetone, toluene), reduced pressure 0.02 to 0.8597, mass flux 200 to 3798, temperature glide 2.1 to 21.9 K, and critical quality −0.46 to 0.99. From the results of this data analysis and the study of CHF during pool boiling of mixtures, a range is identified in which pure fluid correlations can be used for mixtures without the need of any correction. The results of the present research are presented, and suggestions are made for further research. Previous work related to this topic is first briefly discussed.
2. Previous Work
The topic of CHF of mixtures has been reviewed by Collier and Thome (1994) [2], Celata et al. (1994a) [3], and Shah (2021) [4]. While there are numerous studies on CHF in pool boiling, there are only a few for flow boiling. A couple of those on pool boiling pertinent to the present work are first discussed.
To help in the following discussions, the phase equilibrium diagram of a typical binary mixture is shown in Figure 1. Point A is the bubble point, point C is the dew point. The difference in temperature between points A and C is the glide. Points A and B show the mole fractions of the more volatile component in the liquid and vapor phases, respectively, at the same temperature. The symbols for these are x’ and y’, respectively.
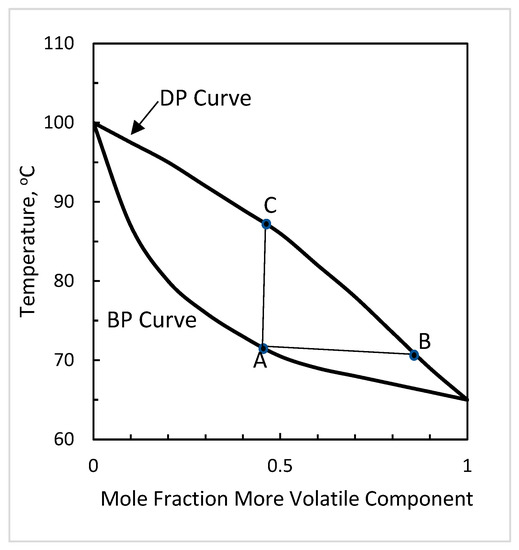
Figure 1.
Equilibrium curve of a typical binary mixture.
2.1. Pool Boiling CHF
Fujita and Bai (1997) [5] performed pool boiling CHF tests on seven mixtures and compared their measured CHF with the Zuber (1959) [6] hydrodynamic theory. They noted that the deviation from the Zuber model was related to Δσ = (σA − σB) where the subscripts “A” and “B” refer to the points in Figure 1. This is the difference in surface tensions at the composition in the liquid phase and the vapor phase at the bubble point temperature. When it is positive, CHF is higher than that given by the Zuber model. When it is negative, CHF is lower than that by the Zuber model. All mixtures showed these trends, but a strong effect was found only in aqueous mixtures. Mixtures of water with alcohols showed up to 2.5 times higher CHF than the Zuber formula. A water–ethylene glycol mixture had a CHF up to 50% lower than the Zuber formula. The four other mixtures were of methanol, ethanol, n-butanol, benzene, and n-heptane. The CHF of these mixtures was close to the Zuber theory. They attributed the variations of CHF to Marangoni flow induced at the vapor–liquid interface as a consequence of the surface tension gradient due to a concentration difference and correlated their data in terms of the Marangoni number. They have also discussed other hypotheses to explain the trends of CHF of mixtures, including those of Van Stralen and Sluyter (1969) [7] and Reddy and Lienhard (1989) [8].
Yagov (2004) [9] extended his dry spot model of CHF in pool boiling to mixtures and arrived at the following formula.
where qc,ef is the CHF of an equivalent pure fluid with properties of the mixture to be calculated by a correlation for a single-component fluid. He showed this formula to be in satisfactory agreement with mixtures of ethanol and methanol with water from many sources.
2.2. Mixture CHF in Annuli
Sterman et al. (1968) [10] studied the CHF of MIPD–benzene mixtures during boiling in an annulus, 10 mm ID, 16 mm OD. Pressure was 2 bar, subcooling was 20 to 50 K, and velocity was 4 to 12 m/s. They correlated their results by using the following equation. MIPD is the abbreviation for monoisopropyl diphenyl.
where
qc,A is the CHF of pure component A, and qc,B is that of pure component B. x′ is the mole fraction of component A in the liquid phase. The parameter β was given as:
y′ is the mole fraction of component A in the vapor phase.
Carne (1963) [11] performed tests on binary mixtures of acetone/toluene and benzene/toluene in a vertical annulus. Andrews et al. (1968) [12] tested the same mixtures in an annulus of dimensions close to that used by Carne.
Tests on mixtures of MIPD/dipheny have been performed by Naboichenko et al. (1965) [13]. Annulus ID was 2.94 mm and OD 16.37 mm, subcooling was 25 to 125 K, and velocity 4 to 8 m/s.
2.3. Mixture CHF in Tubes
Tolubinsky and Matorin (1973) [14] measured CHF for benzene–ethanol mixtures and various aqueous mixtures in a 4 mm diameter tube. Pressure was 3.3 to 13.2 bar, subcooling 10 to 110 K, and liquid velocity 2.5 to 10 m/s. They do not say whether they compared their data with the Sterman et al. correlation, Equation (2) with Equation (4) for β. They correlated their data with Equation (2) but with β as below.
This suggests that their data did not agree with the Sterman et al. correlation.
Celata et al. (1994b) [15] performed tests with mixtures of R-12/R-114 in a vertical tube. Data were in excellent agreement with the Sterman et al. correlation, Equations (2)–(4), using the measured values of qc for pure R-12 and R-114. They also found good agreement with the Katto and Ohno (1984) [16] correlation for pure fluids using mixture mean properties.
Sindhuja et al. (2008) [17] studied the CHF of R-407C in a vertical tube over a wide range of flow rate, pressure, and quality. They compared their data with three pure fluid correlations. These are the CHF lookup table of Groeneveld et al. (1993) [18], the Katto and Ohno (1984) [16] correlation, and Vijayarangan et al. (2006) [19]. The first two gave large deviations while the last one gave good agreement with their data.
Mori et al. (1990) [20] performed tests with R-22/R-114 mixtures in a vertical tube of 9 mm diameter at 2.3 to 4.8 MPa. No significant effect of mol fraction of components was found.
Auracher and Marroquin (1995) [21] performed tests with R-13B1/R-114 mixtures flowing up in a vertical tube of 17 mm diameter. Pressure was 11 bar, mass flux 1000 kg/m2s, and quality −0.4 to 0.2.
Robinson and Lurie (1962) [22] performed tests with organic reactor coolant mixtures. Their tests were performed in an 8.4-mm diameter vertical tube. The pressure was 1.6 to 10.3 bar, mass flux 1088 to 7122 kg/m2s, and subcooling 19 to 157 K.
In some of the above studies, it was found that at some mixture concentrations CHF can be higher than either of the pure components by a small amount.
3. Present Data Analysis
It is clear from Section 2 that there is no well-verified correlation for the CHF of mixtures in tubes or annuli. The correlation of Sterman et al. (1968) [10] for annuli was based only on their own data and was later found to be also in good agreement with the data of Celata et al. (1994b) [15]. While this is encouraging, more verification is needed to gain confidence in its reliability. Considering the widespread and increasing use of mixtures, there is clearly a need for a well-verified correlation. To achieve this goal, it was decided to first compare the available test data to correlations that have been shown to be accurate for pure fluids over a wide range of parameters, study the deviations of the data from these correlations, and then modify an existing correlation or develop a completely new one.
3.1. Choice of Correlations for Evaluation
The first step was to choose the pure-fluid correlations for comparison with data. All the available data are for vertical upflow in channels. Hence only such correlations need to be looked into. For tubes, the most verified general correlations are Shah (1987) [23] and Katto and Ohno (1984) [16]. Shah (1987) [23] analyzed data for 23 fluids (water, refrigerants, cryogens, chemicals, and liquid metals), tube diameters 0.315 to 37.5 mm, mass flux 4 to 2905 kgm−2s−1, reduced pressure 0.0014 to 0.96, and critical quality −0.26 to 0.96. The MAD of the Shah and the Katto–Ohno correlations were 16.0 and 22.3%. With the increasing interest in mini channels (usually considered those with D < 3 mm), Shah (2017) [24] collected a database of CHF in minichannels with diameters 0.13 to 3 mm. He compared this database with the correlations of Shah (1987) [23], Katto–Ohno (1984) [16], Zhang et al. (2006) [25], and Wojtan et al. (2006) [26]. Their MAD for all data were, respectively, 18.9, 33.2, 23.4, and 59.7%. In view of the poor performance of the Wojtan et al. correlation, it was decided to compare the tube data only to the correlations of Shah, Katto–Ohno, and Zhang et al.
For annuli, only two general correlations, i.e., those applicable to a wide range of fluids and parameters, have been published. These are Shah (2015a) [27] and Katto (1979) [28]. The Shah correlation is applicable to internally, externally, and bilaterally heated annuli while the Katto correlation is essentially limited to internally heated annuli. The Katto correlation has three regimes, namely L, H, and N. The correlation requires a factor K for each regime, which was provided for regimes L and H but was not provided for regime N. Shah (2015a) compared these two correlations to a wide-ranging database that included all three heating types. The Shah correlation had a MAD of 16.5% for all data while that of the Katto correlation for internally heated annuli in the L and H regimes was 233%. Doerffer et al. (1994) [29] and Hung and Yao (1983) [30] had also found it unsatisfactory. It was therefore decided to compare the annuli CHF data to only the Shah correlation.
3.2. Selection of Test Data
The published test data have been identified in Section 2.2 and Section 2.3. It is certainly desirable to analyze all available test data. The difficulty in doing so is in not being able to calculate accurately the properties of some mixtures. The concentration of components of mixtures is different in the vapor and liquid phases, and it changes along the tube length as the liquid evaporates, the more volatile component evaporating faster. Therefore, the properties of the phases change as the evaporation progresses. Calculating mixture properties is therefore very difficult without the support of a reliable software. The present author uses REFPROP 9.1, Lemmon et al. (2013) [1]. REFPROP is the most widely used property software. Developing programs to reliably predict properties of mixtures not supported by REFPROP will itself be a major project. Therefore, data for mixtures not supported by REFPROP were not analyzed. REFPROP 9.1 and its latest version does not provide transport properties of mixtures containing water or alcohols, as reliable general models for this purpose are not available to the developers of this program (Huber 2022 [31]). Further, it does not have properties of R-13B1, MIPD, and organic reactor coolants used by Robinson and Lurie (1962) [22]. For this reason, only the data listed in Table 1 and Table 2 could be analyzed. These data were read from the figures in the publications.

Table 1.
Results of comparison of data for CHF in tubes with some correlations. All tubes are vertical, and flow is upward.

Table 2.
Range of data for CHF in annuli and results of comparison with the Shah correlation. Mixture composition varied between 10 and 90% of each component.
3.3. Results of Data Analysis
The results for data analyzed for tubes are listed in Table 1, and those for annuli are in Table 2. The range of all data analyzed is listed in Table 3. The deviations listed in the tables are the mean absolute deviation (MAD) and the average deviation (AD). These are defined as below.

Table 3.
Range of parameters in the data analyzed.
Average deviation (AD) is defined as:
Results for the pure fluids have also been listed to permit comparison with those of their mixtures.
It is seen in Table 1 that the data of mixtures in tubes are in close agreement with the Shah correlation. The MAD for mixtures is comparable to that for the pure components. The other two correlations also do fairly well. Their deviations are higher than those of the Shah correlation but are comparable with their deviations for the pure components.
Table 2 for annuli shows that the data for mixtures are in good agreement with the Shah correlation, and deviations for mixtures are comparable to those of their pure components.
4. Discussion
4.1. Variation of CHF with Mixture Composition
Figure 2, Figure 3, Figure 4 and Figure 5 show the variations of CHF as a fraction of the more volatile component of the mixture varies from 0 to 1. It is seen that in some cases CHF at some composition is a little higher than of either component, but the excess is small and is within the margin of experimental uncertainty. The predictions of the Shah (2015a) [27] correlation are always close to the measured values. As is seen in Figure 2, it also predicts a CHF higher than that of either pure component. So, the variations in CHF are accounted for by the change in properties with change in composition.
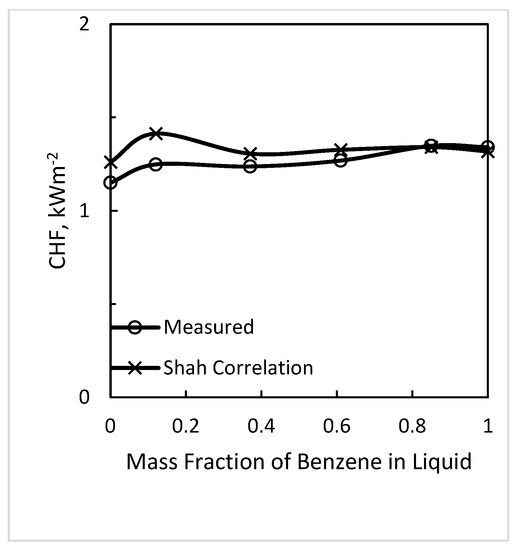
Figure 2.
Comparison of the data from Andrews et al. (1968) [12] for the benzene–toluene mixture in an annulus with the Shah (2015a) [27] correlation. Liquid velocity is 2.18 ms−1, inlet subcooling is 40 K, and pressure is atmospheric.
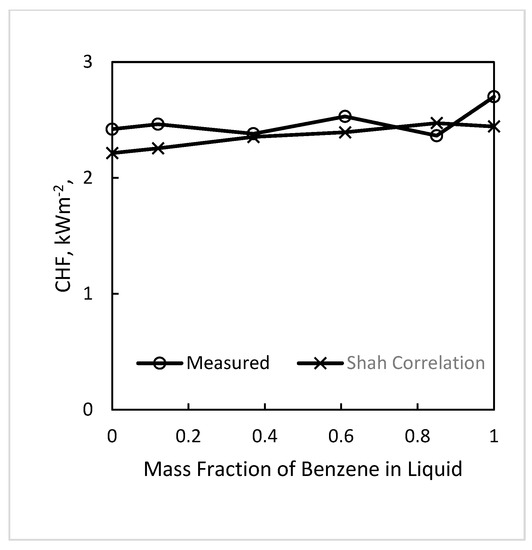
Figure 3.
Comparison of the data from Carne (1963) [11] for benzene–toluene mixture in an annulus with the Shah (2015a) [27] correlation. Liquid velocity is 4.36 ms−1, inlet subcooling is 80 K, and pressure is 2.23 bar.
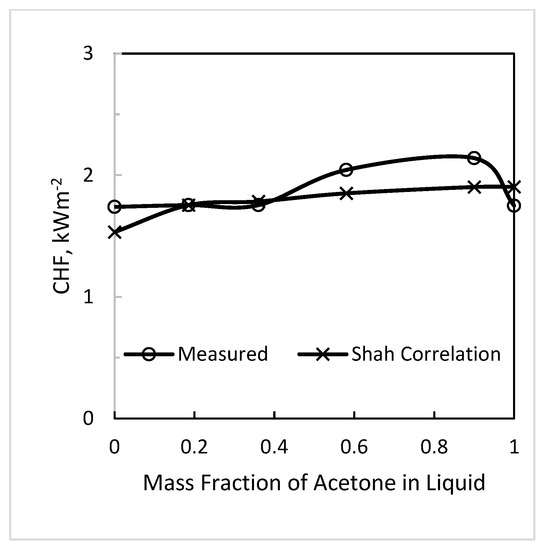
Figure 4.
Comparison of the data from Carne (1963) [11] for acetone–toluene mixture in an annulus with the Shah (2015a) [27] correlation. Liquid velocity is 2.18 ms−1, inlet subcooling is 60 K, and pressure = 2.23 bar.
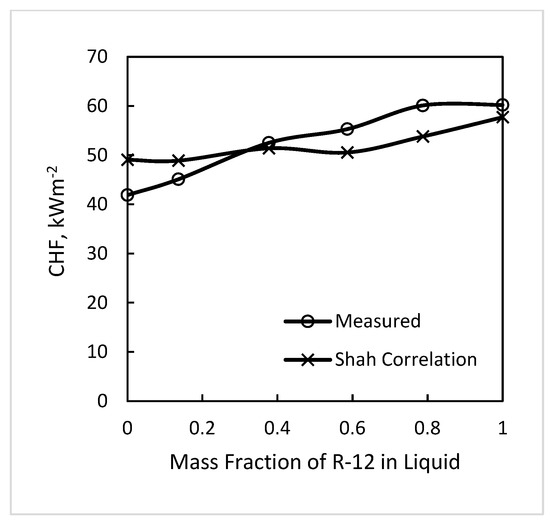
Figure 5.
Effect of the component mass fraction on CHF. R-12/R-114 is in a vertical tube. Pressure is 1.2 MPa, subcooling is 23 K, and mass flux is 559–612 kgm−2s−1. Data of Celata et al. (1994b) [15] compared with the Shah (1987) [23] correlation.
Some data show very complex variations of CHF with composition. An example is the data of Carne (1963) [11] shown in Figure 3, in which CHF has almost sinusoidal variations with composition. Note that there was considerable scatter in the data while Figure 3 gives the data points on the curve drawn through the data by Carne. Carne himself says about this figure that in view of the data scatter, these maxima have no significance, and the existence of the turning point itself is doubtful. Note that the Shah correlation agrees fairly closely with the measured CHF values.
It can be concluded that for the data analyzed, the Shah correlations for tubes and annuli adequately predict the variations of CHF with composition. However, this may not be the case for mixtures in which surface tension differences are large, as discussed in Section 4.2.
4.2. Effect of Surface Tension Difference
As was discussed in Section 2.1, Fujita and Bai (1997) [5] measured pool boiling CHF of seven mixtures. For mixtures with Δσ variation between −2.4 to 2.0 mN/m, they found that CHF of the mixture was close to the prediction of the Zuber model. By contrast, CHF was 2.5 times the Zuber prediction when Δσ was 20 mN/m and 50% lower than the Zuber prediction when Δσ was −10 mN/m.
As seen in Table 1, Table 2 and Table 3, Δσ in the present data analysis varied from −0.02 to 2.8 mN/m, and data over the entire range are in satisfactory agreement with the Shah correlations. Deviations of the Shah (2015a) [27] correlation with annulus data are plotted against Δσ in Figure 6. There is no indication in it that deviations are related to Δσ. Deviations of a few data points are high at both small and large Δσ. All such data are for mixtures of acetone. Some data for pure acetone also had similar deviations. This behavior may be due to small amounts of impurities in acetone. No data other than those for acetone and its mixtures had deviations greater than 25%.
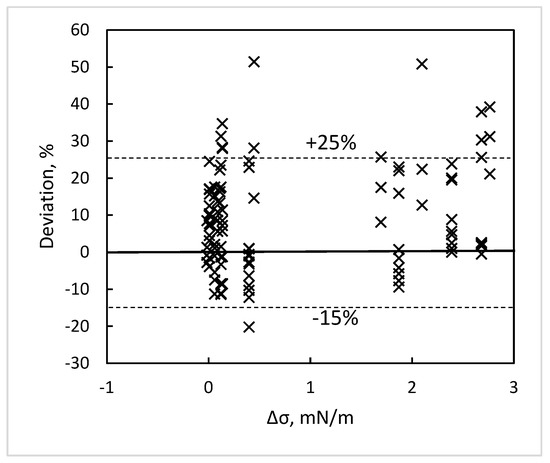
Figure 6.
Effect of Δσ on deviations of the Shah (2015a) [21] correlation with data for CHF in annuli.
Based on the present data analysis and the pool boiling results of Fujita and Bai, it seems that the Shah correlations for tubes and annuli can be used without any correction in the range of Δσ from −2.4 to 2.8 mN/m.
4.3. Effect of Glide
As seen in Table 1, Table 2 and Table 3, the glide of mixtures was up to 21.9 K. Data over this entire range of the glide for tubes and annuli are in satisfactory agreement with the Shah correlations. The glide is used as a parameter in the Bell and Ghaly (1973) [32] correction factor for the heat transfer coefficient of mixtures. The larger the glide, the greater the reduction in the heat transfer coefficient compared to pure fluid. The glides of most mixtures in use or being considered for use in refrigeration systems is well below 20 K.
4.4. Mass Flux
Mass flux in the data analyzed varied from 200 to 3798 kgm−2s−1, a very wide range. As seen in Table 1 and Table 2, the data over the entire range are satisfactorily predicted. Figure 7 and Figure 8 show the comparison of data of mixtures in tubes over a wide range of mass flux with the correlations of Shah, Katto and Ohno, and Zhang et al. The Shah correlation is seen to be in close agreement with the data. The predictions of the other two correlations are not too far off.
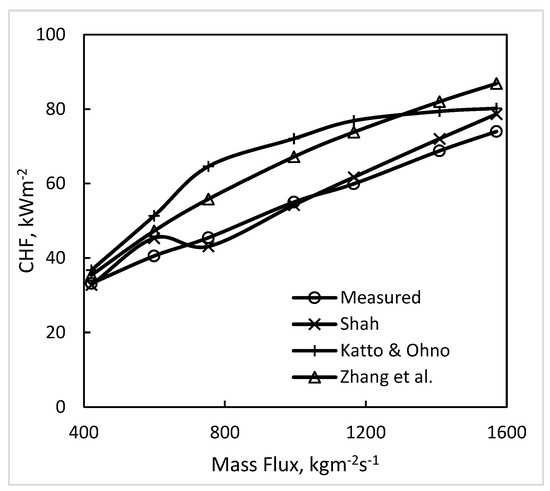
Figure 7.
Comparison of data from Celata et al. (1994b) [15], Shah [23], Katto and Ohno [16] and Zhang et al. [25] for the R-12/R-114 mixture of 0.787/0.223 mole in tube with some general correlations. Pressure is 2.8 MPa, and inlet subcooling is 23 K.
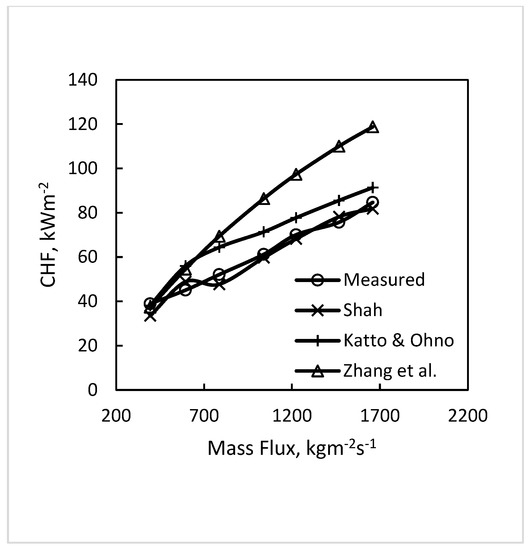
Figure 8.
Comparison of the data from Celata et al. (1994b) [15], Shah [23], Katto and Ohno [16] and Zhang et al. [25] for the R-12/R-114 mixture of 0.0.136/0.864 mole in a tube with some general correlations. Pressure is 1.2 MPa, and inlet subcooling is 23 K.
4.5. Reduced Pressure
Reduced pressure is a very important parameter as properties of fluids vary strongly with reduced pressure. Many correlations are known to fail at extremes of reduced pressure. The reduced pressure in the mixture data analyzed varied from 0.021 to 0.677, a wide range. For the pure components, the reduced pressure was up to 0.86. In fact, the reduced pressure in the pure fluid data analyzed in Shah (1987) [23] for tubes was up to 0.96 and in Shah (2015a) [27] for annuli up to 0.906. As the mixture data analyzed were limited to 0.677 reduced pressure, applicability to higher reduced pressures is subject to verification.
4.6. Inlet and Critical Qualities
CHF is basically of two types. One is DNB (departure from nucleate boiling) and the other is dryout. DNB occurs because of the inability of liquid to reach the tube surface due to intense vapor generation. Dryout occurs due to drying out of the liquid in contact with the surface due to evaporation. DNB occurs at a subcooled condition (negative quality) or at low vapor qualities. Dryout occurs at higher vapor qualities. As seen in Table 1, Table 2 and Table 3, critical quality varied from −0.46 to 0.99. Thus, both types of CHF are included in the data analyzed. The inlet quality varied from −0.78 to −0.03. There were no positive quality data in the present data analysis. However, the Shah (1987) [23] correlation for tubes and the Shah (2015a) [27] correlation for annuli were verified with pure fluid data that included large positive inlet qualities.
4.7. Orientations Other Than Vertical Upflow
All the data analyzed in the present study are for vertical upflow. Use of horizontal channels is widespread. In horizontal channels, stratification occurs at lower flow rates. This causes the upper part of channel to dry out and have CHF while the lower part remains in contact with liquid. Several correlations have been developed for CHF of pure fluids in horizontal channels. These were reviewed in Shah (2015b) [33] and Shah (2021) [4]. Shah (2015b) [33] developed a correlation for CHF in horizontal tubes, which is in the form of a correction factor to the CHF in vertical upflow calculated with the Shah (1987) [23] correlation. It was verified with a wide range of data and was shown to be much more accurate than other correlations. It is likely to be applicable to mixtures but needs to be verified when data become available.
For orientations other than vertical upflow and horizontal, there are no well-verified prediction methods even for pure fluids. Gong et al. (2022) [34] have reviewed the literature on the effect of orientation on the CHF of pure fluids.
4.8. Correlations for Mixture CHF
The correlation of Sterman et al. (1968) [10] was discussed in Section 2.2. It predicts the CHF of mixtures using the values of CHF of the pure components. It was shown by them to be in good agreement with their data for MIPD/benzene mixtures in a vertical tube. CHF occurred under a subcooled condition. They used their measured values of CHF of the pure components. Celata et al. (1994b) [15] found it to be in good agreement with their data for the R-12/R-114 mixture, again using the measured values of CHF of the pure components; CHF occurred at high vapor qualities. Thus, this correlation has been shown to agree with data for both DNB and dryout and could be generally applicable. As it requires the CHF of pure components to be inserted in it, its accuracy is limited by the accuracy of the correlations to predict pure fluid CHF. As the Shah (1987) [23] correlation predicted the CHF of mixtures with the same accuracy as for pure fluids, it is not possible to evaluate the accuracy of the Sterman et al. correlation using the data analyzed in the present study. Some doubts about the general applicability of the Sterman et al. correlation are raised by the fact that Tolubinsky and Matorin (1973) [14] gave their own formula for β to fit their data. This might have been because β from the Sterman et al. formula did not agree with their data.
The correlation of Tolubinsky and Matorin (1973) [14], Equation (5), was verified only with their own data. Hence, its general applicability is unknown. Note that this correlation also requires the value of CHF of the pure components, which have to be calculated by a suitable correlation.
5. Conclusions
- Data for CHF mixtures of halocarbon refrigerants (R-407C, R-12, R-114) and mixtures of chemicals (benzene, acetone, toluene) in annuli and tubes were compared to well-verified general correlations for pure fluids. The data included subcooled CHF as well as at high qualities. The range of flow rates and reduced pressures was very wide.
- Based on the results of this data analysis and results of pool boiling CHF, the best recommendation is that correlations for pure fluids can be used without any correction to predict CHF of mixtures provided that Δσ is the range −2.4 to +2.8 mN/m. Δσ is the difference between surface tension of the mixture at a vapor phase composition and that at a liquid phase composition, both at the same liquid phase temperature. The data analyzed were in this range and were in good agreement with the correlations of Shah (1987) for tubes and Shah (2015a) for annuli, both well verified for pure fluids.
- Most refrigerant mixtures have Δσ in the range stated above, and hence, this result will be particularly useful in the design of refrigerant evaporators.
- There is no verified method for calculation of CHF when Δσ is outside the range −2.4 to +2.8 mN/m.
- A number of available data sets for mixture CHF could not be analyzed due to the unavailability of software for calculating their properties. There is a need to develop software to predict properties of such fluids and mixtures.
- There is a great need for more experimental studies on the CHF of mixtures so that reliable methods to calculate the CHF of all types of fluid mixtures could be developed.
Funding
This research received no external funding.
Data Availability Statement
All data analyzed in this study is from publications whose references have been provided.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
| Nomenclature | |
| D | diameter, m |
| DHP | equivalent diameter of annulus based on heated perimeter, m |
| G | mass flux, kgm−2s−1 |
| L | length of channel from entrance to CHF location, m |
| N | number of data points, (-) |
| pr | reduced pressure = (actual pressure)/(critical pressure) (-) |
| qc | critical heat flux, kWm−2 |
| TSAT | saturation temperature, K |
| x’ | mole fraction of more volatile component in liquid phase at bubble point temperature, (-) |
| xc | quality at CHF location (called critical quality), (-) |
| xin | inlet quality, (-) |
| y’ | mole fraction of more volatile component in vapor phase at bubble point temperature, (-) |
| Greek | |
| β | parameter in Equation (2), (-) |
| σ | surface tension, Nm−1 |
| Δσ | σ at liquid phase composition minus σ at vapor phase composition both at bubble point temperature, Nm−1 |
| μ | dynamic viscosity, Pa.s |
| Subscripts | |
| I | ideal pure fluid with properties of mixture |
| mix | mixture |
Appendix A. Shah Correlation (1987) for CHF in Vertical Tubes
This correlation consists of two correlations, which are used in different ranges. These are the upstream condition correlation (UCC) and the local condition correlation (LCC). In the UCC, the CHF at a location depends on the upstream conditions, namely the inlet quality and the distance from the tube inlet. In the LCC, CHF depends only on the local quality except for very short tubes.
The UCC is as follows.
Y is a correlating parameter defined as:
When Y ≤ 104, n = 0 for all fluids.
For Y > 104, n is given by the following relations.
For helium at all values of Y > 104,
For all fluids other than helium,
The effective length LE and effective inlet quality xIE are defined below.
When xin ≤ 0, LE = Lc and xIE = xin
When xin > 0, LE = LB and xIE = 0
LB is the boiling length defined as the length of the tube between x = 0 and x = xc. For uniformly heated tubes, heat balance yields the following expression for it.
The LCC is given by the expression:
FE is the entrance effect factor given by the equation below.
If the above equation gives FE < 1, then use FE = 1.
Bo0 is the boiling number at xc = 0 and is the highest of those given by the following three equations.
For xc > 0, Fx is given by the following expression.
When pr ≤ 0.6, c = 0. When pr > 0.6, c = 1.
When xc < 0, Fx is calculated by the following equation.
When pr ≤ 0.6, b = 0; otherwise, b = 1.
When Y ≤ 1.4 × 107,
When Y > 1.4 × 107, use the above equation with Y = 1.4 × 107.
The choice between UCC and LCC is made as follows. For helium, always use UCC. For all other fluids, select as follows.
For Y ≤ 106, use the UCC.
For Y > 106, use the correlation, which gives the lower value of Bo. The only exception to this rule is that UCC is used if LE > (160/pr1.14).
Appendix B. Shah (2015a) Correlation for CHF in Vertical Annuli
The correlating parameters are L/Dhp; the inlet quality is xin, Y, and Bo. If the quality at CHF, xc, is negative, then it also becomes a correlating parameter. When xin ≤ 0, L is the heated length of tube up to the CHF location. If xin > 0, then L equals the boiling length, which is the tube length between xin = 0 and the location of CHF. LB is given by:
Use of LB implies that xin = 0 has been assumed, and this value has to be used when xin > 0 in all equations that follow.
Y is given by Equation (A2) in Appendix A for tubes where D is the diameter of the tube on which CHF occurs.
DHP is the equivalent diameter based on the heated perimeter and is defined as flow area divided by heated perimeter. Thus, for cylindrical annuli:
D is the diameter of the tube on which CHF occurs, and D2 is the diameter of the other tube of the annulus.
The boiling number at CHF is given by:
Bo1 is the boiling number for Y < 104 at the actual inlet quality. It is calculated as follows.
Bo0 is the boiling number at xin = 0 with Y < 104, given by:
The factor K = 1 for (L/Dhp) ≤ 120.
For (L/Dhp) > 120, K = 0.336 + 0.0055(L/Dhp)
If K from Equation (A23) > 2.2, then use K = 2.2.
For L/DHP between 30 and 85, calculate E1 using equations for L/DHP < 30 and L/DHP > 85 and use the larger of the two.
F1 is calculated as follows. F1 = 1 for Y ≤ 104. For Y > 104,
F2 is calculated as follows.
When xc ≥ 0, F2 = 1.
For xc < 0, F2 is calculated as below.
F2 = 1 for Y < 3.5 × 105 for all values of xc.
For Y > 3.5 × 105,
where
n = −1.143xc ≤ 0.24
For Y between 3.5 × 105 and 5.5 × 105, interpolate linearly between F2 = 1 at Y = 3.5 × 105 and F2 at Y = 5.5 × 105, calculated as given above. As there were no test data in this range, this recommendation to interpolate is tentative.
The above equations are applicable to annuli with one heated tube. The same are also applicable to bilaterally heated annuli by adjusting the vapor inlet quality to take into account the vapor generated at the other tube. To do so, xin in the above equations is replaced by an effective inlet quality xin,ef defined as:
where DHP,2 is the heated equivalent diameter of the tube other than that on which CHF occurs, and q2 is the heat flux on it. If xin,ef from Equation (A34) is positive, then xin,ef replaces xin in Equation (A18) for calculating the boiling length; all other calculations are the same as for annuli with one tube heated. Using this effective inlet quality, calculations proceed as if only one tube is heated. DHP,2 is calculated as:
If heat fluxes on both tubes are high, then calculations should be performed for each tube in this way to determine on which one the CHF occurs.
Shah recommends that for water, this correlation be used only when:
where G is in kg/m2s, and p is the pressure in bar.
References
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST Reference Fluid Thermodynamic and Transport Properties, REFPROP Version 9.1; NIST: Gaithersburg, MD, USA, 2013.
- Collier, J.G.; Thome, J.R. Convective Boiling & Condensation, 2nd ed.; Chapter 4; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Celata, G.P.; Cumo, M.; Setaro, T. A Review of Pool and Forced Convective Boiling of Binary Mixtures. Exp. Therm. Fluid Sci. 1994, 9, 367–381. [Google Scholar] [CrossRef]
- Shah, M.M. Two-Phase Heat Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Fujita, Y.; Bai, Q. Critical heat flux of binary mixtures in pool boiling and its correlation in terms of Marangoni number. Int. J. Refrig. 1997, 20, 616–622. [Google Scholar] [CrossRef]
- Zuber, N. Hydrodynamic Aspects of Boiling Heat Transfer, AECU-4439; University of California: Los Angeles, CA, USA, 1959. [Google Scholar]
- Van Stralen, S.J.D.; Sluyter, W.M. Investigations on the critical heat flux of pure liquids and mixtures under various conditions. Int. J. Heat Mass Transf. 1969, 12, 1353–1384. [Google Scholar] [CrossRef]
- Reddy, R.P.; Lienhard, J.H. The peak boiling heat flux in saturated ethanol-water mixtures. J. Heat Transf. 1989, 111, 480–486. [Google Scholar] [CrossRef]
- Yagov, V.V. Critical heat flux prediction for pool boiling of binary mixtures. Chem. Eng. Res. Des. 2004, 82, 457–461. [Google Scholar] [CrossRef]
- Sterman, L.A.; Abramov, A.; Checheta, G. Investigation of boiling crisis at forced motion of high temperature organic heat carriers and mixtures. In International Symposium on Research into Co-Current Gas-Liquid Flow; Paper E2, Quoted in Collier and Thome (1994); University of Waterloo: Waterloo, ON, Canada, 1968. [Google Scholar]
- Carne, M. Studies of the Critical Heat Flux for some Binary Mixtures and their Components. Can. J. Chem. Eng. 1963, 41, 235–240. [Google Scholar] [CrossRef]
- Andrews, D.G.; Hooper, F.C.; Butt, P. Velocity, Subcooling and Surface Effects in the Departure from Nucleate Boiling of Organic Binaries. Can. J. Chem. Eng. 1968, 46, 194–199. [Google Scholar] [CrossRef]
- Naboichenko, K.V.; Kiryutin, A.A.; Gribov, B.S. A study of critical heat flux with forced flow of monoisopropyldiphenyl- benzene mixture. Teploenergetika 1965, 12, 81–86, Quoted in Collier & Thome (1994). [Google Scholar]
- Tolubinsky, V.I.; Matorin, P.S. Forced Convection Boiling Heat Transfer Crisis with Binary Mixtures. Heat Transf.—Sov. Res. 1973, 5, 98–101. [Google Scholar]
- Celata, G.P.; Cumo, M.; Setaro, T. Critical heat flux in upflow convective boiling of refrigerant binary mixtures. Int. J. Heat Mass Transf. 1994, 37, 1143–1153. [Google Scholar] [CrossRef]
- Katto, Y.; Ohno, H. An improved version of the generalized correlation of critical heat flux for the forced convection boiling in uniformly heated vertical tubes. Int. J. Heat Mass Transf. 1984, 27, 1641–1648. [Google Scholar] [CrossRef]
- Sindhuja, R.; Balakrishnan, A.R.; Murthy, S.S. Critical heat flux of R-407C in upflow boiling in a vertical pipe. Appl. Therm. Eng. 2008, 28, 1058–1065. [Google Scholar] [CrossRef]
- Groeneveld, D.C.; Leung, L.K.H.; Erbacher, F.J.; Zeggel, W. An improved table look-up method for predicting critical heat flux. In Proceedings of the NURETH-6, Sixth International Topical Meeting on Nuclear Reactor Thermal Hydraulics, Grenoble, France, 5–8 October 1993; Volume 1, pp. 223–230. [Google Scholar]
- Vijayarangan, B.R.; Jayanti, S.; Balakrishnan, A.R. Studies on critical heat flux in flow boiling under near critical pressures. Int. J. Heat Mass Transf. 2006, 49, 259–268. [Google Scholar] [CrossRef]
- Mori, H.; Yoshida, S.; Ohno, M.; Kusumoto, K.; Itoh, T. Critical heat flux for non-azeotropic binary mixtures at high pressure. Proc. JSME 1990, 908, 210–214, Quoted in Auracher and Marroquin (1995). [Google Scholar]
- Auracher, H.; Marroquin, A. Forced Convection Critical Heat Flux and Transition Boiling of Mixtures Flowing Upward in a Vertical Tube. In Convective Flow Boiling; Chen, J., Ed.; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Robinson, J.M.; Lurie, H. Critical heat flux of some polyphenyl coolants. In Proceedings of the Symposium on Boiling Phenomena in Nuclear Heat Transfer, Fifty-fifth Annual Meeting of AIChE, Chicago, IL, USA, 2–6 December 1962. Preprint 156. [Google Scholar]
- Shah, M.M. Improved general correlation for critical heat flux in uniformly heated vertical tubes. Int. J. Heat Fluid Flow 1987, 8, 326–335. [Google Scholar] [CrossRef]
- Shah, M.M. Applicability of general correlations for CHF in conventional tubes to mini/macro channels. Heat Transf. Eng. 2017, 38, 1–10. [Google Scholar] [CrossRef]
- Zhang, W.; Hibiki, T.; Mishima, K.; Mi, Y. Correlation of critical heat flux for flow boiling of water in mini-channels. Int. J. Heat Mass Transf. 2006, 49, 1058–1072. [Google Scholar] [CrossRef]
- Wojtan, L.; Revellin, R.; Thome, J.R. Investigation of saturated critical heat flux in a single uniformly heated microchannel. Exp. Therm. Fluid Sci. 2006, 30, 765–774. [Google Scholar] [CrossRef]
- Shah, M.M. Improved general correlation for CHF in vertical annuli with upflow. Heat Transf. Eng. 2015, 37, 557–570. [Google Scholar] [CrossRef]
- Katto, Y. Generalized Correlation of Critical Heat Flux for the Forced Convection Boiling in Vertical Uniformly Heated Annuli. Int. J. Heat Mass Transf. 1979, 22, 575–584. [Google Scholar] [CrossRef]
- Doerffer, S.; Groeneveld, D.C.; Cheng, S.C.; Rudzinski, K.F. A Comparison of Critical Heat Flux in Tubes and Annuli. Nucl. Eng. Des. 1994, 149, 167–175. [Google Scholar] [CrossRef]
- Hung, Y.H.; Yao, S.C. Critical Heat Flux of Convective R-113 in Very Narrow Annuli; ASME Paper 83-HT-10; ASME: New York, NY, USA, 1983. [Google Scholar]
- Huber, M.L.; National Bureau of Standards, Washington, DC, USA. Personal communication, 21 November 2022.
- Bell, K.J.; Ghaly, M.A. An approximate generalized method for multicomponent partial condenser. Am. Inst. Chem. Eng. Symp. Ser. 1973, 69, 72–79. [Google Scholar]
- Shah, M.M. A general correlation for CHF in horizontal channels. Int. J. Refrig. 2015, 59, 37–52. [Google Scholar] [CrossRef]
- Gong, S.; Dong, S.; Mei, Y.; Zhang, B.; Yuan, Y.; Zhang, Z. Separate factors’ effects on CHF for flow boiling in an inclined rectangular channel under low mass flux. Appl. Therm. Eng. 2022, 207, 118207. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).