Conjugate Heat Transfer in Thermal Inkjet Printheads
Abstract
1. Introduction
1.1. Literature Review
1.1.1. Flow in Heated Ducts
1.1.2. Convection against Conduction
1.1.3. Backward-Facing Step with Downstream Heated Wall
1.1.4. More Complicated Problems
2. Theoretical Models
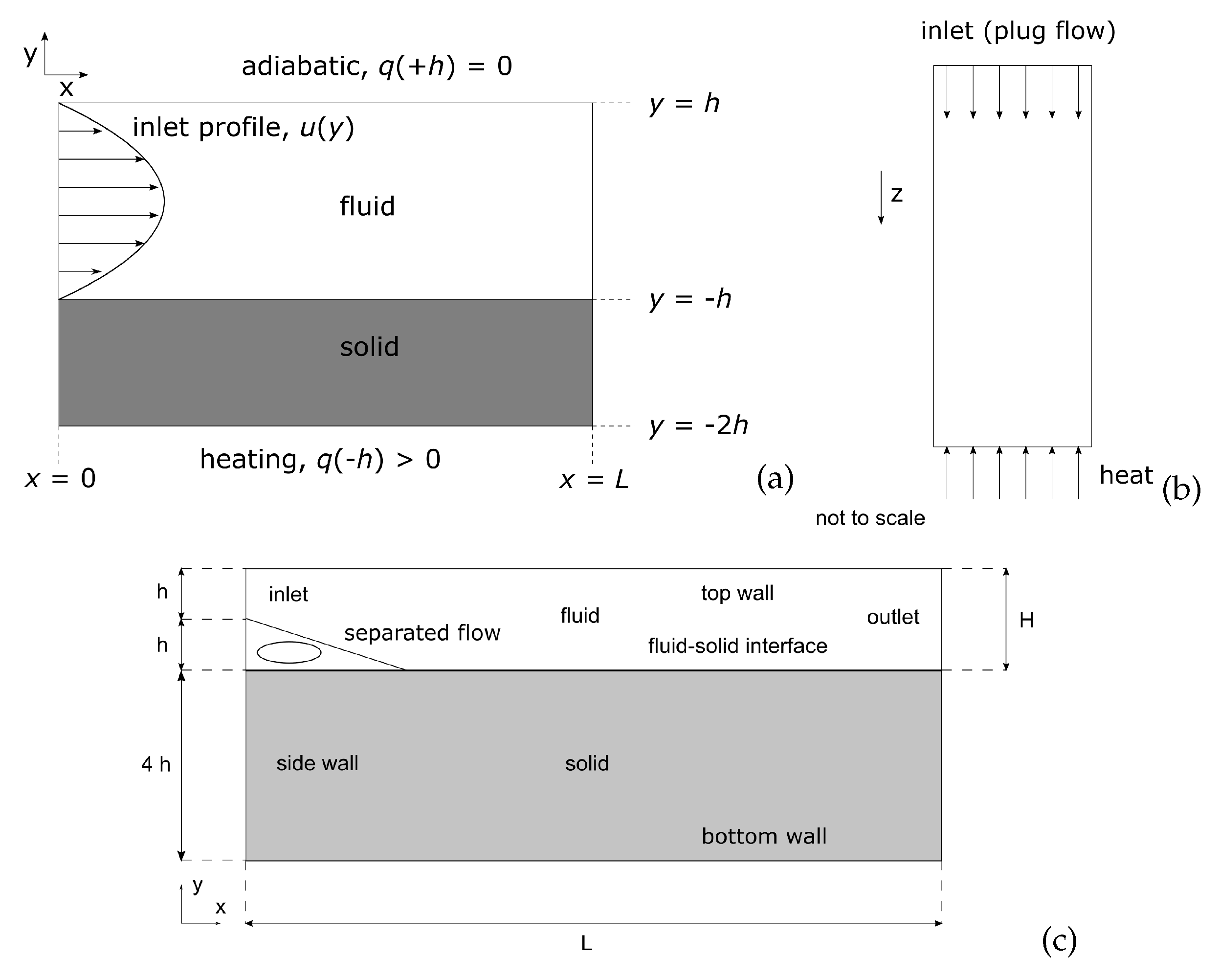
2.1. Fully-Developed Planar Channel Flow with Forced Convection
Extension to Conjugate Heat Transfer
2.2. One-Dimensional Transient Conduction against Convection
3. Methods
3.1. Equations for Advection–Diffusion
3.2. Solvers, Discretization and Boundary Conditions
4. Results
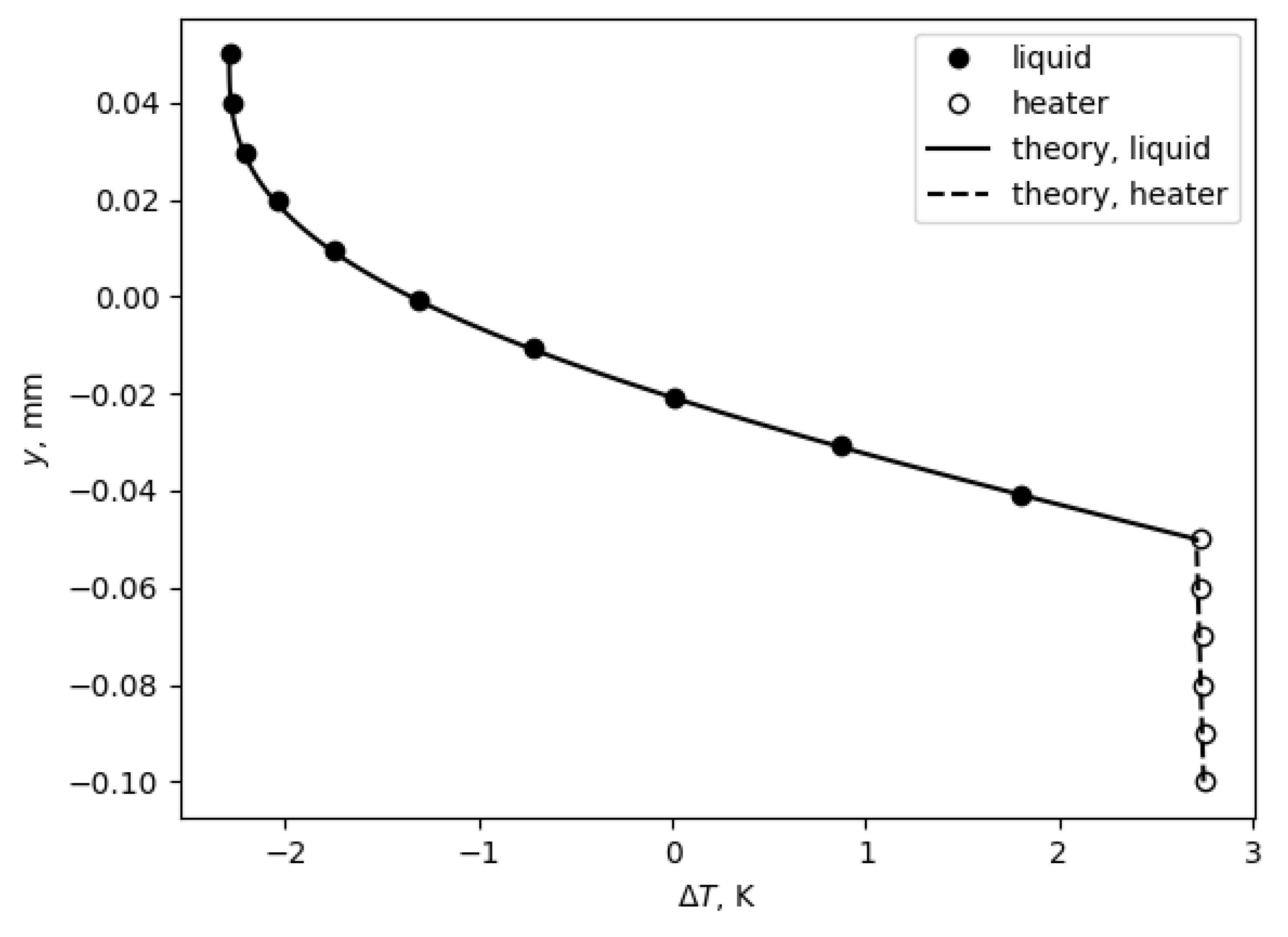
4.1. Comparison with Analytical Models
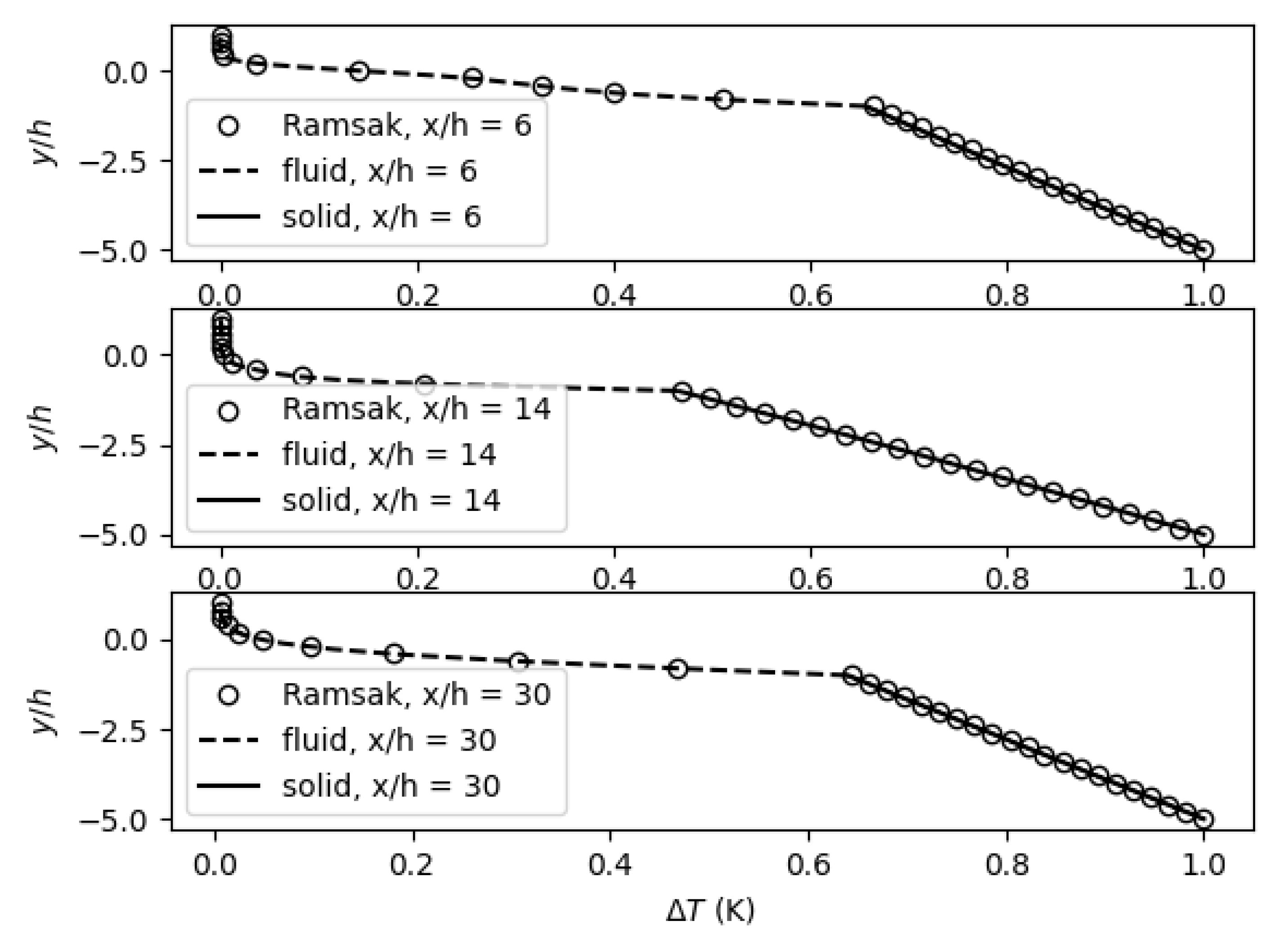
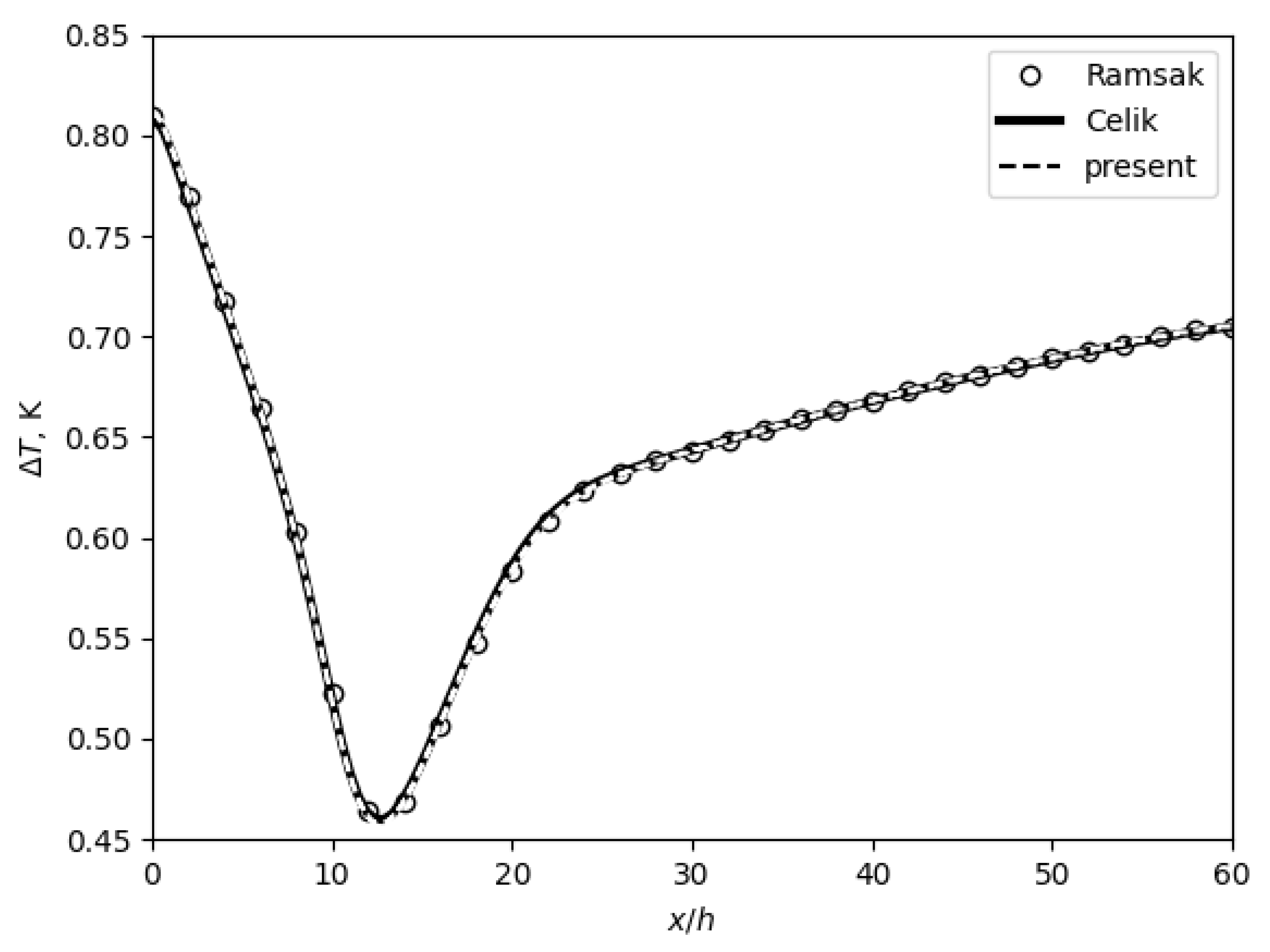
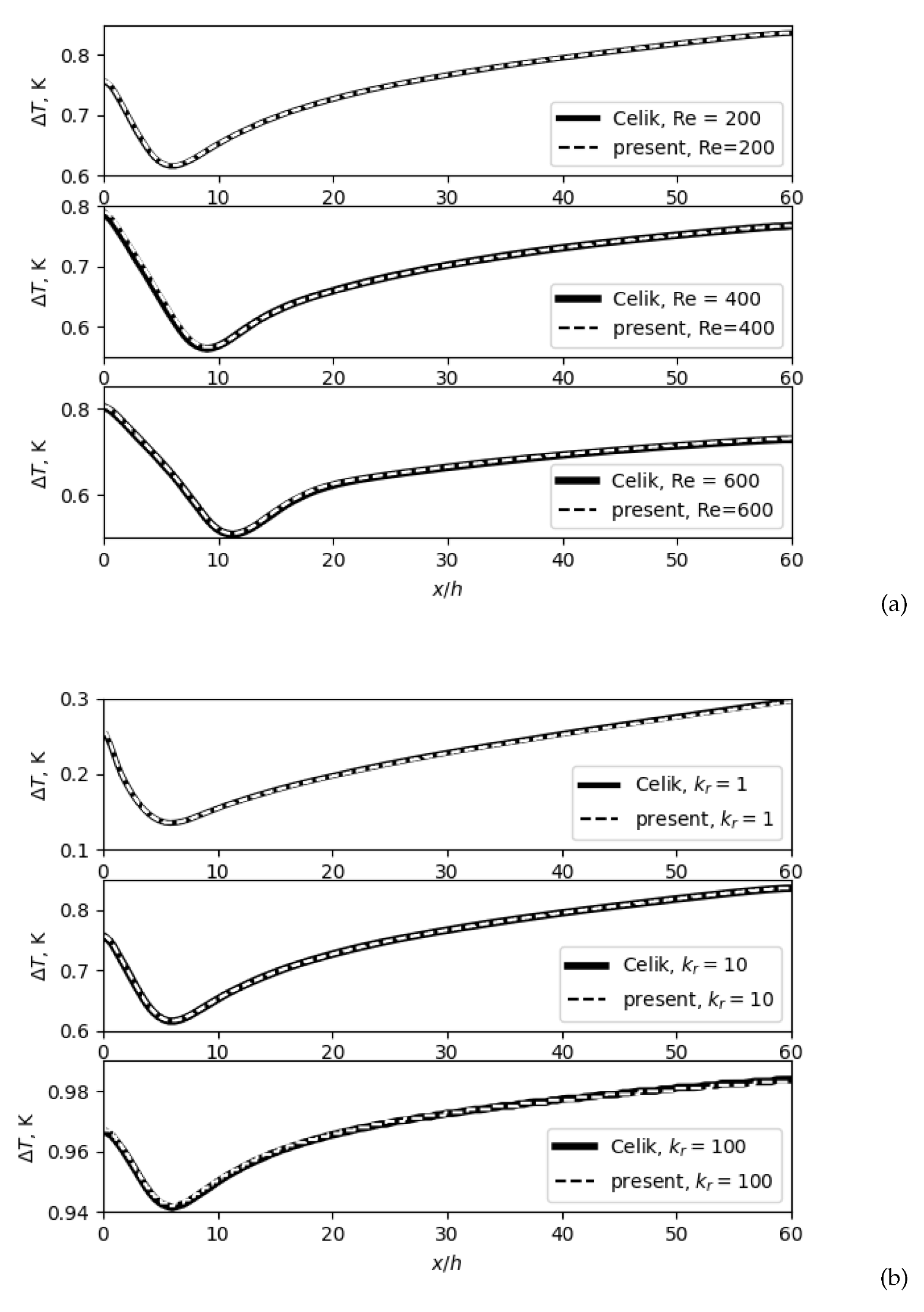
4.2. Backward-Facing Step
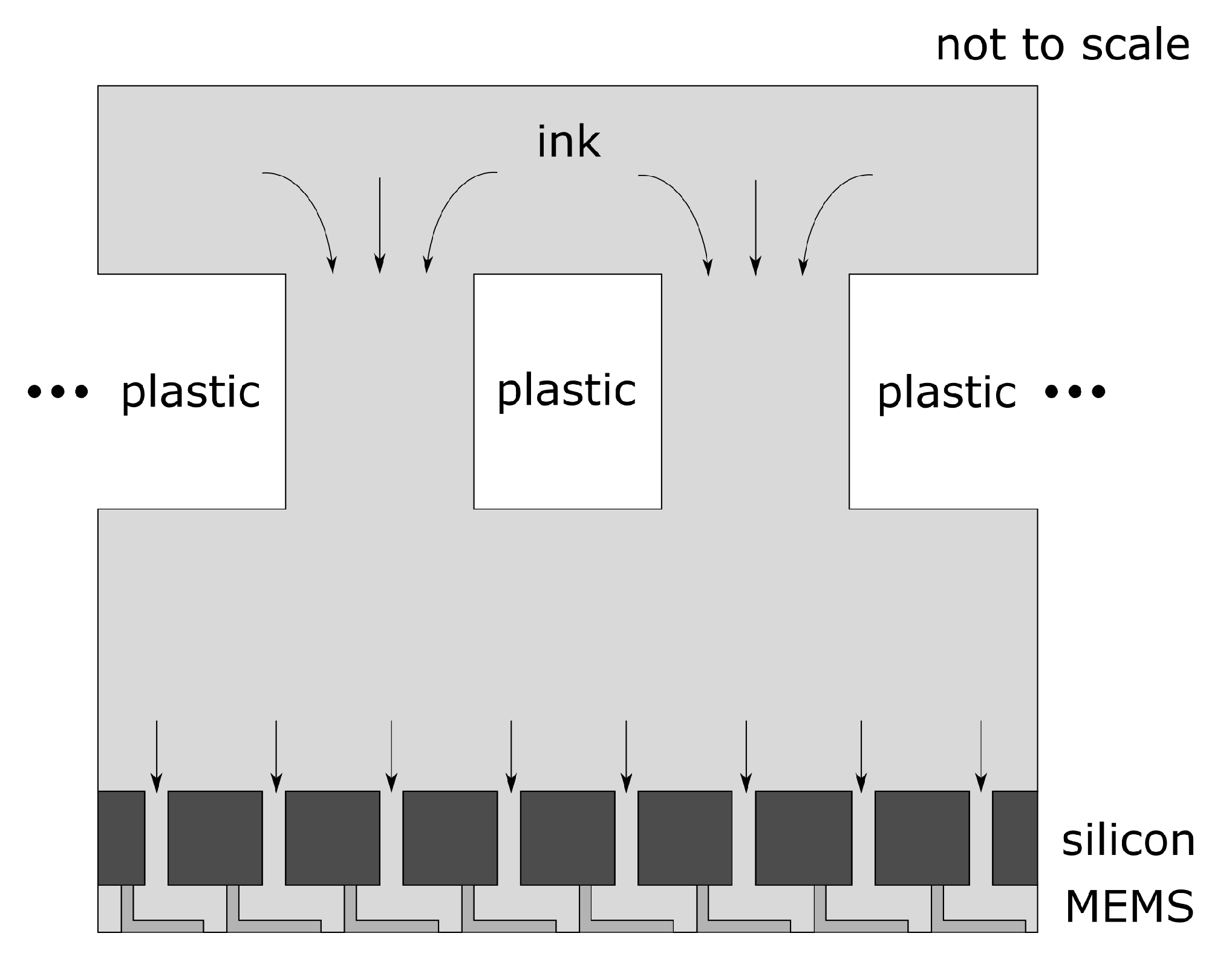
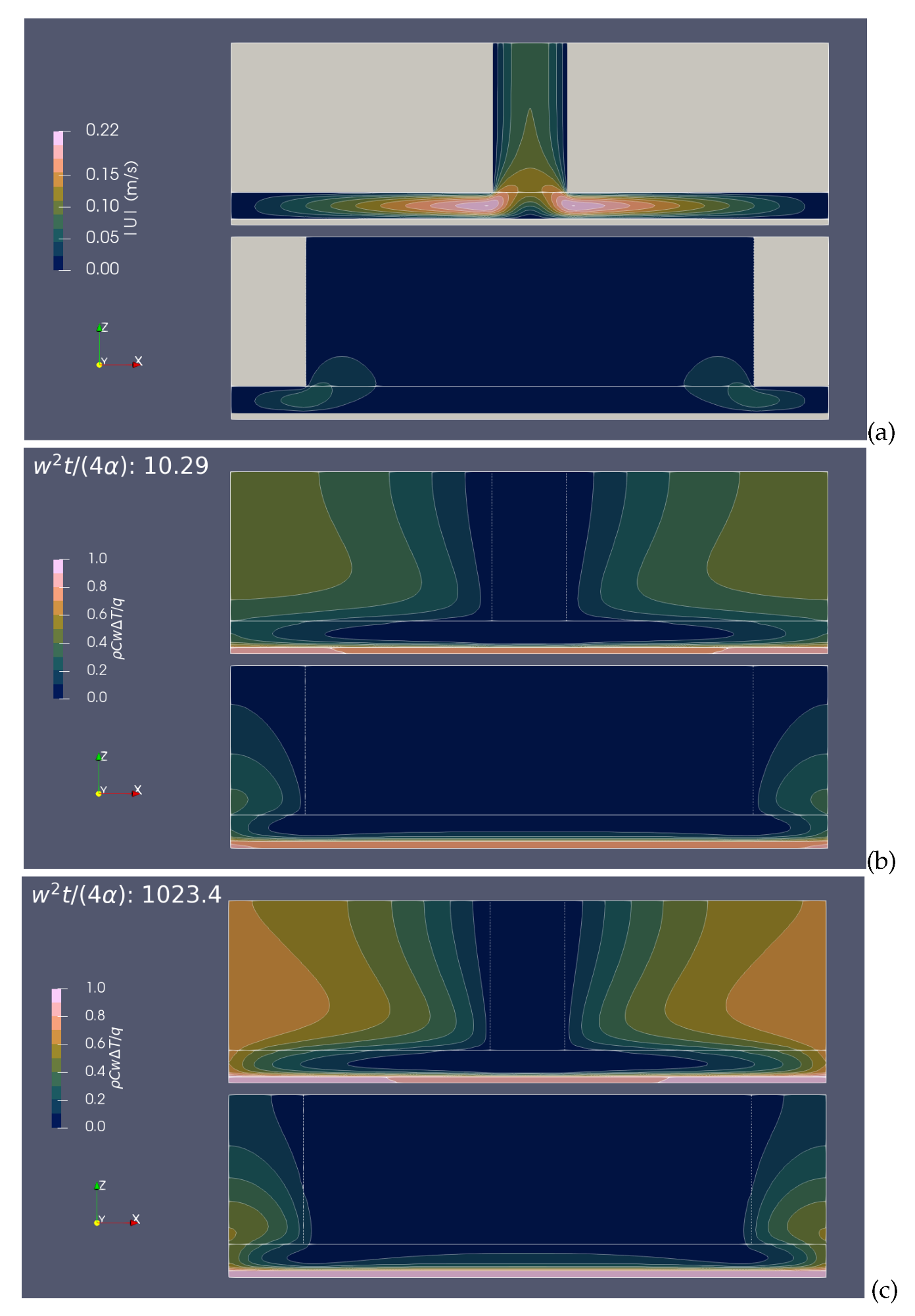
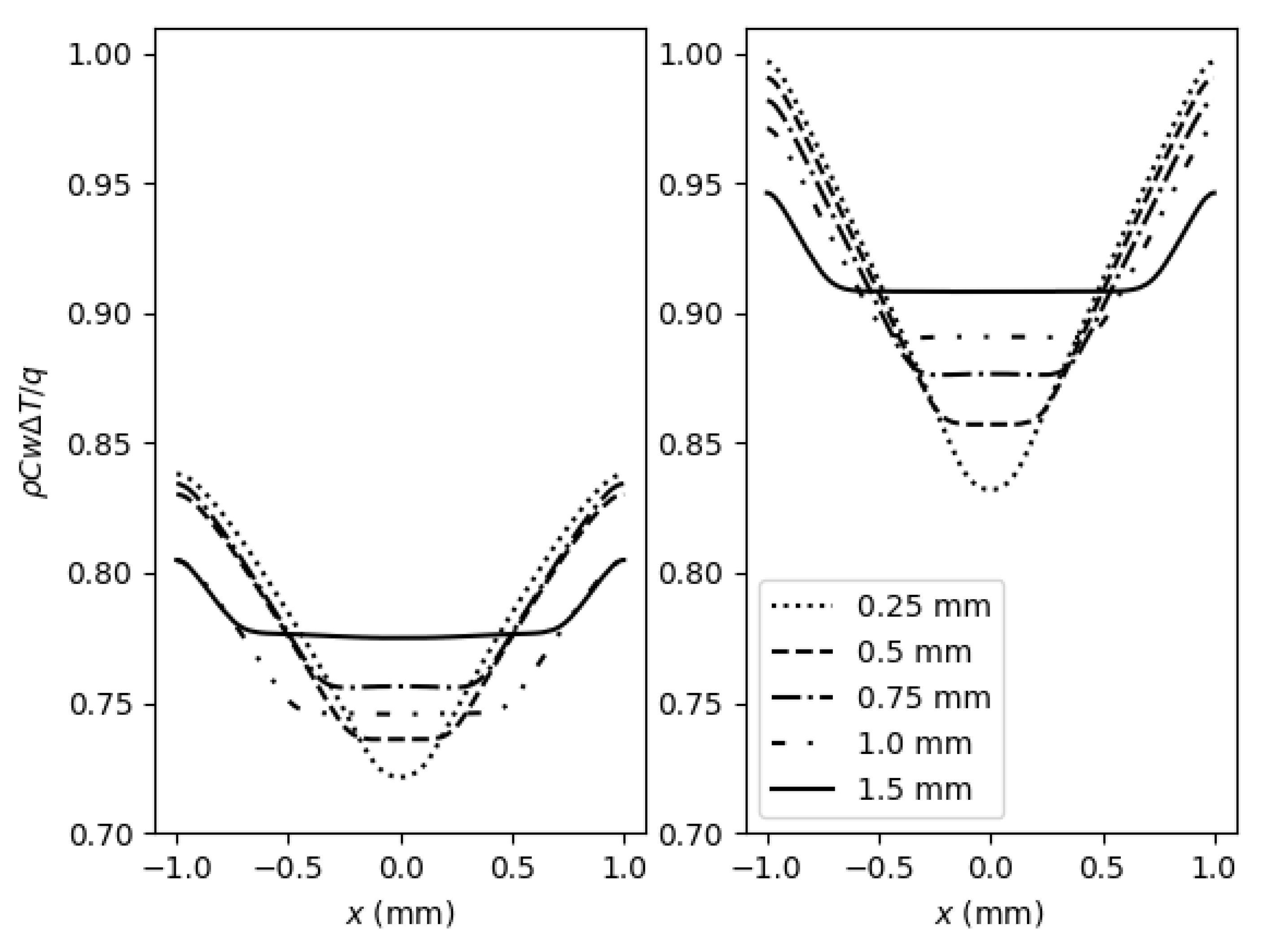
4.3. Thermal Inkjet Printhead
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PHIC | printhead integrated circuit |
| PPS | printhead-to-paper spacing |
| CHT | conjugate heat transfer |
References
- Graetz, L. Ueber die Wärmeleitungsfähigkeit von Flüssigkeiten. Ann. Der Phys. Und Chem. 1885, 25, 337–357. [Google Scholar] [CrossRef]
- Papoutsakis, E.; Ramkrishna, M. Conjugated Graetz problems—I: General formalism and a class of solid-fluid problems. Chem. Eng. Sci. 1981, 36, 1381–1391. [Google Scholar] [CrossRef]
- White, F.M. Viscous Fluid Flow, 2nd ed.; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Sugavanam, R.; Ortega, A.; Choi, C.Y. A numerical investigation of conjugate heat transfer from a flush heat source on a conductive board in laminar channel flow. Int. J. Heat Mass Transf. 1995, 38, 2969–2984. [Google Scholar] [CrossRef]
- Wansophark, N.; Malatip, A.; Dechaumphai, P. Streamline upwind finite element method for conjugate heat transfer problems. Acta Mech. Sin. 2005, 21, 436–443. [Google Scholar] [CrossRef]
- Mori, S.; Sakakibara, M.; Tanimoto, A. Steady laminar heat transfer in a circular tube with conduction in tube wall. Chem. Eng. 1974, 38, 144–150. [Google Scholar] [CrossRef]
- Sucec, J. Unsteady conjugated forced convective heat transfer in a duct with convection from the ambient. Int. J. Heat Mass Transf. 1987, 30, 1963–1970. [Google Scholar] [CrossRef]
- Yan, W.M.; Tsay, Y.L.; Lin, T.F. Transient conjugated heat transfer in laminar pipe flows. Int. J. Heat Mass Transf. 1989, 32, 775–777. [Google Scholar] [CrossRef]
- Nagendra, K.; Tafti, D.K.; Viswanath, K. A new approach for conjugate heat transfer problems using immersed boundary method for curvilinear grid based solvers. J. Comp. Phys. 2014, 267, 225–246. [Google Scholar] [CrossRef]
- Sucec, J.; Sawant, A.M. Unsteady, conjugated, forced convection heat transfer in a parallel plate duct. Int. J. Heat Mass Transf. 1984, 27, 95–101. [Google Scholar] [CrossRef]
- Karvinen, R. Transient conjugated heat transfer to laminar flow in a tube or channel. Int. J. Heat Mass Transf. 1988, 31, 1326–1328. [Google Scholar] [CrossRef]
- Gallegos-Muñoz, A.; Balderas-Bernal, J.A.; Violante-Cruz, C.; Rangel-Hernández, V.H.; Belman-Flore, J.M. Analysis of the conjugate heat transfer in a multi-layer wall including an air layer. Appl. Therm. Eng. 2010, 30, 599–604. [Google Scholar]
- Omosehin, O.S.; Adelaja, A. Numerical simulation of conjugate heat transfer in forced convective boundary bilayered cylindrical pipe with different Peclet numbers. Fed. Univ. Oye-Ekiti J. Eng. Tech. 2019, 4, 158–163. [Google Scholar] [CrossRef]
- Bilir, Ş.; Ateş, A. Transient conjugated heat transfer in thick walled pipes with convective boundary conditions. Int. J. Heat Mass Transf. 2003, 46, 2701–2709. [Google Scholar] [CrossRef]
- Manna, P.; Chakraborty, D. Numerical investigation of conjugate heat transfer problems. Indian J. Aerosp. Sci. Tech. 2004, 56, 166–175. [Google Scholar]
- Mason, M.; Weaver, W. The settling of small particles in a fluid. Phys. Rev. 1924, 23, 412–426. [Google Scholar] [CrossRef]
- Pérez Guerrero, J.S.; Pimentel, L.C.G.; Skaggs, T.H.; van Genuchten, M.T. Analytical solution of the advection–diffusion transport equation using a change-of-variable and integral transform technique. Int. J. Heat Mass Transf. 2009, 52, 3297–3304. [Google Scholar] [CrossRef]
- Wang, J.; Shao, M.; Huang, L.; Jia, X. A general polynomial solution to convection–dispersion equation using boundary layer theory. J. Earth Syst. Sci. 2017, 126, 40. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Oxford University Press: Oxford, UK, 1959. [Google Scholar]
- van Genuchten, M.T.; Alves, W.J. Analytical Solutions of the One-Dimensional Convective-Dispersive Solute Transport Equation; Tech. Bull. number 1661; U. S. Salinity Laboratory, Agricultural Research Service, United States Department of Agriculture: Washington, DC, USA, 1982. [Google Scholar]
- Armaly, B.F.; Durst, F.; Pereira, J.C.F.; Schonung, B. Experimental and theoretical investigation of backward-facing step flow. J. Fluid Mech. 1983, 127, 473–496. [Google Scholar] [CrossRef]
- Biswas, G.; Breuer, M.; Durst, F. Backward–facing step flows for various expansion ratios at low and moderate Reynolds numbers. J. Fluids Eng. 2004, 126, 362–374. [Google Scholar] [CrossRef]
- Kaiktsis, L.; Karniadakis, G.E.; Orsz, S.A. Onset Three-Dimens. Equilibria, Early Transit. Flow A Backward-Facing Step. J. Fluid Mech. 1991, 231, 501–528. [Google Scholar] [CrossRef]
- Ramšak, M. Conjugate heat transfer of backward-facing step flow: A benchmark problem revisited. Int. J. Heat Mass Transf. 2015, 84, 791–799. [Google Scholar] [CrossRef]
- Gartling, D.K. A test problem for outflow boundary conditions - flow over a backward-facing step. Int. J. Num. Methods Fluids 1990, 11, 953–967. [Google Scholar] [CrossRef]
- Gresho, P.M.; Gartling, D.K.; Torczynski, J.R.; Cliffe, K.A.; Winters, K.H.; Garratt, T.J.; Spence, A.; Goodrich, J.W. Is the steady viscous incompressible two-dimensional flow over a backward-facing step at Re = 800 stable? Int. J. Num. Methods Fluids 1993, 17, 501–541. [Google Scholar] [CrossRef]
- Celik, B. Conjugate heat transfer characteristics of laminar flows through a backward facing step duct. Süleyman Demirel Univ. Inst. Sci. Tech. Mag. 2017, 21, 820–830. [Google Scholar] [CrossRef]
- Nouri–Borujerdi, A.; Moazezi, A. Investigation of obstacle effect to improve conjugate heat transfer in backward facing step channel using fast simulation of incompressible flow. Heat Mass Transf. 2018, 54, 135–150. [Google Scholar] [CrossRef]
- Yu, E.; Joshi, Y. Heat transfer enhancement from enclosed discrete components using pin-fin heat sinks. Int. J. Heat Mass Transf. 2002, 45, 4957–4966. [Google Scholar] [CrossRef]
- Balakin, V.; Churbanov, A.; Gavriliouk, V.; Makarov, M.; Pavlov, A. Verification and validation of EFD.lab code for predicting heat and fluid flow. In CHT-04-Advances in Computational Heat Transfer III. Proceedings of the Third International Symposium; Begel House Inc.: Danbury, CT, USA, 2004. [Google Scholar]
- Nakayama, W.; Park, S.-H. Conjugate heat transfer from a single surface-mounted block to forced convective air flow in a channel. J. Heat Transf. 1996, 118, 301–309. [Google Scholar] [CrossRef]
- Kumar, A.U.; Javed, A.; Dubey, S.K. Material selection for microchannel heatsink: Conjugate heat transfer simulation. IOP Conf. Ser. Mater. Sci. Eng. 2018, 346, 012024. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; Wiley: New York, NY, USA, 1960. [Google Scholar]
- Eckert, E.R.G.; Gross, J.F. Introduction to Heat and Mass Transfer. McGraw-Hill Series in Mechanical Engineering; McGraw-Hill: New York, NY, USA, 1963. [Google Scholar]
- Boyce, W.E.; DiPrima, R.C. Elementary Differential Equations and Boundary Value Problems, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1969. [Google Scholar]
- Dorfman, A.S. Conjugate Problems in Convective Heat Transfer; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Faghri, A.; Zhang, Y.; Howell, J. Advanced Heat and Mass Transfer; Global Digital Press: Columbia, MO, USA, 2010. [Google Scholar]
- Greenshields, C.J. Energy Equation in OpenFOAM. Available online: https://cfd.direct/openfoam/energy-equation/ (accessed on 16 November 2022).
- Greenshields, C.J.; Weller, H.G. Notes on Computational Fluid Dynamics: General Principles; CFD Direct Limited: Reading, UK, 2022. [Google Scholar]
- Holzmann, T.; Nagy, J. Mathematics, Numerics, Derivations and OpenFOAM; Holzmann CFD: Augsburg, Germany, 2021. [Google Scholar]
- Shackelford, J.F.; Alexander, W. (Eds.) CRC Materials Science and Engineering Handbook; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Touloukian, Y.S.; Powell, R.W.; Ho, C.Y.; Klemens, P.G. Thermal Conductivity—Metallic Elements and Alloys; Thermophysical Properties of Matter; Plenum: New York, NY, USA, 1970; Volume 1. [Google Scholar]


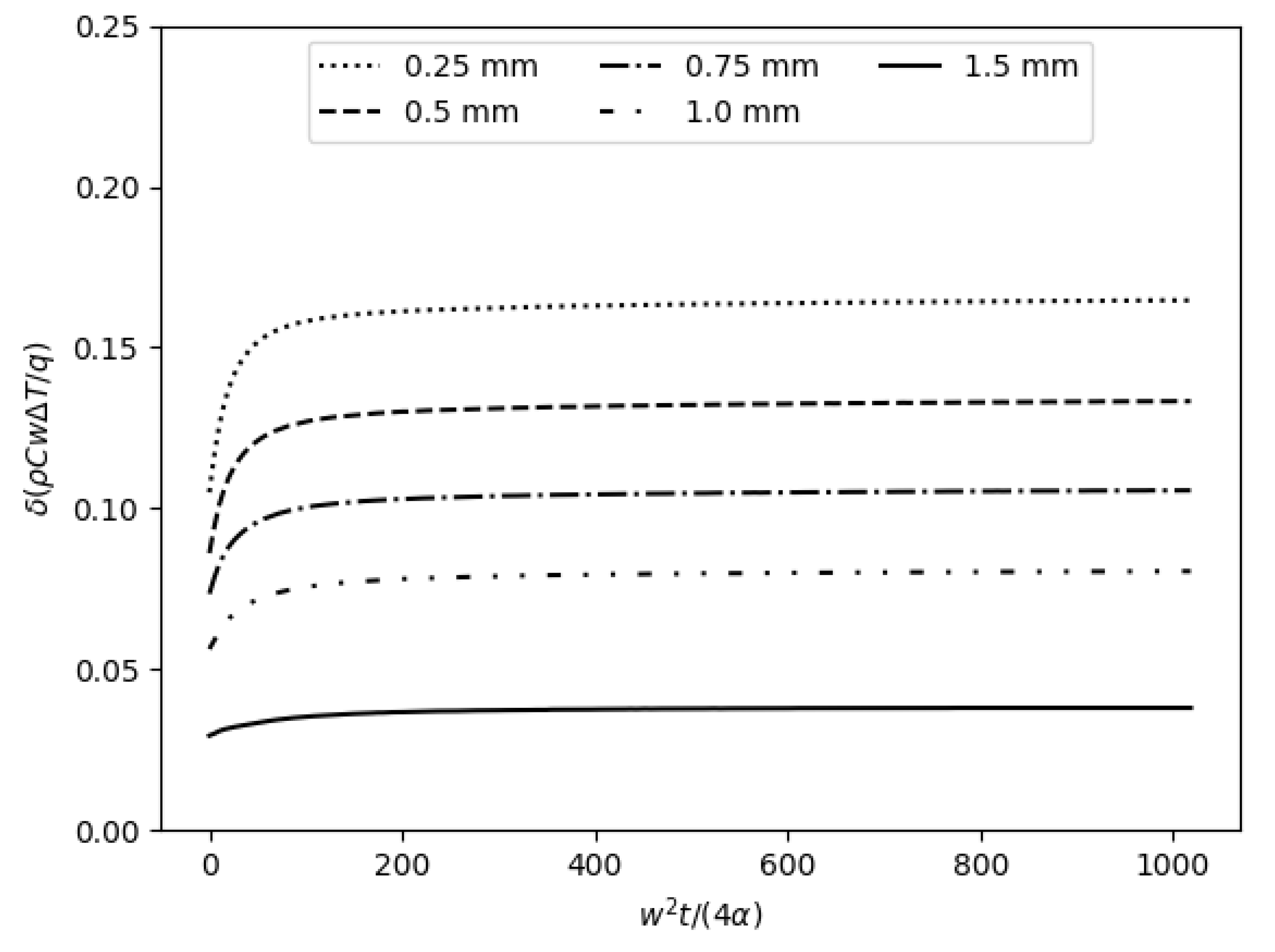
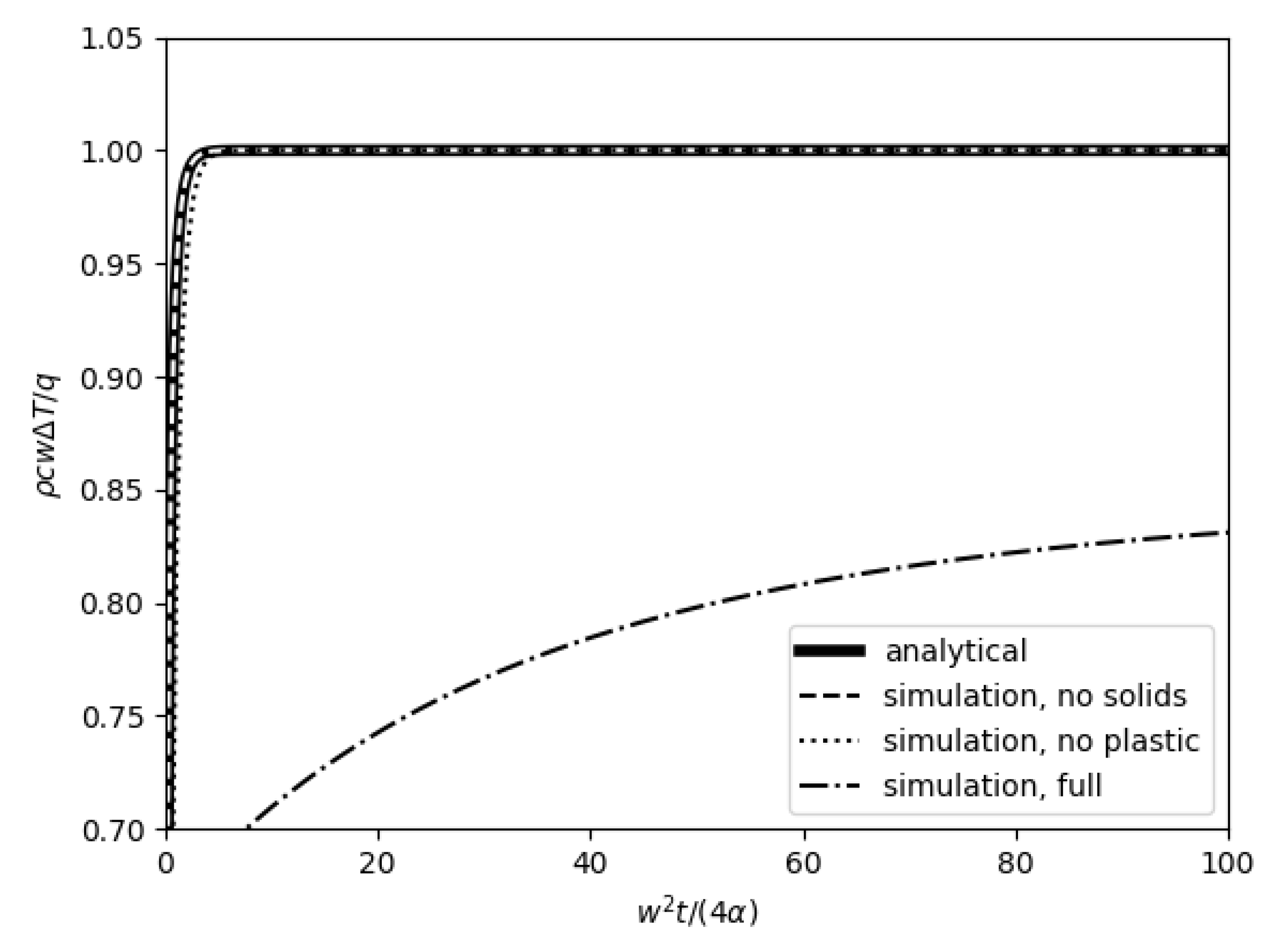
| Mesh Size/Channel Height | (−)/ (%) |
|---|---|
| 0.17 | 0.69 |
| 0.1 | 0.49 |
| 0.05 | 0.39 |
| 0.025 | 0.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mallinson, S.G.; McBain, G.D.; Brown, B.R. Conjugate Heat Transfer in Thermal Inkjet Printheads. Fluids 2023, 8, 88. https://doi.org/10.3390/fluids8030088
Mallinson SG, McBain GD, Brown BR. Conjugate Heat Transfer in Thermal Inkjet Printheads. Fluids. 2023; 8(3):88. https://doi.org/10.3390/fluids8030088
Chicago/Turabian StyleMallinson, S. G., G. D. McBain, and B. R. Brown. 2023. "Conjugate Heat Transfer in Thermal Inkjet Printheads" Fluids 8, no. 3: 88. https://doi.org/10.3390/fluids8030088
APA StyleMallinson, S. G., McBain, G. D., & Brown, B. R. (2023). Conjugate Heat Transfer in Thermal Inkjet Printheads. Fluids, 8(3), 88. https://doi.org/10.3390/fluids8030088








