Abstract
This review paper aims to summarize recent advancements in time-marching schemes for solving Navier–Stokes (NS) equations in multiphase flow simulations. The focus is on dual-time stepping, local preconditioning, and artificial compressibility methods. These methods have proven to be effective in achieving high time accuracy in simulations, as well as converting the incompressible NS equations into a hyperbolic form that can be solved using compact schemes, thereby accelerating the solution convergence and allowing for the simulation of compressible flows at all Mach numbers. The literature on these methods continues to grow, providing a deeper understanding of the underlying physical processes and supporting technological advancements. This paper also highlights the imposition of dual-time stepping on both incompressible and compressible NS equations. This paper provides an updated overview of advanced methods for the CFD community to continue developing methods and select the most suitable two-phase flow solver for their respective applications.
1. Introduction
Two-phase flows such as gas–gas, gas–liquid, liquid–liquid, and three-phase (liquid, gas, and vapor) flows are of great interest in many natural phenomena, engineering, and industrial applications. Numerical simulations and analyses of two-phase flows to obtain an understanding of the mechanism and physical characteristics of the flows in applications have become routine activities. In design and development, computational fluid dynamic (CFD) programs based on the Navier–Stokes (NS) equations are now considered to be standard numerical tools to predict the nonlinear motions of the interface between two phases (two fluids), its deformations and breaks, phase change, heat transfer, turbulence, shockwaves, and violent interaction with devices/systems [1,2,3,4,5].
Both incompressible and compressible NS systems are commonly used for predicting multiphase flows. The governing equations for multiphase incompressible flows generally consist of the mixture continuity equation, mixture momentum equations, and phasic volume fraction equations, which are given as:
where is the flow velocity vector, is the pressure, is the physical time, is the volume fraction of the ith phasic component and g is the gravity acceleration.
Mixture rules are given as
To predict the mechanism and physical characteristics of flows with transient effects accurately, the governing equations require advanced temporal discretization and time-marching schemes. For the incompressible system (1–3), the time derivative term does not appear in the continuity Equation (1). The numerical solution of these equations presents a major difficulty, and to overcome this, a special equation was derived for solving pressure, e.g., employing the nonlinear Poisson equation for pressure, and then obtaining other state variables by using prediction and correction procedures [6,7,8]. However, to apply the well-developed compressible flow algorithms to the incompressible problem, the incompressible NS equation system must be hyperbolic as compressible NS equation systems.
The dual-time preconditioning approach originally is a numerical technique used to simulate unsteady incompressible flows. It was first proposed by Merkle [9] as a modification of the artificial compressibility method developed by Chorin [10]. The approach involves adding pseudo-time derivative terms to the incompressible NS equations and treating the time variation of the incompressible flow as a compressible flow, allowing for the coupling of the velocity and pressure fields in each time iteration [11,12,13,14,15]. One of the key advantages of the dual-time preconditioning approach is the direct coupling of the continuity and momentum equations in the incompressible flow equations, which eliminates the factorization error in factored implicit schemes [2]. Additionally, this approach eliminates errors due to approximations made in the implicit operator, improves numerical efficiency, and eliminates errors due to lagged boundary conditions at both solid and internal fluid boundaries [2,15,16,17]. By using preconditioned iterative methods, the dual-time preconditioning approach can also achieve a more efficient convergence of the sub-iterations.
The concept of artificial compressibility involves transforming elliptic equations describing incompressible flows into a hyperbolic compressible system, making it amenable to a solution using standard time-marching methods, such as explicit or implicit methods [2,18,19,20]. This allows the use of established numerical techniques for solving compressible flows to be applied to the simulation of incompressible flows. The specific procedure for adding artificial time derivatives to the incompressible NS equations is discussed in detail in Section 2.1.
Multiphase flows are assumed either incompressible or compressible flows depending on the range of Mach numbers of the flows. A flow can be assumed an incompressible one as the Mach number is less than 0.1, in which the compressibility is small and can be ignored. Examples of small Mach numbers are free-surface flows [21,22], dynamics of rising bubbles [23,24,25], and boiling flows [26,27]. A flow, at a Mach number greater than 0.3, is usually assumed a compressible one. At supersonic speeds, the Mach number is greater than 1.0, supercavitating flow around projectiles characterizes by shock waves, thermodynamic behavior, and compressibility dominates [28]. The physical aspects also were observed in supersonic flows in nozzles and/or separators [29,30,31]. Traditional time-marching algorithms that are based on physical time derivatives have been widely used and have proven to be effective in simulating transonic and supersonic flows. These algorithms have been successful in capturing the temporal evolution of the flow and have been widely adopted in many engineering and scientific applications. Despite their success, these algorithms may face challenges in the simulation of unsteady incompressible flows, which require the solution of elliptic equations and may suffer from convergence issues. Weakly compressible flow models were introduced for multiphase flows where the compressibility is not very significant [32,33,34]. Moreover, in realistic problems, the flows are often mixed flows involving both high and low local Mach numbers, e.g., cavitating flows [35], water entry of objects [36], cavitation bubble collapse [37,38] where the sound speed varies largely, or unsteady flows around accelerating and decelerating objects at all Mach number speeds. A major difficulty encountered in most compressible flow solvers is their inability to efficiently solve the problems of very low Mach numbers in the flows. At the low Mach numbers, most of these numerical solvers encounter degraded convergence speeds due to the wide disparity between the fluids and acoustic wave speeds. To overcome these challenges, alternative numerical techniques, such as the artificial compressibility method and the dual-time preconditioning approach, have been developed to improve the accuracy and efficiency of simulations of incompressible flows.
It is worth noting that there are two types of preconditioning techniques. The first type is the linear system level, which is purely mathematical. This approach solves a linear system to accelerate convergence in the initial iterations by preconditioning the matrix. The second type is the partial differential equation level, in which preconditioning terms are introduced in the partial differential equations to overcome difficulties in solving the equation. In this paper, our focus is mainly on the second type, specifically dual-time preconditioning derivatives introduced to the NS equation system to modify the way the solution evolves in pseudo-time towards convergence. The paper will review dual-time preconditioning methods for both steady and unsteady cases.
The subsequent sections provide a detailed mathematical background on the implementation of artificial time derivatives in both incompressible and compressible NS equations for multiphase flows. These sections present summaries of efficient simulation techniques for various multiphase flows, and serve as an informative resource for interested readers.
Subsequently, we conduct a comprehensive review and analysis of current trends, advanced simulation results, and complex numerical methods reported in the literature. This analysis provides researchers with a comprehensive overview of the successful applications of dual-time preconditioning methods in the field.
We conclude by recommending further research in the improvement of numerical methods for the simulation of complex multiphase flow problems. Additionally, we discuss several ways to enhance the accuracy and conductivity of these methods and provide potential areas for future research. Overall, this study contributes to the growing body of literature on the effective use of dual-time preconditioning methods in the simulation of multiphase flows.
2. Incompressible Multiphase Flows
This section focuses on the review of the mathematical foundations of various forms of preconditioning and artificial compressibility methods for multi-phase flows. The review begins with an overview of the incompressible flow models, including the dual-time homogeneous mixture model with a preconditioning parameter and the artificial compressibility model with a pseudo density and pressure function. The latest research and simulations on multi-phase flow modeling are then discussed and presented.
2.1. Preconditioning Dual-Time Stepping Method
As aforementioned, the ideas of artificial compressibility for incompressible flow are to transform the elliptic incompressible equations into a hyperbolic compressible system, which can be solved by standard, explicit or implicit, time-marching methods. The continuity equation can be rewritten as
where the artificial equation of state is , is artificial density, and is artificial compressibility. In order to ensure a consistently high convergence rate, the condition number of the Jacobian matrix of the governing equations system should be as close as possible to one for all flow conditions.
At each physical time step of the numerical solver, a pseudo-time iterative procedure is applied such that the term approaches zero upon convergence. Conversely, when approaches zero, the solution of the artificial equations converts back to the solution of the original equations.
The artificial compressibility method is effective in solving single-phase flows. However, when the computational domain involves more than one fluid, a challenging difficulty arises due to the appearance of an interface that separates fluids and behaves as an additional type of discontinuity. The application of single-phase schemes to multi-phase flows can result in problematic issues related to the mixture of two phases, mixture density, and sound speed, which can ultimately affect the entire flow field. To achieve rapid convergence rates and high computational accuracies near material interfaces in multiphase flow systems, it is necessary to modify the preconditioning formulation for single-phase flow systems due to the significantly different densities of the fluids involved.
In order to solve multiphase flows, various formulations of the preconditioning formulation for the continuity equation have been proposed. One such formulation, suggested by Kunz et al. [39,40], is given by . Another formulation, proposed by Owis and Neyfeh [41], is given by . The different forms of preconditioning result in different convergence rates and accuracies of the methods. To evaluate these rates and accuracies, Nguyen et al. [2] introduced a general formulation:
The convergence rates and accuracy of the methods were accessed using a variety of . The detailed effects of each formulation can be found in the study.
The dual-time preconditioning formulations can be applied to the mixture continuity, mixture momentum, and phasic volume fraction equations. The mass transfer was considered to model cavitation around the projectiles. In our previous study [2], a dual time-stepping algorithm was developed for the unsteady computation of multiphase flow. The algorithm is based on the NS equations, which are expressed as follows:
where is the preconditioning compressibility parameter, is the pressure, is the physical time, is the pseudo time, is the flow velocity vector, is the volume fraction of the ith phasic component and g denotes the gravity vector.
As described by the governing equations, the dual time-stepping algorithm introduces novel pseudo-time terms into the mixture continuity and phasic volume fraction equations. These terms are presented in the general form , where represents an exponential factor of the mixture density. The general forms reduce to the form suggested by Kunz et al. [39,40] when , and to the form modified by Owis and Neyfeh [41] when . This exponential factor provides a convenient mechanism for controlling the magnitude of the pseudo-time terms, thereby enabling the adjustment of the convergence rate for a given multiphase flow simulation. Accordingly, the pseudo terms are generalized forms in order to effectively evaluate the numerical stability and computational efficiency of the model.
Thanks to the ideas of artificial compressibility, it can transform the elliptic incompressible equations into a hyperbolic compressible system, allowing solving the system by standard, explicit or implicit, time-marching methods [2,18,19,20]. The governing Equations (6)–(8) can be rewritten in a compact vector form for two-phase flows as follows:
where the preconditioning matrix is given as
, is the flux tensor, is viscous terms and is the source term.
Here,
2.2. Numerical Method and Body-Fitted Curvilinear Coordinate System
The dual-time preconditioning approach treats the time variation of the incompressible flow as a compressible flow, which enables the coupling of the velocity and pressure fields in each time iteration [2,23]. This approach uses sub-iterations in pseudo-time and offers several advantages over traditional time-marching algorithms. For example, it provides a direct coupling of the continuity and momentum equations in the incompressible flow equations, eliminates the factorization error in factored implicit schemes, reduces errors due to approximations made in the implicit operator for improved numerical efficiency, eliminates errors due to lagged boundary conditions at both solid and internal fluid boundaries, and allows for the use of nonphysical, preconditioned iterative methods for more efficient convergence of the sub-iterations. These benefits of the dual-time preconditioning approach make it a promising technique for the numerical simulation of unsteady incompressible flows.
By adding a pseudo-time derivative term into the NS systems, the incompressible NS equation system can be formulated in a hyperbolic form, which can be solved using advanced compact schemes where the eigensystem and eigenvectors can be derived, and the wave propagation can be determined by applying Godunov-type methods and upwind solvers. Solving the NS equation in a system that can be implicitly solved and obtain highly accurate simulations [2,15,16].
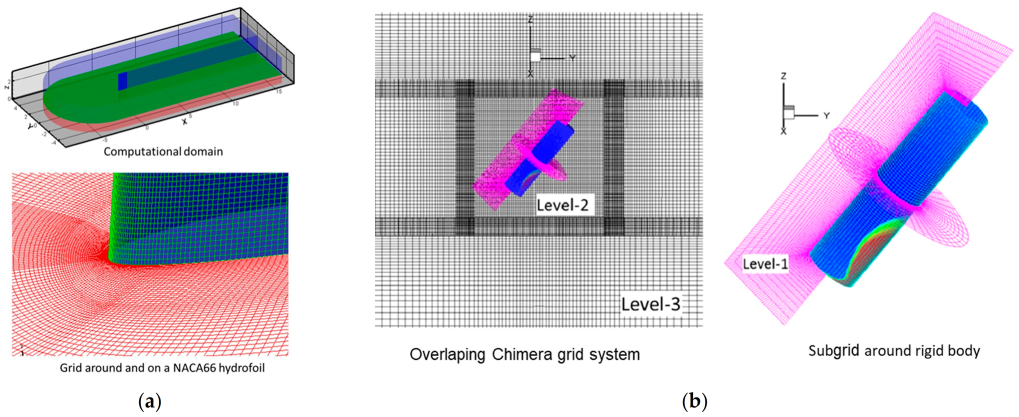
The preconditioning dual-time multiphase flow model (9) can be solved on a curvilinear body-fitted grid for complex geometries, as illustrated in Figure 1. Accordingly, the governing equations can be transformed from the physical space to the computational space in the general curvilinear coordinate system using the following relations [34]:
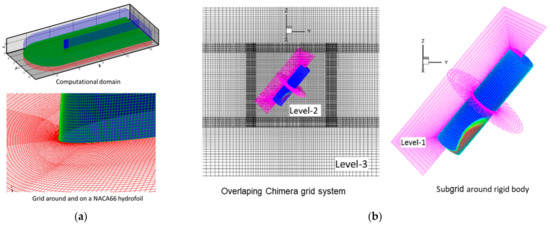
Figure 1.
Body-Fitted grid system. (a) Grid around a NACA66 hydrofoil (From [1]) and (b) Overlapping Chimera grids (From [2]).
The Cartesian derivatives can be expressed using the chain rule of differential derivatives:
For convenience, the differential derivatives of are defined similarly. The derivatives of the metrics are given as:
where the Jacobian of the transformation is defined as:
By applying Equations (12)–(15), Equation (1) can be transformed into a general curvilinear coordinate system . Note that the time ; therefore, the system can be rewritten in vector form as:
where , is the state vector, , and convective flux vector and viscous flux vector given as;
To build a moving grid algorithm, the grid velocities ,, and are introduced, and the contravariant velocities are defined as:
2.3. Coupling Artificial Density-Based Dual-Time Method and Sharp Interface Methods
The pseudo-compressibility method used in this study is based on the fundamental principles of classical methods, but it introduces pseudo-time derivative terms by replacing the true density with a pseudo-density, denoted by , and calculating the pressure as a function of the pseudo-density, referred to as the pseudo-law of state [1,21,42]. This pseudo-law of state provides a mechanism for controlling the magnitude of the pseudo-time terms and adjusting the convergence behavior for a given simulation, as described in the governing equations. The introduction of pseudo-density and the use of a pseudo-law of state provide a means of effectively and efficiently simulating unsteady incompressible flows in a manner that couples the velocity and pressure fields in each time iteration.
where the parameters are set in accordance to or , in which , and , are equal to the local values of the respective velocities obtained at a previous iteration.
Using the pseudo-law of state (19), the incompressible NS Equations (1) and (2) can be solved in a hyperbolic form using density-based solvers, where the pseudo-density and velocity field can be obtained at each time step and, subsequently the pressure can be obtained from Equation (19). The governing equations can be expressed as follows:
For the simulation of immiscible fluid flows, such as free surface flows and bubble dynamics, which involve a sharp interface separating the two fluids, it is crucial to maintain the accuracy and sharpness of the interface. In order to achieve this, a volume of fluid (VOF) equation is used to track the interface position. The advection equation is solved using a known velocity field to update the density and viscosity fields in the next time step. The VOF equation takes the form of:
This equation ensures that the interface is captured accurately, even in the presence of complex flow physics, and allows for the simulation of multiphase flows with sharp interface transitions. The use of the VOF equation in conjunction with the governing equations of the flow helps to accurately model and simulate the behavior of immiscible fluid systems. The geometric VOF/PLIC methods [21] or algebraic VOF methods [22] have been successfully coupled to incompressible flow solutions for free surface flows.
2.4. Simulations of Incompressible Multiphase Flows
2.4.1. Modeling Two-Phase Flows with Sharp Interface
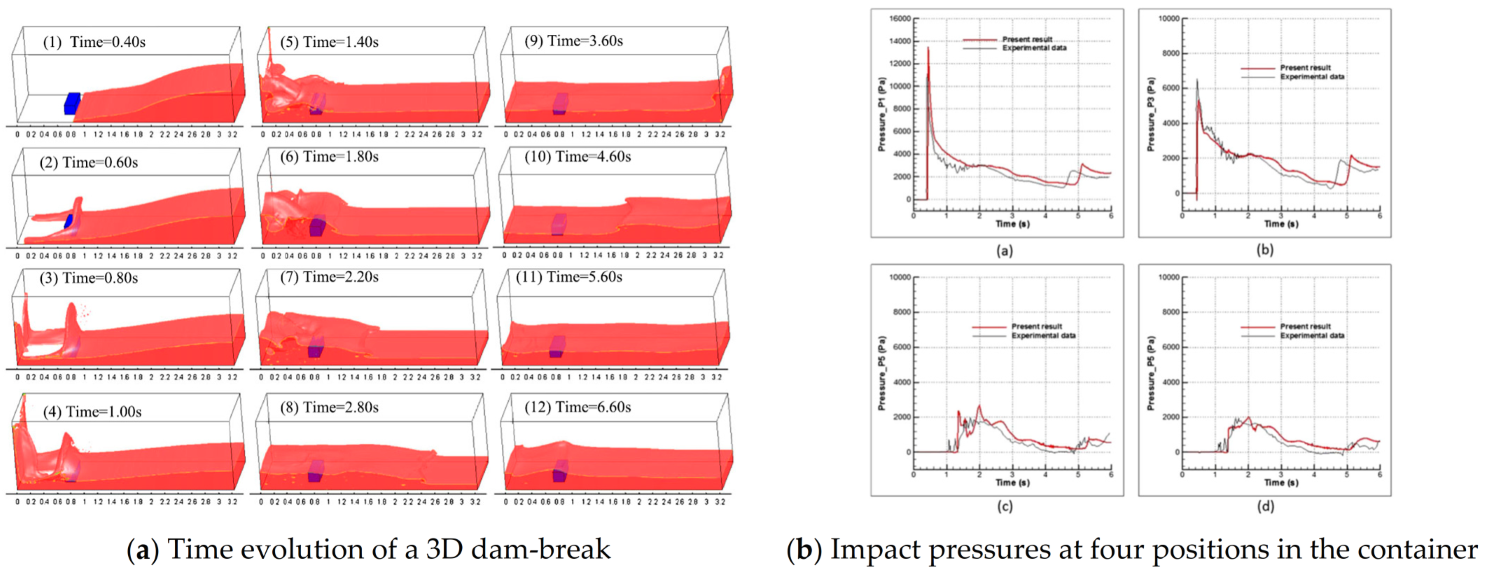
The dual-time preconditioning and artificial compressibility methods have been utilized in the simulation of multiphase flows in the incompressible NS equations. These techniques have led to successful reports of two-phase flow simulations. Extensive numerical analyses have been conducted to study the free surface and fluid-structure interactions with moving bodies [1,2,20,21,22,42,43,44,45]. A novel numerical model that integrates a fully 3D, dual-time, pseudo-compressibility model with a VOF interface tracking algorithm was introduced for multiphase flows [21]. The model is designed for the analysis of free surface flows and water impact problems. The numerical solver is validated through simulations of various water impact problems, including the water entries of free-falling hemisphere and cone, the initial stages of the dam-break problem with dynamic pressure loads, and a long-term simulation of the wave impact on a container and a tall structure. A typical simulation of a three-dimensional falling water column on a container and impact pressures at four positions in the container is illustrated in Figure 2. The time sequence of a falling water column on a container in 3D shows complex and violent fluid dynamics, including wave impact, breaking, jets, mixing, and entrapment of fluids. The simulation results of pressure peak, initial slope, water level, and arrival times of the primary wave show good agreement with experimental data. These findings demonstrate the model’s potential for accurate analysis and prediction of fluid dynamics in free surface flows and water impact problems.
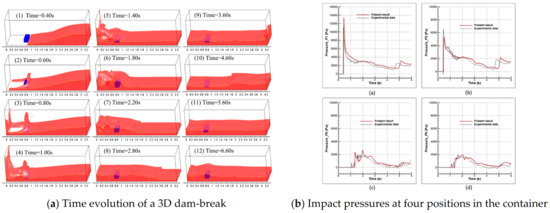
Figure 2.
Simulation of a 3D falling water column in a container (This figure has been adapted from [21]).
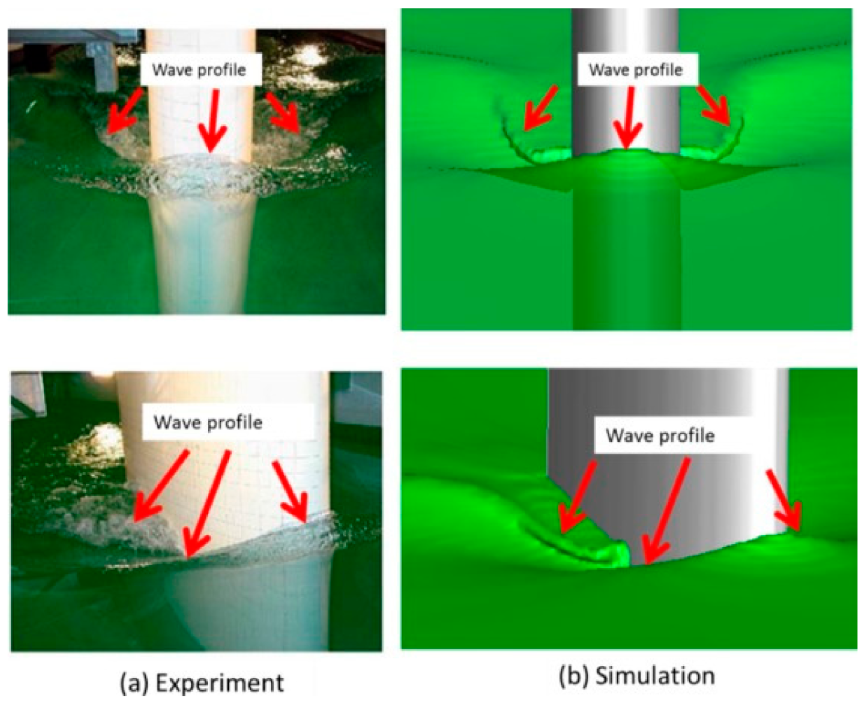
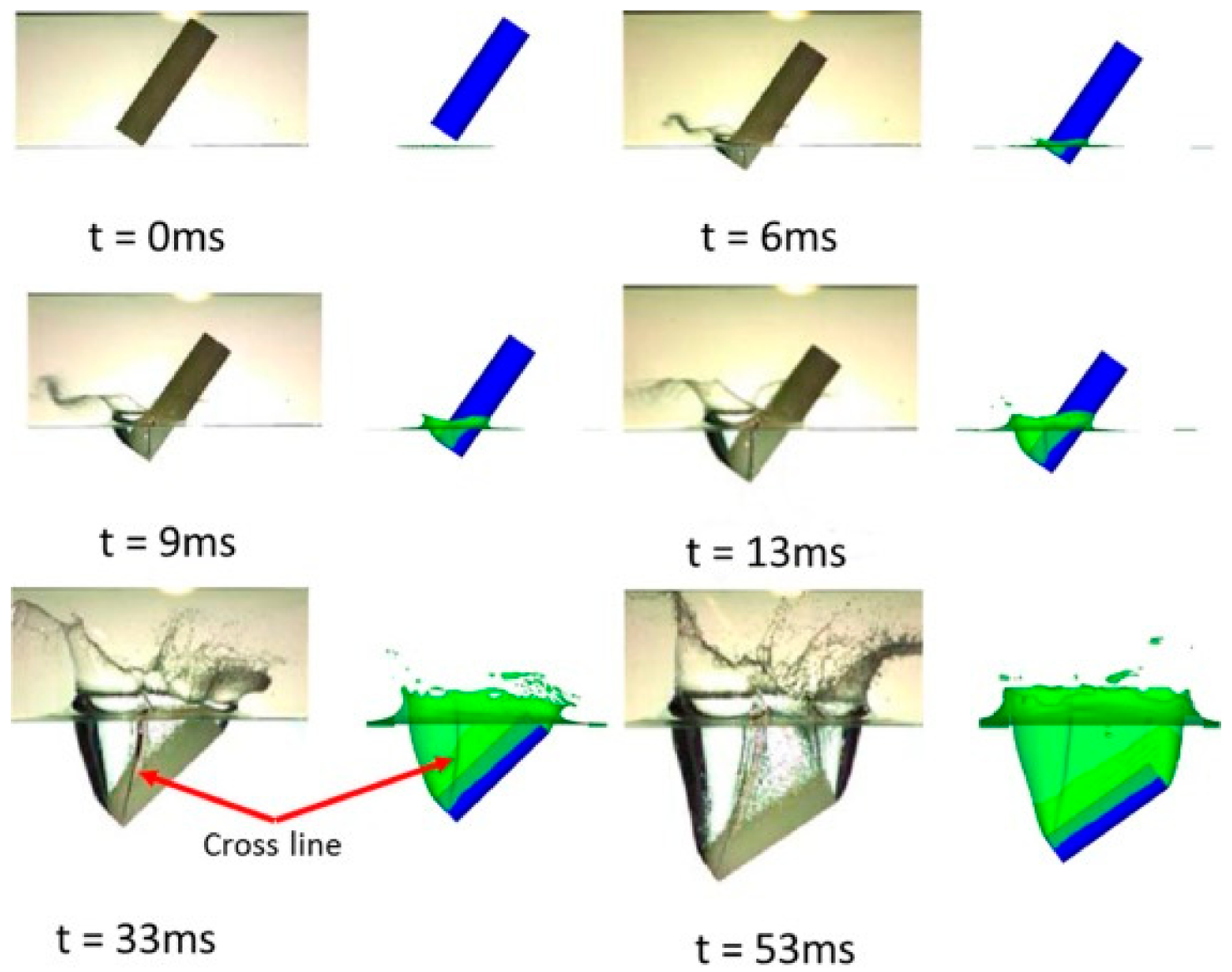
A research article was published describing an advanced technique that uses a volume-of-fluid (VOF)-based method and a dual-time, pseudo-compressibility method on overset grids for 3D free-surface flow problems in engineering [21]. The technique employs overset grids to enable simulations of complex geometries and object motions, enhancing computational efficiency by utilizing the flexibility of these grids. The nonlinear six degrees of freedom (6DOF) motion equations are strongly coupled with the flow solver to enable the simultaneous solution of rigid body motion. A range of complex problems, featuring a broad variety of Froude numbers and large density ratios, was selected to showcase the method’s capabilities on a complex, moving overset grid system. Figure 3 illustrates simulations of free-surface wave profiles surrounding a NACA0024 foil using the free-surface flow solver. The numerical results are well compared with experimental photographs from [46]. The numerical simulations of a bubble-bursting phenomenon in two tandem bubbles at the free surface are conducted to explore the influence of another bubble behind it [47]. The problems of water entry and exit of rigid bodies have been numerically simulated to study the slamming effect on structures near the free surface [1]. Figure 4 shows a 3D simulation of an oblique cylinder entering the water. The dual-time preconditioning method was used in ANSYS Fluent software to model flow-front advancement during the impregnation of woven fabrics of a 3D curved mold for a fillet L-shaped structure [48]. The studies show the capability of the methods for simulation and analysis of incompressible two-phase flows with sharp interfaces.

Figure 3.
Simulated and experimental free-surface wave profiles around a surface-piercing NACA0024 foil (This figure has been adapted from [1]).
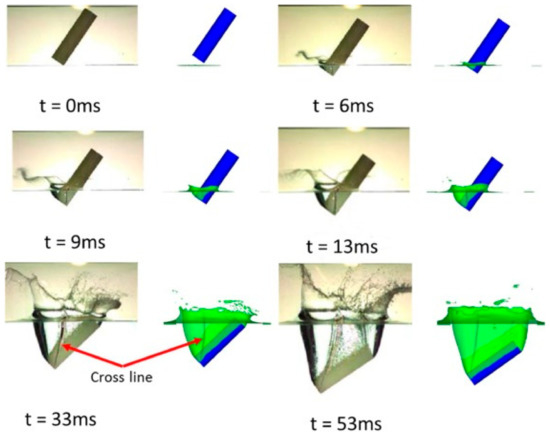
Figure 4.
Water entry of an oblique cylinder (This figure has been adapted from [1]).
2.4.2. Modeling Cavitating Flows
To model phase change in cavitating flows, vaporization and condensation are taken into the account [2,20]. Accordingly, the mass transfer rates are added in the source terms of the continuity and phasic volume fraction equations as follows.
The source term for the mass transfer rate in multiphase flows is represented as the sum of two terms: . The term represents the mass rate of vapor generation, while represents the mass rate of condensation. The source term of the mass transfer rate takes into account the generation and condensation of vapor, which are essential processes in the simulation of multiphase flows. The accurate representation of the mass transfer rate is crucial in ensuring the accuracy of the simulation results and the proper prediction of the behavior of the flow. The source term of the mass transfer rate has been widely studied in the literature and various models have been proposed to account for the generation and condensation of vapor in multiphase flows [26,34].
The mass transfer rates can be characterized and modeled based on the vapor pressure , and the scaling theory of static critical phenomena [2,35,49] as follows:
where the constant coefficients, and , represent the transfer rates from fluid 2 to fluid 1 and from fluid 1 to fluid 2, respectively. The damping parameter, , accounts for the pressure difference between the vapor and liquid pressures.
Alternative models of cavitation based on the vapor pressure , and the scaling theory of static critical phenomena can be also employed in this governing equation system such as the Merkle cavitation model [2,50], Kunz cavitation model [39,40], Schnerr and Sauer cavitation model [51,52] Singhal cavitation model [53], and ZGB cavitation model [54,55].
The cavitation number is defined as follows:
where the is the initial pressure in air, is the vapor pressure, is the liquid density, and is the initial velocity.
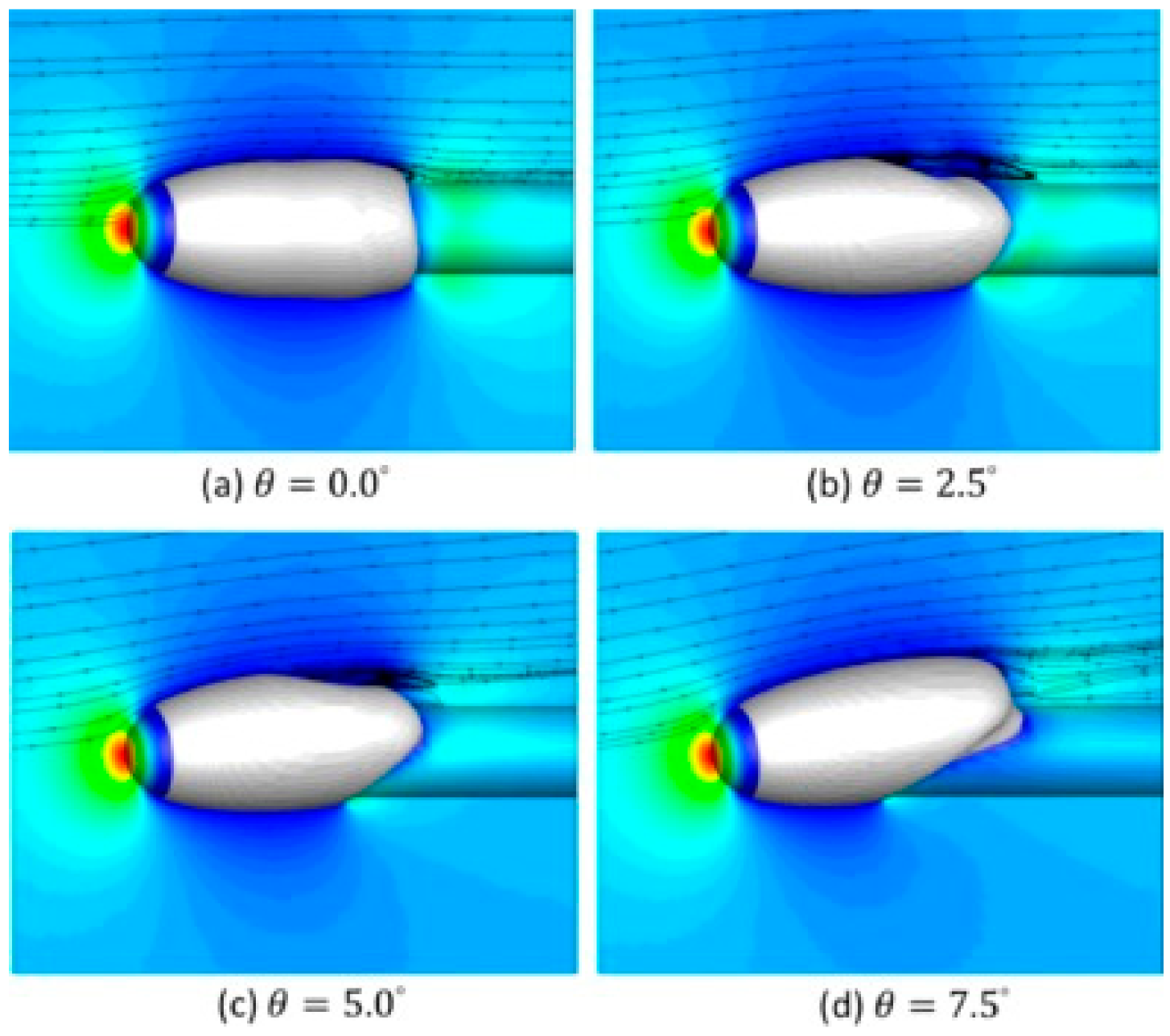
This technique was also employed in many studies to analyze cavitating flows. The super- and partial-cavitating flow over submerged projectiles were modeled and reported [2,41,56,57,58]. Using the general form of the dual-time preconditioning terms [2], the cavitating flows around the projectile with different angles of attack have been simulated as shown in Figure 5. Furthermore, in the study, the simulations of water entry for high-speed projectiles involve modeling the fluid flow as a mixture of liquid, condensable vapor, and non-condensable gases. Separate volume fraction equations are used for each species and solved to capture their behavior. The interface-capturing method can distinguish between the species and is crucial for accurately modeling supercavitation, which occurs when a cavity of vapor is created around the projectile. This enables a more accurate prediction of supercavitating water entry and provides valuable design insights.
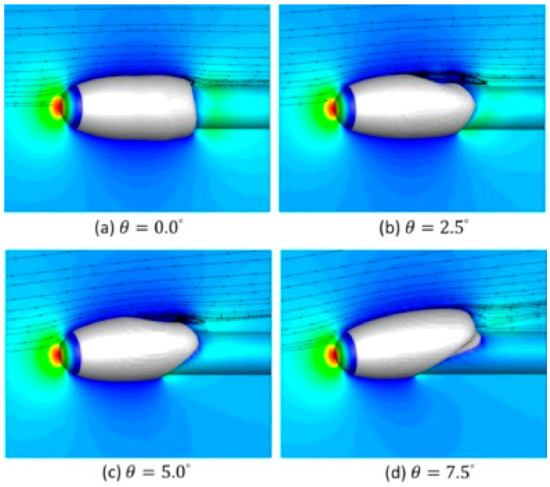
Figure 5.
Simulation of cavitating flows over a hemispherical body with different angles of attack (This figure has been adapted from [2]).
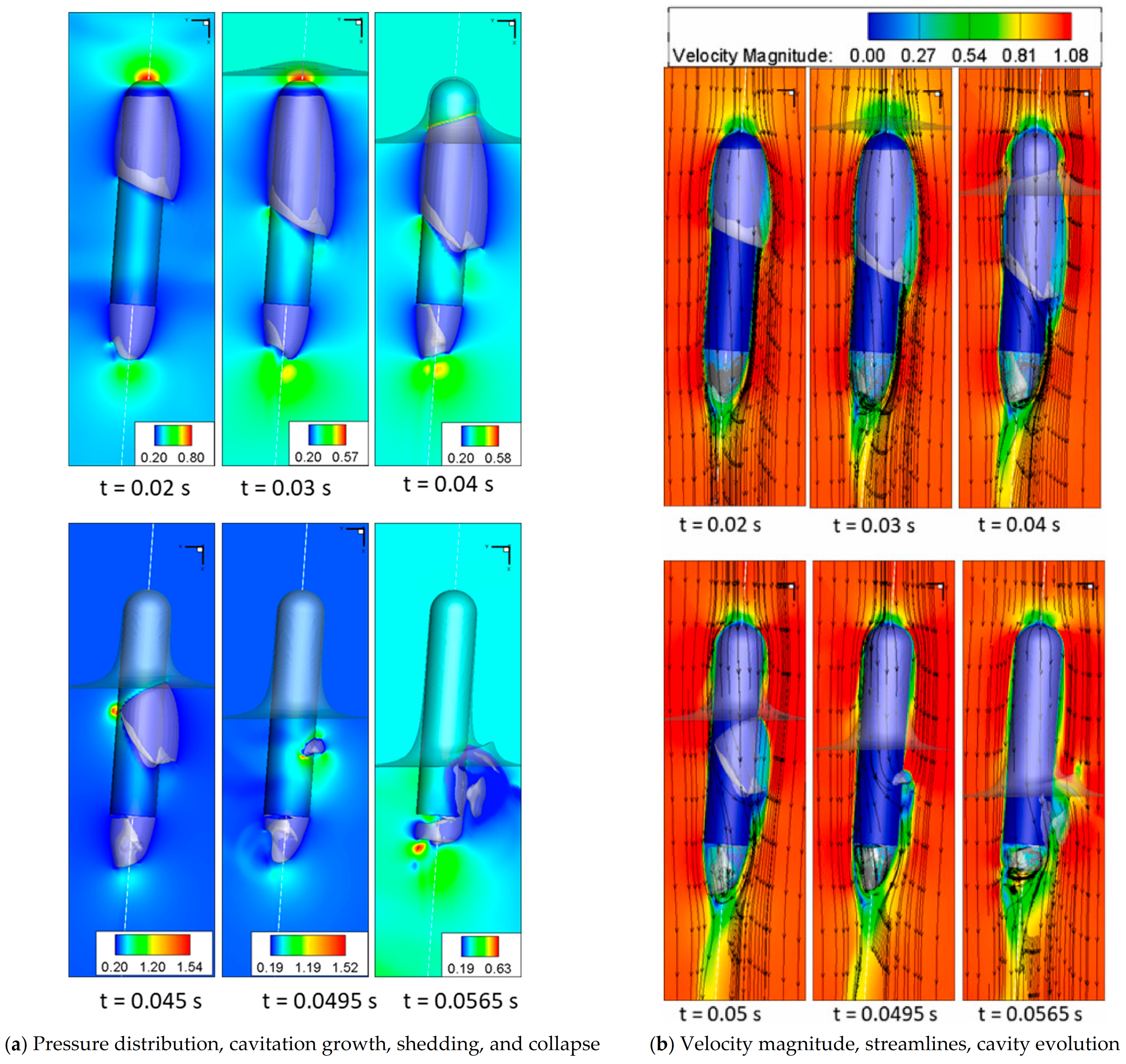
The dual-time preconditioning NS solver was employed to study the cavitation behavior of projectiles moving below a free surface and exiting it [20]. The results of the simulation can be used to improve the design of underwater systems and make them more resilient to high-pressure peaks caused by collapsing bubbles. Figure 6 demonstrates the asymmetric cavitation shedding and collapse during the exit of an axisymmetric projectile at an angle of attack of 4 degrees. The simulation accurately captured pressure distribution, cavitation growth, shedding, collapse, velocity magnitude, streamlines, and cavity evolution. These findings can aid in the design and control of submerged vehicles or projectiles operating in similar fluid flows, as they provide insight into the interaction between these objects and their environment.
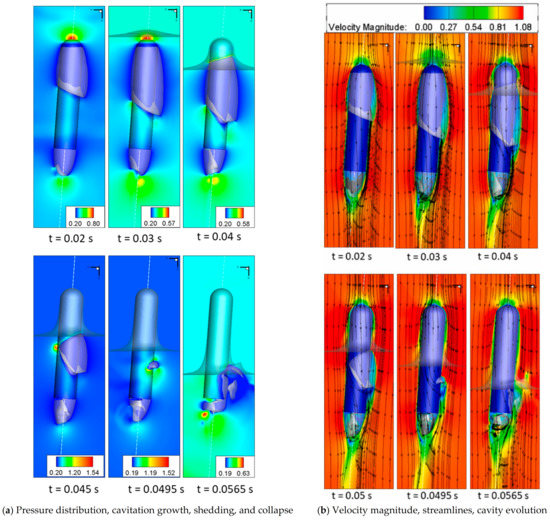
Figure 6.
Cavitation evolution during oblique water exits of a projectile (This figure has been adapted from [20]).
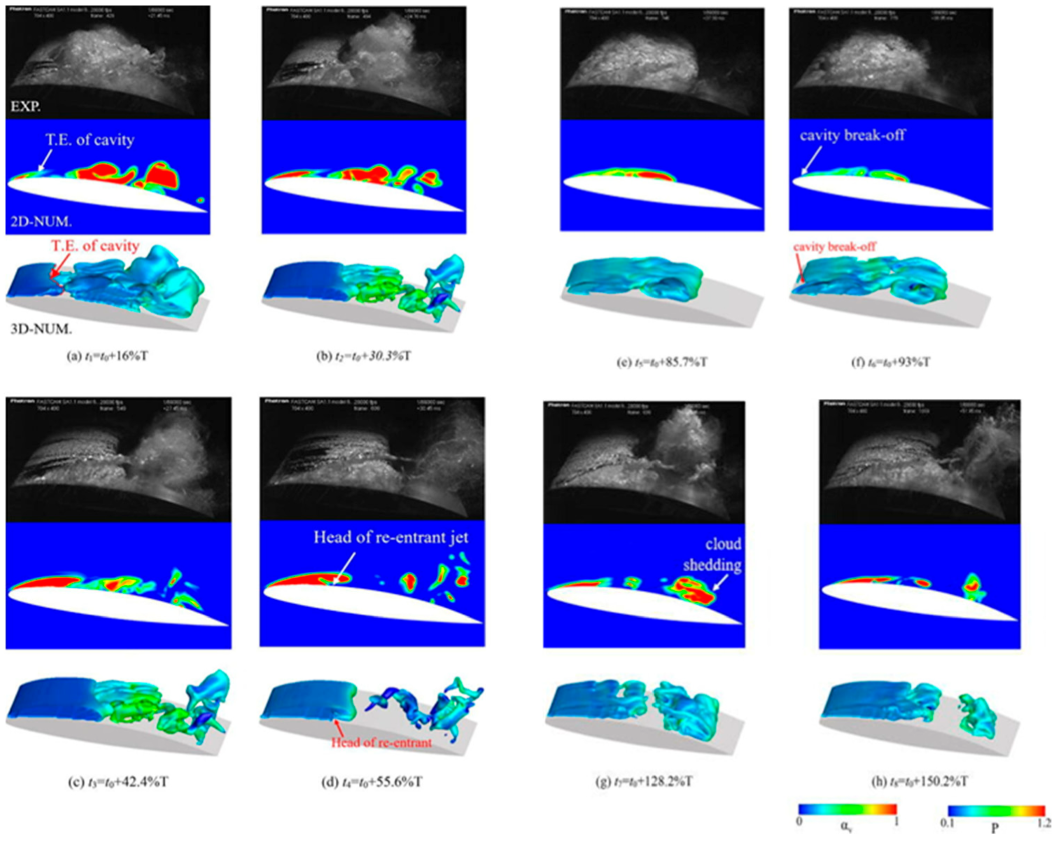
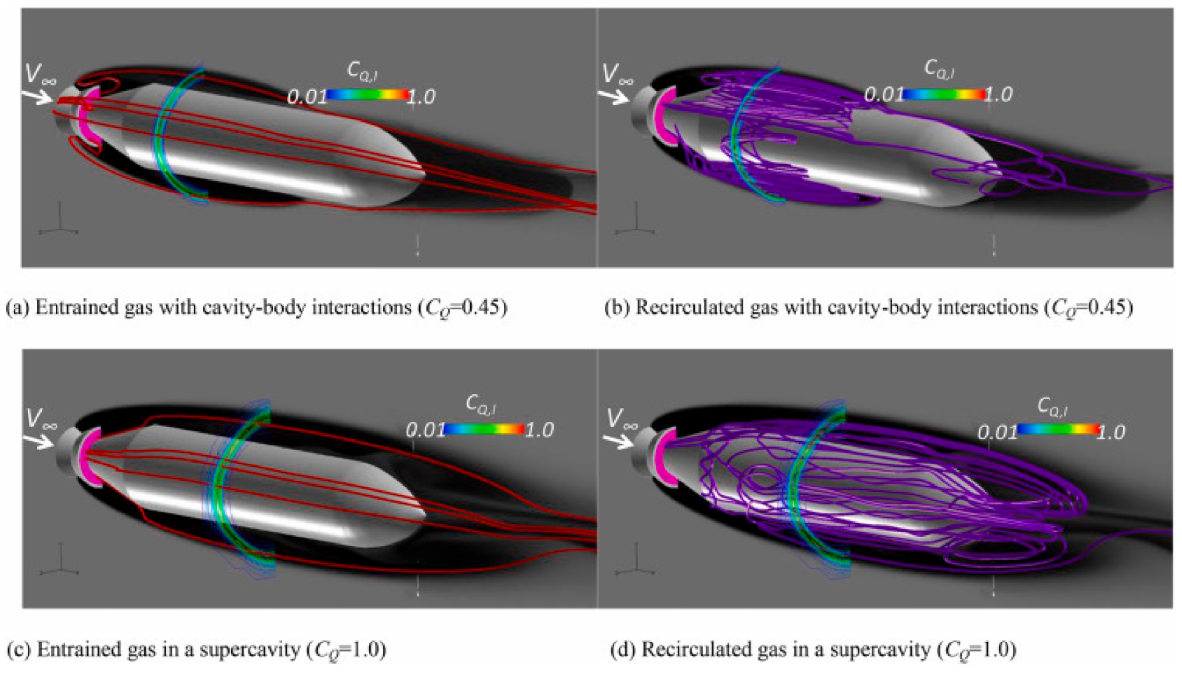
The dual-time preconditioning method has also been employed with a cut-cell method utilizing 2D cartesian meshes with embedded boundaries to simulate steady-state, turbulent, and cavitating flows over isolated hydrofoils. The numerical solver can characterize two hydrofoils featuring mid-chord and leading-edge cavitation and the simulation results show satisfactory agreement with numerical and experimental data [59]. The cavitation of many different hydrofoils is widely analyzed because of the important application of this shape in ship engineering. A 3D NACA66 hydrofoil fixed at an 8° angle of attack and sheet/cloud cavitating conditions has been simulated and compared with experimental data as shown in Figure 7. The unsteady behavior of transient cavitating flow, the results at eight typical instants are presented and the formation, growth, and breakdown of the cavity well agree with the experimental photograph. The dual-time preconditioning method has been used to predict instabilities due to cavitation in turbopump inducers [60]. The method was successful to analyze steady cavitating flows around the NACA 0012 and NACA 66 (MOD) hydrofoils and also an axisymmetric hemispherical fore-body under different conditions, and the results are compared with the available numerical and experimental data [61]. A high-order nodal discontinuous Galerkin method was applied to solve the dual-time preconditioned multiphase NS equations for cavitating flows on unstructured grids, showing accurate results of the cavitation around hydrofoil and axisymmetric bodies [62]. The artificially ventilated supercavities covering an underwater vehicle are shown in Figure 8. The numerical method shows its capability and is a powerful tool for computation of the complex multiphase flows.
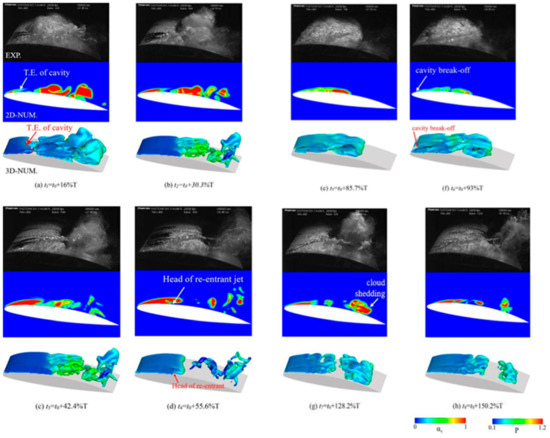
Figure 7.
Cavitation about a 3D NACA66 hydrofoil fixed at an 8° angle of attack (This figure has been adapted from [63]).
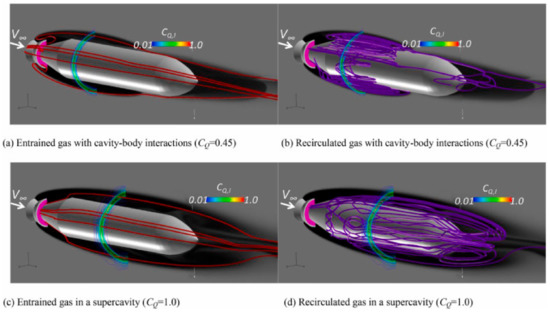
Figure 8.
Ventilated cavitating flow over a body at FrN = 26.7, ReN = 56,000 (This figure has been adapted from [64]).
3. Compressible Multiphase Flows
This section provides a review of the mathematical foundation of dual-time preconditioning techniques for compressible multiphase flows. The focus will be on the description of the dual-time stepping methods and preconditioning approach for the compressible NS equation system, as well as the computation of multiphase flows for a range of Mach numbers.
3.1. Dual-Time Preconditioning Method for Compressible NS Equation System
Almost numerical solvers for compressible flows can well simulate transonic and supersonic flows, however, for problems with mixed flows of very different Mach numbers, the solver can overcome the stiffness of the compressible flows at low Mach numbers and the large discrepancy of wave propagation in the hyperbolic system of the compressible NS equations. Local preconditioning techniques with dual-time stepping methods were introduced to the compressible NS equation to control the wave propagation velocities of the various modes. The preconditioning techniques eliminate the inconsistent scaling behavior of numerical flux functions of Godunov-like schemes. The techniques should be improved and applied to full two-fluid models and DNS-like flow simulations for realistic flow problems [65].
For the compressible homogeneous mixture flow model, the preconditioning matrix is introduced into the compressible Euler/NS equations with pseudo-time derivative terms [66]. The dual-time preconditioning methods not only moderate the stiffness of the system of equations but also improve the accuracy of simulations of flows at low Mach numbers. The preconditioning technique involves the alteration of the time derivatives used in time-marching CFD methods with the primary objective of enhancing their convergence. The preconditioning is introduced by multiplying the time derivative in Equation (17) by a preconditioning matrix as follows [36]:
In formulation (17), the alteration of the time derivative, as the time is replaced by a pseudo time , can negatively impact the time accuracy, particularly for transient problems. However, the time accuracy can be restored by using a dual time-stepping method.
To improve the efficiency of numerical simulations, the equation is transformed from the conservative variables Q to a more suitable set of variables, to reduce the system Jacobian matrix to a sparse and easier-to-manipulate form. The derivation of the preconditioning matrix starts with this transformation.
In the case of a mixture of multi-species real gases, the primitive variables are considered the most suitable set of variables. After the preconditioning steps, a transformation back to the conservative set of variables is necessary for numerical implementation. The preconditioning matrix will be modified in different forms according to the numerical models to which is applied [67,68,69,70,71,72]. Here, the formulation of the dual-time preconditioning NS equation system of a homogeneous mixture flow model based on mass fraction variables is presented. The system is given in a vector form in curvilinear coordinates as follows [36]:
where , is the state vector, , and convective flux vector and viscous flux vector given as;
where .
The preconditioning matrix is given as
where, . The characteristics of the preconditioned system result in a well-conditioned dissipation formulation and ensure reliable accuracy, in which the pseudo-time derivative, ; is defined as the pseudo-speed of sound and this control the wave propagation velocities of the various modes of the system.
The fluids’ properties can be modeled based on equations of state (EOS) from ideal to real fluids. Examples of EOS equations are adiabatic/Isentropic EOS, Tait EOS, Stiffened Gas EOS, Noble-Abel Stiffened-Gas EOS, and Industrial Association for the Properties of Water and Steam (IAPWS).
3.2. Numerical Solution Procedures
The Dual-Time Preconditioned System (18) can be discretized on a structured grid utilizing a subclass of the lower-upper symmetric Gauss-Seidel (LU-SGS) method [73]. An upwind non-MUSCL total variation diminishing (TVD) algorithm is employed in conjunction with a suitable limiter function to eliminate the generation of unphysical solutions in the vicinity of strong gradients [36]. The discretization of the convective flux terms is accomplished through this approach. Meanwhile, the viscous flux terms are treated using a second-order accurate central difference scheme. The physical-time derivative is approximated using a second-order accurate backward difference method, while the pseudo-time derivative is determined through the application of the Euler finite-difference formula. The pseudo-time step is established based on the largest eigenvalue of the system, and the local pseudo-time step is defined accordingly. For steady-state solutions, the physical-time step is set to infinity, while in unsteady computations, the physical-time step is set to the global pseudo-time step at each pseudo-time level. A hybrid formulation, combining a conservative preconditioned Roe method and a nonconservative preconditioned characteristic-based method, is presented to extend the method to transonic and supersonic flows with the presence of shocks. This hybrid approach allows for a more comprehensive and accurate treatment of flow physics in these challenging regimes [74].
Alternatively, the application of the linearization procedure to System (18) results in the derivation of an implicit unfactored numerical scheme. The solution to this implicit unfactored scheme can be obtained through the utilization of the alternating direction implicit (ADI) method [75]. Furthermore, the dual-time preconditioned system can alternatively be discretized by employing the advection upstream splitting method (AUSM), and the multi-dimensional limiting process (MLP) limiter was utilized to ensure efficient and accurate computation of convective fluxes [76,77].
3.3. Simulations of Compressible Multiphase Flows
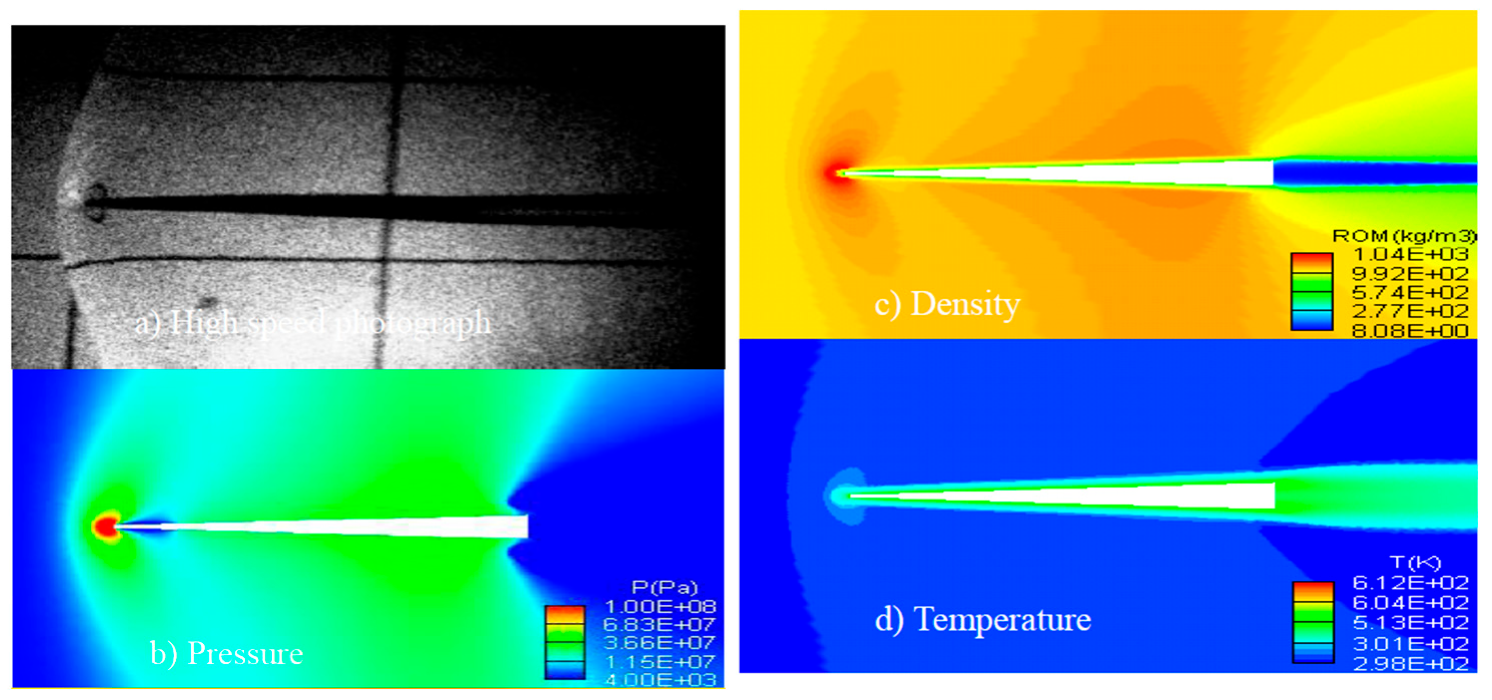
The initial preconditioning algorithm designed for the computation of compressible single-phase flow [66] was expanded to accommodate multiphase flow simulations [36]. This study presents a numerical solver for multiphase flows capable of simulating various fluid-structure interactions in underwater environments, such as cavitation flows over underwater projectiles, transonic flow past an underwater projectile, water impact of a circular cylinder, and water entry of a hemisphere with one degree of freedom. The solver has been shown to provide results that are in good agreement with available experimental data or previously published results for various quantities of interest, such as surface pressure coefficients, water impact forces, vertical accelerations, and impact velocities. Figure 9 presents typical results of the contours of pressure, density, and temperature for a transonic flow over a projectile, where the free stream velocity is 1540 m/s. Additionally, the study also examines key aspects of supercavitating flows over axisymmetric projectiles during entry and exit from the water, including the shape of the cavity, phase topography, and drag coefficients.
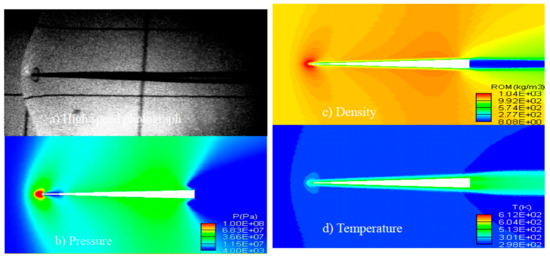
Figure 9.
The contours of pressure, density, and temperature for a transonic flow over a projectile, where the free stream velocity is 1540 m/s (This figure has been adapted from [36]).
Given that a significant portion of cavitating flows involve both an incompressible liquid region and a compressible cavity region, it is imperative to employ a system preconditioning technique that appropriately scales the numerical speed of sound in order to improve the convergence rate in low Mach number flow simulations [35,67,75,78,79,80].
Furthermore, the Dual-Time Preconditioned method has been demonstrated to be highly effective in the simulation of cavitation bubble dynamics using real fluid properties of IAPWS [37,81]. The cavitation bubble dynamics, which refers to the formation of vapor-filled bubbles in a liquid, is a potent phenomenon with significant ramifications in various fields such as nature, science, and industrial engineering and technologies. In applications such as hydrofoils, propellers, pipes, control valves and nozzles, and ultrasonic cavitation, repeated instances of cavitation bubble collapse over time can result in high local energy and cause detrimental effects on the mechanical components. Conversely, the repeated occurrences of cavitation bubble collapse can also generate high local energy that can be harnessed for practical applications, such as hydrodynamic cavitation processes, surface cleaning, extraction of natural products, industrial production of food and beverages, microbial inactivation, and others. During the collapse phase of a cavitation bubble, high local energy can be generated through shock waves and high-speed microjets, resulting in hot spots of high temperature and pressure.
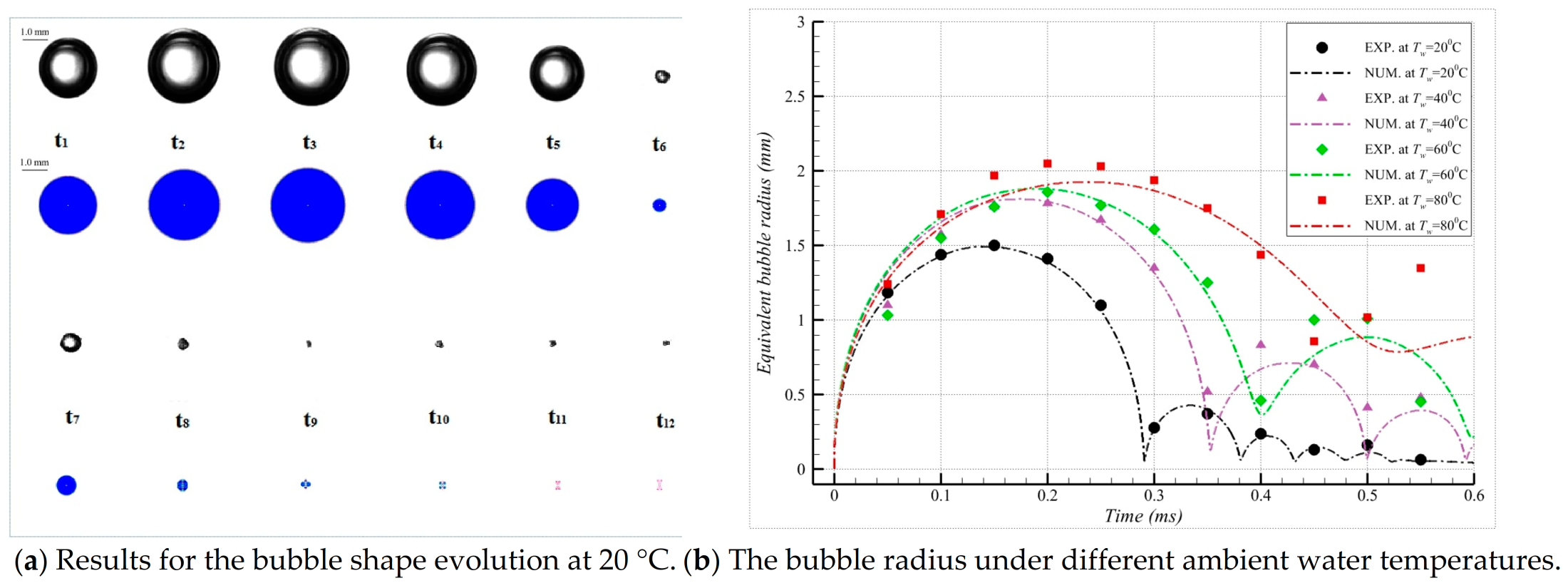
The numerical computations can analyze the thermodynamic effects on single cavitation bubble dynamics under various ambient temperature conditions [37,38]. The results of these studies can be used to improve our understanding of how different temperatures affect the behavior and intensity of bubbles in a variety of applications as simulations in Figure 10, such as medical imaging or industrial processes that involve fluid flow with high-pressure gradients. The maximum bubble radius, first minimum bubble radius, and collapsing time increase with an increase in ambient temperature. However, the peak values of internal pressure and internal temperature decrease as the ambient temperature increases. Generally speaking, bubbles collapse less violently at higher temperatures than the lower ones.
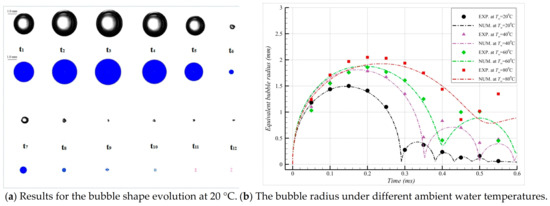
Figure 10.
Thermodynamic effects on single cavitation bubble dynamics (This figure has been adapted from [37]).
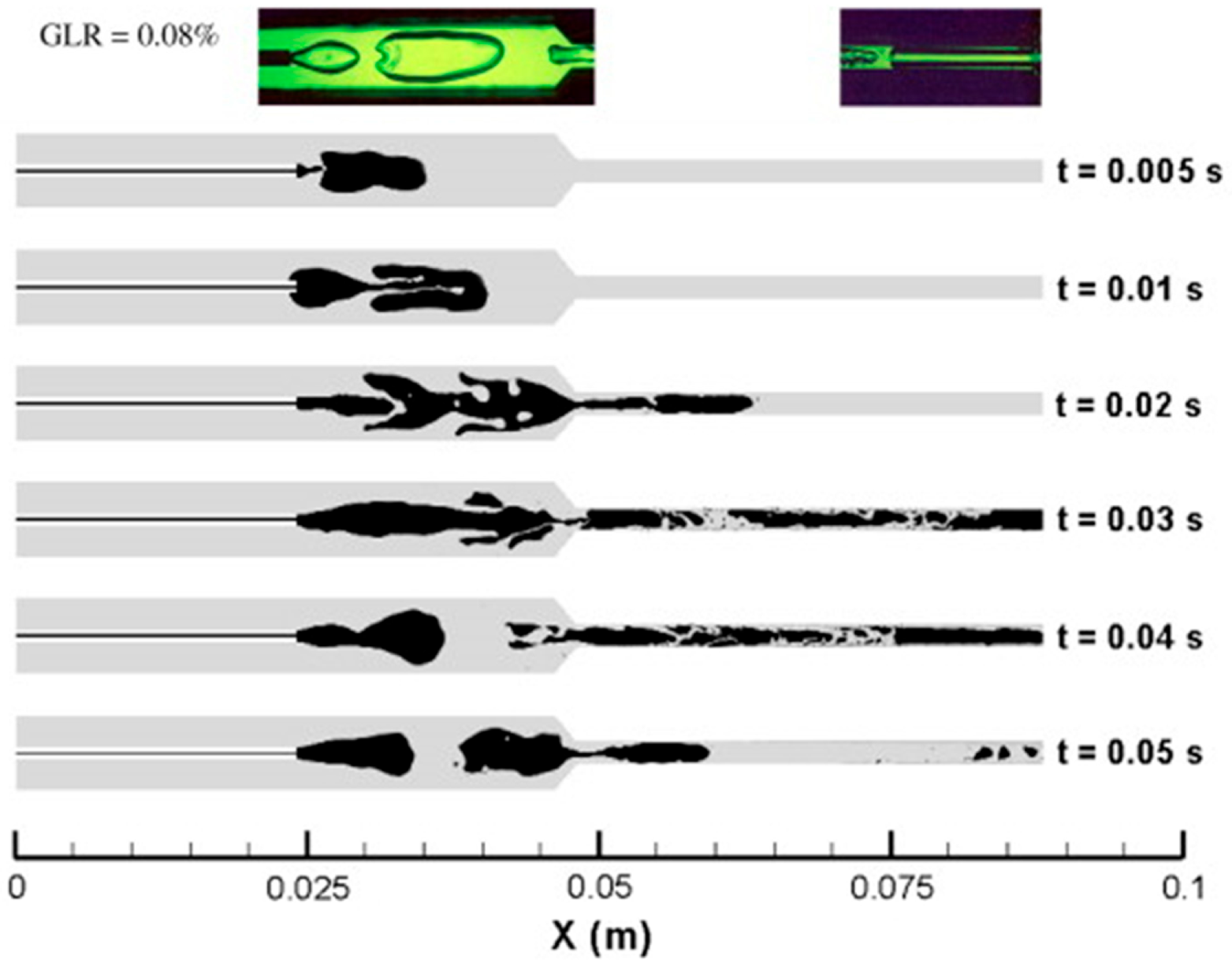
For capturing a sharper interface between two fluids, novel level-set approaches [82], and tangent of hyperbola for interface-capturing methods (THINC) [83,84] were introduced for the simulation of all-Mach multiphase flows. The proposed all-Mach level-set method utilizes the concept of signed distance functions within the framework of a species mass conservation equation to provide accurate evolution of the interface. The method also encompasses multiple reinitialization techniques to address subgrid scale interfacial fragmentation, ensuring the maintenance of accuracy. From a practical perspective, this study has the potential to enhance simulations related to high-speed marine vehicles, particularly in the context of supercavitation, which refers to the formation of gaseous cavities around moving objects such as ships or submarines at very high velocities. The other works have evaluated several approaches for sharp interface capturing in computations of multi-phase mixture flows using the preconditioning method [83]. The practical implications are that these strategies can be used to accurately capture the volume fraction discontinuities, which is important when simulating complex flow phenomena such as Rayleigh Taylor instability and axisymmetric jet instabilities. These methods also provide an accurate representation of fluid properties at interfaces between different phases such as the evolution of vapor volume fraction in an aerated-liquid injector shown in Figure 11. The inception of bubbles occurs in the fluid upstream of the discharge tube, which is characterized by a relatively low flow velocity. As these bubbles progress through the discharge tube, they experience rapid deformation and fragmentation due to the presence of shearing stresses. This allows engineers to better understand how fluids interact with each other under various conditions.
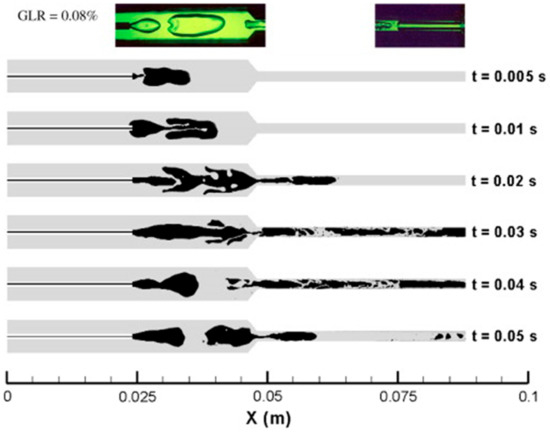
Figure 11.
Evolution of vapor volume fraction in an aerated-liquid injector. Numerical computation using the preconditioning method and interface sharpening technique (This figure has been adapted from [83]).
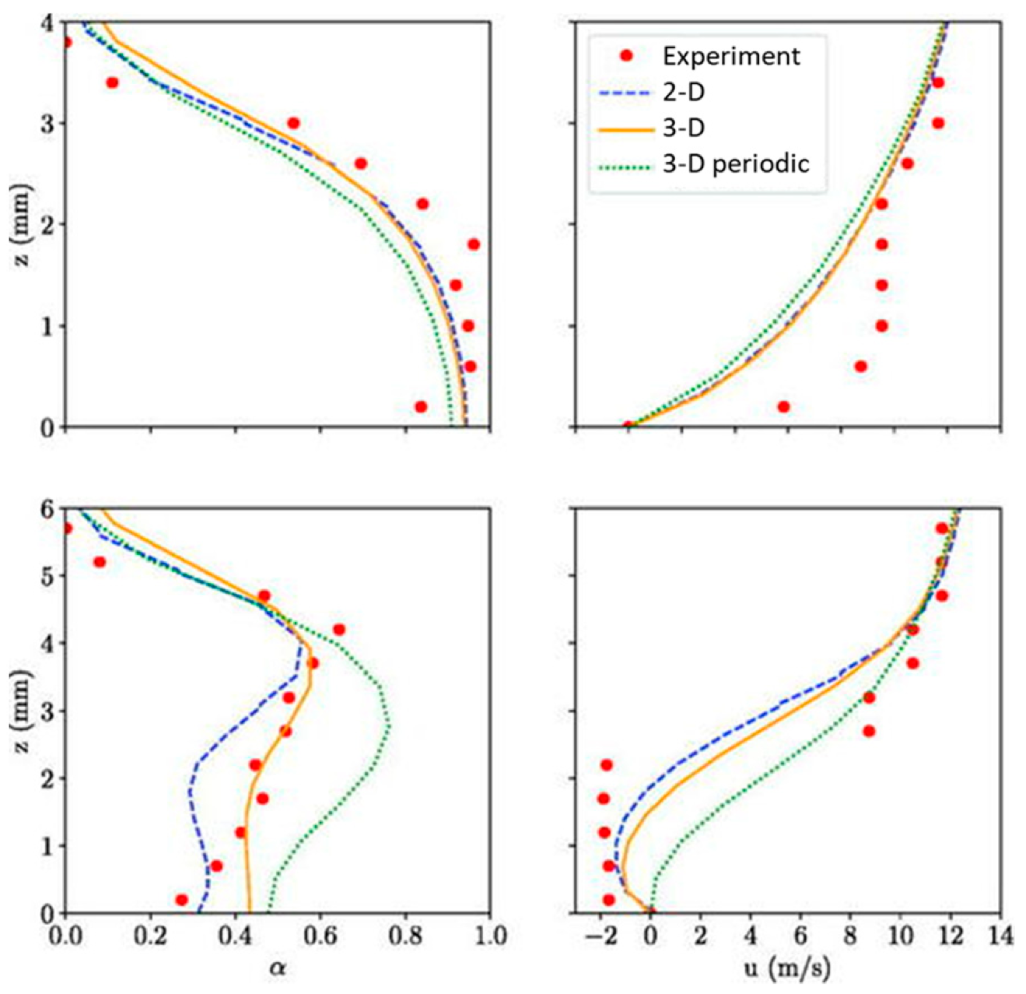
Using the preconditioning method, a comprehensive examination of the behavior of sheet cavitation in 3D Venturi geometries has been studied [85]. The research provides a deeper understanding of the dynamics of sheet cavitation, which is crucial for improving design decisions in hydraulic applications. The correlation between the numerical results and the experimental data for the capture of the re-entrant jet is found to be substantial in Figure 12 This is evidenced by the accurate determination of negative velocity values as depicted in the velocity profiles. Through a comparison of numerical results obtained under both sidewall and periodic conditions, the researchers were able to identify 3D effects that are not directly tied to the presence or absence of walls.
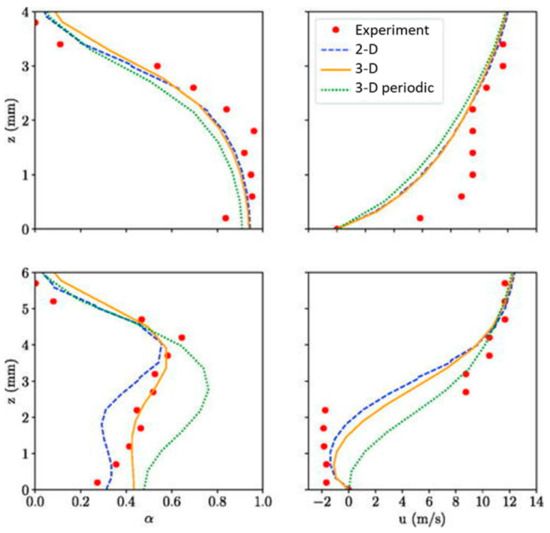
Figure 12.
Dynamics of partial cavitation developing in a 3D Venturi geometry and the interaction with sidewalls. Time-averaged comparison at midspan at stations S1 (top) and S2 (bottom) (This figure has been adapted from [85]).
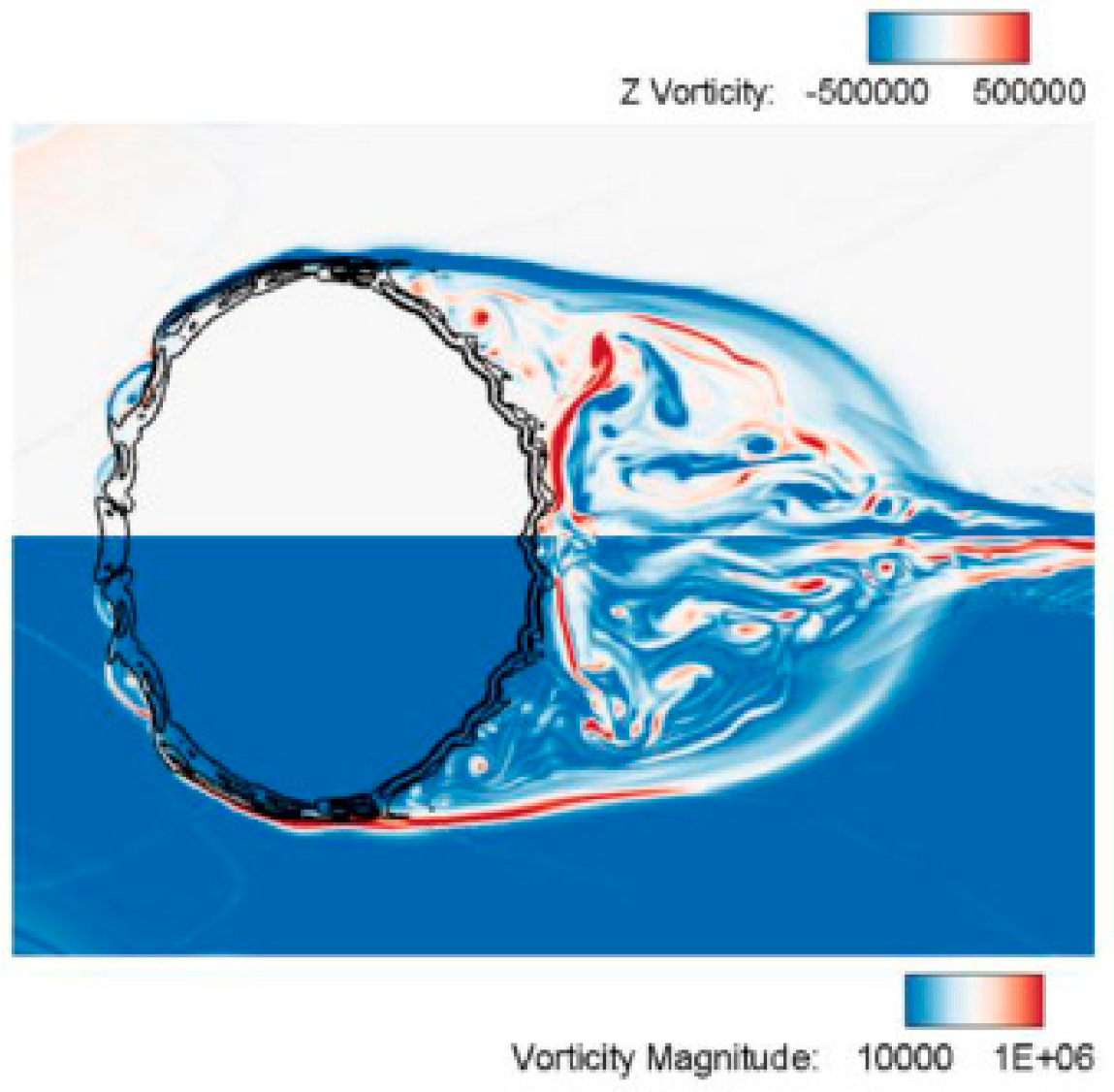
The homogeneous mixture model simulation of compressible multi-phase flows at all Mach numbers was also applied for a numerical simulation of compressible multi-phase flows utilizing the Noble–Abel stiffened gas (NASG) equation of state for fluid properties [86]. The simulation takes into account the effects of gravity and surface tension forces, which allows for the examination of oscillations in elliptical drops and unsteady water surfaces in dam break scenarios. The preconditioning technique was utilized to achieve improved convergence at low speeds without introducing numerical dissipation. The results obtained from this research were compared against analytic solutions and experimental data, such as Schlieren images, and were found to be in good agreement. The method provided a highly resolved result of the vortex formed around the bubble in Figure 13, showing the bubble transformed into an elliptical shape. Additionally, the simulation was able to accurately predict the deformation and evolution of bubbles during air/helium shock interactions, as well as the mixing and heat transfer between liquid and gas phases in underwater explosion scenarios, under various conditions.
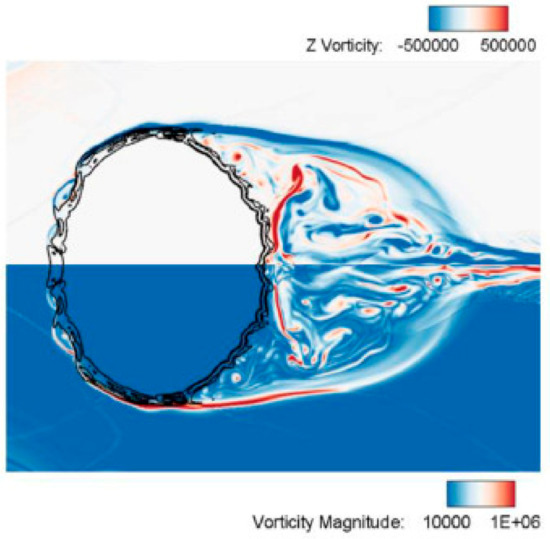
Figure 13.
Shock/water-column interaction problem. The z-vorticity and vorticity magnitude contour results at 194 μs (This figure has been adapted from [86]).
Furthermore, the preconditioning method has been applied to various multiphase flows and physics. A study presents the results of a numerical simulation investigating the interaction between an ultrasound wave and a bubble [87]. It provides three different numerical methods which are assessed with one-dimensional spherical benchmarks, showing that the compressible projection method is most suitable when considering spatial accuracy and time step stability. Finally, moving deformable bubbles interacting with plane waves have been simulated successfully demonstrating the ability of this new technique in more complex situations. The preconditioning technique was also applied to the development of a two-phase compressible flow model with stiff mechanical relaxation [70,88]. These studies present numerical results for two-dimensional liquid gas channel flows, shocks, and real cavitating flows in Venturi nozzles, which show that the proposed preconditioning techniques are effective in improving accuracy at low Mach number regimes. The order of pressure fluctuations generated by these methods is consistent with theoretical predictions from an asymptotic analysis on continuous relaxed two-phase flow models. A comprehensive and unified approach to general fluid thermodynamics was developed to account for fluid flows across the entire thermodynamic state [89]. The proposed method was validated through several test cases that examined the vaporization of supercritical droplets in both quiescent and convective environments. These test cases demonstrate the efficacy of the current algorithm in accurately modeling the specified physical phenomena. This technique was also applied to a modified flamelet-progress-variable model for combustion under supercritical conditions. The validity of the model is established through comparisons with experimental data from both laminar flames and turbulent combustion. Additionally, the model is used to investigate the influence of pressure on the coaxial injection and combustion of LOx/methane, as well as on the swirling injection and combustion of LOx/kerosene [90]. An algorithm based on the integration of time-derivative preconditioning techniques with low-diffusion upwinding methods was presented and applied to the simulation of multiphase, compressible flows commonly found in the motion of underwater projectiles [91]. The efficacy of the algorithm is demonstrated through the presentation of results from several multiphase shock tube calculations. Furthermore, calculations are presented for a high-speed axisymmetric supercavitating projectile during the crucial water entry phase of flight. an extension of the preconditioned advection upstream splitting method was introduced for the simulation of 3D two-phase flows in circulating fluidized beds [92]. The results of the calculations performed on a straight tube geometry demonstrate that the behavior of the flow, as reported in previous studies, is accurately modeled. The analysis specifically focuses on the effects of inelastic particle-particle collisions, which result in a fluctuating flow field. Another study focuses on the development of simultaneous solution algorithms for Eulerian–Eulerian gas–solid flow models, analyzing the stability and convergence behavior of both a point solver and a plane solver [93].
4. Conclusions
In this review, we analyzed the advancements in dual-time preconditioning and artificial compressibility methods for solving NS equations in both incompressible and compressible multiphase flows. We discussed the latest progress in different forms of dual-time preconditioning and artificial compressibility terms integrated into the NS equations on structured and unstructured grids, overlapping grid systems, and curvilinear coordinates.
These methods have been proven to be robust and widely used for the analysis of multiphase flows. We also highlighted outstanding issues in the simulation of free-surface, fluid-structure interaction, slamming, water entry, and exit of rigid bodies, and cavitation flows and shock waves. The relative advantages of these techniques for simulating mixed flows of different speeds were pointed out, and it was concluded that they are a powerful tool for the computation of multiphase flows at all Mach numbers. Overall, the dual-time preconditioning and artificial compressibility methods are valuable tools for CFD simulations in the field of multiphase flows. However, the dual-time, pseudo-compressibility method can be still improved in several ways:
- (i)
- Incorporating more accurate and efficient numerical schemes for solving dual-time, pseudo-compressibility NS equations.
- (ii)
- Considering the effects of turbulence by implementing various accurate turbulence models and other physical phenomena that may affect the multiphase flow behaviors.
- (iii)
- Additionally, the method can be extended to handle more complex and realistic boundary conditions and geometries. Accordingly, efforts should be focused on reducing the computational cost of the method while preserving its accuracy and robustness.
Funding
This research was funded by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, grant number 2020R1I1A1A01072475.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Phasic volume fraction | |
| Phasic mass fraction | |
| Preconditioning parameter | |
| Density | |
| Exponential factor of mixture density | |
| Preconditioning matrix | |
| Jacobian of physical time derivatives | |
| Molecular viscosity | |
| Pseudo time | |
| Pseudo time step | |
| Physical time step | |
| Cavitation number | |
| Gravity | |
| Pressure | |
| Physical time | |
| Transformation matrix | |
| x-direction velocity of fluid | |
| Contravariant velocity in x-direction | |
| Parameter reference to velocity | |
| Free-stream velocity | |
| y-direction velocity of fluid | |
| Contravariant velocity in y-direction | |
| z-direction velocity of fluid | |
| Contravariant velocity in z-direction | |
| computational space in the general curvilinear coordinate system | |
| Mass transfer rate | |
| Artificial density | |
| Reference to free stream |
References
- Nguyen, V.-T.; Park, W.-G. Enhancement of Navier–Stokes solver based on an improved volume-of-fluid method for complex interfacial-flow simulations. Appl. Ocean. Res. 2018, 72, 92–109. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Vu, D.-T.; Park, W.-G.; Jung, C.-M. Navier–Stokes solver for water entry bodies with moving Chimera grid method in 6DOF motions. Comput. Fluids 2016, 140, 19–38. [Google Scholar] [CrossRef]
- Palomino Solis, D.A.; Piscaglia, F. Toward the Simulation of Flashing Cryogenic Liquids by a Fully Compressible Volume of Fluid Solver. Fluids 2022, 7, 289. [Google Scholar] [CrossRef]
- Yao, J.; Yao, Y. Transient CFD Modelling of Air–Water Two-Phase Annular Flow Characteristics in a Small Horizontal Circular Pipe. Fluids 2022, 7, 191. [Google Scholar] [CrossRef]
- Fayed, H.; Bukhari, M.; Ragab, S. Large-Eddy Simulation of a Hydrocyclone with an Air Core Using Two-Fluid and Volume-of-Fluid Models. Fluids 2021, 6, 364. [Google Scholar] [CrossRef]
- Harlow, F.H.; Welch, J.E. Numerical Calculation of Time-Dependent Viscous Incompressible Flow of Fluid with Free Surface. Phys. Fluids 1965, 8, 2182–2189. [Google Scholar] [CrossRef]
- Puckett, E.G.; Almgren, A.S.; Bell, J.B.; Marcus, D.L.; Rider, W.J. A High-Order Projection Method for Tracking Fluid Interfaces in Variable Density Incompressible Flows. J. Comput. Phys. 1997, 130, 269–282. [Google Scholar] [CrossRef]
- Yu, J.D.; Sakai, S.; Sethian, J.A. A coupled level set projection method applied to ink jet simulation. Interface Free. Bound. 2003, 5, 459–482. [Google Scholar] [CrossRef]
- Merkle, C. Time-accurate unsteady incompressible flow algorithms based on artificial compressibility. In Proceedings of the 8th Computational Fluid Dynamics Conference, Honolulu, HI, USA, 9–11 June 1987. [Google Scholar]
- Chorin, A.J. A Numerical Method for Solving Incompressible Viscous Flow Problems. J. Comput. Phys. 1997, 135, 118–125. [Google Scholar] [CrossRef]
- Štrubelj, L.; Tiselj, I. Modeling of Rayleigh-Taylor instability with conservative level set method. In Proceedings of the ICMF 2007, 6th International Conference on Multiphase Flow, Leipzig, Germany, 9–13 July 2007. [Google Scholar]
- Elmahi, I.; Gloth, O.; Hänel, D.; Vilsmeier, R. A preconditioned dual time-stepping method for combustion problems. Int. J. Comput. Fluid Dyn. 2008, 22, 169–181. [Google Scholar] [CrossRef]
- Lin, H.; Jiang, C.; Hu, S.; Gao, Z.; Lee, C.-H. Disturbance region update method with preconditioning for steady compressible and incompressible flows. Comput. Phys. Commun. 2023, 285, 108635. [Google Scholar] [CrossRef]
- Li, X.-s.; Gu, C.-w.; Xu, J.-z. Development of Roe-type scheme for all-speed flows based on preconditioning method. Comput. Fluids 2009, 38, 810–817. [Google Scholar] [CrossRef]
- Muradoglu, M.; Gokaltun, S. Implicit Multigrid Computations of Buoyant Drops Through Sinusoidal Constrictions. J. Appl. Mech. 2005, 71, 857–865. [Google Scholar] [CrossRef]
- Kinzel, M.P. Computational Techniques and Analysis of Cavitating-Fluid Flows; A Dissertation in Aerospace Engineering; The Pennsylvania State University: State College, PA, USA, 2008. [Google Scholar]
- Maia, A.A.G.; Kapat, J.S.; Tomita, J.T.; Silva, J.F.; Bringhenti, C.; Cavalca, D.F. Preconditioning methods for compressible flow CFD codes: Revisited. Int. J. Mech. Sci. 2020, 186, 105898. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics. A Practical Introduction; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Nguyen, V.-T.; Phan, T.-H.; Duy, T.-N.; Kim, D.-H.; Park, W.-G. Fully compressible multiphase model for computation of compressible fluid flows with large density ratio and the presence of shock waves. Comput. Fluids 2022, 237, 105325. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Phan, T.-H.; Duy, T.-N.; Park, W.-G. Unsteady cavitation around submerged and water-exit projectiles under the effect of the free surface: A numerical study. Ocean. Eng. 2022, 263, 112368. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Park, W.-G. A free surface flow solver for complex three-dimensional water impact problems based on the VOF method. Int. J. Numer. Methods Fluids 2016, 82, 3–34. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Park, W.-G. A volume-of-fluid (VOF) interface-sharpening method for two-phase incompressible flows. Comput. Fluids 2017, 152, 104–119. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Thang, V.-D.; Park, W.-G. A novel sharp interface capturing method for two- and three-phase incompressible flows. Comput. Fluids 2018, 172, 147–161. [Google Scholar] [CrossRef]
- Ansari, M.R.; Nimvari, M.E. Bubble viscosity effect on internal circulation within the bubble rising due to buoyancy using the level set method. Ann. Nucl. Energy 2011, 38, 2770–2778. [Google Scholar] [CrossRef]
- Komrakova, A.E.; Eskin, D.; Derksen, J.J. Lattice Boltzmann simulations of a single n-butanol drop rising in water. Phys. Fluids 2013, 25, 042102. [Google Scholar] [CrossRef]
- Magnini, M.; Pulvirenti, B.; Thome, J.R. Numerical investigation of the influence of leading and sequential bubbles on slug flow boiling within a microchannel. Int. J. Therm. Sci. 2013, 71, 36–52. [Google Scholar] [CrossRef]
- Tomar, G.; Biswas, G.; Sharma, A.; Agrawal, A. Numerical simulation of bubble growth in film boiling using a coupled level-set and volume-of-fluid method. Phys. Fluids 2005, 17, 112103. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Park, W.-G. Numerical study of the thermodynamics and supercavitating flow around an underwater high-speed projectile using a fully compressible multiphase flow model. Ocean. Eng. 2022, 257, 111686. [Google Scholar] [CrossRef]
- Ding, H.; Zhang, Y.; Yang, Y.; Wen, C. A modified Euler-Lagrange-Euler approach for modelling homogeneous and heterogeneous condensing droplets and films in supersonic flows. Int. J. Heat Mass. Tran. 2023, 200, 123537. [Google Scholar] [CrossRef]
- Chen, J.; Huang, Z.; Li, A.; Gao, R.; Jiang, W.; Xi, G. Numerical simulation of carbon separation with shock waves and phase change in supersonic separators. Process. Saf. Environ. 2023, 170, 277–285. [Google Scholar] [CrossRef]
- Heydar Rajaee Shooshtari, S.; Honoré Walther, J.; Wen, C. Combination of genetic algorithm and CFD modelling to develop a new model for reliable prediction of normal shock wave in supersonic flows contributing to carbon capture. Sep. Purif. Technol. 2022, 309, 122878. [Google Scholar] [CrossRef]
- Munz, C.D.; Roller, S.; Klein, R.; Geratz, K.J. The extension of incompressible flow solvers to the weakly compressible regime. Comput. Fluids 2003, 32, 173–196. [Google Scholar] [CrossRef]
- Kajzer, A.; Pozorski, J. A weakly Compressible, Diffuse-Interface Model for Two-Phase Flows. Flow Turbul. Combust. 2020, 105, 299–333. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Nguyen, N.T.; Phan, T.-H.; Park, W.-G. Efficient three-equation two-phase model for free surface and water impact flows on a general curvilinear body-fitted grid. Comput. Fluids 2019, 196, 104324. [Google Scholar] [CrossRef]
- Phan, T.-H.; Shin, J.-G.; Nguyen, V.-T.; Duy, T.-N.; Park, W.-G. Numerical analysis of an unsteady natural cavitating flow around an axisymmetric projectile under various free-stream temperature conditions. Int. J. Heat Mass. Tran. 2021, 164, 120484. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Ha, C.-T.; Park, W.-G. Multiphase Flow Simulation of Water-entry and -exit of axisymmetric bodies. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Diego, CA, USA, 15–21 November 2013. [Google Scholar]
- Phan, T.-H.; Kadivar, E.; Nguyen, V.-T.; el Moctar, O.; Park, W.-G. Thermodynamic effects on single cavitation bubble dynamics under various ambient temperature conditions. Phys. Fluids 2022, 34, 023318. [Google Scholar] [CrossRef]
- Phan, T.-H.; Nguyen, V.-T.; Duy, T.-N.; Kim, D.-H.; Park, W.-G. Numerical study on simultaneous thermodynamic and hydrodynamic mechanisms of underwater explosion. Int. J. Heat Mass. Tran. 2021, 178, 121581. [Google Scholar] [CrossRef]
- Kunz, R.F.; Boger, D.A.; Stinebring, D.R.; Chyczewski, T.S.; Lindau, J.W.; Gibeling, H.J.; Venkateswaran, S.; Govindan, T.R. A preconditioned Navier-Stokes method for two-phase flows with application to cavitation prediction. Comput. Fluids 2000, 29, 849–875. [Google Scholar] [CrossRef]
- Kunz, R.F.; Boger, D.A.; Chyczewski, T.S.; Stinebring, D.; Gibeling, H.; Govindan, T. Multi-phase CFD analysis of natural and ventilated cavitation about submerged bodies. In Proceedings of the 3rd ASME-JSME Joint Fluids Engineering Conference, San Francisco, CA, USA, 18–23 July 1999; Volume 99. [Google Scholar]
- Owis, F.M.; Nayfeh, A.H. Numerical simulation of 3-D incompressible, multi-phase flows over cavitating projectiles. Eur. J. Mech. B-Fluid. 2004, 23, 339–351. [Google Scholar] [CrossRef]
- de Jouëtte, C.; Laget, O.; Le Gouez, J.M.; Viviand, H. A dual time stepping method for fluid–structure interaction problems. Comput. Fluids 2002, 31, 509–537. [Google Scholar] [CrossRef]
- Helluy, P.; Golay, F.; Caltagirone, J.-P.; Lubin, P.; Vincent, S.; Drevard, D.; Marcer, R.; Fraunié, P.; Seguin, N.; Grilli, S.; et al. Numerical simulations of wave breaking. ESAIM Math. Model. Numer. Anal. Model. Math. Anal. Numer. 2005, 39, 591–607. [Google Scholar] [CrossRef]
- Nourgaliev, R.R.; Dinh, T.N.; Theofanous, T.G. A pseudocompressibility method for the numerical simulation of incompressible multifluid flows. Int. J. Multiphas Flow. 2004, 30, 901–937. [Google Scholar] [CrossRef]
- Ha, C.-T.; Lee, J.H. A modified monotonicity-preserving high-order scheme with application to computation of multi-phase flows. Comput. Fluids 2020, 197, 104345. [Google Scholar] [CrossRef]
- Metcalf, B.; Longo, J.; Ghosh, S.; Stern, F. Unsteady free-surface wave-induced boundary-layer separation for a surface-piercing NACA 0024 foil: Towing tank experiments. J. Fluid. Struct. 2006, 22, 77–98. [Google Scholar] [CrossRef]
- GeolLee, C.; YoubLee, S.; Ha, C.-T.; HwaLee, J. Bursting jet in two tandem bubbles at the free surface. Phys. Fluids 2022, 34, 083309. [Google Scholar]
- Alotaibi, H.; Abeykoon, C.; Soutis, C.; Jabbari, M. Numerical Simulation of Two-Phase Flow in Liquid Composite Moulding Using VOF-Based Implicit Time-Stepping Scheme. J. Compos. Sci. 2022, 6, 330. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Phan, T.-H.; Duy, T.-N.; Park, W.-G. Numerical simulation of supercavitating flow around a submerged projectile near a free surface. In Proceedings of the 11th International Symposium on Cavitation, Daejon, Korea, 10–13 May 2021. [Google Scholar]
- Merkle, C.L.; Feng, J.; Buelow, P. Computational modeling of the dynamics of sheet cavitation. In Proceedings of the Third International Symposium on Cavitation, Grenoble, France, 7–10 April 1998. [Google Scholar]
- Schnerr, G.H.; Sauer, J. Physical and numerical modeling of unsteady cavitation dynamics. In Proceedings of the Fourth International Conference on Multiphase Flow, New Orleans, LA, USA, 27 May–1 June 2001. [Google Scholar]
- Ullas, P.K.; Chatterjee, D.; Vengadesan, S. Prediction of unsteady, internal turbulent cavitating flow using dynamic cavitation model. Int. J. Numer. Methods Heat 2022, 32, 3210–3232. [Google Scholar] [CrossRef]
- Singhal, A.K.; Athavale, M.M.; Li, H.; Jiang, Y. Mathematical Basis and Validation of the Full Cavitation Model. J. Fluids Eng. 2002, 124, 617–624. [Google Scholar] [CrossRef]
- Zwart, P.J.; Gerber, A.G.; Belamri, T. A two-phase flow model for predicting cavitation dynamics. In Proceedings of the Fifth International Conference on Multiphase Flow, Yokohama, Japan, 30 May–4 June 2004. [Google Scholar]
- Tauviqirrahman, M.; Jamari, J.; Susilowati, S.; Pujiastuti, C.; Setiyana, B.; Pasaribu, A.H.; Ammarullah, M.I. Performance Comparison of Newtonian and Non-Newtonian Fluid on a Heterogeneous Slip/No-Slip Journal Bearing System Based on CFD-FSI Method. Fluids 2022, 7, 225. [Google Scholar] [CrossRef]
- Hejranfar, K.; Ezzatneshan, E.; Fattah-Hesari, K. A comparative study of two cavitation modeling strategies for simulation of inviscid cavitating flows. Ocean. Eng. 2015, 108, 257–275. [Google Scholar] [CrossRef]
- Lindau, J.W.; Kunz, R.F.; Boger, D.A.; Stinebring, D.R.; Gibeling, H.J. High Reynolds number, unsteady, multiphase CFD modeling of cavitating flows. J. Fluid. Eng. 2002, 124, 607–616. [Google Scholar] [CrossRef]
- Lindau, J.W.; Kunz, R.F.; Mulherin, J.M.; Dreyer, J.J.; Stinebring, D.R. Fully coupled, 6-DOF to URANS, modeling of cavitating flows around a supercavitating vehicle. In Proceedings of the Fifth International Symposium on Cavitation (CAV2003), Osaka, Japan, 1–4 November 2003. [Google Scholar]
- Vrionis, Y.-P.G.; Samouchos, K.D.; Giannakoglou, K.C. Implementation of a conservative cut-cell method for the simulation of two-phase cavitating flows. In Proceedings of the 10th International Conference on Computational Methods (ICCM2019), Singapore, 9–13 July 2019; pp. 440–452. [Google Scholar]
- Coutier-Delgosha, O.; Fortes-Patella, R.; Reboud, J.L.; Hakimi, N.; Hirsch, C. Stability of preconditioned Navier–Stokes equations associated with a cavitation model. Comput. Fluids 2005, 34, 319–349. [Google Scholar] [CrossRef]
- Hejranfar, K.; Fattah-Hesary, K. Assessment of a central difference finite volume scheme for modeling of cavitating flows using preconditioned multiphase Euler equations. J. Hydrodyn. Ser. B. 2011, 23, 302–313. [Google Scholar] [CrossRef]
- Hajihassanpour, M.; Hejranfar, K. A high-order nodal discontinuous Galerkin method to solve preconditioned multiphase Euler/Navier-Stokes equations for inviscid/viscous cavitating flows. Int. J. Numer. Methods Fluids 2020, 92, 478–508. [Google Scholar] [CrossRef]
- Tian, B.; Chen, J.; Zhao, X.; Zhang, M.; Huang, B. Numerical analysis of interaction between turbulent structures and transient sheet/cloud cavitation. Phys. Fluids 2022, 34, 047116. [Google Scholar] [CrossRef]
- Kinzel, M.P.; Lindau, J.W.; Kunz, R.F. Gas entrainment from gaseous supercavities: Insight based on numerical simulation. Ocean. Eng. 2021, 221, 108544. [Google Scholar] [CrossRef]
- Saurel, R.; Pantano, C. Diffuse-Interface Capturing Methods for Compressible Two-Phase Flows. Annu. Rev. Fluid. Mech. 2018, 50, 105–130. [Google Scholar] [CrossRef]
- Weiss, J.M.; Smith, W.A. Preconditioning applied to variable and constant density flows. AIAA J. 1995, 33, 2050–2057. [Google Scholar] [CrossRef]
- Venkateswaran, S.; Lindau, J.W.; Kunz, R.F.; Merkle, C.L. Computation of multiphase mixture flows with compressibility effects. J. Comput. Phys. 2002, 180, 54–77. [Google Scholar] [CrossRef]
- Lindau, J.; Kunz, R.; Venkateswaran, S.; Merkle, C. Development of a fully-compressible multi-phase Reynolds-averaged Navier-Stokes model. In Proceedings of the 15th AIAA Computational Fluid, Dynamics Conference, Anaheim, CA, USA, 11–14 June 2001. [Google Scholar]
- Braconnier, B.; Nkonga, B. An all-speed relaxation scheme for interface flows with surface tension. J. Comput. Phys. 2009, 228, 5722–5739. [Google Scholar] [CrossRef]
- Pelanti, M. Low Mach number preconditioning techniques for Roe-type and HLLC-type methods for a two-phase compressible flow model. Appl. Math. Comput. 2017, 310, 112–133. [Google Scholar] [CrossRef]
- Murrone, A.; Guillard, H. Behavior of upwind scheme in the low Mach number limit: III. Preconditioned dissipation for a five equation two phase model. Comput. Fluids 2008, 37, 1209–1224. [Google Scholar] [CrossRef]
- Gupta, A. Preconditioning Methods for Ideal and Multiphase Fluid Flows. Ph.D. Thesis, The University of Tennessee at Chattanooga, Chattanooga, TN, USA, 2013. [Google Scholar]
- Yoon, S.; Jameson, A. Lower-upper Symmetric-Gauss-Seidel method for the Euler and Navier-Stokes equations. AIAA J. 1988, 26, 1025–1026. [Google Scholar] [CrossRef]
- Housman, J.A.; Kiris, C.C.; Hafez, M.M. Time-Derivative Preconditioning Methods for Multicomponent Flows—Part I: Riemann Problems. J. Appl. Mech. 2009, 76, 021210. [Google Scholar] [CrossRef]
- Ha, C.-T.; Park, W.-G. Evaluation of a new scaling term in preconditioning schemes for computations of compressible cavitating and ventilated flows. Ocean. Eng. 2016, 126, 432–466. [Google Scholar] [CrossRef]
- Kim, H.; Kim, C. A physics-based cavitation model ranging from inertial to thermal regimes. Int. J. Heat Mass. Tran. 2021, 181, 121991. [Google Scholar] [CrossRef]
- Yoo, Y.-L.; Sung, H.-G. A hybrid AUSM scheme (HAUS) for multi-phase flows with all Mach numbers. Comput. Fluids 2021, 227, 105050. [Google Scholar] [CrossRef]
- Kadioglu, S.Y.; Sussman, M.; Osher, S.; Wright, J.P.; Kang, M. A second order primitive preconditioner for solving all speed multi-phase flows. J. Comput. Phys. 2005, 209, 477–503. [Google Scholar] [CrossRef]
- Shin, B.R.; Yamamoto, S.; Yuan, X. Application of Preconditioning Method to Gas-Liquid Two-Phase Flow Computations. J. Fluids Eng. 2004, 126, 605–612. [Google Scholar] [CrossRef]
- Goncalves, E.; Patella, R.F. Numerical simulation of cavitating flows with homogeneous models. Comput. Fluids 2009, 38, 1682–1696. [Google Scholar] [CrossRef]
- Phan, T.-H.; Nguyen, V.-T.; Duy, T.-N.; Kim, D.-H.; Park, W.-G. Influence of phase-change on the collapse and rebound stages of a single spark-generated cavitation bubble. Int. J. Heat Mass. Tran. 2022, 184, 122270. [Google Scholar] [CrossRef]
- Kinzel, M.P.; Lindau, J.W.; Kunz, R.F. A multiphase level-set approach for all-Mach numbers. Comput. Fluids 2018, 167, 1–16. [Google Scholar] [CrossRef]
- Cassidy, D.A.; Edwards, J.R.; Tian, M. An investigation of interface-sharpening schemes for multi-phase mixture flows. J. Comput. Phys. 2009, 228, 5628–5649. [Google Scholar] [CrossRef]
- Kakumanu, N.; Edwards, J.R.; Choi, J.-I. Numerical Simulation of Underwater Burst Events Using Sharp Interface Capturing Methods. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2019. [Google Scholar]
- Gouin, C.; Junqueira-Junior, C.; Goncalves Da Silva, E.; Robinet, J.-C. Numerical investigation of three-dimensional partial cavitation in a Venturi geometry. Phys. Fluids 2021, 33, 063312. [Google Scholar] [CrossRef]
- Yoo, Y.-L.; Kim, J.-C.; Sung, H.-G. Homogeneous mixture model simulation of compressible multi-phase flows at all Mach number. Int. J. Multiphas Flow. 2021, 143, 103745. [Google Scholar] [CrossRef]
- Huber, G.; Tanguy, S.; Béra, J.-C.; Gilles, B. A time splitting projection scheme for compressible two-phase flows. Application to the interaction of bubbles with ultrasound waves. J. Comput. Phys. 2015, 302, 439–468. [Google Scholar] [CrossRef]
- LeMartelot, S.; Nkonga, B.; Saurel, R. Liquid and liquid–gas flows at all speeds. J. Comput. Phys. 2013, 255, 53–82. [Google Scholar] [CrossRef]
- Meng, H.; Yang, V. A unified treatment of general fluid thermodynamics and its application to a preconditioning scheme. J. Comput. Phys. 2003, 189, 277–304. [Google Scholar] [CrossRef]
- Huang, D.; Wang, Q.; Meng, H. Modeling of supercritical-pressure turbulent combustion of hydrocarbon fuels using a modified flamelet-progress-variable approach. Appl. Therm. Eng. 2017, 119, 472–480. [Google Scholar] [CrossRef]
- Neaves, M.D.; Edwards, J.R. All-Speed Time-Accurate Underwater Projectile Calculations Using a Preconditioning Algorithm. J. Fluids Eng. 2005, 128, 284–296. [Google Scholar] [CrossRef]
- De Wilde, J.; Heynderickx, G.J.; Vierendeels, J.; Dick, E.; Marin, G.B. An extension of the preconditioned advection upstream splitting method for 3D two-phase flow calculations in circulating fluidized beds. Comput. Chem. Eng. 2002, 26, 1677–1702. [Google Scholar] [CrossRef]
- De Wilde, J.; Vierendeels, J.; Heynderickx, G.J.; Marin, G.B. Simultaneous solution algorithms for Eulerian–Eulerian gas–solid flow models: Stability analysis and convergence behaviour of a point and a plane solver. J. Comput. Phys. 2005, 207, 309–353. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).