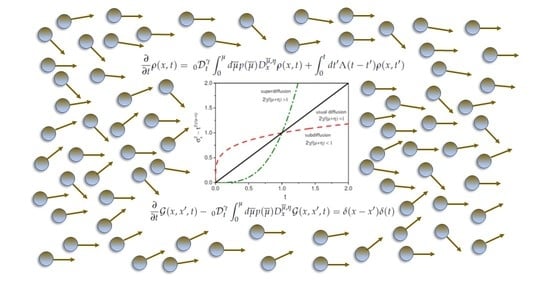
A Generalized Diffusion Equation: Solutions and Anomalous Diffusion
Abstract
1. Introduction
2. Fractional Dynamics and Diffusion
3. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Meerschaert, M.M.; Sikorskii, A. Stochastic Models for Fractional Calculus; de Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Magin, R. Fractional calculus in bioengineering, part 1. Crit. Rev. Biomed. Eng. 2004, 32, 1–104. [Google Scholar] [CrossRef] [PubMed]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists; World Scientific: Singapore, 2011. [Google Scholar]
- Evangelista, L.R.; Lenzi, E.K. Fractional Diffusion Equations and Anomalous Diffusion; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Kuntz, M.; Lavallée, P. Experimental evidence and theoretical analysis of anomalous diffusion during water infiltration in porous building materials. J. Phys. D Appl. Phys. 2001, 34, 2547. [Google Scholar] [CrossRef]
- Rosseto, M.P.; Evangelista, L.R.; Lenzi, E.K.; Zola, R.S.; Ribeiro de Almeida, R.R. Frequency-Dependent Dielectric Permittivity in Poisson–Nernst–Planck Model. J. Phys. Chem. B 2022, 126, 6446–6453. [Google Scholar] [CrossRef]
- Scher, H.; Montroll, E.W. Anomalous transit-time dispersion in amorphous solids. Phys. Rev. B 1975, 12, 2455. [Google Scholar] [CrossRef]
- Jeon, J.H.; Leijnse, N.; Oddershede, L.B.; Metzler, R. Anomalous diffusion and power-law relaxation of the time averaged mean squared displacement in worm-like micellar solutions. New J. Phys. 2013, 15, 045011. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Evangelista, L.; Zola, R.; Scarfone, A. Fractional Schrödinger equation for heterogeneous media and Lévy-like distributions. Chaos Solitons Fractals 2022, 163, 112564. [Google Scholar] [CrossRef]
- Magin, R.L.; Lenzi, E.K. Slices of the Anomalous Phase Cube Depict Regions of Sub-and Super-Diffusion in the Fractional Diffusion Equation. Mathematics 2021, 9, 1481. [Google Scholar] [CrossRef]
- Kenkre, V.; Montroll, E.; Shlesinger, M. Generalized master equations for continuous-time random walks. J. Stat. Phys. 1973, 9, 45–50. [Google Scholar] [CrossRef]
- Swenson, R.J. Derivation of generalized master equations. J. Math. Phys. 1962, 3, 1017–1022. [Google Scholar] [CrossRef]
- Cortes, E.; West, B.J.; Lindenberg, K. On the generalized Langevin equation: Classical and quantum mechanicala. J. Chem. Phys. 1985, 82, 2708–2717. [Google Scholar] [CrossRef]
- Klafter, J.; Sokolov, I.M. First Steps in Random Walks: From Tools to Applications; OUP Oxford: Oxford, UK, 2011. [Google Scholar]
- Giona, M.; Roman, H.E. Fractional diffusion equation on fractals: One-dimensional case and asymptotic behaviour. J. Phys. A Math. Gen. 1992, 25, 2093. [Google Scholar] [CrossRef]
- Hashan, M.; Jahan, L.N.; Imtiaz, S.; Hossain, M.E. Modelling of fluid flow through porous media using memory approach: A review. Math. Comput. Simul. 2020, 177, 643–673. [Google Scholar] [CrossRef]
- Razminia, K.; Razminia, A.; Baleanu, D. Fractal-fractional modelling of partially penetrating wells. Chaos Solitons Fractals 2019, 119, 135–142. [Google Scholar] [CrossRef]
- Raghavan, R.; Chen, C. The Theis solution for subdiffusive flow in rocks. Oil Gas Sci. Technol. Rev. D’Ifp Energies Nouv. 2019, 74, 6. [Google Scholar] [CrossRef]
- Zhokh, A.; Strizhak, P. Macroscale modeling the methanol anomalous transport in the porous pellet using the time-fractional diffusion and fractional Brownian motion: A model comparison. Commun. Nonlinear Sci. Numer. Simul. 2019, 79, 104922. [Google Scholar] [CrossRef]
- Feng, C.; Si, X.; Li, B.; Cao, L.; Zhu, J. An inverse problem to simulate the transport of chloride in concrete by time–space fractional diffusion model. Inverse Probl. Sci. Eng. 2021, 29, 2429–2445. [Google Scholar] [CrossRef]
- Han, M.; Zhou, C.; Silberschmidt, V.V.; Bi, Q. Multiscale heat conduction and fractal oxidation behaviors of needle-punched carbon/carbon composites. Sci. Eng. Compos. Mater. 2022, 29, 508–515. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Evangelista, L. Space–time fractional diffusion equations in d-dimensions. J. Math. Phys. 2021, 62, 083304. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Atangana, A.; Baleanu, D. New Fractional Derivatives with non-local and non-singular kernel. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Tateishi, A.A.; Ribeiro, H.V.; Lenzi, E.K. The role of fractional time-derivative operators on anomalous diffusion. Front. Phys. 2017, 5, 52. [Google Scholar] [CrossRef]
- Fernandez, A.; Baleanu, D. Classes of operators in fractional calculus: A case study. Math. Methods Appl. Sci. 2021, 44, 9143–9162. [Google Scholar] [CrossRef]
- Singh, H. Chebyshev spectral method for solving a class of local and nonlocal elliptic boundary value problems. Int. J. Nonlinear Sci. Numer. Simul. 2021. [Google Scholar] [CrossRef]
- Singh, H. Solving a class of local and nonlocal elliptic boundary value problems arising in heat transfer. Heat Transf. 2022, 51, 1524–1542. [Google Scholar] [CrossRef]
- Singh, H. An efficient computational method for non-linear fractional Lienard equation arising in oscillating circuits. In Methods of Mathematical Modelling; CRC Press: Boca Raton, FL, USA, 2019; pp. 39–50. [Google Scholar]
- Singh, H.; Srivastava, H. Numerical investigation of the fractional-order Liénard and Duffing equations arising in oscillating circuit theory. Front. Phys. 2020, 8, 120. [Google Scholar] [CrossRef]
- Scarfone, A.M.; Barbero, G.; Evangelista, L.R.; Lenzi, E.K. Anomalous Diffusion and Surface Effects on the Electric Response of Electrolytic Cells. Physchem 2022, 2, 163–178. [Google Scholar] [CrossRef]
- Barbero, G.; Evangelista, L.; Lenzi, E.K. Time-fractional approach to the electrochemical impedance: The Displacement current. J. Electroanal. Chem. 2022, 920, 116588. [Google Scholar] [CrossRef]
- Singh, H.; Srivastava, H.; Nieto, J.J. Handbook of Fractional Calculus for Engineering and Science; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Singh, H.; Kumar, D.; Baleanu, D. Methods of Mathematical Modelling: Fractional Differential Equations; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Singh, H.; Kumar, D.; Baleanu, D. Methods of Mathematical Modelling: Infectious Disease; Elsevier Science: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Gómez-Aguilar, J.; Atangana, A. Fractional Hunter-Saxton equation involving partial operators with bi-order in Riemann–Liouville and Liouville–Caputo sense. Eur. Phys. J. Plus 2017, 132, 100. [Google Scholar] [CrossRef]
- Evangelista, L.R.; Lenzi, E.K. An Introduction to Anomalous Diffusion and Relaxation; Springer Nature: Berlin, Germany, 2023. [Google Scholar]
- Ali, I.; Kalla, S. A generalized Hankel transform and its use for solving certain partial differential equations. Anziam J. 1999, 41, 105–117. [Google Scholar] [CrossRef]
- Garg, M.; Rao, A.; Kalla, S.L. On a generalized finite Hankel transform. Appl. Math. Comput. 2007, 190, 705–711. [Google Scholar] [CrossRef]
- Nakhi, Y.B.; Kalla, S.L. Some boundary value problems of temperature fields in oil strata. Appl. Math. Comput. 2003, 146, 105–119. [Google Scholar] [CrossRef]
- Xie, K.; Wang, Y.; Wang, K.; Cai, X. Application of Hankel transforms to boundary value problems of water flow due to a circular source. Appl. Math. Comput. 2010, 216, 1469–1477. [Google Scholar] [CrossRef]
- O’Shaughnessy, B.; Procaccia, I. Diffusion on fractals. Phys. Rev. A 1985, 32, 3073–3083. [Google Scholar] [CrossRef]
- O’Shaughnessy, B.; Procaccia, I. Analytical Solutions for Diffusion on Fractal Objects. Phys. Rev. Lett. 1985, 54, 455–458. [Google Scholar] [CrossRef]
- Richardson, L.F. Atmospheric diffusion shown on a distance-neighbour graph. Proc. Math. Phys. Eng. Sci. 1926, 110, 709–737. [Google Scholar]
- Boffetta, G.; Sokolov, I.M. Relative Dispersion in Fully Developed Turbulence: The Richardson’s Law and Intermittency Corrections. Phys. Rev. Lett. 2002, 88, 094501. [Google Scholar] [CrossRef]
- Ben Avraham, D.; Havlin, S. Diffusion and Reactions in Fractals and Disordered Systems; CUP: Cambridge, UK, 2000. [Google Scholar]
- Su, N.; Sander, G.; Liu, F.; Anh, V.; Barry, D. Similarity solutions for solute transport in fractal porous media using a time- and scale-dependent dispersivity. App. Math. Model. 2005, 29, 852–870. [Google Scholar] [CrossRef]
- He, J.H. Fractal calculus and its geometrical explanation. Results Phys. 2018, 10, 272–276. [Google Scholar] [CrossRef]
- Cai, W.; Chen, W.; Xu, W. The fractal derivative wave equation: Application to clinical amplitude/velocity reconstruction imaging. J. Acoust. Soc. Am. 2018, 143, 1559–1566. [Google Scholar] [CrossRef]
- Chen, W.; Liang, Y. New methodologies in fractional and fractal derivatives modeling. Chaos Solitons Fractals 2017, 102, 72–77. [Google Scholar] [CrossRef]
- Liang, Y.; Chen, W.; Cai, W. Hausdorff Calculus: Applications to Fractal Systems; Walter de Gruyter GmbH & Co KG: Berlin, Germany, 2019; Volume 6. [Google Scholar]
- Evans, M.R.; Majumdar, S.N. Diffusion with stochastic resetting. Phys. Rev. Lett. 2011, 106, 160601. [Google Scholar] [CrossRef] [PubMed]
- Lenzi, M.K.; Lenzi, E.K.; Guilherme, L.; Evangelista, L.R.; Ribeiro, H.V. Transient anomalous diffusion in heterogeneous media with stochastic resetting. Phys. A Stat. Mech. Appl. 2022, 588, 126560. [Google Scholar] [CrossRef]
- Wyld, H.W.; Powell, G. Mathematical Methods for Physics; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Mathai, A.M.; Saxena, R.K.; Haubold, H.J. The H-Function: Theory and Applications; Springer Science & Business Media: Berlin, Germany, 2009. [Google Scholar]
- Lenzi, E.K.; Evangelista, L.; Lenzi, M.K.; Ribeiro, H.V.; de Oliveira, E.C. Solutions for a non-Markovian diffusion equation. Phys. Lett. A 2010, 374, 4193–4198. [Google Scholar] [CrossRef]
- Jiang, X.; Xu, M. The time fractional heat conduction equation in the general orthogonal curvilinear coordinate and the cylindrical coordinate systems. Phys. A Stat. Mech. Appl. 2010, 389, 3368–3374. [Google Scholar] [CrossRef]
- Evans, M.R.; Majumdar, S.N.; Schehr, G. Stochastic resetting and applications. J. Phys. A 2020, 53, 193001. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lenzi, E.K.; Somer, A.; Zola, R.S.; da Silva, L.R.; Lenzi, M.K. A Generalized Diffusion Equation: Solutions and Anomalous Diffusion. Fluids 2023, 8, 34. https://doi.org/10.3390/fluids8020034
Lenzi EK, Somer A, Zola RS, da Silva LR, Lenzi MK. A Generalized Diffusion Equation: Solutions and Anomalous Diffusion. Fluids. 2023; 8(2):34. https://doi.org/10.3390/fluids8020034
Chicago/Turabian StyleLenzi, Ervin K., Aloisi Somer, Rafael S. Zola, Luciano R. da Silva, and Marcelo K. Lenzi. 2023. "A Generalized Diffusion Equation: Solutions and Anomalous Diffusion" Fluids 8, no. 2: 34. https://doi.org/10.3390/fluids8020034
APA StyleLenzi, E. K., Somer, A., Zola, R. S., da Silva, L. R., & Lenzi, M. K. (2023). A Generalized Diffusion Equation: Solutions and Anomalous Diffusion. Fluids, 8(2), 34. https://doi.org/10.3390/fluids8020034