Enhancement of an Air-Cooled Battery Thermal Management System Using Liquid Cooling with CuO and Al2O3 Nanofluids under Steady-State and Transient Conditions
Abstract
:1. Introduction
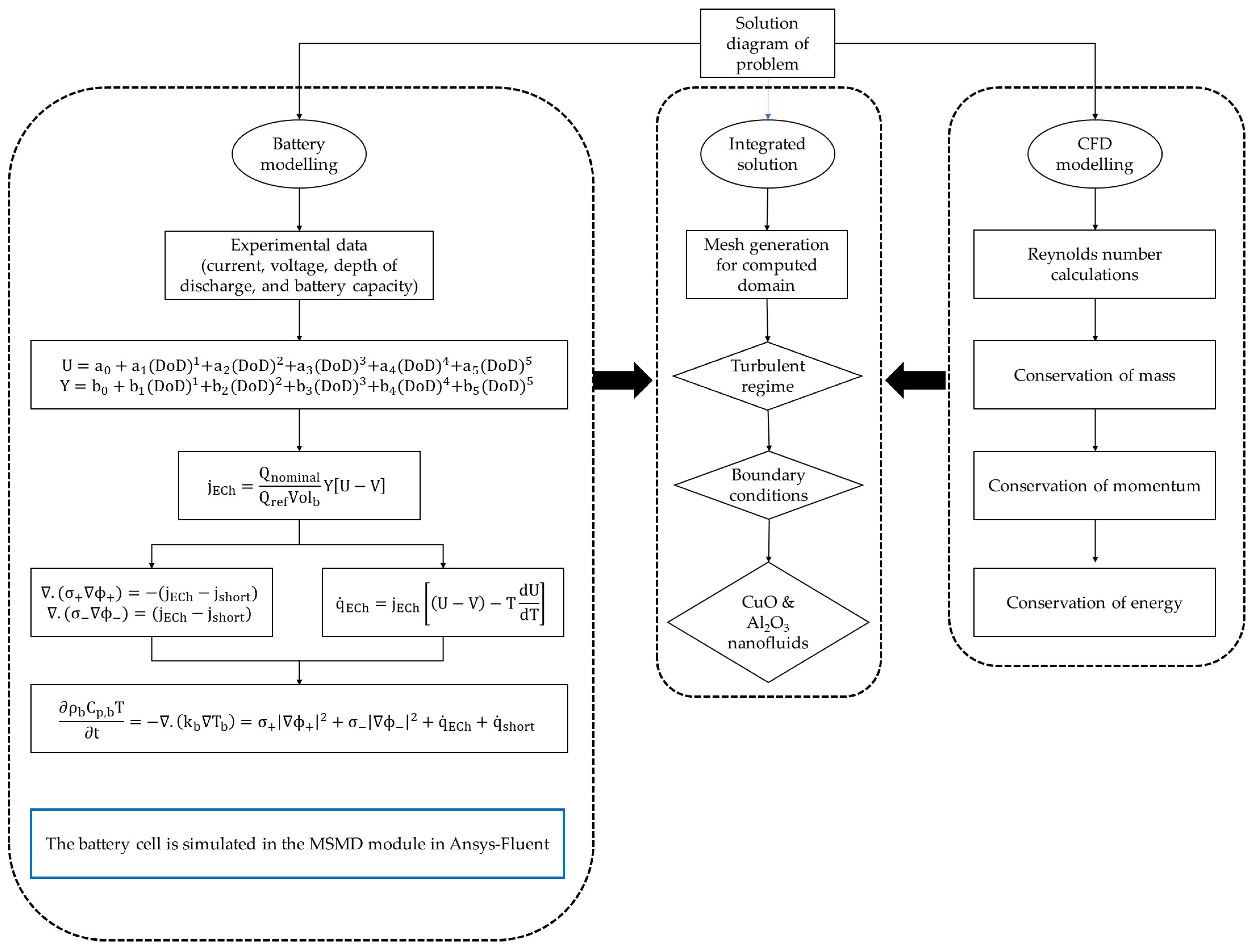
2. Model and Methodology
2.1. Battery Thermal Model Analysis
2.2. Battery Thermal and Electrical Field Models
2.3. High Performance of the EV Model
2.4. Liquid Cooled Model
- Energy equation:
2.5. Thermophysical Properties of Nanofluid
2.6. Data Reduction
3. Numerical Analysis
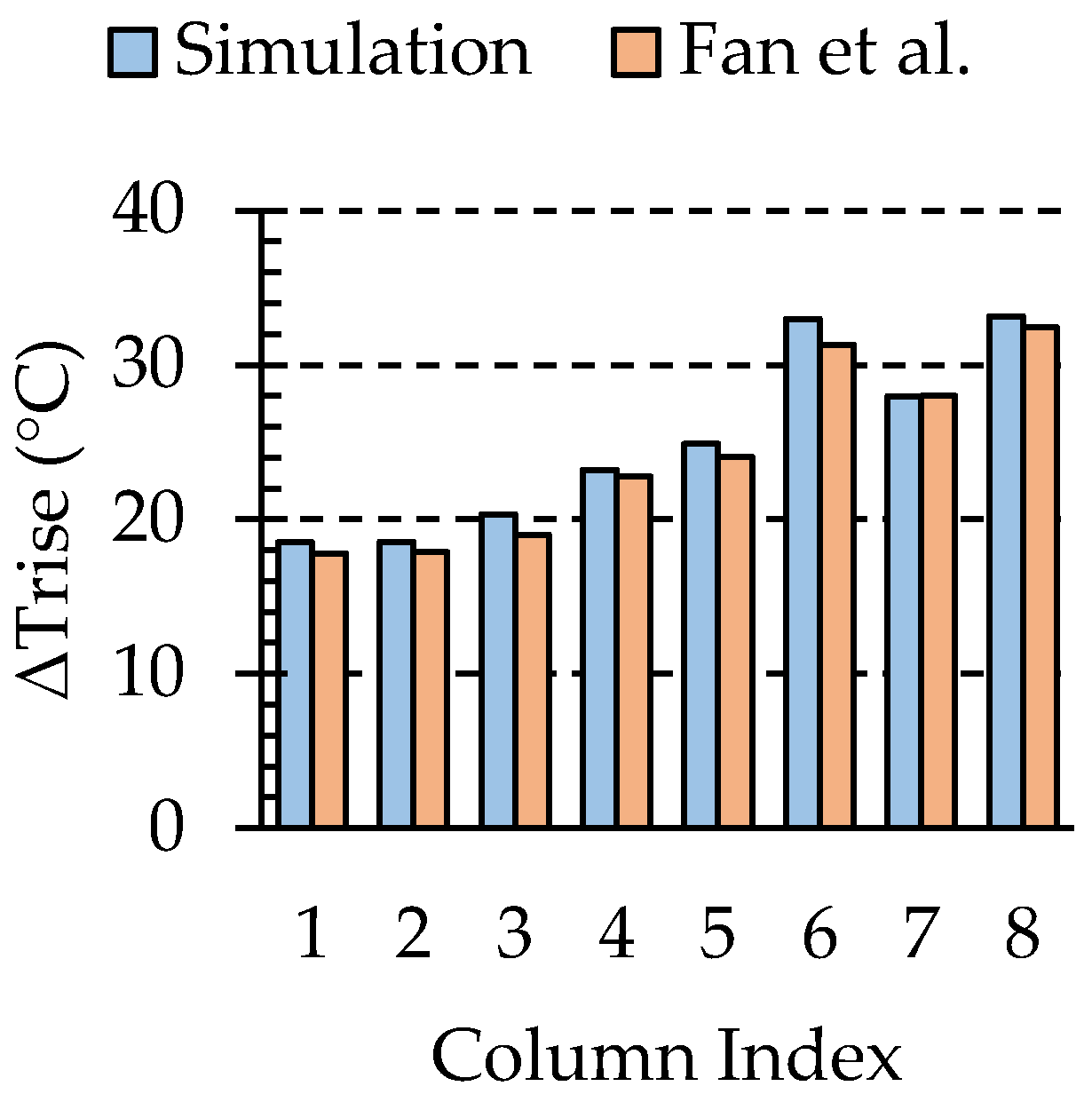
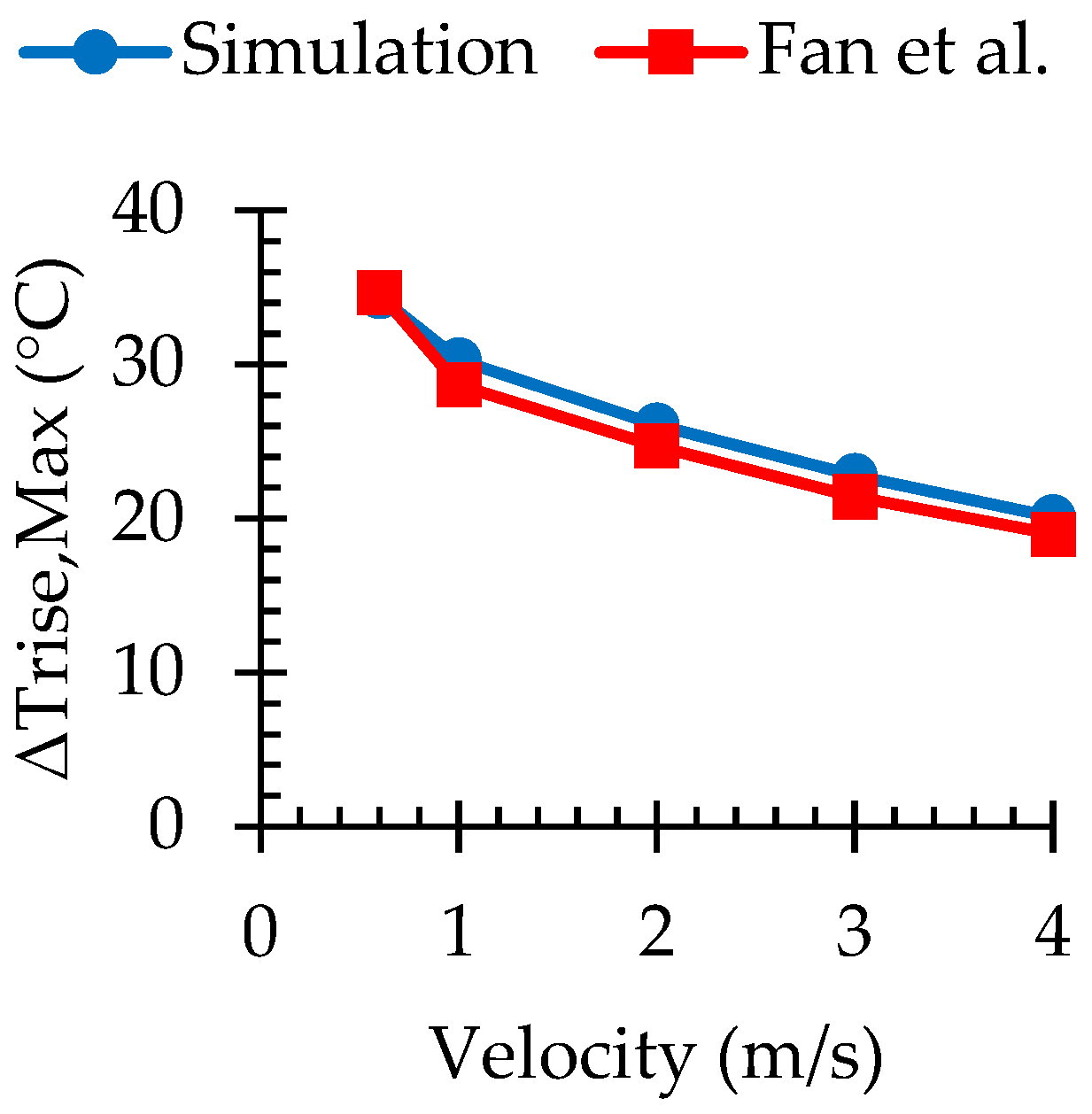
3.1. Numerical Validation
3.2. Grid Independence
4. Results and Discussion
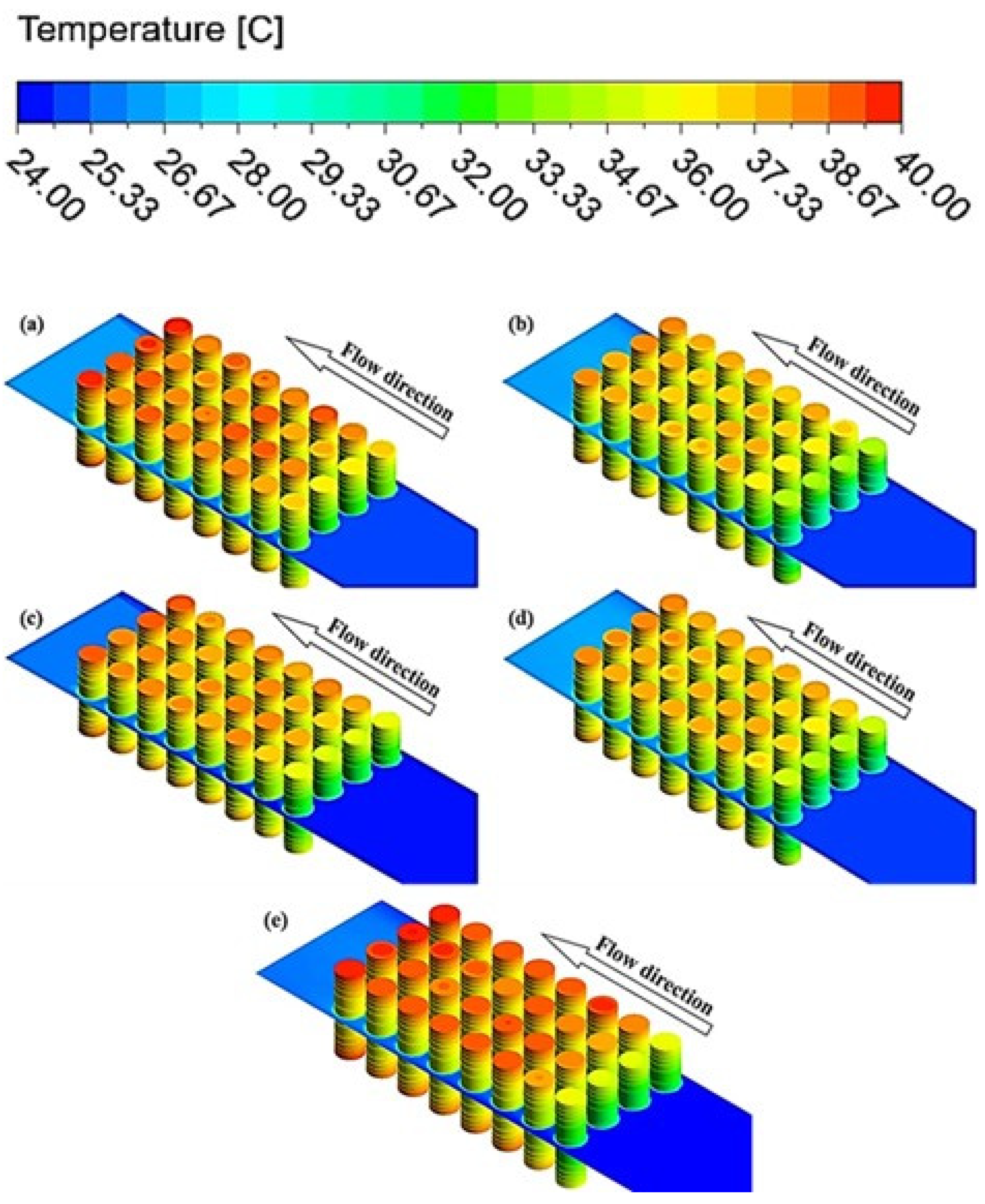
4.1. Effects of Nanoparticle Concentration on Thermal Characteristics of the Batteries
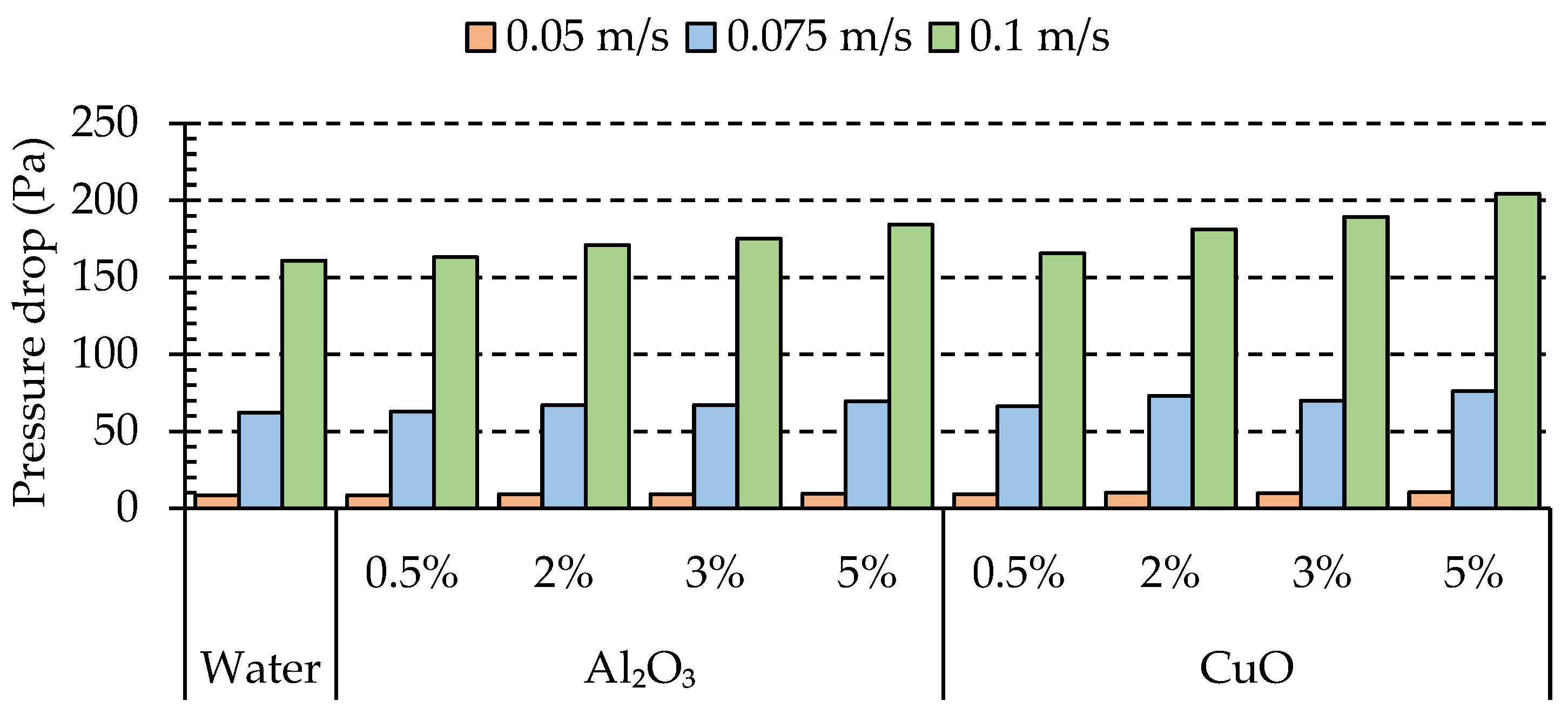
4.2. Effects of Nanoparticle Concentration on Pressure Drop
4.3. Effect of Nanoparticle Material
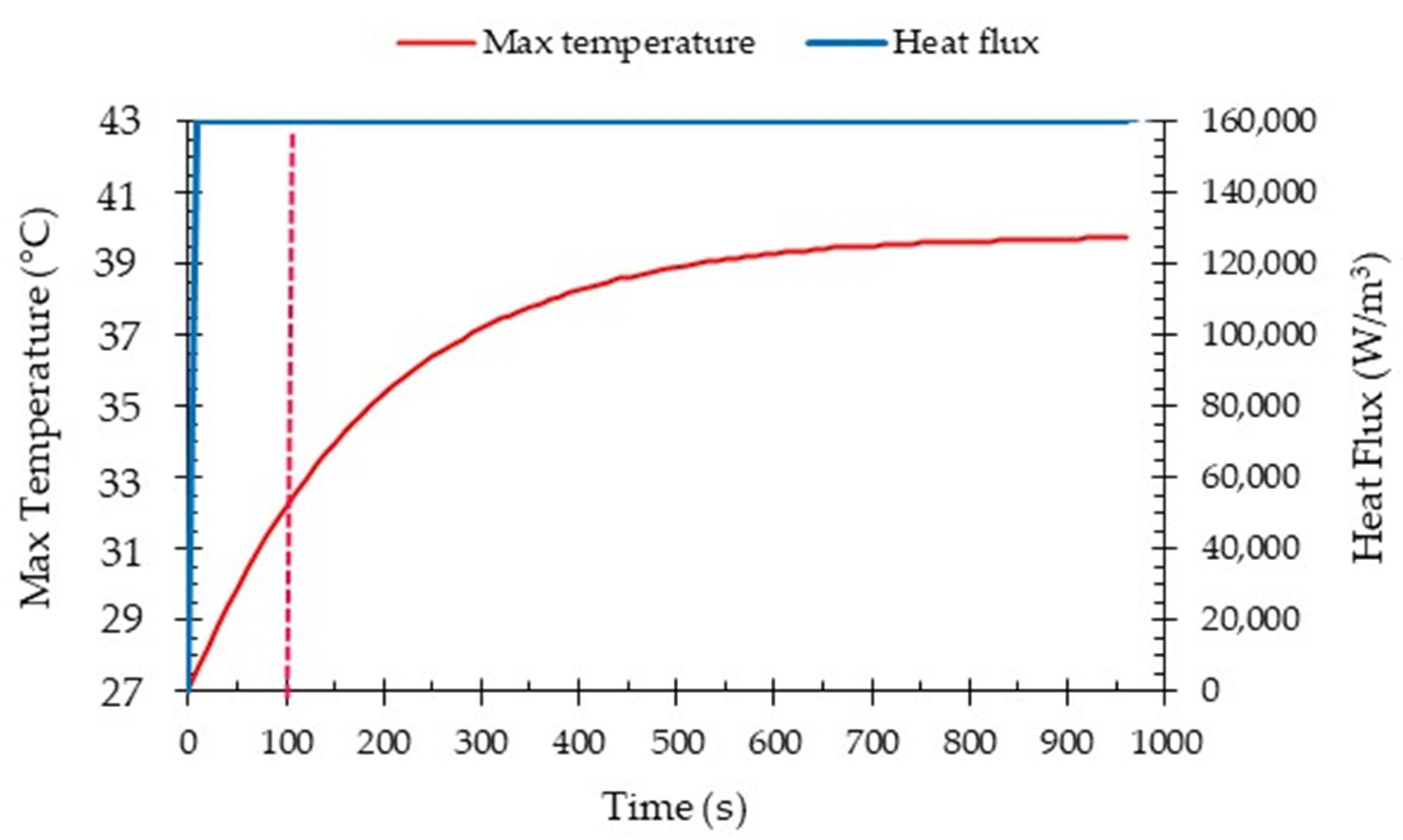
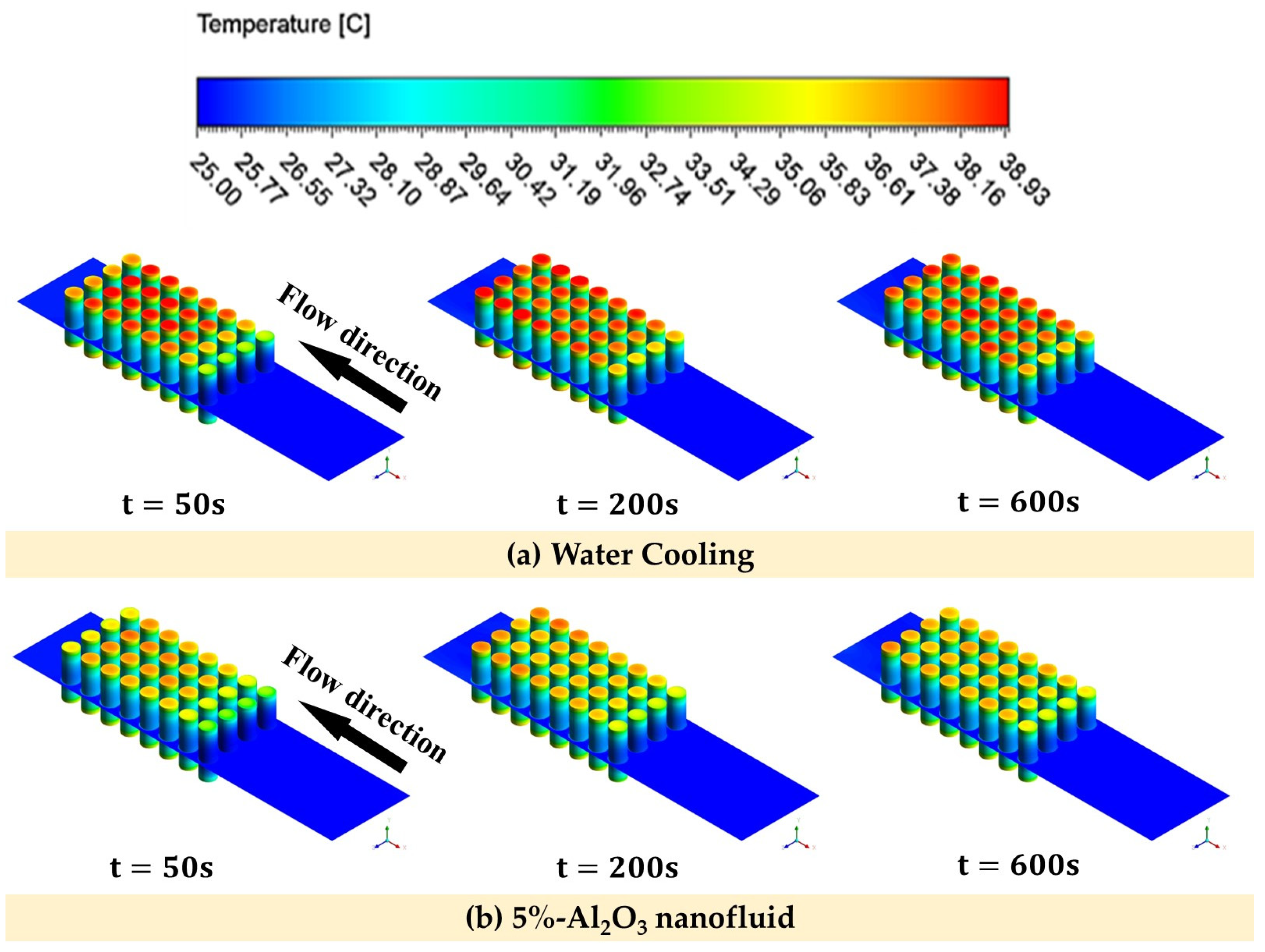
4.4. Transient Analysis
5. Conclusions
- Our results revealed that the utilization of nanofluids results in higher vortex development and enhances heat transfer capabilities of the fluid. Through a comprehensive analysis, we found that Al2O3 exhibited superior heat transfer performance compared to CuO.
- In the case of alumina, we observed that increasing the volume fraction led to improved performance. Similarly, for copper oxide, the performance showed an improvement compared to the base fluid. However, it is worth noting that alumina outperformed CuO, with an average enhancement of 4.37%.
- Due to the possibility of nanoparticle clustering, we found that the optimum performance was achieved at a volume fraction of 5% for Al2O3. This indicates that lower volume fractions can exhibit the opposite effect, reducing the impact on the heat transfer.
- Increasing the velocity of the fluid led to enhanced turbulence, which in turn improved the heat transfer performance. However, this improvement came at the expense of a higher pressure drop.
- During the transient analysis, it was observed that the utilization of 5% Al2O3 and CuO nanofluids resulted in a reduction in the temperature of the batteries. Specifically, the Al2O3 nanofluid exhibited a temperature reduction of 7.89% compared to the base fluid, and the CuO nanofluid showed a reduction of 4.73%.
- In the high-performance mode, the temperature of the batteries was effectively maintained within a safe range through the utilization of liquid cooling. Furthermore, even after operating under the highest power requirement for 600 s, the temperature of the batteries remained within the designated safe range. This demonstrates the effectiveness of the liquid cooling system in managing and controlling the temperature of the batteries even during high demand operations.
- To ensure the batteries’ temperature remained within a safe range during moderate operation mode (2C discharge rate), the maximum inlet coolant velocity considered was set at 0.1 m/s. However, for the high-performance operation mode (5C discharge rate), which depends on the specific conditions, it is necessary to increase the inlet coolant velocity to 0.3 m/s. This adjustment is aimed at achieving improved temperature uniformity and ensuring a safe temperature range.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abdallah, S.R.; Elsemary, I.M.; Altohamy, A.A.; Abdelrahman, M.; Attia, A.A.; Abdellatif, O.E. Experimental investigation on the effect of using nano fluid (Al2O3-Water) on the performance of PV/T system. Therm. Sci. Eng. Prog. 2018, 7, 1–7. [Google Scholar] [CrossRef]
- Soleymani, P.; Saedodin, S.; Rostamian, S.H.; Karimi, N. Experimental investigation of a hybridized flat-plate solar collector/gas burner for low-carbon production of hot water–Analysis of energy, exergy, and GHG emissions. Sustain. Energy Technol. Assess. 2023, 55, 102918. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). World Energy Outlook. Available online: https://www.iea.org/reports/world-energy-outlook-2010 (accessed on 5 May 2022).
- Panchal, S.; Dincer, I.; Agelin-Chaab, M.; Fowler, M.; Fraser, R. Uneven temperature and voltage distributions due to rapid discharge rates and different boundary conditions for series-connected LiFePO4 batteries. Int. Commun. Heat Mass Transf. 2017, 81, 210–217. [Google Scholar] [CrossRef]
- Tran, M.; Banister, D.; Bishop, J.D.; McCulloch, M.D. Realizing the electric-vehicle revolution. Nat. Clim. Change 2012, 2, 328–333. [Google Scholar] [CrossRef]
- Ouyang, D.; He, Y.; Chen, M.; Liu, J.; Wang, J. Experimental study on the thermal behaviors of lithium-ion batteries under discharge and overcharge conditions. J. Therm. Anal. Calorim. 2018, 132, 65–75. [Google Scholar] [CrossRef]
- Wang, Q.; Ping, P.; Zhao, X.; Chu, G.; Sun, J.; Chen, C. Thermal runaway caused fire and explosion of lithium ion battery. J. Power Sources 2012, 208, 210–224. [Google Scholar] [CrossRef]
- Pesaran, A.; Vlahinos, A.; Stuart, T. Cooling and Preheating of Batteries in Hybrid Electric Vehicles. In Proceedings of the 6th ASME-JSME Thermal Engineering Joint Conference, Kohala Coast, HI, USA, 16–20 March 2003; Citeseer: State College, PA, USA, 2003; pp. 1–7. [Google Scholar]
- Saeed, A.; Karimi, N.; Paul, M.C. Analysis of the unsteady thermal response of a Li-ion battery pack to dynamic loads. Energy 2021, 231, 120947. [Google Scholar] [CrossRef]
- Wu, X.; Wang, K.; Chang, Z.; Chen, Y.; Cao, S.; Lv, C.; Liu, H.; Wang, Y. Experimental and numerical study on hybrid battery thermal management system combining liquid cooling with phase change materials. Int. Commun. Heat Mass Transf. 2022, 139, 106480. [Google Scholar] [CrossRef]
- Verma, A.; Shashidhara, S.; Rakshit, D. A comparative study on battery thermal management using phase change material (PCM). Therm. Sci. Eng. Prog. 2019, 11, 74–83. [Google Scholar] [CrossRef]
- He, S.; Xiong, B.; Lei, H.; Dong, K.; Khan, S.A.; Zhao, J. Optimization of low-temperature preheating strategy for Li-ion batteries with supercooling phase change materials using response surface method. Int. Commun. Heat Mass Transf. 2023, 142, 106635. [Google Scholar] [CrossRef]
- Panchal, S.; Dincer, I.; Agelin-Chaab, M.; Fraser, R.; Fowler, M. Experimental temperature distributions in a prismatic lithium-ion battery at varying conditions. Int. Commun. Heat Mass Transf. 2016, 71, 35–43. [Google Scholar] [CrossRef]
- Pesaran, A.A. Battery thermal management in EV and HEVs: Issues and solutions. Battery Man 2001, 43, 34–49. [Google Scholar]
- Pesaran, A.A.; Vlahinos, A.; Burch, S.D. Thermal Performance of EV and HEV Battery Modules and Packs; National Renewable Energy Laboratory: Golden, CO, USA, 1997. Available online: https://www.nrel.gov/docs/legosti/old/23527.pdf (accessed on 5 May 2022).
- Pesaran, A.; Keyser, M.; Burch, S. An Approach for Designing Thermal Management Systems for Electric and Hybrid Vehicle Battery Packs; National Renewable Energy Laboratory: Golden, CO, USA, 1999. Available online: https://www.nrel.gov/docs/fy99osti/25992.pdf (accessed on 5 May 2022).
- Keyser, M.; Pesaran, A.; Oweis, S.; Chagnon, G.; Ashtiani, C. Thermal Evaluation and Performance of High-Power Lithium-Ion Cells; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2000. Available online: https://www.nrel.gov/docs/fy99osti/26616.pdf (accessed on 5 May 2022).
- Wu, W.; Wang, S.; Wu, W.; Chen, K.; Hong, S.; Lai, Y. A critical review of battery thermal performance and liquid based battery thermal management. Energy Convers. Manag. 2019, 182, 262–281. [Google Scholar] [CrossRef]
- Zhang, Q.; White, R.E. Capacity fade analysis of a lithium ion cell. J. Power Sources 2008, 179, 793–798. [Google Scholar] [CrossRef]
- Chen, H.-Q.; Wang, X.; He, L.; Chen, P.; Wan, Y.; Yang, L.; Jiang, S. Chinese energy and fuels research priorities and trend: A bibliometric analysis. Renew. Sustain. Energy Rev. 2016, 58, 966–975. [Google Scholar] [CrossRef]
- Shahid, S.; Agelin-Chaab, M. Development and analysis of a technique to improve air-cooling and temperature uniformity in a battery pack for cylindrical batteries. Therm. Sci. Eng. Prog. 2018, 5, 351–363. [Google Scholar] [CrossRef]
- Fan, Y.; Bao, Y.; Ling, C.; Chu, Y.; Tan, X.; Yang, S. Experimental study on the thermal management performance of air cooling for high energy density cylindrical lithium-ion batteries. Appl. Therm. Eng. 2019, 155, 96–109. [Google Scholar] [CrossRef]
- Liang, J.; Gan, Y.; Li, Y.; Tan, M.; Wang, J. Thermal and electrochemical performance of a serially connected battery module using a heat pipe-based thermal management system under different coolant temperatures. Energy 2019, 189, 116233. [Google Scholar] [CrossRef]
- Deng, Y.; Feng, C.; E, J.; Zhu, H.; Chen, J.; Wen, M.; Yin, H. Effects of different coolants and cooling strategies on the cooling performance of the power lithium ion battery system: A review. Appl. Therm. Eng. 2018, 142, 10–29. [Google Scholar] [CrossRef]
- Kalbasi, R. Introducing a novel heat sink comprising PCM and air-Adapted to electronic device thermal management. Int. J. Heat Mass Transf. 2021, 169, 120914. [Google Scholar] [CrossRef]
- Shahsavani, E.; Afrand, M.; Kalbasi, R. Using experimental data to estimate the heat transfer and pressure drop of non-Newtonian nanofluid flow through a circular tube: Applicable for use in heat exchangers. Appl. Therm. Eng. 2018, 129, 1573–1581. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab. (ANL): Argonne, IL, USA, 1995. Available online: https://www.osti.gov/servlets/purl/196525 (accessed on 5 May 2022).
- Islam, M.R.; Shabani, B.; Rosengarten, G.; Andrews, J. The potential of using nanofluids in PEM fuel cell cooling systems: A review. Renew. Sustain. Energy Rev. 2015, 48, 523–539. [Google Scholar] [CrossRef]
- Moghadasi, R.; Rostami, A.; Hemmati-Sarapardeh, A. Application of nanofluids for treating fines migration during hydraulic fracturing: Experimental study and mechanistic understanding. Adv. Geo-Energy Res. 2019, 3, 198–206. [Google Scholar] [CrossRef]
- Guthrie, D.G.; Torabi, M.; Karimi, N. Combined heat and mass transfer analyses in catalytic microreactors partially filled with porous material-The influences of nanofluid and different porous-fluid interface models. Int. J. Therm. Sci. 2019, 140, 96–113. [Google Scholar] [CrossRef]
- Alizadeh, R.; Abad, J.M.N.; Fattahi, A.; Mohebbi, M.R.; Doranehgard, M.H.; Li, L.K.B.; Alhajri, E.; Karimi, N. A machine learning approach to predicting the heat convection and thermodynamics of an external flow of hybrid nanofluid. J. Energy Resour. Technol. 2021, 143, 070908. [Google Scholar] [CrossRef]
- Singh, D.; Toutbort, J.; Chen, G. Heavy Vehicle Systems Optimization Merit Review and Peer Evaluation; Annual Report; Argonne National Laboratory: Lemont, IL, USA, 2006; Volume 23, pp. 405–411. [Google Scholar]
- Rashidi, S.; Karimi, N.; Sunden, B.; Kim, K.C.; Olabi, A.G.; Mahian, O. Progress and challenges on the thermal management of electrochemical energy conversion and storage technologies: Fuel cells, electrolysers, and supercapacitors. Prog. Energy Combust. Sci. 2022, 88, 100966. [Google Scholar] [CrossRef]
- Nguyen, Q.; Bahrami, D.; Kalbasi, R.; Bach, Q.V. Nanofluid flow through microchannel with a triangular corrugated wall: Heat transfer enhancement against entropy generation intensification. Math. Methods Appl. Sci. 2020. [Google Scholar] [CrossRef]
- Nadooshan, A.A.; Kalbasi, R.; Afrand, M. Perforated fins effect on the heat transfer rate from a circular tube by using wind tunnel: An experimental view. Heat Mass Transf. 2018, 54, 3047–3057. [Google Scholar] [CrossRef]
- Huo, Y.; Rao, Z. The numerical investigation of nanofluid based cylinder battery thermal management using lattice Boltzmann method. Int. J. Heat Mass Transf. 2015, 91, 374–384. [Google Scholar] [CrossRef]
- Sharma, D.K.; Prabhakar, A. A review on air cooled and air centric hybrid thermal management techniques for Li-ion battery packs in electric vehicles. J. Energy Storage 2021, 41, 102885. [Google Scholar] [CrossRef]
- Rahmati, A.R.; Akbari, O.A.; Marzban, A.; Toghraie, D.; Karimi, R.; Pourfattah, F. Simultaneous investigations the effects of non-Newtonian nanofluid flow in different volume fractions of solid nanoparticles with slip and no-slip boundary conditions. Therm. Sci. Eng. Prog. 2018, 5, 263–277. [Google Scholar] [CrossRef]
- Khan, S.A.; Eze, C.; Dong, K.; Shahid, A.R.; Patil, M.S.; Ahmad, S.; Hussain, I.; Zhao, J. Design of a new optimized U-shaped lightweight liquid-cooled battery thermal management system for electric vehicles: A machine learning approach. Int. Commun. Heat Mass Transf. 2022, 136, 106209. [Google Scholar] [CrossRef]
- Saeed, A.; Karimi, N.; Paul, M.C. Computational assessment of the thermal response of a Li-ion battery module to transient loads. J. Power Sources 2022, 552, 232217. [Google Scholar] [CrossRef]
- Wang, H.; He, F.; Ma, L. Experimental and modeling study of controller-based thermal management of battery modules under dynamic loads. Int. J. Heat Mass Transf. 2016, 103, 154–164. [Google Scholar] [CrossRef]
- Ling, Z.; Wang, F.; Fang, X.; Gao, X.; Zhang, Z. A hybrid thermal management system for lithium ion batteries combining phase change materials with forced-air cooling. Appl. Energy 2015, 148, 403–409. [Google Scholar] [CrossRef]
- Li, B.; Mao, Z.; Song, B.; Chen, P.; Wang, H.; Sunden, B.; Wang, Y.-F. Enhancement of phase change materials by nanoparticles to improve battery thermal management for autonomous underwater vehicles. Int. Commun. Heat Mass Transf. 2022, 137, 106301. [Google Scholar] [CrossRef]
- Chen, R.; Ge, X.; Zhong, Y.; Jiang, L.; Zhang, G.; Zhang, J.; Ke, X. Experimental study of phase change microcapsule-based liquid cooling for battery thermal management. Int. Commun. Heat Mass Transf. 2023, 146, 106912. [Google Scholar] [CrossRef]
- Yu, X.; Lu, Z.; Zhang, L.; Wei, L.; Cui, X.; Jin, L. Experimental study on transient thermal characteristics of stagger-arranged lithium-ion battery pack with air cooling strategy. Int. J. Heat Mass Transf. 2019, 143, 118576. [Google Scholar] [CrossRef]
- Sarah, M.; Jacob, T.; Jacopo, T. Tracking Report-November 2021; International Energy Agency (IEA): Paris, France, 2021; Available online: https://www.iea.org/reports/tracking-transport-2021 (accessed on 5 May 2022).
- Hssain, M.A.; Mir, R.; El Hammami, Y. Numerical Simulation of the cooling of heated electronic blocks in horizontal channel by mixed convection of nanofluids. J. Nanomater. 2020, 2020, 4187074. [Google Scholar] [CrossRef]
- Zhao, J.; Rao, Z.; Li, Y. Thermal performance of mini-channel liquid cooled cylinder based battery thermal management for cylindrical lithium-ion power battery. Energy Convers. Manag. 2015, 103, 157–165. [Google Scholar] [CrossRef]
- Zhou, H.; Zhou, F.; Xu, L.; Kong, J. Thermal performance of cylindrical Lithium-ion battery thermal management system based on air distribution pipe. Int. J. Heat Mass Transf. 2019, 131, 984–998. [Google Scholar] [CrossRef]
- Zhang, F.; Lin, A.; Wang, P.; Liu, P. Optimization design of a parallel air-cooled battery thermal management system with spoilers. Appl. Therm. Eng. 2021, 182, 116062. [Google Scholar] [CrossRef]
- Zhang, H.; Li, C.; Zhang, R.; Lin, Y.; Fang, H. Thermal analysis of a 6s4p Lithium-ion battery pack cooled by cold plates based on a multi-domain modeling framework. Appl. Therm. Eng. 2020, 173, 115216. [Google Scholar] [CrossRef]
- Tran, M.-K.; Mevawala, A.; Panchal, S.; Raahemifar, K.; Fowler, M.; Fraser, R. Effect of integrating the hysteresis component to the equivalent circuit model of Lithium-ion battery for dynamic and non-dynamic applications. J. Energy Storage 2020, 32, 101785. [Google Scholar] [CrossRef]
- Heenan, T.M.M.; Jnawali, A.; Kok, M.D.R.; Tranter, T.G.; Tan, C.; Dimitrijevic, A.; Jervis, R.; Brett, D.J.I.; Shearing, P.R. An advanced microstructural and electrochemical datasheet on 18650 Li-ion batteries with nickel-rich NMC811 cathodes and graphite-silicon anodes. J. Electrochem. Soc. 2020, 167, 140530. [Google Scholar] [CrossRef]
- Reis, G.D.; Strange, C.; Yadav, M.; Li, S. Lithium-ion battery data and where to find it. Energy AI 2021, 5, 100081. [Google Scholar] [CrossRef]
- Patil, M.S.; Seo, J.-H.; Lee, M.-Y. A novel dielectric fluid immersion cooling technology for Li-ion battery thermal management. Energy Convers. Manag. 2021, 229, 113715. [Google Scholar] [CrossRef]
- Kim, G.-H.; Smith, K.; Lee, K.-J.; Santhanagopalan, S.; Pesaran, A. Multi-domain modeling of lithium-ion batteries encompassing multi-physics in varied length scales. J. Electrochem. Soc. 2011, 158, A955. [Google Scholar] [CrossRef]
- Kim, J.; Oh, J.; Lee, H. Review on battery thermal management system for electric vehicles. Appl. Therm. Eng. 2019, 149, 192–212. [Google Scholar] [CrossRef]
- EVcompare. Available online: https://evcompare.io/cars/tesla/tesla_model_s_100d/ (accessed on 5 May 2022).
- Fluent, A. Ansys Fluent Theory Guide; Ansys Inc.: Canonsburg, PA, USA, 2011; Volume 15317, pp. 724–746. [Google Scholar]
- Bejan, A. Convection Heat Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Xu, Y.; Zhang, H.; Xu, X.; Wang, X. Numerical analysis and surrogate model optimization of air-cooled battery modules using double-layer heat spreading plates. Int. J. Heat Mass Transf. 2021, 176, 121380. [Google Scholar] [CrossRef]
- Panchal, S.; Khasow, R.; Dincer, I.; Agelin-Chaab, M.; Fraser, R.; Fowler, M. Numerical modeling and experimental investigation of a prismatic battery subjected to water cooling. Numer. Heat Transf. Part A Appl. 2017, 71, 626–637. [Google Scholar] [CrossRef]
- Panchal, S.; Khasow, R.; Dincer, I.; Agelin-Chaab, M.; Fraser, R.; Fowler, M. Thermal design and simulation of mini-channel cold plate for water cooled large sized prismatic lithium-ion battery. Appl. Therm. Eng. 2017, 122, 80–90. [Google Scholar] [CrossRef]
- Kalkan, O.; Celen, A.; Bakirci, K. Multi-objective optimization of a mini channeled cold plate for using thermal management of a Li-Ion battery. Energy 2022, 251, 123949. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, J.; Liu, F.; Liu, Y.; Wang, F.; Yang, N.; Lu, D.; Jia, Y. Performance optimisation of Tesla valve-type channel for cooling lithium-ion batteries. Appl. Therm. Eng. 2022, 212, 118583. [Google Scholar] [CrossRef]
- Wan, C. Battery space optimization to limit heat transfer in a lithium-ion battery using adaptive elephant herding optimization. Ionics 2020, 26, 4993–5009. [Google Scholar] [CrossRef]
- Soleymani, P.; Ma, Y.; Saffarifard, E.; Mohebbi, R.; Babaie; Karimi, N.; Saedodin, S. Numerical investigation on turbulent flow, heat transfer, and entropy generation of water-based magnetic nanofluid flow in a tube with hemisphere porous under a uniform magnetic field. Int. Commun. Heat Mass Transf. 2022, 137, 106308. [Google Scholar] [CrossRef]
- Pak, B.C.; Cho, Y.I. Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles. Exp. Heat Transf. Int. J. 1998, 11, 151–170. [Google Scholar] [CrossRef]
- Mehta, S.; Chauhan, K.P.; Kanagaraj, S. Modeling of thermal conductivity of nanofluids by modifying Maxwell’s equation using cell model approach. J. Nanopart. Res. 2011, 13, 2791–2798. [Google Scholar] [CrossRef]
- Brinkman, H.C. The viscosity of concentrated suspensions and solutions. J. Chem. Phys. 1952, 20, 571. [Google Scholar] [CrossRef]
- Xuan, Y.; Roetzel, W. Conceptions for heat transfer correlation of nanofluids. Int. J. Heat Mass Transf. 2000, 43, 3701–3707. [Google Scholar] [CrossRef]
- Kiani, M.; Omiddezyani, S.; Houshfar, E.; Miremadi, S.R.; Ashjaee, M.; Nejad, A.M. Lithium-ion battery thermal management system with Al2O3/AgO/CuO nanofluids and phase change material. Appl. Therm. Eng. 2020, 180, 115840. [Google Scholar] [CrossRef]
- Colangelo, G.; Favale, E.; Milanese, M.; De Risi, A.; Laforgia, D. Cooling of electronic devices: Nanofluids contribution. Appl. Therm. Eng. 2017, 127, 421–435. [Google Scholar] [CrossRef]

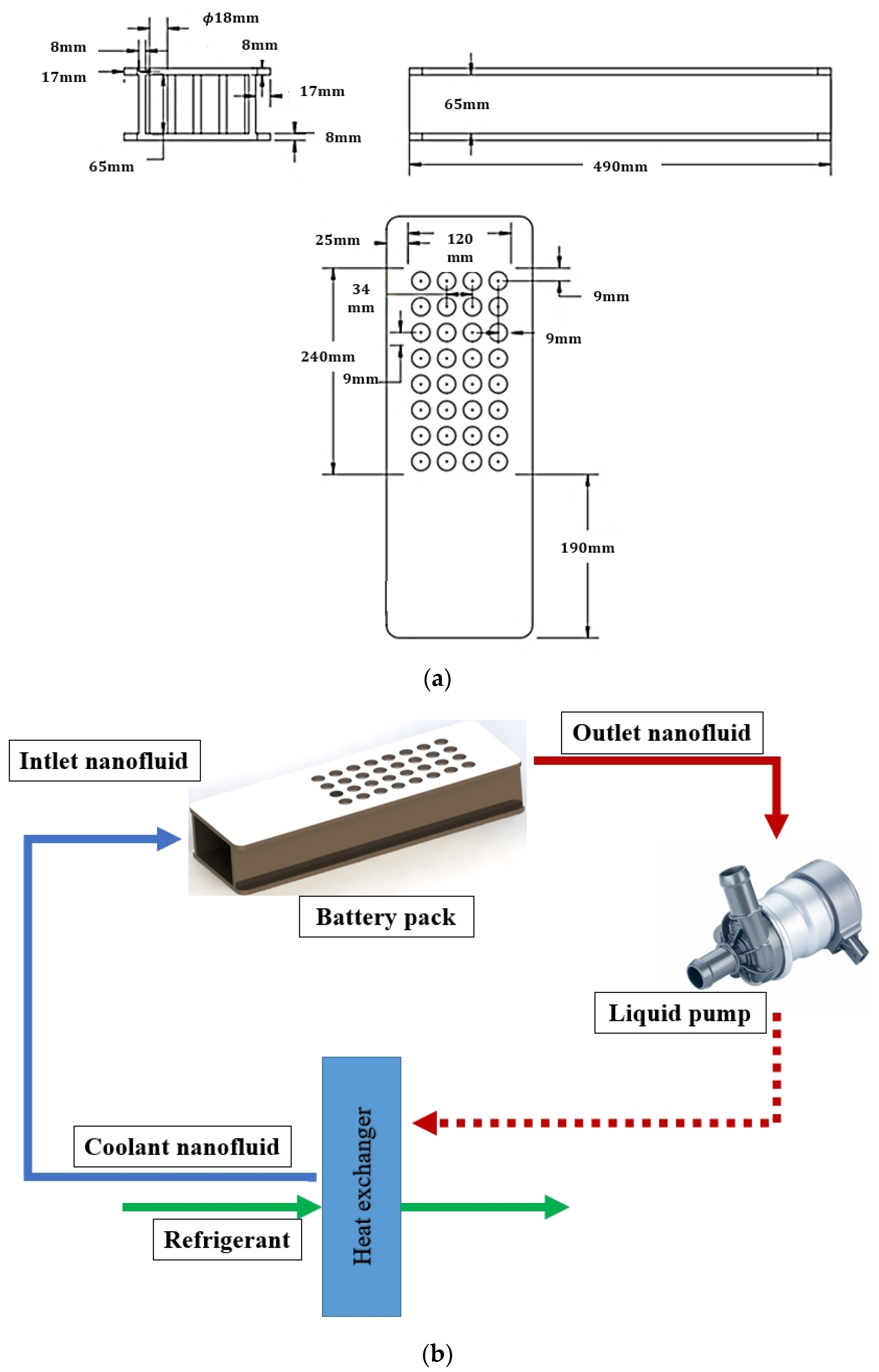
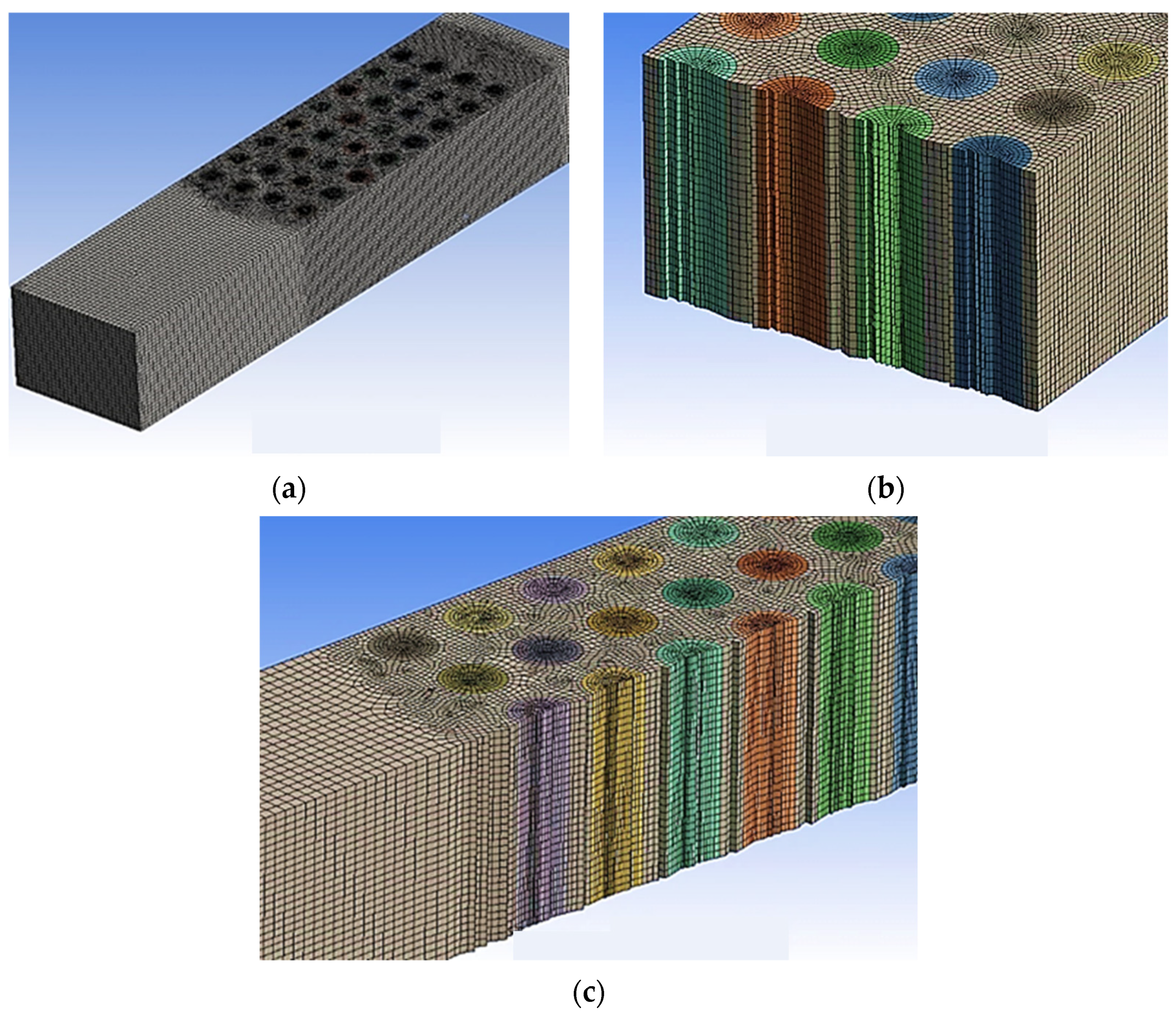
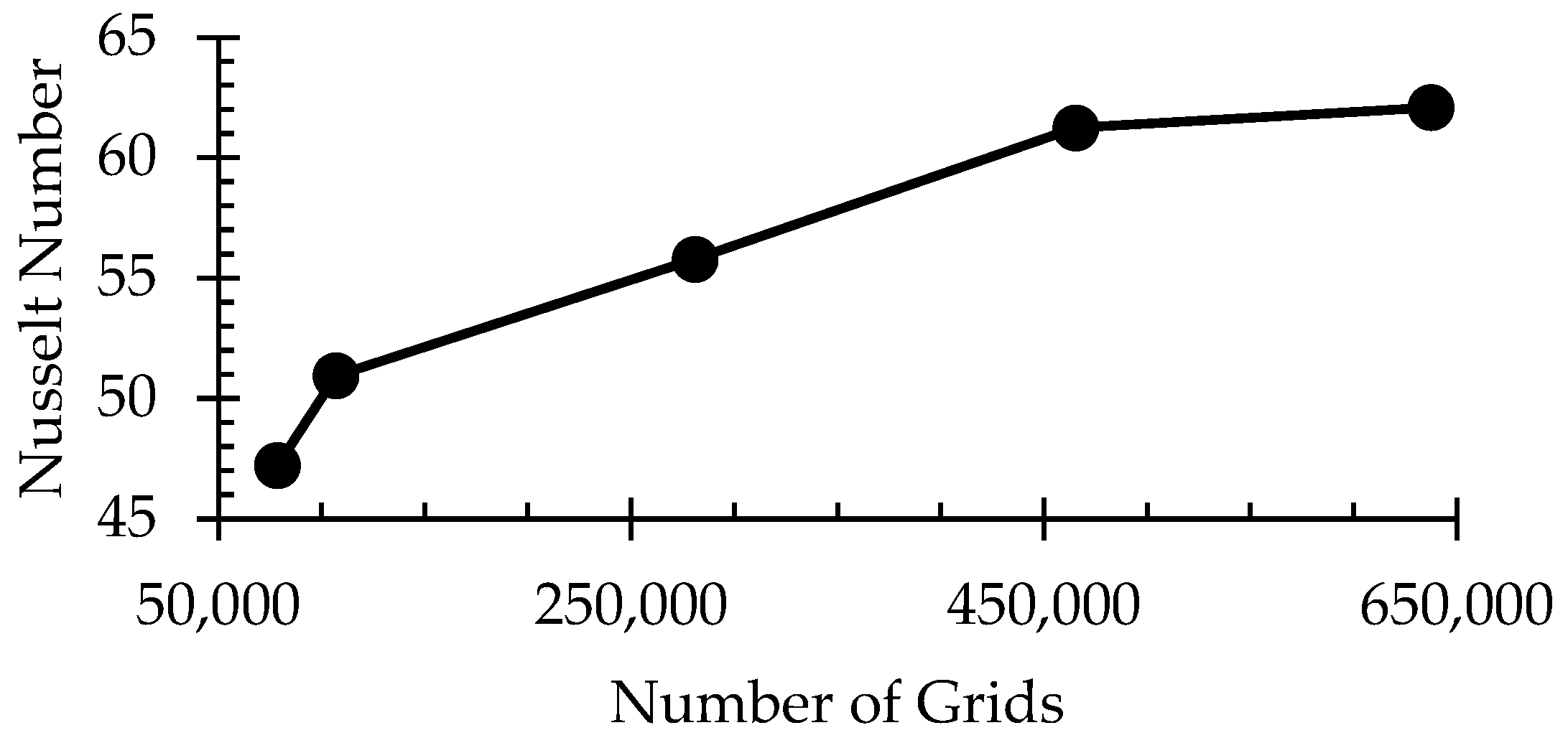

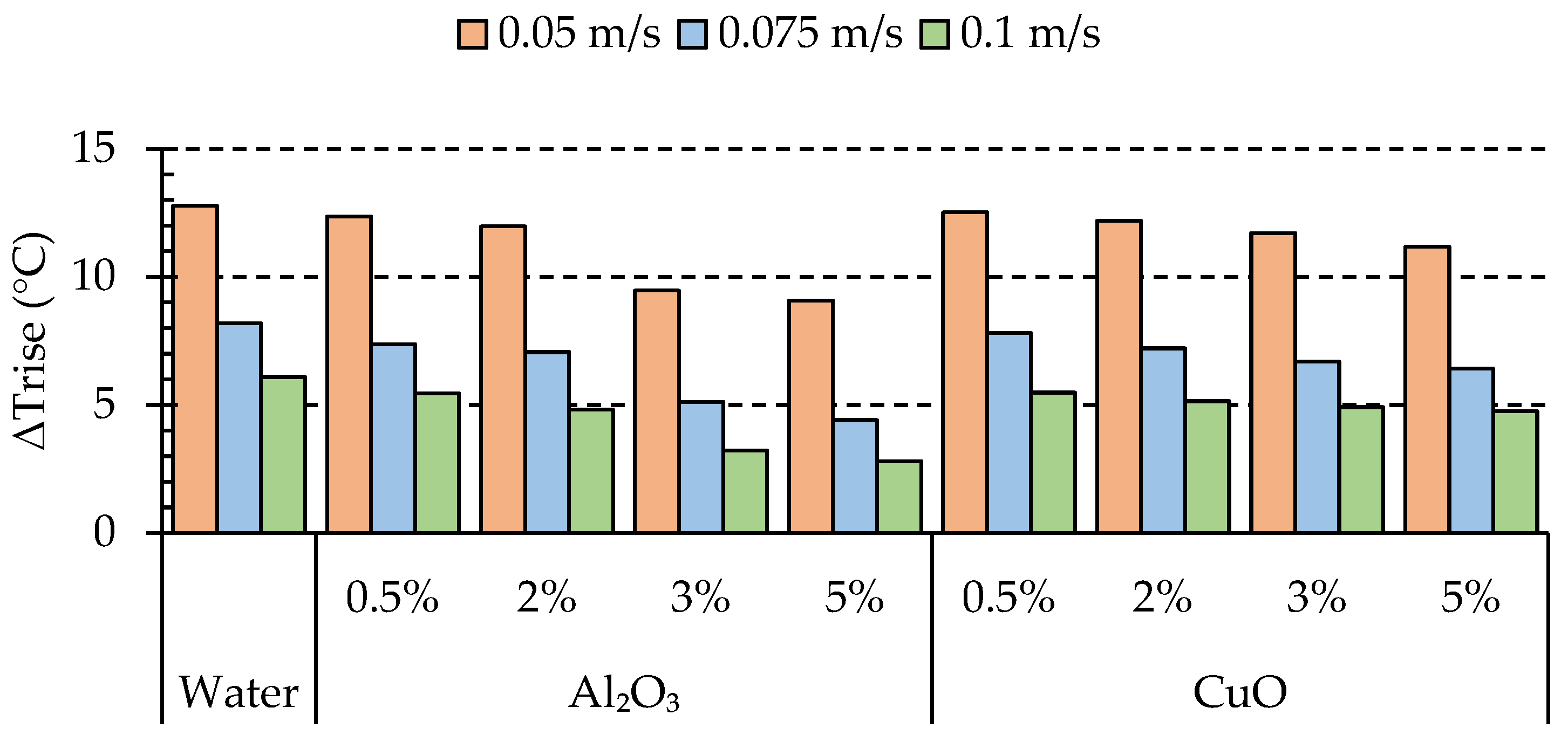
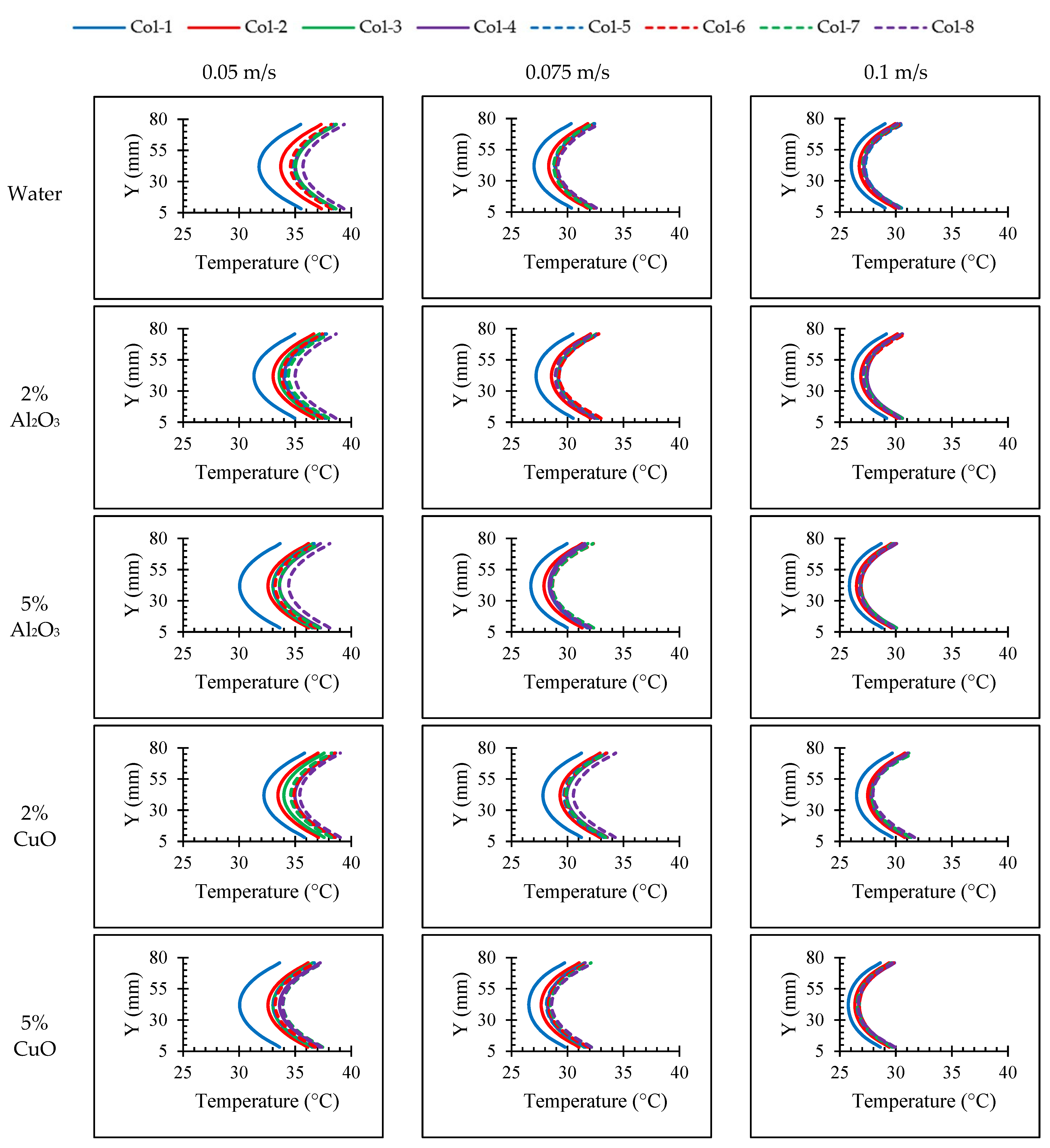
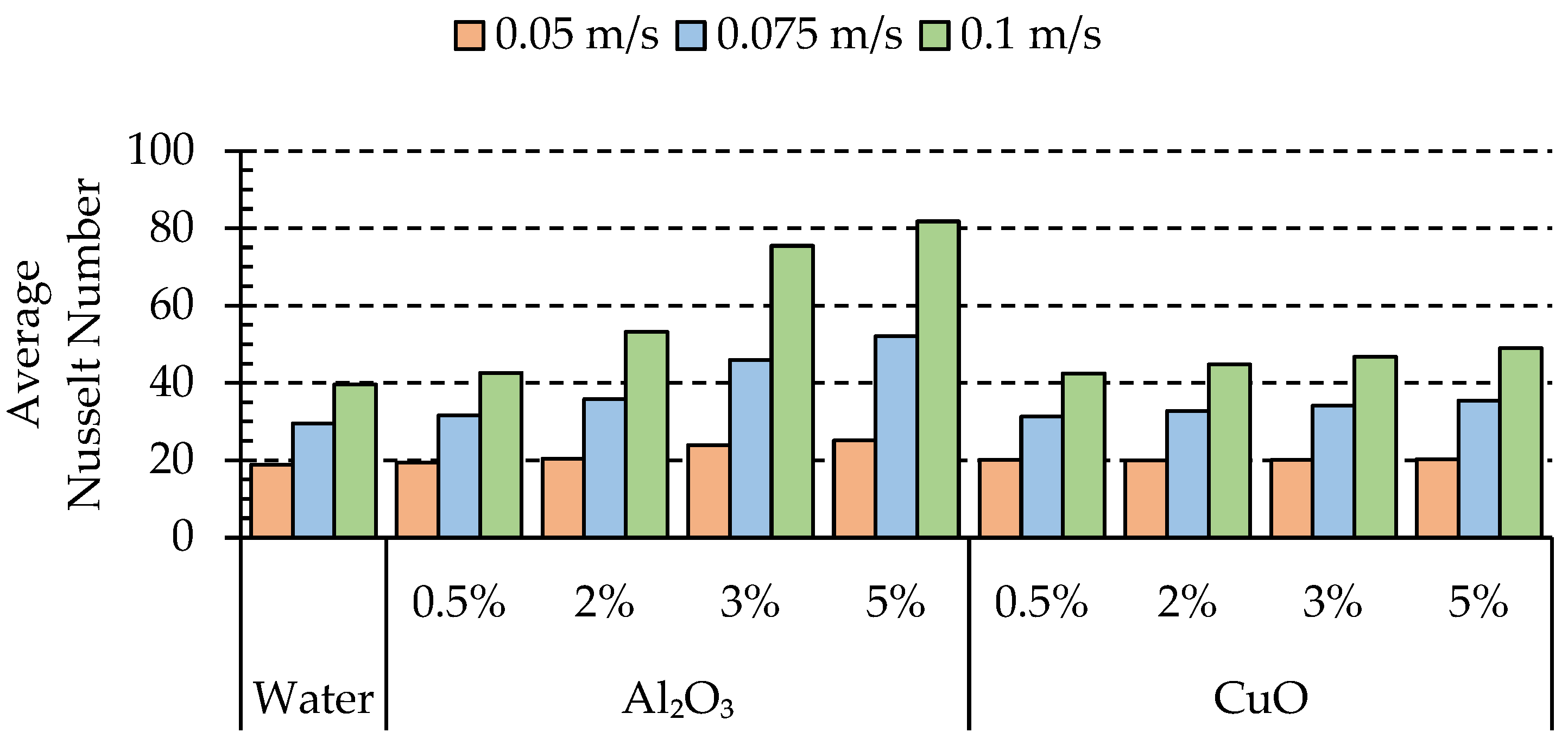



| Boundary Conditions | Value |
|---|---|
| The velocity of the liquid at the inlet in a 2C (corresponds to vehicle moderate operation) | 0.05, 0.075, 0.1 m/s |
| The velocity of the liquid at the inlet in high-performance mode | 0.1, 0.2, 0.3 m/s |
| Outlet condition | Pressure outlet |
| The initial temperature of nanofluid | 25 °C |
| Volumetric heat on batteries in 2C moderate operation | 48 kW/m3 |
| Volumetric heat on batteries in high-performance model | 160 kW/m3 |
| Other walls | No-slip condition |
| Battery Specifications | Type and Values |
|---|---|
| Model | LG INR 18,650 MJ1 |
| Chemical | LiCoMnO2 |
| Nominal voltage (V) | 3.635 |
| Nominal capacity (Ah) | 3.50 |
| Minimum capacity (Ah) | 3.40 |
| The nominal energy density (Wh/kg) | 260 |
| Maximum charge voltage (V) | 4.2 |
| Cut-off voltage (V) | 2.5 |
| Operating temperature during charge (°C) | 0–45 |
| Parameters | SI Unit | Water 25 °C [46] | ||
|---|---|---|---|---|
| Al2O3 [47] | CuO | |||
| Density (ρ) | kg/m3 | 997.1 | 3970 | 6450 |
| Dynamic viscosity (µ) | kg/ms | 0.0008905 | - | - |
| Specific heat (Cp) | J/kgK | 3970 | 765 | 561 |
| Thermal conductivity (K) | W/mK | 0.5948 | 40 | 20 |
| Nanofluid volume concentration | - | - | 0.5, 2, 3, 5% | 0.5, 2, 3, 5% |
| Constants | Cμ | C1ε | C2ε | σk | σε | σt |
|---|---|---|---|---|---|---|
| Values | 0.09 | 1.44 | 1.92 | 1.00 | 1.30 | 1.00 |
| Properties of Nanofluid | Correlations | Model |
|---|---|---|
| Effective density | Pak [68] | |
| Effective Thermal Conductivity | Maxwell [69] | |
| Effective Viscosity | Brinkman [70] | |
| Specific Heat Capacity | Xuan [71] |
| Nanofluid Concentrations | Al2O3 | CuO | ||||
|---|---|---|---|---|---|---|
| 0.05 m/s | 0.075 m/s | 0.1 m/s | 0.05 m/s | 0.075 m/s | 0.1 m/s | |
| 0.5% | 3.34 | 9.93 | 10.50 | 2.10 | 4.62 | 10.10 |
| 2% | 6.32 | 13.66 | 20.89 | 4.72 | 11.84 | 15.60 |
| 3% | 25.93 | 37.46 | 47.26 | 8.44 | 18.13 | 19.31 |
| 5% | 29.07 | 46.09 | 54.18 | 12.62 | 21.43 | 21.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soleymani, P.; Saffarifard, E.; Jahanpanah, J.; Babaie, M.; Nourian, A.; Mohebbi, R.; Aakcha, Z.; Ma, Y. Enhancement of an Air-Cooled Battery Thermal Management System Using Liquid Cooling with CuO and Al2O3 Nanofluids under Steady-State and Transient Conditions. Fluids 2023, 8, 261. https://doi.org/10.3390/fluids8100261
Soleymani P, Saffarifard E, Jahanpanah J, Babaie M, Nourian A, Mohebbi R, Aakcha Z, Ma Y. Enhancement of an Air-Cooled Battery Thermal Management System Using Liquid Cooling with CuO and Al2O3 Nanofluids under Steady-State and Transient Conditions. Fluids. 2023; 8(10):261. https://doi.org/10.3390/fluids8100261
Chicago/Turabian StyleSoleymani, Peyman, Ehsan Saffarifard, Jalal Jahanpanah, Meisam Babaie, Amir Nourian, Rasul Mohebbi, Zineb Aakcha, and Yuan Ma. 2023. "Enhancement of an Air-Cooled Battery Thermal Management System Using Liquid Cooling with CuO and Al2O3 Nanofluids under Steady-State and Transient Conditions" Fluids 8, no. 10: 261. https://doi.org/10.3390/fluids8100261
APA StyleSoleymani, P., Saffarifard, E., Jahanpanah, J., Babaie, M., Nourian, A., Mohebbi, R., Aakcha, Z., & Ma, Y. (2023). Enhancement of an Air-Cooled Battery Thermal Management System Using Liquid Cooling with CuO and Al2O3 Nanofluids under Steady-State and Transient Conditions. Fluids, 8(10), 261. https://doi.org/10.3390/fluids8100261








