Analysis of Particle-Resolved CFD Results for Dispersion in Packed Beds
Abstract
:1. Introduction
2. Methods
2.1. Packing Generation
2.2. CFD for Flow and Passive Transport
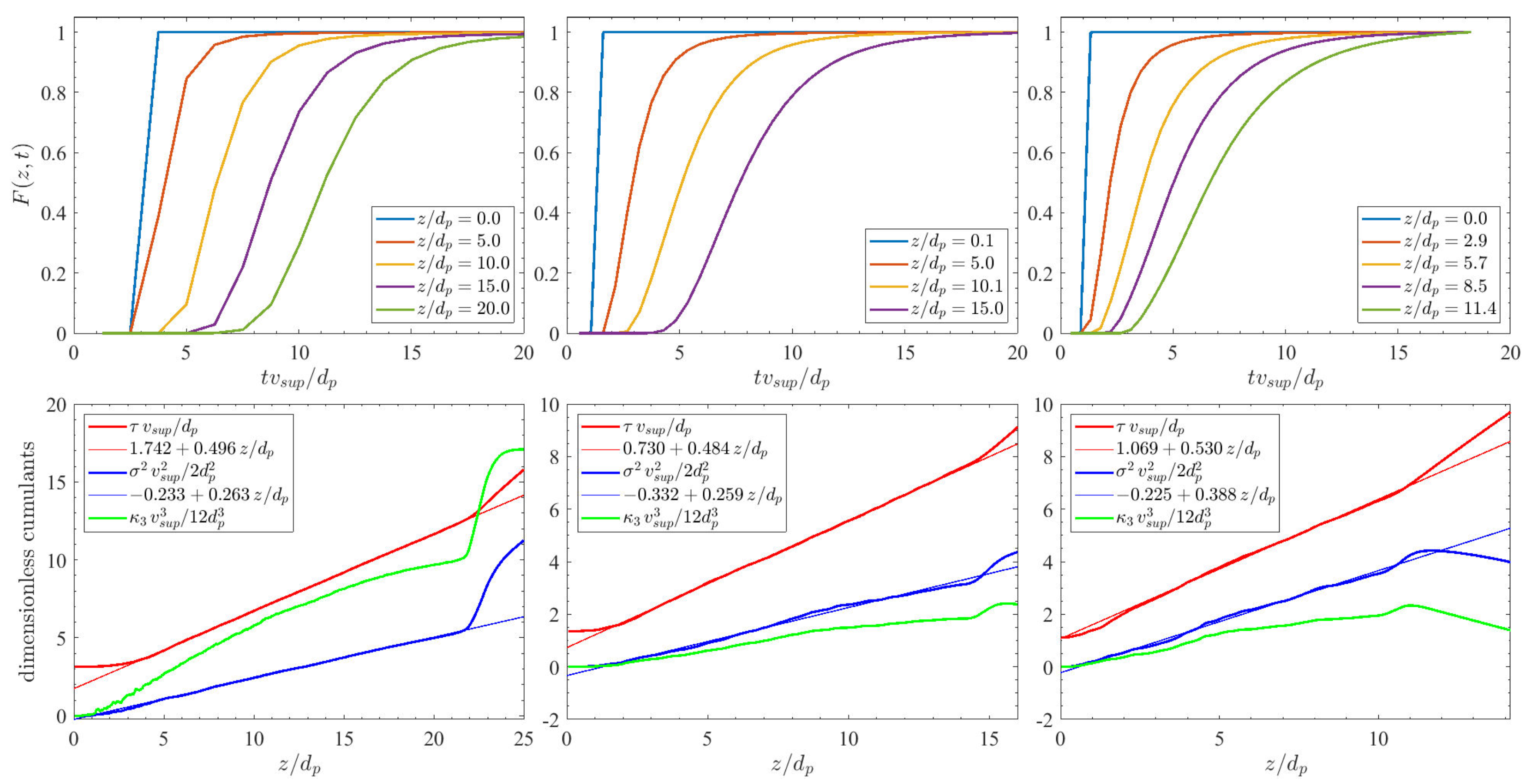
2.3. Analysis of Residence Time Distributions
2.4. Interpretation Models for Dispersion
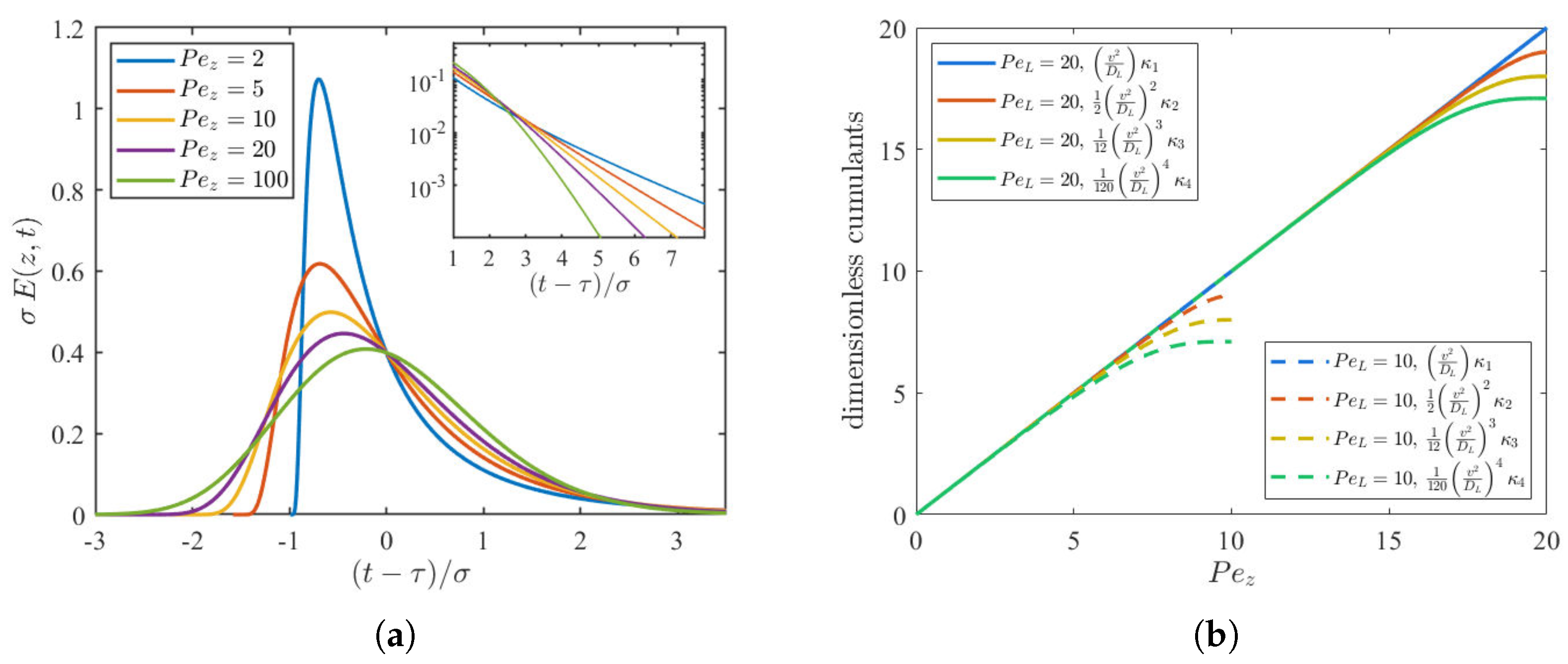
2.4.1. 1D Convection-Diffusion Model
2.4.2. 2D Convection-Diffusion Model
2.5. Post-Processing
3. Results
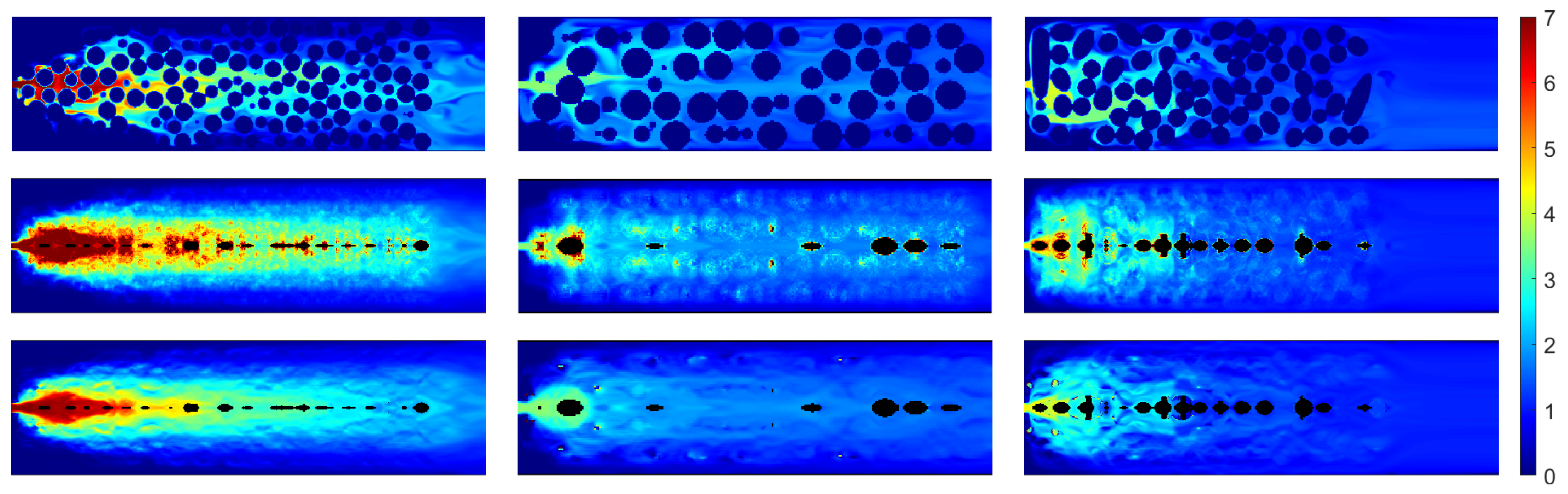
3.1. Porosity, Velocity and Concentration Profiles
3.2. Residence Time Distributions and Axial Dispersion
3.3. Transverse Dispersion
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Residence Time Distribution for 1D Convection-Diffusion
Appendix B. General Expression for Taylor Dispersion
References
- Atmakidis, T.; Kenig, E.E.Y. Numerical analysis of residence time distribution in packed bed reactors with irregular particle arrangements. Chem. Prod. Process Model. 2015, 10, 17–26. [Google Scholar] [CrossRef]
- Zeiser, T.; Lammers, P.; Klemm, E.; Li, Y.W.; Bernsdorf, J.; Brenner, G. CFD-calculation of flow, dispersion and reaction in a catalyst filled tube by the lattice Boltzmann method. Chem. Eng. Sci. 2001, 56, 1697–1704. [Google Scholar] [CrossRef]
- Augier, F.; Idoux, F.; Delenne, J.Y. Numerical simulations of transfer and transport properties inside packed beds of spherical particles. Chem. Eng. Sci. 2010, 65, 1055–1064. [Google Scholar] [CrossRef]
- Icardi, M.; Boccardo, G.; Marchisio, D.L.; Tosco, T.; Sethi, R. Pore-scale simulation of fluid flow and solute dispersion in three-dimensional porous media. Phys. Rev. E 2014, 90, 13032. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jourak, A.; Hellström, J.G.I.; Lundström, T.S.; Frishfelds, V. Numerical derivation of dispersion coefficients for flow through three-dimensional randomly packed beds of monodisperse spheres. AIChE J. 2014, 60, 749–761. [Google Scholar] [CrossRef]
- Yan, X.; Li, N. Simulation of solute dispersion in particle packs by the volume averaging method. Comput. Chem. Eng. 2017, 98, 154–160. [Google Scholar] [CrossRef]
- Schnitzlein, K. Modelling radial dispersion in terms of the local structure of packed beds. Chem. Eng. Sci. 2001, 56, 579–585. [Google Scholar] [CrossRef]
- Magnico, P. Hydrodynamic and transport properties of packed beds in small tube-to-sphere diameter ratio: Pore scale simulation using an Eulerian and a Lagrangian approach. Chem. Eng. Sci. 2003, 58, 5005–5024. [Google Scholar] [CrossRef]
- Acharya, R.C.; Valocchi, A.J.; Werth, C.J.; Willingham, T.W. Pore-scale simulation of dispersion and reaction along a transverse mixing zone in two-dimensional porous media. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef] [Green Version]
- Dixon, A.G.; Medeiros, N.J. Computational Fluid Dynamics Simulations of Gas-Phase Radial Dispersion in Fixed Beds with Wall Effects. Fluids 2017, 2, 56. [Google Scholar] [CrossRef]
- Das, S.; Deen, N.G.; Kuipers, J.A.M. A DNS study of flow and heat transfer through slender fixed-bed reactors randomly packed with spherical particles. Chem. Eng. Sci. 2017, 160, 1–19. [Google Scholar] [CrossRef]
- Yu, C.; Warrick, A.W.; Conklin, M.H. A moment method for analyzing breakthrough curves of step inputs. Water Resour. Res. 1999, 35, 3567–3572. [Google Scholar] [CrossRef]
- Kloss, C.; Goniva, C.; Hager, A.; Amberger, S.; Pirker, S. Models, algorithms and validation for opensource DEM and CFD–DEM. Prog. Comput. Fluid Dyn. Int. J. 2012, 12, 140–152. [Google Scholar] [CrossRef]
- Smilauer, V. Woo Documentation. 2016. Available online: https://woodem.org (accessed on 28 August 2018).
- Deen, N.; Kriebitzsch, S.; van der Hoef, M.; Kuipers, J. Direct numerical simulation of flow and heat transfer in dense fluid-particle systems. Chem. Eng. Sci. 2012, 81, 329–344. [Google Scholar] [CrossRef]
- Deen, N.; Peters, E.; Padding, J.; Kuipers, J. Review of direct numerical simulation of fluid-particle mass, momentum and heat transfer in dense gas-solid flows. Chem. Eng. Sci. 2014, 116, 710–724. [Google Scholar] [CrossRef]
- van Gelder, K.; Westerterp, K. Residence time distribution and hold-up in a cocurrent upflow packed bed reactor at elevated pressure. Chem. Eng. Technol. 1990, 13, 27–40. [Google Scholar] [CrossRef] [Green Version]
- Delgado, J. A critical review of dispersion in packed beds. Heat Mass Transf. 2006, 42, 279–310. [Google Scholar] [CrossRef]
- Koch, D.; Brady, J. Dispersion in fixed beds. J. Fluid Mech. 1985, 154, 399–427. [Google Scholar] [CrossRef]
- Panda, A.; Peters, E.; Baltussen, M.; Kuipers, J. Fully resolved scalar transport for high Prandtl number flows using adaptive mesh refinement. Chem. Eng. Sci. X 2019, 4, 100047. [Google Scholar] [CrossRef]
- Van Swaaij, W.P.M.; Charpentier, J.C.; Villermaux, J. Residence time distribution in the liquid phase of trickle flow in packed columns. Chem. Eng. Sci. 1969, 24, 1083–1095. [Google Scholar] [CrossRef]
- Otake, T.; Kunigita, E. Mixing characteristics of irrigated packed towers. Kagaku Kogaku 1958, 22, 144. [Google Scholar] [CrossRef] [Green Version]



| Reference | Domain Size and Shape | Methodology | Range |
|---|---|---|---|
| Atmakidis and Kenig [1] | Random packing of spheres in a cylindrical column with N from 1 to 7. | Evaluation of RTD with tracer and post-processing method. | from 14 to 78 |
| Zeiser et al. [2] | Random packing of spheres in a cylindrical column with N from 5 to 10. | Lattice Boltzmann method. | 4.3 and 5.2 |
| Augier et al. [3] | Random packing of spheres in a cylindrical column with N = 17. | Solving hydrodynamics and transport equations. | from 1 to 80 |
| Icardi et al. [4] | Periodic random packing of irregular and polydisperse objects. | CFD with high-order numerical schemes and advanced meshing techniques. | from 10 to 10 |
| Jourak et al. [5] | Periodic random and regular packing of spheres. | Minimization of the dissipation rate of energy for the dual stream function. | up to 10 |
| Yan and Li [6] | Periodic random packing of spheres. | Volume averaging method. | less than 1 |
| Schnitzlein [7] | Random packing of spheres in a cylindrical column with N = 10. | Solution of flow field and tracer mass balance. | from 1 to 1000 |
| Magnico [8] | Random packings of spheres in a cylindrical column with N = 5.96 and N = 7.8. | Eulerian and Lagrangian approach. | from 7 to 200 |
| Acharya et al. [9] | Periodic, random and macroscopically trending packings of cylinders. | Lattice Boltzmann method and 2D pore-scale simulation. | from 10 to 10 |
| Dixon and Medeiros [10] | Random packings of spheres in a cylindrical column with N from 5.04 to 9.3. | Three-parameter model based on classical two-layer mixing length theory. | from 87 to 870 |
| Parameter | Value | Unit |
|---|---|---|
| Particle diameter (d) | , , | m |
| Particle shaft (h) | –, –, | m |
| Column diameter (D) | m | |
| Number of particles | 900, 200, 120 | – |
| Particle density | 900, 900, 1130 | kg/m |
| Young’s modulus | , , | Pa |
| Poisson’s ratio | , , | – |
| Coefficient of restitution | , , | – |
| Coefficient of friction | , , | – |
| Time step | , , | s |
| Parameter | Value | Unit |
|---|---|---|
| Computational grid | , , | – |
| Grid size | , , | m |
| Time step | s | |
| Bed diameter | m | |
| Particle diameter | , , | m |
| Particle shaft | –, –, | m |
| Particle equivalent | ||
| diameter | –, –, | m |
| Number of particles | 900, 200, 120 | – |
| Fluid density | kg/m | |
| Fluid viscosity | Pa · s | |
| Background fluid velocity | , , | m/s |
| Tracer molecular diffusion | ||
| coefficient | m/s | |
| Tracer inlet concentration | 6 | mol/m |
| Tracer flow rate | m/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lovreglio, P.; Buist, K.A.; Kuipers, J.A.M.; Peters, E.A.J.F. Analysis of Particle-Resolved CFD Results for Dispersion in Packed Beds. Fluids 2022, 7, 199. https://doi.org/10.3390/fluids7060199
Lovreglio P, Buist KA, Kuipers JAM, Peters EAJF. Analysis of Particle-Resolved CFD Results for Dispersion in Packed Beds. Fluids. 2022; 7(6):199. https://doi.org/10.3390/fluids7060199
Chicago/Turabian StyleLovreglio, P., K. A. Buist, J. A. M. Kuipers, and E. A. J. F. Peters. 2022. "Analysis of Particle-Resolved CFD Results for Dispersion in Packed Beds" Fluids 7, no. 6: 199. https://doi.org/10.3390/fluids7060199
APA StyleLovreglio, P., Buist, K. A., Kuipers, J. A. M., & Peters, E. A. J. F. (2022). Analysis of Particle-Resolved CFD Results for Dispersion in Packed Beds. Fluids, 7(6), 199. https://doi.org/10.3390/fluids7060199






