Numerical Simulation of Turbulent Flow in Eccentric Co-Rotating Heat Transfer
Abstract
:1. Introduction
2. Methodology
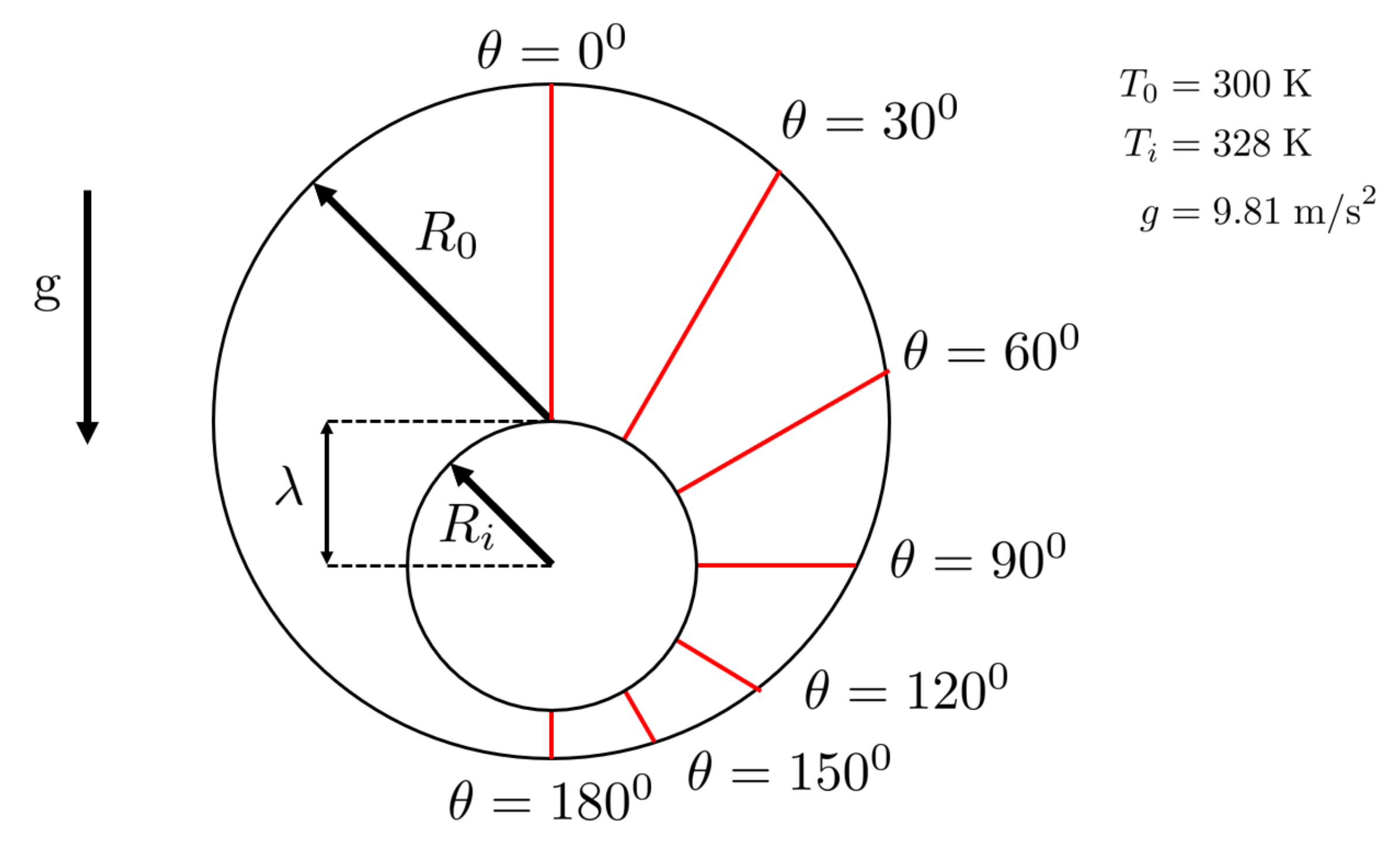
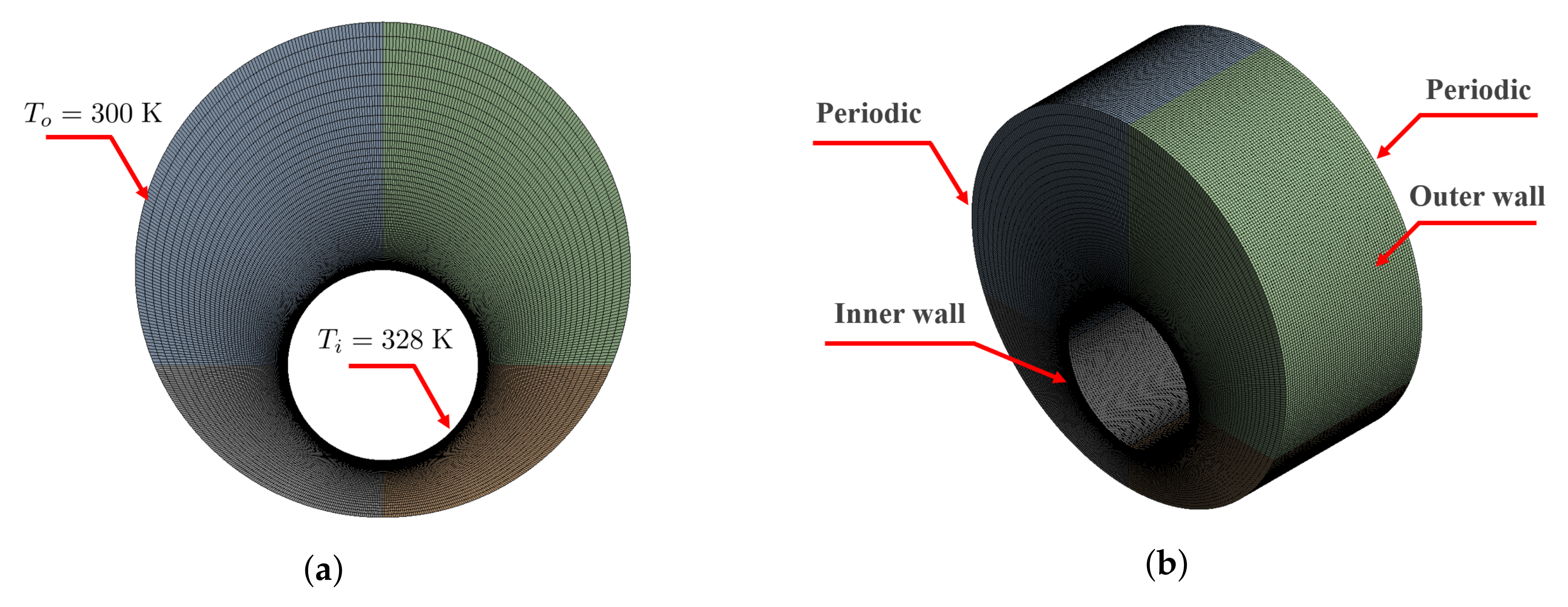
2.1. Geometry and Mesh Details
2.2. Mathematical Model
2.2.1. Turbulent Flow of an Incompressible Ideal Fluid
- The STD model and the transformed model are multiplied by a blending function and added together. The blending function is designed to take a value of one in the near-wall region, which activates the STD model, and zero away from the surface, which activates the transformed model.
- A damped cross-diffusion derivative term is included in the BSL model equation.
- The model includes a new source term in order to capture the natural convection turbulent heat transfer.
- The modeling constants are different.
2.2.2. Initial and Boundary Conditions
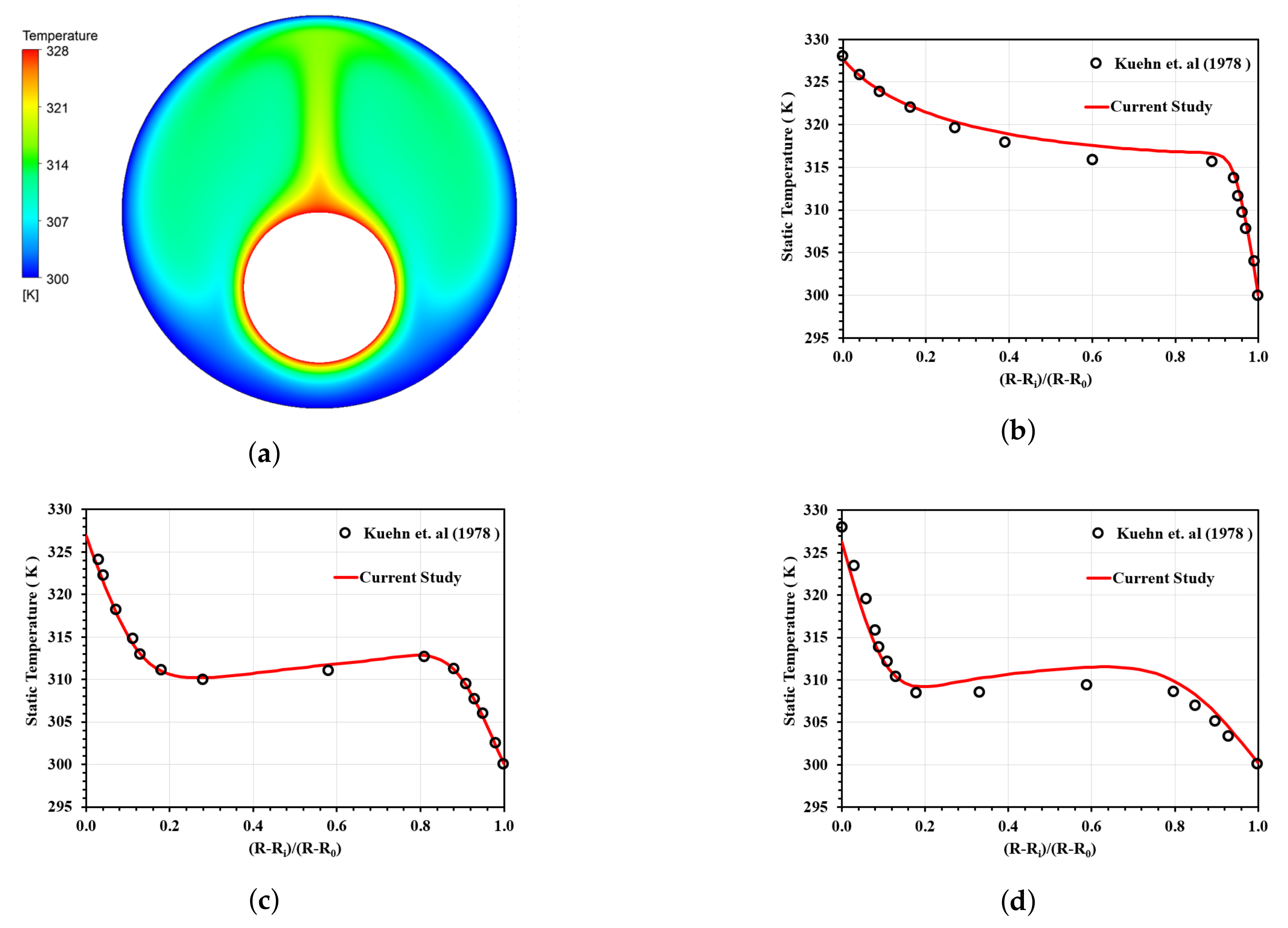
3. Validation Study
4. Results
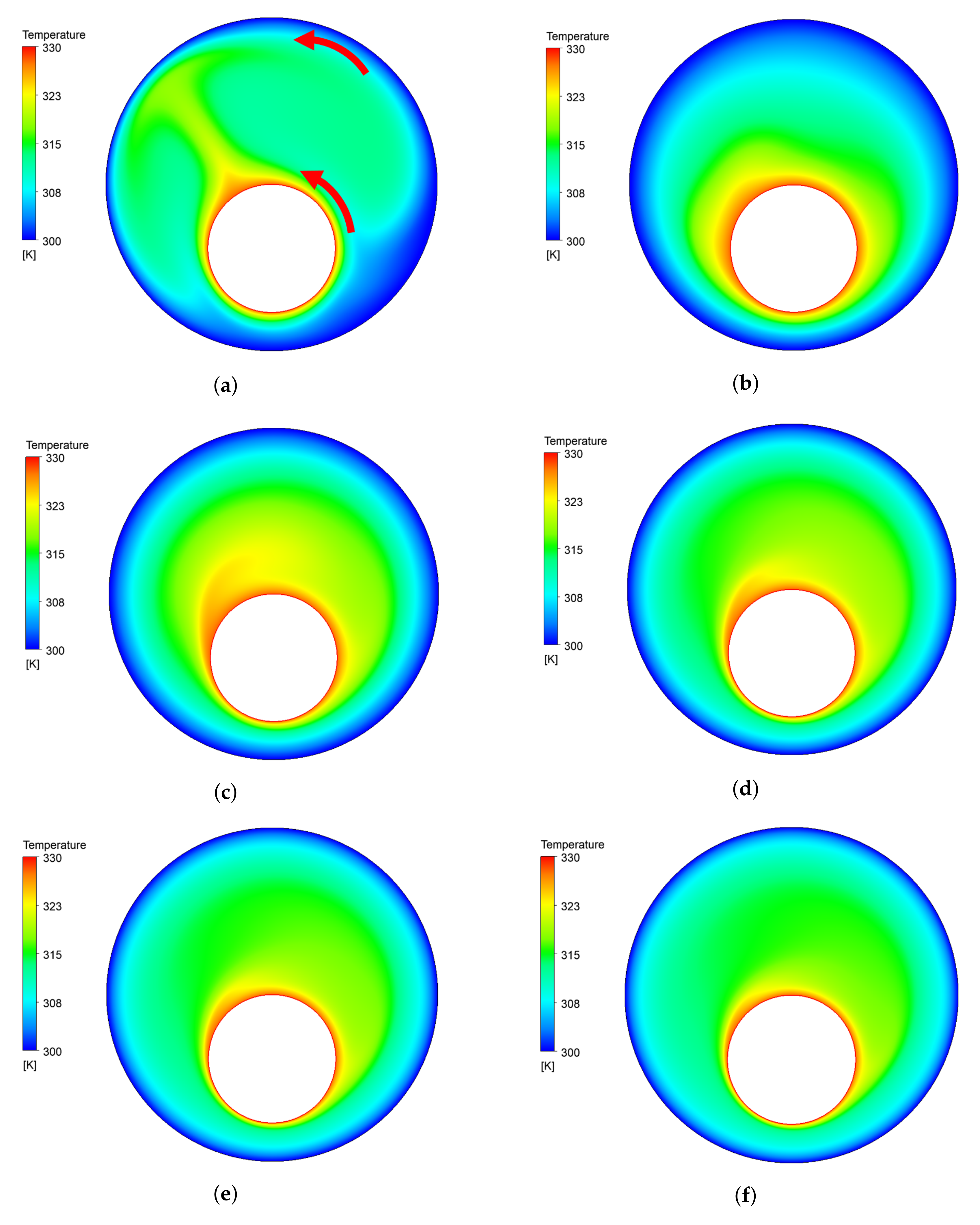
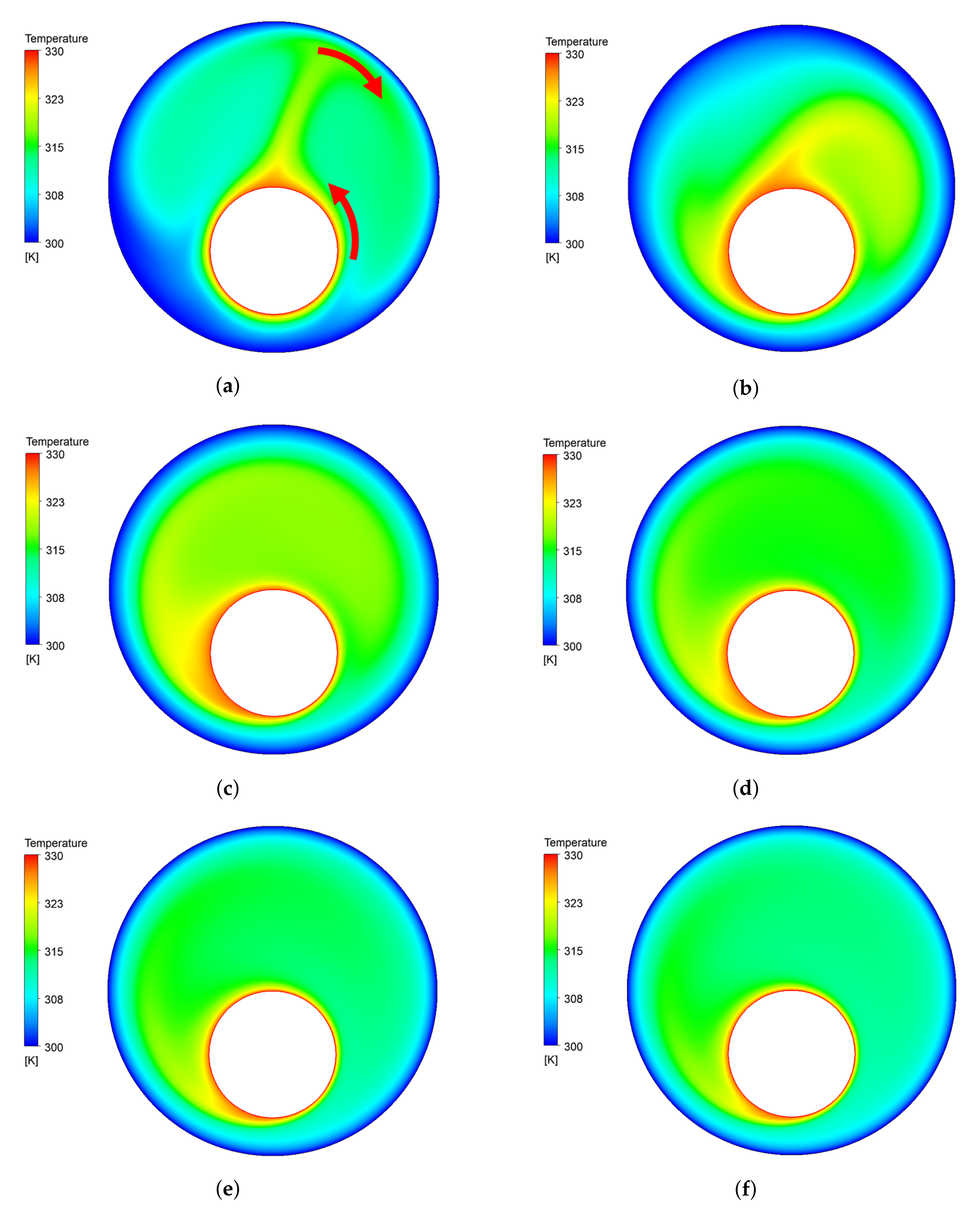
4.1. The Effect of the Inner Counterclockwise Rotating Velocity
4.2. The Effect of Outer Counterclockwise Rotating Velocity
4.3. The Effect of Inner–Outer Counterclockwise Rotating Velocity
4.4. The Effect of Inner Clockwise, Outer Counterclockwise Velocity
4.5. Temperature Mixing Performance
4.6. Velocity Distribution
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Garai, A.; Kleissl, J. Air and Surface Temperature Coupling in the Convective Atmospheric Boundary Layer. J. Atmos. Sci. 2011, 68, 2945–2954. [Google Scholar] [CrossRef]
- Hilland, R.V.J.; Bernhofer, C.; Bohmann, M.; Christen, A.; Katurji, M.; Maggs-Kölling, G.; Krauß, M.; Larsen, J.A.; Marais, E.; Pitacco, A.; et al. The Namib Turbulence Experiment: Investigating Surface–Atmosphere Heat Transfer in Three Dimensions. Bull. Am. Meteorol. Soc. 2021, 103, E741–E760. [Google Scholar] [CrossRef]
- Curic, M.; Zafirovski, O.; Spiridonov, V. Meteorological and Weather Elements. In Essentials of Medical Meteorology; Springer International Publishing: Cham, Switzerland, 2022; pp. 39–62. [Google Scholar]
- Abdillah, H.; Saputra, G.; Novitrian; Permana, S. Study of Natural Convection Passive Cooling System for Nuclear Reactors. J. Phys. Conf. Ser. 2017, 877, 012047. [Google Scholar] [CrossRef]
- Zitek, P.; Valenta, V. Solution of heat removal from nuclear reactors by natural convection. EPJ Web Conf. 2014, 67, 02133. [Google Scholar] [CrossRef] [Green Version]
- Tamdogan, E.; Arik, M. Natural Convection Immersion Cooling with Enhanced Optical Performance of Light-Emitting Diode Systems. J. Electron. Packag. Trans. ASME 2015, 137, 1–8. [Google Scholar] [CrossRef]
- Al-Khateeb, A.; Khashan, M.; Khashan, M.; Mutaib, A. Enhancement of natural convection heat transfer for cooling of electronic power chips. AIP Conf. Proc. 2021, 2404, 080001. [Google Scholar] [CrossRef]
- Klimanek, A.; Cedzich, M.; Białecki, R. 3D CFD modeling of natural draft wet-cooling tower with flue gas injection. Appl. Therm. Eng. 2015, 91, 824–833. [Google Scholar] [CrossRef]
- Takata, K.; Michioka, T.; Kurose, R. Prediction of a visible plume from a dry and wet combined cooling tower and its mechanism of abatement. Atmosphere 2016, 7, 59. [Google Scholar] [CrossRef] [Green Version]
- Yang, G.; Li, X.; Ding, L.; Zhu, F.; Wang, Z.; Wang, S.; Xu, Z.; Xu, J.; Qiu, P.; Guo, Z. CFD simulation of pollutant emission in a natural draft dry cooling tower with flue gas injection: Comparison between LES and RANS. Energies 2019, 12, 3630. [Google Scholar] [CrossRef] [Green Version]
- Liao, C.C.; Lin, C.A. Mixed convection of a heated rotating cylinder in a square enclosure. Int. J. Heat Mass Transf. 2014, 72, 9–22. [Google Scholar] [CrossRef]
- Abou-Ziyan, H.; Ameen, R.; Elsayed, K. Fluid flow and convection heat transfer in concentric and eccentric cylindrical annuli of different radii ratios for Taylor-Couette-Poiseuille flow. Adv. Mech. Eng. 2021, 13, 16878140211040731. [Google Scholar] [CrossRef]
- Bagheri, E.; Wang, B.C. Direct numerical simulation of turbulent heat transfer in concentric annular pipe flows. Phys. Fluids 2021, 33, 055131. [Google Scholar] [CrossRef]
- Abed, W.M.; Al-Damook, A.; Khalil, W.H. Convective heat transfer in an annulus of concentric and eccentric cylinders with an inner rotating cylinder. Int. J. Heat Technol. 2021, 39, 61–72. [Google Scholar] [CrossRef]
- Alnakeeb, M.A.; Abdel Salam, M.A.; Hassab, M.A. Eccentricity optimization of an inner flat-tube double-pipe latent-heat thermal energy storage unit. Case Stud. Therm. Eng. 2021, 25, 100969. [Google Scholar] [CrossRef]
- Tang, M.; He, L.; Ma, R.; He, S.; Yao, G. Modeling of yield-power-law fluid flow in an eccentric annulus with fixed horizontal cuttings bed. Energy Sources Part A Recover. Util. Environ. Eff. 2019, 1–16. [Google Scholar] [CrossRef]
- Phongthanapanich, S.; Dechaumphai, P. Finite volume element method for analysis of unsteady reaction-diffusion problems. Acta Mech. Sin. 2009, 25, 481–489. [Google Scholar] [CrossRef]
- Hassan, B.; Yohei, S.; Matthias, B.; Bojan, N. A Three-Dimensional, Immersed Boundary, Finite Volume Method for the Simulation of Incompressible Heat Transfer Flows around Complex Geometries. Int. J. Chem. Eng. 2017, 2017, 1726519. [Google Scholar]
- Goodarzi, M.; Safaei, M.R.; Karimipour, A.; Hooman, K.; Dahari, M.; Kazi, S.N.; Sadeghinezhad, E. Comparison of the Finite Volume and Lattice Boltzmann Methods for Solving Natural Convection Heat Transfer Problems inside Cavities and Enclosures. Abstr. Appl. Anal. 2014, 2014, 762184. [Google Scholar] [CrossRef]
- Svacek, P.; Louda, P.; Kozel, K. On numerical simulation of three-dimensional flow problems by finite element and finite volume techniques. J. Comput. Appl. Math. 2014, 270, 451–461. [Google Scholar] [CrossRef]
- Asadi, A.; Zaboli, M.; Mogharrebi, A.R.; Saedodin, S.; Ganji, D.D. Numerical analysis of turbulence-inducing elements with various geometries and utilization of hybrid nanoparticles in a double pipe heat exchanger. Alex. Eng. J. 2022, 61, 3633–3644. [Google Scholar] [CrossRef]
- Kuehn, T.H.; Goldstein, R.J. An experimental and theoretical study of natural convection in the annulus between horizontal concentric cylinders. J. Fluid Mech. 1976, 74, 695–719. [Google Scholar] [CrossRef]
- Kuehn, T.H.; Goldstein, R.J. An Experimental Study of Natural Convection Heat Transfer in Concentric and Eccentric Horizontal Cylindrical Annuli. J. Heat Transf. 1978, 100, 635–640. [Google Scholar] [CrossRef]
- Chauhan, A.K.; Prasad, B.V.S.S.S.; Patnaik, B.S.V. Numerical simulation of flow through an eccentric annulus with heat transfer. Int. J. Numer. Methods Heat Fluid Flow 2014, 24, 1864–1887. [Google Scholar] [CrossRef]
- Ataíde, C.H.; Pereira, F.A.R.; Barrozo, M.A.S. CFD predictions of drilling fluid velocity and pressure profiles in laminar helical flow. Braz. J. Chem. Eng. 2007, 24, 587–595. [Google Scholar] [CrossRef]
- Shahsavar, A.; Talebizadeh Sardari, P.; Toghraie, D. Free convection heat transfer and entropy generation analysis of water-Fe3O4/CNT hybrid nanofluid in a concentric annulus. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 915–934. [Google Scholar] [CrossRef]
- Kaewbumrung, M.; Tangsopa, W.; Thongsri, J. Investigation of the trailing edge modification effect on compressor blade aerodynamics using SST k-ω turbulence model. Aerospace 2019, 6, 48. [Google Scholar] [CrossRef] [Green Version]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Launder, B.; Spalding, D. Mathematical Models of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]
- ANSYS, Solver Theory, Fluent Theory Guide 2021 R1. In Fluent Theory Guide 2021 R1; ANSYS Inc.: Canonsburg, PA, USA, 2021.
- Lopez-Santana, G.; Kennaugh, A.; Keshmiri, A. Experimental Techniques against RANS Method in a Fully Developed Turbulent Pipe Flow: Evolution of Experimental and Computational Methods for the Study of Turbulence. Fluids 2022, 7, 78. [Google Scholar] [CrossRef]
- Guestal, M.; Kadja, M.; Ton Hoang, M. Study of heat transfer by natural convection of nanofluids in a partially heated cylindrical enclosure. Case Stud. Therm. Eng. 2018, 11, 135–144. [Google Scholar] [CrossRef]





| Solution Methods | Setting |
|---|---|
| Pressure–Velocity Coupling | Coupled |
| Gradient | Least Squares Cell Based |
| Pressure | Body Force Weighted |
| Density | Second Order Upwind |
| Momentum | Second Order Upwind |
| Turbulent Kinetic Energy | Second Order Upwind |
| Specific Dissipation Rate | Second Order Upwind |
| Energy | Second Order Upwind |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaewbumrung, M.; Charoenloedmongkhon, A. Numerical Simulation of Turbulent Flow in Eccentric Co-Rotating Heat Transfer. Fluids 2022, 7, 131. https://doi.org/10.3390/fluids7040131
Kaewbumrung M, Charoenloedmongkhon A. Numerical Simulation of Turbulent Flow in Eccentric Co-Rotating Heat Transfer. Fluids. 2022; 7(4):131. https://doi.org/10.3390/fluids7040131
Chicago/Turabian StyleKaewbumrung, Mongkol, and Akapak Charoenloedmongkhon. 2022. "Numerical Simulation of Turbulent Flow in Eccentric Co-Rotating Heat Transfer" Fluids 7, no. 4: 131. https://doi.org/10.3390/fluids7040131
APA StyleKaewbumrung, M., & Charoenloedmongkhon, A. (2022). Numerical Simulation of Turbulent Flow in Eccentric Co-Rotating Heat Transfer. Fluids, 7(4), 131. https://doi.org/10.3390/fluids7040131







