1. Introduction
The main legacy of the Einsteinian theory of Brownian motion to modern physics lies in the confirmation of the atomistic nature of matter and in the equivalence between random molecular motion at the microscopic level and the macroscopic phenomenon of diffusion [
1,
2].
Thanks also to the contributions by Langevin, Smoluchowski and many others [
3,
4,
5], it is now common knowledge in applied transport theory [
6] that any transport equation, expressed in the form of an advection-diffusion equation for the concentration field
of some solute diffusing in a fluid phase,
where
is the macroscopic velocity field experienced by the solute (coinciding in most of the applications with the fluid phase velocity
), and
D its isotropic diffusivity, can be represented in terms of the microscopic motion of the solute particles by means of a Langevin equation of the form
where
is the increment of a three-dimensional Wiener process in the time interval
. This equivalence is also computationally important as it enables to solve parabolic transport equations in complex geometries by means of stochastic simulations of the Langevin Equation (
2) [
7,
8,
9,
10].
The description of physical processes in terms of stochastic Langevin equations, both in equilibrium and in out-of equilibrium conditions, has become one of the strongest and more fruitful research lines in modern statistical physics, providing useful insights in all the fields of physical investigation, including quantum and particle physics [
11,
12,
13].
The Langevin Equation (
2), expressed exclusively with respect to the particle position
, can be derived from a stochastic dynamics (stochastic Newton equation) of the form
where
,
,
m is the particle mass,
the friction factor,
T the absolute temperature and
the Boltzmann constant, in the limit for
, i.e., in the case particle inertia could be neglected. This simplification is not only important in transport theory, but also in the thermodynamics of fluctuations as it implies the simplest form of fluctuation-dissipation relation [
14,
15],
that, in the case of spherical particles for which
(
is the fluid viscosity,
the particle radius) is referred to as the Stokes-Einstein relation. Equation (
4) connects a transport parameter, related to the intersity of fluctuations (the diffusivity
D) to a hydrodynamic quantity, related to dissipation (the friction factor
) at constant temperature
T.
The rise of microfludics as an autonomous hydrodynamic discipline has informed recent research in the theory of fluid motion, with relevant practical applications in analytical chemistry, molecular biology and biomedicine, production of high-quality pharmaceuticals, etc. [
16,
17,
18,
19]
The analysis of flow systems at microscale in devices (microchannels, microreactors) of almost comparable size than that of solute particles, necessarily implies a more detailed understanding of all the physical processes at small lengthscales, and thus a unitary and integrated use of theoretical tools deriving from practically all the branches of physics coupled to hydrodynamic problems [
20]: optical methods for trapping, particle manipulation and detection [
21,
22] are of common use in microfluidics, and electrosmotic [
23,
24,
25] and acoustic effects [
26,
27], either for fluid mixing or for separation purposes can be conveniently integrated within a microfluidic device. On the other hand, microscale hydrodynamics represents the natural realm where thermal and hydrodynamic fluctuations play a leading role. This admits also interesting practical implications related to the use of micrometric particles for detecting and measuring superficial phenomena and surface interactions (Brownian probes) [
28,
29,
30]. For 1
m particles, quantum effects and forces become measurable, and this opens the way for testing quantum theories, such as the occurrence of the Casimir effect, using “macroscopic” microfluidic systems [
31,
32], paving the way for a better understanding of the quantum-to-classical transition.
In most of the microfluidic applications, linearized hydrodynamic equations can be used with reasonable accuracy [
33,
34]. For timescales much larger than the dissipation time
, the instantaneous Stokes equations
where
are the velocity, the pressure and the stress tensor of the fluid respectively, provides a good approximation for modeling fluid-particle interactions, and the no-slip boundary conditions at the particle surface (
)
where
is the velocity and the angular velocity of the particle, and
a reference point, say the center of mass of the particle, describe with sufficient accuracy fluid-particle interactions.
Consequently, all the theory of Stokesian hydrodynamics [
33,
34,
35,
36], developed throughout more than one and half century, finds in microfluidics a vast field of application. Exceptions to the applicability of the Stokesian hydrodynamics in microfluidics occur for specific inertial effects such as the Segre-Silberberg effect [
37,
38,
39], and the use of “high-Reynolds number flows” (with a Reynolds number order of 100–1000) in microchannels (T- and Y-junctions) for nanoparticle production [
40,
41,
42].
The linearity of the Stokes equations and of the boundary conditions at the fluid-particle interface yields a the linear relation between the velocity of the particle and the hydrodynamic force acting on it, that in the case of a sphere moving in an unbounded fluid consist in the well known Stokes’ laws, and , ( is the force and the torque), where and are scalar coefficients due to the isotropy of the problem and the uniformity of the fluid.
On the other hand, whenever the fluid is confined into a bounded device, corresponding to the hydrodynamic domain bounded by walls, both the symmetries (isotropy and uniformity) are generically broken. Therefore, the hydrodynamic resistance law attains a more general position-dependent and tensorial character
where
is the
overall resistance matrix of the hydrodynamic interactions, possessing a block structure
where (i)
, and
are the translational and rotational friction matrices, respectively, (ii)
, and
are the roto-translational coupling matrices. By the Lorentz’s reciprocal theorem it is possible to prove [
33] that
and
are symmetric matrices, while
and
satisfy the property
, where the superscript “
T” indicates the transpose. Correspondingly, the overall resistance matrix
is symmetric and positive definite.
This automatically implies, due to the fluctuation-dissipation relation (
4), a tensorial and position-dependent diffusivity. The latter two properties have deep and non trivial implications whenever a stochastic equation of motion, in the form of Equation (
3) is considered, due to the highly singular nature of the Wiener description of the thermal/hydrodynamic fluctuations. For the sake of completeness, it should be also mentioned that a position dependent effective diffusivity arises in modeling solute transport in microchannels with undulated walls, in the case the transport problem is referred exclusively to the channel axial coordinate [
43,
44]. This is referred to as the Fick-Jacobs approximation and it is essentially a geometrical effect within an approximate transport model unrelated to any hydrodynamic interactions.
The scope of this article is to analyze in detail the problems and the peculiarities of particle transport in microfluidic systems, originating from the confined nature of the flow, starting from the stochastic description of the microscopic particle motion, in a way that may also be useful for researchers in microfluidics that are not fully familiar with stochastic differential equations. While stochastic modeling of particle transport involving constant effective diffusivities is widely used in the analysis of microfluidic devices, the inclusion of hydrodynamic effects, deriving from fluid confinement, represents a completely new and unexplored field of theoretical and numerical investigation. This article attempts to fill this gap, providing a methodological bridge between hydrodynamic theory and the stochastic formulation of transport phenomena in confined geometries, addressing also in a clear and critical way the complexities and the difficulties of this approach. The article addresses also novel original derivations as regards specific topics, such as the use of the overdamped approximation in non-equilibrium conditions and the effect of slippage as regards transport phenomena involving surface effects (such as surface chemical reactions).
In order to illustrate the physical concepts and the resulting analytical approaches, the hydrodynamics of a spherical particle near an infinite planar solid surface is explicitly considered, as a prototypical and paradigmatic case study of the hydrodynamic problems occurring in microfluidic channels. Throughout this article, rigid particles and Newtonian fluids are considered.
The article is organized as follows.
Section 2 addresses the formulation of fluctuation dissipation relations in confined systems, and the computational problems associated with it.
Section 3 analyzes the reduction of the equation of motion in the form of a Langevin Equation (
3), discussing also the case of non-equilibrium thermal conditions (thermophoresis).
Section 4 discusses the problems arising from the non-integrable singularity of the friction factor near a solid no-slip wall, as regards diffusional problems in the presence of superficial phenomena (surface chemical reactions). A way for overcoming these problems lies in relaxing the no-slip assumption, as discussed in
Section 5, where we show the necessity of considering slippage effects both at the particle external surface and at the walls of the fluid domain. Finally,
Section 6 discusses in a succinct way the role of the fluid inertial effects in the formulation of the stochastic equations for particle motion.
2. Fluctuation-Dissipation Relations in Confined Geometries
Consider the motion of a rigid spherical particle, of mass
m and momentum of inertia
I, in a microfluidic device. Let
and
be its velocity and angular velocity, respectively. Assume that the particle is dispersed in a fluid flow, characterized by the fluid velocity
and that the particle is also subjected to the action of an external potential field
. The particle equations of motion read
where
and
are the force and the torque deriving from the action of the external flow field
(assuming that the particle velocity and angular velocity are vanishing),
and
are the force and the torque due to the hydrodynamic interactions (described by means of Equation (
7) in the case the external flow velocity is vanishing and the particle possesses a velocity
and an angular velocity
), and
,
represent the the stochastic force and the torque deriving from to thermal fluctuations. This decomposition is made possible because the hydrodynamic equations for the fluid are assumed to be linear. The basic problem in the statistical physics of microparticle motion resides in the determination of the contributions of the thermal perturbations
and
, since all the other terms in Equation (
9) stem from a classical hydrodynamic analysis.
Following the original approach due to Einstein and Langevin [
15], in the case the fluid is described by means of an instantaneous response (Stoke’s regime), it is natural to represent
and
in the form of a linear superposition of vector-valued Wiener processes, i.e., as
where
and
are the increments in the time interval
of two mutually independent vector-valued Wiener processes. This observation is a consequence of the fact that Wiener processes are also memoryless, in the meaning that if one defines
, interpreted in a distributional meaning, than the correlation function
is impulsive (here
indicates indifferently either ensemble or temporal averages, and
is any time instant) [
45].
Henceforth, in order to simplify the notation, the explicit dependence of the matrices
on the position
will be omitted. While the determination of
,
and
,
follows for the simple application of the Stokesian hydrodynamics, the estimate of the matrices entering Equation (
10) and defining the thermal perturbations requires a statistical physical ansatz that, at constant temperature
T, the thermal fluctuations described by Equation (
10) would provide the known result of equilibrium statistical physics [
14]. This is the essence of the fluctuation-dissipation ansatz, and for this reason, owing to linearity, it is sufficient to consider the statistical properties for the particle dynamics in the absence of external forcings, i.e., for
,
. Under these conditions, by substituting Equations (
7), (
8) and (
10) into the equations of motion (
9) one obtains,
where also for
the explicit dependence on the position has been omitted.
The matrices
,
,
,
are the stochastic amplitude matrices, and the final goal of fluctuation-dissipation analysis is their determination from physical principles enforcing equilibrium properties. Let
be the overall
stochastic amplitude matrix entering Equation (
11),
and define the
matrix
, the entries of which are
as
In matrix form,
which is, by definition, symmetric. Expressing Equation (
11) componentwise
so that the associated Fokker-Planck equation for the probability density function
attains the form [
45]
The statistical equilibrium properties can be ascertained from the analysis of the lower-order (first and second) moments of
. The first-order moments relax to zero in the long-term regime, as a consequence of the fact that the hydrodynamic interaction matrix
is positive definite. It is therefore sufficient to consider the second-order moments for the translational/angular velocities,
To begin with, consider
. From the Fokker-Planck Equation (
16) one obtains
In the long-term limit (equilibrium), it follows from Equation (
18) that
Next, consider
, the entries of which satisfy the equations
so that the value attained at equilibrium is
Finally, consider the mixed second-order roto-translational moments
admitting the equilibrium condition
Fluctuation-dissipation conditions, and the explicit expression for the stochastic amplitude matrices follow by enforcing the equilibrium properties [
14]
where
I is the moment of inertia, and
the identity matrix. These conditions stem from the Maxwellian equilibrium velocity distribution, and from the energy equipartition theorem applied to a rigid particle, admitting 6 degrees of freedom. Making use of Equation (
24) and of the equilibrium expression Equation (
19) for
, one obtains that the matrix
should be symmetric and
A similar analysis for
Equation (
21) at equilibrium provides
The equilibrium results deriving from the analysis of the mixed roto-translational moments yield
a solution of which is
and
Once the “diffusional” matrices , , , have been expressed in terms of the hydrodynamic resistance matrices, the next step is to derive the expression for the stochastic amplitude matrices , , , .
Because of Equation (
28), the
matrix
defined by Equation (
12) is symmetric, and satisfies the algebraic matrix equation
Mutuating this property from the symmetry of hydrodynamic matrices, the matrix
is symmetric and positive definite, and it is known from matrix theory [
46] that there exists a unique, symmetric, and positive definite matrix
solution of Equation (
29), formally
In order to determine the explicit expression for the matrix
, it is convenient to normalize its entries, expressing the force/torque and the velocity/angular velocity in the same physical dimensions. If
is the characteristic particle length,
for spherical particle of radius
, set
,
. In this way,
has the dimension of a force, and
the dimension of a velocity, so that Equations (
7) and (
8) become
where
is the normalized overall resistance matrix possessing the block structure
and the normalized moment of inertia is given by
. In this way, Equation (
11) attains the normalized representation
with
,
,
,
. The normalized matrix Equation (
29) thus becomes
and
.
For symmetric and positive definite matrices
, the estimate of their square root
reduces to an eigenvalue problem [
46]. Let
,
, be the eigenvalues of
, and
the corresponding unit eigenvectors. The solution of Equation (
34) can be expressed as
where
is the eigenbasis transformation matrix, the column of which are orderly the eigevectors of
, i.e.,
and
is a diagonal matrix, the diagonal entries of which are the square roots of the eigenvalues
,
.
An Example: Systems with Axialsymmetric Geometry
As an application of the previous analysis, consider a system with axialsymmetric geometry. Typical axisymmetric systems in microfluidics are spherical particles moving in a slit channel or near an infinitely extended planar wall. The symmetries of the problem reduces the 21 independent coefficients of the hydrodynamic resistance matrix to 5. By taking a Cartesian coordinate system
with
lying on the axis of symmetry as in
Figure 1, the resistance matrix takes the form [
33]
Therefore, the matrix
, chosing
, becomes
where
The eigenvalues of
are
where
. The eigenvector matrix
entering Equation (
36) takes in this case the expression
By applying Equations (
36) and (
38), we obtain for
where
As
, i.e., far away from the wall, the coupling term
, and the quantity
r take the limit form
where
Substituting these values into Equation (
43), we obtain the expected results in the free space
and therefore
where
is the
identity matrix. In order to recover the Stokesian limit values in the free space
,
, the argument of the square root in Equation (
43) should be positive, i.e.,
Inequality (
48) is fulfilled in the free space as follows from Equation (
45).
3. Adiabatic Elimination of the Velocity Variables
In this section we consider the formulation of the overdamped approximation for micrometric rigid particles in confined geometries. The overdamped approximation consists in expressing the equations of motion in the form of a kinematic equation for the mechanical degrees of freedom associated with translational and rotational motions. This is made possible due to the fact that velocity variables are customarily characterized by a faster relaxation dynamics than position and orientational variables. This is certainly true for micrometric particles if one considers their transport properties at time scales much larger than the characteristic dissipation timescale
, the order of magnitude of which falls between
–
s for micrometric particles in water at room temperature. For this reason, the overdamped approximation is often referred to as the adiabatic elimination of the fast velocity variables, and this follows by imposing the condition
and extracting out of Equation (
49) the expression for
and
, entering the kinematic equation
where
is the vector-valued angular variable accounting for the particle orientation.
The overdamped approximation in confined geometries presents intrinsic peculiarities, just because the hydrodynamic resistance matrix depends on the position
, and in general of the orientation
, and this raises delicate issues when the thermal fluctuations are expressed as linear superposition of increments of Wiener processes, owing to their highly singular local structure [
45]. This problem in the physical literature is usually referred to as the Ito-Stratonovich dilemma [
47,
48]. The most convenient and simple approach to perform the adiabatic elimination of the fast velocity variable is due to Sancho et al. [
49]. The starting point in this derivation is that the configurational coordinates of a particle driven by Wiener fluctuations still represent a locally smooth, and almost everywhere differentiable continuous stochastic process with probability 1, and this property determines the way Equation (
49) is interpreted. Without loss of generality, let us suppose that the particle is subjected to an external potential
, and that no additional flow contribution are present. The latter can be added at the end of the adiabatic elimination process.
In order to perform this analysis in the simplest formal way, it is convenient to group together configurational and velocity variables, thus introducing the 6-dimensional configurational and velocity variables,
and
, respectively, and the overall stochastic forcing
so that the equations of motion can be compactly expressed as
where
is the mass/moment-of inertial tensor,
for a spherical particle,
the hydrodynamic resistance matrix,
the nabla operator with respect to the
-variable and
is the matrix of thermal fluctuation intensity satisfying, as discussed in the previous Section, the condition at thermal equilibrium,
The overdamped approximation corresponds to the limit for mass and momentum of inertia tending to zero. In performing this limit, upon correct physical grounds, it should be ensured that the configurational variable
is a smooth stochastic process. To this end, the Wong-Zakai theorem can be enforced [
50,
51], implying that the stochastic differential equation describing particle dynamics should be interpreted in a Stratonovich way [
52], Technically, this means that, in performing the limit process, the quantity
should be interpreted as
where “∘” indicates the Stratonovich rule in the definition of stochastic integrals and differentials. It is also convenient to recall a known result, deriving from the Ito lemma, namely that [
45]
where
are the Kronecker’s symbols (entries of the identity matrix), and
is a quantity going to zero for
faster than
.
The final goal of this analysis is to derive a kinematic equation for the configurational particle degrees of freedom (Langevin equation) expressed in the Ito way and, out of it, the transport equation for particle density, corresponding to the Fokker-Planck equation for the statistical characterization of the so-obtained Langevin equation.
Making use of the Wong-Zakai result, expressed by Equation (
54), the overdamped approximation of Equation (
52) is thus given componentwise by
Expanding the first term at the r.h.s. of Equation (
56) in Taylor series to the leading order,
The quantity
can be evaluated from Equation (
56), by considering for the first term at the r.h.s. of Equation (
56) its Ito interpretation, namely
that provides the leading order contribution as the remainder in this approximation is order of
. Thus, enforcing also Equation (
55), one obtains
where
, and in deriving the last relation we have made use of Equation (
53). Substituting Equations (
57) and (
58) into Equation (
56) it follows that
where the
-terms have been neglected. Correspondingly, the Langevin equation in the configuration
-space becomes
where
The Fokker-Planck equation for the probability density
associated with Equation (
61) is thus given by
where
and the generalized diffusivity tensor
takes the form
i.e., the generalized diffusivity tensor
is related to the resistance matrix
by the relation
generalizing the fluctuation-dissipation relation Equation (
4). Next, consider the contribution of the vector field
entering the Fokker-Planck Equation (
62). From the identity
, it follows componentwise, for any
,
and thus,
The latter expression implies that the entries
of
defined by Equation (
61) reduce to
Substituting Equations (
63) and (
67) into Equation (
62), the Fokker-Planck equation for
attains the simpler form
that can be rewritten in a more compact way as
The latter corresponds to an advection-diffusion equation in the configuration space in the presence of the effective velocity
, stemming from the potential
and of the tensor diffusivity
. Conversely, Equation (
68) represents the classical formulation of the Fokker-Planck equation associated with a Langevin dynamics interpreted in the Ito way, attaining the following expression
where
are the entries of the square root matrix
of the diffusivity tensor
,
. It is also clear from the Ito representation of the Langevin Equation (
70) the occurrence of an additional convective contribution depending on the divergence of the diffusivity tensor. This term admits a physical meaning as, even for
, it provides a biasing average velocity
,
where
is the average value of the particle velocity evaluated when the particle configuration is at
[
53,
54].
In the case of a spherical particle, the hydrodynamic matrices depends solely on
and not on
. Consequently it is easy to obtain the evolution equation for the marginal distribution
, where
. Assume also that the spherical particles are immersed in a flow, and that the force exterted by the flow onto a generic particle located at
is
. In this case, the spatial particle density function
satisfies the balance equation
where
, is the
diffusivity tensor,
.
3.1. An Application
As a simple application of the overdamped theory, consider the vertical motion of a spherical particle in the upper half-plane delimited by a planar wall at
in isothermal conditions at temperature
T. Indicate with
the distance of the particle from the wall, and assume that the particle is subjected to an external potential
, as in [
28,
29], where
stems from gravity and from a local double-layer repulsive potential near the wall. In this case the problem is spatially one-dimensional, since
, and
depends solely from the distance
x from the wall. Setting
, and similarly for
, the Fokker-Planck equation for the density function
reads
and this equation corresponds to the Langevin-Ito equation
where
is the increment of a one-dimensional Wiener process. Assuming that the potential is attractive towards
at large distances, so that
, it follows from Equation (
73) that in the limit for
, the density
converges towards a stationary density
, solution of the equation
corresponding, as expected, to the Boltzmann distribution
This is a classical result, starting from which, micrometric particles may be used as Brownian probes, upon recording their statistical properties i.e. their stationary density function
, in order to investigate and measure surface properties of materials [
28,
29].
It is instructive to analyze in greater detail the mathematical properties of Equation (
73). This is a one-dimensional parabolic equation for
, and as the wall at
is impermeable to particle transport,
for any
. To solve Equation (
73), it should be equipped with initial and boundary conditions. As regards the initial condition,
, with
. The boundary condition at infinity,
is the classical regularity condition, namely
meaning that
and
should decay faster than any power
of
x for
. At
, the zero-flux boundary condition applies, implying in the present case
Two cases should be discussed. If, (i)
, since
, the wall boundary condition at
blows up, reducing Equation (
78) to a trivial identity that does not provide any condition on the local behavior of
near
. Conversely, if (ii)
, and moreover
, where the constant
C may even diverge to
∞, the boundary condition (
78) reduces to a homogeneous Dirichlet condition,
As in principle, the condition on the potential
U leading to Equation (
79) could not be verified in a physical systems, as for the case analyzed in [
28,
29], it follows from the above analysis that the simple transport model Equation (
73) displays a singular behavior as regards the wall boundary conditions. This singular phenomenon is a peculiar feature of the transport equations involving a hydrodynamic Stokesian description of the fluid-particle interactions in confined geometries, deriving from the singularity of some entries of the resistance matrix near a solid wall.
3.2. Thermophoresis from the Overdamped Approximation
An interesting byproduct of the overdamped analysis discussed above is the derivation of thermophoretic effects from the stochastic equations of motion. For simplicity, let us consider the case of a spherical particle in its translational motion, neglecting rotational effects and in the absence of any external or fluid forcing. It has been shown in [
55] (see also [
56]) that even in the presence of a non-equilibrium steady temperature profile
the fluctuation-dissipation relation can be applied, so that the equations of motion in the present case read
Within the overdamped approximation, enforcing the same Stratonovich-approach developed in
Section 2 to the term
, one obtains
Since,
This leads to the following Langevin equation
From the fluctuation-dissipation relation extended to non-equilibrium steady thermal conditions,
, it follows, for any
, that
which implies
From the latter expression it follows that
Therefore, Equation (
82) becomes
and the corresponding Fokker-Planck equations reads
providing the occurrence of an additional convective contribution to the flux, depending on the temperature gradient, and equal to
providing a thermophoretic velocity
equal to
[
57]. This result shows that thermophoretic effects naturally follow from the accurate description of stochastic particle motion in thermal non-equilibrium conditions.
4. Wall Singularities: Superficial Phenomena
In the previous Section we have outlined the physical problems associated with the setting of boundary conditions for transport equations in confined geometries due to the singularities of the entries of the resistance matrix. The asymptotic trends of all the entries of
of two smooth no-slip surfaces almost in contact, such as the case of a particle very close to a solid surface, has been studied by Cox [
58] for any value of the walls’ curvatures. From the Cox’s analysis, it results that the drag force on a particle moving towards the wall is inversely proportional to gap between the surfaces (particle and wall surfaces). To simplify the analysis, let us focus on a spherical particle of radius
. By considering a Cartesian reference system
with the origin on the wall and with
colinear to the axis passing between the two contact points of the two surfaces, we have that
as
. For example, the drag force on a sphere moving towards a planar wall can be expressed to the leading order by the Taylor approximation [
59]
for small gaps
h between sphere and planar wall. At larger distances, Lorentz [
60] found
and, since
, a reasonable approximation over the whole range of
h values is given by
The singularity of
at the wall implies that a particle, initially at
and moving towards the solid surface due to the action of a constant force
, say gravity, reaches the surface in an infinity time
, being the integral
divergent to infinity. The characteristic time
is referred to as the wall touching time. This result poses severe problems in predicting the kinetics of coalescence and deposition of dispersed particles from hydrodynamic theories based on the Stokes model Equation (
5). To complete the picture, let us consider the scaling behavior of the remaining resistance coefficients. As regards the other coefficients, they are all logarithmically singular as
with the exception of the rotational resistance around the normal axis to the surfaces attaining a finite value close to the wall, i.e.,
as
. Singularities at a contact point between surfaces are typical of Stoke’s flows due to the no-slip conditions at solid boundaries. For example, in contact line motions [
61] and for flows near a corner [
62] it has be found that unphysical singularities can be eliminated or mollified by introducing slippage at solid boundaries [
63,
64]. Before, addressing the effect of slip boundary conditions, it is useful to investigate further the pathologies arising from the classical no-slip hydrodynamic description in dealing with surface phenomena.
Surface Phenomena and Hydrodynamic Singularities
All the surface phenomena (particle coalescence, surface aggregation, adsorption, surface chemical reactions) depending on a transfer mechanism of molecules and particles from the fluid phase onto the surface are deeply influenced by the spatial dependence of the entries of the hydrodynamic resistance matrix. Paradoxes arise due to the singularities of these entries at the solid walls (for incompressible flows, assuming no-slip boundary conditions at the solid boundaries).
In order to highlight these phenomena, it is sufficient to consider a simple problem, namely the pure diffusional motion of solute particles (nanoparticles) in the neighborhood of a solid wall (located at
), undergoing at the solid wall a surface chemical reaction characterized by a linear, first-order kinetics. To simplify the analysis, let us assume that far away from the wall, say at
, the particle concentration is kept fixed, and equal to
. The problem is thus specified by the parabolic diffusion equation for the particle concentration
,
equipped with the boundary conditions
Consider the steady-state solution
of Equation (
94). From Equation (
94) it follows that,
where
B is a constant, and thus
where
A is a second constant to be determined from the boundary conditions. From Equation (
97) it follows that a solution exists provided that
is locally integrable near
. But this is not the case when the hydrodynamic modeling deriving from incompressible Stokes equations imposing no-slip boundary conditions at the solid walls, as
.
On the other hand, in the case
would be locally integrable near
, the steady-state solution
would attain the expression
It is clear from the above problem that Stokes’ hydrodynamics applied to transport phenomena coupled to any form of superficial chemical physical processes determines unphysical paradoxes. In the present case, the paradox can be resolved within a classical hydrodynamic formulation by deriving, from more general hydrodynamic conditions, a diffusion coefficient that is integrable near , i.e., such that , with and . Indeed, this property can be recovered by relaxing the no-slip boundary conditions as addressed in the next Section.
5. Effect of Slip Boundary Conditions
Although the no-slip assumption,
, at the interface between a Newtonian fluid and a solid boundary is largely accepted due to its capability of predicting mechanical and hydrodynamical properties involving macroscopic bodies and large-scale systems, the nature of the proper boundary conditions for the tangential velocity at a solid interface has been a long-debated issue over more than two centuries of hydrodynamic research [
65]. As an alternative to the no-slip hypothesis, Navier [
66] proposed that the tangential stresses at any point on the solid surface should be the same as the stresses at a neighboring internal point of the fluid, providing the boundary condition
where
is the identity matrix,
, the unit normal vector to the surface of the solid,
a friction constant and “⊗” indicates dyadic composition,
. Since the isotropic pressure contribution entering
vanishes at the r.h.s of Equation (
99), the Navier’s boundary condition (
99) can be written as
where
, having the dimension of a length, is the so called slip length. It is evident that the slip length represents a new parameter in modeling Stokes flow. In fact, while the no-slip model describes an idealized fluid/solid interface, the slip model introduces an additional parameter related to the chemical physical interactions at the solid-liquid interface.
Slip phenomena can be distinguished in two main classes: intrinsic slip and apparent slip [
67]. The first one is due exclusively to the molecular dynamics at the solid-liquid interface. The second one is due to artifacts at the surfaces that can increase or decrease the slippage, such as the presence of gas bubbles or the surface roughness. However, these artifacts have necessarily a characteristic length below which no-slip conditions applies. In addition, as shown by Cox [
58], the nature of the singularity does not depend on the curvature of the approaching surfaces. In considering very small gaps between the surfaces (
), the apparent slip vanishes. Therefore, in the remainder, we will refer solely to the intrinsic (molecular) slip. The occurrence of slippage depends in principle, either on hydrodynamic conditions or on the gap length. In fact, as shown by molecular dynamic simulations [
68], the slip length for the system (PA-6,6 oligomer)-graphene increases by increasing the shear rate and by reducing the gap between the solid walls. Being such behavior, due to the molecular rearrangement of the fluid, it is appreciable solely when the gap is small enough to be comparable with the characteristic size of the molecular structure of the fluid. However, at this lengthscale scale, it is not possible to mark a clear distinction between the solid surface and the domain of the fluid used in continuous hydrodynamic models, due to solvation and diffusive phenomena. Therefore, a constant slip length, used in hydrodynamic theories (and in the remainder), should be considered as a parameter emerging from the complexity of the molecular system. A review of typical slip lengths for several fluid-surface systems obtained experimentally is given in [
67]. Non vanishing values of the slip length are in the range
nm, whereas typical characteristic lengthscales of colloids are
nm. Correspondingly, the dimensionless slip length for a colloid attains values in the range
.
Owing to the linearity of the slip boundary conditions Equation (
100), a linear relation between resistance and particle velocity Equation (
7) still holds. In [
33], a purely mechanical proof of the symmetry of the resistance matrix has been provided, alternative to the thermodynamic approach followed in [
69]. However, this proof, as opposed to the thermodynamic one, considers solely no-slip conditions at the solid surfaces. To fill this gap,
Appendix A provides a more general proof of the symmetry of the resistance matrix also in the presence of slippage enforcing mechanical arguments.
Either the problems of translating or rotating sphere in an unbounded fluid have been solved by Basset [
70] in the presence of the Navier’s slip obtaining the following expressions for the force and the torque acting on the sphere
Being , larger spherical particles experience the force and the torque corresponding to no-slip boundary conditions and , whereas for smaller colloids the Basset’s correction becomes necessary.
For a particle in a confined geometry, the slip boundary conditions can be considered either at the surface of the particle (
), with a slip length
, or at the surface of the walls (
) with a slip length
. Therefore, the boundary conditions for the flow become
Spherical Particle Moving Perpendicular to a Planar Wall
Let us to consider the problem of a spherical particle near a planar wall as depicted in
Figure 1. Hocking has shown [
71] that, in the presence of the same slip on both the surfaces (
), the touching time in Equation (
93) becomes finite although the singularity of the transversal resistance at the wall still remains [
71]. The functional dependence of the resistance to perpendicular translations on
h in the limit
, derived by Hocking using lubrication methods, attains the form
where
. Consequently, the drag force is logarithmically singular at the wall, Equation (
91) becomes integrable and the touching time attains a finite value.
A seminalytical expression for the drag force over a sphere translating perpendicularly to a plane has been obtained by Goren [
72] over the entire range of positions and for any values of
and
using a bispherical coordinate system. However, the author [
72] has provided only few numerical values for
corresponding to relatively large gaps and slip lengths, and considering solely the case
. In point of fact, in order to obtain the numeric values for the transversal resistance from the Goren’s solution is in principle necessary to solve an infinite dimensional linear system of equations for any position of the sphere. On the other hand, the infinite linear system, truncated to a finite number
N of equations, provides approximate but accurate values for the force experienced by the particle with an error that decreases as
N increases, while the number of the equations from a fixed accuracy increases as
and the slip lengths increase.
In order to obtain the values of
for different slip lengths and at any distance from the wall, we have either performed FEM simulations, the detail of which are reported in the
Appendix B, or solved the Goren’s equations up to
. The data depicted in
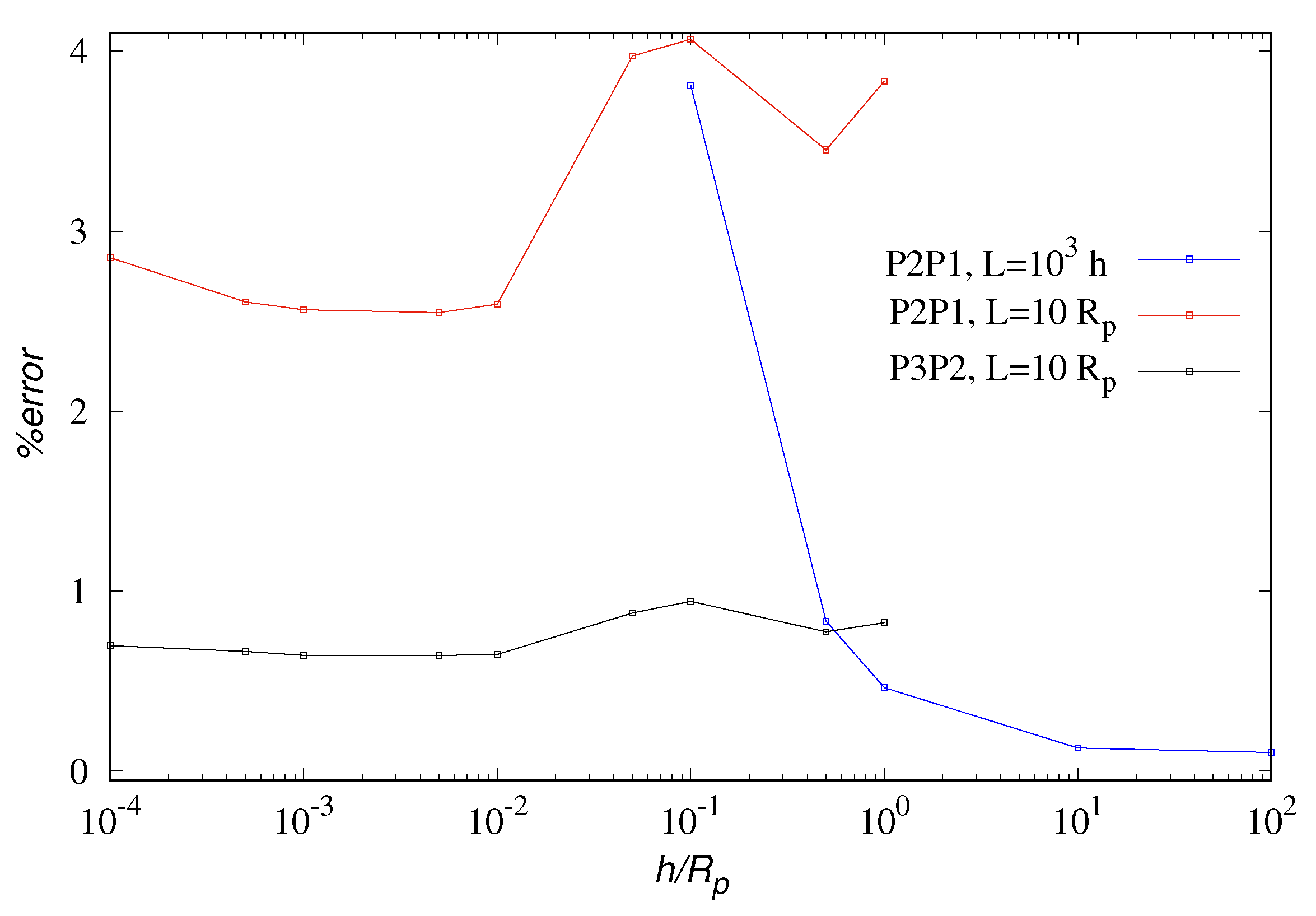
Figure 2 show that the Hocking asymptotic Equation (
104) matches accurately the FEM simulations and the Goren solution in the range of
and that the predicted logarithmic scaling starts to appear for gaps smaller then the slip length (
), after a transition zone, where
.
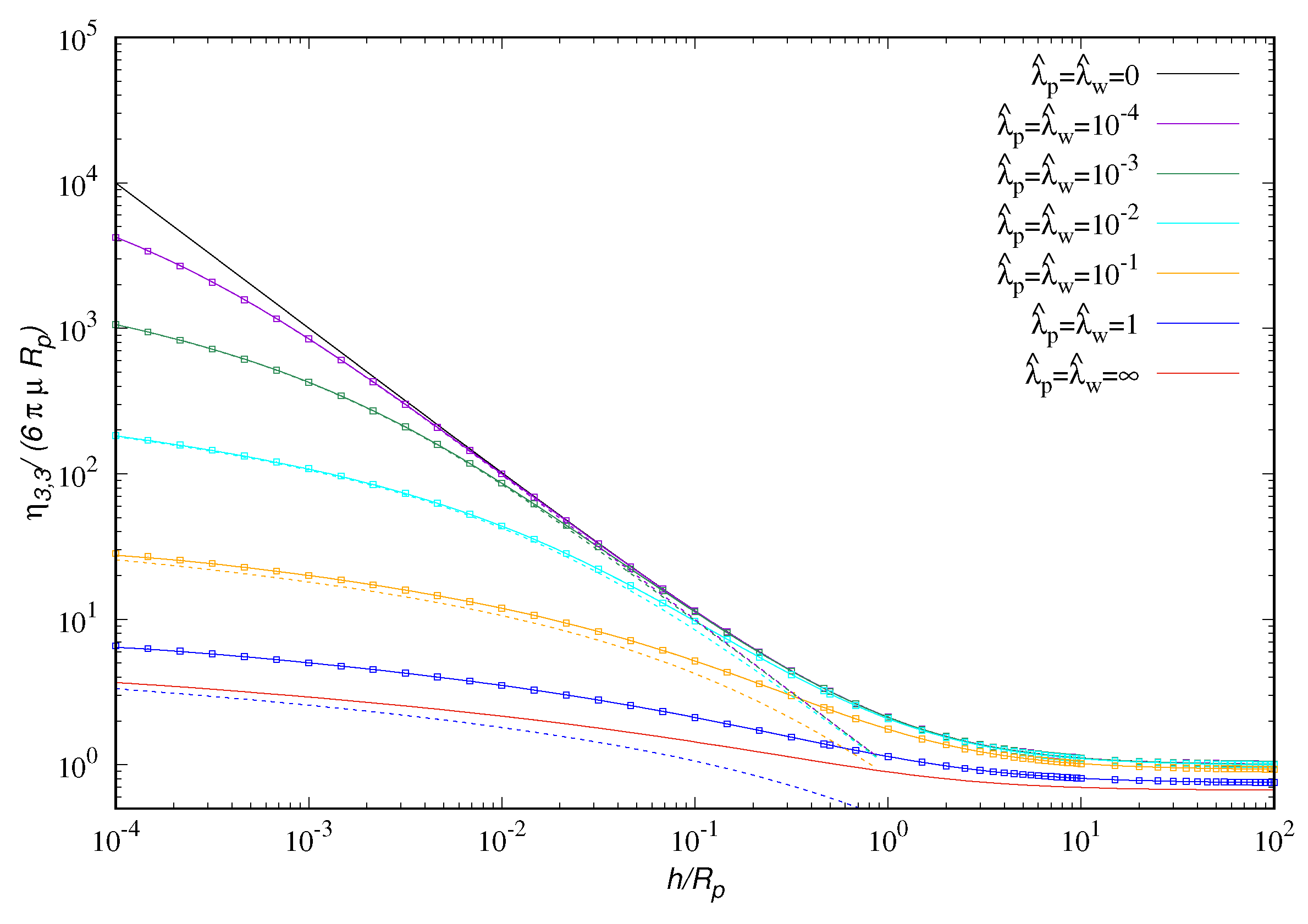
On the other hand, as depicted in
Figure 3, if the no-slip boundary condition is imposed on solely one of the surfaces, the singular scaling
remains no matter the value of the slip length imposed on the other surface. In the latter conditions, we can distinguish three different regimes: (i) the scaling
for
, (ii) an apparent logarithmic behavior for
and (iii) the asymptotic regime where
for
.
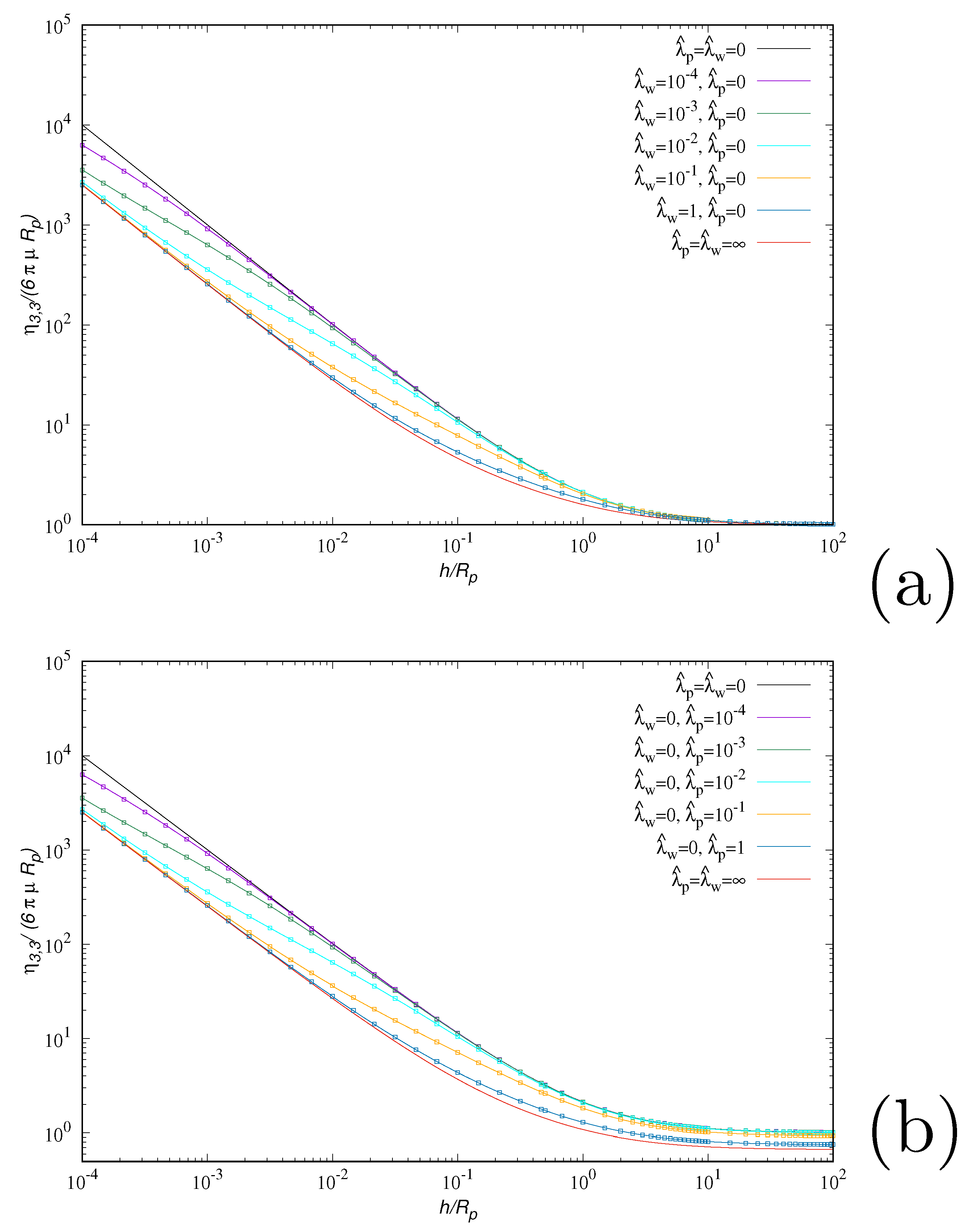
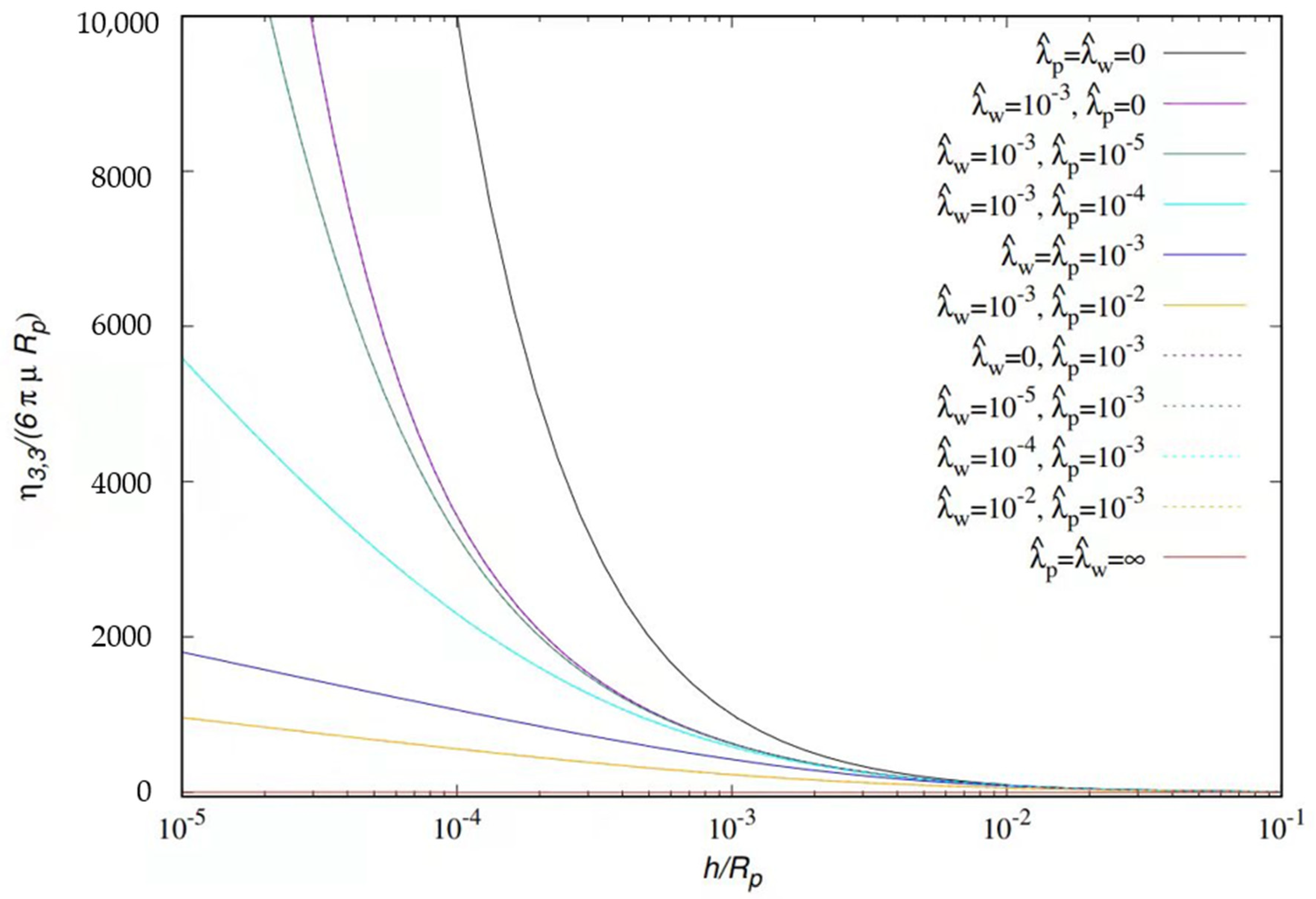
To complete the analysis the data in
Figure 4 show that, keeping fixed the slip length at one of the surfaces (
,
) and increasing the slip length on the other
,
, the logarithmic scaling occurs for
. This means that an arbirarily small slip on both the surfaces is sufficient to determine an asymptotic logarithmic scaling of the transversal resistance and thus the occurrence of a finite value of the touching time.
6. Fluid Inertial Effects
So far we have considered fluid-particle interaction within the instantaneous Stokes regime, neglecting fluid inertia. In point of fact, while the Reynolds number is smaller that 1 in most of the microfluidic applications, this is not the case of the product of the Reynolds number times the Strouhal number, which is order of 1 or higher due to the high frequency of the thermal fluctuations. This means that a more accurate description of particle motion at short time and length scales would involve a hydrodynamic description of fluid inertia, which in the present case corresponds to the time-dependent Stokes regime [
69],
with
.
It is well known that the force
exerted by a fluid with density
and viscosity
on a spherical particle of radius
moving with velocity
in a still fluid, can be expressed in the Laplace domain
as [
34]
The first term at the r.h.s of Equation (
106) is the Stokesian friction factor, the second one corresponds in the time domain to the convolutional Basset force
and the third term is the added-mass contribution
where
is the particle volume, equal to half the mass of the fluid occupying the particle volume. Physically, the added mass contribution corresponds to the back action on the particle of the correlated motion of nearby fluid elements originating from the particle movement within the fluid [
73]. In confined geometries, the added mass
becomes a tensorial quantity dependent on particle position. For instance, for a spherical particle near a solid planar wall,
where
, and
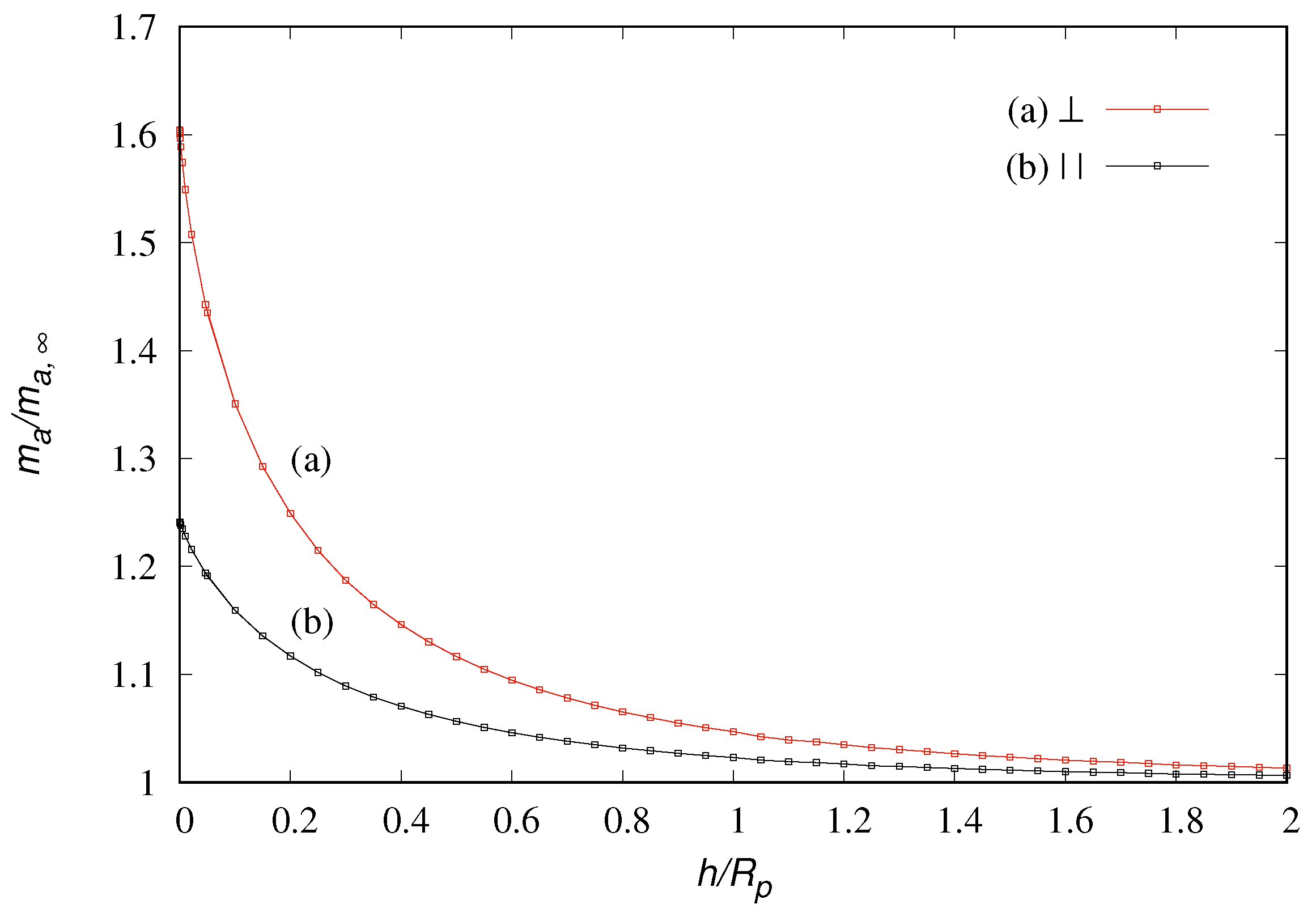
, corresponding to the parallel and transversal added masses, are smooth functions of the particle distance from the wall, as depicted in
Figure 5 attaining a finite value for
.
Similarly, the Basset contribution attains in confined geometries a tensorial, position-dependent character,
where
and
. There are very few works on the characterization of the Basset force in confined geometries [
74], and the detailed study of fluid inertial effects in microchannels and in the presence of solid walls represents an almost virgin field of theoretical and experimental investigation.
Gathering these contributions, and considering also the action of a potential
and of a flow force
, deriving e.g., by a (pressure-drive) flow in the fluid, the equations of motion for a microparticle become,
where
is the stochastic fluctuational contributions, to be determined by enforcing fluctuation-dissipation relations. But also this aspect, owing to the explicit dependence of
on the position
, represents a challenging problem in statistical physics, especially if one is interested in determining the velocity autocorrelation function. Fortunately, for
, corresponding to typical conditions in microfluidic applications, the fluid inertia can be neglected, and the stochastic description of particle motion can be based on the theory addressed in
Section 2 and
Section 3.
7. Concluding Remarks
Microfluidics is not only an emerging field as regards practical applications but it provides a fertile playground for analyzing fundamental physical questions. This is because particle motion at microscale is controlled by thermal stochastic fluctuations, the understanding of which would not only improve the performances of micofluidic devices (e.g. for separation purposes), but also could test the validity of classical physical theories (hydrodynamics) down to the scale where quantum effects should start to appear (going down to the nanoscale).
The fundamental peculiarity of microhydrodynamics in confined geometries is that fluid-particle interactions depend on the position and, owing to fluctuation-dissipation relations, these spatial nonuniformities are transferred to mass-transport properties (diffusion) giving rise to delicate theoretical issues and paradoxes.
As long as fluid inertia is negligible, it is still possible to derive a rather complete characterization of thermal fluctuations, and to perform a simplification of the equations of motion, eliminating the fast velocity variables, thus reducing the statistical description to the Fokker-Planck equation for the particle spatial density corresponding to a classical advection-diffusion equation in physical space and time. However, even in this case, transport paradoxes arise due to the singularity of the hydrodynamic resistances in the neighbourhood of a solid wall.
We have thoroughly analyzed how the lack of integrability of mass-transport models (diffusion equation) in the presence of a surface chemical reaction depend on the simplifying assumption of no-slip boundary conditions. The inclusion of slippage effects at all the solid surfaces (walls and particle) transforms the non-integrable -singularity in the transversal resistance coefficient near a planar wall into a logarithmic singularity (∼) resolving the above mentoned integrability problem. Hovewer, there are physical reasons to conjecture that a more refined modeling of fluid-particle interactions (including compressibility and acoustic effects) could completely eliminate the singularity in at the wall. This issue will be addressed in forthcoming works.
The inclusion of fluid inertia in confined microfluidics opens up other interesting and fundamental problems. The theoretical and numerical estimate of the Basset force even in simple confined systems is a basic ingredient in order to tackle the formulation of fluctuation-dissipation relations, and the efficient determination of the fluctuational force
, similarly to what developed in the free space, in order to determine the short-time behavior of the velocity autocorrelation functions. In this framework, the development of more elaborate statistical physical methods should proceed hand-in-hand with the accurate experimental analysis of particle motion at short time and length scales near a solid surface, following and extending the experimental investigations recently performed for Brownian particles in the free space [
75,
76].