Analysis of Tip Clearance Effect on the Transportation Characteristics of a Multiphase Rotodynamic Pump Based on the Non-Uniform Bubble Model
Abstract
:1. Introduction
2. Physical Model and Numerical Methods
2.1. Geometrical Model of the Pump
2.2. Mesh Arrangement
2.3. Non-Uniform Bubble Model (NUBM)
2.4. Drag Force Model
2.5. Calculation Settings
3. Experimental Setup
4. Results and Discussion
4.1. Validation of the Simulation
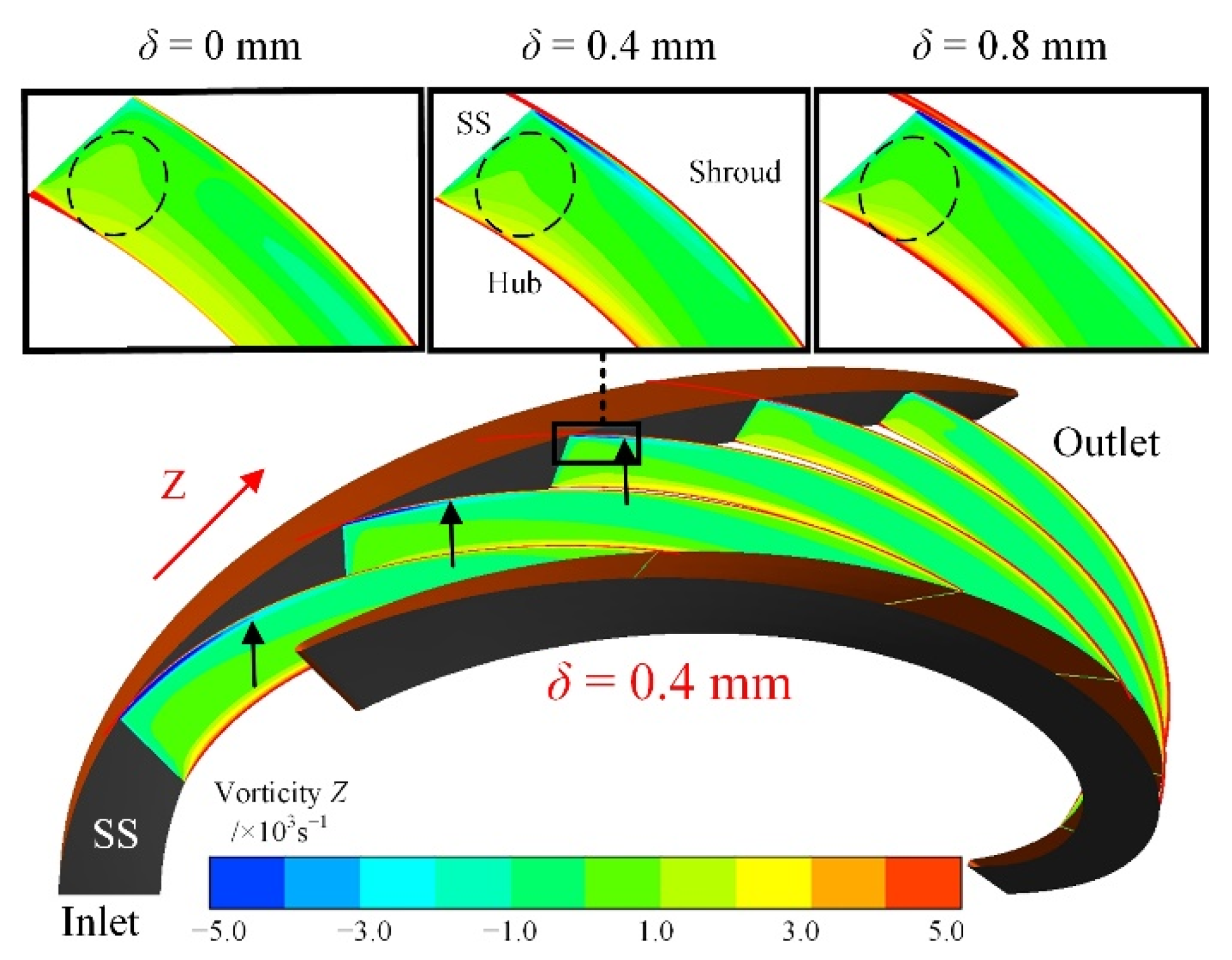
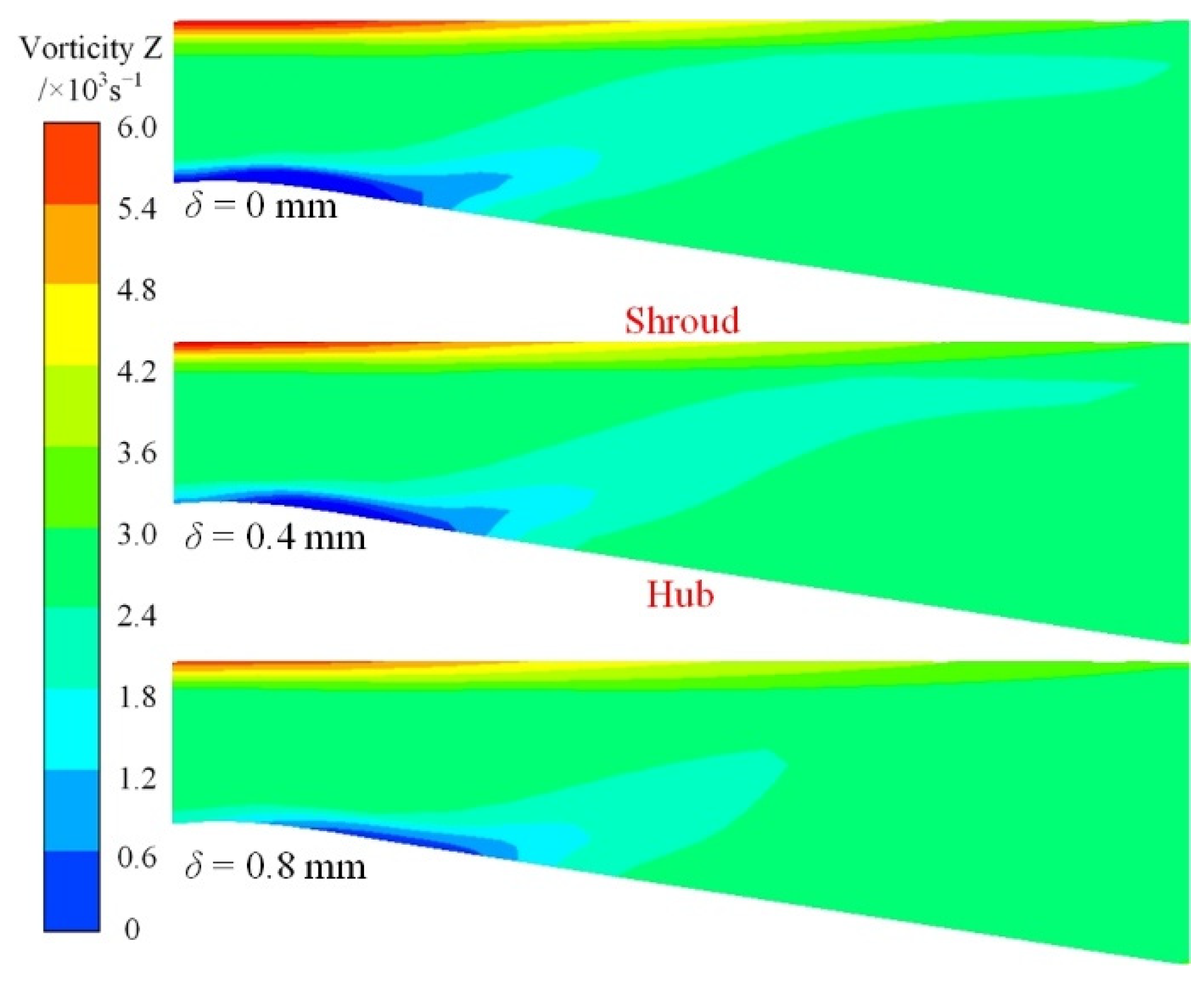
4.2. Leakage Flow Rate and Leakage Vortex
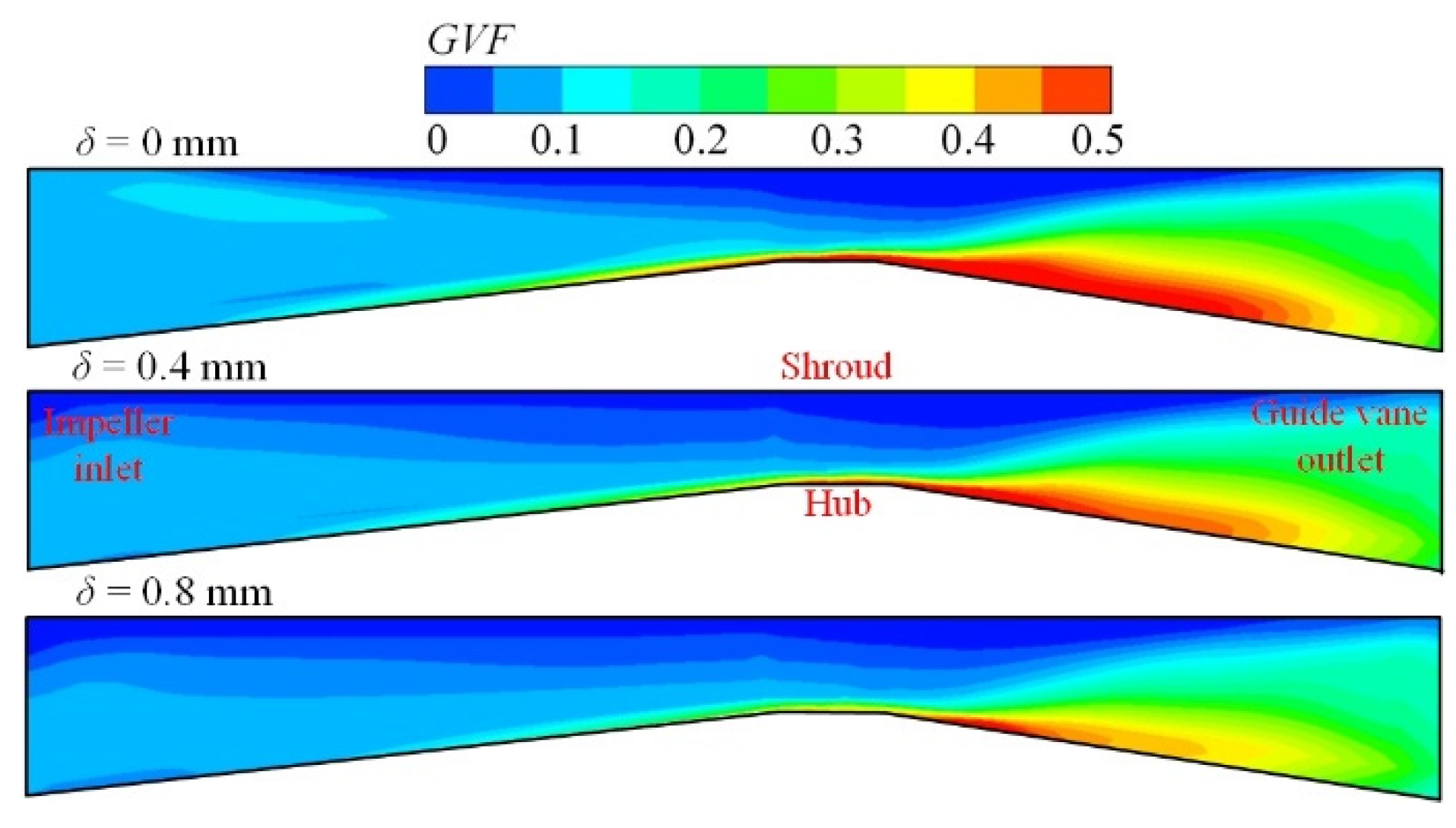
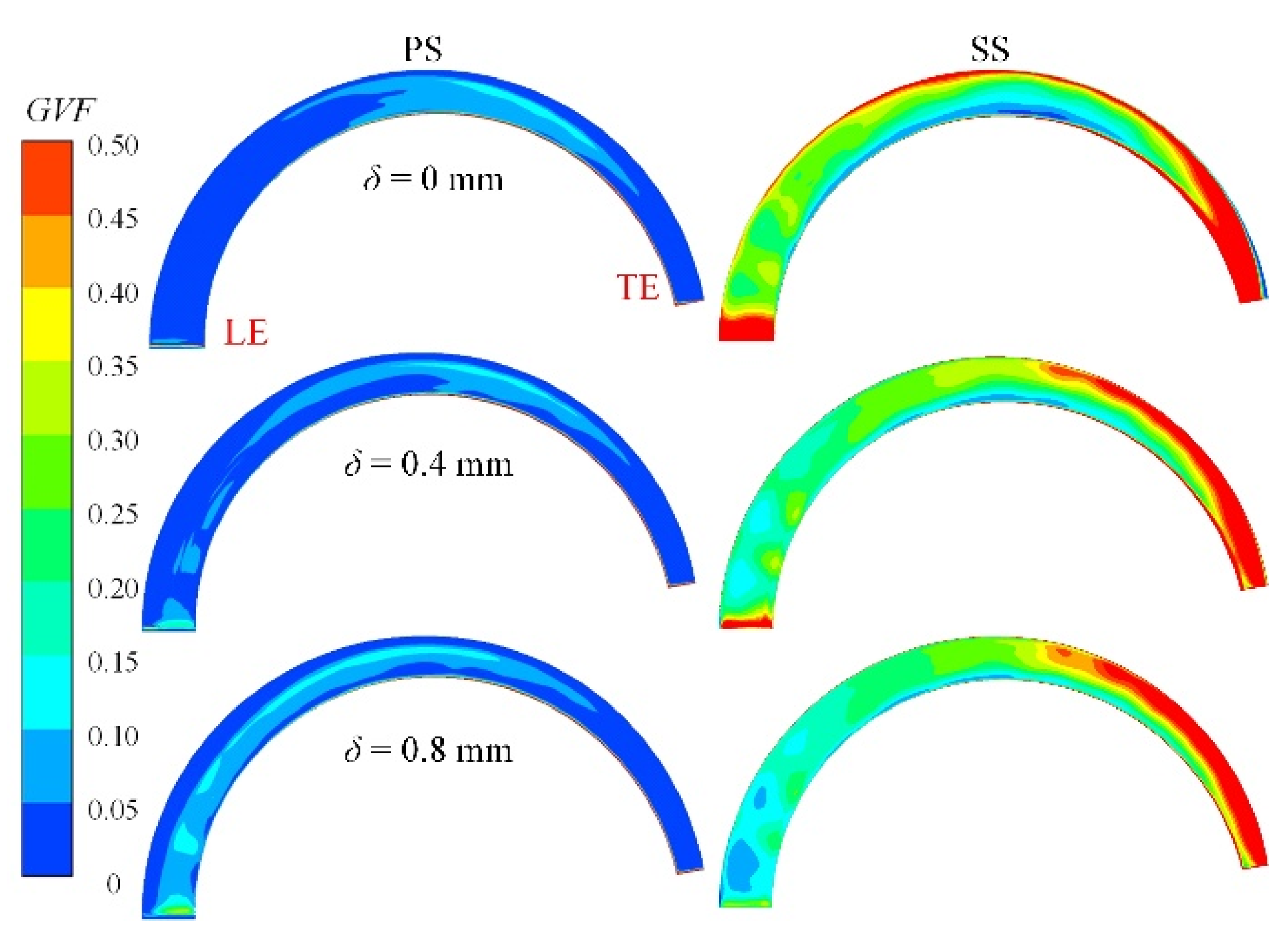
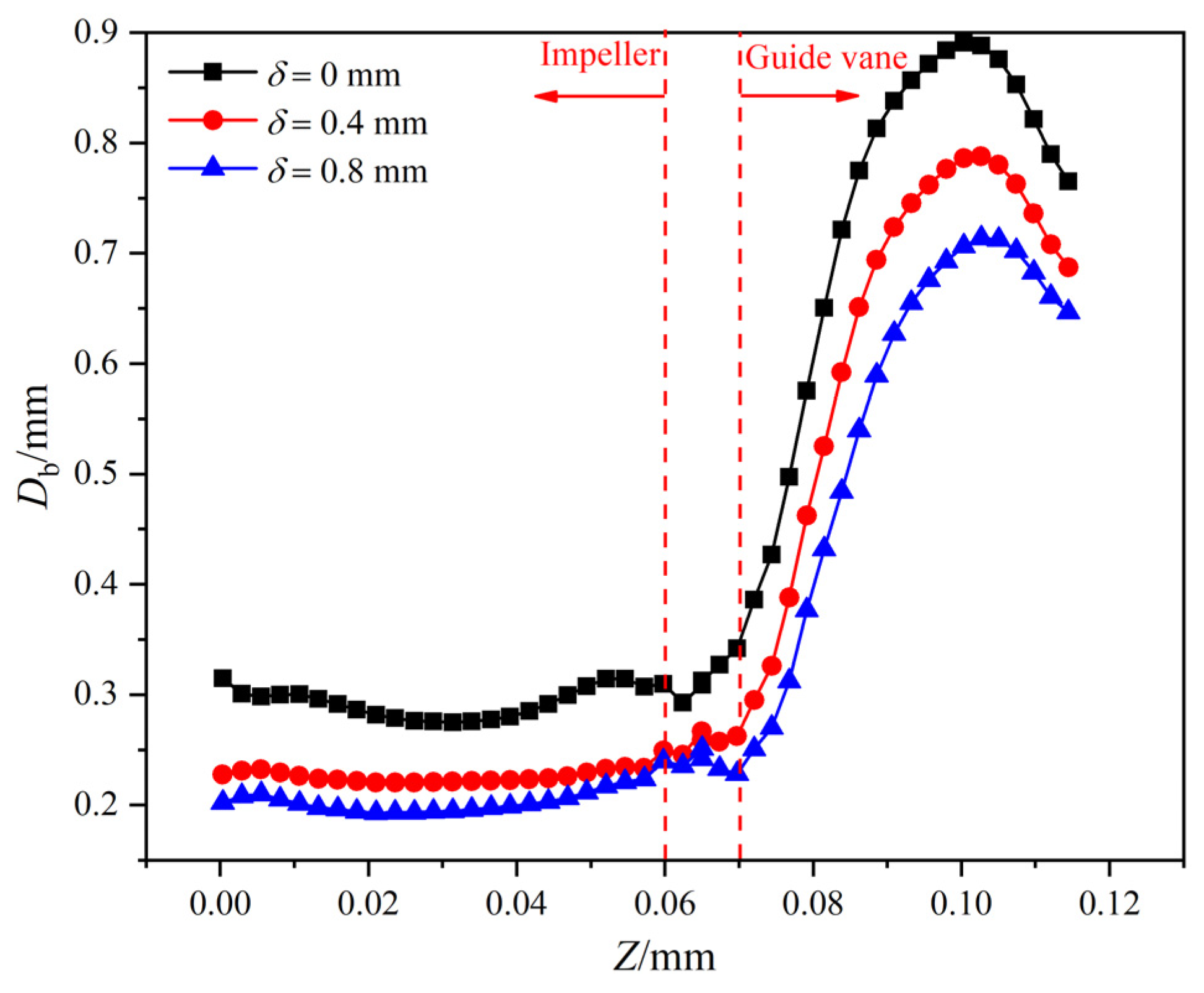
4.3. Gas Phase Distribution
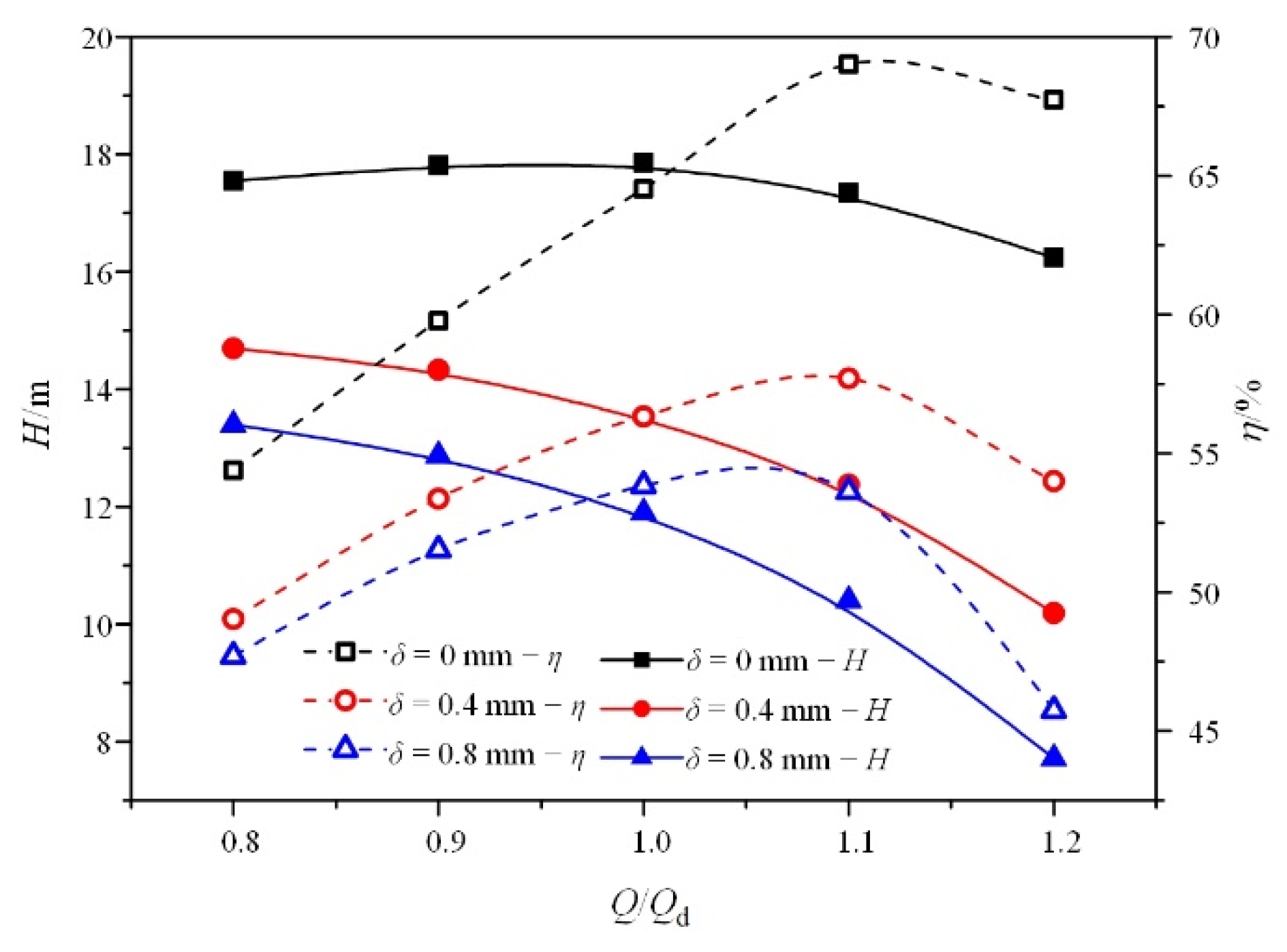
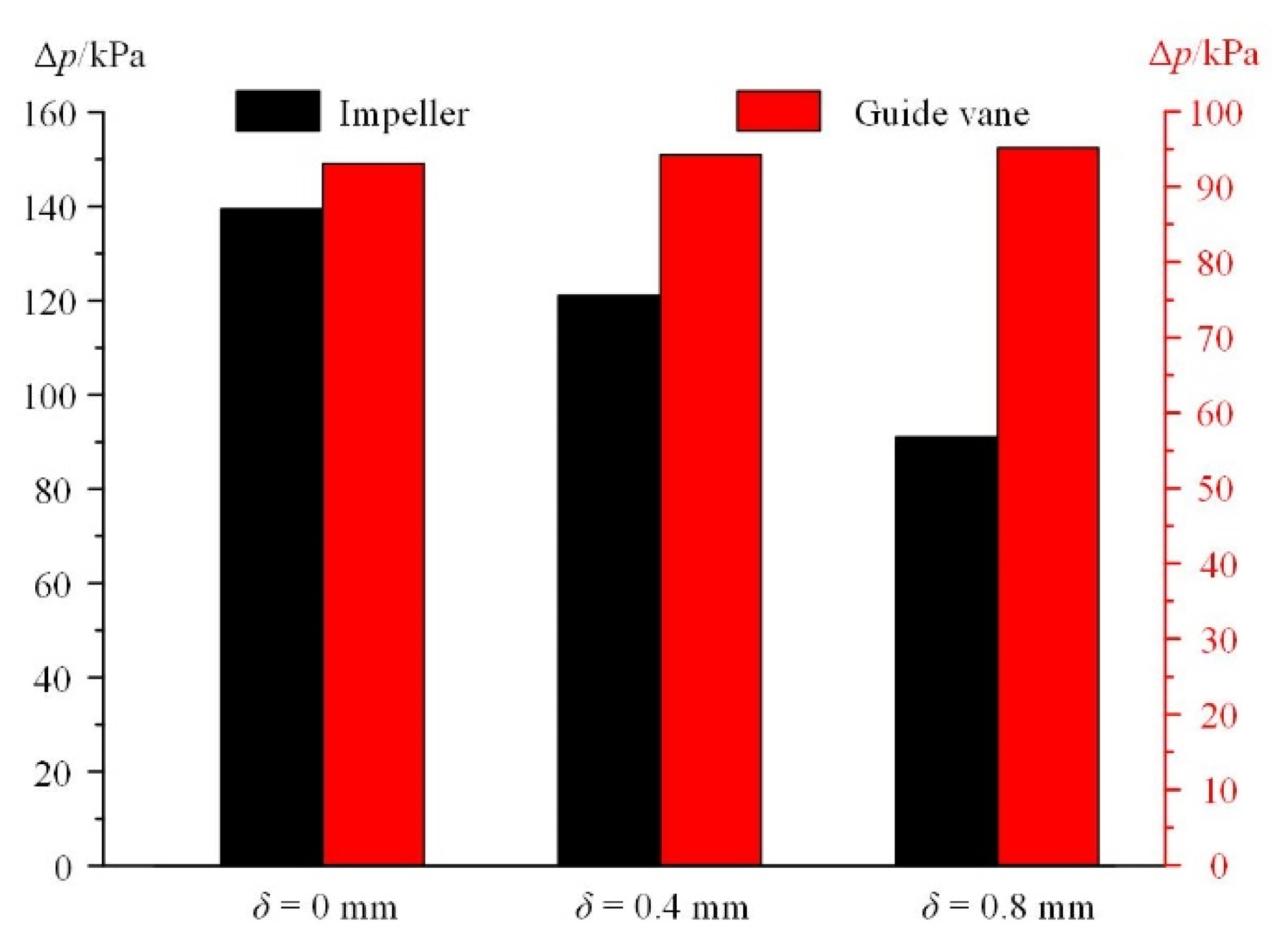
4.4. Energy Performance
5. Conclusions
- (1)
- A larger δ causes a rise in the leakage flow rate and further strengthens the leakage vortex. However, due to the higher flow loss in the impeller, the separation vortex is reduced in the guide vane passage with increasing δ;
- (2)
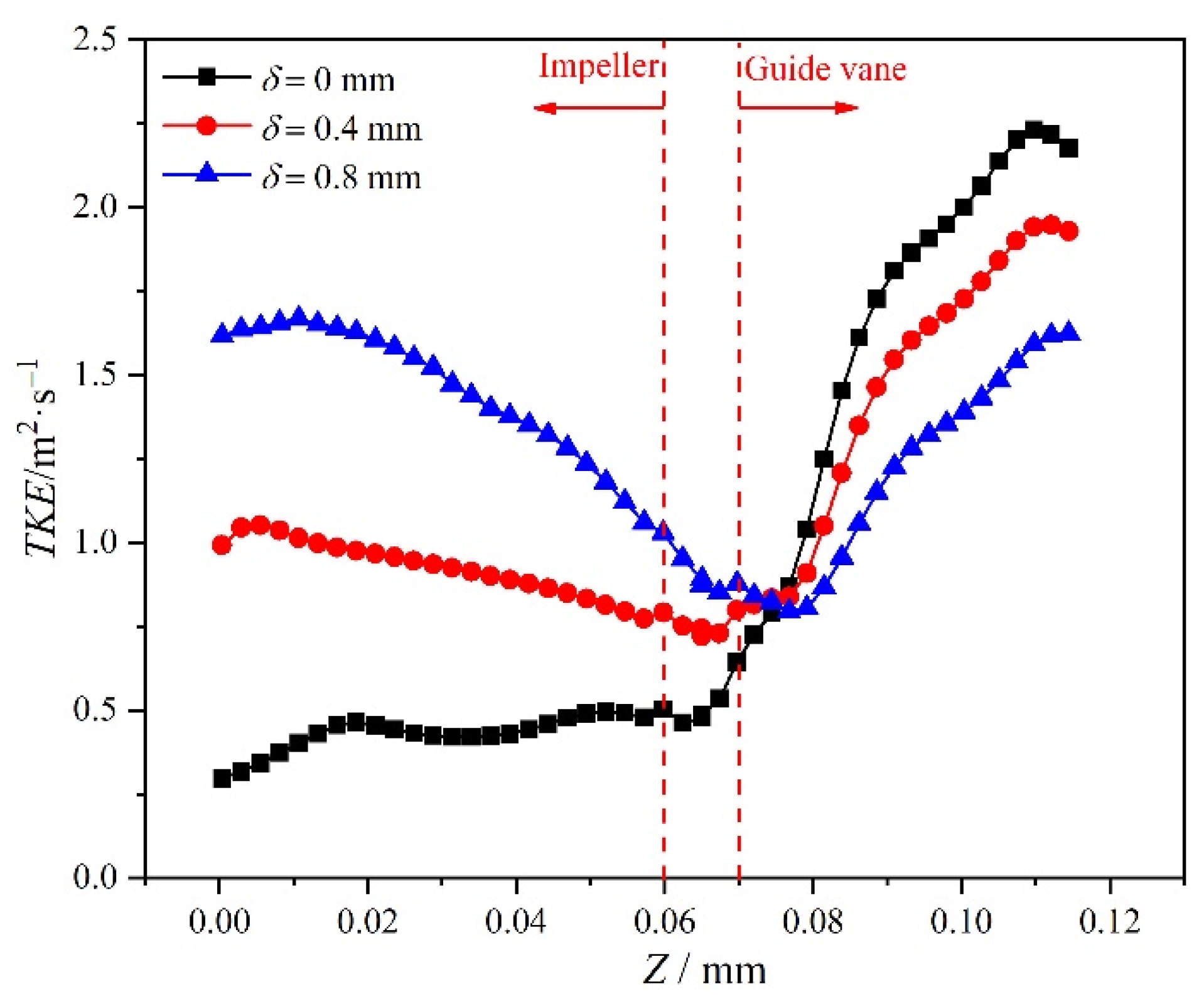
- As δ increases, the disturbance of the tip leakage vortex makes the average TKE increase obviously in the impeller region. The variation in TKE shows the opposite trends with or without tip clearance, and the vortex strength weakens along the streamwise direction, which leads to a decreasing trend of TKE when the tip clearance is considered;
- (3)
- In the impeller inlet, a larger δ leads to more severe accumulation on the PS and decreased gas content on the SS. The blocking effect of the tip leakage vortex makes the liquid kinetic energy increase near the impeller hub; thus, gas accumulation weakens in this region;
- (4)
- Due to the combined effect of more severe gas accumulation and higher flow loss caused by the leakage flow, the pressure increment drops sharply in the impeller region as the δ increases. In the guide vane, however, the pressure increment is raised slightly with a larger δ because of the weaker flow separation in this condition.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Cbr | break-up coefficient, constant |
| Cco | coalescence coefficient, constant |
| CD | drag coefficient, dimensionless |
| CD_mod | modified drag coefficient, dimensionless |
| CD_SN | drag coefficient calculated by the Schiller Naumann model, dimensionless |
| Db | bubble diameter, m |
| FD,k | drag force, N/m3 |
| FL,k | lift force, N/m3 |
| FA,k | added mass force, N/m3 |
| FT,k | turbulent dispersion force |
| H | design head, m |
| IGVF | inlet gas volume fraction, dimensionless |
| n | rotating speed, r/min |
| ns | specific speed, dimensionless |
| p | pressure, Pa |
| P | power, kw |
| Qd | design flow rate, m3/h |
| Re | Reynolds number, dimensionless |
| Reb | modified Reynolds number, dimensionless |
| t | time, s |
| TKE | turbulence kinetic energy, m2/s2 |
| Ug | gas phase relative velocity vector, m/s |
| Ul | liquid phase relative velocity vector, m/s |
| We | Weber number, dimensionless |
| Wec | critical Weber number, dimensionless |
| Greek symbols | |
| δ | tip clearance size, m |
| αg | gas phase volume fraction, dimensionless |
| ξ | bubble number density, m−3 |
| ε | turbulence dissipation rate, m2/s3 |
| σ | surface tension coefficient, N/m |
| ηco | coalescence efficiency, dimensionless |
| ρg | gas phase density, kg/m3 |
| ρl | liquid phase density, kg/m3 |
| μl | liquid phase dynamic viscosity, N·s/m2 |
References
- Xiao, W.Y.; Tan, L. Design method of controllable velocity moment and optimization of pressure fluctuation suppression for a multiphase pump. Ocean Eng. 2021, 220, 108402. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Cai, S.J.; Li, Y.J.; Zhu, H.W.; Zhang, Y.X. Optimization design of multiphase pump impeller based on combined genetic algorithm and boundary vortex flux diagnosis. J. Hydrodyn. 2017, 29, 1023–1034. [Google Scholar] [CrossRef]
- Liu, M.; Tan, L.; Xu, Y.; Cao, S.L. Optimization design method of multi-stage multiphase pump based on Oseen vortex. J. Petrol. Sci. Eng. 2020, 184, 106532. [Google Scholar] [CrossRef]
- Yang, X.; Qu, Z.; Wu, Y.Y. Frictional loss studies and experimental performance of a new synchronal rotary multiphase pump. J. Fluid. Eng. 2011, 133, 041303. [Google Scholar] [CrossRef]
- Kim, J.H.; Lee, H.C.; Kim, J.H.; Choi, Y.S.; Yoon, Y.H.; Yoo, S.; Choi, W.C. Improvement of hydrodynamic performance of a multiphase pump using design of experiment techniques. J. Fluid. Eng. 2015, 137, 181301. [Google Scholar] [CrossRef]
- Cao, S.L.; Peng, G.; Yu, Z.Y. Hydrodynamic design of rotodynamic pump impeller for multiphase pumping by combined approach of inverse design and CFD analysis. J. Fluid. Eng. 2005, 127, 330–338. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Cai, S.J.; Zhu, H.W.; Zhang, Y.X. Experimental investigation of the flow at the entrance of a rotodynamic multiphase pump by visualization. J. Petrol. Sci. Eng. 2015, 126, 254–261. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Cai, S.J.; Li, Y.J.; Zhu, H.W.; Zhang, Y.X. Visualization study of gas-liquid two-phase flow patterns inside a three-stage rotodynamic multiphase pump. Exp. Therm. Fluid Sci. 2016, 70, 125–138. [Google Scholar] [CrossRef]
- Shi, Y.; Zhu, H.W.; Zhang, J.Y.; Zhang, J.T.; Zhao, J.L. Experiment and numerical study of a new generation three-stage multiphase pump. J. Petrol. Sci. Eng. 2018, 169, 471–484. [Google Scholar] [CrossRef]
- Zhu, J.J.; Zhu, H.W.; Zhang, J.C.; Zhang, H.Q. A numerical study on flow patterns inside an electrical submersible pump (ESP) and comparison with visualization experiments. J. Petrol. Sci. Eng. 2019, 173, 339–350. [Google Scholar] [CrossRef]
- Suh, J.; Kim, J.; Choi, Y. Development of numerical Eulerian-Eulerian models for simulating multiphase pumps. J. Petrol. Sci. Eng. 2010, 22, 35–43. [Google Scholar] [CrossRef]
- Yu, Z.Y.; Zhu, B.S.; Cao, S.L.; Liu, Y. Effect of virtual mass force on the mixed transport process in a multiphase rotodynamic pump. Adv. Mech. Eng. 2014, 6, 958352. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.W.; Xie, X.; Zhu, B.S.; Ma, Z. Analysis of phase interaction and gas holdup in a multistage multiphase rotodynamic pump based on a modified Euler two-fluid model. Renew. Energ. 2021, 164, 1496–1507. [Google Scholar] [CrossRef]
- Yu, Z.Y.; Zhu, B.S.; Cao, S.L. Interphase force analysis for air-water bubbly flow in a multiphase rotodynamic pump. Eng. Computation. 2015, 32, 2166–2180. [Google Scholar] [CrossRef] [Green Version]
- Pourtousi, M.; Sahu, J.; Ganesan, P. Effect of interfacial forces and turbulence models on predicting flow pattern inside the bubble column. Chem. Eng. Process. 2014, 75, 38–47. [Google Scholar] [CrossRef]
- Zhang, W.W.; Yu, Z.Y.; Li, Y.J. Application of a non-uniform bubble model in a multiphase rotodynamic pump. J. Petrol. Sci. Eng. 2018, 173, 1316–1322. [Google Scholar] [CrossRef]
- Li, Y.J.; Yu, Z.Y. Distribution and motion characteristics of bubbles in a multiphase rotodynamic pump based on modified non-uniform bubble model. J. Petrol. Sci. Eng. 2020, 195, 107569. [Google Scholar] [CrossRef]
- Li, Y.J.; Yu, Z.Y.; Sun, W.H. Drag coefficient modification for turbulent gas-liquid two-phase flow in a rotodynamic pump. Chem. Eng. J. 2021, 417, 128570. [Google Scholar] [CrossRef]
- Zhang, H.; Shi, W.D.; Chen, B.; Zhang, Q.H.; Cao, W.D. Experimental study of flow field in interference area between impeller and guide vane of axial flow pump. J. Hydrodyn. 2014, 26, 894–901. [Google Scholar] [CrossRef]
- Liu, Y.B.; Tan, L. Tip clearance on pressure fluctuation intensity and vortex characteristic of a mixed flow pump as turbine at pump mode. Renew. Energ. 2018, 129, 606–615. [Google Scholar] [CrossRef]
- Hayat, T.; Yasmin, H.; Ahmad, B.; Chen, G.Q. Exact solution for peristaltic transport of a micropolar fluid in a channel with convective boundary conditions and heat source/sink. Z. Für Nat. A 2014, 69, 425–432. [Google Scholar] [CrossRef]
- Yasmin, H.; Iqbal, N. Convective mass/heat analysis of an electroosmotic peristaltic flow of ionic liquid in a symmetric porous microchannel with soret and dufour. Math. Probl. Eng. 2021, 2021, 2638647. [Google Scholar] [CrossRef]
- Iqbal, N.; Yasmin, H.; Bibi, A.; Attiya, A.A. Peristaltic motion of Maxwell fluid subject to convective heat and mass conditions. Ain. Shams. Eng. J. 2021, 12, 3021–3031. [Google Scholar] [CrossRef]
- Xu, Y.; Tan, L.; Liu, Y.B.; Cao, S.L. Pressure fluctuation and flow pattern of a mixed-flow pump with different blade tip clearances under cavitation condition. Adv. Mech. Eng. 2017, 9, 2071938710. [Google Scholar] [CrossRef]
- Hao, Y.; Tan, L. Symmetrical and unsymmetrical tip clearances on cavitation performance and radial force of a mixed flow pump as turbine at pump mode. Renew. Energ. 2018, 127, 368–376. [Google Scholar] [CrossRef]
- Huang, Z.W.; Huang, Z.; Fan, H.G. Influence of C groove on energy performance and noise source of a NACA0009 hydrofoil with tip clearance. Renew. Energ. 2020, 159, 726–735. [Google Scholar] [CrossRef]
- Zhang, D.S.; Shi, L.; Shi, W.D.; Zhao, R.J.; Wang, H.Y.; van Esch, B.P.M. Numerical analysis of unsteady tip leakage vortex cavitation cloud and unstable suction-side-perpendicular cavitating vortices in an axial flow pump. Int. J. Multiphas. Flow 2015, 77, 244–259. [Google Scholar] [CrossRef]
- Zhang, J.S.; Fan, H.G.; Zhang, W.; Xie, Z.F. Energy performance and flow characteristics of a multiphase pump with different tip clearance sizes. Adv. Mech. Eng. 2019, 11, 1–14. [Google Scholar] [CrossRef]
- Liu, Y.B.; Tan, L.; Hao, Y.; Xu, Y. Energy performance and flow patterns of a mixed flow pump with different tip clearance sizes. Energies 2017, 10, 191. [Google Scholar] [CrossRef]
- Han, C.Z.; Xu, S.; Cheng, H.Y.; Ji, B.; Zhang, Z.Y. LES method of the tip clearance vortex cavitation in a propelling pump with special emphasis on the cavitation-vortex interaction. J. Hydrodyn. 2020, 32, 736–746. [Google Scholar] [CrossRef]
- Wang, L.K.; Lu, J.L.; Liao, W.L.; Guo, P.C.; Feng, J.J.; Luo, X.Q.; Wang, W. Numerical investigation of the effect of T-shaped blade on the energy performance improvement of a semi-open centrifugal pump. J. Hydrodyn. 2021, 11, 2072152310. [Google Scholar] [CrossRef]
- Liu, Y.B.; Tan, L. Method of T shape tip on energy improvement of a hydrofoil with tip clearance in tidal energy. Renew. Energ. 2020, 149, 42–54. [Google Scholar] [CrossRef]
- Liu, Y.B.; Tan, L. Method of C groove on vortex suppression and energy performance improvement for a NACA0009 hydrofoil with tip clearance in tidal energy. Energy 2018, 155, 448–461. [Google Scholar] [CrossRef]
- Tan, L.; Xie, Z.; Liu, Y.B.; Hao, Y.; Xun, Y. Influence of T-shape tip clearance on performance of a mixed-flow pump. P. I. Mech. Eng. A-J. Pow. 2018, 232, 386–396. [Google Scholar]
- Lane, G.; Schwarz, M.; Evans, G. Numerical modelling of gas-liquid flow in stirred tanks. Chem. Eng. Sci. 2005, 60, 2203–2214. [Google Scholar] [CrossRef]
- Tabib, M.; Schwarz, P. Quantifying sub-grid scale (SGS) turbulent dispersion force and its effect using one-equation SGS large eddy simulation (LES) model in a gas-liquid and a liquid-liquid system. Chem. Eng. Sci. 2011, 66, 3071–3086. [Google Scholar] [CrossRef]
- Sun, W.H.; Tan, L. Cavitation-vortex-pressure fluctuation interaction in a centrifugal pump using bubble rotation modified cavitation model under partial load. J. Fluid. Eng. 2020, 142, 051206. [Google Scholar] [CrossRef]

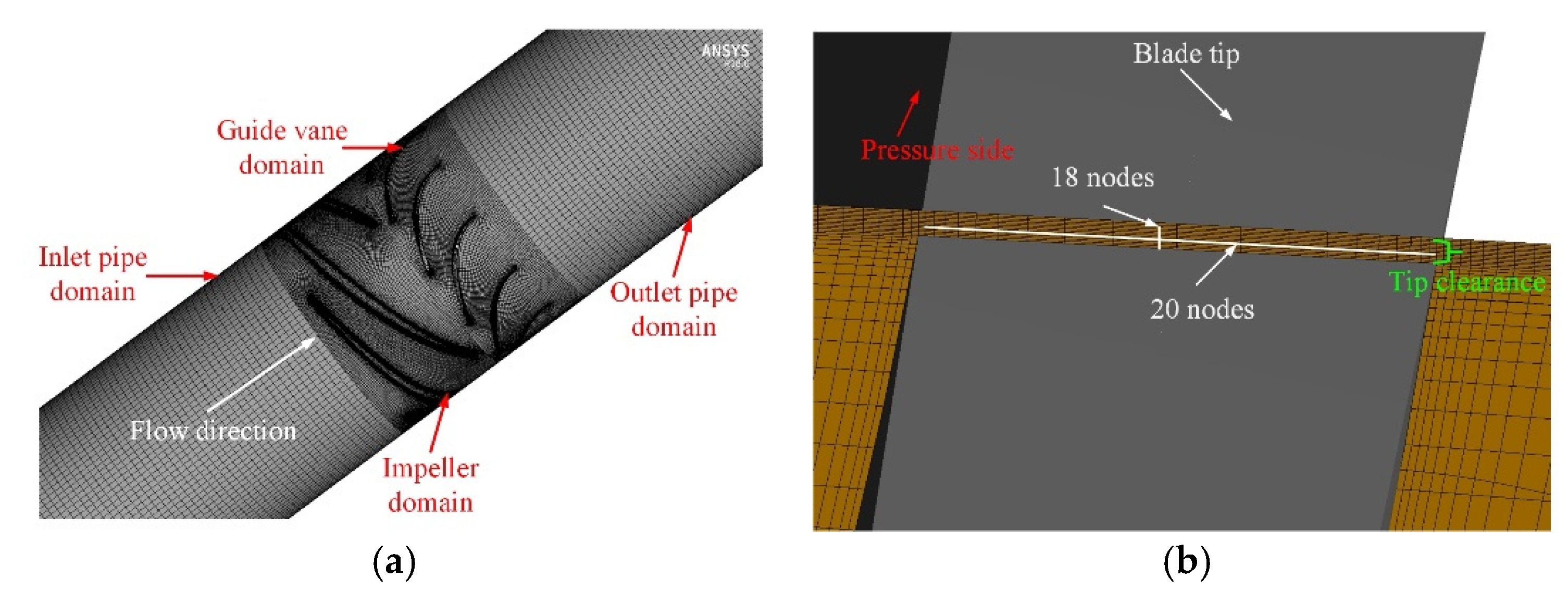
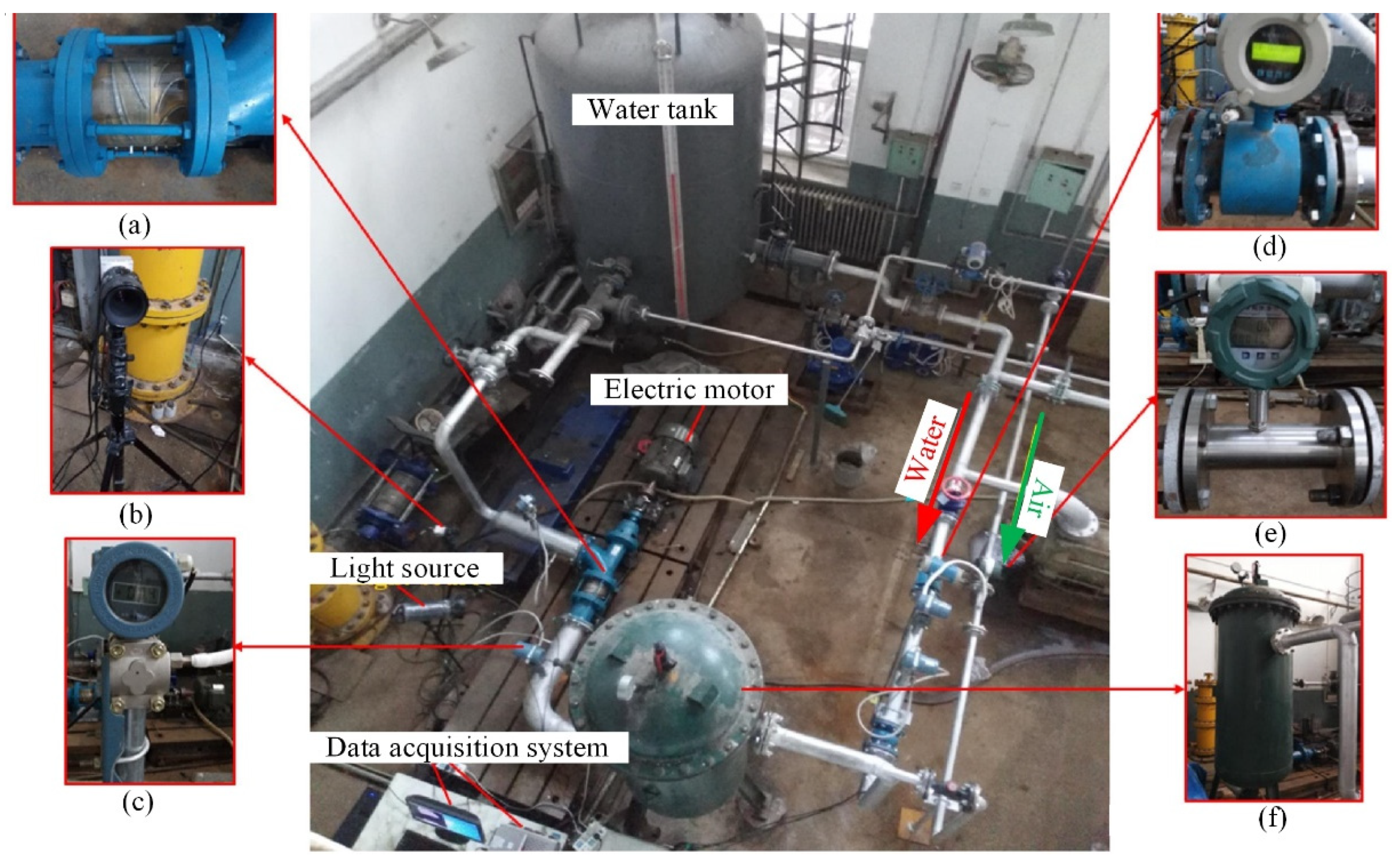
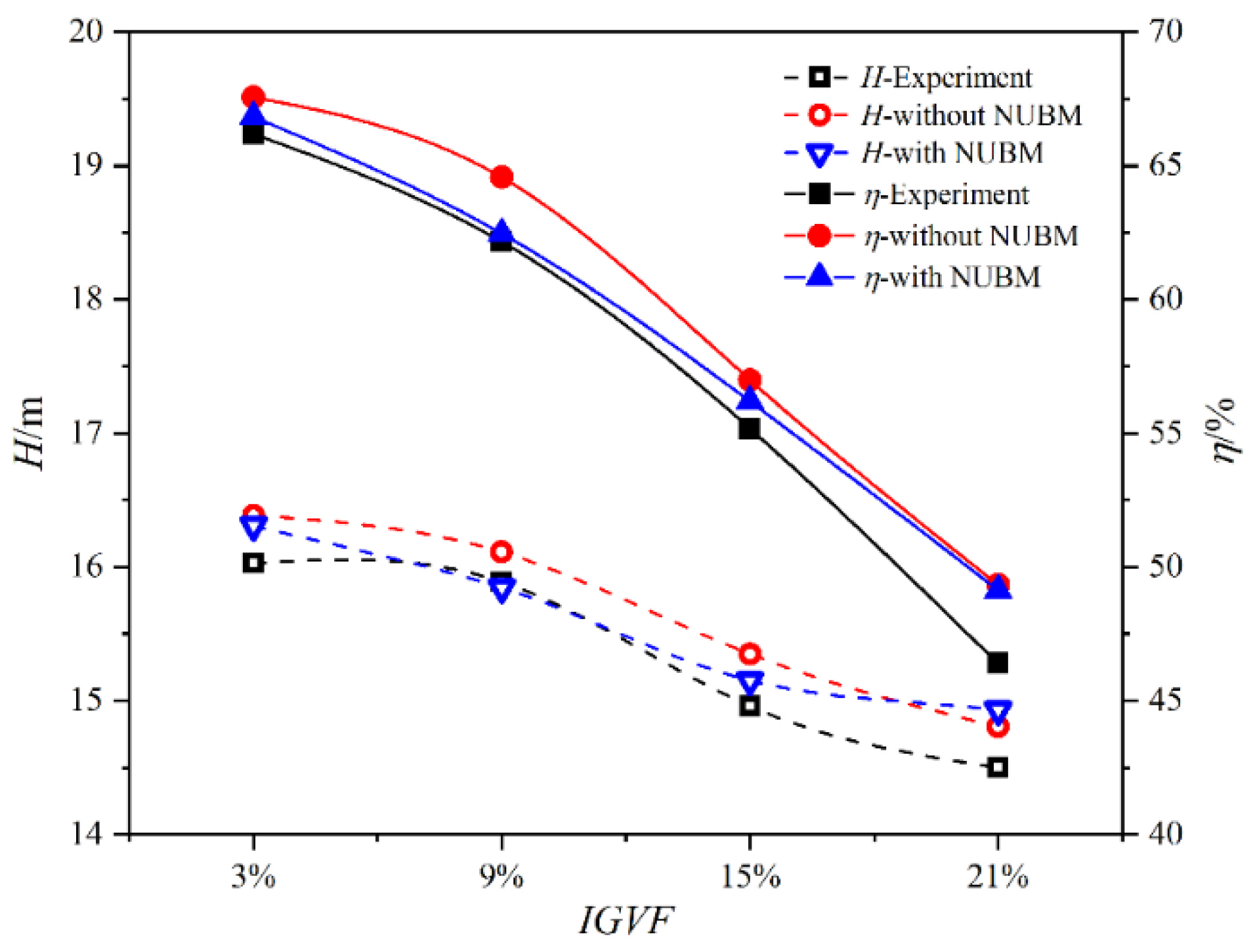
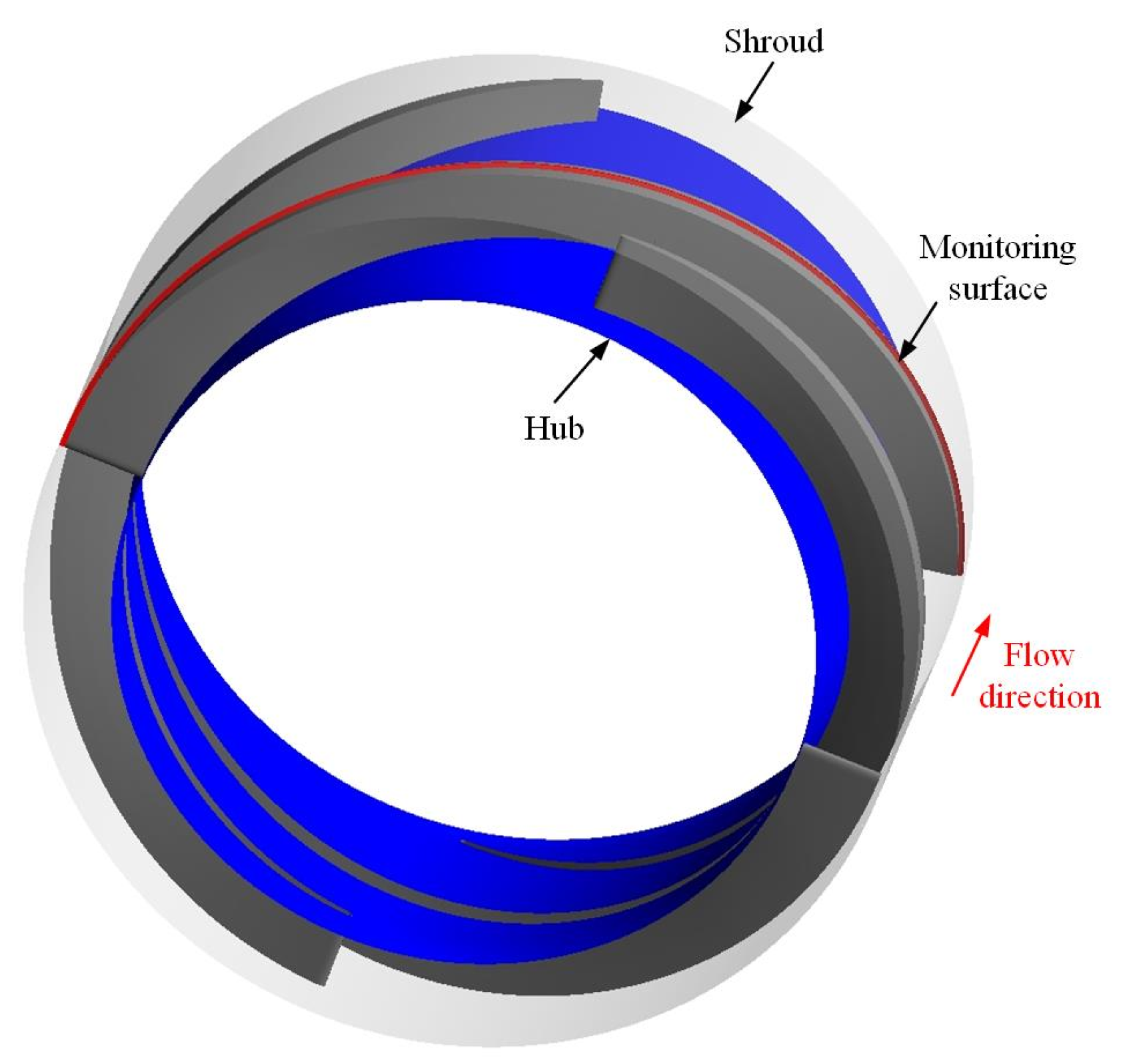


| Multiphase Pump | Items | Values | Units |
|---|---|---|---|
| Impeller | Number of impeller blade | 4 | - |
| Shroud diameter of impeller inlet | 150 | mm | |
| Shroud diameter of impeller outlet | 150 | mm | |
| Hub diameter of impeller inlet | 120 | mm | |
| Hub diameter of impeller outlet | 134 | mm | |
| Guide vane | Number of guide vane blade | 11 | - |
| Shroud diameter of guide vane outlet | 150 | mm | |
| Hub diameter of guide vane outlet | 120 | mm | |
| Design operating point | Rotating speed n | 2950 | r/min |
| Specific speed ns | 166 | - | |
| Design head H | 15 | m | |
| Design flow rate Qd | 50 | m3/h | |
| Power P | 7.35 | KW |
| Item | Mesh1 | Mesh2 | Mesh3 | Mesh4 |
|---|---|---|---|---|
| Pipe | 54,516 | 54,516 | 54,516 | 54,516 |
| Impeller | 660,384 | 1,226,640 | 2,364,667 | 3,237,444 |
| Guide vane | 386,848 | 619,080 | 1,164,240 | 1,424,192 |
| Total | 1,101,748 | 1,900,236 | 3,583,423 | 4,716,152 |
| Δp/Δp1 | 1.0000 | 0.9831 | 0.9783 | 0.9775 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Yu, Z.; Zhang, K.; Liu, Z. Analysis of Tip Clearance Effect on the Transportation Characteristics of a Multiphase Rotodynamic Pump Based on the Non-Uniform Bubble Model. Fluids 2022, 7, 58. https://doi.org/10.3390/fluids7020058
Sun W, Yu Z, Zhang K, Liu Z. Analysis of Tip Clearance Effect on the Transportation Characteristics of a Multiphase Rotodynamic Pump Based on the Non-Uniform Bubble Model. Fluids. 2022; 7(2):58. https://doi.org/10.3390/fluids7020058
Chicago/Turabian StyleSun, Weihua, Zhiyi Yu, Ke Zhang, and Zheng Liu. 2022. "Analysis of Tip Clearance Effect on the Transportation Characteristics of a Multiphase Rotodynamic Pump Based on the Non-Uniform Bubble Model" Fluids 7, no. 2: 58. https://doi.org/10.3390/fluids7020058
APA StyleSun, W., Yu, Z., Zhang, K., & Liu, Z. (2022). Analysis of Tip Clearance Effect on the Transportation Characteristics of a Multiphase Rotodynamic Pump Based on the Non-Uniform Bubble Model. Fluids, 7(2), 58. https://doi.org/10.3390/fluids7020058






