Abstract
The dynamic contact line plays a key role in various fields of interfacial physics, including bioprinting, nano-scale printing, three-dimensional printing, biomaterials, tissue engineering, smart materials, flexible printed electronics, biomedicine, and healthcare. However, there is still a lack of thorough physical understanding of its real behavior in numerous complex problems in nature and technology. The dynamic contact line exhibits a complex conformation in real-life fluid dynamics problems. Therefore, this review presents two main long-standing models that describe the physics of the dynamic contact line: hydrodynamics theory and molecular kinetics theory. Next, the role of the dynamic contact line in current advanced technologies is discussed. Finally, this review discusses future research directions to enhance the power of current physical models of the dynamic contact line.
1. Introduction
When a liquid is in contact with a substrate in a gaseous environment, a contact line is formed. The contact line, also known as the three-phase contact line, is a line of intersection of three phases: solid, liquid, and gas. The contact line moves on the substrate until the total energy of the contact line reaches its minimum value, which is the thermodynamic equilibrium state. In this dynamic condition, the contact line is defined as the dynamic contact line [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22].
The physics of the dynamic contact line has been an important subject in the field of interfacial science. The physics of the dynamic contact line is a multidisciplinary topic, and it involves numerous scientific areas, including anti-icing of air planes, various conventional coatings, smart coatings, functional coatings, inkjet printing, bio-printing, tissue engineering, functional organs, flexible printed electronics, biomaterials, smart materials, microfluidics, nanofluidics, phase-change heat exchangers, oil recovery, power plants, and various biological systems [2,3,4,5,6,7,8,9,10,11,12,13,14,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60].
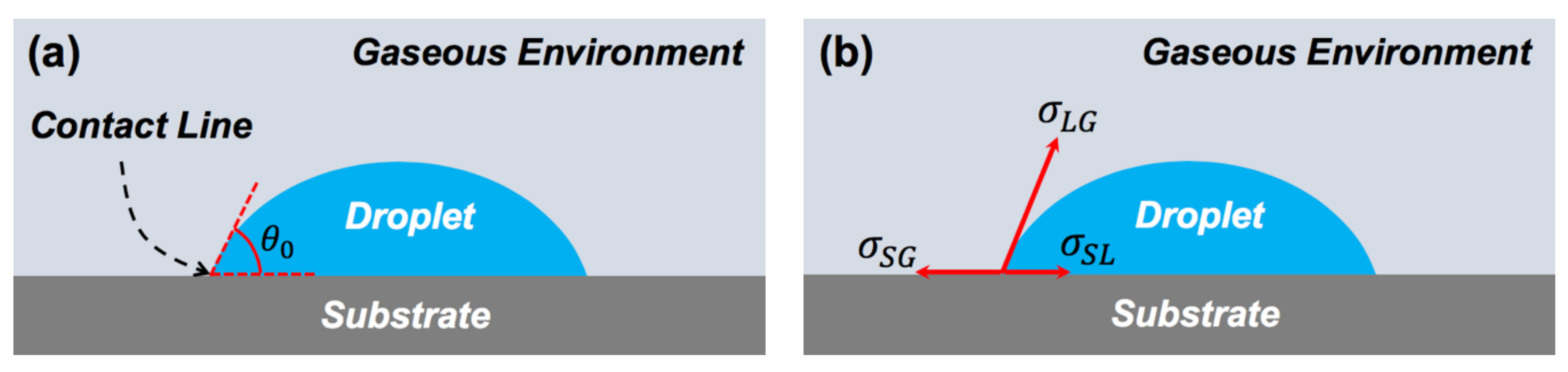
The angle between the liquid–air interface and liquid–substrate interface at the dynamic contact line is known as the dynamic contact angle (). When the dynamic contact line reaches the equilibrium state, the dynamic contact angle becomes the static contact angle () [61,62]. The static contact angle is defined by the balance of the interfacial tensions at the contact line, as demonstrated by Figure 1 and formulated by Equation (1) [63]:
in which is the interfacial tension at the liquid–gas interface, is the interfacial tension at the solid–gas interface, and is the interfacial tension at the solid–liquid interface.
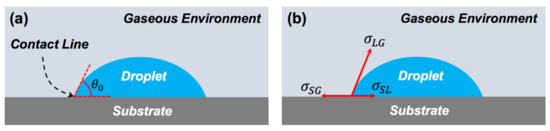
Figure 1.
(a) Schematic representation of the contact line and the static contact angle. (b) A droplet, deposited on a substrate, is in the equilibrium state with the balance of the interfacial tensions along the contact line.
There are two mechanisms for contact line dynamics: spontaneous and forced [64,65,66]. In the spontaneous mechanism, the contact line moves on a substrate to reach the equilibrium state without any external driving force. In spontaneous mode, the capillary force and gravity play key roles in inducing the motion of the contact line on the substrate to reduce the dynamic contact angle to achieve the minimum energy value in the equilibrium state (static contact angle). For the case of a droplet spreading on a substrate, the gravitational effect is negligible as the droplet size is less than the capillary length (), where is the droplet surface tension, is the droplet density, and is the gravitational acceleration [67].
In the forced mechanism, the contact line dynamics are governed by an external driving force (or forces). In forced contact line dynamics, the balance of the forces is between the tendency of the contact line to achieve the equilibrium condition and the external force(s) to induce the contact line to deviate from the equilibrium condition [68]. There are two modes of the forced contact line dynamics: advancing and receding. In advancing contact line dynamics, the dynamic contact angle is denoted as the advancing dynamic contact angle (). In receding contact line dynamics, the dynamic contact angle is denoted as the receding dynamic contact angle ().
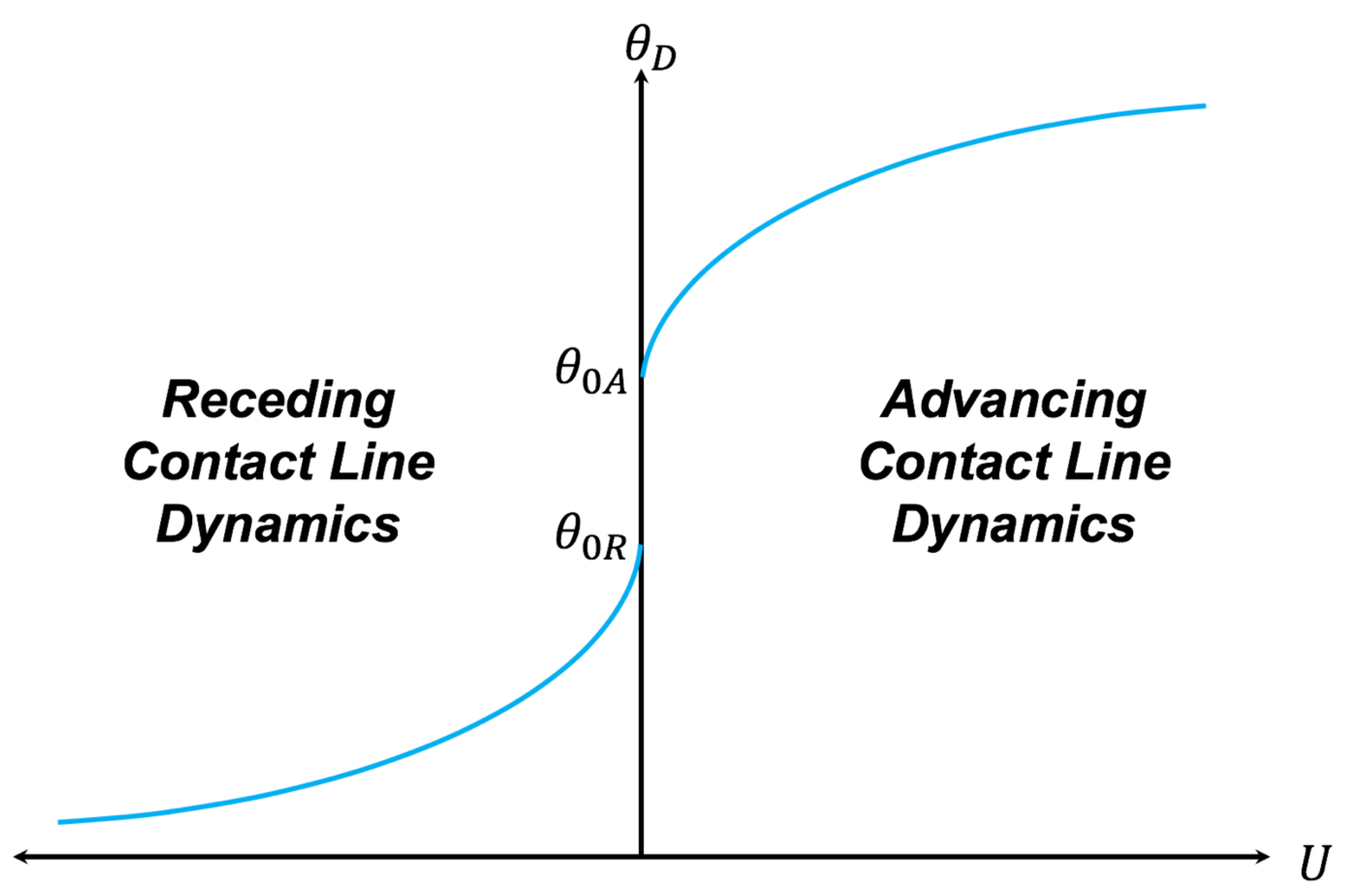
The physics of the dynamic contact line is conventionally defined in terms of the relation between the dynamic contact angle () and the contact line velocity (), as represented in Figure 2 [19,69,70,71,72]. It is important to note that the contact line velocity is not necessarily constant in the contact line dynamics, as shown in Figure 2. It depends on the mode of contact line motion: spontaneous or forced. In forced contact line motion, the contact line velocity can be controlled to be constant. In spontaneous contact line motion, the contact line velocity might not be constant, such as a droplet spreading on a smooth glass surface in which the contact line velocity reduces as the dynamic contact angle decreases until the droplet reaches the equilibrium state. In the physical relation between the dynamic contact angle and the contact line velocity, the equilibrium advancing contact angle () and equilibrium receding contact angle () are also important [68,69,70,71,72]. Various experimental techniques have been used to measure the contact angle, including capillary rise, the Wilhelmy plate, a continuous vertical fiber, and a continuous moving tape [73,74,75,76,77,78,79].
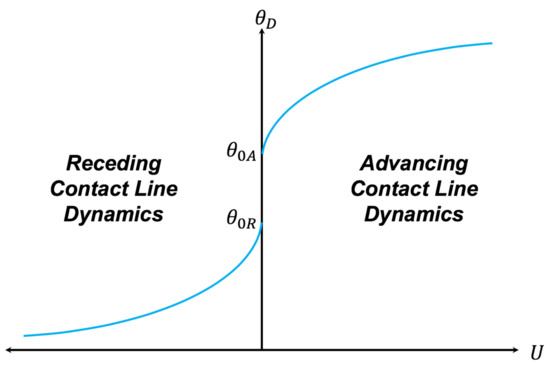
Figure 2.
Relation between contact line velocity and dynamic contact angle for advancing contact line dynamics and receding contact line dynamics.
The difference in value between the equilibrium of the advancing and receding contact angles is known as the contact angle hysteresis, as shown in Figure 2. The contact angle hysteresis signifies the heterogeneity in substrate roughness and substrate chemistry [80,81,82,83,84,85,86,87,88,89,90]. The contact angle hysteresis causes the pinning event and stick–slip behavior of the dynamic contact line on the substrate.
The stick–slip behavior is the phenomenon in which the dynamic contact line remains stationary for most of the time, and only from time to time does it move rapidly and abruptly [91]. The pinning event is a phenomenon in which the dynamic contact line does not move until the contact angle reaches the critical values (critical advancing and receding dynamic contact angles). The difference between the critical advancing and receding dynamic contact angles is defined as the contact angle hysteresis, which features the pinning effect. The pinning effect prevents the dynamic contact line from moving over the substrate [92].
Numerous studies have attempted to reach a physical understanding of the underlying mechanism of the dynamic contact line. Several theories have been proposed to define the physics of the moving contact line by determining the relation between the dynamic contact angle and the contact line velocity [21,22,64,65,66,68,69,70,71,72,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122]. Among them, two long-standing theories have been largely accepted in the interfacial physics community: hydrodynamics and molecular kinetics.
Regarding the significance of the dynamic contact line in various scientific fields and technologies, a recent comprehensive review outlined the challenges of the computational approach to describe the physics of the dynamic contact line [123]. There are several well-established computational models that numerically describe the flow physics of the dynamic contact line [123]. These computational models are based on direct numerical simulations of the dynamic contact line using the volume of the fluid technique [123]. There have been advancements in the volume-of-fluid-based computations to describe the dynamics of a moving contact line [123]. One of the advancements in the field of numerical simulation of the dynamic contact line was the combination of the simulation of the flow physics in a macroscopic region with the theory of hydrodynamics in the proximity of the dynamic contact line. The other main advancement in this field was the computational explanation of the dynamic contact line in a microscopic region by considering the van der Waals force [123].
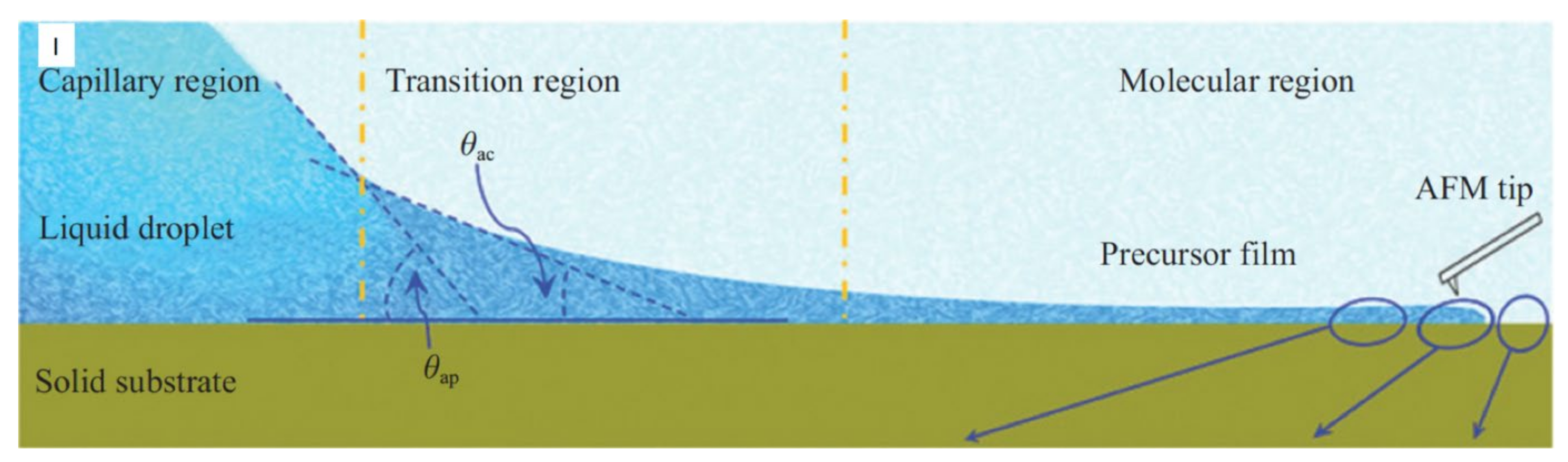
The physics of the dynamic contact line involves multidisciplinary research. Physically understanding the dynamic contact line problems, such as flexible printed electronics, biosensors, functional smart nano-bio-materials, and printable solar cells, requires collaboration between numerous fields, including electrical engineering, materials science, mechanical engineering, applied physics, applied mathematics, biology, chemistry, and nanoscience [50,124]. Moreover, the dynamic contact line is a multi-scale physical problem that requires deep insights from all scales to define the true physics of the dynamic contact line (Figure 3). At the micro scale, a thin liquid layer known as the precursor film forms on a substrate, which advances the dynamic contact line [124]. At the macro scale, the hydrostatic pressure from the bulk of the liquid affects the physics of the dynamic contact line to achieve equilibrium [124]. At the mesoscopic scale, the physics of the dynamic contact line are governed by hydrostatic pressure and disjoining pressure [124].
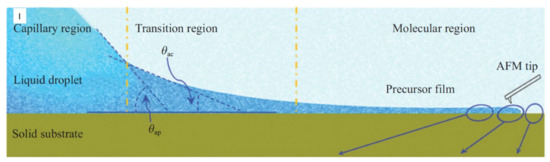
Figure 3.
Multi-scale representation of the physics of contact line dynamics [124].
In the following sections, the role of the dynamic contact line in some current advanced technologies, including printings/coatings and biotechnology/healthcare, is demonstrated. After, the two long-standing physical theories that have been frequently used to describe the physics of the dynamic contact line are thoroughly reviewed. These two theories are hydrodynamics and molecular–kinetic. Moreover, the drawbacks and advantages of both theories are discussed. Finally, future research directions to enhance the power of these two theories to explain the physics of the dynamic contact line in real-life problems are discussed.
2. Applications of the Dynamic Contact Line
2.1. Coating and Printing
The dynamic contact line has a remarkable role in numerous areas of printing, covering conventional inkjet printing, bioprinting, three-dimensional printing, soft materials, nanoprinting, tissue engineering, functional organs, and smart materials. Furthermore, the dynamic contact line has a prominent role in different coatings modes in various areas of technology, including anti-icing of airplanes, smart materials, and the automobile industry [27,125,126,127,128,129,130,131].
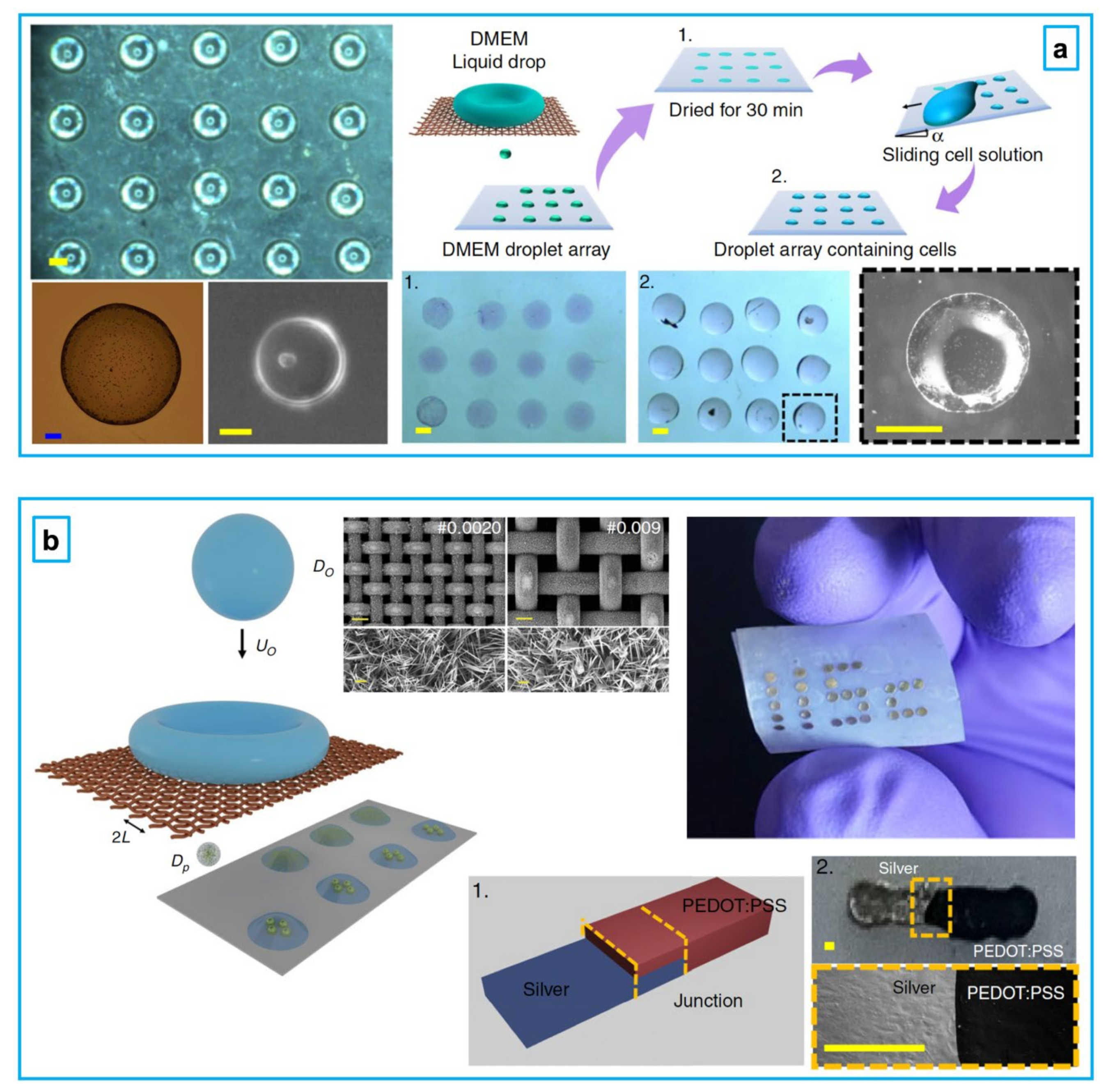
Droplet-based printing on soft materials is of significant interest in leading-edge state-of-the-art technologies, including modern, flexible printed electronics; robotics; tissue engineering; functional organs; and soft biomaterials, as demonstrated in Figure 4 [132]. In droplet-based printing for biotechnology/healthcare and medical purposes, droplets contain biological solutions such as DNA samples, living cells, viruses, bacteria, and proteins. In droplet-based printing for electronics purposes, droplets consist of electrical-conducting solutions, such as silver inks and polymeric samples.
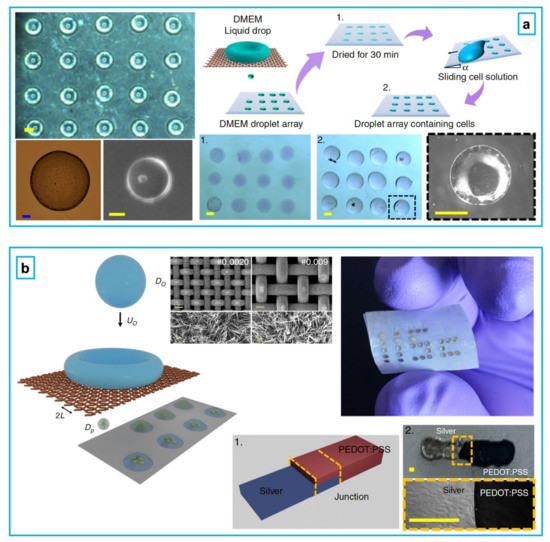
Figure 4.
(a) Droplet-based bioprinting of droplets containing biological solutions to produce biomaterials [132]. (b) Droplet-based printing of electrically conducting droplets containing silver inks on soft materials to produce soft elastic printed electronics [132].
Coatings and printings of evaporative droplets on various substrates show remarkable applications in numerous technologies, such as self-assembly of volatile suspensions of nanoparticles, flexible electronics products, soft materials, photovoltaics products, and biosensors [133,134,135,136,137].
Contact line dynamics has remarkable usefulness in advanced state-of-the-art biotechnology for the production of new-generation biosensors [138,139]. Moreover, contact line dynamics plays an important role in the diagnosis of various diseases via the imaging of a spreading blood droplet and its drying process at various steps, including flow, adhesion, gelation, and fracturing [126,137].
2.2. Healthcare
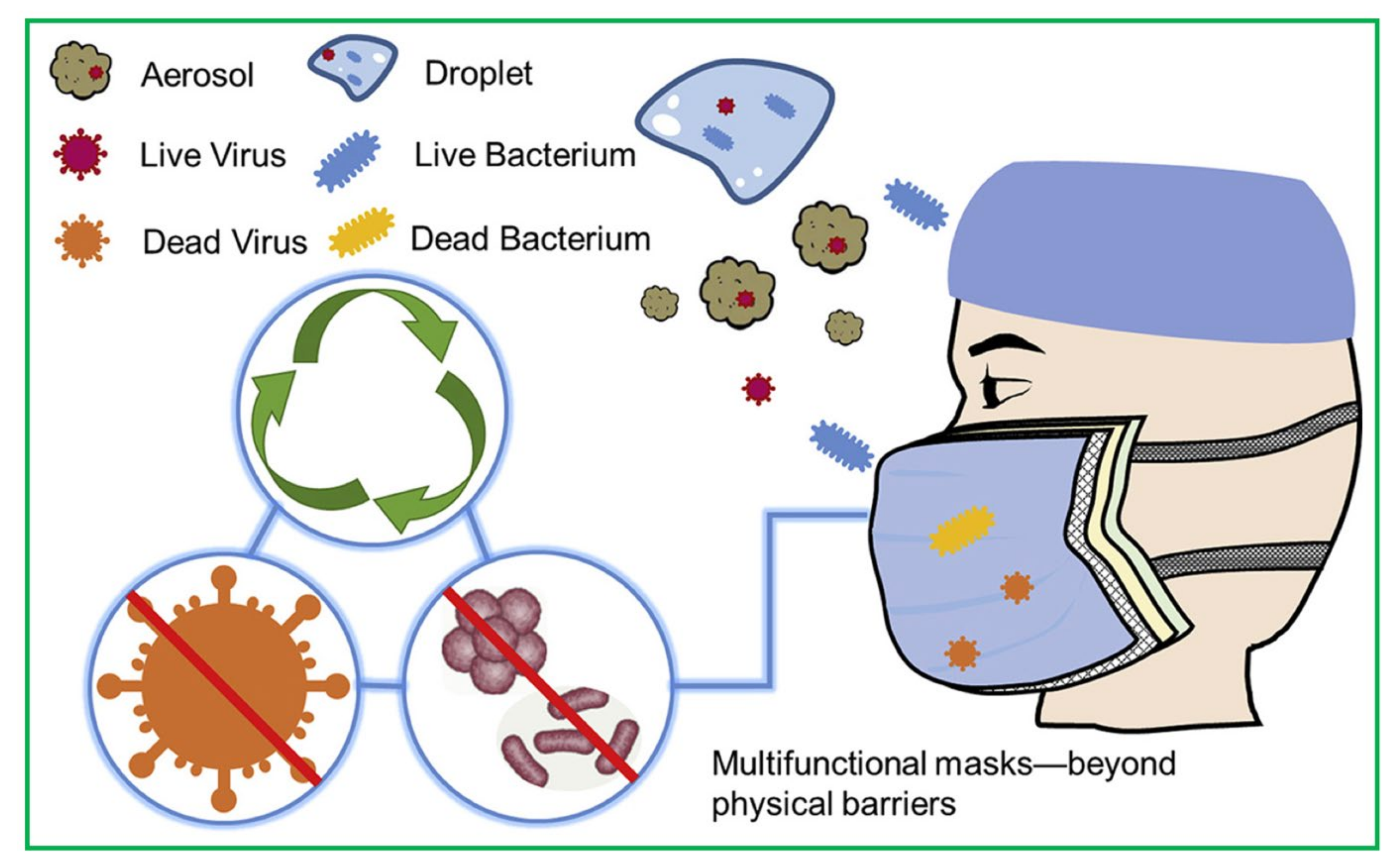
Due to the seriousness of the COVID-19 pandemic, the dynamic contact line of respiratory droplets on various substrates and soft materials such as face masks has a remarkable role in the fight against the spread of the coronavirus in the public (Figure 5). Currently, the scientific community in various fields is trying to develop a physical understanding of the interactions of SARS-CoV-2-virus-laden droplets with diverse materials. The interfacial interactions between virus-laden droplets on substrates with various wetting properties, such as hydrophilic, hydrophobic, and superhydrophobic surfaces, have been investigated. Moreover, recent studies have attempted to investigate the interactions of virus-contained droplets on materials with different mechanical properties, such as rigid, soft, and elastic substrates [140,141,142].
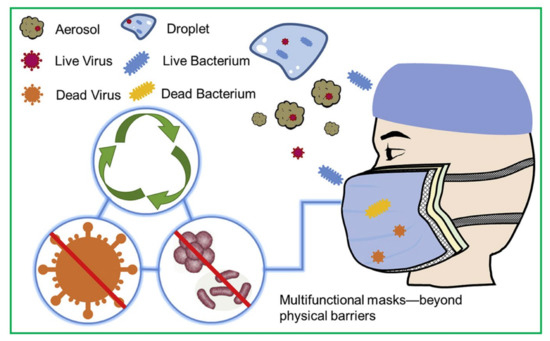
Figure 5.
Significance of SARS-CoV-2-virus-containing droplet interfacial interaction with a soft superhydrophobic material such as a face mask [142].
It is important to note that extensive, full-scale computational efforts have been made to clarify the underlying physical process of droplet motion in various droplet-based applications such as droplet-based microfluidics in Polymerase Chain Reaction continuous flow and single-cell DNA analysis [143].
3. Molecular Kinetic Theory
Molecular kinetic theory explains the molecular dynamics of the liquid–air interface at the vicinity of the dynamic contact line in terms of surface diffusion and adjacent bulk phases [68,95,101]. Molecular kinetic theory considers a solid surface containing many adsorption sites over which the liquid molecules move. The liquid molecular motion near the dynamic contact line is dependent on potential barriers. Molecular kinetic theory explains the physics of the dynamic contact line according to the strength of the potential barriers at the vicinity of the contact line.
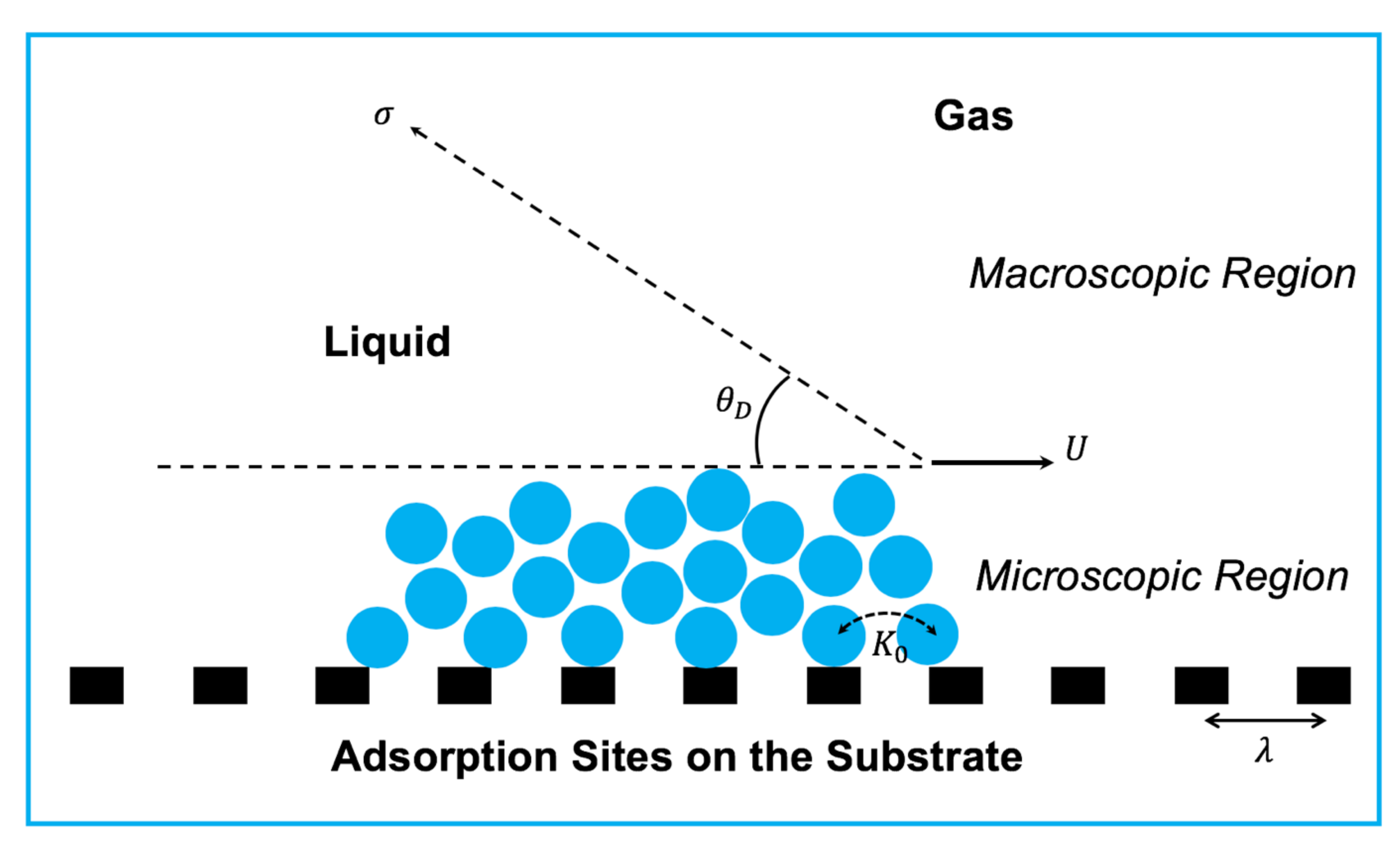
Molecular kinetic theory outlines the physical process of contact line motion on a substrate in terms of the attachment of the liquid molecules on the adsorption sites of the solid surface as the gas molecules of the environment detach from the adsorption sites, as represented in Figure 6 [95,101]. Molecular kinetic theory regards the balance of interfacial tensions with friction () at the dynamic contact line (Equation (2)):
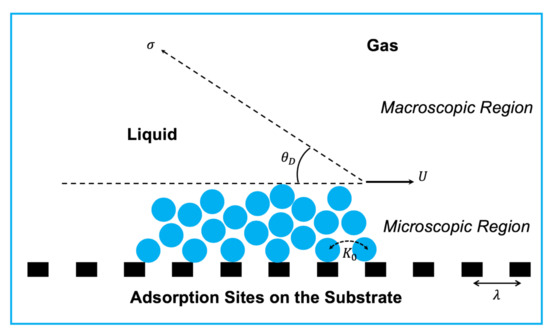
Figure 6.
Schematic representation of molecular kinetic theory to explain the physics of dynamic contact line based on two parameters: and .
Therefore, molecular kinetic theory describes the physics of contact line dynamics on a substrate in terms of molecular motion near the contact line as a result of energy dissipation due to friction [101]. It is assumed that the substrate has number of adsorption sites per unit surface area over which the molecules move. The adsorption sites are equally distant by . The number density of adsorption sites () and the corresponding distance between them () are related by . The frequency of molecular motion near the dynamic contact line is denoted by .
Molecular kinetic theory shows the relation between the velocity () of the dynamic contact line and the dynamic contact angle () in terms of the molecular kinetic parameters and , as represented by (Equation (3)) [95,101]:
in which presents the temperature and represents the Boltzmann constant. In Equation (3), the positive sign stands for the dynamic contact line advancement on a substrate, and the negative sign denotes that the dynamic contact line recedes on the substrate.
The frequency () of molecular motion at the vicinity of the dynamic contact line is described by Eyring’s theory of absolute reaction rates [144], as shown in Equation (4):
in which stands for activation free energy, related to adsorption energy; denotes Avogadro’s number; and represents Planck’s constant. It is necessary to know that there is no definitive method to specify the molecular kinetic parameters ( and ) to describe the physics of the dynamic contact line. As a result, their values are normally estimated by fitting the experimental data with the molecular kinetic model (Equation (3)) based on known values for surface tension (), temperature (), and the static contact angle ().
4. Hydrodynamics Theory
Hydrodynamics theory characterizes the physics of flow near the dynamic contact line. However, there has been a contradiction between the motion of the liquid at the dynamic contact line and the long-established no-slip boundary condition at the liquid–substrate interface. This is due to the fact that the shear stress and pressure diverge to infinity as the flow approaches the dynamic contact line [70]. Moreover, the total force applied on the substrate due to liquid flow becomes unbounded as the flow nears the dynamic contact line [70].
This issue in hydrodynamics theory was resolved by relaxing the well-established no-slip boundary condition, along the liquid–substrate interface, at the proximity of the dynamic contact line over the distance called the slip length [70,93,103,104,105]. This method resolves the issue of divergence of the force by the flow on the solid surface at the dynamic contact line. However, the shear stresses are still not finite at the dynamic contact line [68]. This approach adapts hydrodynamics theory to explain the physics of the dynamic contact line without divergence of the force applied on the substrate at the contact line. It is important to note that adapted hydrodynamics theory is only suitable for flow at low capillary numbers so that the liquid-free surface geometry maintains its static condition away from the dynamic contact line [68].
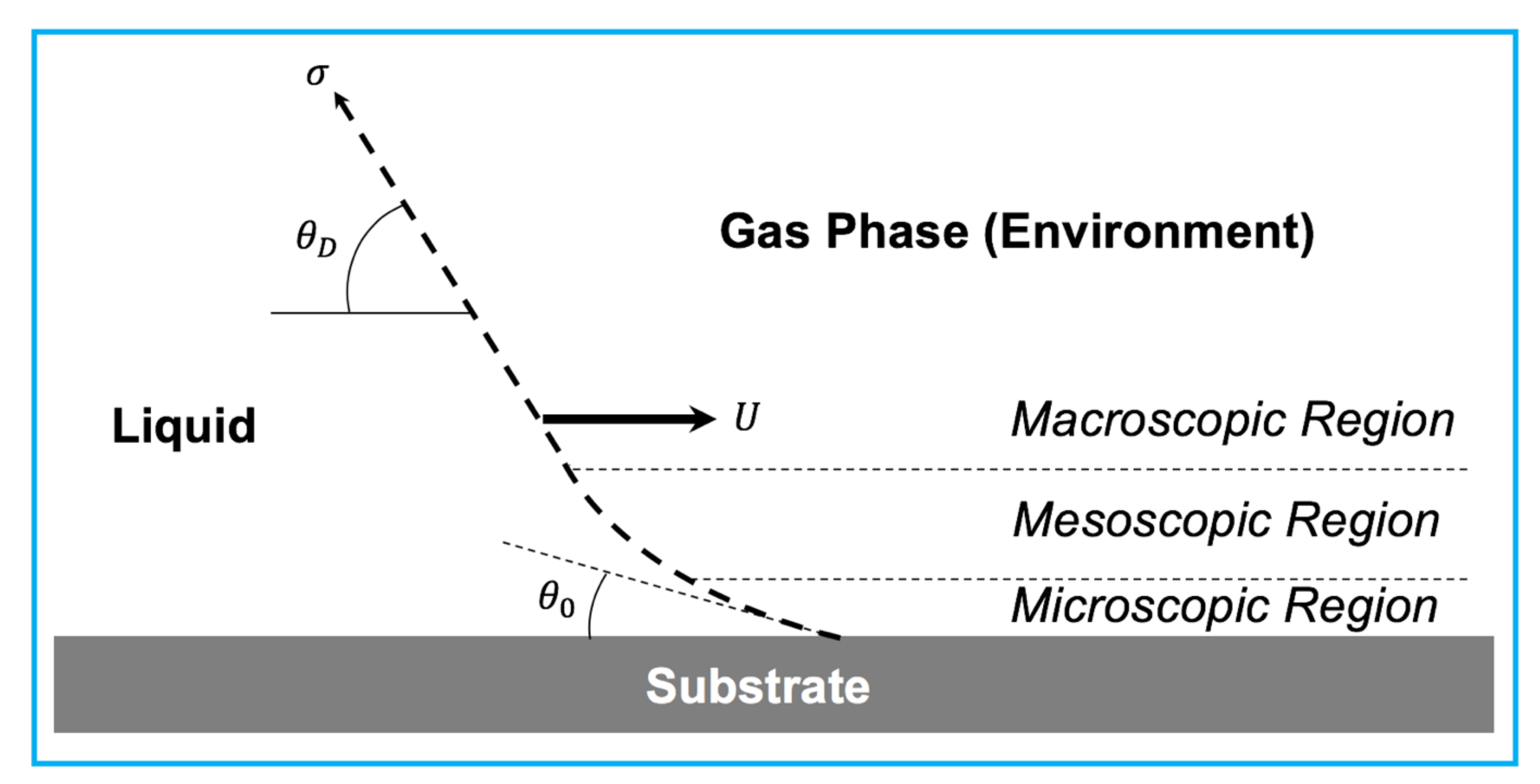
Hydrodynamics theory explains the physics of the dynamic contact line based on viscous bending of the liquid-free surface geometry, which is formed at the mesoscopic region of the flow. The dynamic contact angle in the macroscopic region of the flow is determined by the extrapolation of the static liquid-free surface all the way to the substrate [68]. Therefore, hydrodynamics theory defines the physics of the dynamic contact line using the matched asymptotic expansions approach, as represented in Figure 7 [68,122].
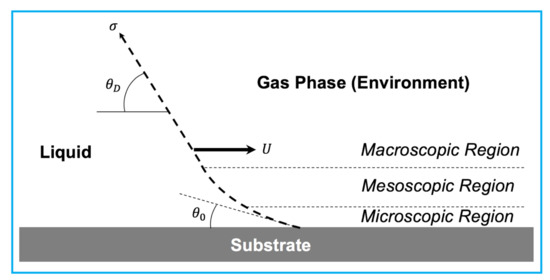
Figure 7.
Schematics of hydrodynamics theory to explain the physics of dynamic contact line due to viscous bending near the contact line.
The relation between the capillary number and the dynamic contact angle, , in the macroscopic region, during the motion of a liquid-free interface on a substrate, is shown in Equation (5) [71]:
Equation (5) is valid for a steady state two-dimensional flow of a viscous liquid on a smooth horizontal solid surface at a low Reynolds number. In Equation (5), denotes the macroscopic characteristic length and represents the microscopic characteristic length, also called the slip length. presents the static contact angle in the microscopic region, and represents the dynamic contact angle in the macroscopic region. denotes the capillary number (), in which is the surface tension of the liquid, is the shear viscosity of the liquid, and presents the dynamic contact line velocity.
Lubrication assumption is assumed for the Navier–Stokes equations for the flow of the viscous liquid on the solid surface [71]. A steady-state wedge shape of the viscous liquid at the proximity of the dynamic contact line is also assumed. Therefore, Voinov (1976) formulated hydrodynamics theory to describe the physics of the dynamic contact line using Equations (6) and (7) [71]:
Here, the positive sign stands for the advancement of the dynamic contact line on a smooth substrate, and the negative sign denotes the receding of the dynamic contact line on the substrate. Similar findings were obtained by Cox’s theoretical study [69] in which gas viscosity was assumed to be negligible. Therefore, Equations (6) and (7) are called “Cox-Voinov” equations of hydrodynamics theory and are used for describing the physics of the dynamic contact line.
The characteristic length for the macroscopic region, , is directly related to the capillary length (): . The proportionality constant depends on several factors, including the flow condition, fluid boundary conditions, and capillary number of the flow [8].
The microscopic characteristic length (slip length) is used to remove the long-established stress singularity at the dynamic contact line. It is shown to be dependent on the speed of the dynamic contact line and the liquid physical characteristics, and its magnitude is estimated on the order of several angstroms [2]. The magnitude of the microscopic characteristic length also depends on other parameters, including surface roughness, substrate geometry, solid surface chemistry, flow condition, and shear rate [145,146]. The prediction of the physics of the dynamic contact line by hydrodynamics theory is strongly influenced by the microscopic characteristic length [145,146].
Numerous studies on the development of hydrodynamics theory to describe the physics of the dynamic contact line have provided experimental, theoretical, and numerical attempts. Table 1 summarizes the list of alternative forms of hydrodynamics theory that explain the physics of the dynamic contact line for various conditions of flow and substrate.

Table 1.
Summary of alternative forms of hydrodynamics theory in experimental, theoretical, and numerical studies.
5. Molecular Kinetic Theory: Advantages and Limitations
Molecular kinetic theory is a qualitative approach to describe the physics of the dynamic contact line by examining the energy dissipation at the proximity of the dynamic contact line due to friction force. Molecular kinetic theory is less suitable to precisely describe the physics of dynamic contact line problems compared to hydrodynamics theory. Furthermore, molecular kinetic theory is qualitatively a perfect theory to outline the physics of the dynamic contact line on a solid surface with heterogeneity in chemistry or roughness [50,124,154]. Molecular kinetic theory is normally applied for a dynamic contact line with large contact angles. Molecular kinetic theory was reported to be appropriate for explaining the physics of forced movement of the dynamic contact line on rough substrates and smooth inclined substrates [55,155,156,157,158]. Molecular kinetic theory was also shown to be a promising model for describing the physics of the dynamic contact line in the area of electrowetting and cell-adhesion problems [50,124,154].
It is important to note that molecular kinetic theory normally hypothesizes the physics of the dynamic contact line. However, it was shown that in the case of contact line dynamics of a superfluid on a substrate, molecular kinetic theory successfully describes the relationship between the dynamic contact angle and contact line velocity at various temperatures [101,102]. This result demonstrates the strength of molecular kinetic theory in defining the physics of the dynamic contact line by considering the role of the environment temperature. Moreover, it was reported that molecular kinetic theory is a suitable theory for defining the dynamic contact line on a substrate with nano-size heterogeneities that cause pinning–depinning events [101,102]. This result highlights the possibility of the successful role of molecular kinetic theory in describing the physics of the dynamic contact line on a substrate with orderly or non-orderly nano-size pores.
To apply molecular kinetic theory to define the physics of the dynamic contact line, obtaining extensive experimental results without any noise is required so that the fitting of the data with the molecular kinetic model is successful in perfectly estimating the molecular kinetic parameters. This requirement is a significant challenge for many experimental studies of the dynamic contact line. Therefore, two factors are important in applying molecular kinetic theory to explain the physics of the dynamic contact line: reproducibility and reliability of the estimated molecular kinetic parameters and level of uncertainty in the fitting of data with the molecular kinetic model. Another drawback of molecular kinetic theory is its limitation to the microscopic region. Molecular kinetic theory does not consider the mesoscopic and macroscopic regions of the dynamic contact line [95]. Molecular kinetic theory is not suitable for predicting the physics of the dynamic contact line of non-Newtonian liquids [16,18,19,57,68,159,160,161].
6. Hydrodynamics Theory: Advantages and Limitations
On the other hand, hydrodynamics theory normally quantitatively explains the physics of the dynamic contact line, and it is mostly used for describing the physics of dynamic contact lines with small contact angles. Hydrodynamics theory assumes lubrication in the Navier–Stokes equations. Hydrodynamics theory concludes that dissipation mainly occurs in the bulk of flow due to viscosity and presumes that dissipation at the contact line is not significant. Hydrodynamics theory was shown to be a suitable theory for describing the physics of forced motion of the dynamic contact line on a chemically treated substrate [1].
In general, hydrodynamics was demonstrated to be a suitable theory for defining the physics of spontaneous liquid motion (i.e., Newtonian and non-Newtonian) on a substrate [22,46,47,162,163,164,165,166,167,168]. It was reported that hydrodynamics is an appropriate theory for describing the physics of motion of a liquid on biological materials, synthetic superhydrophobic surfaces, bio-inspired materials, superoleophobic materials, biomaterials, and smart substrates [50,122,160,169,170].
Hydrodynamics theory also has some weaknesses. Hydrodynamics theory is generally applicable to the physics of Newtonian liquid motion on homogeneous surfaces [114,171,172,173,174,175,176]. Hydrodynamics theory does not perfectly describe the physics of the dynamic contact line for the forced motion of a liquid on heterogeneous materials with roughness and heterogeneous surface chemistry [50,93,114,160,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183]. Additionally, hydrodynamics theory is not suitable for explaining the physics of the dynamic contact line for the motion of complex fluids on real substrates with natural heterogeneous roughness and complex surface chemistry [114,122,171,172,173,174,175,176,177,178].
Furthermore, hydrodynamics theory does not consider the role of micro- or nano-scale pores on substrates when describing the physics of the dynamic contact line. These drawbacks significantly limit the applicability of hydrodynamics theory in describing the physics of the dynamic contact line on real interfacial problems [15,20,46,47,50,60,89,114,140,141,160,169,170,171,172,173,174,175,176,177,178,184,185,186,187,188,189,190,191,192,193,194,195,196,197,198].
7. Future Perspectives
Molecular kinetic theory and hydrodynamics theory necessitate estimating physical parameters: the rate of molecular activity near the contact line, the distance between adsorptions sites of the substrate, and the microscopic characteristics length. These parameters are only estimated and not exact. Therefore, both theories cannot provide a real physical understanding of the mechanism of the dynamic contact line.
As hydrodynamics theory is mostly suitable for the macroscopic and mesoscopic regions of the flow and molecular kinetic theory is generally applicable for describing the microscopic region of the dynamic contact line, it is beneficial to apply both theories simultaneously to describe dynamic contact line problems. However, the parameters that define the dynamic contact line in these two well-established theories (hydrodynamics and molecular kinetic) can only currently be estimated through fitting analyses. Therefore, the combined model currently is not applicable to precisely describe real-life dynamic contact line problems. For this reason, it is vital to pay significant attention to precisely determining physical parameters by applying current advanced technologies, including quantum computation, imaging techniques such as atomic force microscopy and cryogenic electron microscopy, and the power of machine learning.
Nanofluidics is the current advanced technology used for the production of nanofilms. The physics of the dynamic contact line in nanofluidics needs to be investigated by considering the complex fluids. The physical properties of nanofluids, such as rheology, change rapidly in the proximity to the dynamic contact line. The change in physical properties of nanofluids can influence the physical parameters that define the dynamic contact line via hydrodynamics theory and molecular kinetic theory. These physical dependencies need to be thoroughly investigated. For instance, as the slip condition strongly depends on the rheology of fluids, in nanofluidics, the slip condition can abruptly change and consequently affects hydrodynamics theory.
Another issue is the real characteristics of the substrates, which complicate the relationship between the physical parameters that define the hydrodynamics and molecular kinetic theories and the heterogenous roughness, heterogeneous surface chemistry, and flexibility of the substrates. Therefore, it is significantly important to enhance the physical understanding of this subject by applying state-of-the-art nanotechnologies such as atomic force microscopy and cryogenic electron microscopy to look closely at the influence of the substrate features on the physics of the dynamic contact line for real-life natural substrates.
Both theories are not suitable for application to real interfacial-related problems. Problems in healthcare and biomedicine that deal with interfacial physics urgently require enhanced knowledge of the dynamic contact line and its real underlying physical mechanism. The physics of the dynamic contact line is a multi-scale phenomenon that requires understanding the details of flow in microscopic, mesoscopic, and macroscopic regions simultaneously. Moreover, a dynamic contact line problem is an interdisciplinary physical event that requires thorough knowledge in various fields, such as chemistry, materials science, electrical engineering, mechanical engineering, physics, mathematics, and biology.
The dynamic contact line in real-life problems involves complexity in the liquid environment and substrate. The liquid, environment, and substrate can have complicated mixtures of phases in real-life situations. Most problems, such as bioprinting; tissue engineering; and designing smart biomaterials, which involve DNA molecules, cells, peptides, and viruses; and state-of-the-art biosensors, deal with very complex liquid models and substrates [46,47,165,166,167,168,197,198].
The present models of hydrodynamics and molecular kinetic do not consider such complexities. Therefore, it is highly recommended that the interfacial physics community directs experimental and theoretical efforts to more complex systems of solid–liquid–gas systems for an enhanced physical understanding of the dynamic contact line in such complicated real-life conditions.
Author Contributions
Conceptualization, A.M.K.; methodology, A.M.K.; software, A.M.K.; validation, A.M.K., W.J.S.; formal analysis, A.M.K.; investigation, A.M.K.; resources, A.M.K.; data curation, A.M.K.; writing—original draft preparation, A.M.K.; writing—review and editing, A.M.K.; visualization, A.M.K.; supervision, A.M.K.; project administration, A.M.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This study did not require ethical approval.
Informed Consent Statement
This study did not involve humans.
Data Availability Statement
Data sharing is not applicable to this article as no new data were created or analyzed in this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ren, W.; Weinan, E. Contact Line Dynamics on Heterogeneous Surfaces. Phys. Fluids 2011, 23, 072103. [Google Scholar] [CrossRef]
- Eggers, J.; Stone, H.A. Characteristic Lengths at Moving Contact Lines for a Perfectly Wetting Fluid: The Influence of Speed on The Dynamic Contact Angle. J. Fluid Mech. 2004, 505, 309–321. [Google Scholar] [CrossRef]
- Diaz, M.E.; Cerro, R.L. A General Solution of Dewetting Flow with a Moving Contact Line. Phys. Fluids 2021, 33, 103601. [Google Scholar] [CrossRef]
- Dodds, S.; Carvalho, M.D.S.; Kumar, S. Stretching and Slipping of Liquid Bridges Near Plates and Cavities. Phys. Fluids 2009, 21, 092103. [Google Scholar] [CrossRef]
- Dodds, S.; Carvalho, M.; Kumar, S. Stretching Liquid Bridges with Moving Contact Lines: The Role of Inertia. Phys. Fluids 2011, 23, 092101. [Google Scholar] [CrossRef]
- Dodds, S.; Carvalho, M.S.; Kumar, S. The Dynamics of Three-Dimensional Liquid Bridges with Pinned and Moving Contact Lines. J. Fluid Mech. 2012, 707, 521–540. [Google Scholar] [CrossRef]
- Ghosh, A.; Bandyopadhyay, D.; Sharma, A. Micro-Patterning of Coatings on A Fiber Surface Exploiting the Contact Instabilities of Thin Viscoelastic Films. Phys. Fluids 2018, 30, 114101. [Google Scholar] [CrossRef]
- Harikrishnan, A.R.; Dhar, P.; Agnihotri, P.K.; Gedupudi, S.; Das, S.K. Correlating Contact Line Capillarity and Dynamic Contact Angle Hysteresis in Surfactant-Nanoparticle Based Complex Fluids. Phys. Fluids 2018, 30, 042006. [Google Scholar] [CrossRef]
- Kumar, S. Liquid Transfer in Printing Processes: Liquid Bridges with Moving Contact Lines. Annu. Rev. Fluid Mech. 2015, 47, 67–94. [Google Scholar] [CrossRef]
- Liu, C.-Y.; Vandre, E.; Carvalho, M.S.; Kumar, S. Dynamic Wetting Failure and Hydrodynamic Assist in Curtain Coating. J. Fluid Mech. 2016, 808, 290–315. [Google Scholar] [CrossRef]
- Liu, C.-Y.; Vandre, E.; Carvalho, M.S.; Kumar, S. Dynamic wetting failure in surfactant solutions. J. Fluid Mech. 2016, 789, 285–309. [Google Scholar] [CrossRef]
- Liu, C.-Y.; Carvalho, M.S.; Kumar, S. Mechanisms of Dynamic Wetting Failure in the Presence of Soluble Surfactants. J. Fluid Mech. 2017, 825, 677–703. [Google Scholar] [CrossRef]
- Liu, C.-Y.; Carvalho, M.S.; Kumar, S. Dynamic Wetting Failure in Curtain Coating: Comparison of Model Predictions and Experimental Observations. Chem. Eng. Sci. 2018, 195, 74–82. [Google Scholar] [CrossRef]
- Liu, M.; Chen, X.-P. Numerical Study on the Stick-Slip Motion of Contact Line Moving on Heterogeneous Surfaces. Phys. Fluids 2017, 29, 082102. [Google Scholar] [CrossRef]
- Ding, H.; Spelt, P.D.M. Inertial Effects in Droplet Spreading: A Comparison Between Diffuse-Interface and Level-Set Simulations. J. Fluid Mech. 2007, 576, 287–296. [Google Scholar] [CrossRef]
- Biance, A.-L.; Clanet, C.; Quéré, D. First Steps in the Spreading of a Liquid Droplet. Phys. Rev. E 2004, 69, 016301. [Google Scholar] [CrossRef]
- Foister, R.T. The Kinetics of Displacement Wetting in Liquid/Liquid/Solid Systems. J. Colloid Interface Sci. 1990, 136, 266–282. [Google Scholar] [CrossRef]
- Spelt, P.D. A level-Set Approach for Simulations of Flows with Multiple Moving Contact Lines with Hysteresis. J. Comput. Phys. 2005, 207, 389–404. [Google Scholar] [CrossRef]
- Wang, H. From Contact Line Structures to Wetting Dynamics. Langmuir 2019, 35, 10233–10245. [Google Scholar] [CrossRef]
- Popescu, M.N.; Oshanin, G.; Dietrich, S.; Cazabat, A.-M. Precursor Films in Wetting Phenomena. J. Phys. Condens. Matter 2012, 24, 243102. [Google Scholar] [CrossRef]
- Pham, T.; Kumar, S. Imbibition and Evaporation of Droplets of Colloidal Suspensions on Permeable Substrates. Phys. Rev. Fluids 2019, 4, 034004. [Google Scholar] [CrossRef]
- Charitatos, V.; Kumar, S. A Thin-Film Model for Droplet Spreading on Soft Solid Substrates. Soft Matter 2020, 16, 8284–8298. [Google Scholar] [CrossRef]
- Raske, N.; Hewson, R.W.; Kapur, N.; De Boer, G. A Predictive Model for Discrete Cell Gravure Roll Coating. Phys. Fluids 2017, 29, 062101. [Google Scholar] [CrossRef]
- Karim, A.M.; Suszynski, W.J.; Griffith, W.B.; Pujari, S.; Francis, L.F.; Carvalho, M.S. Effect of Viscoelasticity on Stability of Liquid Curtain. J. Non-Newton. Fluid Mech. 2018, 257, 83–94. [Google Scholar] [CrossRef]
- Karim, A.M.; Suszynski, W.J.; Griffith, W.B.; Pujari, S.; Francis, L.F.; Carvalho, M.S. Effect of Rheological Properties of Shear Thinning Liquids on Curtain Stability. J. Non-Newton. Fluid Mech. 2018, 263, 69–76. [Google Scholar] [CrossRef]
- Karim, A.M.; Suszynski, W.J.; Pujari, S.; Francis, L.F.; Carvalho, M.S. Delaying Breakup and Avoiding Air Entrainment in Curtain Coating Using a Two-Layer Liquid Structure. Chem. Eng. Sci. 2019, 213, 115376. [Google Scholar] [CrossRef]
- Karim, A.M. Experimental Dynamics of Newtonian and Non-Newtonian Droplets Impacting Liquid Surface with Different Rheology. Phys. Fluids 2020, 32, 043102. [Google Scholar] [CrossRef]
- Karim, A.M.; Suszynski, W.J.; Pujari, S.; Francis, L.F.; Carvalho, M.S. Contact Line Dynamics in Curtain Coating of Non-Newtonian Liquids. Phys. Fluids 2021, 33, 103103. [Google Scholar] [CrossRef]
- Karim, A.M.; Suszynski, W.J.; Pujari, S. Liquid Film Stability and Contact Line Dynamics of Emulsion Liquid Films in Curtain Coating Process. J. Coat. Technol. Res. 2021, 18, 1531–1541. [Google Scholar] [CrossRef]
- Mohammad Karim, A.; Pujari, S.; Suszynski, W.J.; Francis, L.F.; Carvalho, M.S.; Yadav, V. Methods for Curtain Coating Substrates. U.S. Patent No: 11,369,988 B2, 28 June 2022. [Google Scholar]
- Mohammad Karim, A.; Pujari, S.; Suszynski, W.J.; Francis, L.F.; Carvalho, M.S.; Yadav, V. Methods for Curtain Coating Substrates. Application Publication No: WO 2019/190623 A1, 3 October 2019. [Google Scholar]
- Omori, T.; Kajishima, T. Apparent and Microscopic Dynamic Contact Angles in Confined Flows. Phys. Fluids 2017, 29, 112107. [Google Scholar] [CrossRef]
- Patil, N.D.; Shaikh, J.; Sharma, A.; Bhardwaj, R. Droplet Impact Dynamics Over a Range of Capillary Numbers and Surface Wettability: Assessment of Moving Contact Line Models and Energy Budget Analysis. Phys. Fluids 2022, 34, 052119. [Google Scholar] [CrossRef]
- Peschka, D. Variational Approach to Dynamic Contact Angles for Thin Films. Phys. Fluids 2018, 30, 082115. [Google Scholar] [CrossRef]
- Park, J.; Kumar, S. Droplet Sliding on an Inclined Substrate with a Topographical Defect. Langmuir 2017, 33, 7352–7363. [Google Scholar] [CrossRef]
- Vandre, E.; Carvalho, M.S.; Kumar, S. Delaying the Onset of Dynamic Wetting Failure through Meniscus Confinement. J. Fluid Mech. 2012, 707, 496–520. [Google Scholar] [CrossRef]
- Vandre, E.; Carvalho, M.S.; Kumar, S. On the Mechanism of Wetting Failure during Fluid Displacement along a Moving Substrate. Phys. Fluids 2013, 25, 102103. [Google Scholar] [CrossRef]
- Vandre, E.; Carvalho, M.S.; Kumar, S. Characteristics of Air Entrainment during Dynamic Wetting Failure along a Planar Substrate. J. Fluid Mech. 2014, 747, 119–140. [Google Scholar] [CrossRef]
- Xia, Y.; Qin, J. Dynamics of Moving Contact Line on a Transversely Patterned Inclined Surface. Phys. Fluids 2020, 32, 042101. [Google Scholar] [CrossRef]
- Xu, X.; Wang, X. Theoretical Analysis for Dynamic Contact Angle Hysteresis on Chemically Patterned Surfaces. Phys. Fluids 2020, 32, 112102. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, P.; Borg, M.K.; Reese, J.; Wen, D. A Critical Assessment of the Line Tension Determined by the Modified Young’s Equation. Phys. Fluids 2018, 30, 082003. [Google Scholar] [CrossRef]
- Zheng, W.; Wen, B.; Sun, C.; Bai, B. Effects of Surface Wettability on Contact Line Motion in Liquid–Liquid Displacement. Phys. Fluids 2021, 33, 082101. [Google Scholar] [CrossRef]
- Bergeron, V.; Bonn, D.; Martin, J.Y.; Vovelle, L. Controlling Droplet Deposition with Polymer Additives. Nature 2000, 405, 772–775. [Google Scholar] [CrossRef]
- Sansom, M.S.; Biggin, P.C. Water at the Nanoscale. Nature 2001, 414, 157–159. [Google Scholar] [CrossRef]
- Xu, J.; Yan, X.; Liu, G.; Xie, J. The Critical Nanofluid Concentration as the Crossover between Changed and Unchanged Solar-Driven Droplet Evaporation Rates. Nano Energy 2019, 57, 791–803. [Google Scholar] [CrossRef]
- Wang, H.; Garimella, S.V.; Murthy, J.Y. Characteristics of an Evaporating Thin Film in a Microchannel. Int. J. Heat Mass Transf. 2007, 50, 3933–3942. [Google Scholar] [CrossRef]
- Wang, X.D.; Lee, D.J.; Peng, A.X.F.; Lai, J.Y. Spreading Dynamics and Dynamic Contact Angle of Non-Newtonian Fluids. Langmuir 2007, 23, 8042–8047. [Google Scholar] [CrossRef]
- Wang, X.D.; Zhang, Y.; Lee, D.J.; Peng, X.F. Spreading of Completely Wetting or Partially Wetting Power-Law Fluid on Solid Surface. Langmuir 2007, 23, 9258–9262. [Google Scholar] [CrossRef]
- Raghupathi, P.A.; Kandlikar, S.G. Contact Line Region Heat Transfer Mechanisms for an Evaporating Interface. Int. J. Heat Mass Transf. 2016, 95, 296–306. [Google Scholar] [CrossRef]
- Lu, G.; Wang, X.D.; Duan, Y.Y. A Critical Review of Dynamic Wetting by Complex Fluids: From Newtonian Fluids to Non-Newtonian Fluids and Nanofluids. Adv. Colloid Interface Sci. 2016, 236, 43–62. [Google Scholar] [CrossRef]
- Sui, Y.; Ding, H.; Spelt, P.D. Numerical Simulations of Flows with Moving Contact Lines. Annu. Rev. Fluid Mech. 2014, 46, 97–119. [Google Scholar] [CrossRef]
- Abe, Y.; Zhang, B.; Gordillo, L.; Mohammad Karim, A.; Francis, L.F.; Cheng, X. Dynamic Self-Assembly of Charged Colloidal Strings and Walls in Simple Fluid Flows. Soft Matter 2017, 13, 1681–1692. [Google Scholar] [CrossRef]
- Karim, A.M.; Suszynski, W.J.; Francis, L.F.; Carvalho, M.S. Effect of Viscosity on Liquid Curtain Stability. AIChE J. 2017, 64, 1448–1457. [Google Scholar] [CrossRef]
- Dwivedi, R.K.; Jain, V.; Muralidhar, K. Dynamic Contact Angle Model for Resolving Low-Viscosity Droplet Oscillations During Spreading Over a Surface with Varying Wettability. Phys. Rev. Fluids 2022, 7, 034002. [Google Scholar] [CrossRef]
- Kim, J.-H.; Kavehpour, H.P.; Rothstein, J.P. Dynamic Contact Angle Measurements on Superhydrophobic Surfaces. Phys. Fluids 2015, 27, 032107. [Google Scholar] [CrossRef]
- Fernández-Toledano, J.C.; Blake, T.D.; De Coninck, J. Taking a Closer Look: A Molecular-Dynamics Investigation of Microscopic and Apparent Dynamic Contact Angles. J. Colloid Interface Sci. 2021, 587, 311–323. [Google Scholar] [CrossRef]
- Qian, T.; Wang, X.-P.; Sheng, P. Molecular Scale Contact Line Hydrodynamics of Immiscible Flows. Phys. Rev. E 2003, 68, 016306. [Google Scholar] [CrossRef]
- Wang, X.-P.; Qian, T.; Sheng, P. Moving Contact Line on Chemically Patterned Surfaces. J. Fluid Mech. 2008, 605, 59–78. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Xu, X. Analysis of the Cahn–Hilliard Equation with a Relaxation Boundary Condition Modeling the Contact Angle Dynamics. Arch. Ration. Mech. Anal. 2014, 213, 1–24. [Google Scholar] [CrossRef]
- Savva, N.; Kalliadasis, S. Dynamics of Moving Contact Lines: A Comparison between Slip and Precursor Film Models. Eur. Lett. 2011, 94, 64004. [Google Scholar] [CrossRef]
- Nosonovsky, M.; Ramachandran, R. Geometric Interpretation of Surface Tension Equilibrium in Superhydrophobic Systems. Entropy 2015, 17, 4684–4700. [Google Scholar] [CrossRef]
- Nikolayev, V.S. Evaporation Effect on the Contact Angle and Contact Line Dynamics. In The Surface Wettability Effect on Phase Change; Marengo, M., De Coninck, J., Eds.; Springer Nature: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Young, T. III. An essay on the cohesion of fluids. Philos. Trans. R. Soc. Lond. 1805, 95, 65–87. [Google Scholar] [CrossRef]
- Shikhmurzaev, Y. The Moving Contact Line on a Smooth Solid Surface. Int. J. Multiph. Flow 1993, 19, 589–610. [Google Scholar] [CrossRef]
- Shikhmurzaev, Y.D. Mathematical Modeling of Wetting Hydrodynamics. Fluid Dyn. Res. 1994, 13, 45–64. [Google Scholar] [CrossRef]
- Shikhmurzaev, Y.D. Moving Contact Lines in Liquid/Liquid/Solid Systems. J. Fluid Mech. 1997, 334, 211–249. [Google Scholar] [CrossRef]
- De Ruijter, M.J.; De Coninck, J.; Blake, T.D.; Clarke, A.A.; Rankin, A. Contact Angle Relaxation during the Spreading of Partially Wetting Drops. Langmuir 1997, 13, 7293–7298. [Google Scholar] [CrossRef]
- Blake, T.D. The Physics of Moving Wetting Lines. J. Colloid Interface Sci. 2006, 299, 1–13. [Google Scholar] [CrossRef]
- Cox, R.G. The Dynamics of the Spreading of Liquids on a Solid Surface. Part 1. Viscous Flow. J. Fluid Mech. 1986, 168, 169–194. [Google Scholar] [CrossRef]
- Huh, C.; Scriven, J.L.E. Hydrodynamic Model of Steady Movement of a Solid/Liquid/Fluid Contact Line. J. Colloid Interface Sci. 1971, 35, 85–101. [Google Scholar] [CrossRef]
- Voinov, O.V. Hydrodynamics of Wetting. Izv. Akad. Nauk. SSSR Mekhanika Zhidkosti I Gaza 1976, 5, 714–721. [Google Scholar] [CrossRef]
- De Gennes, P.G. Deposition of Langmuir-Blodgett Layers. Colloid Polym. Sci. 1986, 264, 463–465. [Google Scholar] [CrossRef]
- Butt, H.; Liu, J.; Koynov, K.; Straub, B.; Hinduja, C.; Roismann, I.; Berger, R.; Li, X.; Vollmer, D.; Steffen, W.; et al. Contact Angle Hysteresis. Curr. Opin. Colloid Interface Sci. 2022, 59, 101574. [Google Scholar] [CrossRef]
- Bartell, F.E.; Wooley, A.D. Solid-Liquid-Air Contact Angles and Their Dependence upon the Surface Condition of the Solid. J. Am. Chem. Soc. 1933, 55, 3518–3527. [Google Scholar] [CrossRef]
- Schäffer, E.; Wong, P.-Z. Contact Line Dynamics Near the Pinning Threshold: A Capillary Rise and Fall Experiment. Phys. Rev. E 2000, 61, 5257–5277. [Google Scholar] [CrossRef]
- Johnson, R.E.; Dettre, R.H. Wettability and Contact Angles. In Surface and Colloid Science; Matijevic, E., Ed.; Wiley-Interscience: New York, NY, USA, 1969; pp. 85–153. [Google Scholar]
- Wang, J.-H.; Claesson, P.M.; Parker, J.L.; Yasuda, H. Dynamic Contact Angles and Contact Angle Hysteresis of Plasma Polymers. Langmuir 1994, 10, 3887–3897. [Google Scholar] [CrossRef]
- Vega, M.J.; Gouttiere, C.; Seveno, D.; Blake, T.D.; Voue, M.; de Coninck, J. Experimental Investigation of the Link Be-Tween Static and Dynamic Wetting by Forced Wetting of Nylon Filament. Langmuir 2007, 23, 10628–10634. [Google Scholar] [CrossRef]
- Karim, A.M.; Kavehpour, H.P. Effect of Viscous Force on Dynamic Contact Angle Measurement Using Wilhelmy Plate Method. Colloids Surfaces A Physicochem. Eng. Asp. 2018, 548, 54–60. [Google Scholar] [CrossRef]
- Bartell, F.E.; Shepard, J.W. The Effect of Surface Roughness on Apparent Contact Angles and on Contact Angle Hysteresis. I. The System Paraffin−Water−Air. J. Phys. Chem. 1953, 57, 211–215. [Google Scholar] [CrossRef]
- Eick, J.; Good, R.; Neumann, A. Thermodynamics of Contact Angles. II. Rough Solid Surfaces. J. Colloid Interface Sci. 1975, 53, 235–248. [Google Scholar] [CrossRef]
- Oliver, J.F.; Mason, S.G. Liquid Spreading on Rough Metal Surfaces. J. Mater. Sci. 1980, 15, 431–437. [Google Scholar] [CrossRef]
- Good, R.J.A. Thermodynamic Derivation of Wenzel’s Modification of Young’s Equation for Contact Angles, Together with a Theory of Hysteresis. J. Am. Chem. Soc. 1952, 74, 5041–5042. [Google Scholar] [CrossRef]
- Neumann, A.; Good, R. Thermodynamics of Contact Angles. I. Heterogeneous Solid Surfaces. J. Colloid Interface Sci. 1972, 38, 341–358. [Google Scholar] [CrossRef]
- Schwartz, L.W.; Garoff, S. Contact Angle Hysteresis on Heterogeneous surfaces. Langmuir 1985, 1, 219–230. [Google Scholar] [CrossRef]
- Marmur, A. Contact Angle Hysteresis on Heterogeneous Smooth Surfaces. J. Colloid Interface Sci. 1994, 168, 40–46. [Google Scholar] [CrossRef]
- Decker, E.L.; Garoff, S. Contact Line Structure and Dynamics on Surfaces with Contact Angle Hysteresis. Langmuir 1997, 13, 6321–6332. [Google Scholar] [CrossRef]
- Brandon, S.; Marmur, A. Simulation of Contact Angle Hysteresis on Chemically Heterogeneous Surfaces. J. Colloid Interface Sci. 1996, 183, 351–355. [Google Scholar] [CrossRef] [PubMed]
- Yue, P.; Zhou, C.; Feng, J.J. Sharp-Interface Limit of the Cahn–Hilliard Model for Moving Contact Lines. J. Fluid Mech. 2010, 645, 279–294. [Google Scholar] [CrossRef]
- Yue, P.; Zhou, C.; Feng, J.J.; Ollivier-Gooch, C.F.; Hu, H.H. Phase-Field Simulations of Interfacial Dynamics in Viscoelastic Fluids Using Finite Elements with Adaptive Meshing. J. Comput. Phys. 2006, 219, 47–67. [Google Scholar] [CrossRef]
- Shanahan, M.E.R. Simple Theory of “Stick-Slip” Wetting Hysteresis. Langmuir 1995, 11, 1041–1043. [Google Scholar] [CrossRef]
- Kalinin, Y.V.; Berejnov, V.; Thorne, R.E. Contact Line Pinning by Microfabricated Patterns: Effects of Microscale topography. Langmuir 2009, 25, 5391–5397. [Google Scholar] [CrossRef]
- Dussan, V.E.B. On the Spreading of Liquids on Solid Surfaces: Static and Dynamic Contact Lines. Annu. Rev. Fluid Mech. 1979, 11, 371–400. [Google Scholar] [CrossRef]
- Van Der Waals, J.D. The Thermodynamic Theory of Capillarity under the Hypothesis of a Continuous Variation of Density. J. Stat. Phys. 1979, 20, 200–244. [Google Scholar] [CrossRef]
- Blake, T.D.; Berg, J.C. Wettability: Dynamic Contact Angles and Wetting Kinetics; Marcel Dekker: New York, NY, USA, 1993; Volume 49, pp. 251–309. [Google Scholar]
- Blake, T.; Shikhmurzaev, Y. Dynamic Wetting by Liquids of Different Viscosity. J. Colloid Interface Sci. 2002, 253, 196–202. [Google Scholar] [CrossRef]
- Blake, T.D.; Bracke, M.; Shikhmurzaev, Y.D. Experimental Evidence of Non-Local Hydrodynamic Influence on the Dynamic Contact Angle. Phys. Fluids 1999, 11, 1995. [Google Scholar] [CrossRef]
- Cahn, J.W. Critical Point Wetting. J. Chem. Phys. 1977, 66, 3667–3672. [Google Scholar] [CrossRef]
- Jacqmin, D. Contact-Line Dynamics of a Diffuse Fluid Interface. J. Fluid Mech. 2000, 402, 57–88. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free Energy of a Non-Uniform System. Part I. Interfacial Free Energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Blake, T.D.; Haynes, J.M. Kinetics of Liquid/Liquid Displacement. J. Colloid Interf. Sci. 1969, 30, 421–423. [Google Scholar] [CrossRef]
- Prevost, A.; Rolley, E.; Guthmann, C. Thermally Activated Motion of the Contact Line of a Liquid 4 He Meniscus on a Cesium Substrate. Phys. Rev. Lett. 1999, 83, 348–351. [Google Scholar] [CrossRef]
- Huh, C.; Mason, S.G. The Steady Movement of a Liquid Meniscus in a Capillary Tube. J. Fluid Mech. 1977, 81, 401–419. [Google Scholar] [CrossRef]
- Dussan, V.E.B. The Moving Contact Line: The Slip Boundary Condition. J. Fluid Mech. 1976, 77, 665–684. [Google Scholar] [CrossRef]
- Ngan, C.G.; Dussan, V.E.B. On the Dynamics of Liquid Spreading on Solid Surfaces. J. Fluid Mech. 1989, 209, 191–226. [Google Scholar] [CrossRef]
- Hoffman, R.L. A Study of the Advancing Interface. I. Interface Shape in Liquid—Gas Systems. J. Colloid Interface Sci. 1975, 50, 228–241. [Google Scholar] [CrossRef]
- Tanner, L.H. The Spreading of Silicone Oil Drops on Horizontal Surfaces. J. Phys. D Appl. Phys. 1979, 12, 1473–1484. [Google Scholar] [CrossRef]
- Hocking, L.M. A Moving Fluid Interface. Part 2. The Removal of the Force Singularity by A Slip Flow. J. Fluid Mech. 1977, 79, 209–229. [Google Scholar] [CrossRef]
- Petrov, P.G.; Petrov, J.G. A Combined Molecular-Hydrodynamic Approach to Wetting Kinetics. Langmuir 1992, 8, 1762–1767. [Google Scholar] [CrossRef]
- Brochard-Wyart, F.; de Gennes, P. Dynamics of Partial Wetting. Adv. Colloid Interface Sci. 1992, 39, 1–11. [Google Scholar] [CrossRef]
- De Ruijter, M.J.; De Coninck, J.; Oshanin, G. Droplet Spreading: Partial Wetting Regime Revisited. Langmuir 1999, 15, 2209–2216. [Google Scholar] [CrossRef]
- Blake, T.D.; Ruschak, K.J. Liquid Film Coating; Schweizer, P.M., Kistler, S.F., Eds.; Chapman & Hall: London, UK, 1997; Volume 63. [Google Scholar]
- Petrov, J.G.; Ralston, J.; Schneemilch, A.M.; Hayes, R.A. Dynamics of Partial Wetting and Dewetting in Well-Defined Systems. J. Phys. Chem. B 2003, 107, 1634–1645. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhao, Y.-P. Precursor Film in Dynamic Wetting, Electrowetting, and Electro-Elasto-Capillarity. Phys. Rev. Lett. 2010, 104, 246101. [Google Scholar] [CrossRef]
- Hardy, W.B., III. The Spreading of Fluids on Glass. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1919, 38, 49–55. [Google Scholar] [CrossRef]
- Espín, L.; Kumar, S. Sagging of Evaporating Droplets of Colloidal Suspensions on Inclined Substrates. Langmuir 2014, 30, 11966–11974. [Google Scholar] [CrossRef]
- Karapetsas, G.; Sahu, K.C.; Matar, O.K. Evaporation of Sessile Droplets Laden with Particles and Insoluble Surfactants. Langmuir 2016, 32, 6871–6881. [Google Scholar] [CrossRef]
- Maki, K.L.; Kumar, S. Fast Evaporation of Spreading Droplets of Colloidal Suspensions. Langmuir 2011, 27, 11347–11363. [Google Scholar] [CrossRef]
- Wray, A.W.; Papageorgiou, D.T.; Craster, R.V.; Sefiane, K.; Matar, O.K. Electrostatic Suppression of the Coffee Stain Effect. Langmuir 2014, 30, 5849–5858. [Google Scholar] [CrossRef]
- Charitatos, V.; Kumar, S. Droplet Evaporation on Soft Solid Substrates. Soft Matter 2021, 17, 9339–9352. [Google Scholar] [CrossRef]
- Derjaguin, B.; Churaev, N. Structural Component of Disjoining Pressure. J. Colloid Interface Sci. 1974, 49, 249–255. [Google Scholar] [CrossRef]
- Karim, A.M. A Review of Physics of Moving Contact Line Dynamics Models and Its Applications in Interfacial Science. J. Appl. Phys. 2022, 132, 080701. [Google Scholar] [CrossRef]
- Afkhami, S. Challenges of Numerical Simulation of Dynamic Wetting Phenomena: A Review. Curr. Opin. Colloid Interface Sci. 2022, 57, 101523. [Google Scholar] [CrossRef]
- Zhao, Y. Moving Contact Line Problem: Advances and Perspectives. Theor. Appl. Mech. Lett. 2014, 4, 034002. [Google Scholar] [CrossRef]
- Soltman, D.; Smith, B.; Kang, H.; Morris, S.J.S.; Subramanian, V. Methodology for Inkjet Printing of Partially Wetting Films. Langmuir 2010, 26, 15686–15693. [Google Scholar] [CrossRef]
- Tarasevich, Y.Y.; Pravoslavnova, D.M. Segregation in Desiccated Sessile Drops of Biological Fluids. Eur. Phys. J. E 2007, 22, 311–314. [Google Scholar] [CrossRef]
- Karim, A.M. Experimental Dynamics of Newtonian Non-Elastic and Viscoelastic Droplets Impacting Immiscible Liquid Surface. AIP Adv. 2019, 9, 125141. [Google Scholar] [CrossRef]
- Backholm, M.; Molpeceres, D.; Vuckovac, M.; Nurmi, H.; Hokkanen, M.J.; Jokinen, V.; Timonen, J.V.I.; Ras, R.H.A. Water droplet friction and rolling dynamics on superhydrophobic surfaces. Commun. Mater. 2020, 1, 64. [Google Scholar] [CrossRef]
- De Coninck, J. An Introduction to Wettability and Wetting Phenomena. In The Surface Wettability Effect on Phase Change; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Mugele, F.; Baret, J.-C. Electrowetting: From Basics to Applications. J. Phys. Condens. Matter 2005, 17, R705–R774. [Google Scholar] [CrossRef]
- Jarosz, J.; Molliex, N.; Chenon, G.; Berge, B. Adaptive Eyeglasses for Presbyopia Correction: An Original Variable-Focus Technology. Opt. Express 2019, 27, 10533–10552. [Google Scholar] [CrossRef] [PubMed]
- Modak, C.D.; Kumar, A.; Tripathy, A.; Sen, P. Drop Impact Printing. Nat. Commun. 2020, 11, 4327. [Google Scholar] [CrossRef] [PubMed]
- Biswas, S.; Gawande, S.; Bromberg, V.; Sun, Y. Effects of Particle Size and Substrate Surface Properties on Deposition Dynamics of Inkjet-Printed Colloidal Drops for Printable Photovoltaics Fabrication. J. Sol. Energy Eng. 2010, 132, 021010. [Google Scholar] [CrossRef]
- Joshi, A.S.; Sun, Y. Numerical Simulation of Colloidal Drop Deposition Dynamics on Patterned Substrates for Printable Electronics Fabrication. J. Disp. Technol. 2010, 6, 579–585. [Google Scholar] [CrossRef]
- Chhasatia, V.H.; Joshi, A.S.; Sun, Y. Effect of Relative Humidity on Contact Angle and Particle Deposition Morphology of An Evaporating Colloidal Drop. Appl. Phys. Lett. 2010, 97, 231909. [Google Scholar] [CrossRef]
- Bigioni, T.P.; Lin, X.-M.; Nguyen, T.; Corwin, E.I.; Witten, T.A.; Jaeger, H.M. Kinetically Driven Self Assembly of Highly Ordered Nanoparticle Monolayers. Nat. Mater. 2006, 5, 265–270. [Google Scholar] [CrossRef]
- Sobac, B.; Brutin, D. Structural and Evaporative Evolutions in Desiccating Sessile Drops of Blood. Phys. Rev. E 2011, 84, 011603. [Google Scholar] [CrossRef]
- Gosselin, E.; Eynde, J.J.V.; Petit, A.; Conti, J.; De Coninck, J. Designing a High Performance, Stable Spectroscopic Biosensor for the Binding of Large and Small Molecules. J. Colloid Interface Sci. 2017, 508, 443–454. [Google Scholar] [CrossRef]
- Yao, M.; Tijing, L.D.; Naidu, G.; Kim, S.-H.; Matsuyama, H.; Fane, A.G.; Shon, H.K. A Review of Membrane Wettability for the Treatment of Saline Water Deploying Membrane Distillation. Desalination 2020, 479, 114312. [Google Scholar] [CrossRef]
- Melayil, K.R.; Mitra, S.K. Wetting, Adhesion, and Droplet Impact on Face Masks. Langmuir 2021, 37, 2810–2815. [Google Scholar] [CrossRef]
- Sharma, S.; Pinto, R.; Saha, A.; Chaudhuri, S.; Basu, S. Video: On Secondary Atomization and Blockage of Surrogate Cough Droplets in Single and Multi-Layer Face Masks. Sci. Adv. 2020, 7, eabf0452. [Google Scholar] [CrossRef]
- Liao, M.; Liu, H.; Wang, X.; Hu, X.; Huang, Y.; Liu, X.; Brenan, K.; Mecha, J.; Nirmalan, M.; Lu, J.R. A Technical Review of Face Mask Wearing in Preventing Respiratory COVID-19 Transmission. Curr. Opin. Colloid Interface Sci. 2021, 52, 101417. [Google Scholar] [CrossRef]
- Montessori, A.; Lauricella, M.; Tiribocchi, A. Computational Droplets: Where We Stand and How Far We Can Go. Eur. Lett. 2022, 138, 67001. [Google Scholar] [CrossRef]
- Powell, R.E.; Roseveare, W.E.; Eyring, H. The Theory of Rate Processes. Ind. Eng. Chem. 1941, 33, 430. [Google Scholar] [CrossRef]
- Niavarani, A.; Priezjev, N. The Effective Slip Length and Vortex Formation in Laminar Flow over a Rough Surface. Phys. Fluids 2009, 21, 052105. [Google Scholar] [CrossRef]
- Niavarani, A.; Priezjev, N. Modeling the Combined Effect of Surface Roughness and Shear Rate on Slip Flow of Simple Fluids. Phys. Rev. E 2010, 81, 011606. [Google Scholar] [CrossRef]
- Xiaodong, W.; Xiaofeng, P.; Yuanyuan, D.; Buxuan, W. Dynamics of Spreading of Liquid on Solid Surface. Chin. J. Chem. Eng. 2007, 15, 730–737. [Google Scholar] [CrossRef]
- Cazabat, A.-M. How Does a Droplet Spread? Contemp. Phys. 1987, 28, 347–364. [Google Scholar] [CrossRef]
- Roques-Carmes, T.; Mathieu, V.; Gigante, A. Experimental Contribution to the Understanding of the Dynamics of Spreading of Newtonian Fluids: Effect of Volume, Viscosity and Surfactant. J. Colloid Interface Sci. 2010, 344, 180–197. [Google Scholar] [CrossRef]
- Eddi, A.; Winkels, K.G.; Snoeijer, J.H. Short time dynamics of viscous drop spreading. Phys. Fluids 2013, 25, 013102. [Google Scholar] [CrossRef]
- Legendre, D.; Maglio, M. Numerical Simulation of Spreading Drops. Colloids Surf. A Physicochem. Eng. Asp. 2013, 432, 29–37. [Google Scholar] [CrossRef]
- Zeid, W.B.; Brutin, D. Beyond Tanner’s Law: Role of Contact Line Evaporation on the Spreading of Viscous Droplet. Interfacial Phenom. Heat Transf. 2015, 3, 221–229. [Google Scholar] [CrossRef]
- Blake, T.D.; Dobson, R.A.; Ruschak, K.J. Wetting at High Capillary Numbers. J. Colloid Interface Sci. 2004, 279, 198–205. [Google Scholar] [CrossRef]
- Sedev, R. The Molecular-Kinetic Approach to Wetting Dynamics: Achievements and Limitations. Adv. Colloid Interface Sci. 2015, 222, 661–669. [Google Scholar] [CrossRef]
- Mohammad Karim, A. Parametric Study of Liquid Contact Line Dynamics: Adhesion vs. Hydrodynamics. Ph.D. Thesis, University of California, Los Angeles, CA, USA, 2015. [Google Scholar]
- Karim, A.M.; Kavehpour, H.P. Dynamics of Spreading on Ultra-Hydrophobic Surfaces. J. Coat. Technol. Res. 2015, 12, 959–964. [Google Scholar] [CrossRef]
- Karim, A.M.; Rothstein, J.P.; Kavehpour, H.P. Experimental Study of Dynamic Contact Angles on Rough Hydrophobic Surfaces. J. Colloid Interface Sci. 2018, 513, 658–665. [Google Scholar] [CrossRef]
- Karim, A.M.; Fujii, K.; Kavehpour, H.P. Contact Line Dynamics of Gravity Driven Spreading of Liquids. Fluid Dyn. Res. 2021, 53, 035503. [Google Scholar] [CrossRef]
- Seppecher, P. Moving Contact Lines in the Cahn-Hilliard Theory. Int. J. Eng. Sci. 1996, 34, 977–992. [Google Scholar] [CrossRef]
- Bonn, D.; Eggers, J.; Indekeu, J.; Meunier, J.; Rolley, E. Wetting and Spreading. Rev. Mod. Phys. 2009, 81, 739–805. [Google Scholar] [CrossRef]
- Zheng, L.; Wang, Y.-X.; Plawsky, J.L.; Wayner, P.C. Accuracy of Measurements of Curvature and Apparent Contact Angle in a Constrained Vapor Bubble Heat Exchanger. Int. J. Heat Mass Transf. 2002, 45, 2021–2030. [Google Scholar] [CrossRef]
- Karim, A.M.; Davis, S.H.; Kavehpour, H.P. Forced versus Spontaneous Spreading of Liquids. Langmuir 2016, 32, 10153–10158. [Google Scholar] [CrossRef]
- Karim, A.M.; Kavehpour, H.P. Spreading of Emulsions on a Solid Substrate. J. Coat. Technol. Res. 2013, 11, 103–108. [Google Scholar] [CrossRef]
- Carré, A.; Eustache, F. Spreading Kinetics of Shear-Thinning Fluids in Wetting and Dewetting Modes. Langmuir 2000, 16, 2936–2941. [Google Scholar] [CrossRef]
- Betelu, S.; Fontelos, M. Capillarity Driven Spreading of Power-Law Fluids. Appl. Math. Lett. 2003, 16, 1315–1320. [Google Scholar] [CrossRef]
- Betelú, S.; Fontelos, M. Capillarity Driven Spreading of Circular Drops of Shear-Thinning Fluid. Math. Comput. Model. 2004, 40, 729–734. [Google Scholar] [CrossRef]
- Starov, V.M.; Tyatyushkin, A.N.; Velarde, M.G.; Zhdanov, S.A. Spreading of Non-Newtonian Liquids over Solid Substrates. J. Colloid Interface Sci. 2003, 257, 284–290. [Google Scholar] [CrossRef]
- Liang, Z.-P.; Wang, X.-D.; Duan, Y.-Y.; Min, Q. Energy-Based Model for Capillary Spreading of Power-Law Liquids on a Horizontal Plane. Colloids Surf. A Physicochem. Eng. Asp. 2012, 403, 155–163. [Google Scholar] [CrossRef]
- Liang, Z.-P.; Wang, X.-D.; Lee, D.-J.; Peng, X.-F.; Su, A. Spreading Dynamics of Power-Law Fluid Droplets. J. Phys. Condens. Matter 2009, 21, 464117. [Google Scholar] [CrossRef]
- Liu, K.; Tian, Y.; Jiang, L. Bio-Inspired Superoleophobic and Smart Materials: Design, Fabrication, and Application. Prog. Mater. Sci. 2013, 58, 503–564. [Google Scholar] [CrossRef]
- Blake, T.; De Coninck, J. The Influence of Solid–Liquid Interactions on Dynamic Wetting. Adv. Colloid Interface Sci. 2002, 96, 21–36. [Google Scholar] [CrossRef]
- Ferrari, M.; Ravera, F. Surfactants and Wetting at Superhydrophobic Surfaces: Water Solutions and Non Aqueous Liquids. Adv. Colloid Interface Sci. 2010, 161, 22–28. [Google Scholar] [CrossRef]
- Yan, Y.; Gao, N.; Barthlott, W. Mimicking Natural Superhydrophobic Surfaces and Grasping the Wetting Process: A Review on Recent Progress in Preparing Superhydrophobic Surfaces. Adv. Colloid Interface Sci. 2011, 169, 80–105. [Google Scholar] [CrossRef]
- Bhushan, B.; Jung, Y.C. Natural and Biomimetic Artificial Surfaces for Superhydrophobicity, Self-Cleaning, Low Adhesion, and Drag Reduction. Prog. Mater. Sci. 2011, 56, 1–108. [Google Scholar] [CrossRef]
- Oberli, L.; Caruso, D.; Hall, C.; Fabretto, M.; Murphy, P.J.; Evans, D. Condensation and Freezing of Droplets on Superhydrophobic Surfaces. Adv. Colloid Interface Sci. 2014, 210, 47–57. [Google Scholar] [CrossRef]
- Webb, H.K.; Crawford, R.J.; Ivanova, E.P. Wettability of Natural Superhydrophobic Surfaces. Adv. Colloid Interface Sci. 2014, 210, 58–64. [Google Scholar] [CrossRef]
- Ma, M.; Hill, R.M. Superhydrophobic Surfaces. Curr. Opin. Colloid Interface Sci. 2006, 11, 193–202. [Google Scholar] [CrossRef]
- Koch, K.; Bhushan, B.; Barthlott, W. Multifunctional Surface Structures of Plants: An Inspiration for Biomimetics. Prog. Mater. Sci. 2009, 54, 137–178. [Google Scholar] [CrossRef]
- Savva, N.; Kalliadasis, S. Two-Dimensional Droplet Spreading Over Topographical Substrates. Phys. Fluids 2009, 21, 092102. [Google Scholar] [CrossRef]
- Savva, N.; Pavliotis, G.A.; Kalliadasis, S. Contact Lines Over Random Topographical Substrates. Part 2. Dynamics. J. Fluid Mech. 2011, 672, 384–410. [Google Scholar] [CrossRef]
- Pham, T.; Kumar, S. Drying of Droplets of Colloidal Suspensions on Rough Substrates. Langmuir 2017, 33, 10061–10076. [Google Scholar] [CrossRef]
- Charitatos, V.; Pham, T.; Kumar, S. Droplet Evaporation on Inclined Substrates. Phys. Rev. Fluids 2021, 6, 084001. [Google Scholar] [CrossRef]
- Espín, L.; Kumar, S. Droplet Spreading and Absorption on Rough, Permeable Substrates. J. Fluid Mech. 2015, 784, 465–486. [Google Scholar] [CrossRef]
- Ren, W.; Hu, D.; Weinan, E. Continuum Models for the Contact Line Problem. Phys. Fluids 2010, 22, 102103. [Google Scholar] [CrossRef]
- Lukyanov, A.V. Non-Locality of the Contact Line in Dynamic Wetting Phenomena. J. Colloid Interface Sci. 2021, 608, 2131–2141. [Google Scholar] [CrossRef]
- Li, X.; Pozrikidis, C. Shear Flow Over a Liquid Drop Adhering to a Solid Surface. J. Fluid Mech. 1996, 307, 167–190. [Google Scholar] [CrossRef]
- Moriarty, J.A.; Schwartz., L.W. Unsteady Spreading of Thin Liquid Films with Small Surface Tension. Phys. Fluids A Fluid Dyn. 1991, 3, 733–742. [Google Scholar] [CrossRef]
- Myers, T. Thin Films with High Surface Tension. SIAM Rev. 1998, 40, 441–462. [Google Scholar] [CrossRef]
- Wang, X.; Min, Q.; Zhang, Z.; Duan, Y. Effect of Moving Contact Line’s Curvature on Dynamic Wetting of non-Newtonian Fluids. Langmuir 2018, 34, 15612–15620. [Google Scholar] [CrossRef] [PubMed]
- Thompson, P.A.; Robbins, M.O. Simulations of Contact-Line Motion: Slip and the Dynamic Contact Angle. Phys. Rev. Lett. 1989, 63, 766–769. [Google Scholar] [CrossRef] [PubMed]
- Thompson, P.A.; Brinckerhoff, W.; Robbins, M.O. Microscopic Studies of Static and Dynamic Contact Angles. J. Adhes. Sci. Technol. 1993, 7, 535–554. [Google Scholar] [CrossRef]
- Romero, O.J.; Suszynski, W.J.; Scriven, L.E.; Carvalho, M.S. Low-Flow Limit in Slot Coating of Dilute Solutions of High Molecular Weight Polymer. J. Non-Newton. Fluid Mech. 2004, 118, 137–156. [Google Scholar] [CrossRef]
- Wei, Y.; Ramé, E.; Walker, L.; Garoff, S. Dynamic wetting with viscous Newtonian and non-Newtonian Fluids. J. Phys. Condens. Matter 2009, 21, 464126. [Google Scholar] [CrossRef] [PubMed]
- Cohu, O.; Benkreira, H. Entrainment of Air by a Solid Surface Plunging into a Non-Newtonian Liquid. AIChE J. 1998, 44, 2360–2368. [Google Scholar] [CrossRef]
- Charitatos, V.; Suszynski, W.J.; Carvalho, M.S.; Kumar, S. Dynamic Wetting Failure in Shear-Thinning and Shear-Thickening Liquids. J. Fluid Mech. 2020, 892, A1. [Google Scholar] [CrossRef]
- Liang, Z.-P.; Wang, X.-D.; Duan, Y.; Min, Q.; Wang, C.; Lee, D.-J. Dynamic Wetting of Non-Newtonian Fluids: Multicomponent Molecular-Kinetic Approach. Langmuir 2010, 26, 14594–14599. [Google Scholar] [CrossRef]
- Carré, A.; Woehl, P. Hydrodynamic Behavior at the Triple Line of Spreading Liquids and the Divergence Problem. Langmuir 2002, 18, 3600–3603. [Google Scholar] [CrossRef]
- Carré, A.; Woehl, P. Spreading of Silicone Oils on Glass in Two Geometries. Langmuir 2005, 22, 134–139. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).