Uncertainty Quantification of Trajectory Clustering Applied to Ocean Ensemble Forecasts
Abstract
1. Introduction
2. Method
2.1. Spectral Clustering Method with Soft Memberships for Trajectory Clustering
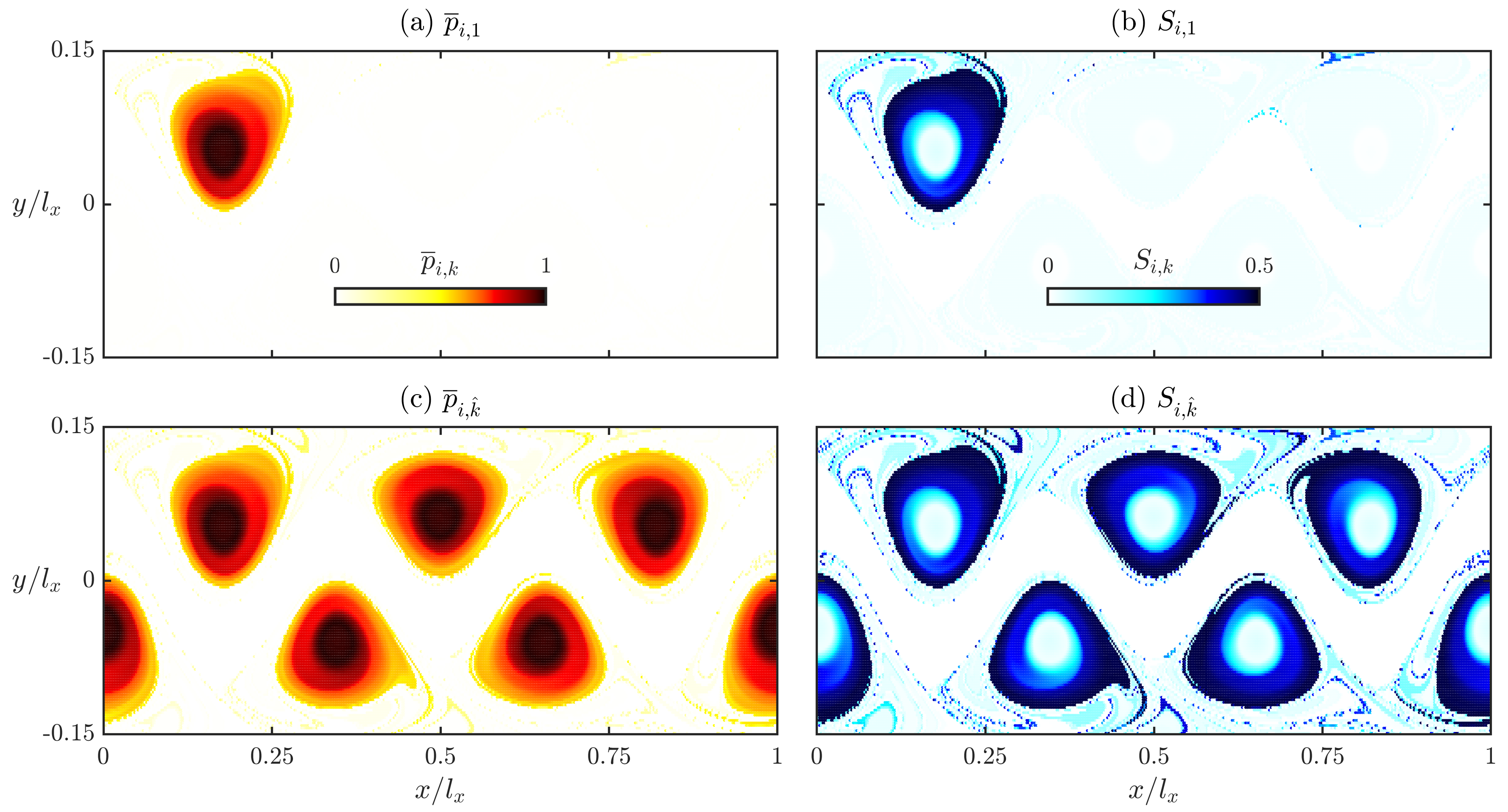
2.2. Uncertainty Quantification for Multiple Realizations
3. The Bickley Jet System and Sensitivity to Method Free-Parameters
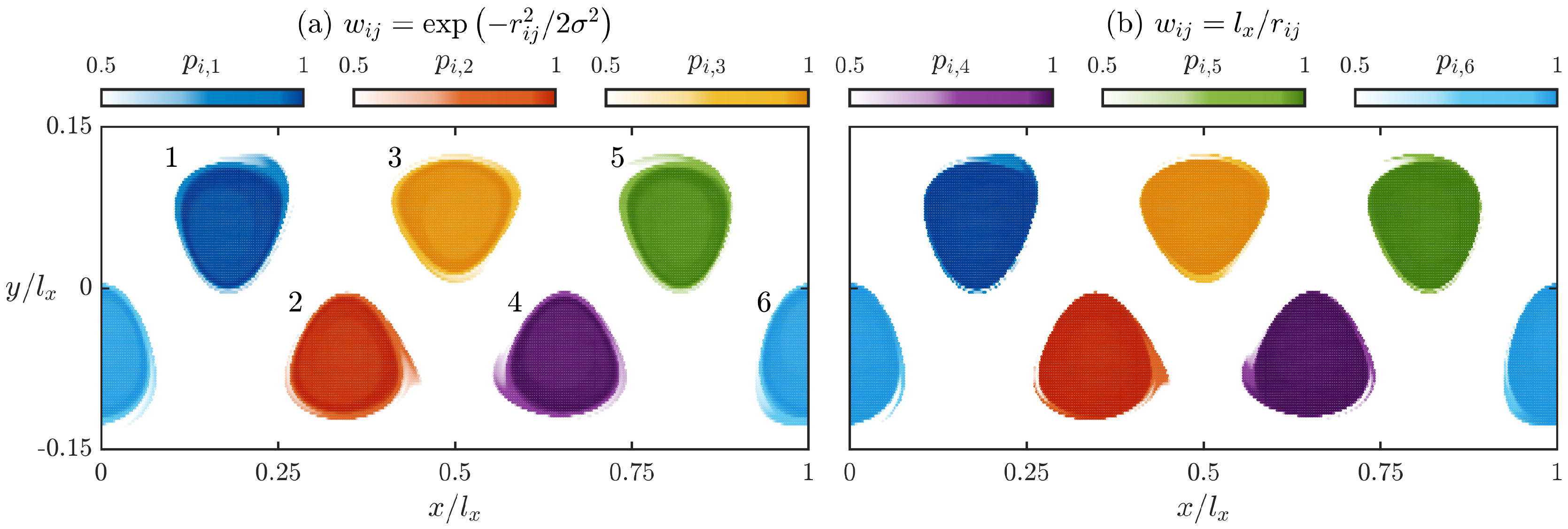
3.1. Gaussian Similarity Measure
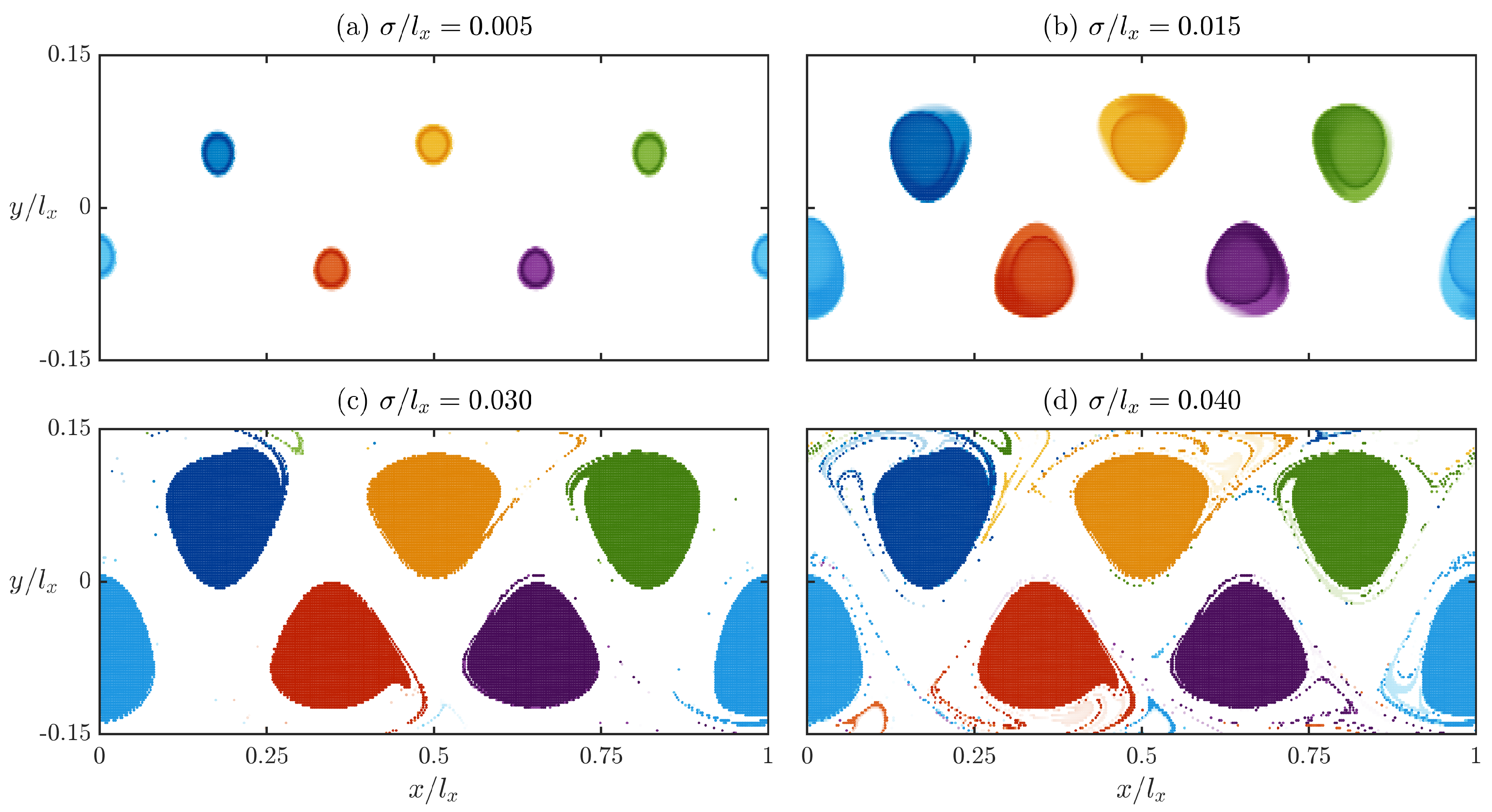
3.2. Similarity Radius
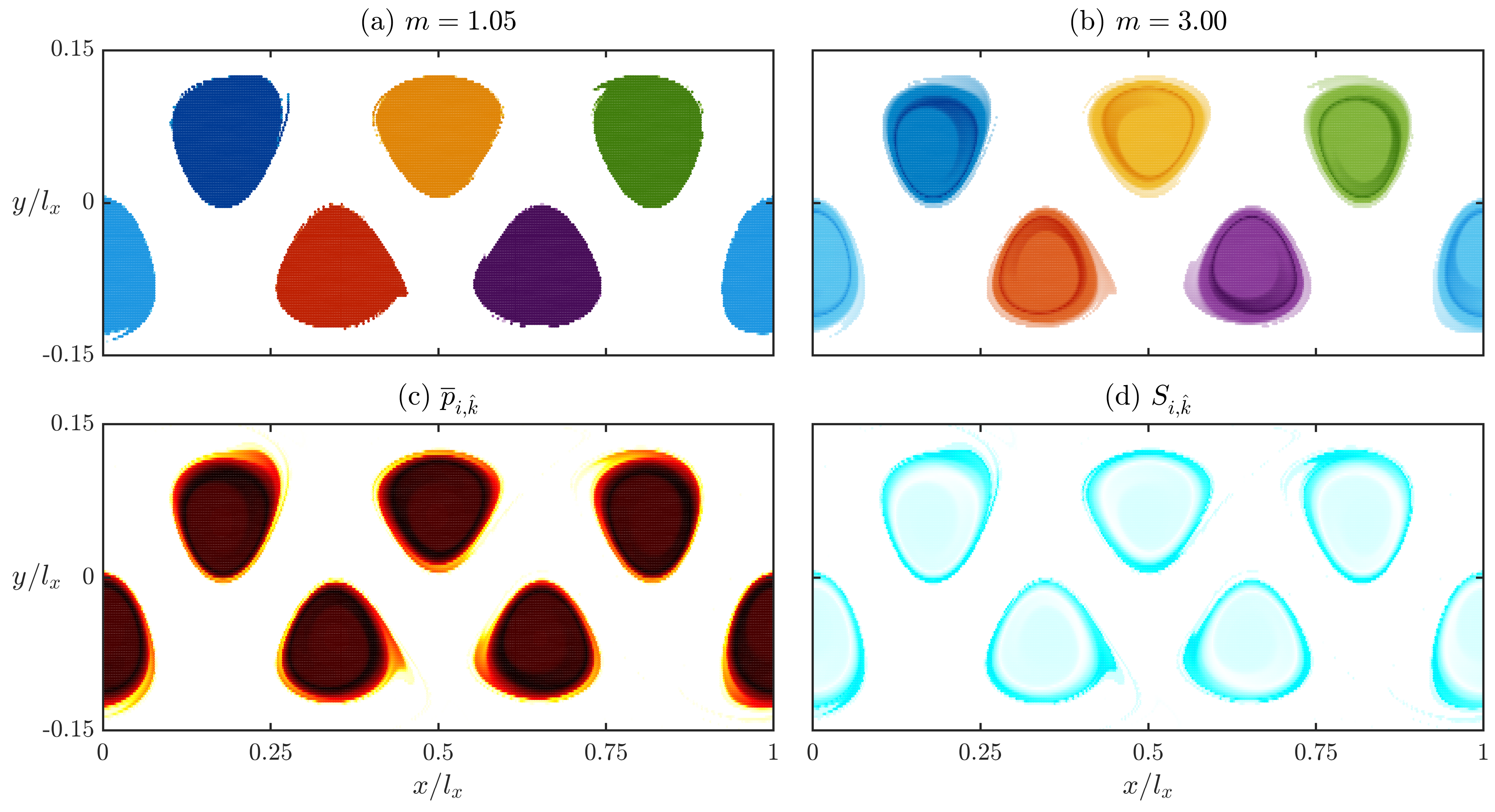
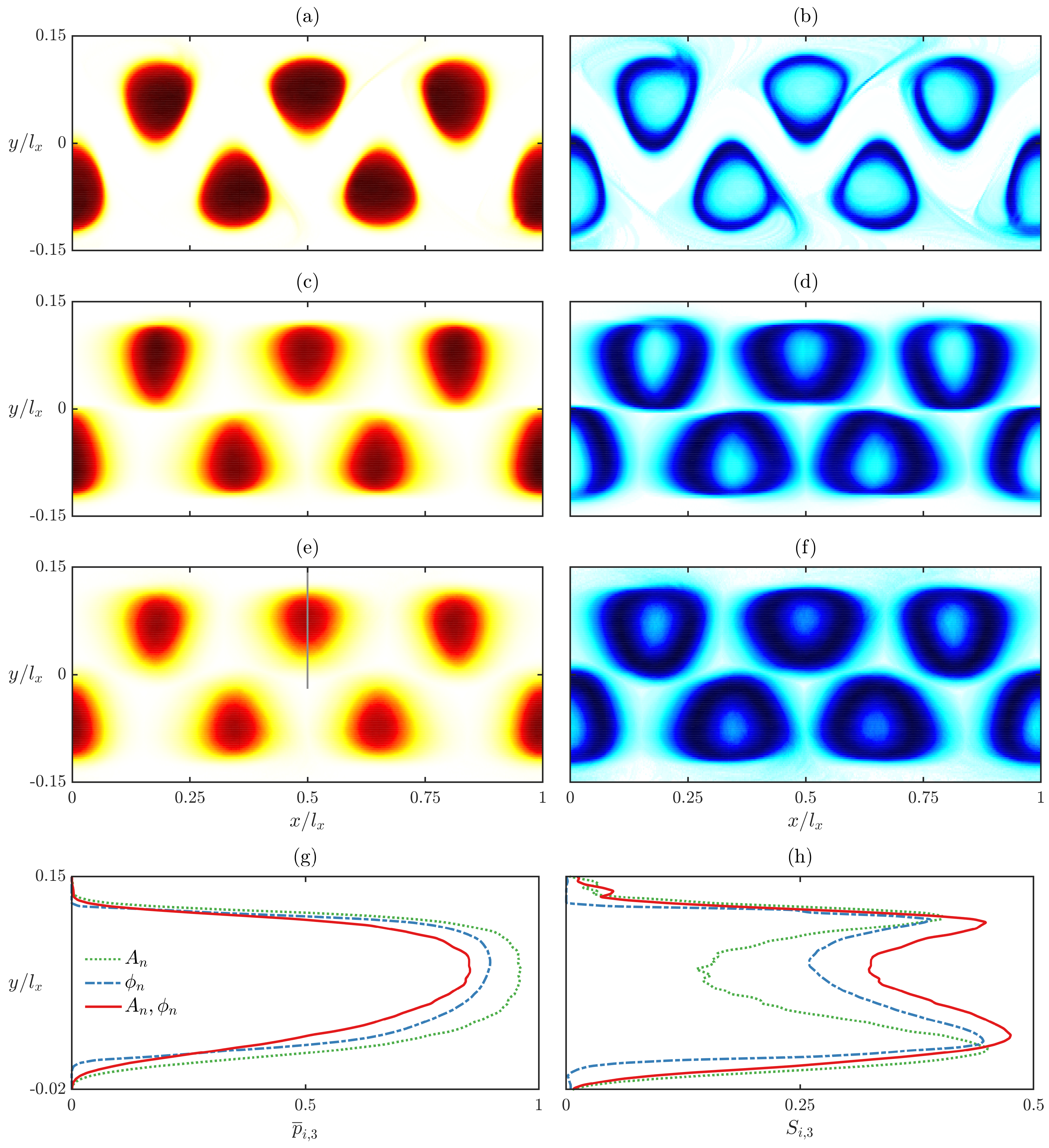
3.3. Fuzziness Parameter
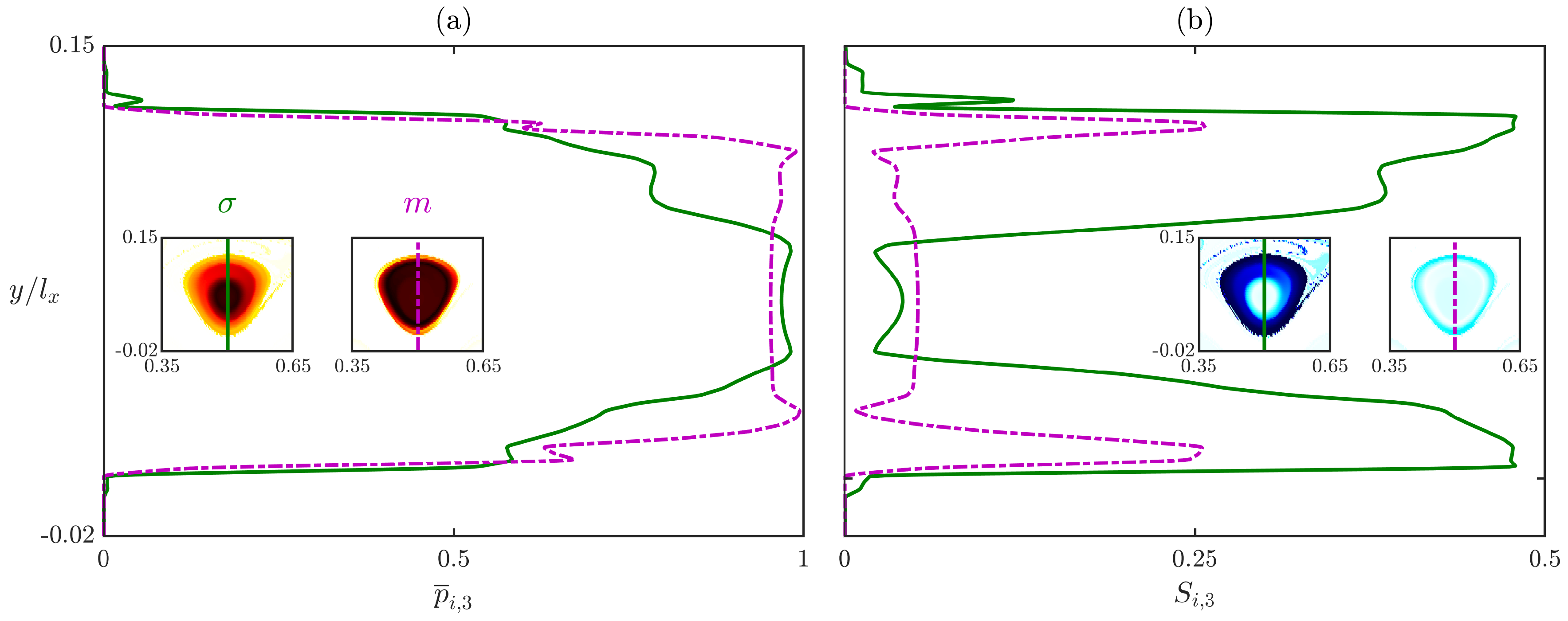
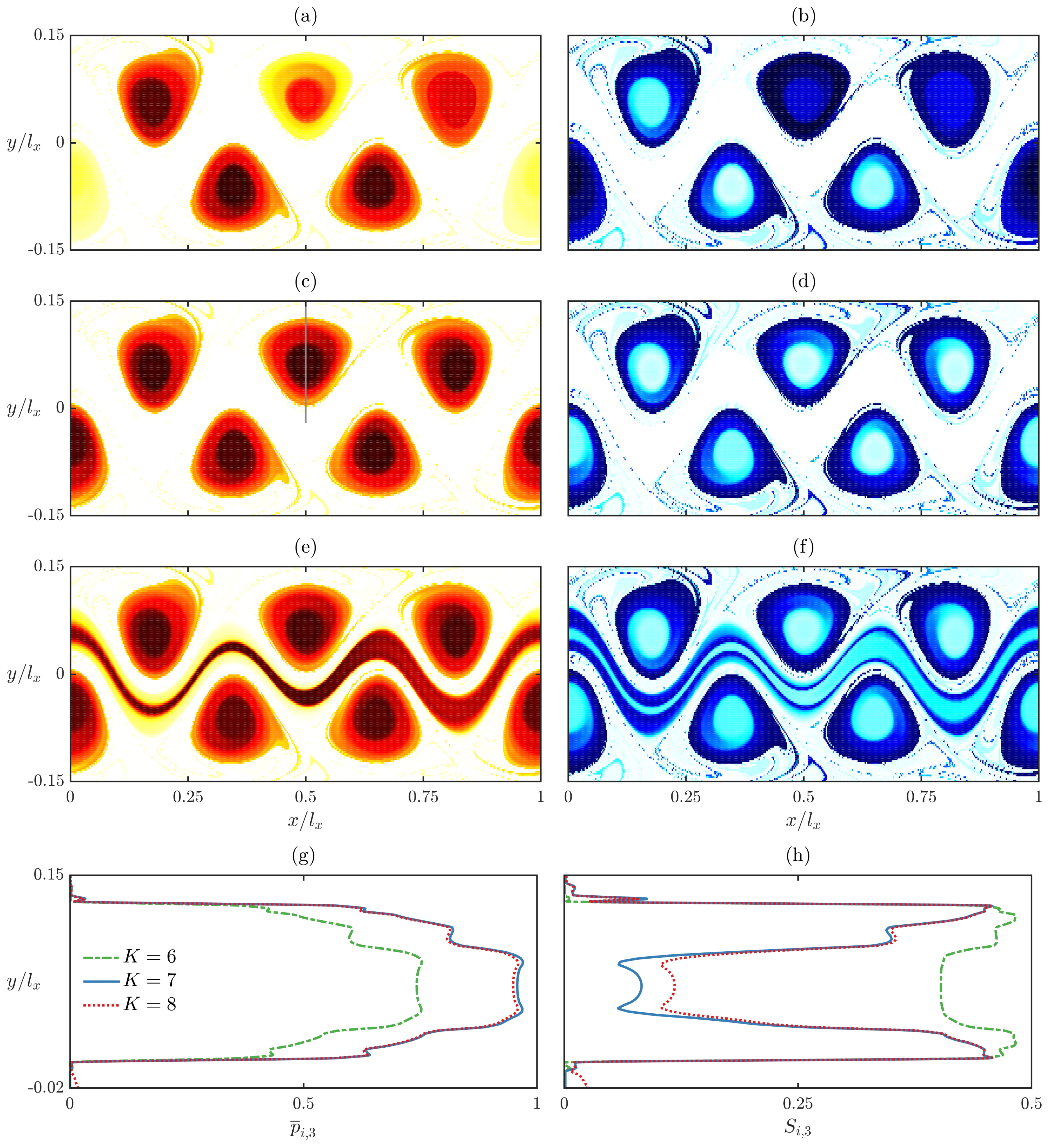
3.4. Number of Clusters
4. Ensemble Realizations and Uncertainty to Model Parameters and System Dynamics
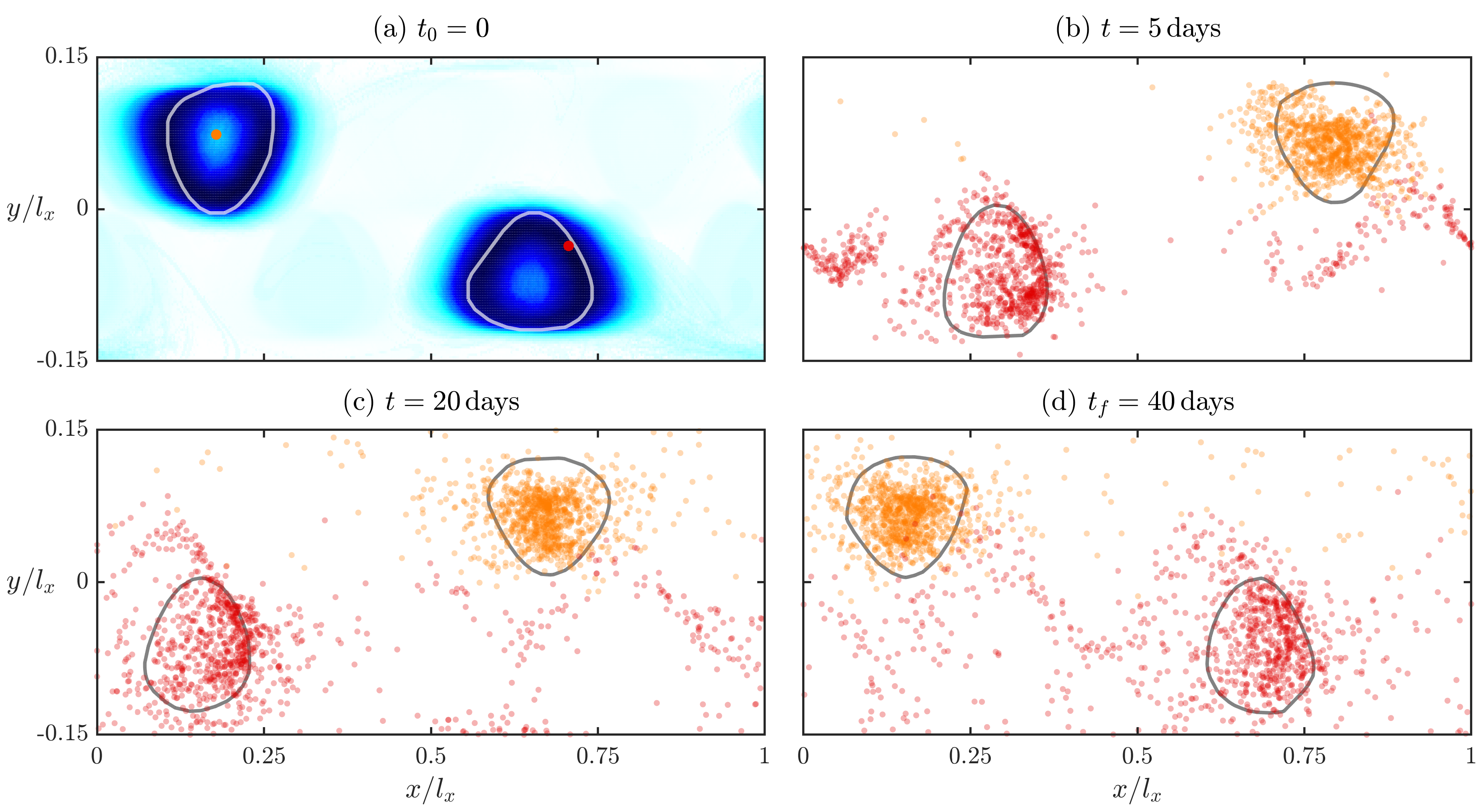
4.1. Perturbing the Bickley Jet Dynamics
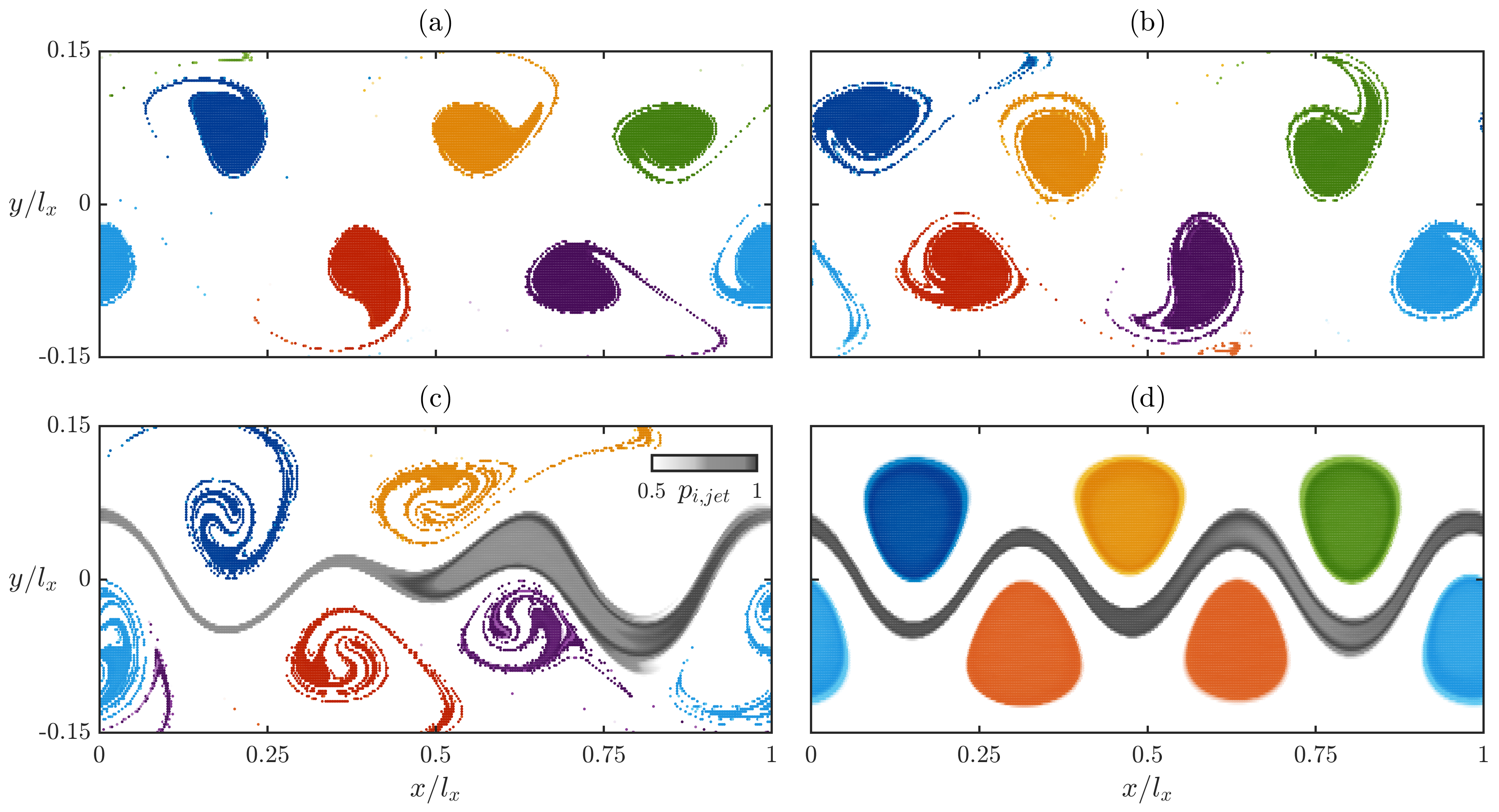
4.2. Uncertainty Quantification of Ensemble Simulations
5. Martha’s Vineyard Ensemble Forecast and Surface Drifter Trajectories
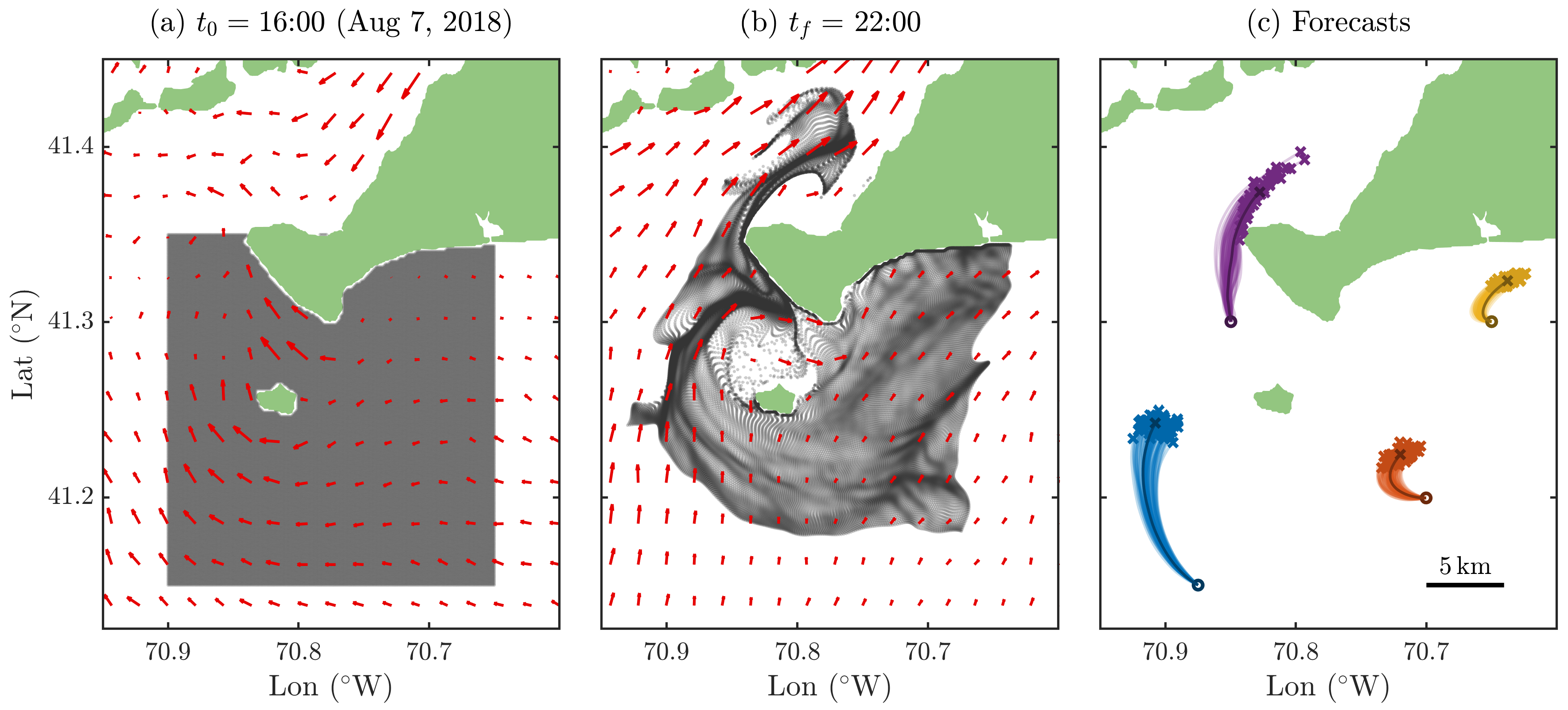
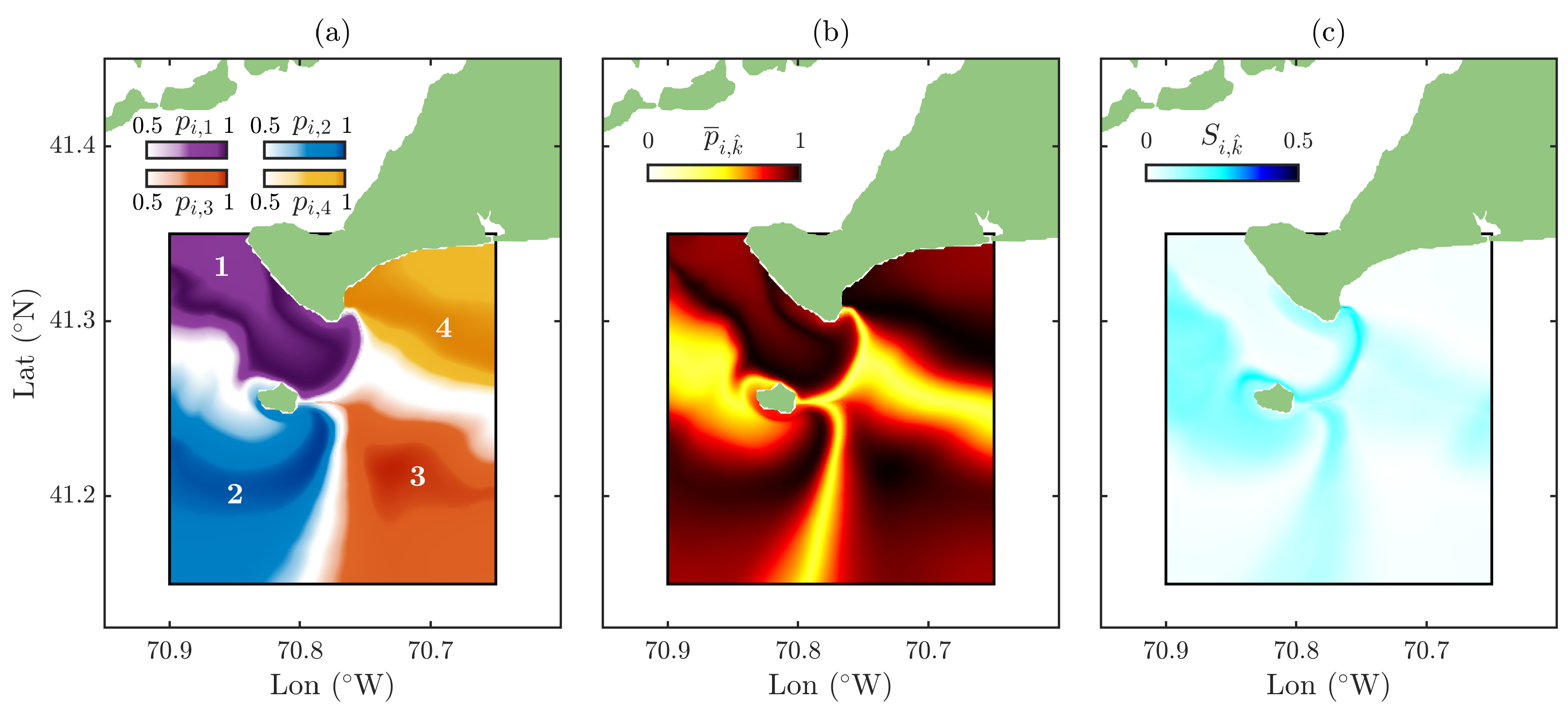
5.1. Velocity Model Ensemble Forecast and Uncertainty Quantification
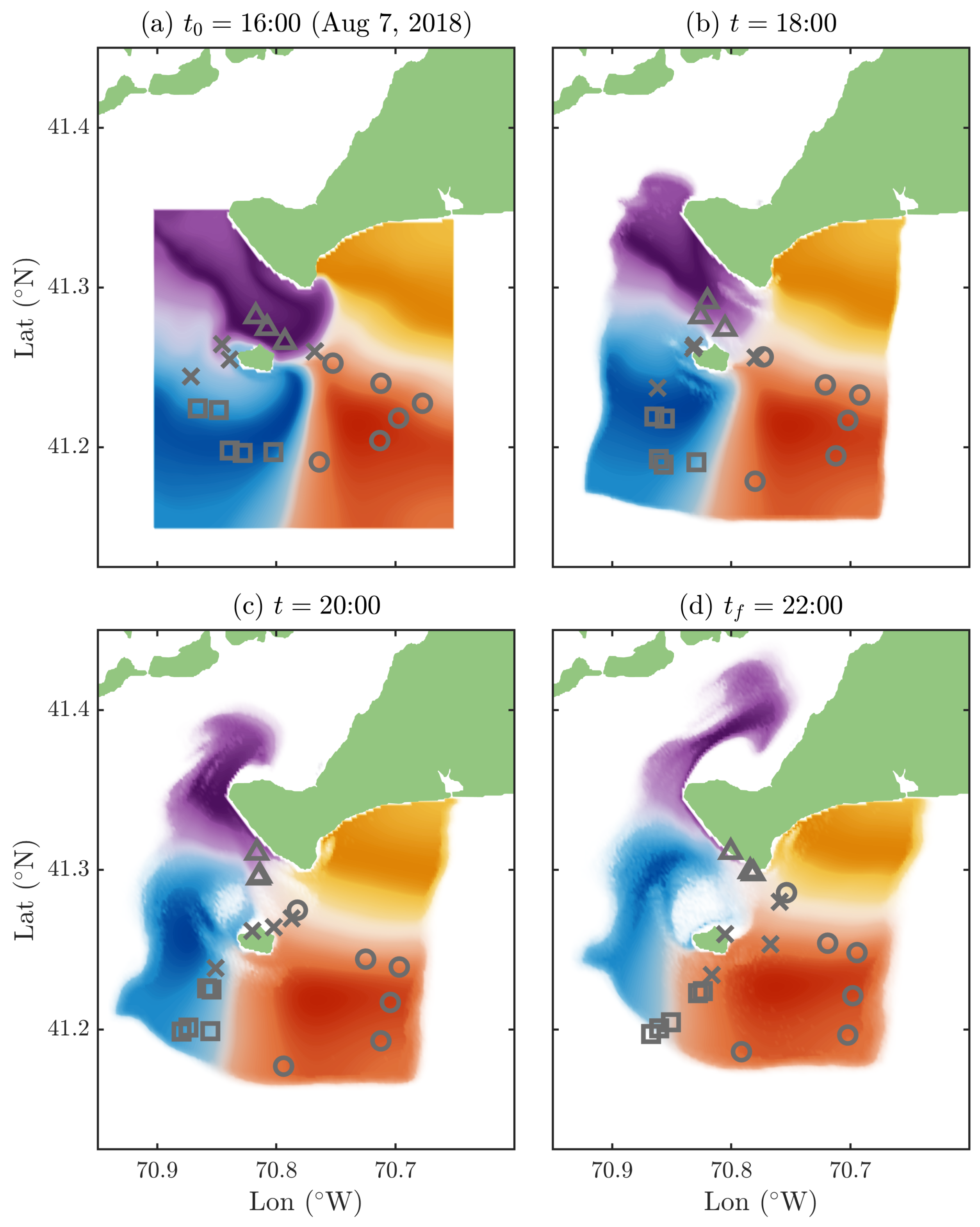
5.2. Drifter Data and Forecast Cluster Dynamics
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McWilliams, J.C. The emergence of isolated coherent vortices in turbulent flow. J. Fluid Mech. 1984, 146, 21–43. [Google Scholar] [CrossRef]
- Provenzale, A. Transport by coherent barotropic vortices. Annu. Rev. Fluid Mech. 1999, 31, 55–93. [Google Scholar] [CrossRef]
- Haller, G. Lagrangian coherent structures. Annu. Rev. Fluid Mech. 2015, 47, 137–162. [Google Scholar] [CrossRef]
- Haller, G.; Beron-Vera, F.J. Geodesic theory of transport barriers in two-dimensional flows. Physica D 2012, 241, 1680–1702. [Google Scholar] [CrossRef]
- Froyland, G.; Padberg-Gehle, K. A rough-and-ready cluster-based approach for extracting finite-time coherent sets from sparse and incomplete trajectory data. Chaos Interdiscip. J. Nonlinear Sci. 2015, 25, 087406. [Google Scholar] [CrossRef]
- Allshouse, M.R.; Peacock, T. Lagrangian based methods for coherent structure detection. Chaos Interdiscip. J. Nonlinear Sci. 2015, 25, 097617. [Google Scholar] [CrossRef]
- Allshouse, M.R.; Thiffeault, J.L. Detecting coherent structures using braids. Phys. D Nonlinear Phenom. 2012, 241, 95–105. [Google Scholar] [CrossRef]
- Froyland, G. Dynamic isoperimetry and the geometry of Lagrangian coherent structures. Nonlinearity 2015, 28, 3587. [Google Scholar] [CrossRef]
- Beron-Vera, F.J.; Wang, Y.; Olascoaga, M.J.; Goni, G.J.; Haller, G. Objective detection of oceanic eddies and the Agulhas leakage. J. Phys. Oceanogr. 2013, 43, 1426–1438. [Google Scholar] [CrossRef]
- Haller, G.; Beron-Vera, F.J. Coherent Lagrangian vortices: The black holes of turbulence. J. Fluid Mech. 2013, 731. [Google Scholar] [CrossRef]
- Boffetta, G.; Lacorata, G.; Redaelli, G.; Vulpiani, A. Detecting barriers to transport: A review of different techniques. Phys. D Nonlinear Phenom. 2001, 159, 58–70. [Google Scholar] [CrossRef]
- Peacock, T.; Dabiri, J. Introduction to focus issue: Lagrangian coherent structures. Chaos Interdiscip. J. Nonlinear Sci. 2010, 20, 017501. [Google Scholar] [CrossRef]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data clustering: A review. ACM Comput. Surv. (CSUR) 1999, 31, 264–323. [Google Scholar] [CrossRef]
- Everitt, B.; Landau, S.; Leese, M.; Stahl, D. Cluster Analysis, 5th ed.; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Hadjighasem, A.; Karrasch, D.; Teramoto, H.; Haller, G. Spectral-clustering approach to Lagrangian vortex detection. Phys. Rev. E 2016, 93, 063107. [Google Scholar] [CrossRef]
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 888–905. [Google Scholar]
- Ng, A.Y.; Jordan, M.I.; Weiss, Y. On spectral clustering: Analysis and an algorithm. In Advances in Neural Information Processing Systems; 2002; pp. 849–856. Available online: http://papers.nips.cc/paper/2092-on-spectral-clustering-analysis-and-an-algorithm.pdf (accessed on 11 October 2020).
- von Luxburg, U. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Filippone, M.; Camastra, F.; Masulli, F.; Rovetta, S. A survey of kernel and spectral methods for clustering. Pattern Recognit. 2008, 41, 176–190. [Google Scholar] [CrossRef]
- Hadjighasem, A.; Farazmand, M.; Blazevski, D.; Froyland, G.; Haller, G. A critical comparison of Lagrangian methods for coherent structure detection. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 053104. [Google Scholar] [CrossRef]
- Vieira, G.S.; Allshouse, M.R. Internal wave boluses as coherent structures in a continuously stratified fluid. J. Fluid Mech. 2020, 885, A35. [Google Scholar] [CrossRef]
- Lermusiaux, P.F. Uncertainty estimation and prediction for interdisciplinary ocean dynamics. J. Comput. Phys. 2006, 217, 176–199. [Google Scholar] [CrossRef]
- Lermusiaux, P.F.; Chiu, C.S.; Gawarkiewicz, G.G.; Abbot, P.; Robinson, A.R.; Miller, R.N.; Haley, P.J.; Leslie, W.G.; Majumdar, S.J.; Pang, A.; et al. Quantifying uncertainties in ocean predictions. Oceanography 2006, 19, 92–105. [Google Scholar] [CrossRef]
- Kratzke, T.M.; Stone, L.D.; Frost, J.R. Search and rescue optimal planning system. In Proceedings of the 2010 13th International Conference on Information Fusion, Edinburgh, UK, 26–29 July 2010; pp. 1–8. [Google Scholar]
- Serra, M.; Sathe, P.; Rypina, I.; Kirincich, A.; Ross, S.D.; Lermusiaux, P.; Allen, A.; Peacock, T.; Haller, G. Search and rescue at sea aided by hidden flow structures. Nat. Commun. 2020, 11, 2525. [Google Scholar] [CrossRef] [PubMed]
- Haller, G. Lagrangian coherent structures from approximate velocity data. Phys. Fluids A 2002, 14, 1851–1861. [Google Scholar] [CrossRef]
- Olascoaga, M.J.; Beron-Vera, F.J.; Haller, G.; Trinanes, J.; Iskandarani, M.; Coelho, E.; Haus, B.K.; Huntley, H.; Jacobs, G.; Kirwan, A.; et al. Drifter motion in the Gulf of Mexico constrained by altimetric Lagrangian coherent structures. Geophys. Res. Lett. 2013, 40, 6171–6175. [Google Scholar] [CrossRef]
- Jacobs, G.A.; Bartels, B.P.; Bogucki, D.J.; Beron-Vera, F.J.; Chen, S.S.; Coelho, E.F.; Curcic, M.; Griffa, A.; Gough, M.; Haus, B.K.; et al. Data assimilation considerations for improved ocean predictability during the Gulf of Mexico Grand Lagrangian Deployment (GLAD). Ocean Model. 2014, 83, 98–117. [Google Scholar] [CrossRef]
- Beron-Vera, F.J.; Olascoaga, M.J.; Haller, G.; Farazmand, M.; Triñanes, J.; Wang, Y. Dissipative inertial transport patterns near coherent Lagrangian eddies in the ocean. Chaos Interdiscip. J. Nonlinear Sci. 2015, 25, 087412. [Google Scholar] [CrossRef] [PubMed]
- Williams, M.O.; Rypina, I.I.; Rowley, C.W. Identifying finite-time coherent sets from limited quantities of Lagrangian data. Chaos Interdiscip. J. Nonlinear Sci. 2015, 25, 087408. [Google Scholar] [CrossRef]
- Rypina, I.; Kirincich, A.; Limeburner, R.; Udovydchenkov, I. Eulerian and Lagrangian correspondence of high-frequency radar and surface drifter data: Effects of radar resolution and flow components. J. Atmos. Ocean. Technol. 2014, 31, 945–966. [Google Scholar] [CrossRef][Green Version]
- Rypina, I.I.; Kirincich, A.; Lentz, S.; Sundermeyer, M. Investigating the eddy diffusivity concept in the coastal ocean. J. Phys. Oceanogr. 2016, 46, 2201–2218. [Google Scholar] [CrossRef]
- Rypina, I.I.; Pratt, L.J. Trajectory encounter volume as a diagnostic of mixing potential in fluid flows. Nonlinear Process. Geophys. 2017, 24, 189–202. [Google Scholar] [CrossRef]
- Haza, A.; Griffa, A.; Martin, P.; Molcard, A.; Özgökmen, T.; Poje, A.; Barbanti, R.; Book, J.; Poulain, P.; Rixen, M.; et al. Model-based directed drifter launches in the Adriatic Sea: Results from the DART experiment. Geophys. Res. Lett. 2007, 34, 6. [Google Scholar] [CrossRef]
- Haza, A.C.; Özgökmen, T.M.; Griffa, A.; Molcard, A.; Poulain, P.M.; Peggion, G. Transport properties in small-scale coastal flows: Relative dispersion from VHF radar measurements in the Gulf of La Spezia. Ocean Dyn. 2010, 60, 861–882. [Google Scholar] [CrossRef]
- Filippi, M.; Rypina, I.I.; Hadjighasem, A.; Peacock, T. A parameter-free spectral clustering approach to coherent structure detection in geophysical flows. Fluids 2020. submitted. [Google Scholar]
- Rypina, I.; Brown, M.G.; Beron-Vera, F.J.; Koçak, H.; Olascoaga, M.J.; Udovydchenkov, I. On the Lagrangian dynamics of atmospheric zonal jets and the permeability of the stratospheric polar vortex. J. Atmos. Sci. 2007, 64, 3595–3610. [Google Scholar] [CrossRef]
- Beron-Vera, F.J.; Olascoaga, M.J.; Brown, M.G.; Koçak, H.; Rypina, I.I. Invariant-tori-like Lagrangian coherent structures in geophysical flows. Chaos Interdiscip. J. Nonlinear Sci. 2010, 20, 017514. [Google Scholar] [CrossRef]
- Haley, P.J.; Lermusiaux, P.F. Multiscale two-way embedding schemes for free-surface primitive equations in the “Multidisciplinary Simulation, Estimation and Assimilation System”. Ocean Dyn. 2010, 60, 1497–1537. [Google Scholar] [CrossRef]
- Haley, P.J., Jr.; Agarwal, A.; Lermusiaux, P.F. Optimizing velocities and transports for complex coastal regions and archipelagos. Ocean Model. 2015, 89, 1–28. [Google Scholar] [CrossRef]
- Nock, R.; Vaillant, P.; Henry, C.; Nielsen, F. Soft memberships for spectral clustering, with application to permeable language distinction. Pattern Recognit. 2009, 42, 43–53. [Google Scholar] [CrossRef]
- Schlueter-Kuck, K.L.; Dabiri, J.O. Coherent structure colouring: Identification of coherent structures from sparse data using graph theory. J. Fluid Mech. 2017, 811, 468–486. [Google Scholar] [CrossRef]
- Lermusiaux, P. On the mapping of multivariate geophysical fields: Sensitivities to size, scales, and dynamics. J. Atmos. Ocean. Technol. 2002, 19, 1602–1637. [Google Scholar] [CrossRef]
- Ameli, S.; Shadden, S.C. A transport method for restoring incomplete ocean current measurements. J. Geophys. Res. Ocean. 2019, 124, 227–242. [Google Scholar] [CrossRef]
- Ameli, S.; Shadden, S.C. Trajectory Reconstruction and Analysis for Coherent Structure Evaluation (TRACE). 2020. Available online: http://transport.me.berkeley.edu/trace/ (accessed on 11 October 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vieira, G.S.; Rypina, I.I.; Allshouse, M.R. Uncertainty Quantification of Trajectory Clustering Applied to Ocean Ensemble Forecasts. Fluids 2020, 5, 184. https://doi.org/10.3390/fluids5040184
Vieira GS, Rypina II, Allshouse MR. Uncertainty Quantification of Trajectory Clustering Applied to Ocean Ensemble Forecasts. Fluids. 2020; 5(4):184. https://doi.org/10.3390/fluids5040184
Chicago/Turabian StyleVieira, Guilherme S., Irina I. Rypina, and Michael R. Allshouse. 2020. "Uncertainty Quantification of Trajectory Clustering Applied to Ocean Ensemble Forecasts" Fluids 5, no. 4: 184. https://doi.org/10.3390/fluids5040184
APA StyleVieira, G. S., Rypina, I. I., & Allshouse, M. R. (2020). Uncertainty Quantification of Trajectory Clustering Applied to Ocean Ensemble Forecasts. Fluids, 5(4), 184. https://doi.org/10.3390/fluids5040184




