Experiments on Flexible Filaments in Air Flow for Aeroelasticity and Fluid-Structure Interaction Models Validation
Abstract
1. Introduction
2. Materials and Methods
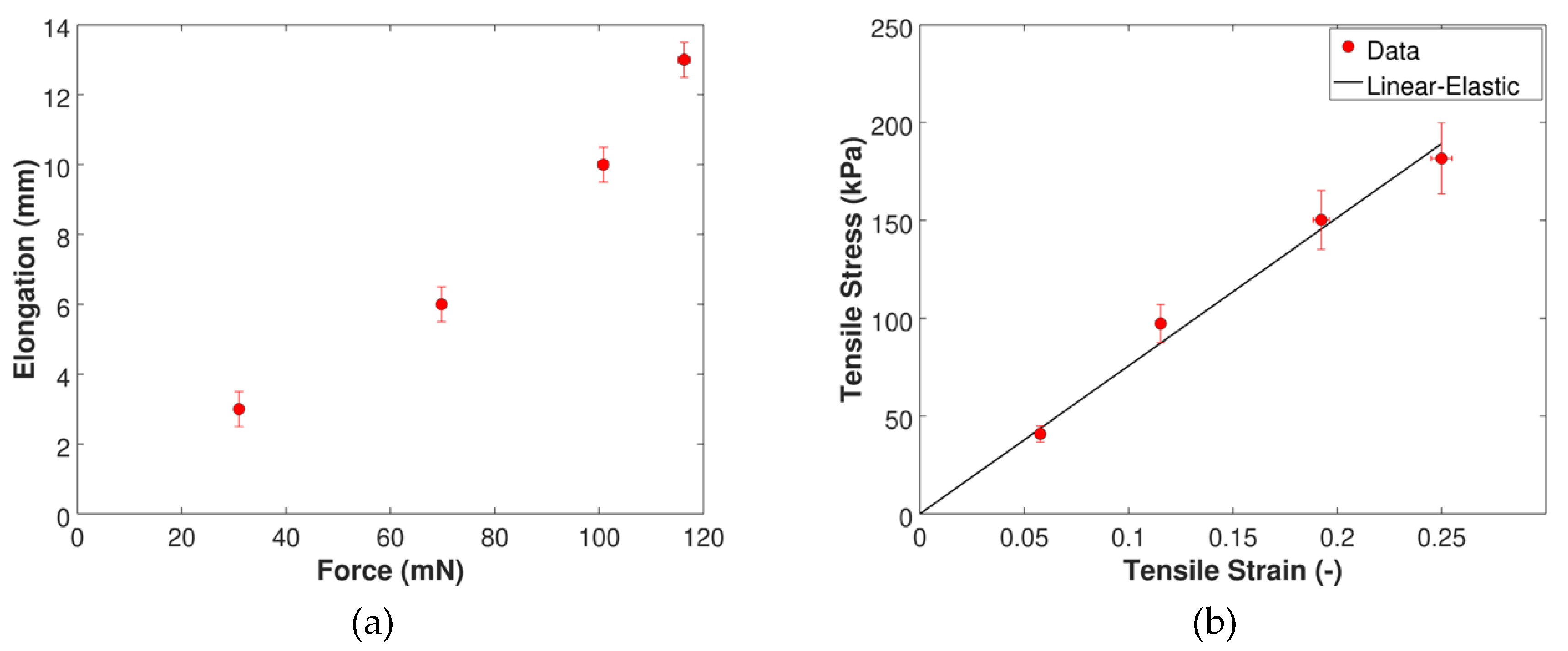
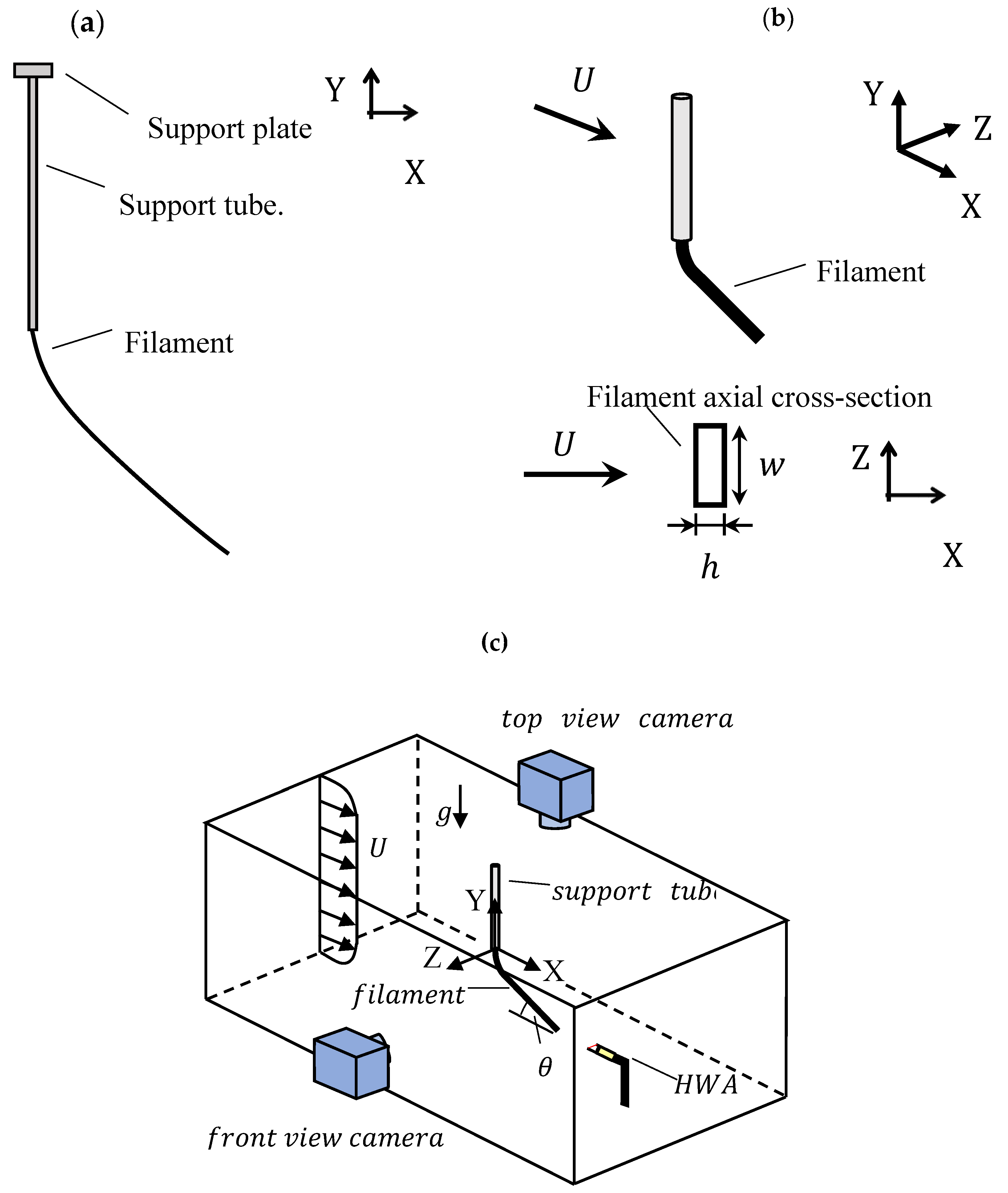
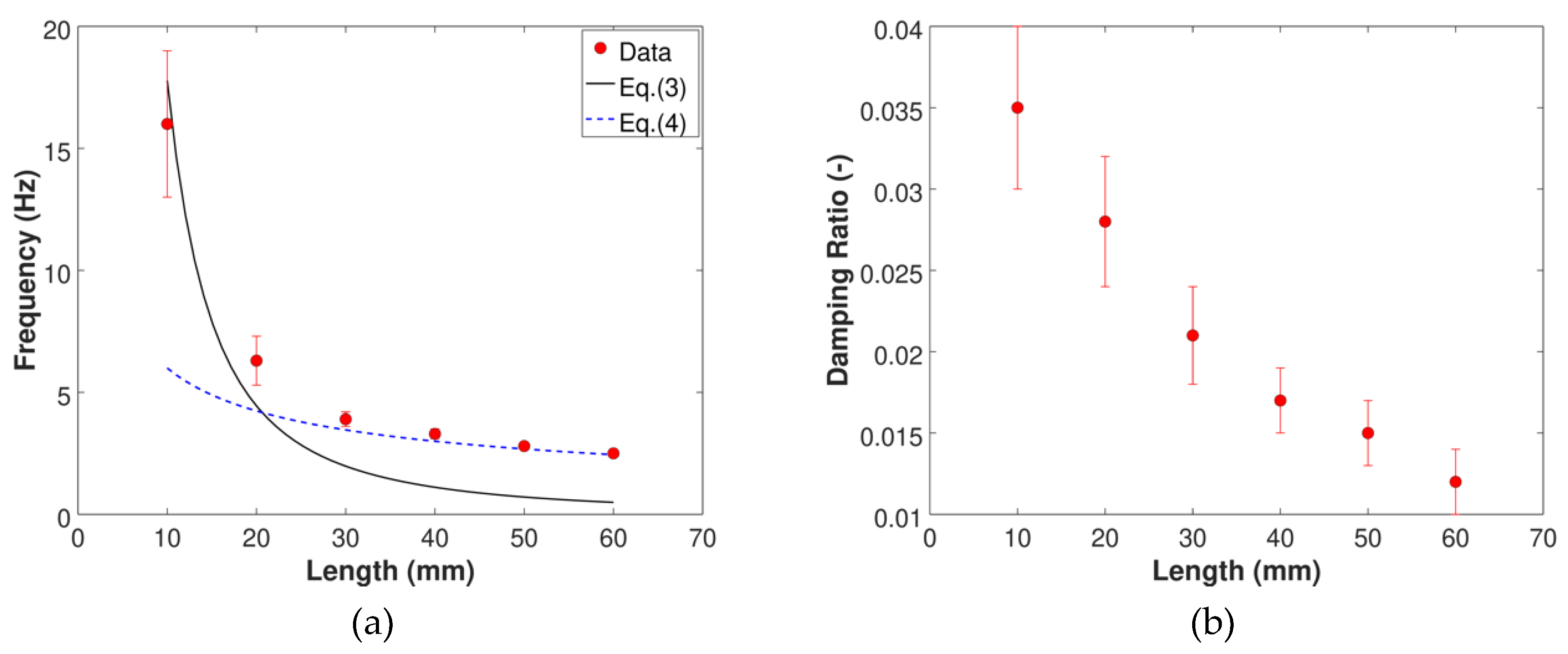
2.1. Flexible Filament Manufacturing and Characterization
2.2. Test Piece Description and Preliminary Characterization
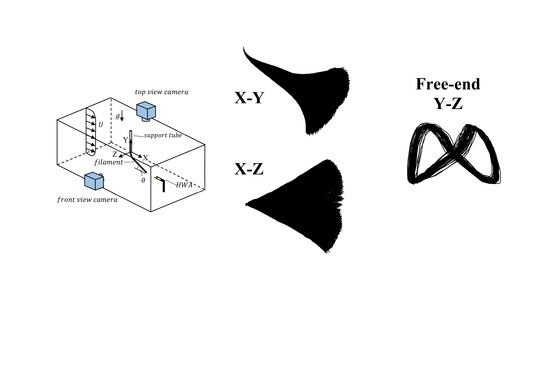
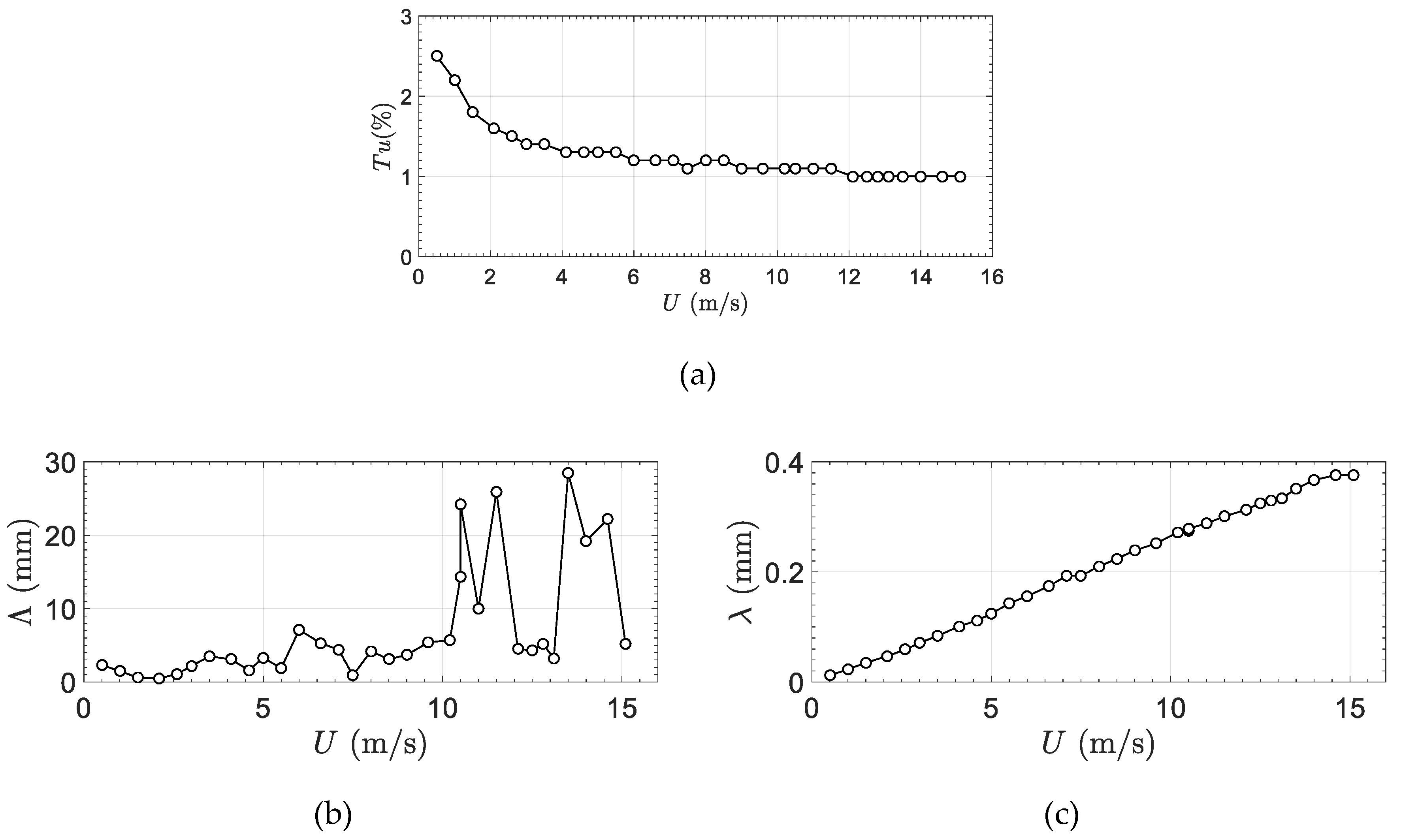
2.3. Wind Tunnel Flow Characterization
2.4. Experimental Procedure
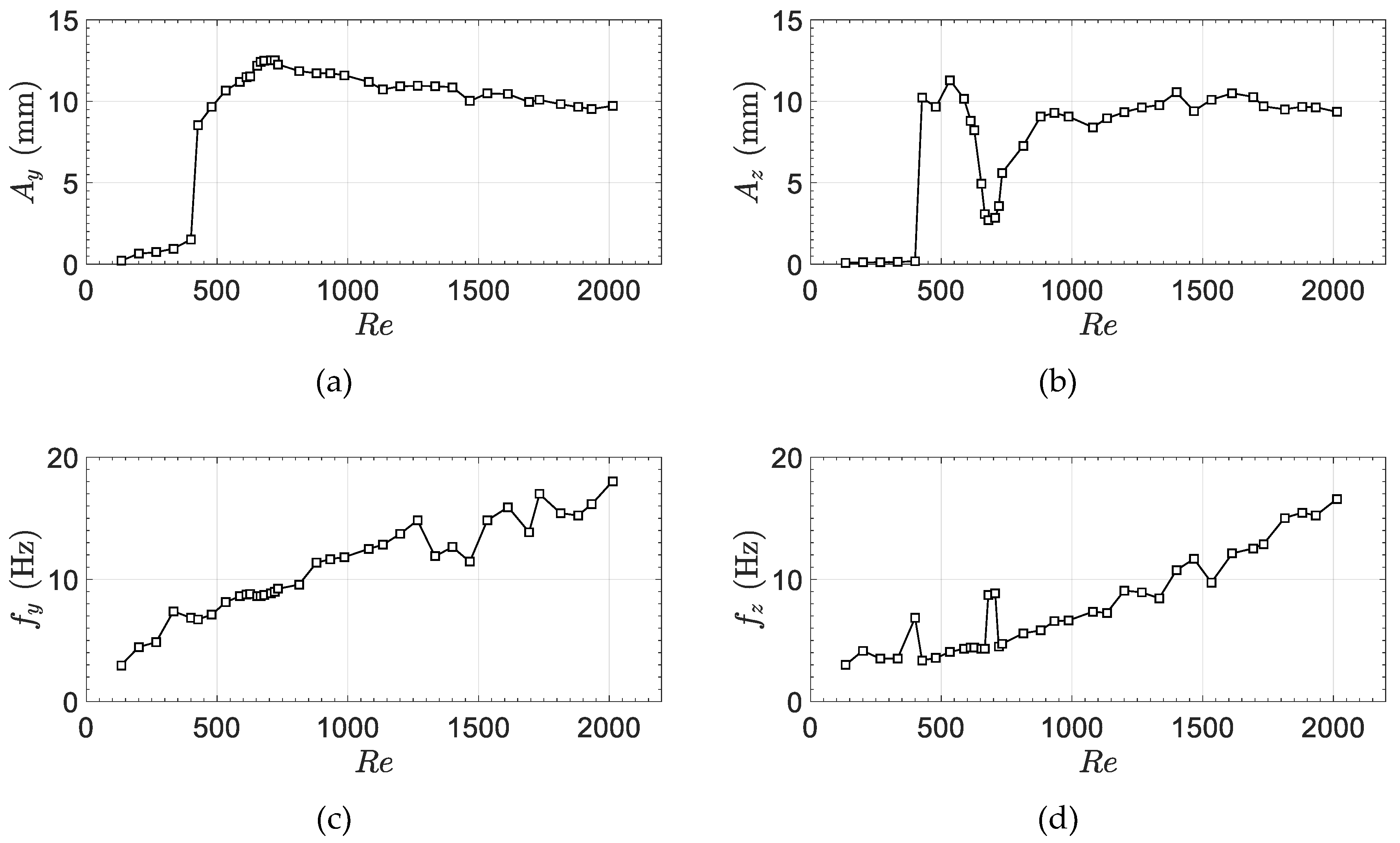
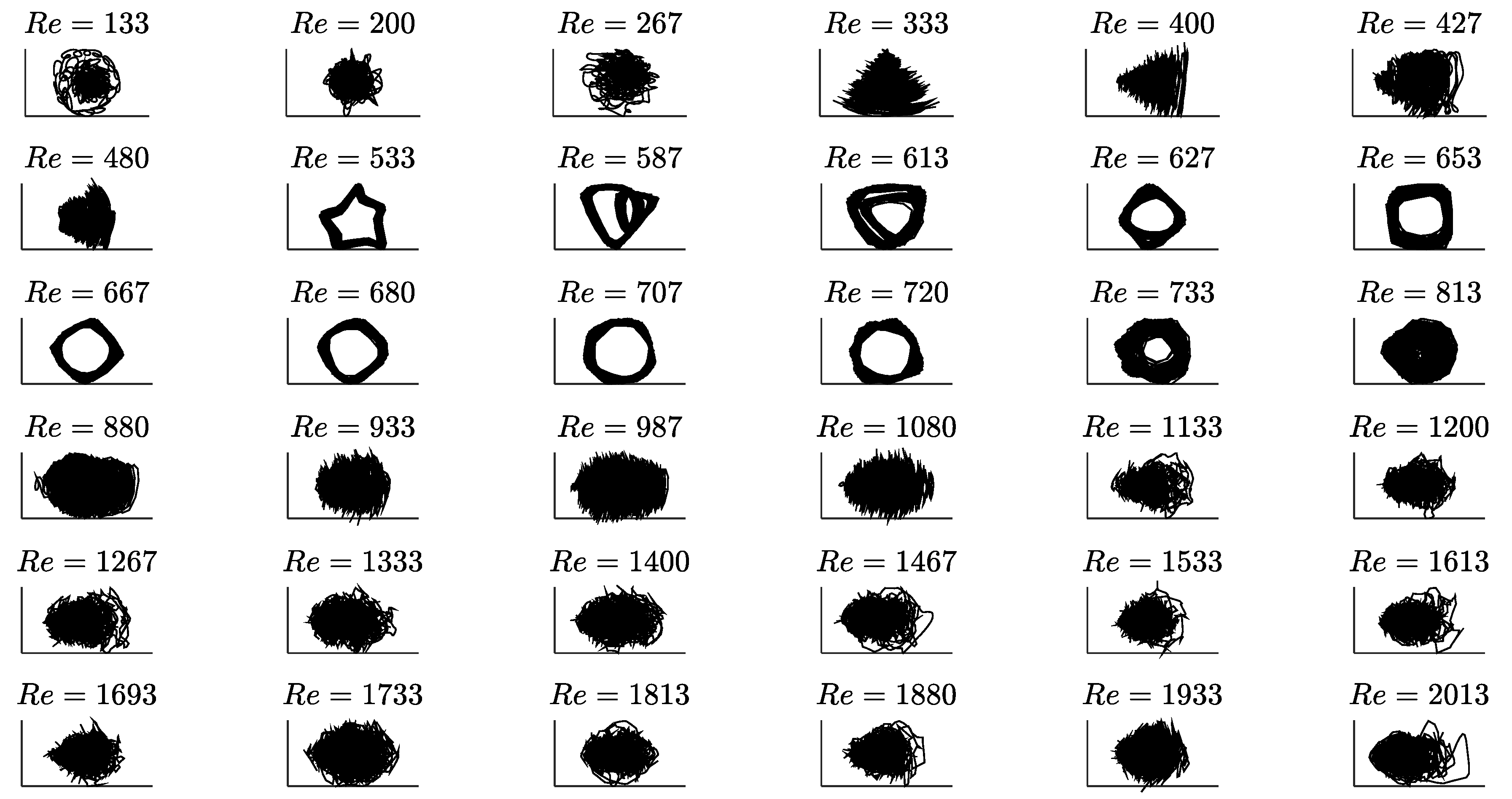
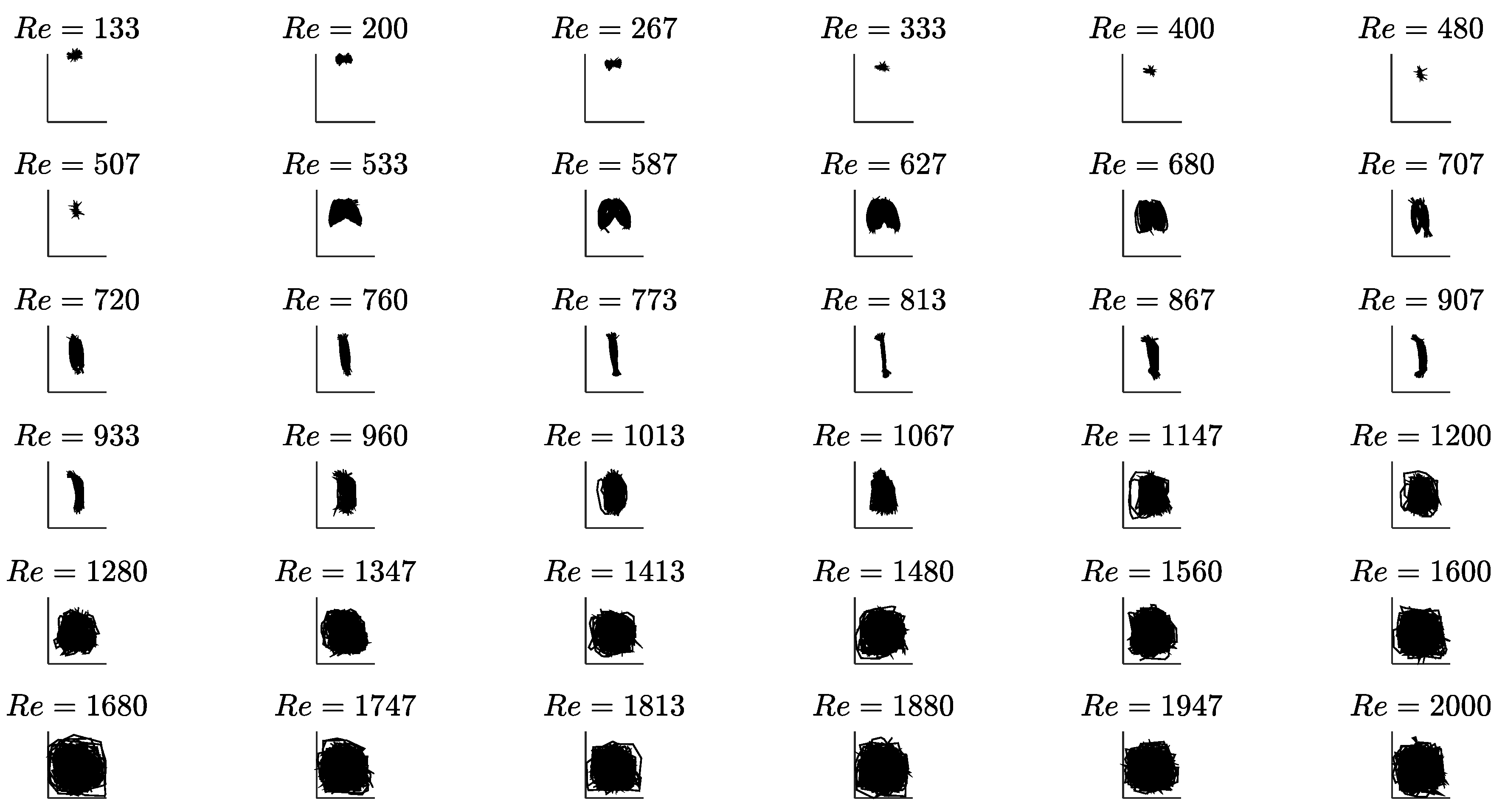
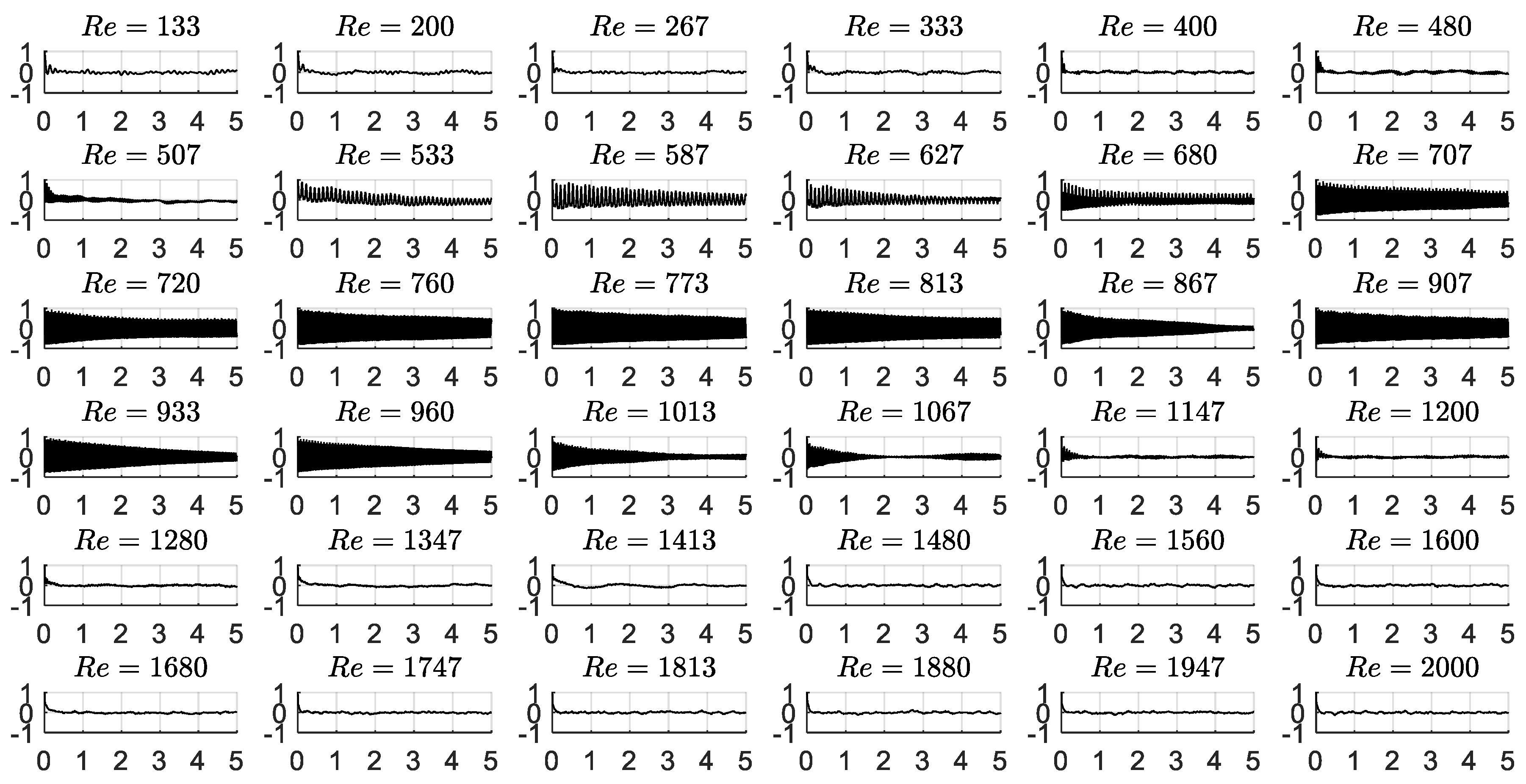
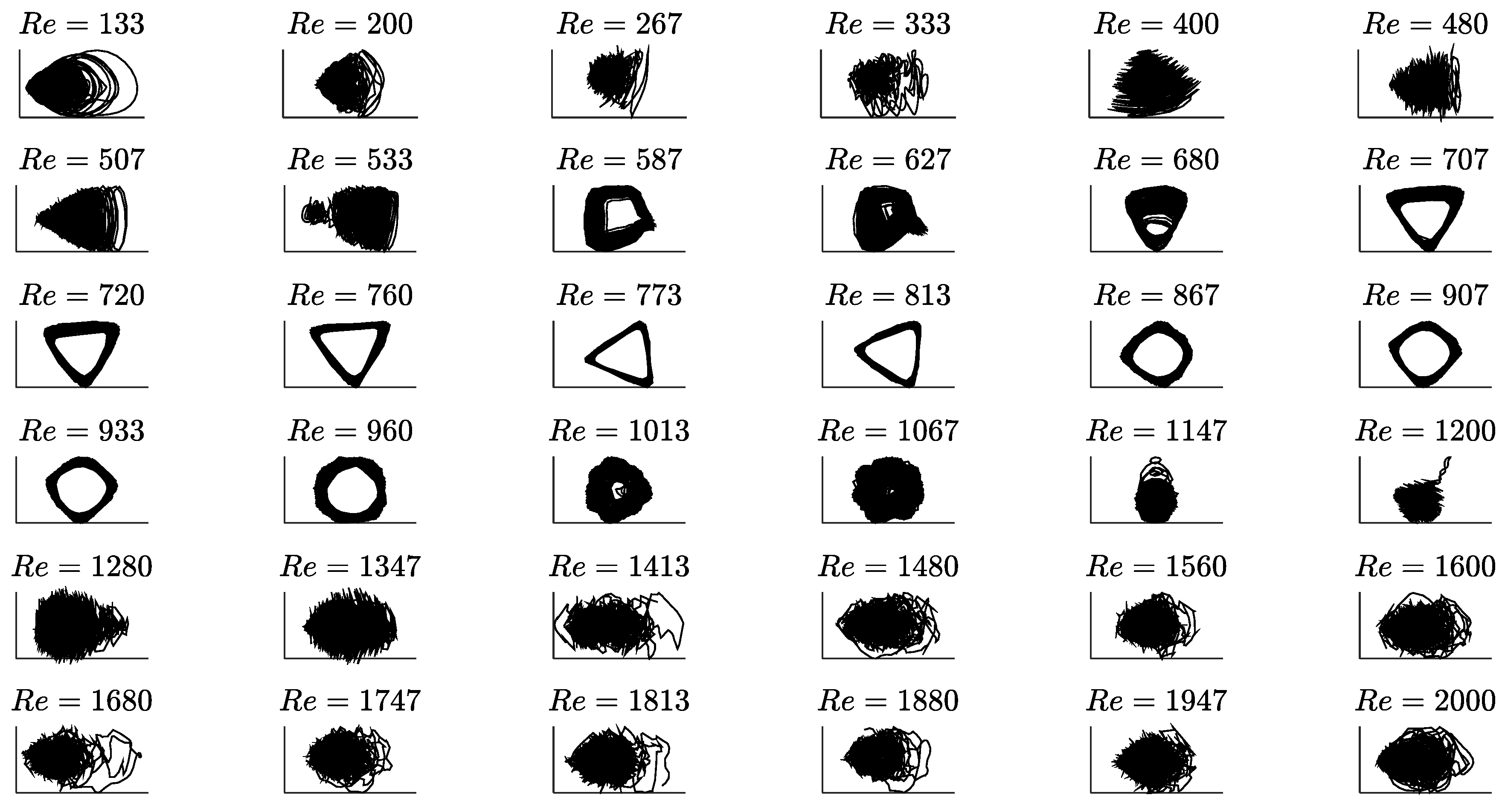
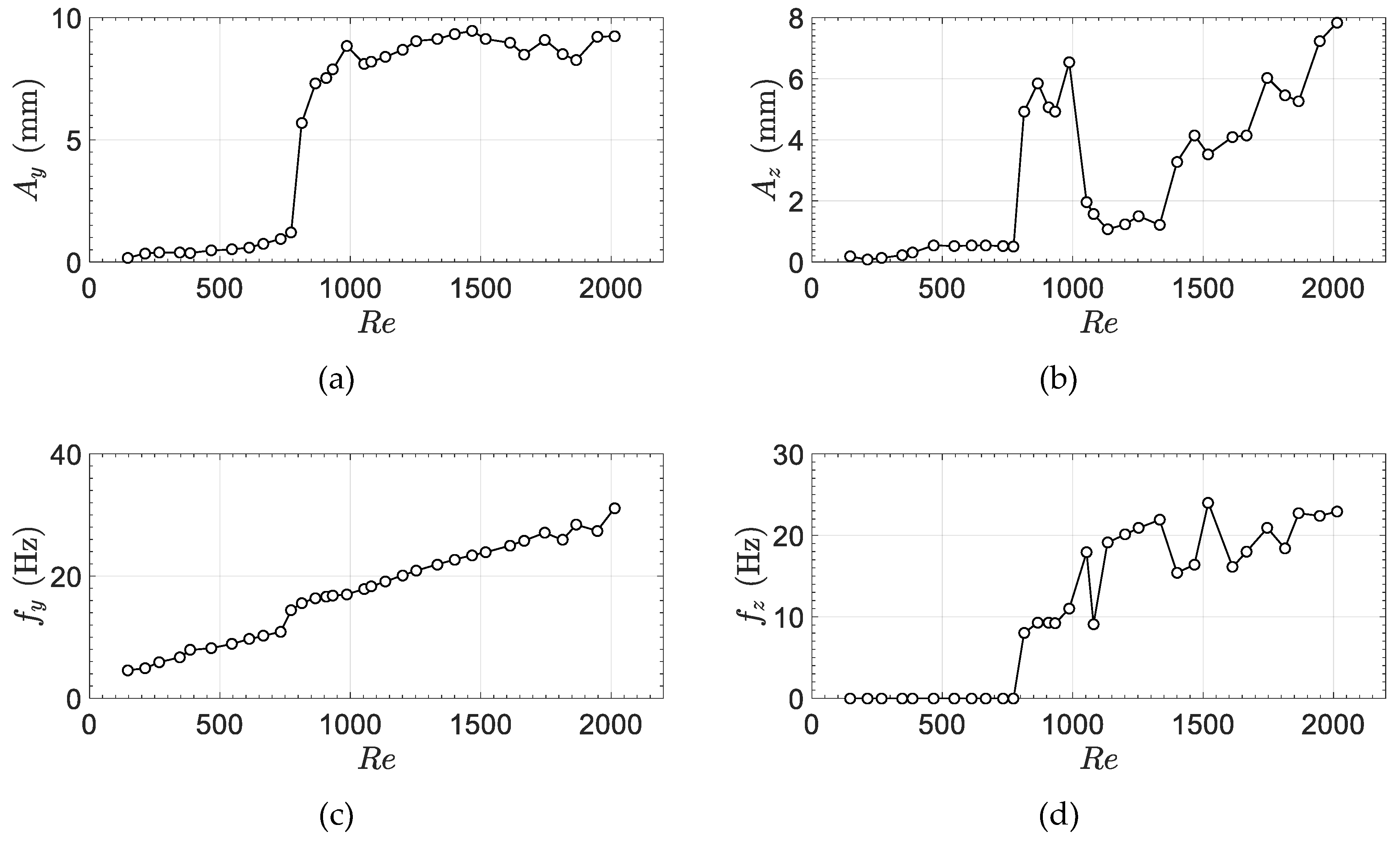
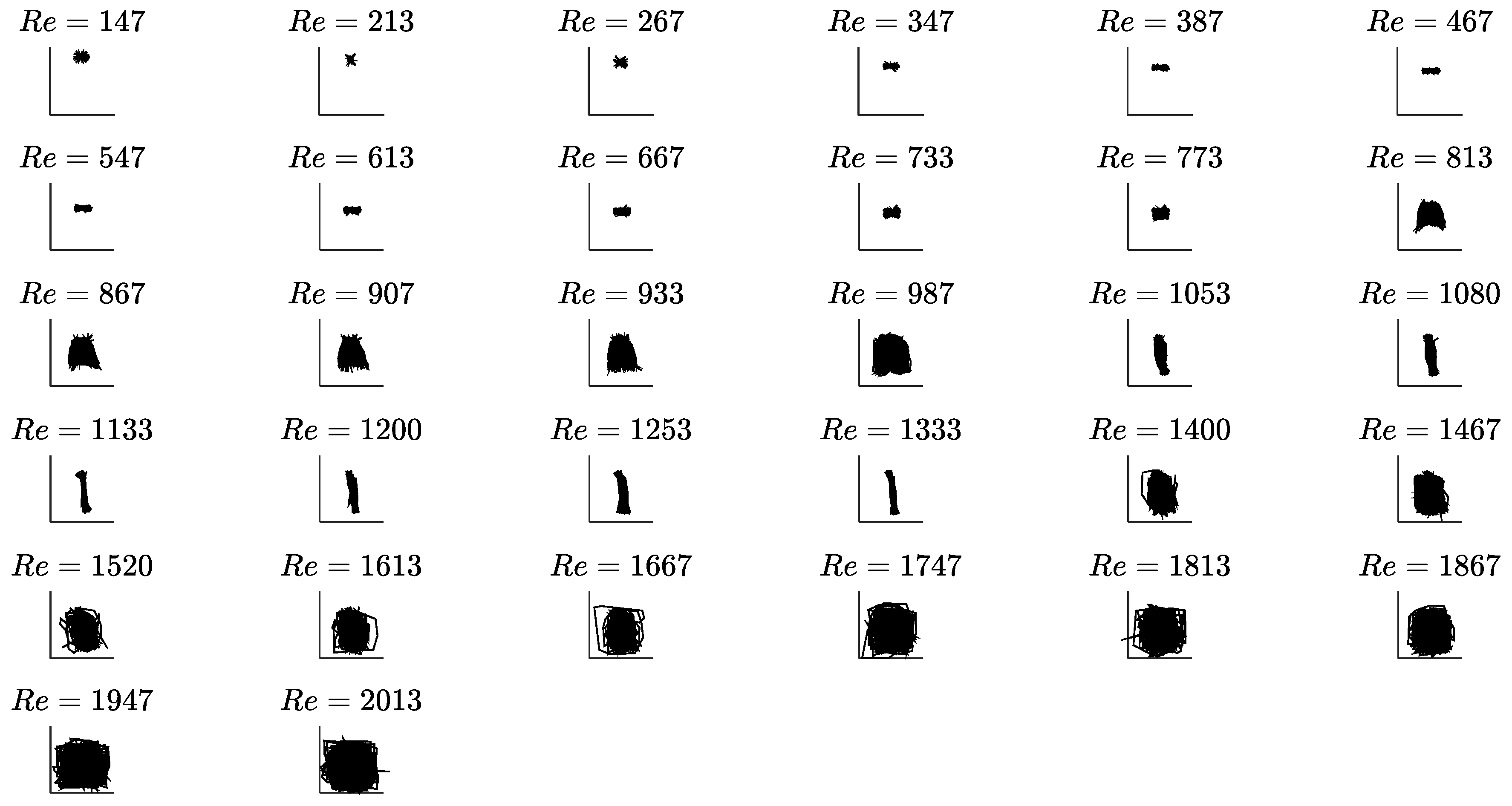
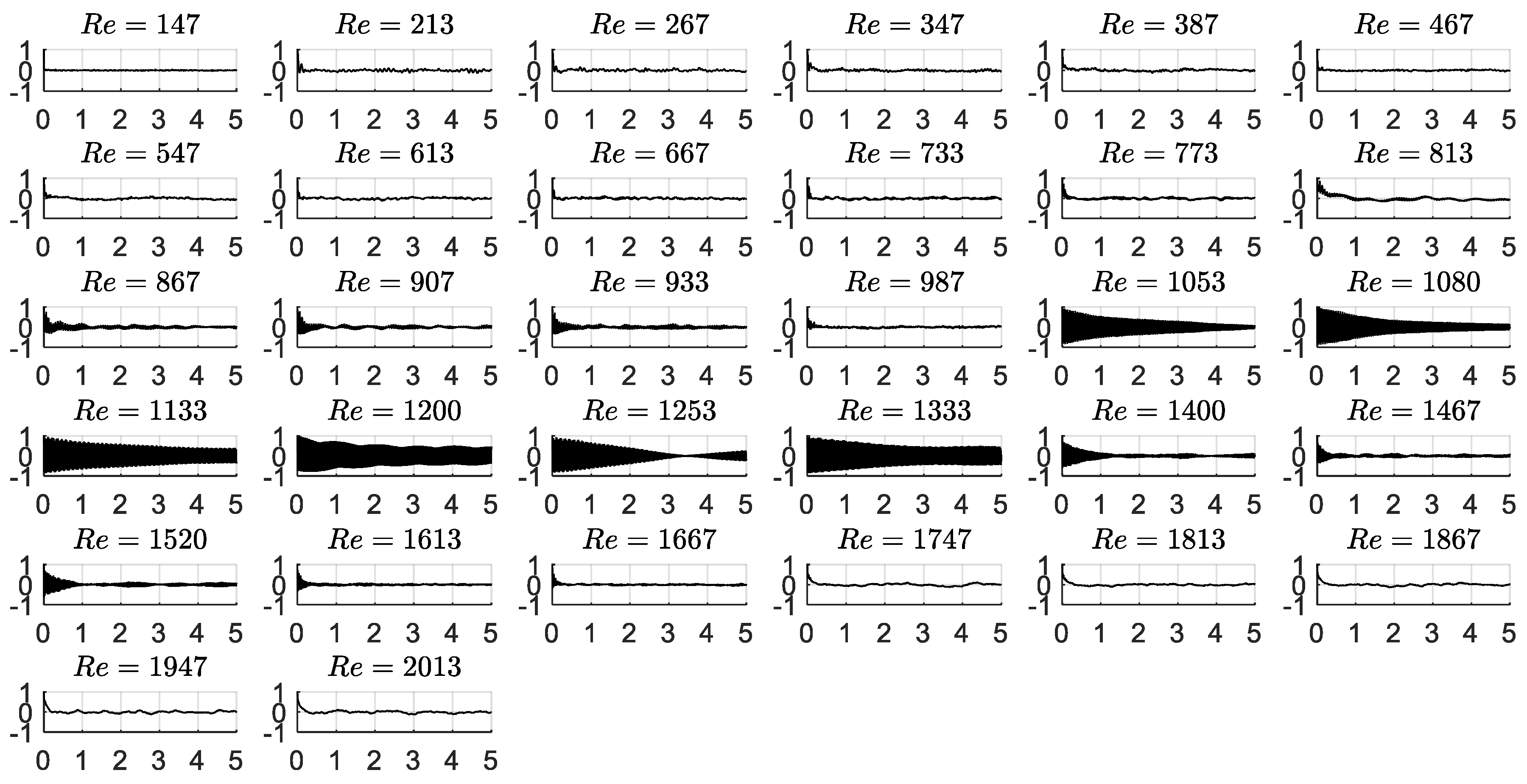
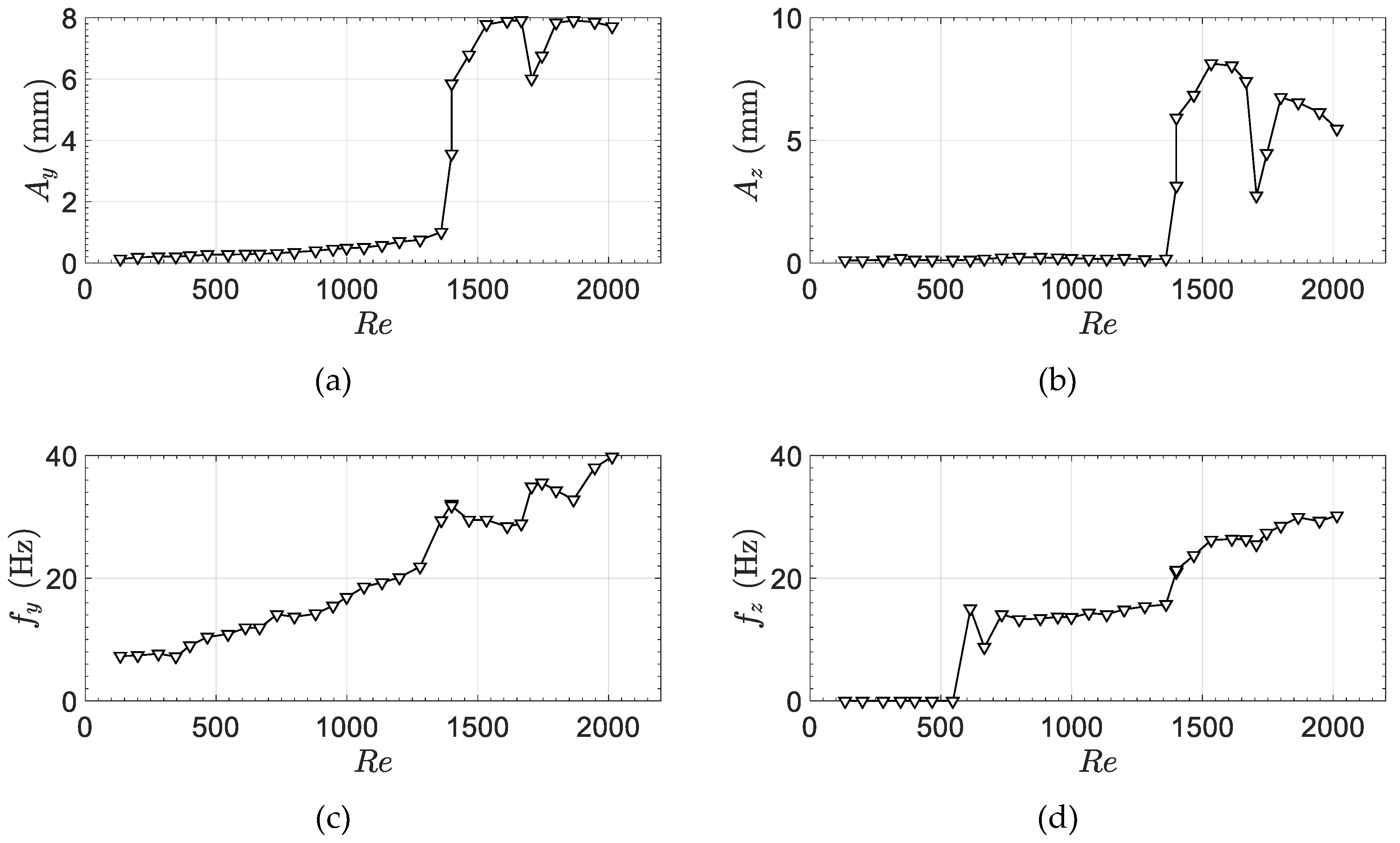
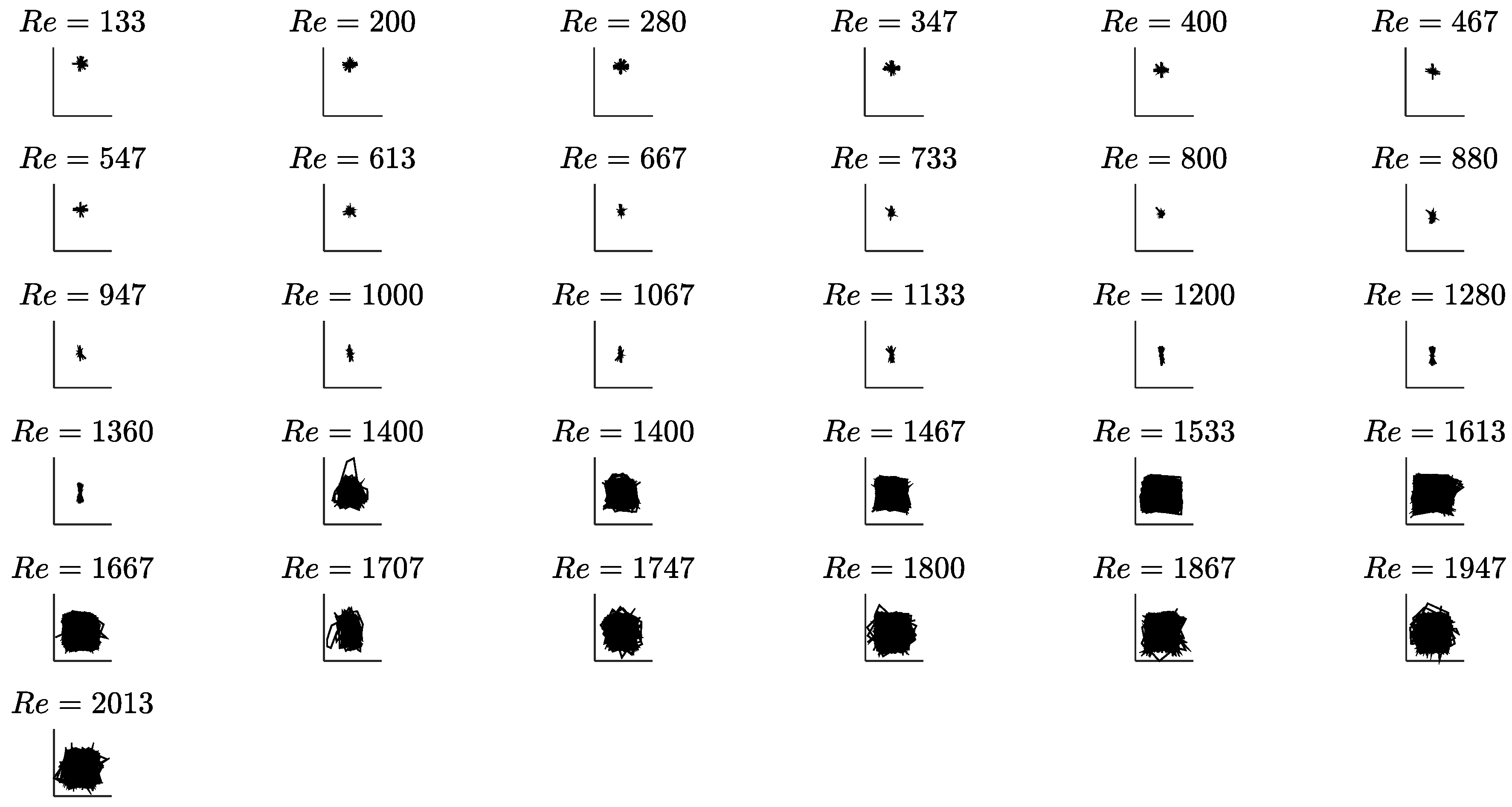
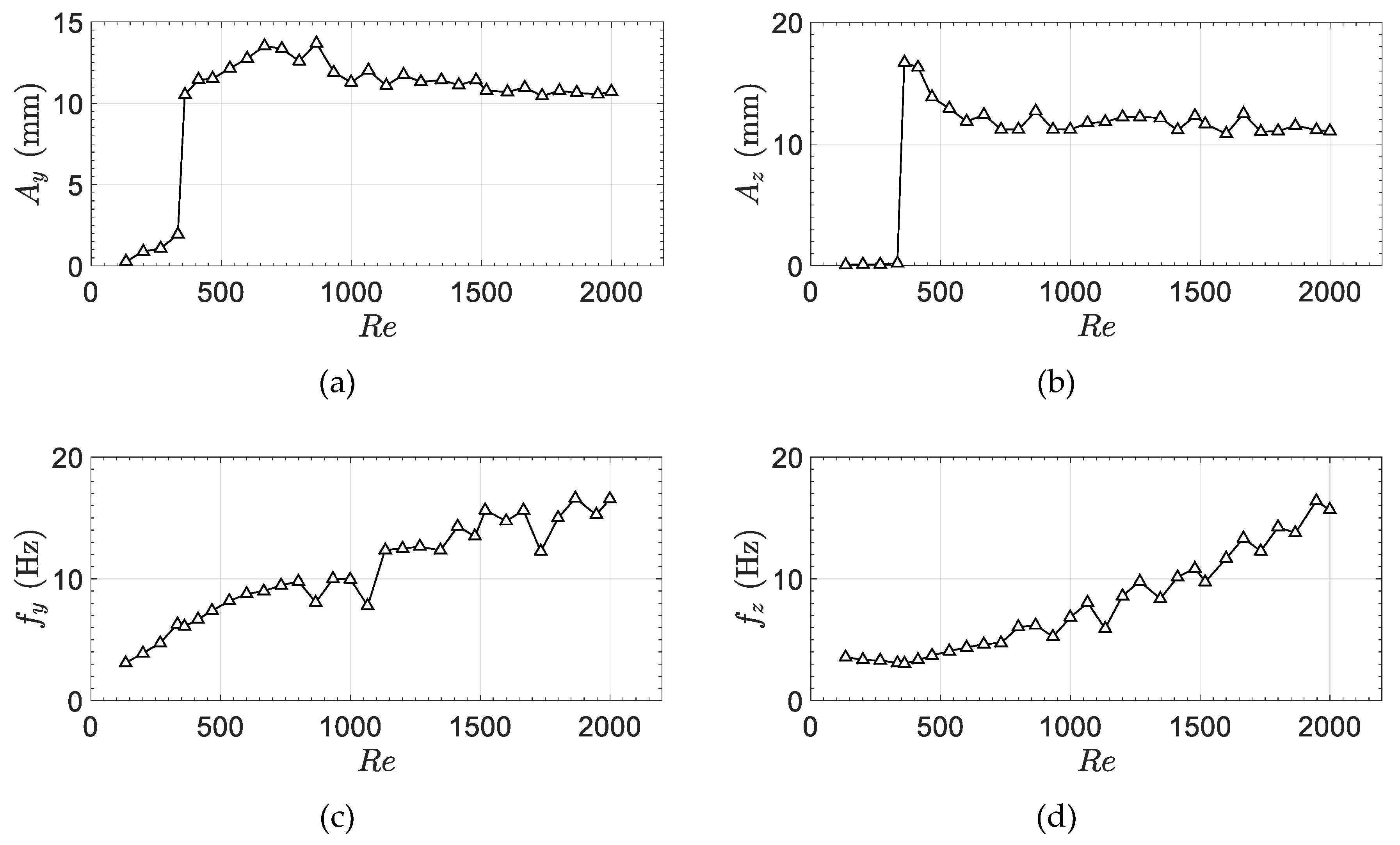
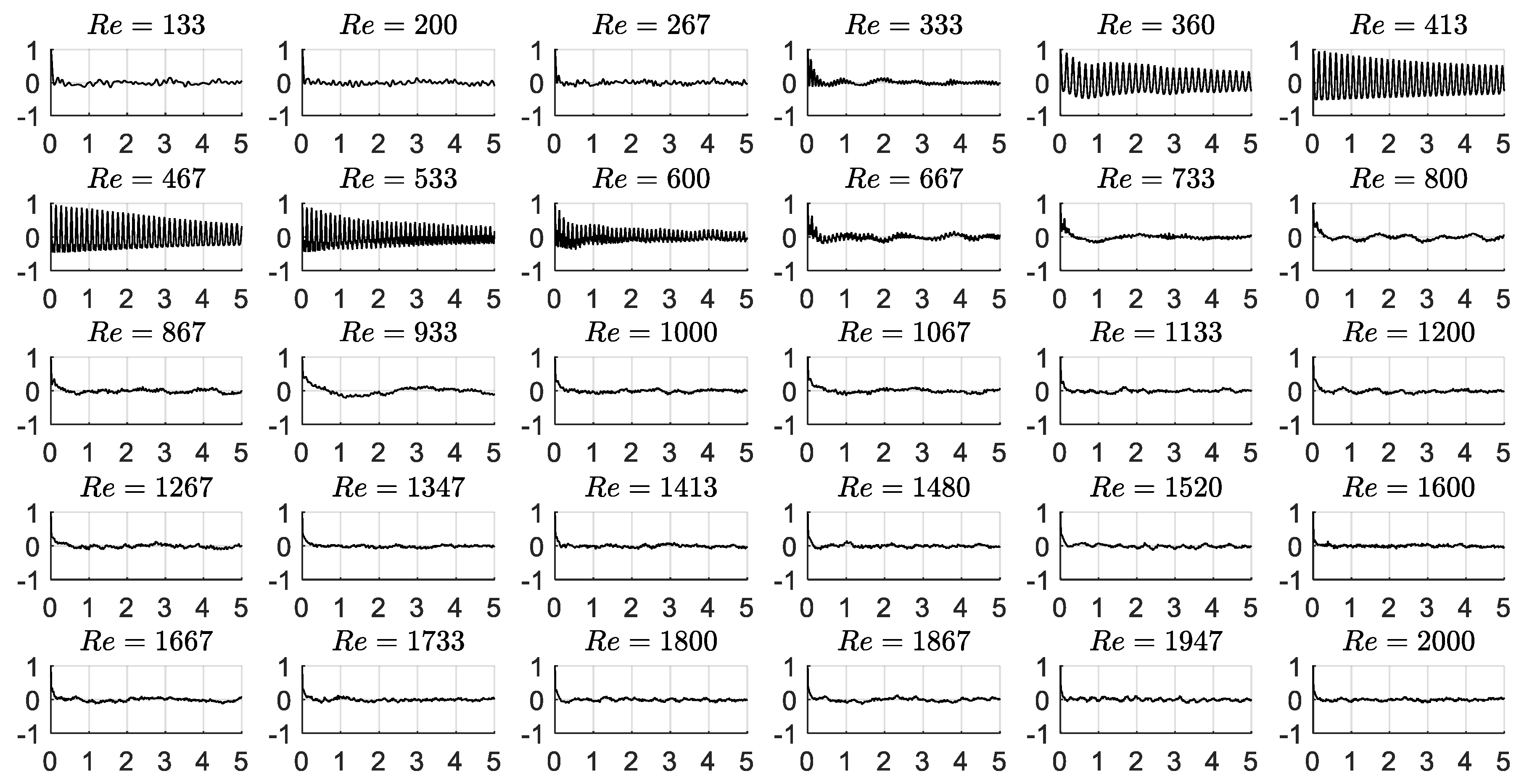
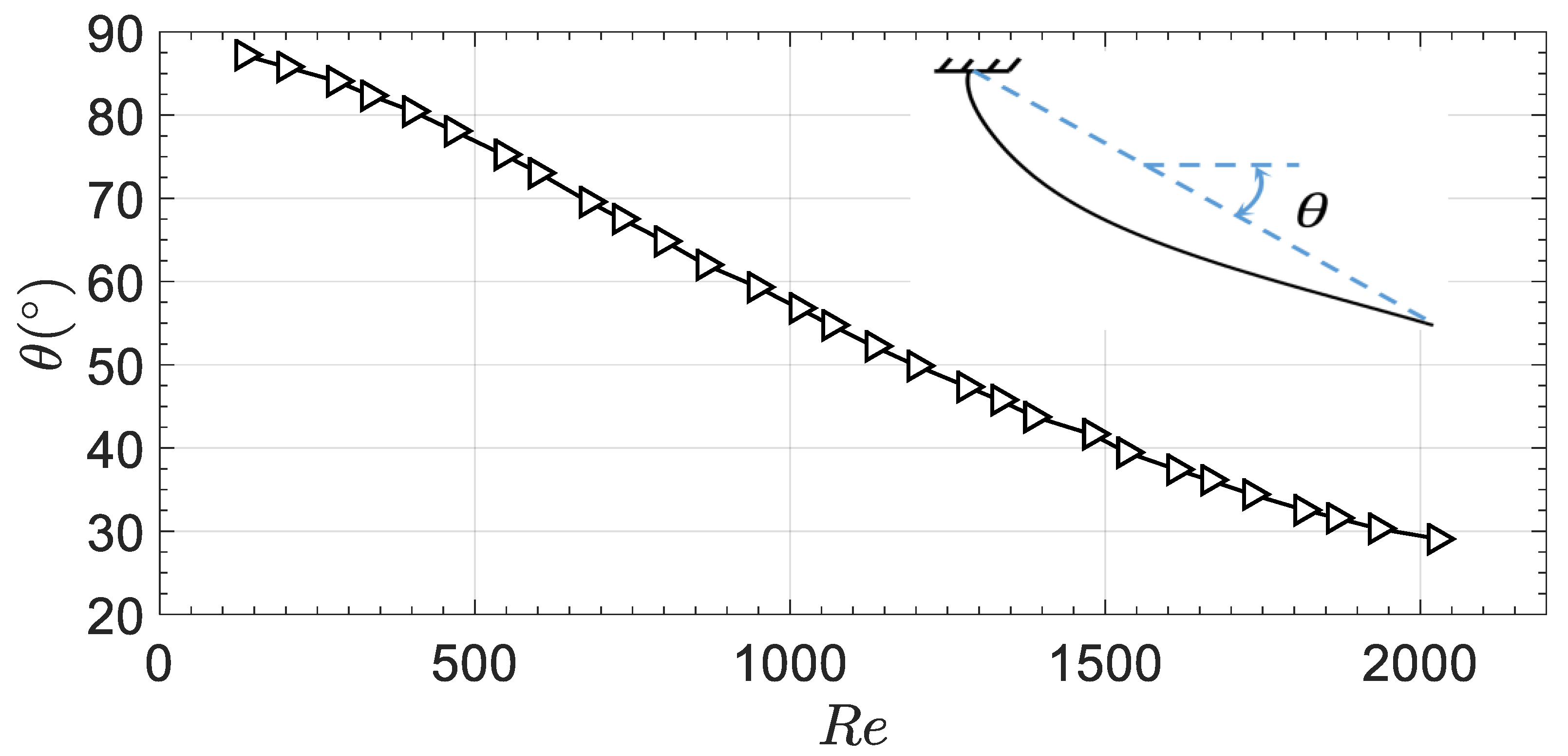
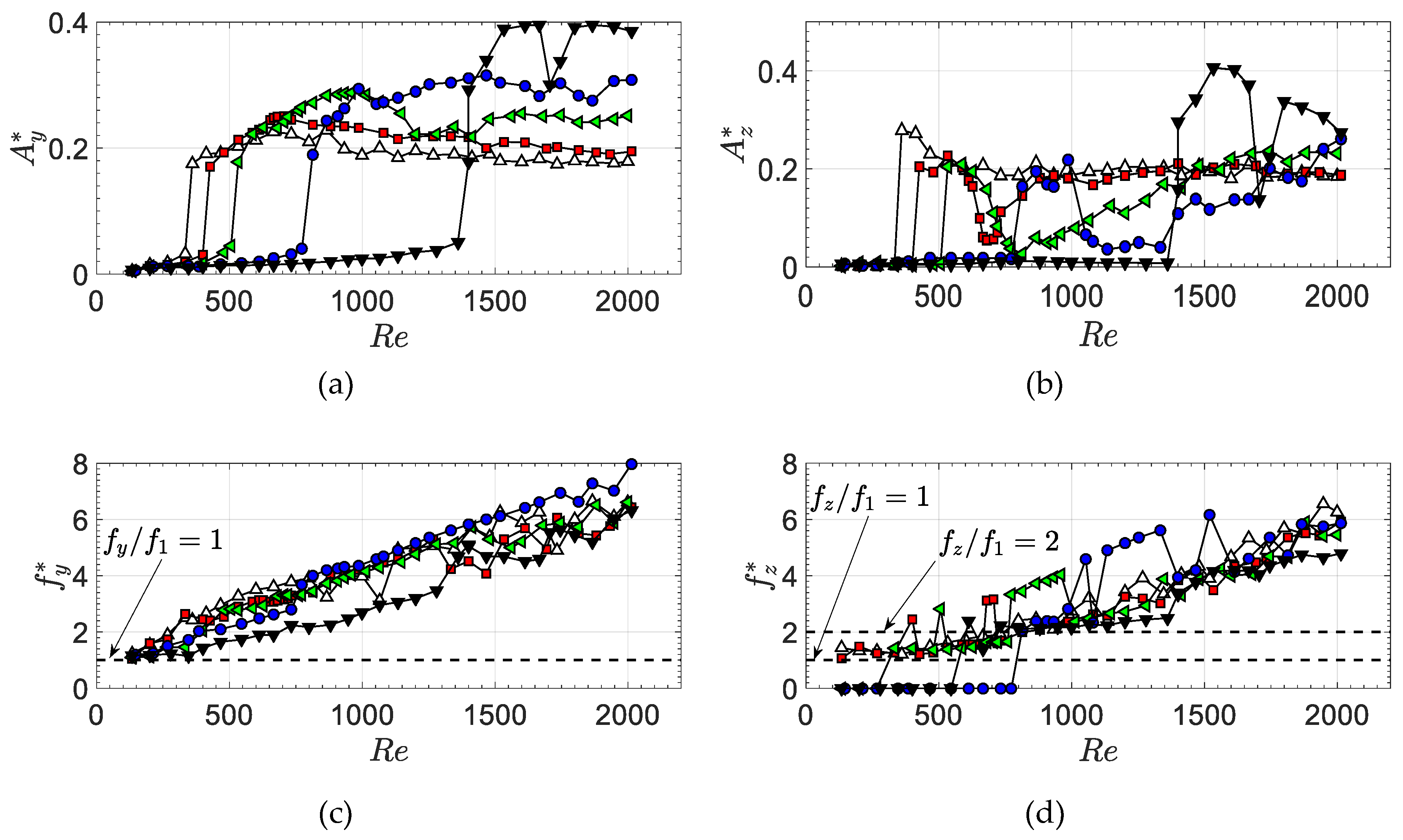
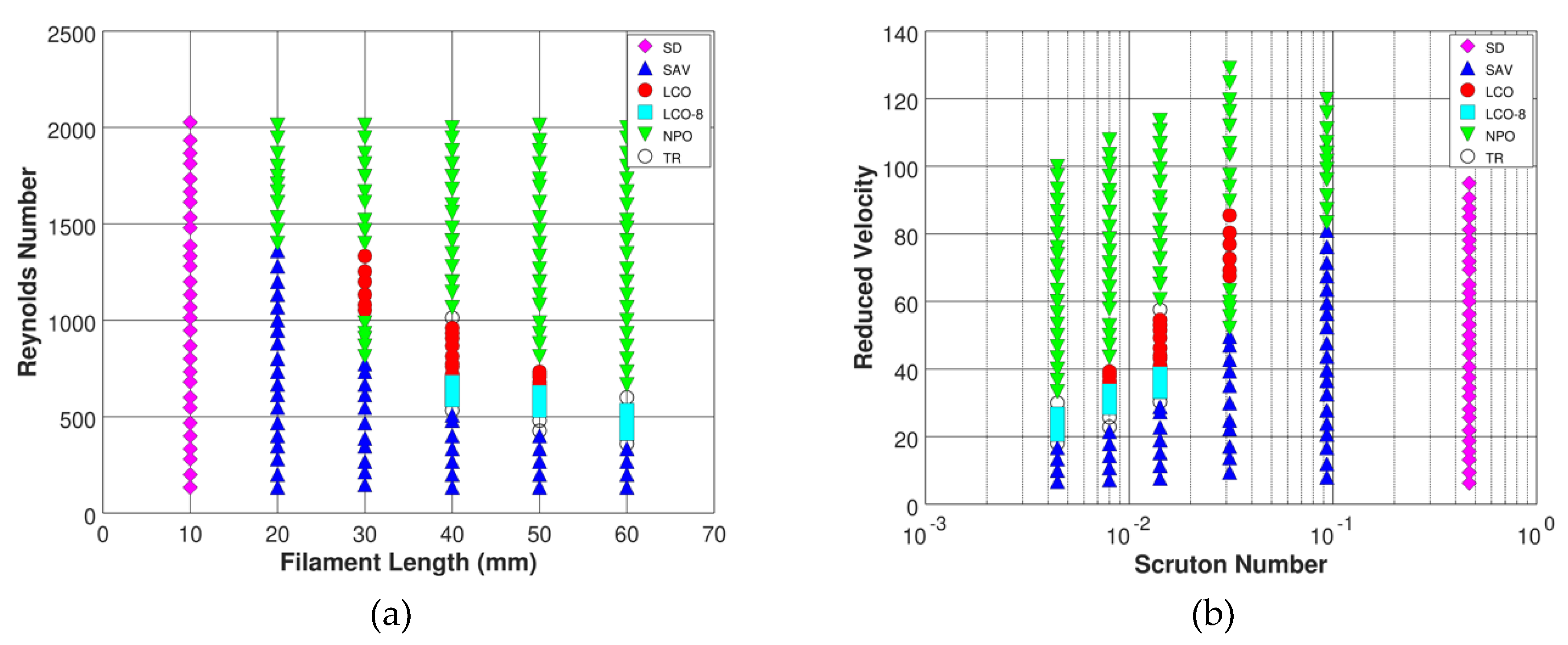
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A






References
- Afonso, F.; Vale, J.; Oliveira, É.; Lau, F.; Suleman, A. A review on non-linear aeroelasticity of high aspect-ratio wings. Prog. Aerosp. Sci. 2017, 89, 40–57. [Google Scholar] [CrossRef]
- Jonsson, E.; Riso, C.; Lupp, C.A.; Cesnik, C.E.S.; Martins, J.R.R.A.; Epureanu, B.I. Flutter and post-flutter constraints in aircraft design optimization. Prog. Aerosp. Sci. 2019, 109, 100537. [Google Scholar] [CrossRef]
- Helbling, E.F.; Wood, R.J. A review of propulsion, power, and control architectures for insect-scale flapping-wing vehicles. Appl. Mech. Rev. 2018, 70, 010801. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, T. A review of design and fabrication of the bionic flapping wing micro air vehicle. Micromachines 2019, 10, 144. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Shang, X.; Tian, X.; Li, X.; Lu, W. A review on fluid dynamics of flapping foils. Ocean Eng. 2020, 195, 106712. [Google Scholar] [CrossRef]
- Young, Y.L. Fluid-structure interaction analysis of flexible composite marine propellers. J. Fluid Struct. 2008, 24, 799–818. [Google Scholar] [CrossRef]
- Campbell, R.L.; Paterson, E.G. Fluid-structure interaction analysis of flexible turbomachinery. J. Fluid Struct. 2011, 27, 1376–1391. [Google Scholar] [CrossRef]
- Kallekar, L.; Viswanath, C.; Anand, M. Effect of wall flexibility on the deformation during flow in a stenosed coronary artery. Fluids 2017, 2, 16. [Google Scholar] [CrossRef]
- Gilmanov, A.; Barker, A.; Stolarski, H.; Sotiropoulos, F. Image-guided fluid-structure interaction simulation of transvalvular hemodynamics: Quantifying the effects of varying aortic valve leaflet thickness. Fluids 2019, 4, 119. [Google Scholar] [CrossRef]
- Stergiou, Y.G.; Kanaris, A.G.; Mouza, A.A.; Paras, S.V. Fluid-structure interaction in abdominal aortic aneurysms: Effect of haematocrit. Fluids 2019, 4, 11. [Google Scholar] [CrossRef]
- Hirschhorn, M.; Tchatchaleishvili, V.; Stevens, R.; Rossano, J.; Throckmorton, A. Fluid-structure interaction modelling in cardiovascular medicine—A systematic review 2017−2019. Med. Eng. Phys. 2020, 78, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Elgeti, J.; Winkler, R.G.; Gompper, G. Physics of microswimmers—Single particle motion and collective behaviour: A review. Rep. Prog. Phys. 2015, 78, 056601. [Google Scholar] [CrossRef] [PubMed]
- Jeznach, C.; Olson, S.D. Dynamics of swimmers in fluids with resistance. Fluids 2020, 5, 14. [Google Scholar] [CrossRef]
- McCarty, J.M.; Watkins, S.; Deivasigamani, A.; John, S.J. Fluttering energy harvesters in the wind: A review. J. Sound Vib. 2016, 361, 355–377. [Google Scholar] [CrossRef]
- Nabavi, S.; Zhang, L. Portable wind energy harvesters for low-power applications: A survey. Sensors 2016, 16, 1101. [Google Scholar] [CrossRef]
- Hou, G.; Wang, J.; Layton, A. Numerical methods for fluid-structure interaction—A review. Commun. Comput. Phys. 2012, 12, 337–377. [Google Scholar] [CrossRef]
- Borazjani, I. A review of fluid-structure interaction simulations of prosthetic heart valves. J. Long Term Eff. Med. Implants 2015, 25, 75–93. [Google Scholar] [CrossRef]
- Chiang, C.-Y.; Pironneau, O.; Sheu, T.W.H.; Thiriet, M. Numerical study of a 3D Eulerian monolithic formulation for incompressible fluid-structures systems. Fluids 2017, 2, 34. [Google Scholar] [CrossRef]
- Murea, C.M. Three-dimensional simulation of fluid-structure interaction problems using monolithic semi-implicit algorithm. Fluids 2019, 4, 94. [Google Scholar] [CrossRef]
- Bathe, K.J.; Ledezma, G.A. Benchmark problems for incompressible fluid flows with structural interactions. Comput. Struct. 2007, 85, 628–644. [Google Scholar] [CrossRef]
- Küttler, U.; Gee, M.W.; Förster, C.; Comerford, A.; Wall, W.A. Coupling strategies for biomedical fluid-structure interaction problems. Int. J. Numer. Meth. Eng. 2009, 26, 305–321. [Google Scholar] [CrossRef]
- Turek, S.; Hron, J.; Razzaq, M.; Wobker, H.; Schäfer, M. Numerical benchmarking of fluid-structure interaction: A comparison of different discretization and solution approaches. In Fluid Structure Interaction II, The First International Workshop on Computational Engineering, Herrsching, Germany, October 2009; Bungartz, H.J., Mehl, M., Schäfer, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 413–424. [Google Scholar]
- Fernández, M.A. Coupling schemes for incompressible fluid-structure interaction: Implicit, semi-implicit and explicit. SeMA J. 2011, 55, 59–108. [Google Scholar] [CrossRef]
- Degroote, J. Partitioned simulation of fluid-structure interaction. Arch. Comput. Methods Eng. 2013, 20, 185–238. [Google Scholar] [CrossRef]
- Pereira Gomes, J.; Yigit, S.; Lienhart, H.; Schäfer, M. Experimental and numerical study on a laminar fluid-structure interaction reference test case. J. Fluids Struct. 2011, 27, 43–61. [Google Scholar] [CrossRef]
- Pereira Gomes, J.; Lienhart, H. Fluid-structure interaction-induced oscillations of flexible structures in laminar and turbulent flows. J. Fluid Mech. 2013, 715, 537–572. [Google Scholar] [CrossRef]
- Kalmbach, A.; Breuer, M. Experimental PIV/V3V measurements of vortex-induced fluid-structure interaction in turbulent flow-A new benchmark FSI-PfS-2a. J. Fluids Struct. 2013, 42, 369–387. [Google Scholar] [CrossRef]
- De Nayer, G.; Kalmbach, A.; Breuer, M.; Sicklinger, S.; Wüchner, R. Flow past a cylinder with a flexible splitter plate: A complementary experimental-numerical investigation and a new FSI test case (FSI-PfS-1a). Comput. Fluids 2014, 99, 18–43. [Google Scholar] [CrossRef]
- Hessenthaler, A.; Gaddum, N.R.; Holub, O.; Sinkus, R.; Röhrle, O.; Nordsletten, D. Experiment for validation of fluid-structure interaction models and algorithms. Int. J. Numer. Meth. Biomed. Eng. 2017, 33, e2848. [Google Scholar] [CrossRef]
- Taylor, J.R. An Introduction to Error Analysis; University Science Books: Sausalito, CA, USA, 1997. [Google Scholar]
- Yong, D. Strings, chains, and ropes. SIAM Rev. 2006, 48, 771–781. [Google Scholar] [CrossRef]
- Silva-Leon, J.; Cioncolini, A.; Filippone, A.; Domingos, M. Flow-induced motions of flexible filaments hanging in cross-flow. Exp. Therm. Fluid Sci. 2018, 97, 254–269. [Google Scholar] [CrossRef]
- Silva-Leon, J.; Cioncolini, A. Modulation of flexible filaments dynamics due to attachment angle relative to the flow. Exp. Therm. Fluid Sci. 2019, 102, 232–244. [Google Scholar] [CrossRef]
- Roach, P.E. The generation of nearly isotropic turbulence by means of grids. Int. J. Heat Fluid Flow 1987, 8, 82–92. [Google Scholar] [CrossRef]
- Blevins, R.D. Flow-Induced Vibrations, 2nd ed.; Krieger Publishing Company: Malabar, FL, USA, 2001. [Google Scholar]
- Cioncolini, A.; Silva-Leon, J.; Cooper, D.; Quinn, M.K.; Iacovides, H. Axial-flow-induced vibration experiments on cantilevered rods for nuclear reactor applications. Nucl. Eng. Des. 2018, 338, 102–118. [Google Scholar] [CrossRef]
- Cioncolini, A.; Nabawy, M.R.A.; Silva-Leon, J.; O’Connor, J.; Revell, A. An experimental and computational study on inverted flag dynamics for simultaneous wind-solar energy harvesting. Fluids 2019, 4, 87. [Google Scholar] [CrossRef]
- Silva-Leon, J.; Cioncolini, A.; Nabawy, M.R.A.; Revell, A.; Kennaugh, A. Simultaneous wind and solar energy harvesting with inverted flags. Appl. Energy 2019, 239, 846–858. [Google Scholar] [CrossRef]
- Welch, P.D. The use of Fast Fourier Transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoustics 1967, 15, 70–73. [Google Scholar] [CrossRef]
- Bradley, E.; Kantz, H. Non-linear time-series analysis revisited. Chaos 2015, 25, 097610. [Google Scholar] [CrossRef]
- Silva-Leon, J.; Cioncolini, A. Effect of inclination on vortex shedding frequency behind a bent cylinder: An experimental study. Fluids 2019, 4, 100. [Google Scholar] [CrossRef]
- Silva-Leon, J.; Cioncolini, A.; Filippone, A. Determination of the normal fluid load on inclined cylinders from optical measurements of the reconfiguration of flexible filaments in flow. J. Fluid Struct. 2018, 76, 488–505. [Google Scholar] [CrossRef]
- Alben, S.; Shelley, M. How flexibility induces streamlining in a two-dimensional flow. Phys. Fluids 2004, 16, 1694–1713. [Google Scholar] [CrossRef]
- Gosselin, F.; De Langre, E.; Machado-Almeida, B.A. Drag reduction of flexible plates by reconfiguration. J. Fluid Mech. 2010, 650, 319–341. [Google Scholar] [CrossRef]
- De Langre, E.; Gutierrez, A.; Cossé, J. On the scaling of drag reduction by reconfiguration in plants. Comp. Rend. Mech. 2012, 340, 35–40. [Google Scholar] [CrossRef]



| Reference | Fluid | Structure | Motion |
|---|---|---|---|
| Pereira Gomez et al. [25] | Polyethylene glycol syrup in laminar flow | Flexible metal plate with rear mass at the trailing edge, clamped behind a rigid circular cylinder free to rotate around its axis, oriented in cross-flow | 2D |
| Pereira Gomes and Lienhart [26] | Water and polyethylene glycol syrup in laminar and turbulent flow | Flexible metal plate with rear mass at the trailing edge, clamped behind a rigid cylindrical body (circular or rectangular cross section) oriented in cross-flow | 2D |
| Kalmbach and Breuer [27] | Water in turbulent flow | Flexible rubber membrane with rear mass at the trailing edge, clamped behind a rigid and fixed circular cylinder oriented in cross-flow | 2D |
| De Nayer et al. [28] | Water in turbulent flow | Flexible rubber membrane clamped behind fixed rigid circular cylinder oriented in cross-flow | 2D/3D |
| Hessenthaler et al. [29] | Aqueous glycerol solution in laminar flow | Flexible cantilever-beam plate in merging flow from two inlets | 3D |
| This study | Air in laminar and turbulent flow | Flexible cantilever-beam filaments of variable length in uniform flow | 3D |
| Filament No. | (mm) | ||
|---|---|---|---|
| 1 | 60.0 ± 0.5 | 2.5 ± 0.1 | 0.012 ± 0.002 |
| 2 | 50.0 ± 0.5 | 2.8 ± 0.1 | 0.015 ± 0.002 |
| 3 | 40.0 ± 0.5 | 3.3 ± 0.2 | 0.017 ± 0.002 |
| 4 | 30.0 ± 0.5 | 3.9 ± 0.3 | 0.021 ± 0.003 |
| 5 | 20.0 ± 0.5 | 6.3 ± 1.0 | 0.028 ± 0.004 |
| 6 | 10.0 ± 0.5 | 16 ± 3 | 0.035 ± 0.005 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva-Leon, J.; Cioncolini, A. Experiments on Flexible Filaments in Air Flow for Aeroelasticity and Fluid-Structure Interaction Models Validation. Fluids 2020, 5, 90. https://doi.org/10.3390/fluids5020090
Silva-Leon J, Cioncolini A. Experiments on Flexible Filaments in Air Flow for Aeroelasticity and Fluid-Structure Interaction Models Validation. Fluids. 2020; 5(2):90. https://doi.org/10.3390/fluids5020090
Chicago/Turabian StyleSilva-Leon, Jorge, and Andrea Cioncolini. 2020. "Experiments on Flexible Filaments in Air Flow for Aeroelasticity and Fluid-Structure Interaction Models Validation" Fluids 5, no. 2: 90. https://doi.org/10.3390/fluids5020090
APA StyleSilva-Leon, J., & Cioncolini, A. (2020). Experiments on Flexible Filaments in Air Flow for Aeroelasticity and Fluid-Structure Interaction Models Validation. Fluids, 5(2), 90. https://doi.org/10.3390/fluids5020090