Abstract
While pendulums have been around for millennia and have even managed to swing their way into undergraduate curricula, they still offer a breadth of complex dynamics to which some has still yet to have been untapped. To probe into the dynamics, we developed a computational fluid dynamics (CFD) model of a pendulum using the open-source fluid-structure interaction (FSI) software, IB2d. Beyond analyzing the angular displacements, speeds, and forces attained from the FSI model alone, we compared its dynamics to the canonical damped pendulum ordinary differential equation (ODE) model that is familiar to students. We only observed qualitative agreement after a few oscillation cycles, suggesting that there is enhanced fluid drag during our setup’s initial swing, not captured by the ODE’s linearly-proportional-velocity damping term, which arises from the Stokes Drag Law. Moreover, we were also able to investigate what otherwise could not have been explored using the ODE model, that is, the fluid’s response to a swinging pendulum—the system’s underlying fluid dynamics.
1. Introduction
Historically, pendulums have been used for a multitude of purposes. From seismometers used almost two thousand years ago [1,2], to devices that increase efficiency for societal capacity, such as reciprocating saws and pumps [3,4], to keeping time [5,6], to even medieval torture devices [7], applications of pendulums are far and wide. Edgar Allan Poe even wrote a short story about one, The Pit and the Pendulum [8]. The esteemed polymath Galileo Galilei dreamt of the first pendulum clock in 1637, but it wasn’t constructed until 1656 when Dutch physicist Christiaan Huygens drew out the plans, thus designing it. He enlisted clockmaker Salomon Coster to build it. The introduction of a pendulum clock increased time keeping accuracy from 15 minutes to a quarter of minute [5]— pendulums changed history!
It is no surprise that the study of pendulums swings its way into many foundational courses in science, mathematics, and engineering. Students are introduced to them in courses such as mechanics, dynamics, or differential equations, where they are first exposed to the idea of a simple gravity pendulum. A simple gravity pendulum is an idealized pendulum—a weight (bob) is attached to a massless string, which is tethered to a fixed pivot point, and is allowed to swing freely, without friction [9]. It will continue to swing forever. Realistic? Not unless one lives in a vacuum, but ultimately a good place to begin a student’s exploration of simple harmonic motion.
If represents the angular displacement (in radians) from the vertical at time t (see Figure 1a), the ordinary differential equation (ODE) describing such a simple pendulum system takes the form:
where I, m, and L are the pendulum bob’s moment of inertia and overall mass and length, respectively, and g is the gravitational acceleration. Since the only external force acting on this pendulum is gravity, it will swing forever, with no loss in oscillatory amplitude, see Figure 1b for an example. Figure 1b shows simulated results for different pendulum cases, each with a circular bob of a different radius. Note that the ODE was solved numerically, as no small angle approximation was used [9]. For these cases of circular bobs, of radius R, attached to a massless string of length L, the moment of inertia is calculated to be:
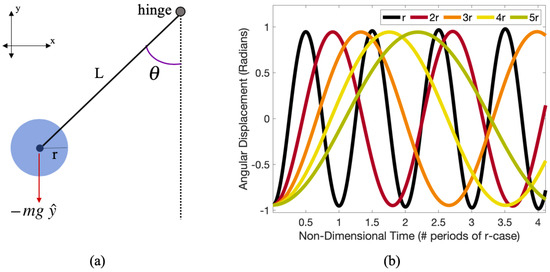
Figure 1.
(a) A pendulum of length L with circular bob of radius, r, and mass, m. (b) Angular displacement (in radians) over time for various gravity pendulums of differing radii. The non-dimensional time is given in terms of the number of periods of the case with radius, r.
There are two things to note from Figure 1b. The first is that over time the oscillation amplitudes do not decay. The second is that although amplitudes of oscillation are not affected, the period of oscillation is affected by bobs of different radii. Larger bobs have larger periods, due to their moment of inertia being greater [9].
In a world (or classroom) like ours which does not exist in a vacuum, a table-sized pendulum demonstration would eventually lead to its angular oscillations reaching zero, i.e., standing still. This is due to the pendulum swinging in air—a fluid. The air resists the pendulum’s motion, effectively pushing back on the pendulum. This is known as fluid drag.
The concept of fluid drag is probably familiar to you already. It is the reason why parachutes work. The equation governing a pendulum swinging in a fluid environment is given by
where the parameter b is deemed a damping parameter. This is a reduced order model of the system, as the contribution of the fluid onto the pendulum is entirely contained within the parameter, b. That is, this equation models how the fluid is believed to affect the swinging motion of the pendulum, while providing no mechanism to understand the underlying fluid’s dynamics. Numerical simulation results from solving Equation (3) are presented in Figure 2.
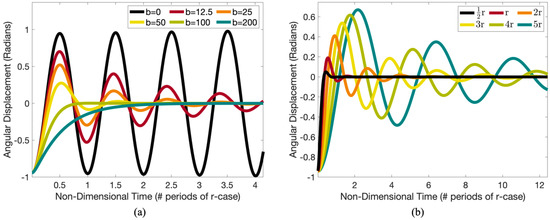
Figure 2.
Angular displacements against non-dimensional time for damped physical pendulums in the case of (a) constant radius and varied damping, b, and (b) constant b and varied radii.
Figure 2a holds the radius constant at r, the same r from Figure 1b, while varying the damping coefficient, b. Compared to Figure 1b, angular oscillations decay in all cases when . The damping induced from will eventually lead to its equilibrium—a stationary pendulum hanging straight down. However, the decay rate is dependent on b; larger values of b lead to a quicker decay of oscillation. Note that b has units of and in realistic situations, . Moreover, depending on the value of b, the pendulum system will exhibit one of three behaviorial cases:
- Under-damped: The pendulum will swing back and forth, although its amplitude of oscillation will steadily decline, until it asymptotically approaches its equilibrium.
- Critically-damped: the pendulum returns to equilibrium as quickly as it can. If the damping parameter were made slightly more or slightly less, it would result in the pendulum returning slower to its equilibrium position.
- Over-damped: the pendulum moves towards its equilibrium position slower than the critically-damped case. There is no oscillation.
The simulations shown in Figure 2b held the damping parameter fixed ( from Figure 2a) and varied the radius of the bob. Note that changing the radius r will vary the moment of inertia (see Equation (2)). This data suggests that as r increases for a given b, this would lead to more oscillatory behavior. That is, smaller r tends to make the pendulum system more damped. Intuitively this doesn’t make much sense as is—a larger pendulum bob should feel more drag since it has a larger surface area. It would be like jumping out of an airplane with a parachute with a surface area of and floating down slower (and more softly) than a parachute of . How could this be?
For the simulations in Figure 2b, we fixed the damping parameter b and then varied r. We did not consider that the damping parameter may depend on the radius (among a variety of other parameters), that is, the geometry of the pendulum bob. Furthermore, we have yet to motivate where the damping term in Equation (3) comes from. Let’s settle that.
It comes from the seminal work of prolific physicist and mathematician Sir George Stokes, who even studied drag force using pendulums [10]! In particular, he derived a drag force equation, now known as Stokes Law, by investigating spheres moving through a fluid at low Reynolds numbers, i.e., situations in which either the fluid is moving extremely slowly or the fluid’s viscosity is very high [11,12]. Stokes Law (for a sphere at low ) is presented as the following:
where is the fluid drag, is the fluid’s dynamic viscosity and r and v are radius and speed of the sphere that is moving through the fluid. Note that the Reynolds number () depends on two fluid parameters, i.e., its density, , and dynamic viscosity, , as well as two parameters based on the physical system being investigated, i.e., a characteristic length and velocity scale, L and V, respectively. The is defined to be
Thus Stokes Drag describes that this damping frictional force acting on the sphere is proportional to its size, , and speed, . Careful to remember that this may only be true in low Reynolds number situations, where either v, r, or both may be small. Notice that the form that the damping term took in Equation (3) was similar, but used angular displacement () and angular velocity (). As suggested by numerical simulations presented above, this damping equation gives rise to exponential decay in angular displacement (Figure 2).
At higher Reynolds numbers, i.e., situations in which fluid viscosity is low or the speed or size of an object is large, the drag force takes a different form. For these situations, the drag law was discovered by none other than the infamous Lord Rayleigh (John William Strutt) using dimensional analysis [13]. For high Reynolds numbers settings, the fluid drag force takes the following form [14,15]:
where is the fluid density, r is the sphere’s radius, v is the sphere’s velocity, and K is a non-dimensional number that is based on the fluid flow’s speed and direction as well as the object’s shape, size, and orientation in respect to the flow, and the fluid’s density and viscosity. In a nutshell, for a specific object, this constant K may significantly change if one or more of these parameters are varied.
This drag force is traditionally represented in the following generalized manner:
where A is a cross-sectional area of an object in flow and is a dimensionless number called the drag coefficient. In this representation is analogous to K above.
Moreover, work in the latter half of the 20th century and early 21st century has shown that in particular situations correction terms must be included into the drag force equations [16,17]. Furthermore there are still unknown dynamics of pendulums involving small amplitude oscillations [18]. Although physical pendulums have been used for thousands of years and studied by students in foundational courses for over a century, they remain an active research area [19].
With the advent of new technologies, e.g., experimental measurement and flow visualization tools, researchers have further probed into the complex interactions of pendulums and the fluid environments they are immersed within [20,21,22,23,24,25]. In particular, Mathai et al. [25] investigated how fluid drag on pendulums may be enhanced due to dynamic interactions with their own vortex wake as they swing—something not quantified previously!
Mathai et al. [25] went on to note Even with the wake history force included, the current model is still quite basic. In reality, the dynamics <of a pendulum> is highly nonlinear, with changes in direction, curvilinear trajectories and wide variations in instantaneous Re <Reynolds number>…Fully resolved direct numerical simulations…can provide better insights into the flow-induced forces. That is exactly where our work on pendulums began, although there have been two previous studies using CFD models of pendulums [26,27].
In this paper we implemented a fluid-structure interaction (FSI) computational model of a swinging pendulum containing a spherical bob (a circular bob in two dimensions). In our FSI model, we varied the size of the circular pendulum bob, i.e., its radius, and its mass. We then analyzed the resulting data in terms of angular displacement, speed of the pendulum bob, and fluid forces acting on it, as well as compared the dynamics between our FSI model and the canonical reduced ODE model for a damped physical pendulum, Equation (3). Furthermore, we visualized (and qualitatively analyzed) the fluids motion in response to a swinging pendulum.
In addition, we provide instructor resources, such as slides and movies, in the Supplemental Materials (the items are listed in Appendix A), with the goal to streamline use of this work in educational settings. Moreover, we also offer the science community the first open-source pendulum models in a fluid-structure interaction framework. The models can be found at github.com/nickabattista/IB2d in the sub-directory:
IB2d → matIB2d → Examples → Examples_Education→ Pendulum.
Note that each example is of a point mass model bob and was selected for its computational speed in comparison to circular bobs (those of non-zero radius). Moreover, three versions are presented, each corresponding to a different grid resolution. The least spatially resolved case, , will be the fastest to run, but also the least accurate of the 3, while the case has the highest spatial resolution, but will run the slowest. The default setting is to only save the pendulum (Lagrangian) data. To store the fluid (Eulerian) data, flags corresponding to the desired fluid quantities may be selected within the input2d file. We also provided the scripts used to solve Equations (1) and (3) that produce Figure 1 and Figure 2.
2. Methods
To investigate the swinging motion of a two-dimensional pendulum bob immersed in a viscous, incompressible fluid, we used computational fluid dynamics (CFD). In our model, the bob starts at rest and begins to swing under gravitational acceleration acting on the mass of the pendulum. An immersed boundary (IB) framework was used to couple the pendulum’s motion and the fluid it is immersed within. Scientists and engineers can use IB to study the interactions of an object and the fluid it is contained within, i.e., you can explore how the fluid affects the object and vice versa.
The immersed boundary method was developed by Charles Peskin, a mathematical physiologist at the Courant Institute of Mathematics [28,29,30]. Even though IB was invented in the 1970s, it is still extensively used for investigating fluid-structure interaction problems today. Many mathematicians, engineers, and scientists have since improved the original algorithm in attempts to increase its accuracy without significantly increasing the computational expense and time required [31,32,33,34,35,36,37,38]. IB is still a leading numerical framework for studying problems in FSI due to its robustness [39,40].
It has previously been applied to study problems ranging from cardiac fluid dynamics [41,42,43,44] to aquatic locomotion [45,46,47,48,49] to insect flight [50,51,52] to dating and relationships [39]. Additional details on the IB method can be found in Appendix B.
In the remainder of this section we will introduce our FSI pendulum’s implementation into the IB2d framework, i.e., the computational geometry, geometrical and fluid parameters, and model assumptions.
2.1. Model Geometry
Figure 3 presents our pendulum model’s computational geometry. In particular, Figure 3a illustrates the modeling idea—a bob (of radius r) is composed of a central point mass (of mass m) and outer neutrally-buoyant shell layer. It is tethered to a particular fixed location, a distance L away. The pendulum is immersed in a viscous, incompressible fluid of uniform density , and dynamic viscosity, . Note that the fluid within and outside the pendulum bob is uniform in its properties. We define the pendulum’s angular displacement, , to be the angle from the vertical dotted line. Gravity acts on the central mass point; as the rest of the pendulum bob’s geometry is neutrally-buoyant, all acceleration of the bob is due to this single gravitational interaction. However, due to the structure properties of the pendulum bob, the neutrally-buoyant shell will undergo fluid drag due to the fluid’s resistance in letting the pendulum bob move through it.
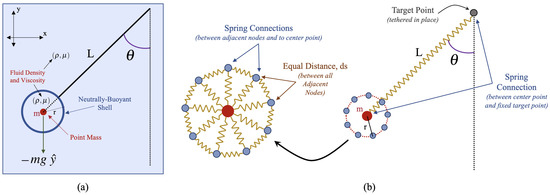
Figure 3.
(a) Model of an immersed pendulum with circular bob of radius r in a viscous, incompressible fluid. The fluid has density and viscosity of and , respectively. The pendulum has length L and the bob has mass m, concentrated at its center. (b) The computational geometry illustrating the fiber model construction of the discretized Lagrangian mesh.
As we wished to vary the pendulum bob’s radius and mass of its central point, we considered the parameters listed in Table 1 for our FSI pendulum model. The explicit radii, r, and masses, m studied are and , respectively. The initial angular displacement, , was radians. We did not vary properties of the fluid, neither its density nor viscosity. Note that the kinematic viscosity in our simulations was . Some common liquids with kinematic viscosities around are sulphuric acid at room temperature or a variety of oils (coconut, SAE Motor Oils, peanut, whale, etc.) at ∼100–130 degrees Fahrenheit [53]. Kinematic viscosity, , measures the fluid’s internal resistance to flow under gravity.

Table 1.
Table of geometric and fluid parameters used in our pendulum study.
2.2. Model Construction
Figure 3b provides a more detailed overview of the computational geometry. In particular it provides details regarding how the structure is modeled using fiber models, which are used to mimic desired material properties between discretized points, i.e., Lagrangian points, that compose the geometry [39]. The single mass point is tethered to the fixed point, a distance L away, via a virtual spring. The static hinge point is tethered in place using the target point model. Target points can be used to hold Lagrangian points nearly rigid. The individual mass point uses a massive point model that tethers the individual Lagrangian point to a mass, which dampens its movement [54]. Note that the target point and massive point models use spring-like mathematical formulations to achieve their desired effects, see [39].
The neutrally-buoyant shell is composed of equally-spaced Lagrangian points, to which are tethered to their neighboring points via virtual spring connections. Furthermore, each of these Lagrangian points are further tethered to the massive point in the center of the pendulum bob by a virtual spring. All of the virtual spring connections in the model use stiff springs with a particular spring resting length in order to keep the geometry from changing shape, i.e., trying to ensure that the Lagrangian points maintain a specific distance from other points. The number of Lagrangian points in a circular shell varies by the radius, see Table 2. Note that due to the coupled nature of the Lagrangian structure and fluid in the standard immersed boundary framework, it was more straightforward for us to approximately model rigid structures in this manner. Additional steps would have been necessary to solve the problem of each Lagrangian point only being allowed to move in a constrained way, due to the imposed rigidity, under forces from the fluid and other external forces (like gravity) pushing on it. Please see [46,55] for further information regarding immersed boundary formulations with rigid bodies.

Table 2.
Table providing number of Lagrangian Points in the circular shell for a particular radius, r.
Fiber models use a variety of different deformation force laws to model material properties. To model virtual (Hookean) springs, deformation forces were calculated as follows,
where is the spring stiffness, is the spring’s resting lengths, and and are the Lagrangian nodes tethered by the spring. Note that in our model the resting lengths are time-independent, hence . As mentioned previously, the spring stiffnesses are large to ensure minimal stretching or compression of the computational geometry. The spring stiffness used to tether the massive point to the fixed hinge point and the pendulum bob points to both one another and the massive point are denoted by and , respectively.
In the simple case where a preferred position is enforced, boundary points are tethered to target points via springs. Its corresponding deformation force equation, which describes the force applied to the fluid by the boundary in Lagrangian coordinates is given by and is explicitly written as,
where is the stiffness coefficient, and is the prescribed Lagrangian position of the target point. In all simulations the hinge point was held nearly rigid by applying a force proportional to the distance between the location of the actual Lagrangian point and its preferred target position. Using a large value of helps mitigate a small deviation between the actual and preferred position.
Artificial mass is modeled using the massive point approach of Kim et al. [54]. It is similar to target points. gives the Cartesian coordinates of the massive points, with associated mass density . Note that such points do not interact with the fluid directly, similar to target points. give the Cartesian coordinates of a neutrally-buoyant Lagrangian boundary point, which do interact with the fluid. Similar to target points, if a Lagrangian point deviates from its massive point, a restoring force drives them back together, as shown in its mathematical description below
where is a stiffness coefficient with , is the mass of the massive point, g is the acceleration due to gravity in vertical direction, , and is the position of the massive point to which the Lagrangian point, , is tethered to at time t.
All numerical stiffness parameters are given in Table 3. The stiffnesses were selected to be as high as possible while also maintaining stability and fidelity of our numerical solver. Each pendulum simulated was of length and was immersed in a square computational domain of size , with a grid resolution of , i.e., . Points that compose the circular pendulum bob were evenly spaced apart at a distance of . Note that this is the standard convention in the immersed boundary literature when choosing the Lagrangian point spacing, . It is used to avoid leaky boundaries [30]. Thus, fluid will not be allowed to flow in or out of the pendulum bob, unless due to numerical error. Moreover, note that the adjacent nodes along the circle were a distance r from the massive point at the center of the pendulum bob, which was tethered a distance of L from the fixed hinge target point. Each of the spring connections between specific points used a spring resting length equal to such corresponding distances in an effort to maintain the geometry while the pendulum was swinging. A time-step of was used to march forward in time.

Table 3.
Table of numerical temporal, spatial, and fiber model parameters used in our pendulum study.
While running the simulations, we stored the following data every of simulation time:
- Position of Lagrangian Points
- Forces on Each Lagrangian Point (Horizontal/Vertical and Normal/Tangential Forces)
- Fluid Velocity
- Fluid Vorticity
- Forces spread from the Lagrangian mesh onto the Eulerian grid
We then used the open-source software VisIt [56], created and maintained by Lawrence Livermore National Laboratory for visualization, see Figure 4, and the data analysis package software within IB2d [39] for data analysis. Figure 4 provides a visualization of some of the data produced for a pendulum of mass and radius of and , respectively, at one snapshot in time. Section 3.4 explores the underlying fluid dynamics in further detail, including the time evolution over a pendulum’s first swing, see Figure 19.
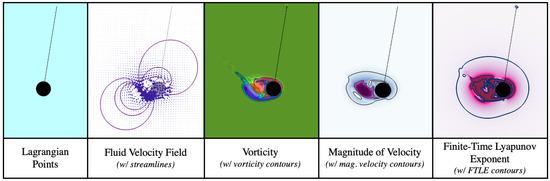
Figure 4.
Snapshots of a single moment in time for a pendulum with mass, , and radius, , providing some of the data stored during the time-step in which the simulation time reached , i.e., positions of Lagrangian points (pendulum), the velocity vector field, magnitude of velocity, and vorticity. Note that data from giving the force spread from the Lagrangian grid (pendulum) onto the Eulerian (fluid) grid is not shown. Lagrangian Coherent Structures (LCS) via finite time Lyapunov exponents (FTLE) are also illustrated, although they were computed during the post-processing stage, after the data was collected.
3. Results
Using an open source implementation of the immersed boundary method, IB2d, we modeled the motion of a pendulum with a circular bob immersed within a fluid undergoing gravity’s influence. For this education focused paper, we explored angular displacement and speed of the pendulum bob as well as forces acting upon the pendulum bob to impede its motion. Upon doing so we quantified the decay in oscillation amplitude and speed damping. This was done for a variety of pendulum bob masses as well as radii (size). We also explored the effect that the motion of the pendulum bob has onto the fluid it was immersed. Lastly, we compared the reduced ODE model of a damped physical pendulum and our FSI model. We organized our results into the following five subsections:
- Angular Displacement of the pendulum bob
- Speed of the pendulum bob
- Forces acting on the pendulum bob
- Effect the pendulum bob has onto the fluid
- Comparison between reduced ODE model and FSI model
3.1. Angular Displacement of the Pendulum Bob
As suggested from Section 1, since the pendulum is immersed within a fluid environment, its oscillation amplitude will decay over time. Figure 5 provides snapshots of multiple pendulums’ angular displacement over time for pendulum bobs of differing radius and . Note that all simulations were run independently of each other and Lagrangian position data is being overlaid during post-processing.
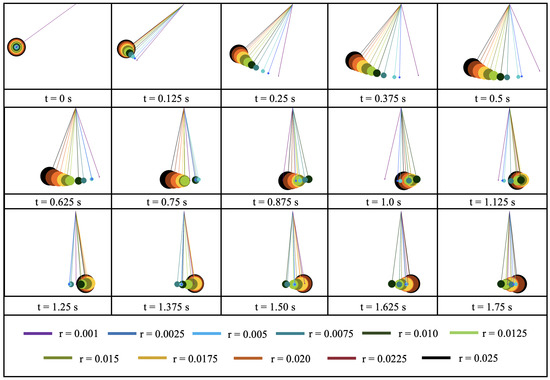
Figure 5.
Snapshots of multiple pendulums’ (of differing radius) angular displacement over time in the case of .
Moreover, both the size of the bob and the mass of the bob will affect its dynamics. Figure 6 illustrates that pendulums with the same size and shape bob may experience significantly different oscillation patterns due to different mass. In particular, depending on the mass, the pendulum could fall into any of the 3 damping cases (under-, over-, or critically-damped). See Figure A1 for the counterpart case where a specific mass is tested for a variety of radii. Consistent dynamics are observed.
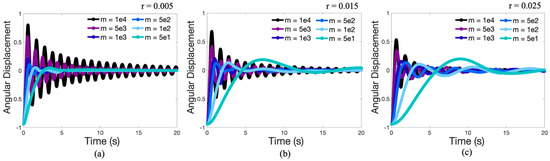
Figure 6.
Depicting the angular displacement (radians) vs. time (s) for pendulums with the same radius but different masses. (a–c) give data for a specific radius, either , or , respectively, for 4 orders of magnitudes in mass in each.
Next we calculated the maximum amplitude during each oscillation cycle for a variety of masses. The amplitude decays exponentially, see Figure 7. Figure 7 presents the displacement amplitude against peak number (number of half swings) for a variety of masses for . The data shows a linear relationship between the logarithm of the amplitude and the peak number, suggesting exponential decay, although lines seem a better fit starting at the first peak, rather than the initial displacement. Note that Figure 8 shows a steady increase in time between successive peaks for three different masses (, and ) for a variety of radii. As mass increases, the time between peaks decreases. Moreover, generally as more swings occur the time become peaks becomes more consistent. We also note that the time between the start of each simulation and their first peak generally does not fit the data. Section 3.2, Section 3.3 and Section 3.5 will also explore this observation in more detail.
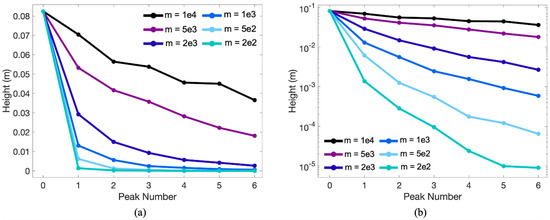
Figure 7.
(a) Plot illustrating the decay of the height (m) that the pendulum bob reaches as the pendulum continues to swing for the case of for a spectrum of masses. The peak amplitude decays exponentially as illustrated by the linear relationship between the logarithm of the amplitude against peak number, as shown in (b).
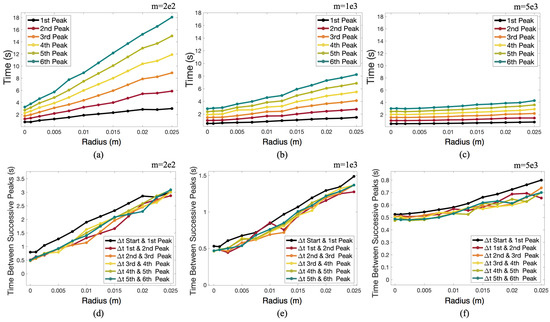
Figure 8.
Plots illustrating the time of the peak in angular displacement against the pendulum bob’s radius for its 1st through 6th peak (a–c) and the time difference between the peaks (d–f) against the pendulum bob’s radius for three different masses: (a,d) , (b,e) , and (c,f) .
From this data, we computed the approximate damped period of oscillation, see Figure 9a,b. Figure 9b provides a colormap with contour lines of the period data from Figure 9a. As mass increases, the approximate period decreases, as suggested previously. Moreover, as radius increases, the period also increases. Note that when mass is high enough (e.g., the case of ), the period does not significantly change between different radii; however, there is still exponential decay in the oscillatory amplitude (see Figure A2). Furthermore, for very small radii there appears to be a non-monotonic trend in period as a function of mass. The period was computed by averaging the time between every other peak over the first 5 full oscillations.
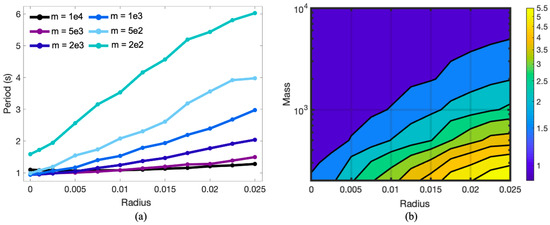
Figure 9.
(a) The period given as a function of a pendulum bob’s radius for a variety of masses. (b) A contour map showing the period as a function of both the pendulum bob’s radius and mass. The highest periods occur for small masses and large pendulum bobs.
Next we explore how the speed of the pendulum bob is affected by variations in its mass and radius in a fluid environment.
3.2. Speed of the Pendulum Bob
Recall that in Section 3.1 we observed that peaks in angular displacement decayed exponentially over time. This suggests that the pendulum bob’s speed is inherently slowing down as well. Figure 10 details the pendulum bob’s speed vs. the number of swings (half a complete oscillatory cycle). The data shown is for the case of for a variety of masses. During each swing the pendulum accelerates to a maximal speed before decelerating. The maximum occurs at roughly halfway through each swing, when the pendulum passes the point of 0 displacement from the vertical. Note that physically the pendulum must hit a speed of zero when it swings from one direction to the other; our data does not reflect this due to the time resolution of the sampled time-points.
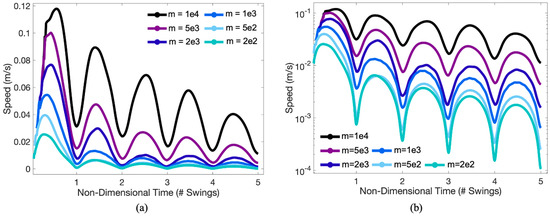
Figure 10.
(a) Plot depicting the linear speed of the pendulum bob against non-dimensional time given as the # of swings (half a full displacement cycle) for the case of and a variety of masses. Speed peaks near the center of each swing. This corresponds to when the pendulum has approximately zero angular displacement from the vertical. The peak speed appears to begin decaying exponentially, starting on the second or third swing in most cases. This can be seen from linear relationships between peak speed and swings in (b).
Furthermore, from Figure 10b, it does not appear that the speed peaks decay exponentially over time from the beginning of the simulation. After a few swings, the peaks in speed appear to satisfy a linear relationship between the logarithm of speed versus time; however, the peak speed significantly decreases from the first to second swing, see Figure 11. Figure 11 illustrates that for most cases from the second swing on, the peak speeds approximately demonstrate exponential decay; however, there is significantly more decay between the first and second swing than successive peaks thereafter. Figure A3 presents the counterpart data of how the speed of pendulum bobs of the same mass decays over time for a variety of radii. Similarly trends are observed in the data.
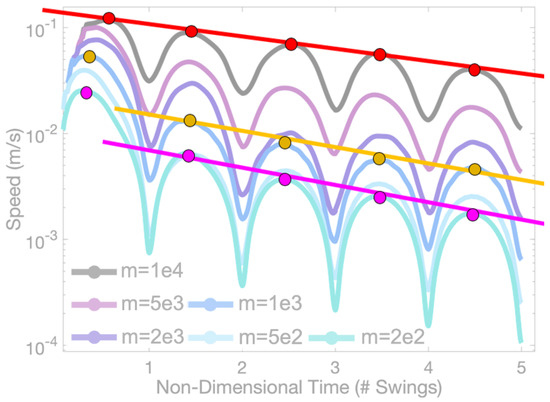
Figure 11.
Plot illustrating that exponential decay appears in peak speed starting with the second swing. There is significantly more decay in peak speed between the first and second swings, than successive swings thereafter.
Next we wished to quantify the amount of damping due to the pendulums immersion in a fluid of kinematic viscosity To do this we computed the theoretical speed of a pendulum bob void of a fluid environment by energy conservation. We set the original potential energy when the pendulum bob was at time zero and computed the kinematic energy when the pendulum was passing 0 displacement, i.e.,
where is the velocity of the pendulum bob outside of a fluid environment and is the initial height of the pendulum bob before it begins swinging. For our initial setup, , since the pendulum is released from an initial angle of radians from the horizontal.
We then defined the speed ratio to be: and the speed damping ratio to be: . If , suggesting only small damping effects. Figure 12 gives the speed damping ratio as a percentage. For this particular fluid environment, even cases of high mass and small radius result in ’s of ∼, i.e., the fluid immersed pendulum bob is moving ∼ slower than its fluid void counterpart. As the radius increases, the increases. Note that smaller masses have less significant increases in . As mass increases, decreases for a given radius.
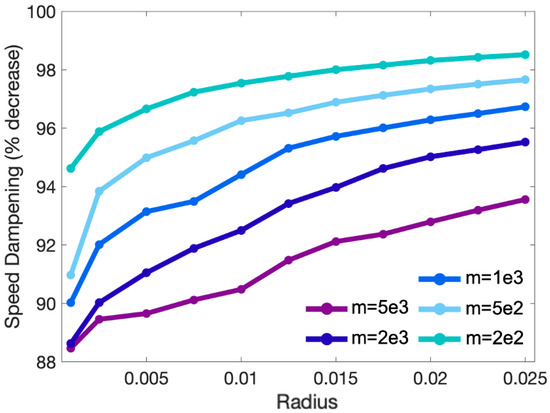
Figure 12.
The percentage decrease in speed when comparing pendulum bob speed once it reaches 0 degree angular displacement on the first swing compared between simulated cases in fluid and theoretical value outside of a viscous fluid environment.
Lastly we explored the phase space between pendulum bob speed and its angular displacement. Figure 13a presents the data for the case of for a spectrum of masses of over 3 orders of magnitude. As suggested by all data previously, the trajectories eventually converge to zero displacement and speed. Interesting, all the trajectories collapse onto an approximate parabolically-capped cone. The last cycle is given for all cases in Figure 13b. Similar topologies are seen in cases of other radii (see Figure A5) over a variety of masses. Furthermore, similar topologies emerge when fixing the mass and exploring trajectories for a variety of radii (see Figure A4).
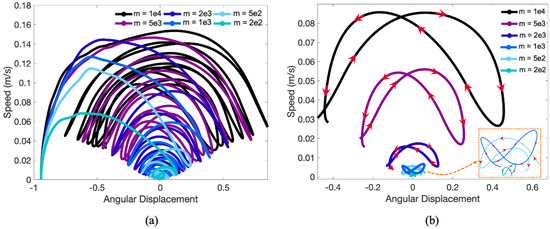
Figure 13.
(a) Phase space of linear speed of the pendulum bob vs. angular displacement (radians) for a variety of masses in the case of . (b) A closer look at the last simulated cycle’s phase space in each case.
3.3. Forces on the Pendulum Bob
We have observed that a fluid-immersed pendulum experiences exponential decay in angular displacement and speed. As discussed in Section 1, this is due to fluid drag on the pendulum bob. In this section we will explore this drag force. We wish to emphasize that our numerical experiments did not prescribe any specific form of the drag forces a priori, or any forces for that matter, beyond gravity acting on the pendulum bob.
First we selected three masses, , and , and investigated the drag force acting on the pendulum versus time for a variety of radii. This data is shown in Figure 14. The drag force was calculated by computing the forces perpendicular to the direction of the pendulum arm as the bob swung. A normal unit vector was computed at each sampled time-point and the drag force was computed using a vector projection in the direction opposite to the swinging motion of the pendulum bob.
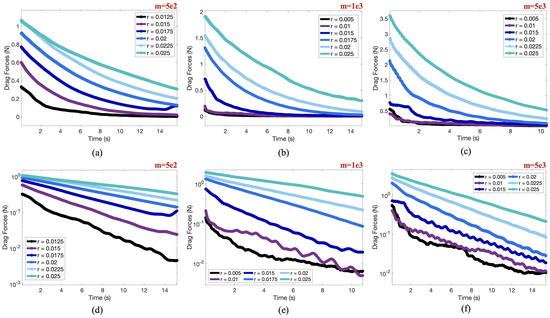
Figure 14.
Drag forces (N) over time in seconds for multiple radii for cases with (a,d) , (b,e) , and (c,f) . The semi-log data is provided in (d–f) to highlight a linear relationship between the logarithm of the drag force and time. This linear relationship suggests an exponential decay in drag force over time.
Figure 14a–c suggest that the drag force exponentially decays as time progressed. This was further confirmed by the linear relationship between the logarithm of drag force vs time in Figure 14d–f. As the radius increases, the surface (circumference) of the circle increases, and thus the amount of drag on the pendulum bob’s body increased for a particular mass as well. Hence the drag on the bob is dependent on its geometry (shape and size), as discussed in Section 1. Furthermore, as mass increases, so does the overall drag on the bob. This can also be seen in the counterpart case, where 3 radii are selected (, and ) and mass was varied, see Figure A6.
Next, we explored the phase space of drag force on the pendulum bob versus angular displacement of the bob. This data is given in Figure 15. Similar to the phase plots of speed versus displacement, the force-displacement trajectories all collapse onto a unique exponentially decaying envelope. Smaller radii (Figure 15a, ) correspond to larger angular displacements and larger spectrum of initial drag forces corresponding to a variety of masses over 3 orders of magnitude. In the case of a larger radii (Figure 15c, ), there are smaller angular displacements, comparatively, and the range of initial drag forces is smaller for the same variety of masses.
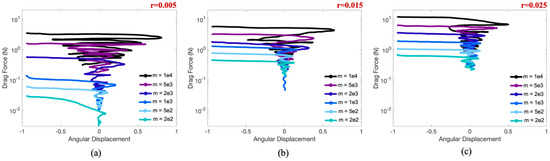
Figure 15.
Phase space of drag force (N) versus angular displacement (radians) for a variety of masses in cases of (a) , (b) , and (c) . The data for each case of a specific radius appears to overlap as well as suggesting that as the peaks in angular displacement decay exponentially (see Figure 7), the drag forces also decay exponentially as well.
Finally, we wish to compare force information across all cases of radii and masses considered. The metric we chose to compare for each is the drag coefficient; recall the term from Equation (7). To justify our use of Equation (7), we verified that the pendulum simulations fell into the appropriate Reynolds number range, i.e., . Recall the Reynolds number, , is defined to be
where and are the fluid’s density and dynamic viscosity, and L and V are a characteristic length and velocity scale, respectively. We chose L to be the length the pendulum’s arm, but rather than select V to be a constant, we used the time-dependent speed of the pendulum bob for each case. Note that this speed is inherently a function of the radius of the pendulum bob itself, see Figure A3 in Appendix C. Figure 16a illustrates that for that the peak in Reynolds number is greater than one. Moreover, where drops down, i.e., at the beginning and end of each swing, is where speed is near zero. Thus we assume the Drag Force Law derived by Lord Rayleigh will suffice for our purposes here (, see Equation (7)). Note that as the pendulums continue to swing, will decrease in every case. Eventually there will be a shift into the regime where Lord Rayleigh’s Drag Force Law begins to fail and one must consider Stokes Drag Law (, see Equation (4)) when . Furthermore, we computed the time-averaged Reynolds number over the first swing of the pendulum for all masses and radii considered, see Figure 16b. Generally, as the mass of the bob increases, the average increases. On the other hand, as the radius increases, average decreases.
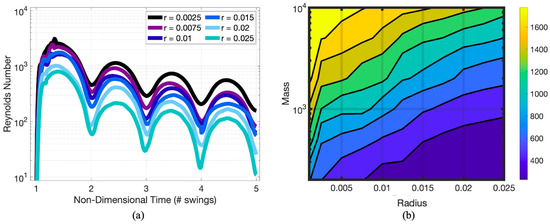
Figure 16.
(a) Re vs. Time for and (b) a colormap depicting the temporally-averaged Reynolds number during the first swing for different masses and radii. Note that over time as the pendulum slows down, the average Reynolds number will decrease.
Upon calculating Equation (7), we also need to describe A, the cross-sectional area of the circular pendulum, and , the drag force on the pendulum. We define A to be the circumference of the circle, i.e., , for each given radius, r. Having computed the speed of the pendulum bob and drag force on the body previously, we could solve for the time-dependent drag coefficient at each sample time-point using Equation (7). Figure 17a,b gives over the first swing (half an oscillation cycle) and 4 swings (2 full oscillation cycles), respectively, for the case of and a variety of radii. Note that the peaks correspond to when the pendulum bob changes direction and thus reach speeds near zero. Moreover, the time-dependent drag coefficients will increase over time due to the pendulum continually slowing down.
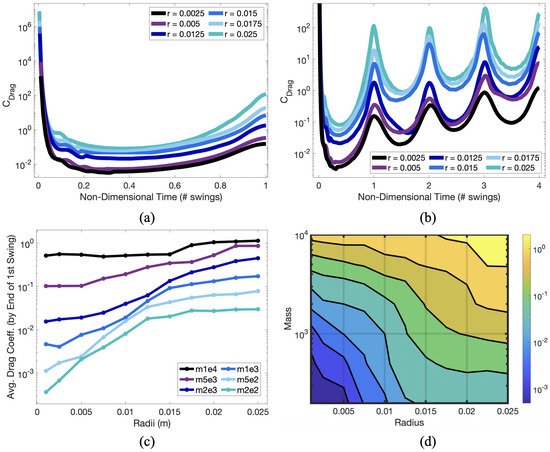
Figure 17.
The drag coefficient, , during the first pendulum’s first swing (a) and first 4-swings (b) for a variety of radius in the case of . Note that the drag coefficient maximizes when the pendulum reaches near zero speed at the end of a swing. (c) The temporally-averaged drag coefficients across the first swing for all mass and radius cases considered. (d) A contour map of the temporally-averaged drag coefficients over the first swing from (c) as a function of both the pendulum bob’s mass and radius. Generally higher drag coefficients are seen for larger mass and size pendulum bobs.
In order to compare all simulations of differing mass and radii, we averaged the time-dependent drag coefficient, , over the first swing, as shown in Figure 17c,d. Figure 17d provides a colormap with contour lines of the time-averaged drag coefficient using the data from Figure 17c. Larger radii pendulums tend to have larger drag coefficients and higher mass pendulum bobs also have larger drag coefficients. Notice that a pendulum bob with same shape (circle) and size (radius) could elicit different drag coefficients based on variations in mass. From Section 3.2 we have already observed that variations in mass give rise to variations in speed, which is also required to compute in the first place. The system is highly coupled in its many dynamical features!
Finally, we highlight the relationship between drag coefficient, , and Reynolds number, , in Figure 18. For a given mass (mass is denoted by a particular shape in the figure), as average increases, decreases. As the system is highly coupled, for a given mass, the average only increases as the pendulum bob’s radius decreases (radius is denoted by the colormap). On the other hand, for a given radius, as the mass increases, the average and also generally increase. The overall trend of decreasing with increasing is common in many fluid dynamics phenomena, not only physical experiments, such as flow past rigid objects [57,58,59], but also in biology, such as tiny insect flight [50,51], or even sports such as baseball [60], American football [61], or football (soccer) [62].
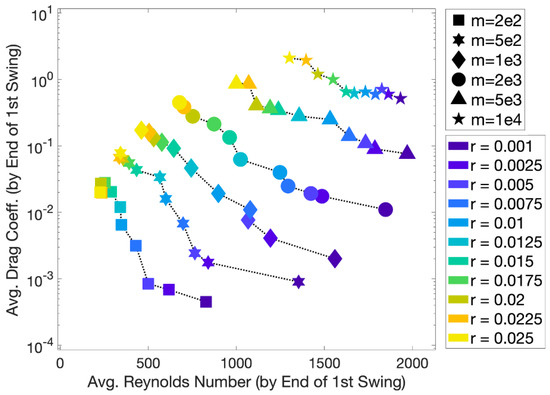
Figure 18.
The average drag coefficient, , vs. average Reynolds number for a variety of masses and radii. The averages were computing over the first swing of the pendulum bob.
3.4. Effect the Pendulum Bob Has onto the Fluid
In addition to the data analysis performed in Section 3.1, Section 3.2 and Section 3.3, which focused primarily on the Lagrangian structure itself—the pendulum, CFD (FSI) simulations grant us the opportunity to analyze how the underlying fluid reacts to a pendulum swinging through it. Also, we are able to visualize the fluid dynamics and observe the evolution of the fluid’s velocity field, , magnitude of velocity, , and vorticity (), see Figure 19, for qualitative analysis.
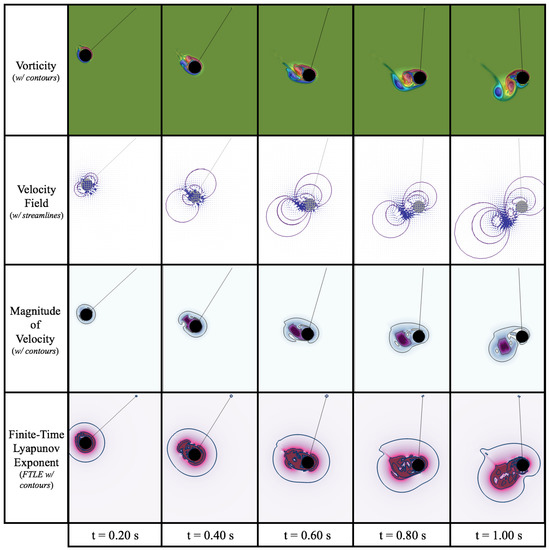
Figure 19.
Colormaps (and its contours) illustrating the time evolution of the fluid’s vorticity, magnitude of velocity, and finite-time Lyapunov Exponent (FTLE), as well as the velocity field (and its streamlines) resulting from the pendulum bob’s first swing in the case of and .
Figure 19 shows the resulting fluid dynamics due to the swinging motion of the pendulum bob of mass, , and radius, , during its first swing. As the pendulum swings, there is a pocket of fast moving fluid directly behind the bob until it passes zero angular displacement, as shown by the Velocity Field and Magnitude of Velocity plots. Note that streamlines are presented on the velocity field’s plots and contours are given on the magnitude of velocity plot, as well. Streamlines illustrate the path of massless tracer particles in the flow at an instantaneous point in time, while the contours give a line in which the quantity (here, magnitude of velocity) has constant value. Note that the direction of the pocket of fast moving fluid is towards the pendulum bob; hence objects directly behind the moving bob receive an fluid dynamic benefit. This phenomenon is commonly called drafting and has been studied in the context of many sports, such as ice skating [63], running [64,65], swimming [66], or cycling [67], as well as biological locomotion [68,69,70,71,72].
Within the region of fast moving fluid there are two interacting, oppositely spinning vortices behind the bob, as illustrated by the Vorticity plots. When the vortices are shed off the bob entirely, i.e., once the bob swings past zero displacement, the vortex pair continues to move vertically downwards, rather than upwards and to the right with the bob. These visualizations were produced using the raw -data produced during the FSI simulations using the open-source software VisIt [56]. We wish to emphasize that one cannot gain knowledge of fluid dynamics from the reduced-order ODE model, Equation (3) alone.
Moreover, because of the FSI simulations we are able to analyze the fluid data further and determine regions that have varying levels of fluid mixing. During data post-processing we could compute the finite-time Lyapunov exponents (FTLE), which can be used characterize the rate of separation in the trajectories of two infinitesimally close fluid blobs. Maxima in the FTLE (called ridges) have been used to determine Lagrangian Coherent Structures (LCSs), which are used to determine distinct flow structures in the fluid [73,74,75,76]. LCSs are a tool to divide the fluid’s complex dynamics into distinct regions to better understand transport properties of flow [77,78,79]. In this paper, we computed forward-time FTLE field, whose maximal ridges give LCSs corresponding to regions of repelling fluid trajectories and low values give rise to regions of attraction [76]. This data is presented in Figure 19 as well. Our desire here is not to emphasize fluid mixing metrics, but merely point out that through CFD one is able to investigate deeper dynamics of a system, even one as well studied as a damped pendulum.
Furthermore, we wish to point out that the resulting fluid dynamics are diverse. Not every pendulum bob sheds vortices in the same way as the case of (as illustrated in Figure 19). Figure 20 illustrates differences in vortex formation and shedding for the case of for a variety of radii during the first swing. In particular the overall size and magnitude of vortices formed is less in the smaller radius cases; however, once shed, the vortex dynamics are different. This would give rise to different dynamics in drafting behind the bob. In the larger radius cases (), the vortices move vertically downwards upon being shed, while they are significantly different in the smaller cases: in the case, the vortex-pair travels along with the pendulum bob, and for two sets of vortex-pairs move on either side of the pendulum bob. Thus, modifying the size of the pendulum results in different dynamics of the underlying fluid, even though all pendulums swing along the same circular arc; however, they do so at different speeds.
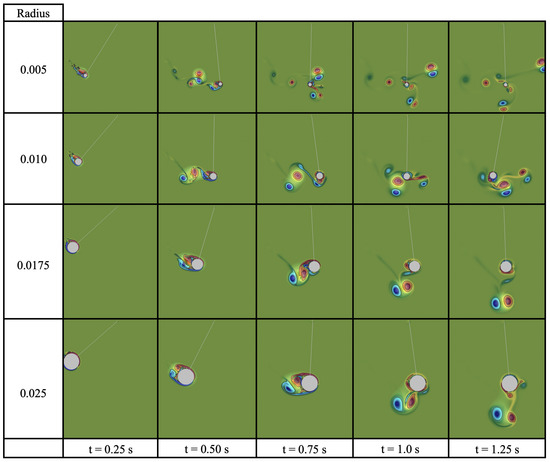
Figure 20.
Comparing vortex dynamics among pendulum bob of different radii for a mass of .
Lastly, taking a further look at the case (for ) reveals that as the pendulum swings, it swings back through its vortex wake, see Figure 21. The act of swinging through its vortex wake has been suggested as a possible mechanism for increased fluid drag on the pendulum bob [25]. However, a vortex could also enhance the speed of the bob if an appropriately spinning vortex interacts with the bob at the right moment in time, see in Figure 21. The vortex in red is spinning counter-clockwise and may give the bob a boost in speed, as it is moving in that same direction. There are complex interwoven dynamics within the system. Figure 22 provides an additional sequence of snapshots depicting these complex interactions. It shows a pendulum bob (, swinging through its own vortex wake during the return swing of the first oscillatory cycle. Such complex interaction mechanisms have not been fully explored and warrant further attention from the scientific community.
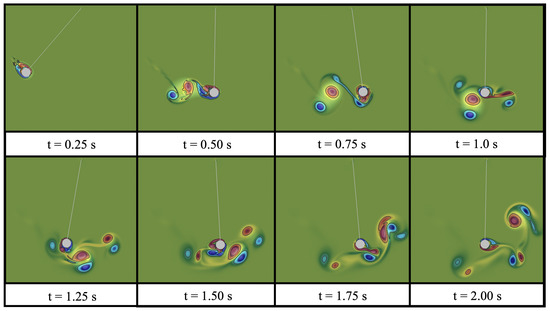
Figure 21.
The vortex dynamics of the case () = () within the first of oscillation.
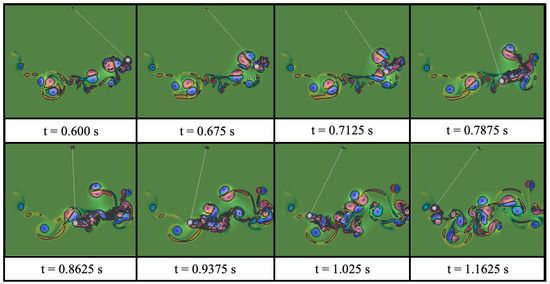
Figure 22.
The vortex dynamics of the case () = () on the return swing during its first oscillatory cycle.
3.5. Numerical Comparison & Validation
Lastly, in this section we will compare and validate the canonical damped physical pendulum equation against our fluid-structure interaction (FSI) model. Recall the damped physical pendulum (Equation (3)) is given by
Our FSI model did not assume any knowledge of the existence of this reduced ordinary differential equations (ODE) model. Instead it placed a spherical (circular) pendulum bob into a fluid environment, tethered it to a fixed location, and under the influence of gravity alone, it swung. This was to mimic a physical experiment, but performed in silica, rather than in a laboratory setting.
To compare Equation (13) and our FSI model, we first matched the parameter values. For each radius and mass considered in our FSI model, we were able to compute the exponential decay of the peaks in angular displacement amplitude using a linear least squares framework to fit a line through the logarithm of the peak values in angular displacement over time (linear regression), see Figure 23a as an illustrative example. The slope of each line was for that particular mass and radius. Hence for the parameter in Equation (13), we multiplied each slope by , i.e.,
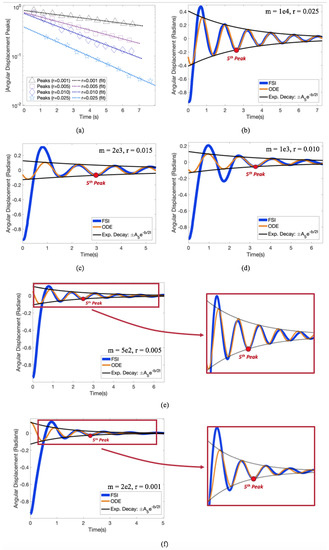
Figure 23.
(a) Slopes of the least squares (linear regression) fits through the peaks of angular displacement over time to compute the exponential decay, , for a variety of radii in the kg case. (b–f) Comparison of the FSI and ODE models’ angular displacement over time for a variety of masses and radii.
Note that the term is the approximate natural (undamped) angular frequency squared of the pendulum bob, i.e.,
Note that this is not the true natural, undamped angular frequency, as we did not invoke the small angle approximation, i.e., for small [9]. Moreover, due to the presence of the fluid, the pendulum bob was not in an undamped setting, so we could not directly calculate from our numerical experiments. However, we used the pendulum’s period, as previously computed in Section 3.1, and to compute . For clarity with the undamped case, we define and to the damped period and angular frequency of our pendulum bob from the FSI experiments. Recall the relationship between and ,
and the relationship between , , and ,
Using Equations (14) and (18) we found the appropriate parameter values for the reduced ODE model, as computed from the FSI simulations. Figure 23b–f provides comparison of the FSI and ODE models’ angular displacement over time for a variety of pendulum bob radii and masses. For comparative purposes, the ODE model was initialized at the 5th peak of the FSI model and its solution was computed by propagating both forwards and backwards in time. Moreover we also plotted the exponential decay, using the 5th peak amplitude as the coefficient, and plotted it in a similar manner both forwards and backwards in time from the 5th peak.
We note that the ODE model only agrees with our FSI model after a few oscillations. If we propagated the ODE model forward in time from the original position of the FSI pendulum, angular displacements were not consistent, see Figure 24. Furthermore, if we used the first peak amplitude (initial angular displacement) as the coefficient on the exponential decay, the FSI model appeared to not agree with its own decay rate. However, the decay rates are consistent, as seen in Figure 23, but the FSI model does not start obeying such decay until after a few oscillations. Thus, the decay rates, , were calculated starting with the third peak rather than the initial displacement. We chose the third peak rather than the second as the linear relationship was more prevalent from that point on. This is the same phenomenon from Figure 11 in Section 3.2, where the exponential decay in peak speeds did not start until what appeared to be the second swing.
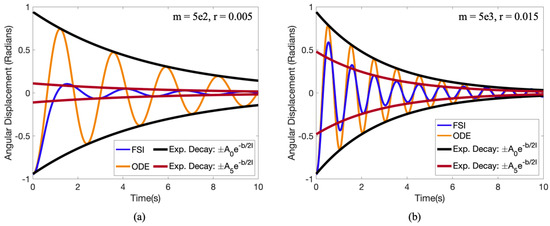
Figure 24.
Depicting the dynamics if the ODE model started from the original angular displacement of the FSI pendulum rather than the the 5th peak for the case and for (a,b), respectively. A visualization of the exponential decay is also provided with the coefficient either being , the original angular angular displacement, or , the displacement of the 5th peak.
Overall the reduced ODE model agrees with the FSI model after a few oscillations for different size pendulum bob radii as well as over a spectrum of masses; however, the dynamics during the first swing are substantially different (see Figure 24). This is possibly due to a different fluid drag law on the pendulum, before it settles into the regime where the drag can be modeled as linearly proportional to its velocity.
Lastly, we computed the damping parameter, b, by itself as a function of the mass and radius of the pendulum bob. To compute this, we first found the effective moment of inertia of each case using Equation (18), e.g.,
and then calculated
Note that we chose to calculate the effective moment of inertia, I, for each simulation here. Our FSI pendulum bob geometry was not a solid structure, but rather, had a singular mass source at its center, a shell composed of neutrally-buoyant points tethered together, and from the IB formulation, its shell enclosed fluid within. This fluid had the same properties as the backward fluid environment in which the pendulum is immersed. Moreover, as the principle of added mass states that inertia is added to a fluid system when an object is accelerating (or decelerating) through it [21]. Thus, the appropriate moment of inertia, I, to use in the ODE model to match the FSI model is non-trivial.
The damping parameter, b, increased as mass increased for a particular radius, see Figure 25. Moreover, as the radius increased for a given mass, b increased as well. While the system appears to be more sensitive to changes in mass, recall that the mass was varied over two orders of magnitudes in value, while the radius varied roughly over one.
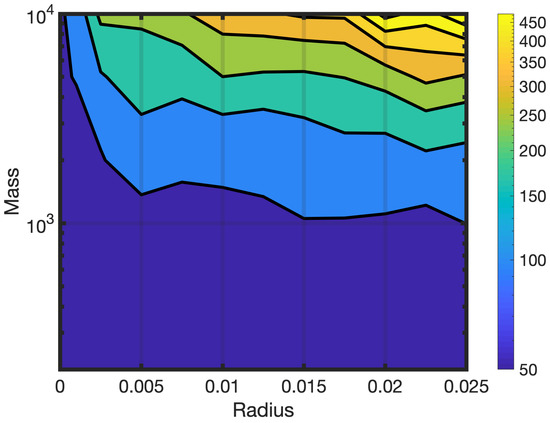
Figure 25.
Values of the damping parameter, b, as a function of the mass and radius of the pendulum bob.
4. Discussion and Conclusions
Two-dimensional immersed boundary simulations were used to model the swinging motion of a circular pendulum bob under the influence of gravity that was contained within a viscous, incompressible fluid environment. In addition, to the authors knowledge, this is the first fluid-structure interaction (FSI) simulation that explores the motion of an ordinary pendulum system which also offers an open-source complement. The angular displacement data collected from the motion of the pendulum bob was directly compared against the reduced-order damping ODE model that is familiar to most STEM students. In general, the oscillatory dynamics agree between the ODE model and the FSI model (see Section 3.5). However, there were discrepancies in the decay rates between the first few swing’s maximal angular displacements and speeds with those following thereafter. The mechanisms underlying these observations are not fully understood. There appear to be interesting dynamics to probe further involving the pendulum bob’s mass and radius, the vortex wake it creates, the interactions of those vortices with each other and the bob itself, and the resulting drag on the bob during large amplitude oscillations.
Moreover, the ODE model’s linearly-proportional-velocity damping term, i.e., Stokes Drag Law, was appropriate once the pendulum has swung a few times after a large initial angular displacement. During the first initial swing there was an enhancement of drag on the pendulum bob, potentially obeying Rayleigh’s Drag Law and/or from the principle of added mass [24] and/or other complex drag mechanisms involving vortex shedding [23].
Furthermore, we were able to determine the approximate damping parameter, b, that fit the ODE model from our FSI model. The damping parameter, b, was found to be dependent on both mass and radius of the pendulum (see Section 3.5). Also, through the FSI simulations, we were able to quantify how the drag coefficient, , increased with both increasing mass and radius of the pendulum bob (see Section 3.3). On that note, we also illustrated how the pendulum’s period of oscillation was a function of both the mass and radius of the pendulum bob (see Section 3.1).
Beyond the dynamics of the pendulum structure itself, using a FSI model allowed us to peek into the resulting dynamics of the underlying fluid (see Section 3.4), which we would not have otherwise been able to do using the reduced-ODE model alone. While the purpose of this study was to explore the dynamics of a FSI pendulum model, which inherently did not assume any particular drag laws a priori, and compare the results to the ODE model, this framework can be used to further probe into new scientific frontiers that could unravel the enhanced contributions to fluid drag, whether from traveling through your own vortex wake, as suggested by Mathai et al., 2019 [25], vortex shedding as suggested by Bolster et al., 2010 [23], or added mass, as suggested by Bandi et al., 2013 [24]. There are still complex relationships to decrypt between oscillatory amplitude, geometry and mass of the pendulum bob, and fluid scale. The aforementioned studies performed physical experiments with pendulums and used sophisticated visualization techniques, either the Baker electrolytic technique [80] or particle image velocimetry (PIV) [81,82] to visualize the underlying fluid dynamics.
Furthermore, using this FSI framework it is possible to couple multiple pendulum together and study the resulting complex dynamics and/or investigate the motion of a variety of geometric objects being swung as pendulum bobs. We have seen that the size of the pendulum bob affects the underlying fluid dynamics, as observed through different vortex dynamics in Section 3.4; however, one has yet to explore how shape affects the fluid dynamics or motion of the bob itself.
While a student’s first brief foray into fluids may have been through the concept of damped simple harmonic motion involving a pendulum, we hope that this manuscript provides the following context for students in an introductory fluid mechanics course:
- A connection to where students may have seen fluid drag laws previously, i.e., the Stokes Drag Law and Pendulum Motion. Furthermore, it illustrates for students that famous laws of physics were discovered with systems that seem as “basic” as that of a pendulum.
- The differences that may arise between modeling a system using a reduced-order ODE model and attempting to computationally model all aspects of the system to a higher degree. We hope this shows students that reduced models are valuable in that they are usually easier to solve while (hopefully) capturing a bulk of a system’s dynamics. However, there are clear disadvantages as illustrated by the discrepancies that arise between the reduced order model and computational model—many dynamics are not captured in the reduced-model, e.g., the vortex wake or drafting, that maybe particularly interesting or important to understanding the system as a whole.
- Similarly, the full dynamical richness of a system may only be explored by investigating its explicit fluid mechanics, even in a system as seemingly “simple” as a single pendulum immersed in a fluid. Moreover, to even study systems involving fluids and objects immersed therein, it requires either sophisticated experimental techniques or computational expertise. This work shows that a computer can be an immensely powerful tool for performing science. More than that, programming knowledge is highly sought after in this day and age [83,84].
- The observation that even systems that are routinely studied in some introductory courses, like a pendulum, may still have open, exciting research questions that scientists and engineers actively pursue.
To conclude, the pendulum may be an old, historic device that has been studied for millennia; however, under the hood, there are a lot of hidden, complex dynamics left to discover.
Supplementary Materials
The following are available online at https://www.mdpi.com/2311-5521/5/2/48/s1.
Author Contributions
Conceptualization, M.M. and N.A.B.; Methodology and Software, N.A.B.; Validation, N.A.B.; Formal Analysis, Investigation, and Data Curation, M.M. and N.A.B.; Writing—Original Draft Preparation, N.A.B.; Writing—Review & Editing, M.M. and N.A.B.; Visualization, M.M. and N.A.B.; Funding Acquisition, N.A.B. All authors have read and agreed to the published version of the manuscript.
Funding
Computational resources were provided by the NSF OAC #1826915 and the NSF OAC #1828163. Support for N.A.B. was provided by the TCNJ Support of Scholarly Activity (SOSA) Grant, the TCNJ Department of Mathematics and Statistics, and the TCNJ School of Science.
Acknowledgments
The authors would like to thank Christina Battista, Robert Booth, Karen Clark, Jana Gevertz, Christina Hamlet, Alexander Hoover, Laura Miller, Matthew Mizuhara, Arvind Santhanakrishnan, Emily Slesinger, Edward Voskanian, and Lindsay Waldrop for comments and discussion.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CFD | Computational Fluid Dynamics |
| FSI | Fluid-Structure Interaction |
| Re | Reynolds Number |
| IB | Immersed Boundary Method |
| ODE | Ordinary Differential Equation |
Appendix A. Instructor Resources
Teaching Resources:
Associated supplemental files contain slides, movies, and open-source codes pertaining to the paper. It encompasses the following:
- Pendulum_Classroom_Supplement.pptx/.pdf: presentations which may be used in class; slides that tell the story of the paper. Note that the file has embedded movies in format.
- Movies: directory containing movies ( format) pertaining to each simulation shown in the manuscript.
- Note that an open-source fluid-structure interaction model of a point-mass pendulum can be found at: https://github.com/nickabattista/IB2d in the sub-directory:IB2d → matIB2d → Examples → Examples_Education→ Pendulum.
- Visualization software used: VisIt (https://visit.llnl.gov/) (v. 2.12.3)
Appendix B. Immersed Boundary Method
The immersed boundary method [30] was used to model the motion of a pendulum under gravitational acceleration, see Section 2. Although, IB is capable of solving fully coupled fluid-structure interaction systems involving flexible or squishy structures, here we use it to model the stiff boundaries of a pendulum bob immersed within an incompressible, viscous fluid. The fluid motion is governed by the Navier-Stokes equations, given as
where is the fluid velocity, is the pressure, is the force per unit volume (area in ) applied to the fluid by the immersed boundary, i.e., the pendulum. The independent variables are the position, , and time, t. Equations (A1) and (A2) are conservation laws for the fluid, i.e., the conservation of momentum and mass, respectively. Note that Equation (A2) is known as the incompressibility condition.
The interaction equations between the fluid and the immersed structure are given by
where gives the Cartesian coordinates at time t of the material point labeled by Lagrangian parameter r, is the force per unit area imposed onto the fluid by elastic deformations in the boundary, as a function of the Lagrangian position, r, and time, t. Equation (A3) applies a force from the immersed boundary to the fluid grid through a delta-kernel integral transformation. Equation (A4) sets the velocity of the boundary equal to the local fluid velocity.
As suggested in Section 2.2, the deformation force equation, F(r,t), is specific to the system being explored. For this pendulum model, it takes the following form
that is the summation of forces arising from spring, target point, and massive point deformations pertaining over each Lagrangian point being modeled with one or more of this model features.
IB Algorithm
In our pendulum model, we imposed periodic boundary conditions on a square domain. To solve Equations (A1)–(A4) we need to update the velocity, pressure, and both the position of the boundary and forces acting on it from the previous time-step data, time n. IB traditionally does this in the following steps [30,39]:
Step 1: Calculate the force density, on the immersed boundary, from its current boundary configuration at time n, .
Step 2: Use Equation (A3) to spread the force from the Lagrangian boundary to the Eulerian (fluid) mesh to compute
Step 3: Solve the Navier-Stokes equations, A1 and A2, on the Eulerian grid, thus updating and from , , and .
Step 4: Update the Lagrangian point positions, , using the local fluid velocities, , computed from and (A4).
Appendix C. Additional Pendulum Data
In this appendix we provide complementary data to the data presented in Section 3, e.g., if we provided a figure that contained a variety of masses for a particular radius (as in Figure 6), here we will provide the opposite—a variety of radii for particular cases of mass (as in Figure A1 below). These figures are provided for additional clarity in regards to the comparisons being discussed and analyzed.
First we provide the angular displacement (in radians) over time (in seconds) for cases of pendulums with the same mass, but different radii in Figure A1. This data is to illustrate clearly that pendulum bobs with the same mass can experience different oscillatory patterns for different radii. Moreover, it appears that by increasing mass orders of magnitude, from to to could result in the pendulum bob undergoing different regimes of oscillation—either underdamped to overdamped.
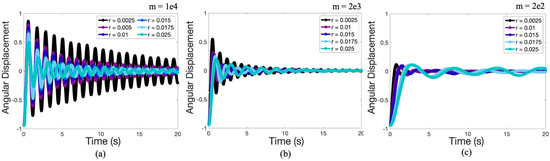
Figure A1.
Depicting the angular displacement (radians) vs. time (s) for pendulums with the same mass but different radii. (a–c) give data for a specific mass, either , or , respectively, and a variety of radii in each.
Next we provide a plot of the height the pendulum reaches (in meters) as a function of the peak number in angular displacement for and a variety of radii in Figure A2. This illustrates that as the radius increases, the height decreases. Not only does the height decreases as the radius increases, the linear speed of the pendulum also decreases as well, as given in Figure A3. Our simulations suggest that smaller pendulum bobs generally move faster than larger ones for a given mass. In both of these figures, among all cases, both the speed and height decay exponentially as illustrated by the semi-logarithmic plots in Figure A2b and Figure A3b. These data are provided to suggest that as the size of the pendulum increases, there must be more drag force acting on the bob to decelerate their speed and thus not allow them to reach as great of heights (angular displacements) as other smaller bobs.
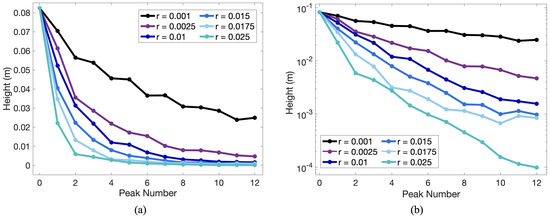
Figure A2.
(a) Plot illustrating the decay of the height (m) that the pendulum bob reaches as the pendulum continues to swing for the case of for a variety of radii. The peak amplitude decays exponentially as illustrated by the linear relationship between the logarithm of the amplitude against peak number, as shown in (b).
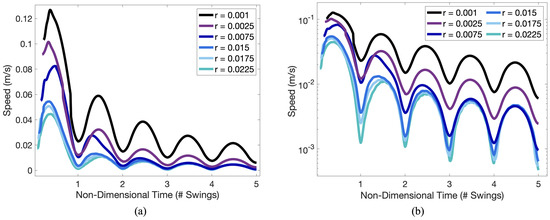
Figure A3.
(a) Plot depicting the linear speed of the pendulum bob against non-dimensional time given as the # of swings (half a full displacement cycle) for the case of for a variety of radii. Speed peaks in the middle of a swing corresponding to when the pendulum has zero angular displacement from the vertical and the peak speed appears to decay exponentially, given by the linear relationship in (b).
Furthermore we also provide more detailed phase space explorations of linear speed () versus angular displacement (radians) in Figure A4 and Figure A5. Figure A4 provides the phase space of linear speed versus angular displacement for the case of and a variety of radii, while Figure A5 selects four radii (, and ) and varies mass. Similar topological structures are observed, where the data collapses onto a parabolically-capped cone. This is intuitive as both the peaks in angular displacement and speed decrease over time; however, what is particularly interesting is that the cone angle looks to be approximately conserved among all cases.
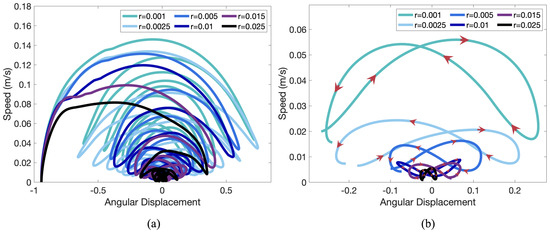
Figure A4.
(a) Phase space of linear speed of the pendulum bob vs. angular displacement (radians) for a variety of radii in the case of . (b) A closer look at the last simulated cycle’s phase space for each case.
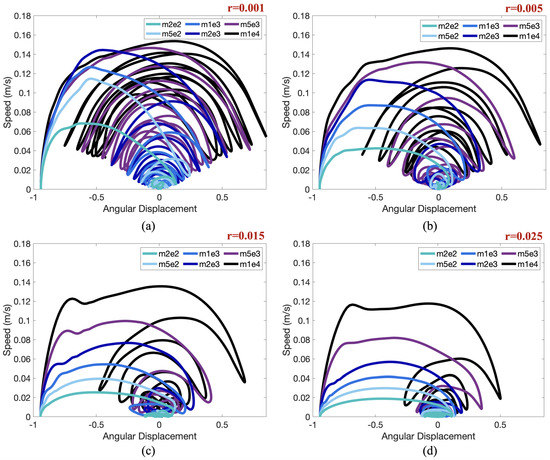
Figure A5.
Phase space of linear speed of the pendulum bob vs. angular displacement (radians) for a variety of masses for cases: (a) , (b) , (c) , and (d) .
Finally we provide data depicting the drag force (N) over time for 3 different radii (, , and ) over a variety of masses. Compared to Figure 14, we notice that for the same radius but different masses, the drag forces begin to overlap with time. Specifically, the drag forces corresponding to larger masses decay more rapidly. This could also be surmised from Figure 17c,d, which show an increased average drag coefficient during the higher mass cases for a specific radius.
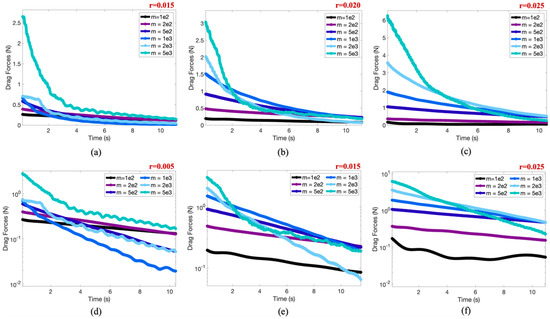
Figure A6.
Drag forces (N) over time in seconds for a variety of masses for cases with (a,d) , (b,e) , and (c,f) . The semi-log data is provided in (d–f) to highlight a linear relationship between the logarithm of the drag force and time. This linear relationship suggests an exponential decay in drag force over time.
References
- Milne, J. Pendulum Seismometers. Nature 1888, 37, 570–571. [Google Scholar] [CrossRef][Green Version]
- Morton, W.S.; Lewis, C.M. China: Its History and Culture; McGraw-Hill, Inc.: New York, NY, USA, 2005. [Google Scholar]
- Matthews, M.R. Time for Science Education: How Teaching the History and Philosophy of Pendulum Motion Can Contribute to Science Literacy; Springer: New York, NY, USA, 2000. [Google Scholar]
- Blackwell, N. Experimental stone-cutting with the Mycenaean pendulum saw. Antiquity 2018, 92, 217–232. [Google Scholar] [CrossRef]
- Bennett, M.; Schatz, M.F.; Rockwood, H.; Wiesenfeld, K. Huygens’ Clocks. Proc. R. Soc. Lond. A 2002, 458, 563–579. [Google Scholar] [CrossRef]
- Boettcher, W.; Merkle, F.; Weitkemper, H.H. History of extracorporeal circulation: The conceptional and developmental period. J. Extra Corpor. Technol. 2003, 3, 172–183. [Google Scholar]
- Scott, G.R. The History of Torture throughout the Ages; Kessinger Publishing, LLC: Whitefish, MT, USA, 2009. [Google Scholar]
- Poe, E.A. The Pit and the Pendulum. In The Gift: A Christmas and New Year’s Present for 1843; Leslie, E., Ed.; Carey & Hart: Philadelphia, PA, USA, 1843; Chapter 12; pp. 133–152. [Google Scholar]
- Halliday, D.; Resnick, R.; Walker, J. Fundamentals of Physics, 7th ed.; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Stokes, G.G. On the Effect of the Internal Friction of Fluids on the Motion of Pendulums. Trans. Camb. Philos. Soc. 1851, 9, 8–106. [Google Scholar]
- Batchelor, G.K. Introduction to Fluid Mechanics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Happel, J.; Brenner, H. Low Reynolds Number Hydrodynamics; Springer: New York, NY, USA, 1981. [Google Scholar]
- Buckingham, E. On physically similar systems; illustrations of the use of dimensional equations. Phys. Rev. 2014, 4, 245–376. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics, 1st ed.; Pergamon: London, UK, 1959. [Google Scholar]
- Mahajan, S. Chapter 4: Fluid Drag. Notes from MIT IAP Course in 2006: Lies and Damn Lies: The Art of Approximation in Science. 2006. Available online: http://www.inference.org.uk/sanjoy/mit/book:04.pdf (accessed on 3 January 2020).
- Nelson, R.A.; Olsson, M.G. The Pendulum-Rich physics from a simple system. Am. J. Phys. 1986, 2, 54. [Google Scholar] [CrossRef]
- Peters, R.D. Nonlinear Damping of the ‘Linear’ Pendulum. 2003. Available online: https://arxiv.org/abs/physics/0306081 (accessed on 15 December 2019).
- Peters, R.D. The Pendulum in the 21st Century-Relic or Trendsetter. Sci. Educ. 2004, 13, 279–295. [Google Scholar] [CrossRef]
- Quiroga, G.D.; Ospina-Henao, P.A. Dynamics of damped oscillations: Physical pendulum. Eur. J. Phys. 2017, 38, 065005. [Google Scholar] [CrossRef]
- Hsu, H.; Capart, H. Enhanced upswing in immersed collisions of tethered spheres. Phys. Fluids 2007, 19, 101701. [Google Scholar] [CrossRef]
- Neill, D.; Livelybrooks, D.; Donnelly, R.J. A pendulum experiment on added mass and the principle of equivalence. Am. J. Phys. 2007, 75, 226. [Google Scholar] [CrossRef]
- Sullivan, I.; Niemela, J.; Hershberger, R.; Bolster, D.; Donnelly, R. Dynamics of thin vortex rings. J. Fluid Mech. 2008, 609, 319–347. [Google Scholar] [CrossRef]
- Bolster, D.; Hershberger, R.E.; Donnelly, R.J. Oscillating pendulum decay by emission of vortex rings. Phys. Rev. E 2010, 13, 046317. [Google Scholar] [CrossRef] [PubMed]
- Bandi, M.M.; Concha, A.; Wood, R.; Mahadevan, L. A pendulum in a flowing soap film. Phys. Fluids 2013, 25, 041702. [Google Scholar] [CrossRef]
- Mathai, V.; Loeffen, L.; Chan, T.; Wildeman, S. Dynamics of heavy and buoyant underwater pendulums. J. Fluid Mech. 2019, 862, 348–363. [Google Scholar] [CrossRef]
- Farnell, D.J.; David, R.; Barton, D.C. Numerical simulations of a filament in a flowing soap film. Int. J. Numer. Methods Fluids 2004, 44, 313–330. [Google Scholar] [CrossRef]
- Orchini, A.; Kellay, H.; Mazzino, A. Galloping instability and control of a rigid pendulum in a flowing soap film. J. Fluids Struct. 2015, 56, 124–133. [Google Scholar] [CrossRef]
- Peskin, C. Flow patterns around heart valves: A numerical method. J. Comput. Phys. 1972, 10, 252–271. [Google Scholar] [CrossRef]
- Peskin, C. Numerical analysis of blood flow in the heart. J. Comput. Phys. 1977, 25, 220–252. [Google Scholar] [CrossRef]
- Peskin, C.S. The immersed boundary method. Acta Numer. 2002, 11, 479–517. [Google Scholar] [CrossRef]
- Fauci, L.; Fogelson, A. Truncated Newton methods and the modeling of complex immersed elastic structures. Commun. Pure Appl. Math 1993, 46, 787–818. [Google Scholar] [CrossRef]
- Lai, M.C.; Peskin, C.S. An Immersed Boundary Method with Formal Second-Order Accuracy and Reduced Numerical Viscosity. J. Comput. Phys. 2000, 160, 705–719. [Google Scholar] [CrossRef]
- Cortez, R.; Minion, M. The Blob Projection Method for Immersed Boundary Problems. J. Comput. Phys. 2000, 161, 428–453. [Google Scholar] [CrossRef]
- Griffith, B.E.; Peskin, C.S. On the order of accuracy of the immersed boundary method: Higher order convergence rates for sufficiently smooth problems. J. Comput. Phys. 2005, 208, 75–105. [Google Scholar] [CrossRef]
- Mittal, R.; Iaccarino, C. Immersed boundary methods. Annu. Rev. Fluid Mech. 2005, 37, 239–261. [Google Scholar] [CrossRef]
- Griffith, B.E.; Hornung, R.; McQueen, D.; Peskin, C.S. An adaptive, formally second order accurate version of the immersed boundary method. J. Comput. Phys. 2007, 223, 10–49. [Google Scholar] [CrossRef]
- Griffith, B.E. An Adaptive and Distributed-Memory Parallel Implementation of the Immersed Boundary (IB) Method. 2014. Available online: https://github.com/IBAMR/IBAMR (accessed on 21 October 2014).
- Griffith, B.E.; Luo, X. Hybrid finite difference/finite element version of the immersed boundary method. Int. J. Numer. Methods Biomed. Eng. 2017, 33, e2888. [Google Scholar] [CrossRef]
- Battista, N.A.; Strickland, W.C.; Miller, L.A. IB2d: A Python and MATLAB implementation of the immersed boundary method. Bioinspir. Biomim. 2017, 12, 036003. [Google Scholar] [CrossRef]
- Battista, N.A.; Strickland, W.C.; Barrett, A.; Miller, L.A. IB2d Reloaded: A more powerful Python and MATLAB implementation of the immersed boundary method. Math. Methods Appl. Sci. 2018, 41, 8455–8480. [Google Scholar] [CrossRef]
- Miller, L.A. Fluid Dynamics of Ventricular Filling in the Embryonic Heart. Cell Biochem. Biophys. 2011, 61, 33–45. [Google Scholar] [CrossRef]
- Griffith, B.E. Immersed boundary model of aortic heart valve dynamics with physiological driving and loading conditions. Int. J. Numer. Methods Biomed. Eng. 2012, 28, 317–345. [Google Scholar] [CrossRef] [PubMed]
- Battista, N.A.; Lane, A.N.; Liu, J.; Miller, L.A. Fluid Dynamics of Heart Development: Effects of Trabeculae and Hematocrit. Math. Med. Biol. 2017, 35, 493–516. [Google Scholar] [CrossRef] [PubMed]
- Battista, N.A.; Douglas, D.R.; Lane, A.N.; Samsa, L.A.; Liu, J.; Miller, L.A. Vortex Dynamics in Trabeculated Embryonic Ventricles. J. Cardiovasc. Dev. Dis. 2019, 6, 6. [Google Scholar] [CrossRef] [PubMed]
- Bhalla, A.; Griffith, B.E.; Patankar, N. A forced damped oscillation framework for undulatory swimming provides new insights into how propulsion arises in active and passive swimming. PLoS Comput. Biol. 2013, 9, e1003097. [Google Scholar] [CrossRef]
- Bhalla, A.; Griffith, B.E.; Patankar, N. A unified mathematical frame- work and an adaptive numerical method for fluid-structure interaction with rigid, deforming, and elastic bodies. J. Comput. Phys. 2013, 250, 446–476. [Google Scholar] [CrossRef]
- Hamlet, C.; Fauci, L.J.; Tytell, E.D. The effect of intrinsic muscular nonlinearities on the energetics of locomotion in a computational model of an anguilliform swimmer. J. Theor. Biol. 2015, 385, 119–129. [Google Scholar] [CrossRef]
- Hoover, A.P.; Griffith, B.E.; Miller, L.A. Quantifying performance in the medusan mechanospace with an actively swimming three-dimensional jellyfish model. J. Fluid Mech. 2017, 813, 1112–1155. [Google Scholar] [CrossRef]
- Miles, J.G.; Battista, N.A. Naut your everyday jellyfish model: Exploring how tentacles and oral arms impact locomotion. Fluids 2019, 4, 169. [Google Scholar] [CrossRef]
- Miller, L.A.; Peskin, C.S. When vortices stick: An aerodynamic transition in tiny insect flight. J. Exp. Biol. 2004, 207, 3073–3088. [Google Scholar] [CrossRef]
- Miller, L.A.; Peskin, C.S. A computational fluid dynamics of clap and fling in the smallest insects. J. Exp. Biol. 2005, 208, 3076–3090. [Google Scholar] [CrossRef]
- Jones, S.K.; Laurenza, R.; Hedrick, T.L.; Griffith, B.E.; Miller, L.A. Lift- vs. drag-based for vertical force production in the smallest flying insects. J. Theor. Biol. 2015, 384, 105–120. [Google Scholar] [CrossRef] [PubMed]
- Engineers Edge, LLC. Kinematic Viscosity Table Chart of Liquids, 2000–2020. Available online: https://www.engineersedge.com/fluid_flow/kinematic-viscosity-table.htm (accessed on 23 October 2019).
- Kim, Y.; Peskin, C.S. 2D parachute simulation by the immersed boundary method. SIAM J. Sci. Comput. 2006, 28, 2294–2312. [Google Scholar] [CrossRef]
- Kallemov, B.; Bhalla, A.; Griffith, B.E.; Donev, A. An immersed boundary method for rigid bodies. Commun. Appl. Math. Comput. Sci. 2016, 11, 79–141. [Google Scholar] [CrossRef]
- Childs, H.; Brugger, E.; Whitlock, B.; Meredith, J.; Ahern, S.; Pugmire, D.; Biagas, K.; Miller, M.; Harrison, C.; Weber, G.H.; et al. VisIt: An End-User Tool For Visualizing and Analyzing Very Large Data. In High Performance Visualization–Enabling Extreme-Scale Scientific Insight; Bethel, E.W., Childs, H., Hansen, C., Eds.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2012; pp. 357–372. [Google Scholar]
- Jones, A.M.; Knudsen, J.G. Drag coefficients at low Reynolds numbers for flow past immersed bodies. AIChE J. 1961, 7, 20–25. [Google Scholar] [CrossRef]
- Hall, N. Drag of a Sphere. National Aeronautics and Space Administration. 2015. Available online: https://www.grc.nasa.gov/WWW/k-12/airplane/dragsphere.html (accessed on 23 March 2020).
- Barry, D.A.; Parlange, J.Y. Universal expression for the drag on a fluid sphere. PLoS ONE 2018, 13, e0194907. [Google Scholar] [CrossRef]
- Sawicki, G.; Hubbard, M.; Stronge, W.J. How to hit home runs: Optimum baseball bat swing parameters for maximum range trajectories. Am. J. Phys. 2003, 71, 1152–1162. [Google Scholar] [CrossRef]
- Watts, R.G.; Moore, G. The drag force on an American football. Am. J. Phys. 2003, 71, 791–793. [Google Scholar] [CrossRef]
- Alam, F.; Chowdhury, H.; George, S.; Mustary, I.; Zimmer, G. Aerodynamic Drag Measurements of FIFA-approved Footballs. Procedia Eng. 2014, 72, 703–708. [Google Scholar] [CrossRef]
- Rundell, K.W. Effects of drafting during short-track speed skating. Med. Sci. Sports Exerc. 1996, 28, 765–771. [Google Scholar] [CrossRef]
- Zouhal, H.; Abderrahman, A.; Prioux, J.; Knechtle, B.; Bouguerra, L.; Kebsi, W.; Noakes, T.D. Drafting’s Improvement of 3000-m Running Performance in Elite Athletes: Is It a Placebo Effect? Int. J. Sports Phys. Perform. 2015, 10, 147–152. [Google Scholar] [CrossRef] [PubMed]
- Beaumont, F.; Bogard, F.; Murer, S.; Polidori, G.; Madaci, F.; Taiar, R. How does aerodynamics influence physiological responses in middle-distance running drafting? Math. Mod. Eng. Probl. 2019, 6, 129–135. [Google Scholar] [CrossRef]
- Silva, A.J.; Rouboa, A.I.; Moreira, A.; Reis, V.M.; Alves, F.; Vilas-Boas, J.P.; Marinho, D.A. Analysis of drafting effects in swimming using computational fluid dynamics. J. Sport Sci. Med. 2008, 7, 60–66. [Google Scholar]
- Blocken, B.; Defraeye, T.; Koninckx, E.; Carmeliet, J.; Hespel, P. CFD simulations of the aerodynamic drag of two drafting cyclists. Comput. Fluids 2013, 71, 435–445. [Google Scholar] [CrossRef]
- Fish, F.E. Energy conservation by formation swimming: Metabolic evidence from ducklings. In Mechanics and Physiology of Animal Swimming; Mattock, L., Bone, Q., Rayner, J.M., Eds.; Cambridge University Press: Cambridge, UK, 1994; Chapter 13; pp. 193–204. [Google Scholar]
- Fish, F.E. Kinematics of ducklings swimming in formation: Consequences of position. J. Exp. Zool. 1995, 273, 1–11. [Google Scholar] [CrossRef]
- Weimerskirch, H.; Martin, J.; Clerquin, Y.; Alexandre, P.; Jiraskova, S. Energy saving in flight formation. Nature 2001, 413, 697–698. [Google Scholar] [CrossRef] [PubMed]
- Hemelrijk, C.K.; Redi, D.A.; Hildenbrandt, H.; Padding, J.T. The increased efficiency of fish swimming in a school. Fish Fish. 2015, 16, 511–521. [Google Scholar] [CrossRef]
- Daghooghi, M.; Borazjani, I. The hydrodynamic advantages of synchronized swimming in a rectangular pattern. Bioinspir. Biomim. 2015, 10, 056018. [Google Scholar] [CrossRef]
- Shadden, S.C.; Lekien, F.; Marsden, J.E. Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows. Physica D 2005, 212, 271–304. [Google Scholar] [CrossRef]
- Shadden, S.C. Lagrangian Coherent Structures: Analysis of Time Dependent Dynamical Systems Using Finite-Time Lyapunov Exponent. 2005. Available online: https://shaddenlab.berkeley.edu/uploads/LCS-tutorial/LCSdef.html (accessed on 19 September 2019).
- Shadden, S.C.; Katija, K.; Rosenfeld, M.; Marsden, J.E.; Dabiri, J.O. Transport and stirring induced by vortex formation. J. Fluid Mech. 2007, 593, 315–331. [Google Scholar] [CrossRef]
- Haller, G.; Sapsis, T. Lagrangian coherent structures and the smallest finite-time Lyapunov exponent. Chaos 2011, 21, 023115. [Google Scholar] [CrossRef] [PubMed]
- Shadden, S.C.; Dabiri, J.O.; Marsden, J.E. Lagrangian analysis of fluid transport in empirical vortex ring flows. Phys. Fluids 2006, 18, 047105. [Google Scholar] [CrossRef]
- Lukens, S.; Yang, X.; Fauci, L. Using Lagrangian coherent structures to analyze fluid mixing by cilia. Chaos 2010, 20, 017511. [Google Scholar] [CrossRef] [PubMed]
- Cheryl, S.; Glatzmaier, G.A. Lagrangian coherent structures in the California Current System—Sensitivities and limitations. Geophys. Astrophys. Fluid Dyn. 2012, 106, 22–44. [Google Scholar]
- Mazo, R.M.; Hershberger, R.; Donnelly, R.J. Observations of flow patterns by electrochemical means. Exp. Fluids 2008, 44, 49–57. [Google Scholar] [CrossRef]
- Kiger, K.; Westerweel, J.; Poelma, C. Introduction to Particle Image Velocimetry. 2016. Available online: http://www2.cscamm.umd.edu/programs/trb10/presentations/PIV.pdf (accessed on 21 October 2016).
- Dantec. Measurement Principles of PIV. 2016. Available online: http://www.dantecdynamics.com/measurement-principles-of-piv (accessed on 21 October 2016).
- Heron, P.; McNeill, L. Phys21: Preparing Physics Students for 21st-Century Careers (A Report by the Joint Task Force on Undergraduate Physics Programs). American Physical Society and the American Association of Physics Teachers. 2016. Available online: https://www.compadre.org/JTUPP/docs/J-Tupp_Report.pdf (accessed on 7 January 2020).
- Heron, P.; McNeill, L. Preparing Physics Students for 21st-Century Careers. Phys. Today 2017, 70, 38. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).