Role of Surface-Layer Coherent Eddies in Potential Vorticity Transport in Quasigeostrophic Turbulence Driven by Eastward Shear
Abstract
1. Introduction
2. Methods
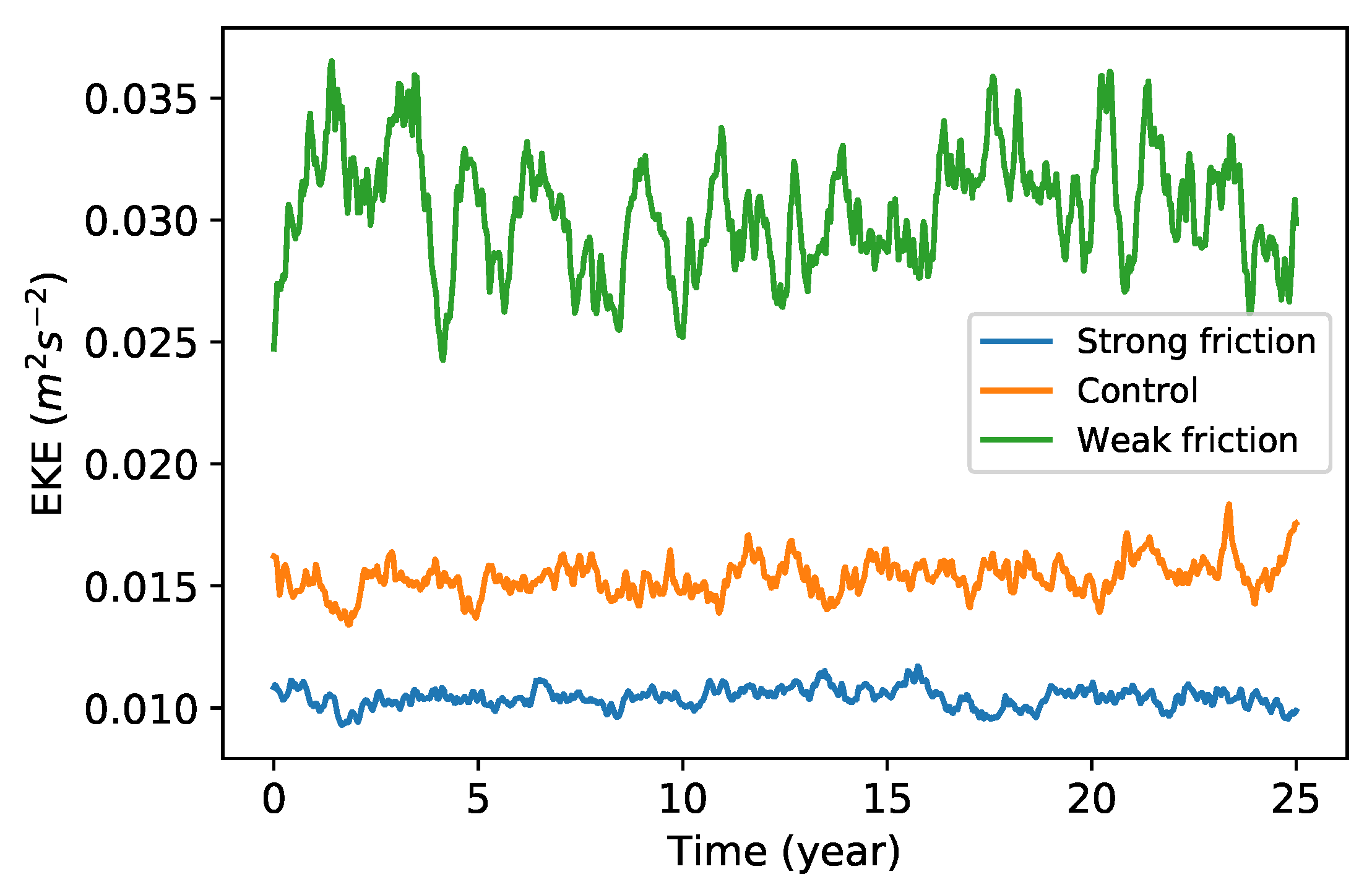
2.1. Model Description
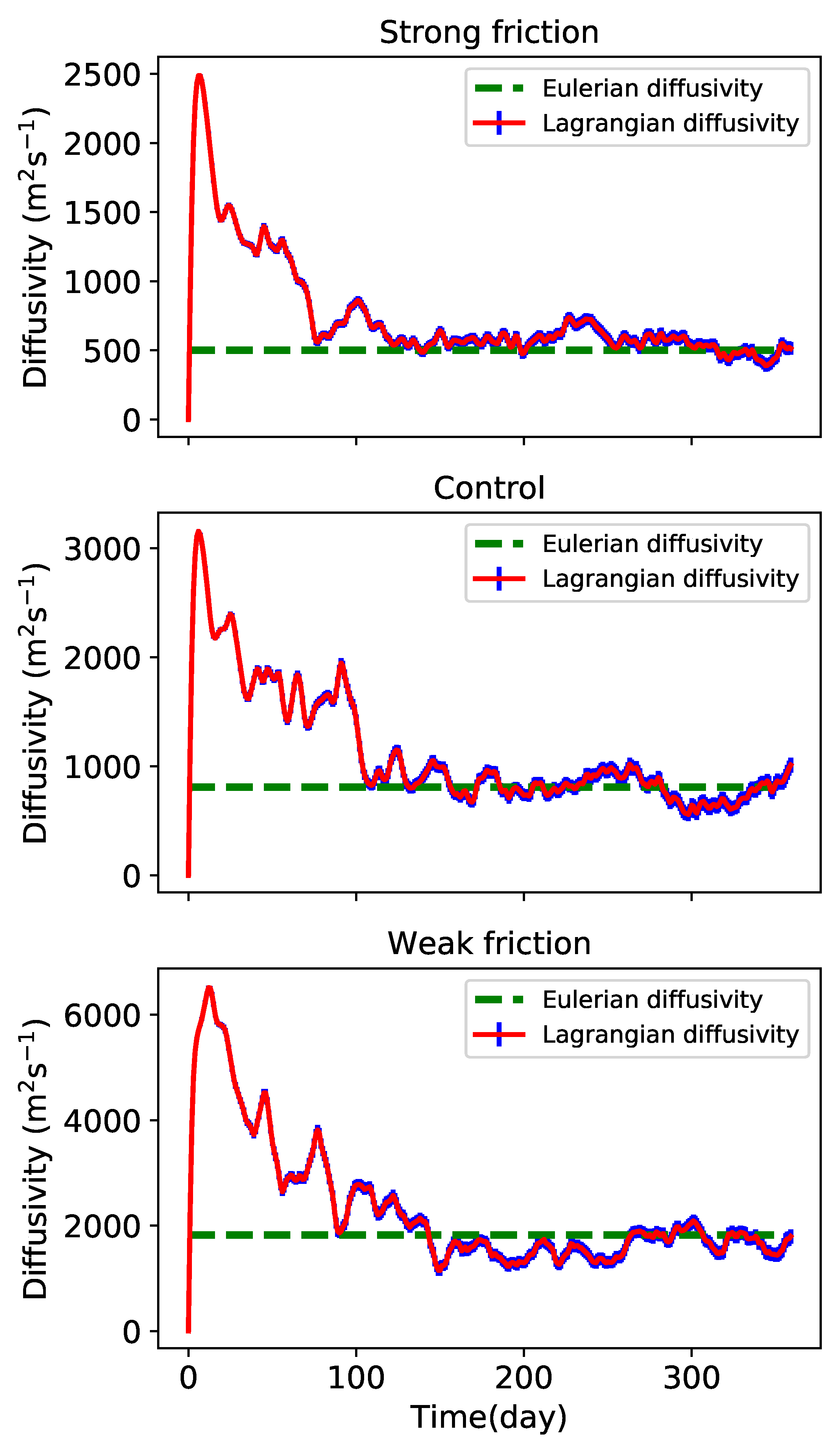
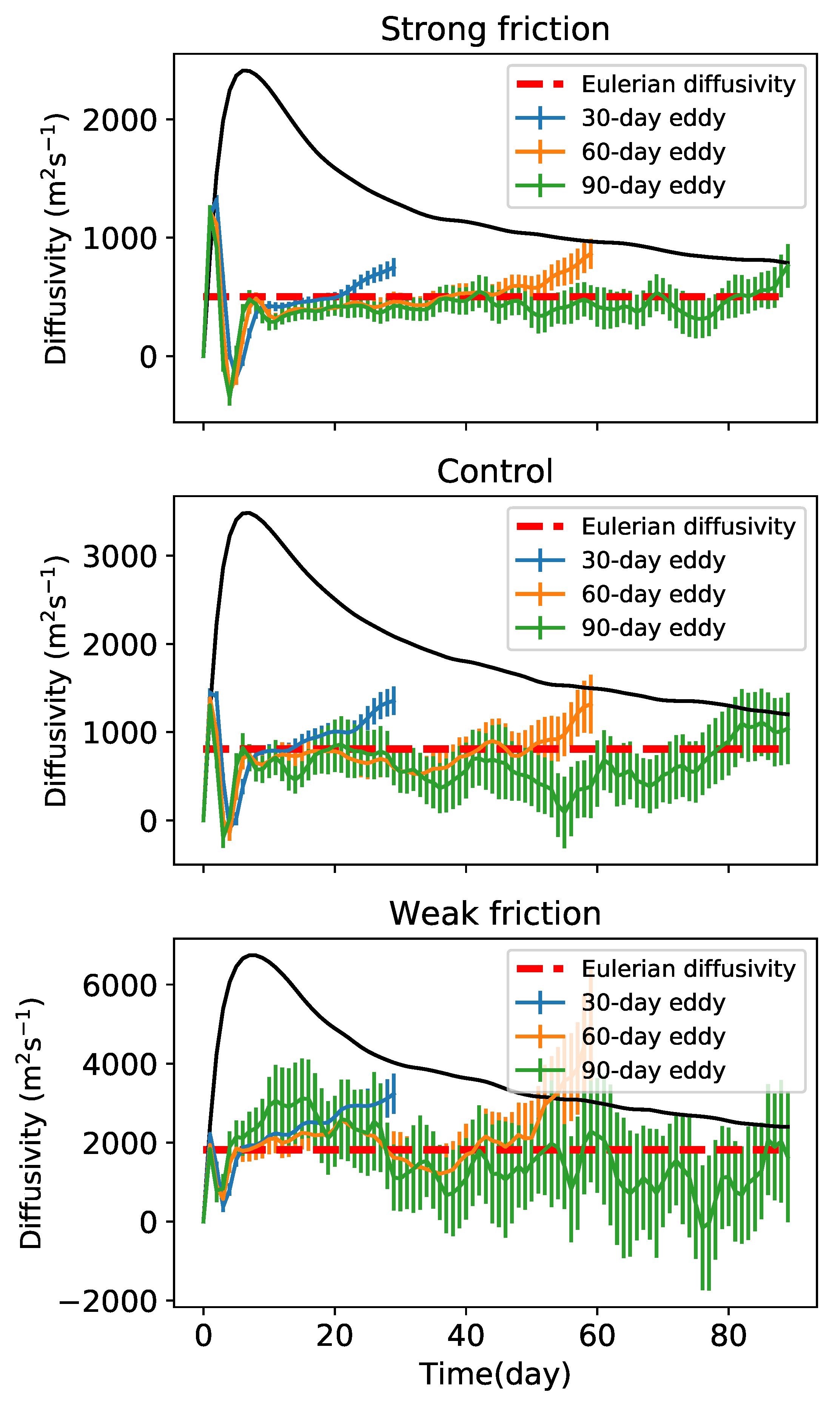
2.2. Lagrangian Particle Advection and Lagrangian Diffusivity
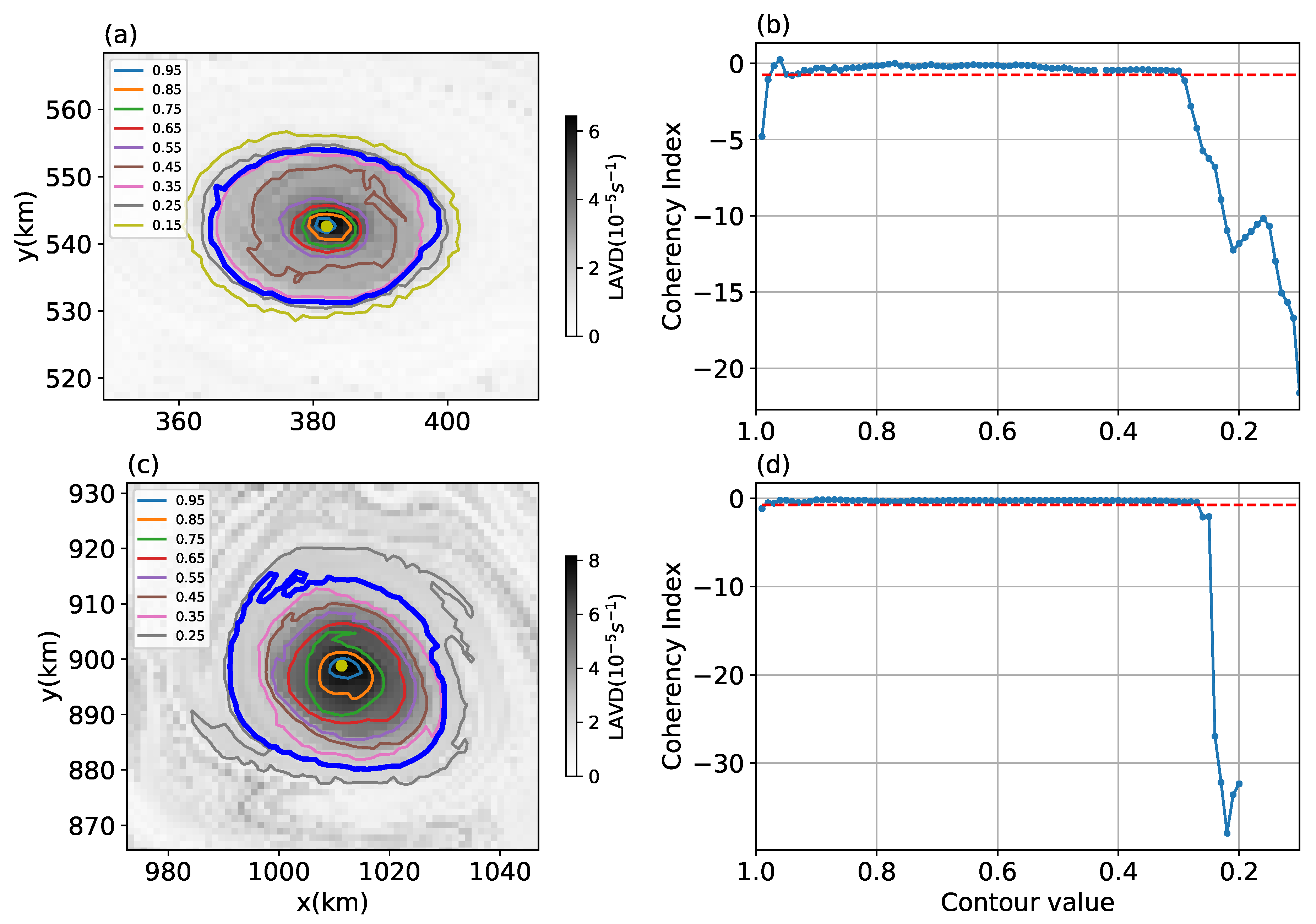
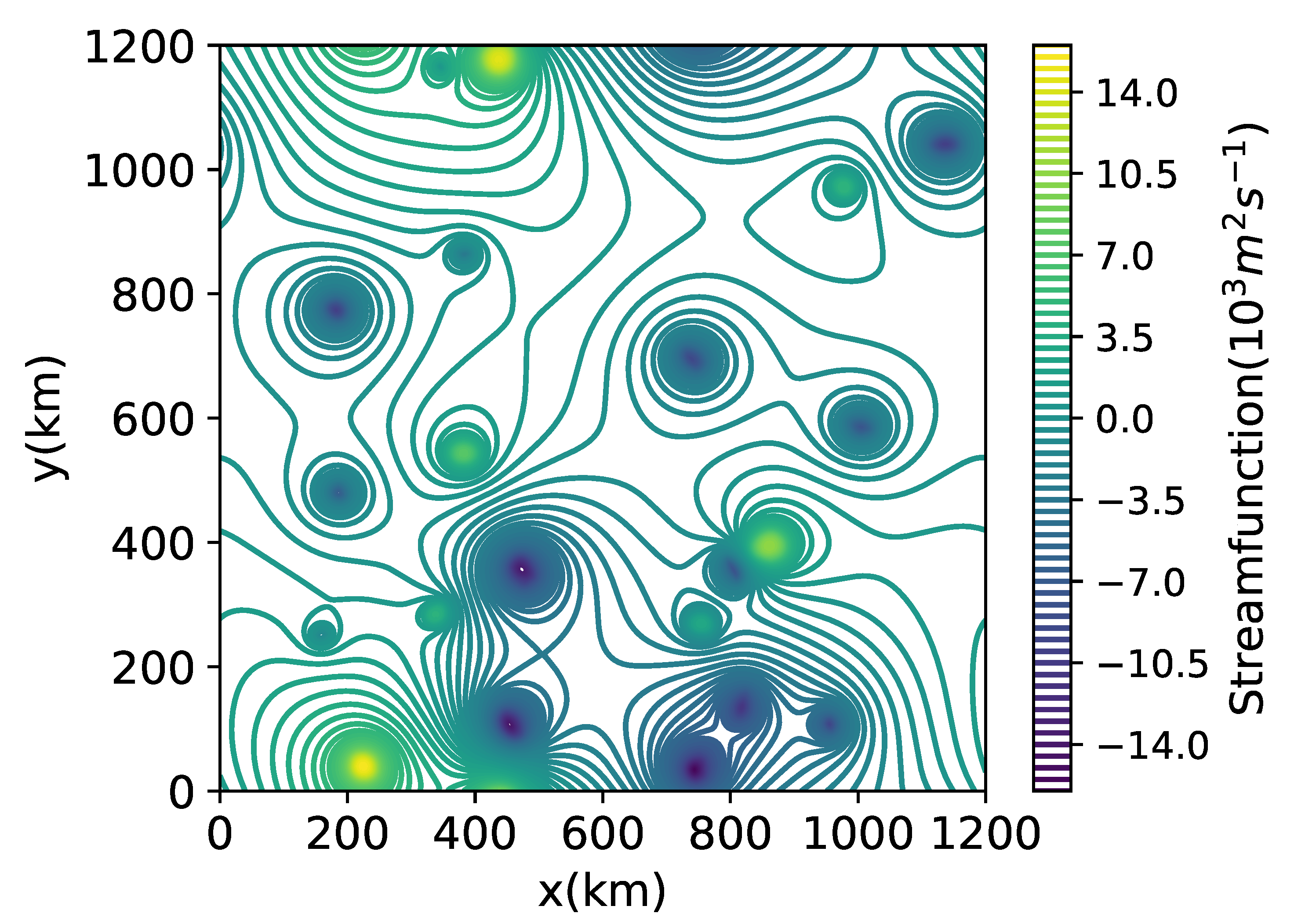
2.3. Identification of Coherent Eddies
- Identify all the LAVD maxima with a minimum separation of 20 pixels (minimum separation suggested by Tarshish et al. [38]).
- Search from each maximum in LAVD for the outermost LAVD contour satisfying CI using the bisection method with an initial contour level of 0.36 times the LAVD value of the maximum.
- Remove eddies containing fewer than 200 particles (approximately equivalent to an area of 274 ).
3. Eddy Statistics
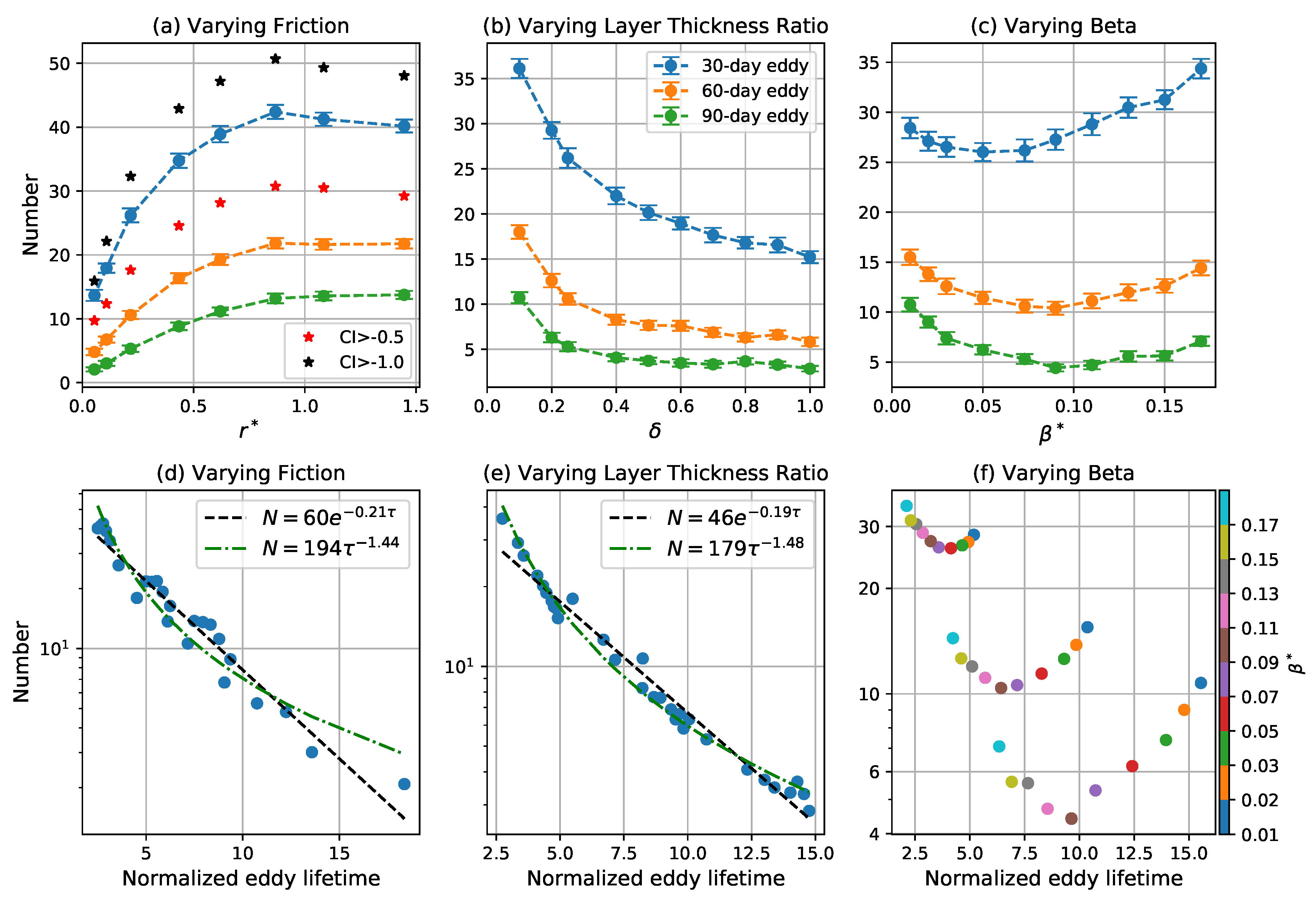
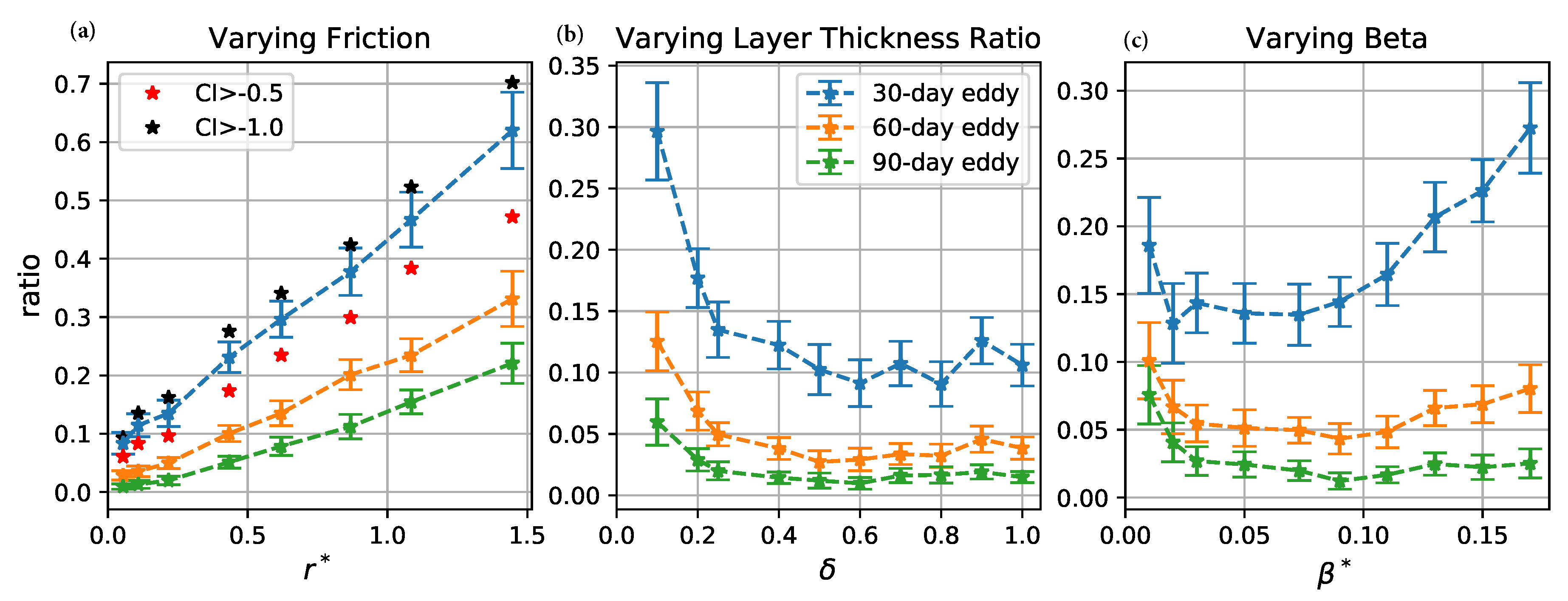
3.1. Occurrence Frequency of Coherent Eddies
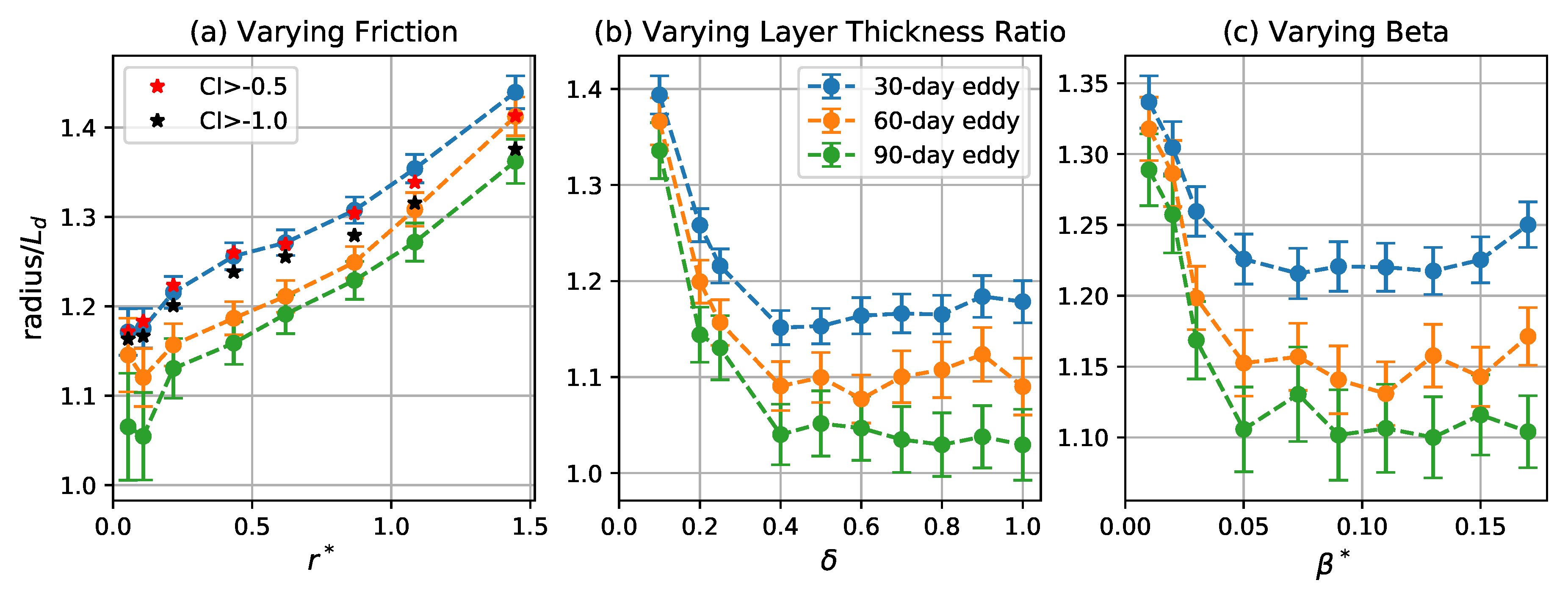
3.2. Eddy Radius Distribution
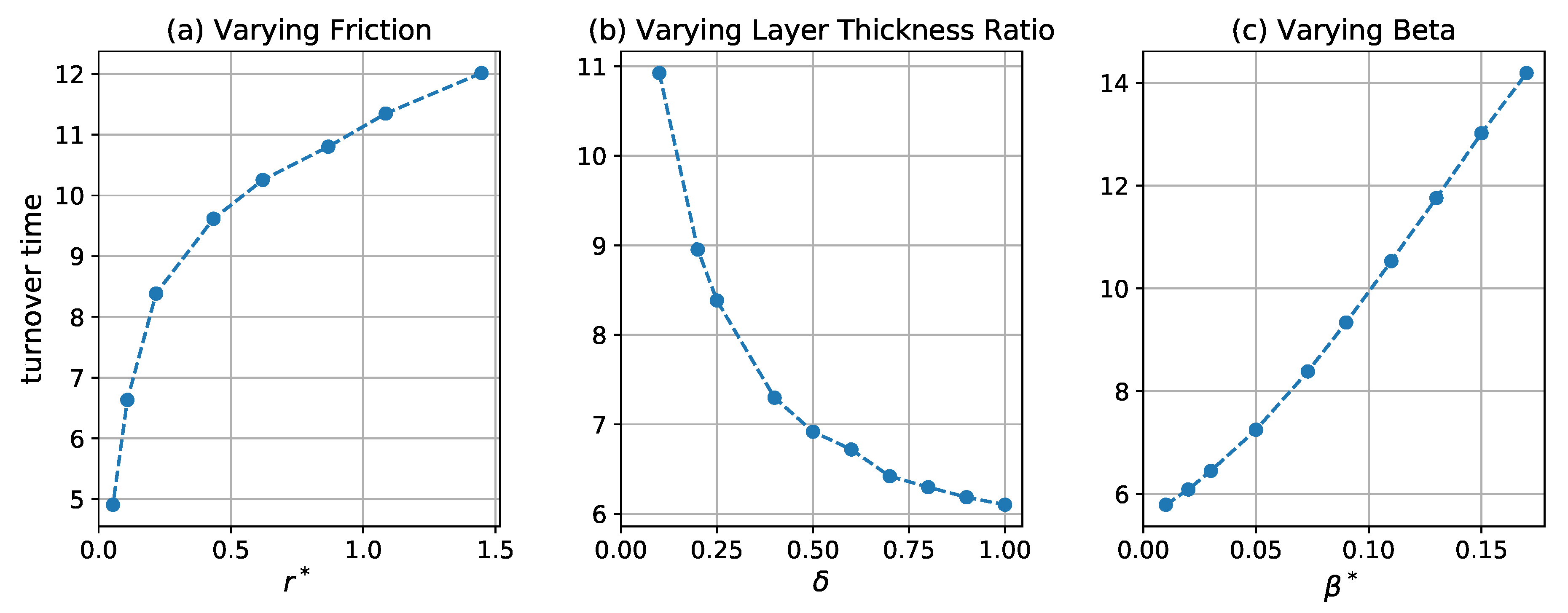
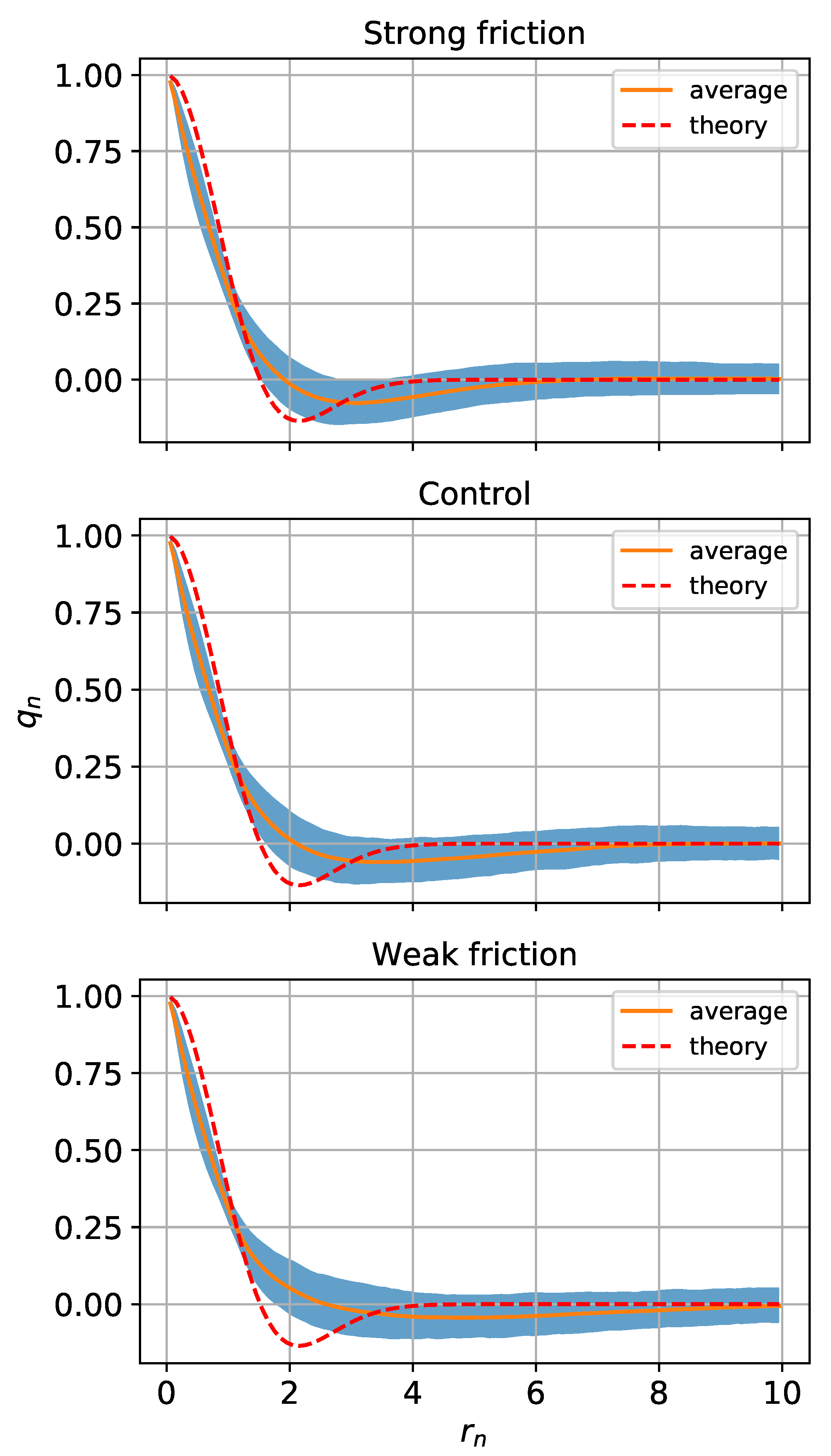
3.3. Radial Structure
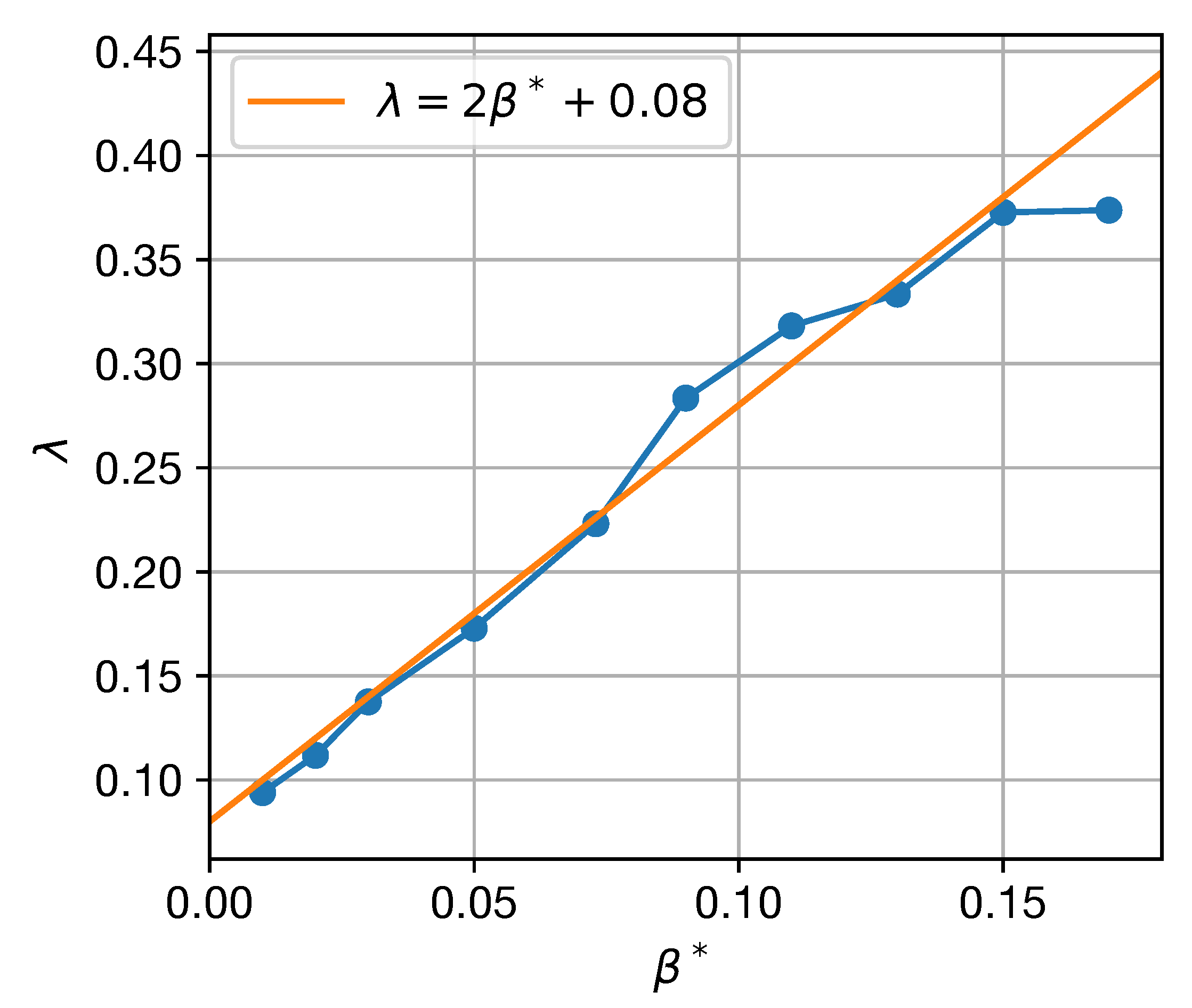
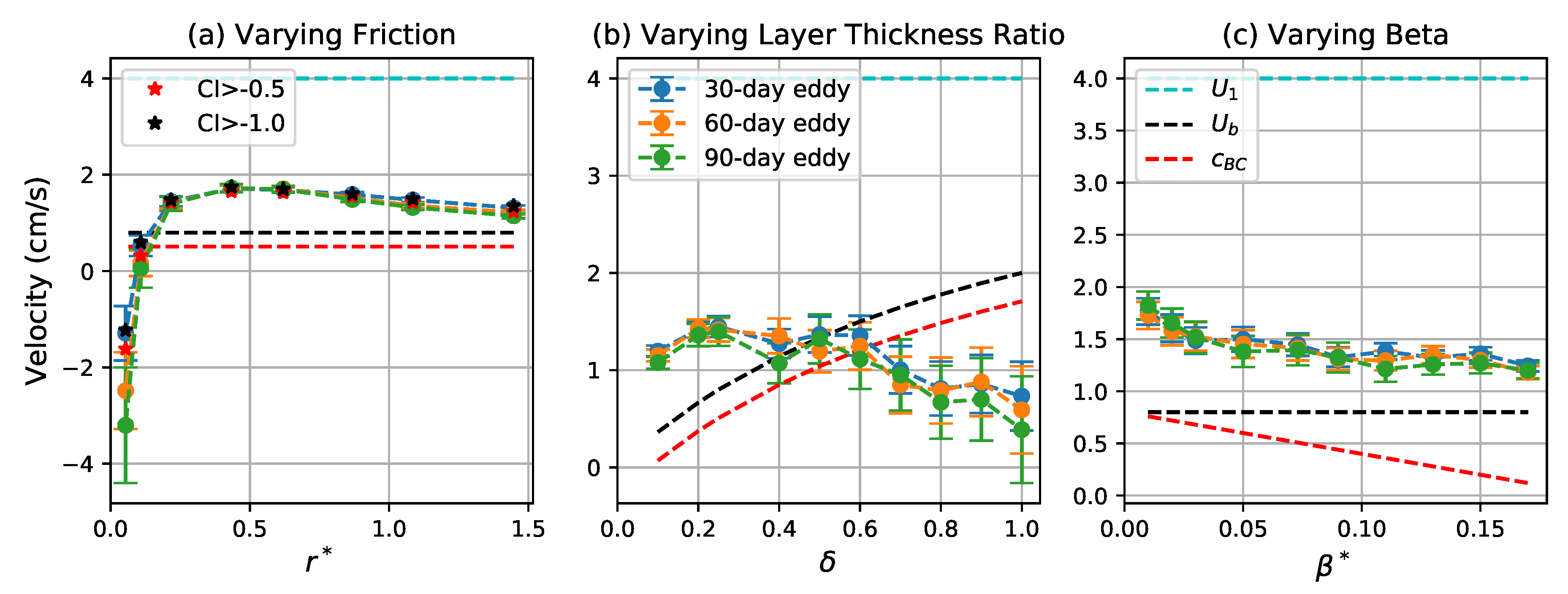
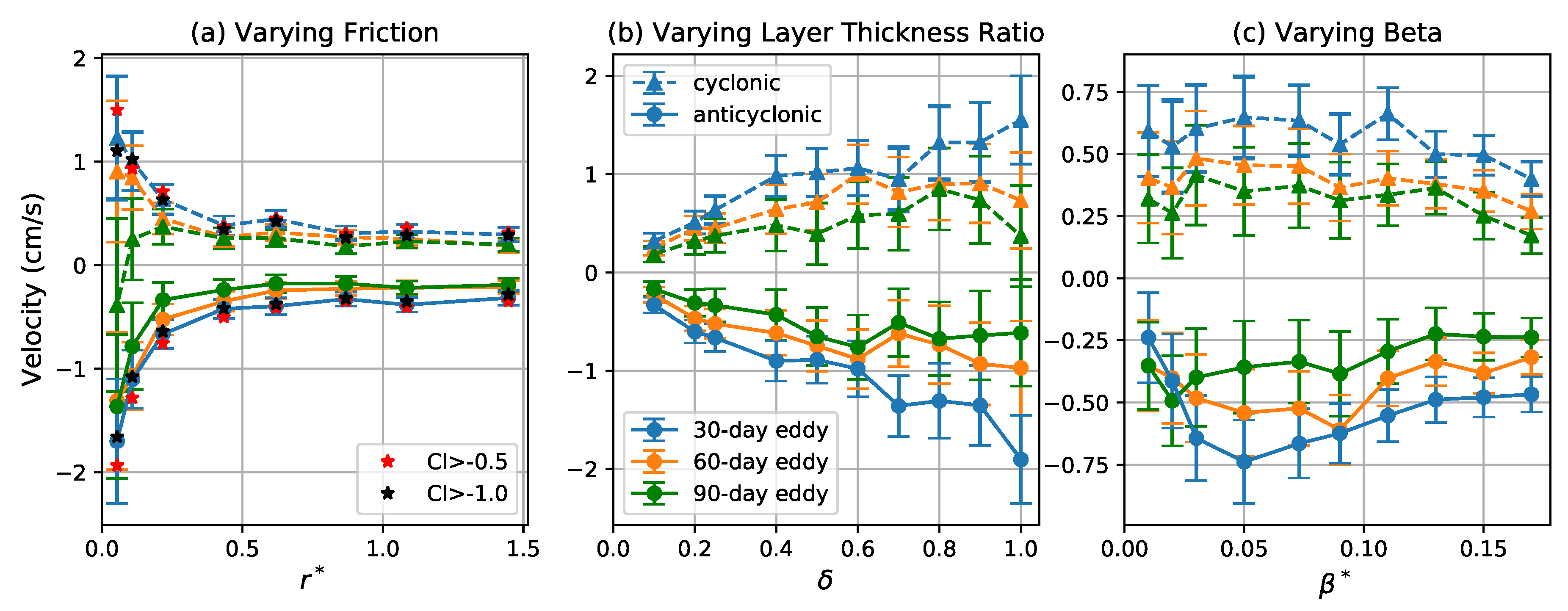
3.4. Eddy Propagation
3.4.1. Zonal Propagation
3.4.2. Meridional Propagation
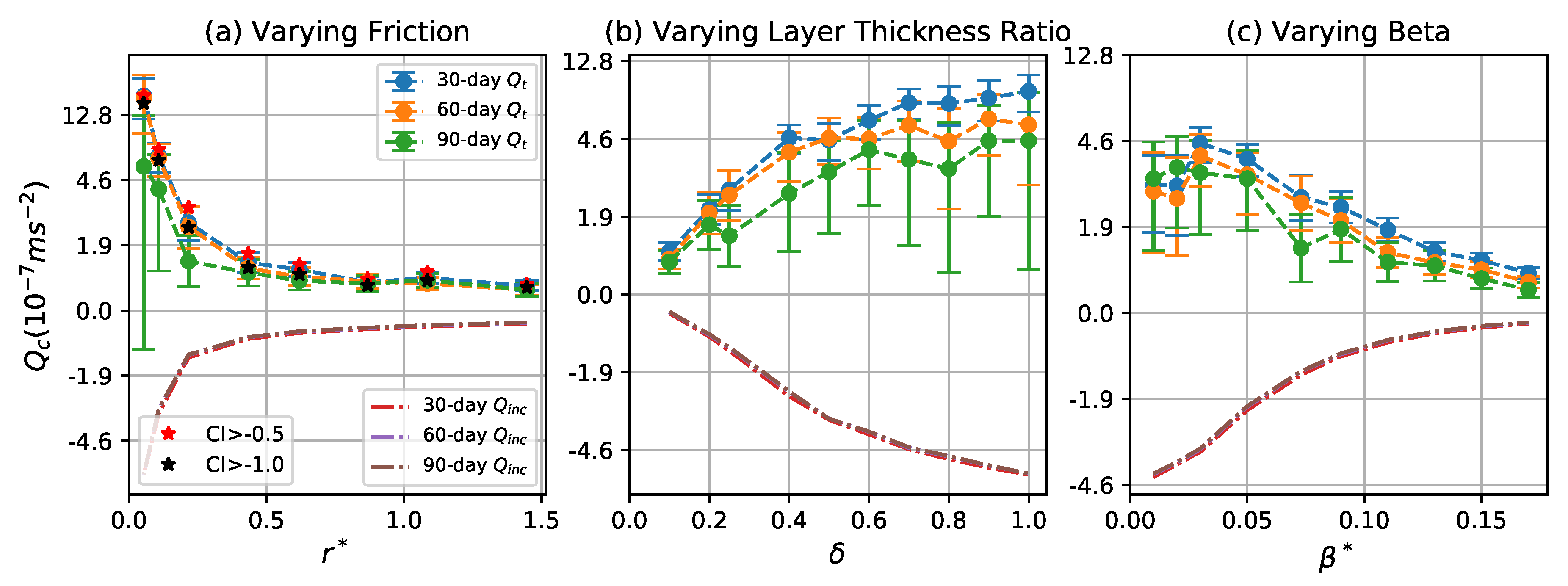
4. PV Transport by Coherent Eddies
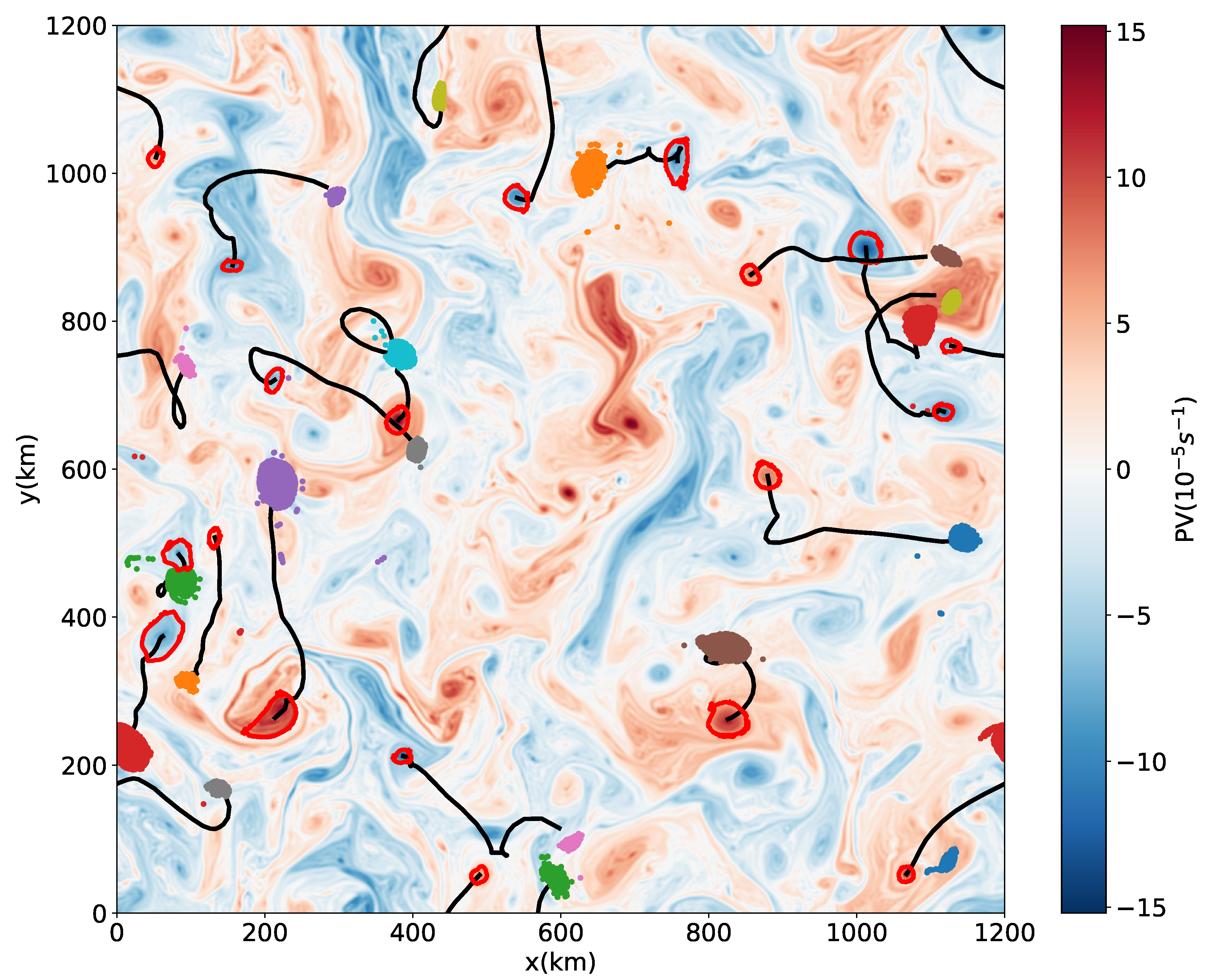
4.1. Transport by Trapping
4.2. Transport by Stirring
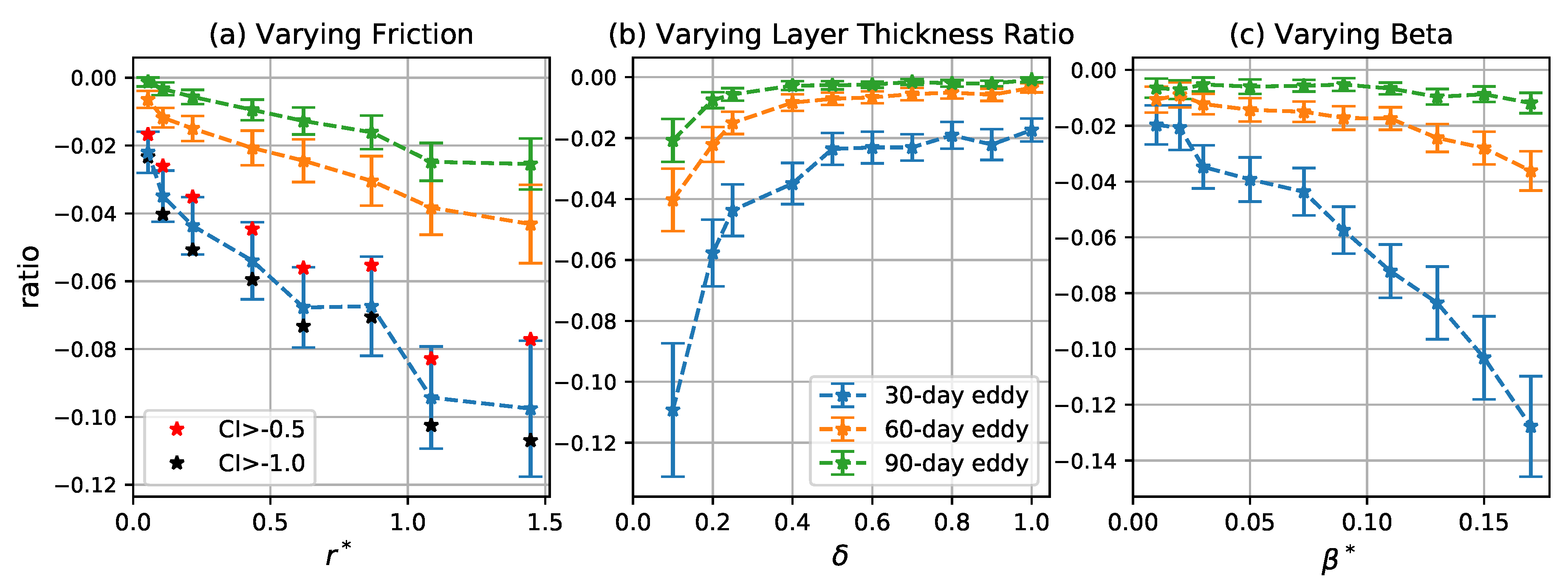
5. Tracer Transport by Coherent Eddies
6. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| LAVD | Lagrangian-averaged vorticity deviation |
| PV | potential vorticity |
| RCLV | rotationally-coherent Lagrangian vortex |
| QG | quasigeostrophic |
| EKE | eddy kinetic energy |
| CI | coherency Index |
| PPVI | piecewise PV inversion |
| NSF | National Science Foundation |
References
- Hallberg, R.; Gnanadesikan, A. The role of eddies in determining the structure and response of the wind-driven Southern Hemisphere overturning: Results from the Modeling Eddies in the Southern Ocean (MESO) project. J. Phys. Oceanogr. 2006, 36, 2232–2252. [Google Scholar] [CrossRef]
- Marshall, J.; Radko, T. Residual-mean solutions for the Antarctic Circumpolar Current and its associated overturning circulation. J. Phys. Oceanogr. 2003, 33, 2341–2354. [Google Scholar] [CrossRef]
- Marshall, J.; Radko, T. A model of the upper branch of the meridional overturning of the Southern Ocean. Prog. Oceanogr. 2006, 70, 331–345. [Google Scholar] [CrossRef]
- Wolfe, C.L.; Cessi, P. Overturning circulation in an eddy-resolving model: The effect of the pole-to-pole temperature gradient. J. Phys. Oceanogr. 2009, 39, 125–142. [Google Scholar] [CrossRef][Green Version]
- Wolfe, C.L.; Cessi, P. What sets the strength of the middepth stratification and overturning circulation in eddying ocean models? J. Phys. Oceanogr. 2010, 40, 1520–1538. [Google Scholar] [CrossRef]
- Griffiths, R.; Pearce, A. Satellite images of an unstable warm eddy derived from the Leeuwin Current. Deep Sea Res. Part A. Oceanogr. Res. Pap. 1985, 32, 1371–1380. [Google Scholar] [CrossRef]
- Fang, F.; Morrow, R. Evolution, movement and decay of warm-core Leeuwin Current eddies. Deep Sea Res. Part II Top. Stud. Oceanogr. 2003, 50, 2245–2261. [Google Scholar] [CrossRef]
- Kurian, J.; Colas, F.; Capet, X.; McWilliams, J.C.; Chelton, D.B. Eddy properties in the California Current System. J. Geophys. Res. Ocean. 2011, 116, C08027. [Google Scholar] [CrossRef]
- Cessi, P.; Wolfe, C.L. Eddy-driven buoyancy gradients on eastern boundaries and their role in the thermocline. J. Phys. Oceanogr. 2009, 39, 1595–1614. [Google Scholar] [CrossRef]
- Colas, F.; Capet, X.; McWilliams, J.C.; Li, Z. Mesoscale eddy buoyancy flux and eddy-induced circulation in Eastern Boundary Currents. J. Phys. Oceanogr. 2013, 43, 1073–1095. [Google Scholar] [CrossRef]
- Pelland, N.A.; Eriksen, C.C.; Lee, C.M. Subthermocline eddies over the Washington continental slope as observed by Seagliders, 2003–09. J. Phys. Oceanogr. 2013, 43, 2025–2053. [Google Scholar] [CrossRef]
- Bire, S.; Wolfe, C.L. The role of eddies in buoyancy-driven eastern boundary currents. J. Phys. Oceanogr. 2018, 48, 2829–2850. [Google Scholar] [CrossRef]
- Steinberg, J.M.; Pelland, N.A.; Eriksen, C.C. Observed evolution of a California Undercurrent eddy. J. Phys. Oceanogr. 2019, 49, 649–674. [Google Scholar] [CrossRef]
- McGillicuddy, D., Jr.; Anderson, L.; Doney, S.; Maltrud, M. Eddy-driven sources and sinks of nutrients in the upper ocean: Results from a 0.1∘ resolution model of the North Atlantic. Glob. Biogeochem. Cycles 2003, 17, 1035. [Google Scholar] [CrossRef]
- Siegenthaler, U. Uptake of excess CO2 by an outcrop-diffusion model of the ocean. J. Geophys. Res. Ocean. 1983, 88, 3599–3608. [Google Scholar] [CrossRef]
- Gnanadesikan, A.; Pradal, M.A.; Abernathey, R. Isopycnal mixing by mesoscale eddies significantly impacts oceanic anthropogenic carbon uptake. Geophys. Res. Lett. 2015, 42, 4249–4255. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, W.; Qiu, B. Oceanic mass transport by mesoscale eddies. Science 2014, 345, 322–324. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Wang, W. Three-compartment structure of subsurface-intensified mesoscale eddies in the ocean. J. Geophys. Res. Ocean. 2017, 122, 1653–1664. [Google Scholar] [CrossRef]
- McWilliams, J.C. The emergence of isolated coherent vortices in turbulent flow. J. Fluid Mech. 1984, 146, 21–43. [Google Scholar] [CrossRef]
- Provenzale, A. Transport by coherent barotropic vortices. Annu. Rev. Fluid Mech. 1999, 31, 55–93. [Google Scholar] [CrossRef]
- Bracco, A.; LaCasce, J.; Pasquero, C.; Provenzale, A. The velocity distribution of barotropic turbulence. Phys. Fluids 2000, 12, 2478–2488. [Google Scholar] [CrossRef][Green Version]
- Berloff, P.S.; McWilliams, J.C.; Bracco, A. Material transport in oceanic gyres. Part I: Phenomenology. J. Phys. Oceanogr. 2002, 32, 764–796. [Google Scholar] [CrossRef]
- Pasquero, C.; Provenzale, A.; Babiano, A. Parameterization of dispersion in two-dimensional turbulence. J. Fluid Mech. 2001, 439, 279–303. [Google Scholar] [CrossRef]
- Thompson, A.F.; Young, W.R. Scaling baroclinic eddy fluxes: Vortices and energy balance. J. Phys. Oceanogr. 2006, 36, 720–738. [Google Scholar] [CrossRef]
- Berloff, P.S.; McWilliams, J.C. Material transport in oceanic gyres. Part II: Hierarchy of stochastic models. J. Phys. Oceanogr. 2002, 32, 797–830. [Google Scholar] [CrossRef]
- Dong, C.; McWilliams, J.C.; Liu, Y.; Chen, D. Global heat and salt transports by eddy movement. Nat. Commun. 2014, 5, 3294. [Google Scholar] [CrossRef]
- Haller, G. An objective definition of a vortex. J. Fluid Mech. 2005, 525, 1–26. [Google Scholar] [CrossRef]
- Beron-Vera, F.J.; Wang, Y.; Olascoaga, M.J.; Goni, G.J.; Haller, G. Objective detection of oceanic eddies and the Agulhas leakage. J. Phys. Oceanogr. 2013, 43, 1426–1438. [Google Scholar] [CrossRef]
- Haller, G.; Beron-Vera, F.J. Coherent Lagrangian vortices: The black holes of turbulence. J. Fluid Mech. 2013, 731, R4. [Google Scholar] [CrossRef]
- Wang, Y.; Olascoaga, M.J.; Beron-Vera, F.J. Coherent water transport across the South Atlantic. Geophys. Res. Lett. 2015, 42, 4072–4079. [Google Scholar] [CrossRef]
- Haller, G.; Hadjighasem, A.; Farazmand, M.; Huhn, F. Defining coherent vortices objectively from the vorticity. J. Fluid Mech. 2016, 795, 136–173. [Google Scholar] [CrossRef]
- Hadjighasem, A.; Farazmand, M.; Blazevski, D.; Froyland, G.; Haller, G. A critical comparison of Lagrangian methods for coherent structure detection. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 053104. [Google Scholar] [CrossRef] [PubMed]
- Abernathey, R.; Haller, G. Transport by Lagrangian vortices in the eastern Pacific. J. Phys. Oceanogr. 2018, 48, 667–685. [Google Scholar] [CrossRef]
- Abernathey, R.P.; Marshall, J. Global surface eddy diffusivities derived from satellite altimetry. J. Geophys. Res. Oceans 2013, 118, 901–916. [Google Scholar] [CrossRef]
- Klocker, A.; Abernathey, R. Global patterns of mesoscale eddy properties and diffusivities. J. Phys. Oceanogr. 2014, 44, 1030–1046. [Google Scholar] [CrossRef]
- Wang, Y.; Beron-Vera, F.J.; Olascoaga, M.J. The life cycle of a coherent Lagrangian Agulhas ring. J. Geophys. Res. Oceans 2016, 121, 3944–3954. [Google Scholar] [CrossRef]
- Tarshish, N.; Abernathey, R.; Zhang, C.; Dufour, C.O.; Frenger, I.; Griffies, S.M. Identifying Lagrangian coherent vortices in a mesoscale ocean model. Ocean Model. 2018, 130, 15–28. [Google Scholar] [CrossRef]
- Spall, M.A. Generation of strong mesoscale eddies by weak ocean gyres. J. Mar. Res. 2000, 58, 97–116. [Google Scholar] [CrossRef]
- Arbic, B.K.; Flierl, G.R. Effects of mean flow direction on energy, isotropy, and coherence of baroclinically unstable beta-plane geostrophic turbulence. J. Phys. Oceanogr. 2004, 34, 77–93. [Google Scholar] [CrossRef]
- Abernathey, R.; Rocha, C.B.; Poulin, F.J.; Jansen, M.; Penn, J. pyqg: v0.2.0. 2016. Available online: https://zenodo.org/record/50569#.Xfwj6Px5vIU (accessed on 14 March 2019).
- Arbic, B.K.; Flierl, G.R. Baroclinically unstable geostrophic turbulence in the limits of strong and weak bottom Ekman friction: Application to midocean eddies. J. Phys. Oceanogr. 2004, 34, 2257–2273. [Google Scholar] [CrossRef]
- Wang, L.; Jansen, M.; Abernathey, R. Eddy phase speeds in a two-layer model of quasigeostrophic baroclinic turbulence with applications to ocean observations. J. Phys. Oceanogr. 2016, 46, 1963–1985. [Google Scholar] [CrossRef]
- Taylor, G.I. Diffusion by continuous movements. Proc. Lond. Math. Soc. 1922, 2, 196–212. [Google Scholar] [CrossRef]
- Abernathey, R. Floater. 2018. Available online: https://github.com/rabernat/floater (accessed on 1 April 2019).
- McWilliams, J.C.; Flierl, G.R. On the evolution of isolated, nonlinear vortices. J. Phys. Oceanogr. 1979, 9, 1155–1182. [Google Scholar] [CrossRef]
- Flierl, G.R. Rossby Wave Radiation from a Strongly Nonlinear Warm Eddy. J. Phys. Oceanogr. 1984, 14, 47–58. [Google Scholar] [CrossRef]
- Sutyrin, G.G.; Hesthaven, J.S.; Lynov, J.P.; Rasmussen, J.J. Dynamical properties of vortical structures on the beta-plane. J. Fluid Mech. 1994, 268, 103–131. [Google Scholar] [CrossRef]
- Korataev, G.K. Radiating Vorticies in Geophysical Fluid Dynamics. Surv. Geophys. 1997, 18, 567–619. [Google Scholar] [CrossRef]
- Early, J.J.; Samelson, R.; Chelton, D.B. The evolution and propagation of quasigeostrophic ocean eddies. J. Phys. Oceanogr. 2011, 41, 1535–1555. [Google Scholar] [CrossRef]
- Rhines, P.B. Waves and turbulence on a beta-plane. J. Fluid Mech. 1975, 69, 417–443. [Google Scholar] [CrossRef]
- Taylor, G. On the dissipation of eddies. In Meteorology, Oceanography and Turbulent Flow; Cambridge University Press: Cambridge, UK, 1918; pp. 96–101. [Google Scholar]
- Trieling, R.; Van Heijst, G. Decay of monopolar vortices in a stratified fluid. Fluid Dyn. Res. 1998, 23, 27. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Wang, W.; Huang, R. Universal structure of mesoscale eddies in the ocean. Geophys. Res. Lett. 2013, 40, 3677–3681. [Google Scholar] [CrossRef]
- Cushman-Roisin, B.; Beckers, J.M. Introduction to Geophysical Fluid Dynamics: Physical and Numerical Aspects; Academic Press: Waltham, MA, USA, 2011; Volume 101. [Google Scholar]
- Rossby, C.G. On a mechanism for the release of potential energy in the atmosphere. J. Meteorol. 1949, 6, 164–180. [Google Scholar] [CrossRef][Green Version]
- Thompson, A.F.; Young, W.R. Two-layer baroclinic eddy heat fluxes: Zonal flows and energy balance. J. Atmos. Sci. 2007, 64, 3214–3231. [Google Scholar] [CrossRef]
- Marshall, J. Eddy-mean-flow interaction in a barotropic ocean model. Q. J. R. Meteorol. Soc. 1984, 110, 573–590. [Google Scholar] [CrossRef]
- Holland, W.R.; Rhines, P.B. An example of eddy-induced ocean circulation. J. Phys. Oceanogr. 1980, 10, 1010–1031. [Google Scholar] [CrossRef]
- Provenzale, A.; Babiano, A.; Bracco, A.; Pasquero, C.; Weiss, J. Coherent vortices and tracer transport. In Transport and Mixing in Geophysical Flows; Springer: Berlin/Heidelberg, Germany, 2008; pp. 101–118. [Google Scholar]
- Hoskins, B.J.; McIntyre, M.E.; Robertson, A.W. On the use and significance of isentropic potential vorticity maps. Q. J. R. Meteorol. Soc. 1985, 111, 877–946. [Google Scholar] [CrossRef]
- Davis, C.A. Piecewise potential vorticity inversion. J. Atmos. Sci. 1992, 49, 1397–1411. [Google Scholar] [CrossRef]
- Egger, J. Piecewise potential vorticity inversion: Elementary tests. J. Atmos. Sci. 2008, 65, 2015–2024. [Google Scholar] [CrossRef]
- Eliassen, A.; Kleinschmidt, E. Dynamic meteorology. In Geophysik II/Geophysics II; Springer: Berlin/Heidelberg, Germany, 1957; pp. 1–154. [Google Scholar]
- Petersen, M.R.; Julien, K.; Weiss, J.B. Vortex cores, strain cells, and filaments in quasigeostrophic turbulence. Phys. Fluids 2006, 18, 026601. [Google Scholar] [CrossRef]
- Chen, R.; Waterman, S. Mixing Nonlocality and Mixing Anisotropy in an Idealized Western Boundary Current Jet. J. Phys. Oceanogr. 2017, 47, 3015–3036. [Google Scholar] [CrossRef]
- Berloff, P.; Karabasov, S.; Farrar, J.T.; Kamenkovich, I. On latency of multiple zonal jets in the oceans. J. Fluid Mech. 2011, 686, 534–567. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Wolfe, C.L.P.; Abernathey, R. Role of Surface-Layer Coherent Eddies in Potential Vorticity Transport in Quasigeostrophic Turbulence Driven by Eastward Shear. Fluids 2020, 5, 2. https://doi.org/10.3390/fluids5010002
Zhang W, Wolfe CLP, Abernathey R. Role of Surface-Layer Coherent Eddies in Potential Vorticity Transport in Quasigeostrophic Turbulence Driven by Eastward Shear. Fluids. 2020; 5(1):2. https://doi.org/10.3390/fluids5010002
Chicago/Turabian StyleZhang, Wenda, Christopher L. P. Wolfe, and Ryan Abernathey. 2020. "Role of Surface-Layer Coherent Eddies in Potential Vorticity Transport in Quasigeostrophic Turbulence Driven by Eastward Shear" Fluids 5, no. 1: 2. https://doi.org/10.3390/fluids5010002
APA StyleZhang, W., Wolfe, C. L. P., & Abernathey, R. (2020). Role of Surface-Layer Coherent Eddies in Potential Vorticity Transport in Quasigeostrophic Turbulence Driven by Eastward Shear. Fluids, 5(1), 2. https://doi.org/10.3390/fluids5010002




