1. Introduction
Permeability is an important macro parameter usually used to characterize porous media. This parameter is a measure of the resistance that fluid faces when flowing through a porous medium. Therefore, this parameter plays an essential role in a great variety of fields, such as soil mechanics, oil prospection, petrophysics, material characterization, etc. The permeability is usually determined in routine laboratory tests by simply applying Darcy’s law. However, laboratory tests can be complex, expensive, time-demanding, and sometimes destructive, and they do not offer a deep understanding of the internal microstructure of the material.
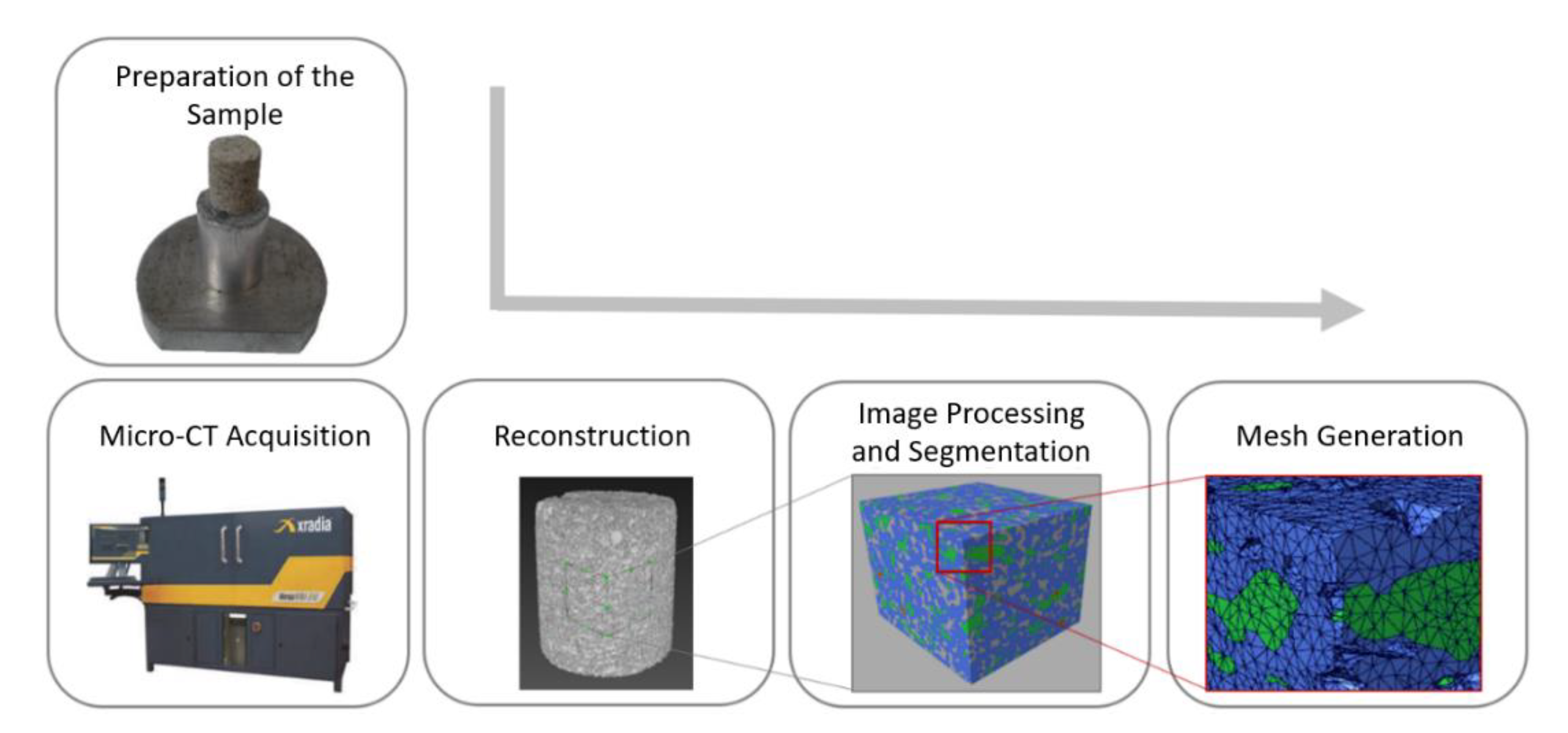
Computer simulations are increasingly applied as an alternative to laboratory tests due to their capability to overcome many difficulties presented in physical testing. Some of the advantages of numerical simulations are their non-destructive characteristic, low cost, ease of performing repeatable analyses, and possibility to perform analyses that cannot (or are very difficult to) be performed in experimental tests. In addition, it is also possible to run simulations on both synthetic and realistic models. Although synthetic models are simpler to be generated, they may introduce inaccuracies in the simulation due to the fact that they are an approximation of reality. Therefore, more accurate results are expected to be obtained with realistic models, which may be generated by means of imaging technologies on several scales (e.g., microcomputed tomography (micro-CT)). Considering those advantages, computational simulations based on numerical methods are an attractive alternative to assess the permeability of porous materials, since this methodology can consider the material internal structure through realistic virtual models.
The work of Andreassen and Andreasen [
1], Aarnes et al. [
2], Sheng and Zhi [
3], Akanji and Mattha [
4], and Yang et al. [
5] are some examples that illustrate the use of the finite element method (FEM), finite volume method, and lattice Boltzmann method to determine permeability through computational homogenization.
The development of computational codes to determine permeability of porous materials has several peculiarities. Finding documents in the literature that address the subtlety in programming this problem is not an easy task. In addition, most of the codes found in the literature have in common the fact that they usually focus on computational efficiency. This often leads to a lack of important steps for the understanding of the reader, who possibly does not have extensive experience with all the subjects involved in the process of permeability determination. Although the work of Andreassen and Andreasen [
1] may be partially included in this context, it presents one of the most relevant educational descriptions of the problem. They described a compact educational program, which adopts a set of interesting strategies, developed in MatLab. For these reasons, the work of Andreassen and Andreasen [
1] was used as a starting point and basic reference for the developments described in our paper.
The main objective of this paper is to present the step-by-step development and implementation of an educational program to determine the effective absolute permeability of porous materials based on the concepts of numerical homogenization. The program aims to determine the mean velocity field value in a single-phase fluid flowing through the connected pores of a given material. This flow is assumed to be governed by the Stokes equation, which is solved with FEM. The program also covers the implementation of periodic boundary conditions, in which the basic assumption is that the numerical model is a representative volume of a non-contoured (statistically homogeneous) medium. By didactic choice, the program was developed for two-dimensional (2D) cases, facilitating the understanding of students, but the extension for three-dimensional (3D) cases is almost straightforward. After program validation, the permeability of a real sandstone sample, modeled by microcomputed tomography, is performed. This paper is suggested as a use case in lectures and trainings for senior undergraduate and graduate students. Since it covers the application of fluid mechanics, numerical methods, and multiscale problems from both theoretical and practical perspectives, it can be a powerful tool when teaching subjects such as fluid dynamics, finite elements, petrophysics, and other classes.
2. Effective Permeability through Numerical Homogenization
The determination of permeability through material microstructure analysis is a multiscale problem. The determination of this macro parameter depends on the determination of the velocity field, which is a function of the material’s microstructure. This means that, to solve the permeability problem of a medium, it is necessary to solve the governing equations of the microscale. The connection between micro and macroscales must be done through homogenization techniques.
Computational homogenization techniques seek to determine relationships between the micro and the macrostructure of the material, which consist of the determination of the effective properties of representative elementary volumes (REV) by considering characteristics and properties of microscopic elements. For determining the effective permeability of a porous medium, a known pressure gradient or body force is applied to the material REV. Under this condition, a velocity field is induced in the domain. The homogenized effective property of the material
is defined as the relationship between the applied pressure gradient
or body force vector
, the fluid viscosity
µ, and the average velocities
at the macroscale, known as Darcy’s law (Ω denotes representative volume).
where
is the average velocity vector resulted from the microscopic scale, i.e.,
Darcy’s law, given by Equation (1), states that the total velocity (units of displacement by time, e.g., m/s) is equal to the product of the medium permeability (m2), the pressure gradient (unit of pressure per length, e.g., Pa/m), and the inverse of the fluid viscosity (Pa∙s).
Considering a two-dimensional problem, the matrix is obtained by two analyses, in which either a unit pressure gradient or a unit body force per direction is applied. The mean velocity vector determined in each analysis is equivalent to that column of matrix
related to the respective direction of the pressure gradient (or body force) applied in each case. To determine the velocity field in the problem domain, the governing equations of the problem must be solved through numerical methods, as described in the next section.
3. Computational Fluid Dynamics with Finite Element Method (FEM)
The continuity equation and the Navier-Stokes equation are the equations that govern the fluid flow problem for most cases of transport in porous medias. As the scale of the problem to be modeled reduces (e.g., nano scales), it is important to be aware that some effects may emerge in the system (e.g., capillarity, chemical interaction). However, this work focuses on viscous fluids at a scale of micrometers; therefore, it can be considered that there is no other effect than those that the Navier-Stokes equation is capable of contemplating. As this work aims to evaluate low-speed incompressible viscous flows only, the convective effects may be neglected (due to low Reynold’s number) and, therefore, the Navier-Stokes equation is reduced to the Stokes equation. Although this simplifies the problem, for the great majority of practical applications, these differential equations that govern the problem still have no analytical solution; thus, numerical methods such as the finite element method (FEM) are employed as an essential tool to obtain reliable and approximate solutions.
The FEM proposes to approximate the problem solution by a finite set of elements connected by a finite number of points (commonly called nodes). The collection of finite elements that represents the continuous space is commonly called the discretized domain. Unlike the continuous domain, in the discretized domain, the variables are calculated only in the nodes of the finite elements. The continuous domain of the problem is represented by interpolation functions, called shape functions, which interpolate the calculated variables at the element nodes.
One of the FEM basic requirements is to transform the differential form (strong form) of the governing equations of the problem into integral equations (weak form). This process can be done by applying the weighted residual method, which allows the exact solution of the problem to be approximated by one with null residuals if integrated in the domain of interest. Therefore, the boundary value problem of the continuous medium can be solved by the mean values of a defined range.
The governing equations of the incompressible Stokes flow problem arise from conservation of linear momentum and conservation of mass, which are expressed, in a closed domain Ω, by Equations (3) and (4), respectively.
where
µ is the viscosity,
is the velocity vector,
p represents the pressure, and
represents the body force. Note that Equation (4) represents the mass continuity equation simplified to incompressible flows, i.e., the density is assumed to be constant (independent of space and time) and the conservation of mass is simplified to the equation of conservation of volume. That assumption is possible because the permeability of porous media is mostly determined in steady-state flow, in which the compressibility effect can be ignored (Akanji and Mattha [
4]).
The solution of a Stokes flow problem requires the specification of boundary conditions in addition to Equations (3) and (4). As mentioned before, there are basically two ways to compute the average velocity field in order to determine the permeability. It is either by applying a known pressure gradient as boundary conditions or by simply applying known body forces in the domain. The latter approach was chosen because applying domain quantities (such as body forces) instead of applying boundary conditions is the simplest and the most natural choice when using a domain-based discretization procedure such as the FEM to compute the velocity fields.
By applying the weighted residual method, the governing equations are multiplied by continuous and differentiable weight functions
. The sum of residues generated by the approximation is considered null within a defined range, resulting in
Using the divergence theorem in the first term of the integral in Equation (5) in combination with the compact support of
, i.e., the vanishing boundary integrals, yields
Different weight functions can be used in the weighted residual method. One of the most common strategies is to assign to the weight functions the interpolation functions of the nodal values, i.e., the shape functions. This method is known as the Galerkin method. The matrix of shape functions is called
N. In classical formulations of the FEM, there arises a matrix whose elements contain derivatives of the shape functions, known as the
B matrix. These matrices establish the following relationships:
where the values
and
represent the nodal values of
u and
p, respectively, and
L is the matrix of the differential operators.
According to Reddy [
4], in order to make an analogy with the virtual powers principle, the weight function vector
presented in Equation (5) can be understood as virtual velocities taken by
u; therefore,
. The weight function
presented in Equation (6) is associated with the volume change of the fluid element; thus, it should be understood as a virtual hydrostatic pressure that causes this volume variation. That way, we define
.
Applying Equations (8)–(10) and the chosen weight functions to Equations (6) and (7), the weak form of the governing equations can be represented as functions of matrices
B and
N. Equations (7) and (6) should be respectively rewritten, in the element domain, as follows:
As the nodal weight values are arbitrary, the terms in the parentheses of Equations (11) and (12) should vanish, resulting in
The terms on the right-hand side of the conservation of momentum equations are the result of the effect of the body forces in each element, called f.
Finally, solving the partial differential Equations (3) and (4) with the application of FEM is simplified to solve the following system of linear algebraic equations:
where
K is the viscosity matrix,
G is the gradient matrix,
and
D is the velocity divergent matrix and is equal to the transpose of
G matrix,
The above model is known as mixed formulation. By mixed formulation, it explains that both pressure and velocity are unknown variables. Considering that, usually, fluid dynamic problems have boundary conditions in terms of both velocity and pressure, it becomes the most intuitive formulation to be used. However, the coupling of velocity and pressure variables brings new difficulties to the resolution of the system of algebraic equations.
According to Reddy [
6], one way to interpret the coupling between velocity and pressure is to understand the continuity equation as a constraint of incompressibility to momentum conservation equations. Due to the fact that the incompressibility constraint does not depend on pressure variables, constructing a finite element model becomes complicated. The direct solution of the system cannot be performed since the coefficient matrix that multiplies the variable vector has a sub-matrix with a diagonal of null coefficients, which makes the coefficient matrix singular and non-inversible. Thus, it is necessary to use other strategies to solve the equation system.
Another common difficulty of mixed formulation is the choice of shape functions. The relationship between the second derivative of the velocity field and the first derivative of the pressure field stated in the Stokes equation shows that the velocity field must have a greater degree than the pressure field. The use of equal-order approximation functions for both pressure and velocity fields generates instability. This instability can be explained by the solvability analysis of the equation system. The solvability of a linear system is explained by several authors as the guarantee of the inf-sup condition, also known as the LBB condition, thanks to the works of Ladyzhenskaya [
7], Babuska [
8], and Brezzi [
9]. According to Elman et al., the inf-sup condition is a sufficient condition for the unique solvability of linear systems of equations in the form of Equation (15). Satisfying the inf-sup condition for Equation (15) will guarantee a unique pressure in a closed domain flow.
The use of approximation functions of the same order does not guarantee the inf-sup condition. Therefore, it does not ensure a unique solution for the problem, and the generated results may be non-reliable Hence, finding a system with unique solution requires the use of other methods to approximate the velocity and pressure fields.
Other approximation methods that are recommended for mixed formulation are found in the literature. Elman et al. [
10] and Bathe [
11] cited the following approximations as satisfactory for the inf-sup condition: Q2-Q1 approximation (bi-quadratic approximation for velocity and bi-linear approximation for pressure), also known as the Taylor-Hood method, Q2-P1 approximation (bi-quadratic approximation for velocity and linear approximation for pressure in each element without guaranteeing continuity), and Q2-P0 approximation (bi-quadratic approximation for velocity and constant for pressure in each element).
However, using same-order shape functions to interpolate pressure and velocity fields has several advantages from a computational perspective. In order to use same-order shape functions for velocity and pressure fields, and to eliminate instability, stabilization techniques can be adopted. Stabilization techniques have the basic idea of relaxing the restriction of incompressibility, ensuring the inf-sup condition. Many authors proposed different methodologies that proved to be very efficient in stabilizing different approximation models.
One of the simplest discretization methodologies is the use of bi-linear form functions for the velocity and pressure domains. This type of approximation is known as Q1-Q1 approximation. The Q1-Q1 approximation, in addition to being easy to implement, produces lower computational cost for solving the system of equations. For this reason, many authors seek to use stabilization techniques to make use of this type of discretization. As an example, we can cite the works of Andreassen and Andreasen [
1], Yang et al. [
5], Karim et al. [
12], Braack and Schieweck [
13], Codina and Blasco [
14], and Becker and Hansbo [
15].
To construct a stable computational model of Q1-Q1 discretization, this work follows the same stabilization adopted by Andreassen and Andreasen [
1]. According to Andreassen and Andreasen [
1], the stabilization of the Q1-Q1 model can be obtained by adding a new term with a stabilization coefficient in the continuity equation. The weak form of the continuity equation with the stabilization term is defined by
where
is the pressure stabilization parameter, defined as
for quadrilateral elements, where
h is the size of the largest diagonal of the finite element.
The integral with the pressure stabilization term results in a matrix that must be added to the equation system of Equation (15), resulting in
where
P represents the pressure stabilization matrix.
The introduction of the new term in the continuity equation causes the coefficient matrix to become positively defined. It allows the system to be solved in the direct form.
5. Octave/Matlab Implementation
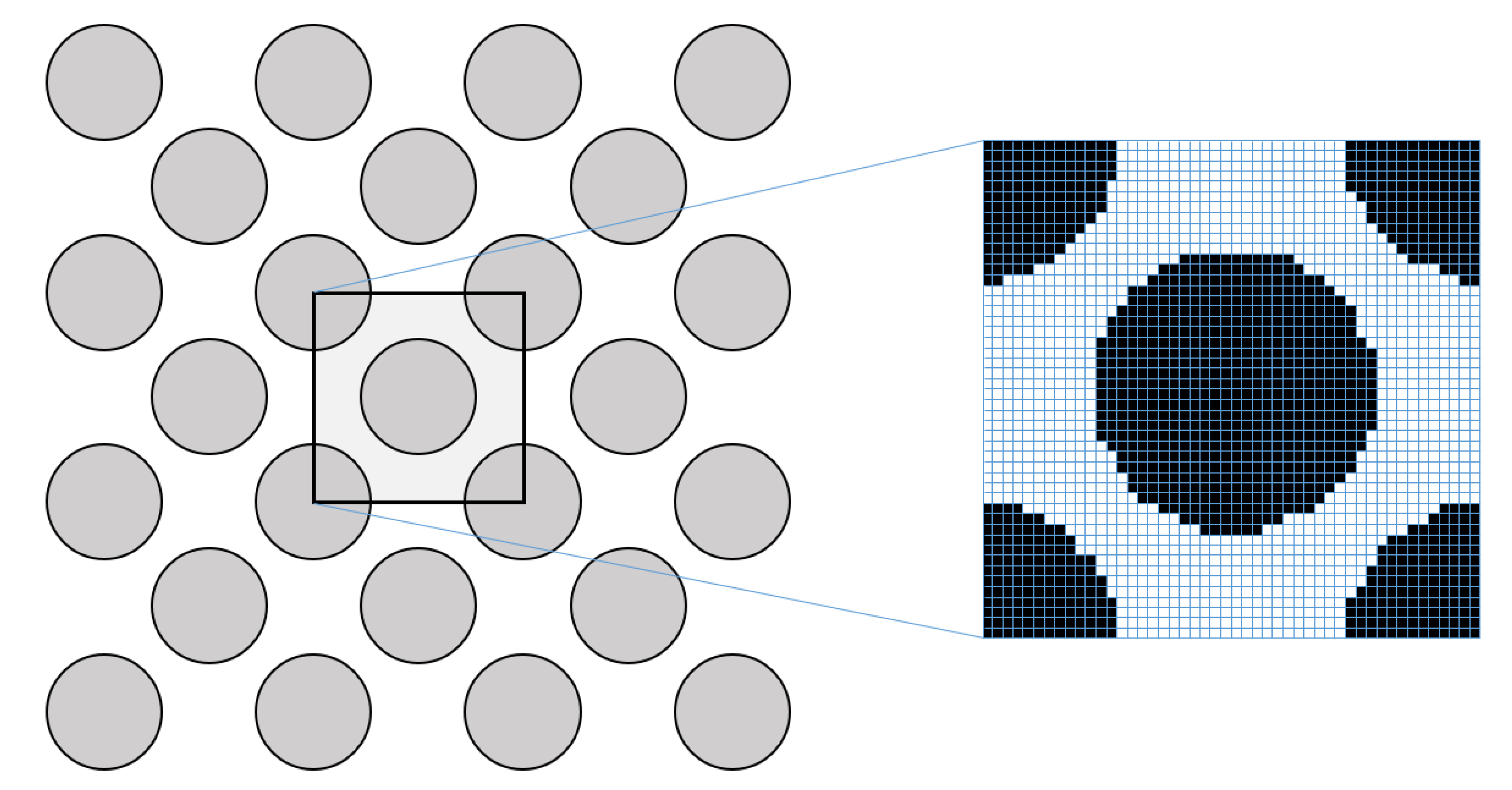
The code proposed in this paper is designed to receive as input an image (in special micro-CT images) of the problem to be modeled. It means that a pixel-based finite element mesh would be a natural choice of modeling strategy. In this approach, each pixel corresponds to a bi-linear finite element. The benefit of this strategy is that it results in a structured regular mesh (all the elements are squares of the same size) and, therefore, in an extremely low computational cost to generate the mesh. Taking full advantage of the fact that all elements in the mesh are of the same size, we compute the element matrices only once, working solely in the “element domain”.
It is important to mention that obtaining accurate values of permeability of real samples through computational simulations relies on contemplating the narrowest constrictions in the porous medium. Covering the material’s fine-scale features requires, firstly, images with high resolutions. The resolution has to be high enough to give good representation of the features in the image. On the other hand, the accuracy of the simulation also relies on modeling the image’s fine features appropriately. It means that narrowest constrictions such as pore throats and cavities represented by few pixels must be modeled with a finer mesh. Therefore, convergence tests are necessary to compute permeability, taking into account the influence of image’s fine-scale features.
5.1. Input and Initialization
The developed program performs simulation of Stokes flow in binary images. As initial data, the user should enter a binary image (line 03 of the code) representing the REV (as in
Figure 1) and the dimensions (lines 11 and 12 of the code) of that image (model) (see Listing 1).
| Listing 1. Implementation of input data and initializations |
| 1 | %% Determining permeability of porous materials |
| 2 | %% Reads the image |
| 3 | z = imread(’filename.tif’); |
| 4 | %% Increases the image resolution by n times |
| 5 | n = 1; |
| 6 | z = repelem(z,n,n); |
| 7 | %% Displays the image |
| 8 | Figure 1 |
| 9 | imshow(z) |
| 10 | %% Determines the effective permeability |
| 11 | lx = 1; % horizontal dimension |
| 12 | ly = 1; % vertical dimension |
| 13 | KH = compute_permeability(lx,ly,z); |
The MatLab function “repelem” (code line 06) is used to refine the mesh by a factor n, dividing each image pixel in a group of n × n square finite elements. This is an important procedure to perform convergence tests.
Note that, in the initialization step, the matrix image is transformed into a vector that indicates the nature of each element in the mesh (whether it is solid or fluid).
It is convenient that input data (lines 01 to 13) be stored in their own file, thus decoupling the main program (which calculates the permeability) from the data inputs (model: image and dimensions). This way, we can save the data of several different problems. Therefore, the main program is defined in its own function, which is presented from line 14 of the code.
To determine permeability, we call the function “compute_permeability”, which takes as parameters the dimensions of the model and the information of each element whether it is solid or fluid (Listing 2):
| Listing 2. Implementation of the main function to compute permeability. |
| 14 | function KH = compute_permeability(lx,ly,z) |
| 15 | %% Initializations |
| 16 | [nely, nelx] = size(z); |
| 17 | dx = lx/nelx; |
| 18 | dy = ly/nely; |
| 19 | nel = nelx*nely; |
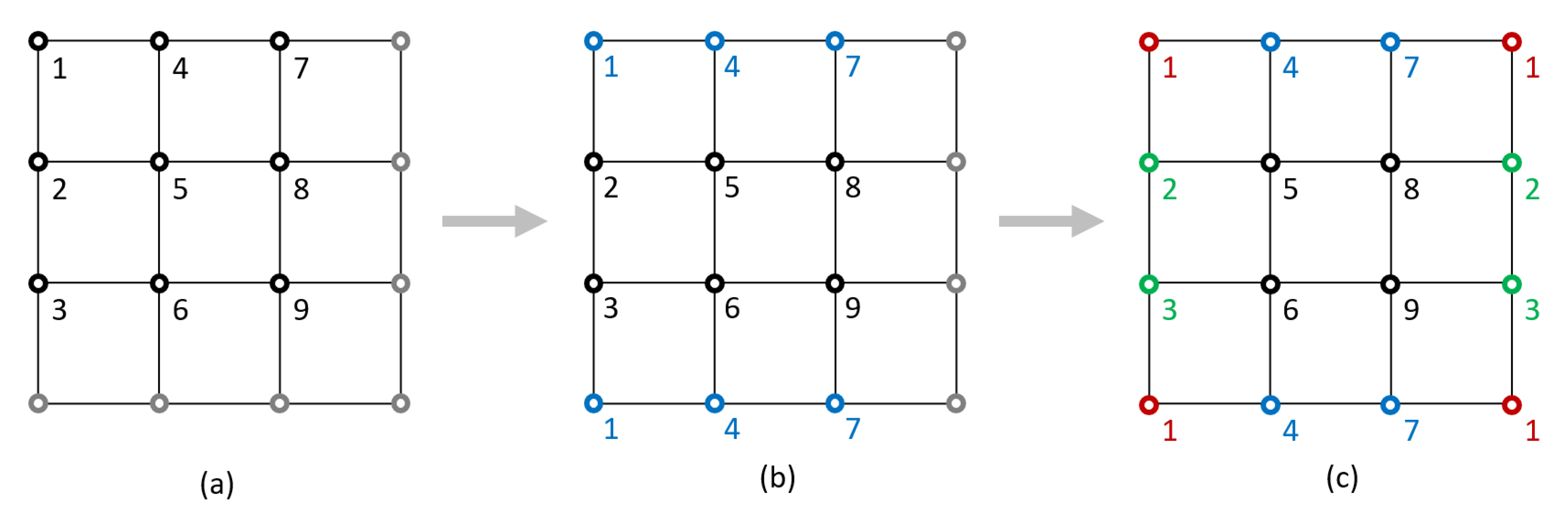
It is also necessary to create a matrix containing the element connectivity, which indicates the nodal incidences of each finite element. The connectivity matrix is assembled so that the image is inserted in a periodic medium. For achieving that, the nodes of the opposite edges are numbered the same.
Figure 2 illustrates how the image nodes are numbered using periodic boundary conditions.
To implement this strategy of mesh node numbering (see lines 21 to 24) and generation of a connectivity matrix (see lines 25 to 29), which considers periodic boundary conditions, Listing 3 is used.
| Listing 3. Implementation of periodic boundary conditions. |
| 20 | %% Periodic boundary conditions (PBC) |
| 21 | nnPBC = nel; %Number of unique nodes |
| 22 | m_IdNodesPBC = reshape(1:nnPBC, nelx, nely); % Matrix of unique nodes |
| 23 | m_IdNodesPBC(end+1,:) = m_IdNodesPBC(1,:); % Numbering bottom nodes |
| 24 | m_IdNodesPBC(:,end+1) = m_IdNodesPBC(:,1); % Numbering right nodes |
| 25 | m_ConnectPBC = zeros(nel,4); % Matrix with element connectivity |
| 26 | m_ConnectPBC = [reshape(m_IdNodesPBC(2:end,1:end-1),nel,1)... |
| 27 | reshape(m_IdNodesPBC(2:end,2:end),nel,1)... |
| 28 | reshape(m_IdNodesPBC(1:end-1,2:end),nel,1)... |
| 29 | reshape(m_IdNodesPBC(1:end-1,1:end-1),nel,1)]; |
| 30 | ndofPBC = 3*nnPBC; |
5.2. Coeficient Matrix and RHS Contribution of Each Element
Since the program proposes performing simulations from images, and the mesh generation uses a pixel-based method, all elements are equal; thus, the viscosity, gradient, and pressure stabilization matrices can be calculated only once. This considerably reduces the simulation time. These matrices are incorporated into the main program using Listing 4.
| Listing 4. Implementation to call the function to compute the element domain matrices. |
| 31 | %% Calculation of element matrices |
| 32 | [ke,ge,pe,fe,SN] = calculate_matrices(dx, dy); |
The calculation of the matrices can be done using Listing 5.
| Listing 5. Implementation of a function to calculate the finite element matrices. |
| 33 | %% Element Matrices |
| 34 | function [k,g,pe,f,SN] = calculate_matrices(dx, dy) |
| 35 | coordsElem = [0 0; dx 0; dx dy; 0 dy]; |
| 36 | rr = [−1/sqrt(3) 1/sqrt(3)]; |
| 37 | ww = [1 1]; |
| 38 | ss = rr; |
| 39 | k = zeros(8); |
| 40 | SN=zeros(2,8); |
| 41 | C = [2 0 0; 0 2 0; 0 0 1]; |
| 42 | g = zeros(8,4); |
| 43 | pe = zeros(4); |
| 44 | h2 = ((dx)^2)+((dy)^2); |
| 45 | stab = h2/12; |
| 46 | f = zeros(4,1); |
| 47 | for i = 1:2
|
| 48 | r = rr(1,i); |
| 49 | for j = 1:2
|
| 50 | s = ss(1,j); |
| 51 | N=(1/4)*[(1−s)*(1−r) 0 (1−s)*(1+r) 0 (1+s)*(1+r) 0 (1−r)*(1+s) 0; |
| 52 | 0 (1−s)*(1−r) 0 (1−s)*(1+r) 0 (1+s)*(1+r) 0 (1−r)*(1+s)]; |
| 53 | dN1dr = −1/4*(1−s); |
| 54 | dN2dr = +1/4*(1−s); |
| 55 | dN3dr = +1/4*(1+s); |
| 56 | dN4dr = −1/4*(1+s); |
| 57 | dN1ds = −1/4*(1−r); |
| 58 | dN2ds = −1/4*(1+r); |
| 59 | dN3ds = +1/4*(1+r); |
| 60 | dN4ds = +1/4*(1−r); |
| 61 | DN = [dN1dr dN2dr dN3dr dN4dr; |
| 62 | dN1ds dN2ds dN3ds dN4ds]; |
| 63 | J = DN*coordsElem; |
| 64 | invJ = 1.0/det(J)*[J(2,2) −J(1,2); −J(2,1) J(1,1)]; |
| 65 | DNxy = invJ*DN; |
| 66 | B = [DNxy(1,1) 0 DNxy(1,2) 0 DNxy(1,3) 0 DNxy(1,4) 0; |
| 67 | 0 DNxy(2,1) 0 DNxy(2,2) 0 DNxy(2,3) 0 DNxy(2,4); |
| 68 | DNxy(2,1) DNxy(1,1) DNxy(2,2) DNxy(1,2) DNxy(2,3) DNxy(1,3) DNxy(2,4) DNxy(1,4)]; |
| 69 | k = k + (B’)*C*B*det(J)*ww(1,i)*ww(1,j); |
| 70 | g = g + (B’)*[1;1;0]*N(1:4:end)*(det(J))*ww(1,i)*ww(1,j); |
| 71 | Bp = inv(J)*[DN(1,:);DN(2,:)]; |
| 72 | pe = pe + stab*(Bp’)*Bp*(det(J))*ww(1,i)*ww(1,j); |
| 73 | f = f + N(1,1:2:end)’*det(J)*ww(1,i)*ww(1,j); |
| 74 | SN = SN + N*det(J)*ww(1,i)*ww(1,j); |
| 75 | end |
| 76 | end |
| 77 | end |
The previous code, although presented in a didactic way, does not make explicitly state the required elements for the calculation of each matrix independently. However, since the shape functions used to interpolate the velocity and pressure fields are the same, the vector f and the matrices k, g, and pe can be calculated within the same function, making the algorithm more compact and elegant.
5.3. Assembly of the Linear Algebraic System
The coefficient matrix is assembled in such a way that the contribution of the degrees of freedom of each element is allocated to the corresponding degrees of freedom of the image mesh. The mapping of the elements’ degrees of freedom is done using a vector that indicates the indices of the coefficient matrix, where the terms of the matrices
K,
G,
GT, and
P are allocated to each element. An intuitive and didactic way to do this assembly is using Listing 6.
| Listing 6. Didactic implementation of assembly in the FEM. |
| | %% Assembling the system of linear algebraic equations with loops |
| v_elemF = find(~z); % vector with fluid region elements only |
| for elem = 1:size(v_elemF,1) |
| e= v_elemF(elem); |
| v_dofF = [m_ConnectPBC(e,1)*2-1; m_ConnectPBC(e,1)*2; |
| m_ConnectPBC(e,2)*2-1; m_ConnectPBC(e,2)*2; |
| m_ConnectPBC(e,3)*2-1; m_ConnectPBC(e,3)*2; |
| m_ConnectPBC(e,4)*2-1; m_ConnectPBC(e,4)*2; |
| 2*nel+m_ConnectPBC(e,1); |
| 2*nel+m_ConnectPBC(e,2); |
| 2*nel+m_ConnectPBC(e,3); |
| 2*nel+m_ConnectPBC(e,4)]; |
| % dof 1, 2 (velocities) of each node and dof 3 (pressure) of each node |
| for i=1:8 |
| for j=1:8 % allocates viscosity matrix |
| A(v_dofF(i), v_dofF(j)) = A(v_dofF(i), v_dofF(j)) + ke(i,j); |
| end |
| for j=1:4 % allocates gradient matrix |
| A(v_dofF(i), v_dofF(8+j)) = A(v_dofF(i), v_dofF(8+j)) + ge(i,j); |
| end |
| end |
| for i=1:4 % allocates right-hand side matrix |
| F(v_dofF(i*2-1),1) = F(v_dofF(i*2-1),1) + f(i); |
| F(v_dofF(i*2),2) = F(v_dofF(i*2),2) + f(i); |
| for j=1:4 % allocates pressure matrix |
| A(v_dofF(8+i),v_dofF(8+j)) = A(v_dofF(8+i),v_dofF(8+j)) - pe(i,j); |
|
end |
|
end |
| end |
| G = A(1:nel*2,nel*2+1:nel *3); |
| A(nel*2+1:nel*3,1:nel*2) = G’; |
However, despite being a more intuitive form, the use of multiple loops causes a significant increase in processing time. A more elegant and optimized approach to performing the same operation is using triplets. Thus, the previous algorithm can be replaced by Listing 7.
| Listing 7. Efficient implementation of assembly in the FEM. |
| 78 | %% Assembling the system of linear algebraic equations with triplets |
| 79 | disp(’--- ASSEMBLY ---’); |
| 80 | v_elemF = find(~z); % Vector containing only fluid elements |
| 81 | nelemF = size(v_elemF,1); |
| 82 | m_dofF = [m_ConnectPBC(v_elemF,1)’*2-1; m_ConnectPBC(v_elemF,1)’*2; |
| 83 | m_ConnectPBC(v_elemF,2)’*2-1; m_ConnectPBC(v_elemF,2)’*2; |
| 84 | m_ConnectPBC(v_elemF,3)’*2-1; m_ConnectPBC(v_elemF,3)’*2; |
| 85 | m_ConnectPBC(v_elemF,4)’*2-1; m_ConnectPBC(v_elemF,4)’*2; |
| 86 | 2*nel+m_ConnectPBC(v_elemF,1)’; % |
| 87 | 2*nel+m_ConnectPBC(v_elemF,2)’; |
| 88 | 2*nel+m_ConnectPBC(v_elemF,3)’; |
| 89 | 2*nel+m_ConnectPBC(v_elemF,4)’]; |
| 90 | % dof 1 and 2 (velocities) of each node and dof 3 (pressure) of each node |
| 91 | iK = repelem(reshape(m_dofF(1:8,1:end),nelemF*8,1),8,1); |
| 92 | jK = reshape(repmat(m_dofF(1:8,1:end),8,1),nelemF*64,1); |
| 93 | iG = repelem(reshape(m_dofF(1:8,1:end),nelemF*8,1),4,1); |
| 94 | jG = reshape(repmat(m_dofF(9:12,1:end),8,1),nelemF*32,1); |
| 95 | iP = repelem(reshape(m_dofF(9:12,1:end),nelemF*4,1),4,1); |
| 96 | jP = reshape(repmat(m_dofF(9:12,1:end),4,1),nelemF*16,1); |
| 97 | iA = [iK;iG;jG;iP]; |
| 98 | jA = [jK;jG;iG;jP]; |
| 99 | clear iK iG iP jK jG jP |
| 100 | ke = reshape(ke’,64,1); |
| 101 | ge = reshape(ge’,32,1); |
| 102 | pe = reshape(pe’,16,1); |
| 103 | coeff = [repmat(ke,nelemF,1);repmat(ge,nelemF,1);repmat(ge,nelemF,1);- |
| 104 | repmat(pe,nelemF,1)]; |
| 105 | A = sparse(iA,jA,coeff); |
| 106 | clear iA jA coeff |
| 107 | iF = [reshape(m_dofF(1:2:8,1:end),nelemF*4,1); |
| 108 | reshape(m_dofF(2:2:8,1:end),nelemF*4,1)]; |
| 109 | jF = [ones(nelemF*4,1);2*ones(nelemF*4,1)]; |
| 110 | sF = repmat(fe,nelemF*2,1); |
| 111 | F = sparse(iF,jF,sF,ndofPBC,2); |
| 112 | clear iF jF sF |
5.4. Boundary Conditions and Linear Equation System Solution
The implementation of zero velocity condition on the fluid-solid interface is done by reducing the coefficient matrix to solve only non-null variables. This process is performed on lines 113 through 123. The system is solved on line 123 (Listing 8).
| Listing 8. Implementation of zero velocity condition on the interface. |
| 113 | %% Solving system of equations |
| 114 | solveF_u = 1:nel*2; |
| 115 | nullnodes = [unique(m_ConnectPBC(find(z),1:4))]; |
| 116 | nulldof = [nullnodes*2-1 nullnodes*2]; |
| 117 | solveF_u(nulldof) = [[]; %Matrix reduction |
| 118 | solveF_p = (nel*2+unique(m_ConnectPBC(find(~z),1:4)))’; |
| 119 | solveF = [solveF_u solveF_p]; |
| 120 | clear solveF_u solveF_p nullnodes nulldof m_ConnectPBC |
| 121 | X = zeros(ndofPBC,2); |
| 122 | disp(’--- SOLVE ---’); |
| 123 | X(solveF,:) = A(solveF,solveF)\F(solveF,:); |
5.5. Obtaining Permeability
After assembling the vector with a nodal variable, permeability is calculated relating the average velocities to the prescribed pressure gradient. In this step, the mean velocities of each element are calculated integrating the velocity field inside each element. The velocity field of each element is achieved using the nodal velocities, and the shape function matrix
N is used to approximate the velocity field. This process can be performed using Listing 9.
| Listing 9. Alternative implementation for permeability calculation. |
| | %% Permeability Calculation |
| KH = zeros(2); |
| for elem=1:nelemF |
| velem_c1(:,elem) = SN*X(m_dofF(1:8,elem),1); |
| velem_c2(:,elem) = SN*X(m_dofF(1:8,elem),2); |
| end |
| vel_c1 = sum(velem_c1,2); |
| vel_c2 = sum(velem_c2,2); |
| KH(1,1) = vel_c1(1,1); |
| KH(1,2) = vel_c1(2,1); |
| KH(2,1) = vel_c2(1,1); |
| KH(2,2) = vel_c2(2,1); |
| KH = KH/nel/dx/dy; |
| end |
In the above algorithm, the element average velocity is calculated in each element during the for loop. The permeability is determined using the micro and macro relationships stated in Equations (1) and (2). However, for a more elegant and efficient way, taking advantage of the already created matrix of degrees of freedom, we use Listing 10.
| Listing 10. Efficient implementation of permeability calculation. |
| 124 | %% Permeability Calculation |
| 125 | % sum of elements’ velocities in case 1 |
| 126 | vel_c1 = SN*sum(reshape(X(m_dofF(1:8,:),1),8,nelemF),2); |
| 127 | %sum of elements’ velocities in case 2 |
| 128 | vel_c2 = SN*sum(reshape(X(m_dofF(1:8,:),2),8,nelemF),2); |
| 129 | KH = [vel_c1’; vel_c2’]/(nel*dx*dy); |
| 130 | disp(KH) |
| 131 | end |
5.6. Validation Test
In order to validate the program presented in this work, a Stokes flow simulation was performed in the porous medium represented in
Figure 3. The permeability obtained by the code demonstrated in this work, which was based on the code of Andreassen and Andreasen [
1], was compared with the analytical solution proposed by Drummond and Tahir [
16]. According to Drummond and Tahir [
16], the permeability of the medium shown in
Figure 3 can be determined using Equation (22).
where permeability (
k) is a function of the grain’s radius (
r) and the volume fraction of solid (
c).
In Reference [
14], the proposed analytical equation is valid for small values of
c. Therefore, for program validation, the REV of the medium was modeled with unit dimensions and grains with radius equal to 0.1. For these adopted values, the corresponding
c can be registered, and the permeability
k = 0.0281 × 10
−3 is obtained via the analytical solution.
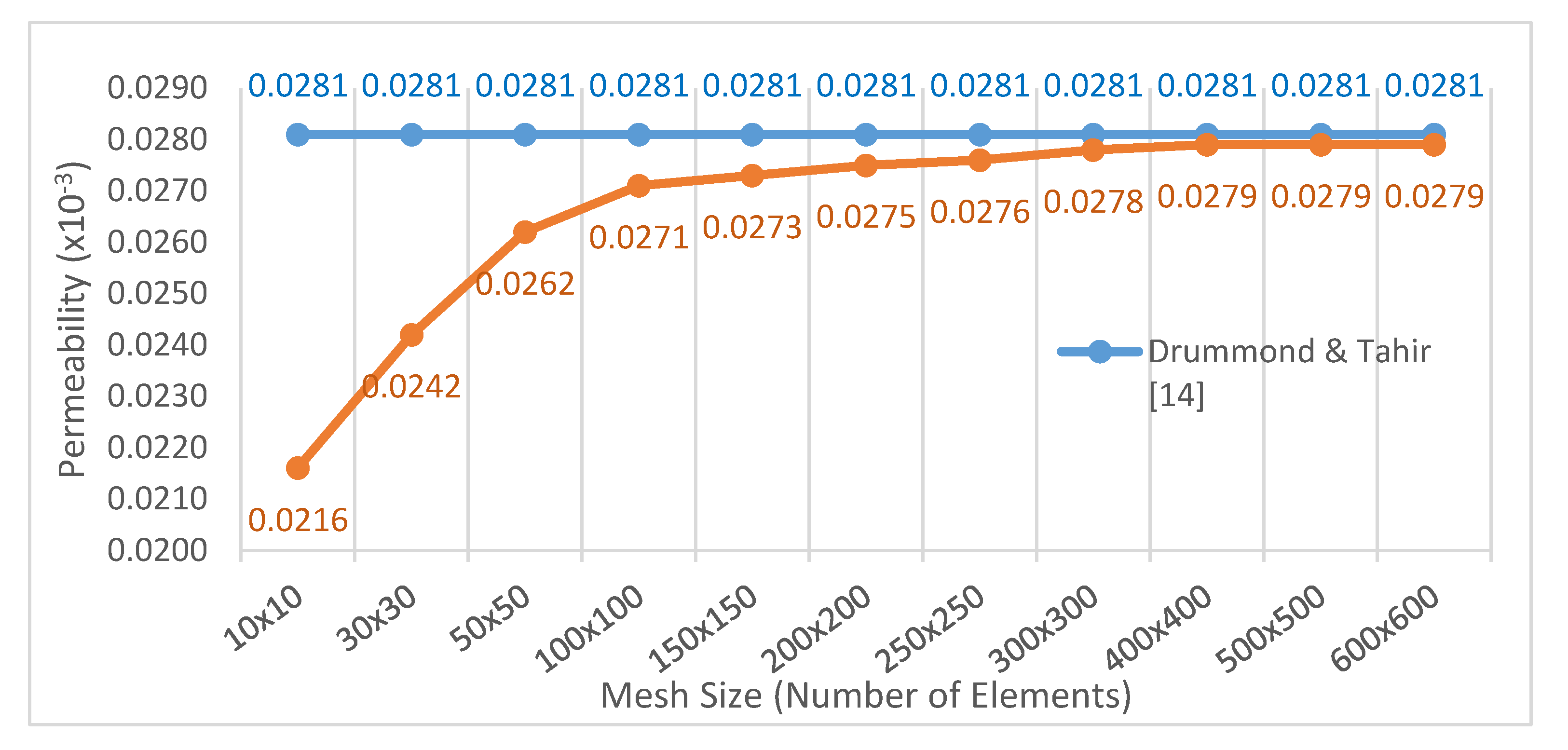
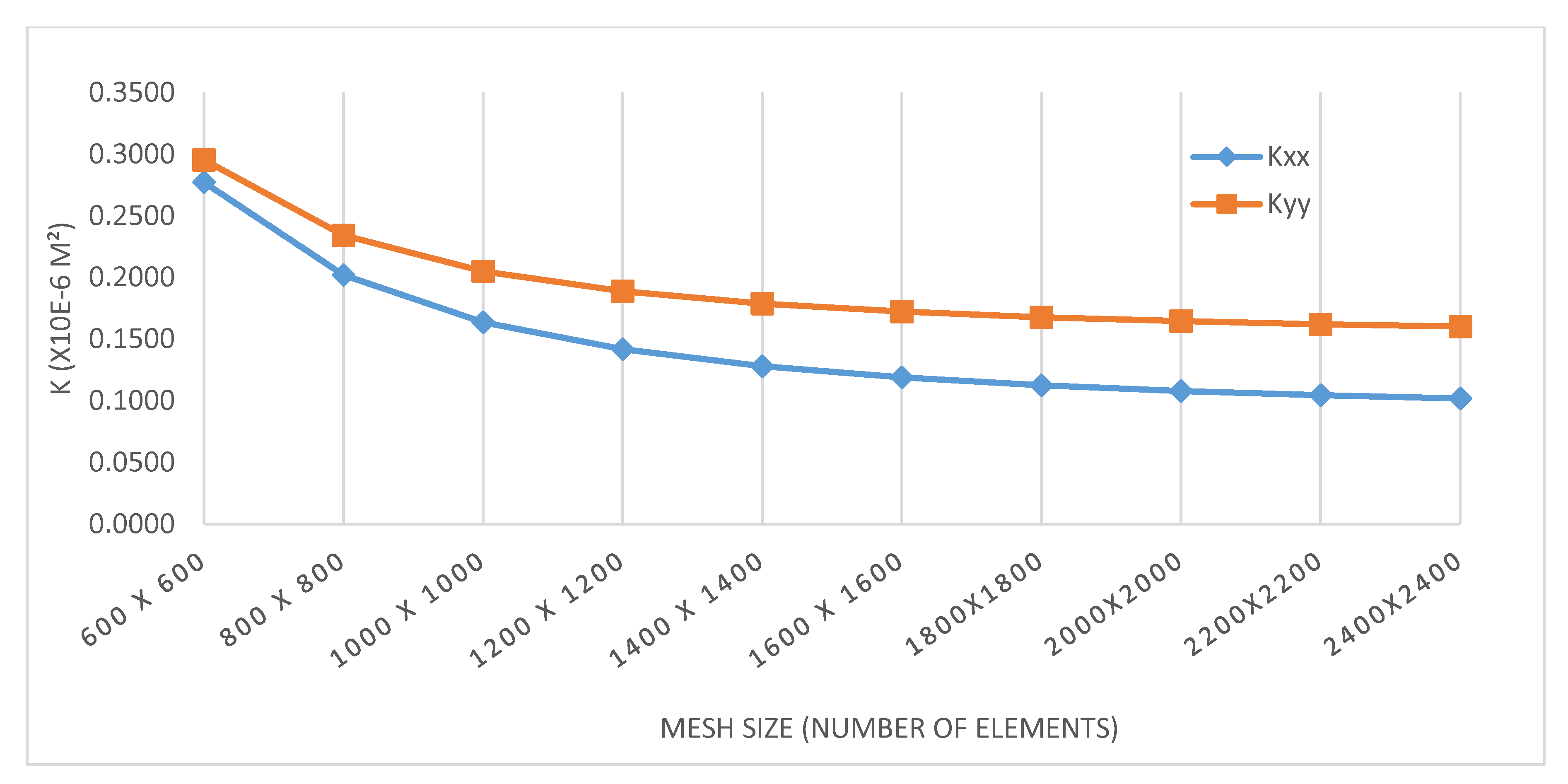
Figure 4 shows the results obtained through numerical modeling using the program proposed in this paper.
As
Figure 4 shows, the convergence of the permeability of the medium displayed in
Figure 3 can be obtained from mesh size 400 × 400. From this mesh size, the difference between the numerical result and analytical result is 0.71%. This means that the program gives good results and fulfills its purpose.