Forty Years’ Experience in Teaching Fluid Mechanics at Strasbourg University
Abstract
1. Introduction
2. Teaching and Learning Fluids with Future Schoolteachers
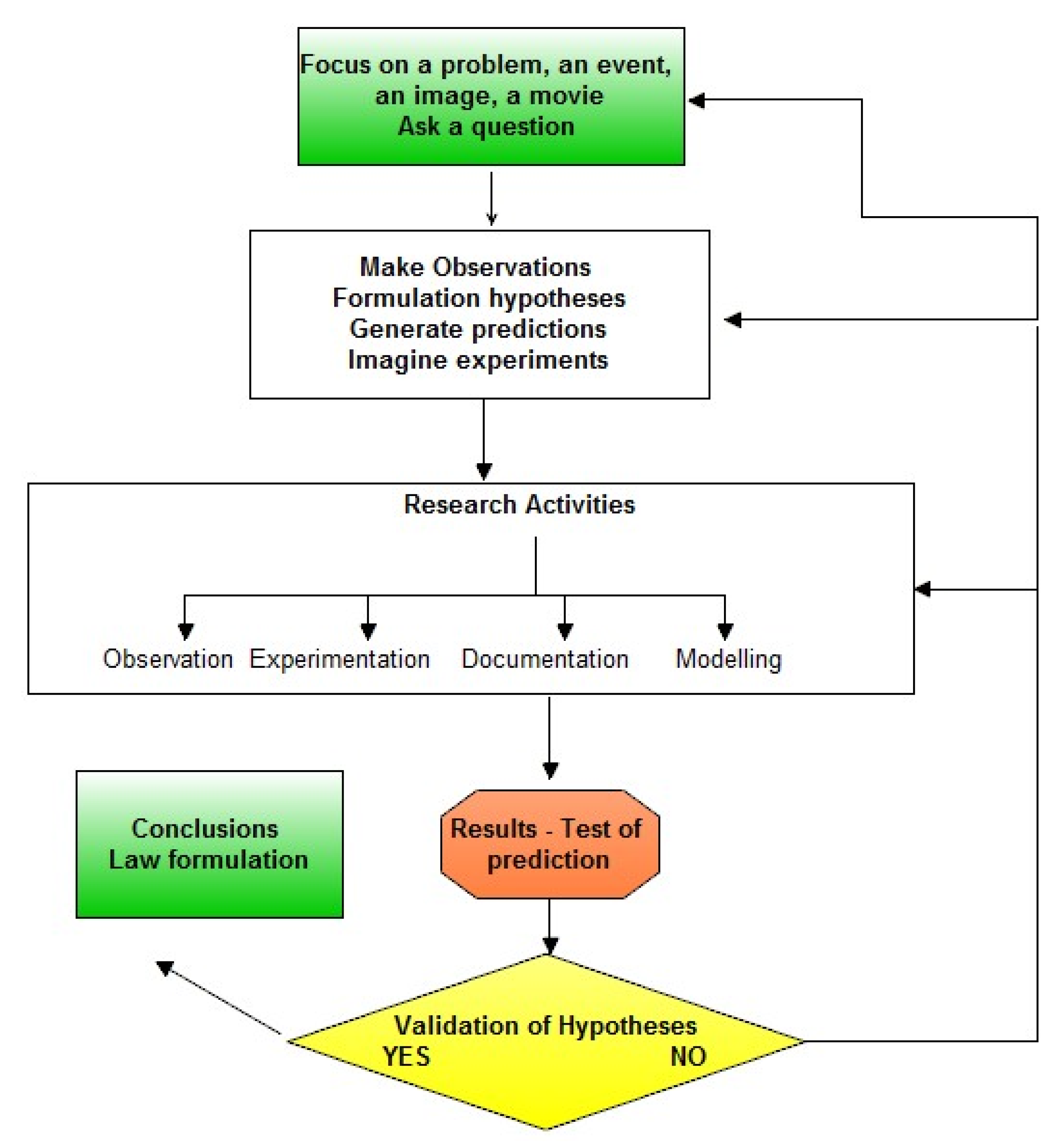
2.1. Hypothetico-Deductive (H-D) Method in Sciences
- Identify a broad problem area;
- Define the problem statement;
- Develop hypotheses;
- Determine measures;
- Data collection;
- Data analysis.
- Observation and questioning related to initial representations, problem identification;
- Theoretical framework, background research, preliminary information gathering;
- Elaboration of hypotheses (testable, falsifiable afterwards);
- Definition, design of test experiments;
- Predictions of results associated to the test experiences;
- Experimentation, data recording and collection, and analysis/interpretation;
- Validation or invalidation of hypotheses and predictions, as well as their assessment;
- Elaboration of a theory or law based on robust validations.
2.2. Practical Work and Projects in Fluid Mechanics
- ➢
- Have two weeks to update their knowledge in fluids (Newton’s laws, free fall bodies in a void, fall in air or water/oil, the Archimedes’ principle, the Bernoulli law of perfect fluids) and investigate the concepts of viscosity and drag force (Reynolds number, Stokes’ law, terminal fall velocity), writing all in a science notebook.
- ➢
- Must imagine simple inexpensive experiments that identify and highlight relevant science notions and concepts, with some available material being listed and some experience items being proposed, such as:
- Galileo’s experiments of falling objects, using sport balls in air from different heights up to 20 m (to observe differences in terminal velocities for different spheres (diameters, density));
- Making a classic Cartesian diver (understanding pressure, Archimedean buoyancy);
- Building a parachute with fabric and string/building a wind turbine;
- Observing the settling of sand grains in water;
- Observing bubbles rising in oil or water, or the fall of a golf ball in water (viscosity calculation);
- Galileo’s experiment with rolling balls down an inclined plane (the calculation of gravity);
- The levitation of a ping pong ball (Coanda effect, Bernoulli equation);
- The measurement of the density of objects (cork, lead sinkers) based on the Archimedes’ principle.
- ➢
- Investigate and execute creative experiments while setting up the hypothetico-deductive teaching strategies.
- ➢
- Elaborate several lesson preparation cards for pupils in primary schools on a topic related to fluid mechanics.
- Improvement in organization of their working hours;
- Efficient use of available information and resources (in books, articles, the internet);
- Investment and teamwork (organizing small students’ groups for interactive pedagogy learning);
- Scientific curiosity, creativity, motivation, and the pleasure of learning;
- Acquisition of reflective practice and scientific questioning;
- Implementing the HD method coupled with a project-based approach;
- Problem solving, formulating and testing hypotheses, theories, or laws;
- Analyzing and understanding scientific phenomena;
- Learning to measure and calculate with efficiency;
- Developing various abilities and skills, including the acquisition of transversal competences such as creativity and critical thinking.
2.2.1. Example of an Experiment: Free Fall of Bodies
2.2.2. Example of an Experiment: Viscosity Calculation
2.2.3. Some Scientific Questions Treated in a Preparation Sheet
3. Teaching Fluid Mechanics from 1976 to 2002
4. Teaching and Learning Fluids after the Bologna Process
4.1. Case of Undergraduate Students
4.2. Case of Graduate Students: A Revealing Illustration
5. Fluid Mechanics Remediation Test
5.1. Conceptual vs. Procedural Knowledge, Misconceptions
5.2. Concept Inventories (CI)
5.3. The American Fluid Mechanics Concept Inventory (FMCI)
- -
- Statics of fluids, seven questions (Q7, Q9, Q10, Q12, Q14, Q18, Q30);
- -
- Ideal fluids and conservation laws (Bernouilli, Euler), 10 questions (Q3, Q4, Q6, Q13, Q17, Q22, Q23, Q25, Q27, Q31);
- -
- External viscous flows, seven questions (Q5, Q19, Q20, Q24, Q26, Q28, Q29);
- -
- Internal viscous flows, six questions (Q8, Q11, Q15, Q16, Q21, Q32).
6. Work in Progress in Learning and Teaching Fluid Mechanics
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Flick, L.B. The Meanings of Hands-On Science. J. Sci. Teach. Educ. 1993, 4, 1–8. [Google Scholar] [CrossRef]
- Sorbonne Declaration. Available online: http://www.ehea.info/cid100203/sorbonne-declaration 1998.html (accessed on 15 June 2019).
- EHEA. The Framework of Qualifications for the European Higher Education Area (PDF). Archived from the Original (PDF) on 23 September 2015. May 2005. Available online: http://www.ehea.info/media.ehea.info/file/BFUG_Meeting/49/6/BFUG_BG_SR_61_4c_AppendixIII_947496.pdf (accessed on 18 March 2016).
- McKinney, K. Attitudinal and structural factors contributing to challenges in the work of the scholarship of teaching and learning. New Dir. Inst. Res. 2006, 129, 37–50. [Google Scholar] [CrossRef]
- Martin, J.; Mitchell, J.; Newell, T. Development of a Concept Inventory for Fluid Mechanics. In Proceedings of the 33th ASEE/IEE Frontiers in Education Conference, Boulder, CO, USA, 5–8 November 2003; p. 20. [Google Scholar]
- Martin, J.K.; Mitchell, J.; Newell, T. Work in Progress: Analysis of Reliability of the Fluid Mechanics Concept Inventory. In Proceedings of the 34th ASEE/IEEE Frontiers in Education Conference, Savannah, GA, USA, 20–23 October 2004. [Google Scholar]
- New Approach to Science Teaching Needed in Europe, Say Experts. Available online: http://europa.eu/rapid/press-release_IP-07-797_en.htm?locale=en (accessed on 15 June 2019).
- Caltech Mourns Professor Emeritus Jerry Pine. Available online: https://www.caltech.edu/about/news/caltech-mourns-professor-emeritus-jerry-pine-80363 (accessed on 28 June 2019).
- Popper, K. Conjectures and Refutations: The Growth of Scientific Knowledge, 5th ed.; Routledge: London, UK, 1989. [Google Scholar]
- Popper, K. Objective Knowledge: An Evolutionary Approached, Revised Edition; Oxford University Press: Oxford, UK, 1979; p. 30. [Google Scholar]
- Popper, K.R. The Logic of Scientific Discovery; Hutchinson & CO: London, UK, 1959. [Google Scholar]
- Lawson, A.E. The generality of hypothetico-deductive reasoning: Making scientific thinking explicit. Am. Biol. Teach. 2000, 62, 482–495. [Google Scholar] [CrossRef]
- Lewis, R.W. Biology: A hypothetico-deductive science. Am. Biol. Teach. 1988, 50, 362–366. [Google Scholar] [CrossRef]
- Available online: http://daniel-huilier.fr (accessed on 28 November 2019).
- The Apollo 15 Hammer-Feather Drop. Available online: https://nssdc.gsfc.nasa.gov/planetary/lunar/apollo_15_feather_drop.html (accessed on 3 July 2019).
- Beard, K.V. Terminal Velocity and Shape of Cloud and Precipitation Drops. J. Atmos. Sci. 1976, 33, 851–864. [Google Scholar] [CrossRef]
- Clanet, C.H. Sport ballistics. Annu. Rev. Fluid Mech. 2015, 45, 455–478. [Google Scholar] [CrossRef]
- Moreau, R.; Sommeria, J. Traînée subie par les corps en mouvement. Encyclopédie de L’environnement. 2019. Available online: https://encyclopedie-environnement.org (accessed on 28 November 2019).
- Munson, B.R.; Okiishi, T.H.; Huebsch, W.W.; Rothmayer, A.P. Fundamentals of Fluid Mechanics, 7th ed.; Wiley: Singapore, 2013; Chapter 9. [Google Scholar]
- Rott, N. Note on the History of the Reynolds Number 1990. Annu. Rev. Fluid Mech. 1990, 22, 1–12. [Google Scholar] [CrossRef]
- Striking Results on Bouncing Balls. Available online: https://staff.fnwi.uva.nl/a.j.p.heck/Research/art/BouncingBall.pdf (accessed on 25 June 2019).
- Bouncing Ball Experiment. Available online: https://www.brooklyn.k12.oh.us/userfiles/66/Classes/13814/Lab%20-Bouncing%20Ball.pdf (accessed on 25 June 2019).
- Hands-on Activity: Reverse Engineering. Available online: https://www.teachengineering.org/activities/view/ball_bounce_experiment (accessed on 25 June 2019).
- Schiller, L.; Naumann, Z. VDI Zeitung 1935. Drag Coeff. Correl. 1935, 77, 318–320. [Google Scholar]
- Milk Viscosity. Available online: https://www.teachengineering.org/activities/view/nyu_milk_activity1 (accessed on 28 June 2019).
- Guyon, E.; Hulin, J.P.; Petit, L.; Mitescu, C. Physical Hydrodynamics, 2nd ed.; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Guyon, É.; Hulin, J.P.; Petit, L. Ce Que Disent Les Fluides, 2nd ed.; Editions Belin: Paris, France, 2011. [Google Scholar]
- De Gennes, P.G.; Brochard-Wyart, F.; Quéré, D. Gouttes, Bulles, Perles Et Ondes; Editions Belin: Paris, France, 2002. [Google Scholar]
- Batchelor, G. An Introduction to Fluid Dynamics; Cambridge Press University: Cambridge, UK, 2000. [Google Scholar]
- Schlichting, H. Boundary Layer Theory, 4th ed.; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Hinze, J.O. Turbulence, 2nd ed.; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Batchelor, G.K. The Scientific Papers of Sir Geoffrey Ingram Taylor; Cambridge Press University: Cambridge, UK, 1960; Volume 2. [Google Scholar]
- Rittle-Johnson, B.; Wagner-Alibali, M.W. Conceptual and procedural knowledge of mathematics: Does one lead to the other? J. Educ. Psychol. 1999, 91, 175–189. [Google Scholar] [CrossRef]
- Barr, C.; Doyle, M.; Clifford, J.; de Leo, T.; Dubeau, C. There Is More to Math: A Framework for Learning and Math Instruction; Waterloo Catholic District School Board: Waterloo, ON, Canada, 2003. [Google Scholar]
- Arslan, S. Traditional instruction of differential equations and conceptual learning. Teach. Math. Appl. Int. J. IMA 2010, 29, 94–107. [Google Scholar] [CrossRef]
- Star, J.R. Re-conceptualizing procedural knowledge: The emergence of “intelligent” performances among equation solvers. In Proceedings of the 28th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Columbus, OH, USA, 26–29 October 2002; Mewborn, D., Sztajn, P., White, D., Wiegel, H., Bryant, R., Nooney, K., Eds.; ERIC Clearinghouse for Science, Mathematics, and Environmental Education: Columbus, OH, USA, 2002; pp. 999–1007. [Google Scholar]
- Rittle-Johnson, B.; Siegler, R. The relations between conceptual and procedural knowledge in learning mathematics: A review, chapter 4. In Studies in Developmental Psychology. The Development of Mathematical Skills; Donlan, C., Ed.; Psychology Press: Hove, UK; Taylor & Francis: London, UK, 1998; pp. 75–110. [Google Scholar]
- Rittle-Johnson, B. Promoting transfer: Effects of self-explanation and direct instruction. Child Dev. 2006, 77, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Piaget, J.; Cook, M.; Norton, W. The Origins of Intelligence in Children; International Universities Press: New York, NY, USA, 1952; Volume 8. [Google Scholar]
- Chi, M.T.; Slotta, J.D.; de Leeuw, N. From things to processes: A theory of conceptual change for learning science concepts. Learn. Instr. 1994, 4, 27–43. [Google Scholar] [CrossRef]
- Madsen, A.; McKagan, S.; Sayre, E. Best Practices for Administering Concept Inventories. Phys. Teach. 2017, 55, 530. [Google Scholar] [CrossRef]
- Sadler, P.M. Psychometric models of student conceptions in science: Reconciling qualitative studies and distractor-driven assessment instruments. J. Res. Sci. Teach. 1998, 35, 265–296. [Google Scholar] [CrossRef]
- Furrow, R.E.; Hsu, J.L. Concept inventories as a resource for teaching evolution. Evol. Educ. Outreach 2019, 12, 11. [Google Scholar] [CrossRef]
- Halloun, I.A.; Hestenes, D. The initial knowledge state of college physics students. Am. J. Phys. 1985, 53, 1043–1055. [Google Scholar] [CrossRef]
- Halloun, I.A.; Hestenes, D. Common sense concepts about motion. Am. J. Phys. 1985, 53, 1056–1065. [Google Scholar] [CrossRef]
- Hestenes, M.; Wells, G. Swackhamer, Force Concept Inventory. Phys. Teach. 1992, 30, 141–158. [Google Scholar] [CrossRef]
- Coalition Foundation. Available online: http://fc.civil.tamu.edu/ (accessed on 25 June 2019).
- Lindell, R.S.; Peak, E.; Foster, T.M. Are They All Created Equal? A Comparison of Different Concept Inventory Development Methodologies. In AIP Conference Proceedings 883; McCullough, L., Heron, P., Hsu, L., Eds.; AIP Press: Melville, NY, USA, 2007; pp. 14–17. [Google Scholar] [CrossRef]
- Adams, W.K.; Wieman, C.E. Development and Validation of Instruments to Measure Learning of Expert-Like Thinking. Int. J. Sci. Educ. 2011, 33, 1289–1312. [Google Scholar] [CrossRef]
- Available online: www.physport.org/assessments (accessed on 7 July 2019).
- Henderson, C. Common Concerns about the Force Concept Inventory. Phys. Teach. 2002, 40, 542. [Google Scholar] [CrossRef]
- Laverty, J.T.; Caballero, M.D. Analysis of the most common concept inventories in physics: What are we assessing? Phys. Rev. Phys. Educ. Res. 2018, 14, 010123. [Google Scholar] [CrossRef]
- Gray, G.L.; Evans, D.; Cornwell, P.; Costanzo, F.; Self, B. Toward a nationwide dynamics concept inventory assessment test. In Proceedings of the American Society for Engineering Education Annual Conference & Exposition, Nashville, TN, USA, 22–25 June 2003. [Google Scholar]
- List of Concept Inventories. Available online: http://fc.civil.tamu.edu/home/keycomponents/concept/index.html (accessed on 28 June 2019).
- David Sands, D.; Parker, M.; Hedgeland, H.; Jordan, S.; Galloway, R. Using concept inventories to measure understanding. High. Educ. Pedagog. 2018, 3, 173–182. [Google Scholar] [CrossRef]
- Watson, K.; Mills, R.; Bower, K.; Brannan, K.; Woo, M.; Welch, R. Revising a Concept Inventory to Assess Conceptual Understanding in Civil Engineering Fluid Mechanics. In Proceedings of the 122nd ASEE Annual Conference & Exhibition, Seattle, WA, USA, 14–16 June 2015. [Google Scholar]
- Suarez, A.; Kahan, S.; Zavala, G.; Marti, A.C. Student Conceptual Difficulties in Hydrodynamics. Phys. Rev. Phys. Educ. Res. 2017, 13, 020132. [Google Scholar] [CrossRef]
- Laverty, J.T.; Underwood, S.M.; Matz, R.L.; Posey, L.A.; Carmel, J.H.; Caballero, M.D.; Fata-Hartley, C.L.; Ebert-May, D.; Jardeleza, S.E.; Cooper, M.M. Characterizing College Science Assessments: The Three-Dimensional Learning Assessment Protocol. PLoS ONE 2016, 11, e0162333. [Google Scholar] [CrossRef]
- National Research Council. A Framework for K-12 Science Education; The National Academies Press: Washington, DC, USA, 2012. [Google Scholar] [CrossRef]
- Besson, U. Students’ conceptions of fluids. Int. J. Sci. Educ. 2004, 26, 1683–1714. [Google Scholar] [CrossRef]
- Loverude, M.E.; Heron, P.R.L.; Kautz, C.H. Identifying and addressing student difficulties with hydrostatic pressure. Am. J. Phys. 2010, 78, 75–85. [Google Scholar] [CrossRef]
- Matewsky, M.; Boyer, A.; Bazan, Z.; Wagner, D.J. Exploring student difficulties with pressure in a fluid. AIP Conf. Proc. 2013, 1513, 154–157. [Google Scholar]
- Nihous, G.C. Notes on hydrostatic pressure. J. Ocean Eng. Mar. Energy 2016, 2, 105–109. [Google Scholar] [CrossRef][Green Version]
- Young, D.; Meredith, D.C. Using the resources framework to design, assess, and refine interventions on pressure in fluids. Phys. Rev. Phys. Educ. Res. 2017, 13, 010125. [Google Scholar] [CrossRef]
- Koumaras, P.; Pierratos, T.H. How Much Does a Half-Kilogram of Water “Weigh”? Phys. Teach. 2015, 53, 174–176. [Google Scholar] [CrossRef]
- Loverude, M.E.; Kautz, C.H.; Heron, P.R. Helping students develop an understanding of Archimedes’ principle. I. Research on student understanding. Am. J. Phys. 2003, 71, 1178–1187. [Google Scholar] [CrossRef]
- Recktenberg, G.W.; Edwards, R.C.; Howe, D.; Faulkner, J. Simple Experiment to Expose Misconceptions about the Bernoulli Equation. In Proceedings of the ASME 2009 International Mechanical Engineering Congress and Exposition, Lake Buena Vista, FL, USA, 13–19 November 2009; Volume 7, pp. 151–160. [Google Scholar] [CrossRef]
- Bedford, D.; Lindsay, R. A misinterpretation of Bernoulli’s theorem. Phys. Educ. 1977, 12, 311–312. [Google Scholar] [CrossRef]
- Eastwell, P. Bernoulli? Perhaps but What about Viscosity? Sci. Educ. Rev. 2007, 6, 1–13. [Google Scholar]
- Eastwell, P. Thinking Some More about Bernoulli. Phys. Teach. 2008, 46, 555–556. [Google Scholar] [CrossRef]
- Kamela, M. Thinking about Bernoulli. Phys. Teach. 2007, 45, 379–381. [Google Scholar] [CrossRef]
- Martin, D.H. Misunderstanding Bernoulli. Phys. Teach. 1983, 21, 37. [Google Scholar] [CrossRef]
- Kusairi, S.; Alfad, H.; Zulaikah, S. Development of Web-Based intelligent (iTutor) to help students learn fluid statics. J. Turkish Sci. Educ. 2017, 14, 1–11. [Google Scholar] [CrossRef]
- Fraser, D.M.; Pillay, R.; Tjatindi, L.; Case, J.M. Enhancing the Learning of Fluid Mechanics Using Computer Simulations. J. Eng. Educ. 2007, 96, 279–289. [Google Scholar] [CrossRef]
- Stern, F.; Xing, T.; Yarbrough, D.B.; Rothmayer, A.; Rajagopalan, G.; Prakashotta, S.; Caughey, D.; Bhaskaran, R.; Smith SHutchings, B.; Moeyke, S. Hands-On CFD Educational Interface for Engineering Courses and Laboratories. J. Eng. Educ. 2006, 95, 63–83. [Google Scholar] [CrossRef]
- Cranston, G.; Lock, G. Techniques to encourage interactive student learning in a laboratory setting. Eng. Educ. 2012, 7, 2–10. [Google Scholar] [CrossRef]
- Lu, H.; Zhang, X.; Jiang, D.; Zhao, Z.; Wang, J.; Liu, J. Several Proposals to Improve the Teaching Effect of Fluid Mechanics. In Emerging Computation and Information Chnologies for Education. Advances in Intelligent and Soft Computing; Mao, E., Xu, L., Tian, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 146. [Google Scholar] [CrossRef]
- Burgher, J.; Finkel, D.; van Wie, B.J.; Adescope, O.O. Comparing misconceptions in fluid mechanics using interview analysis pre and post hands-on learning module treatment. In Proceedings of the 121st ASEE Annual Conference & Exposition, Indianapolis, IN, USA, 15–18 June 2014. [Google Scholar]
- Brown, A. Enhancing learning of fluid mechanics using automated feedback and by engaging students as partners. In Proceedings of the Higher Education Academy Annual Conference, Birmingham, UK, 2–3 July 2014; p. 2. [Google Scholar]
- Albers, L.; Bottomley, L. The Impact of Activity Based Learning, A New Instructional Method, In an Existing Mechanical Engineering Curriculum for Fluid Mechanics. In Proceedings of the 118th ASEE Annual Conference & Exposition, Vancouver, BC, Canada, 26–29 June 2011; Available online: https://www.asee.org/public/conferences/1/papers/781/view (accessed on 25 June 2019).
- Bondehagen, D.L. Inspiring students to learn fluid mechanics through engagement with real world problems. In Proceedings of the 118th ASEE Annual Conference & Exposition, Vancouver, BC, Canada, 26–29 June 2011; Available online: https://peer.asee.org/18190 (accessed on 24 June 2019).
- McClelland, C.J. Flipping a large-enrollment fluid mechanics course—Is it effective? In Proceedings of the 120th ASEE Annual Conference & Exposition, Atlanta, GA, USA, 23 June 2013; Available online: https://www.asee.org/public/conferences/20/papers/7911/view (accessed on 24 June 2019).
- Webster, D.R.; Majerich, D.M.; Madden, A. Flippin’Fluid Mechanics—Comparison Using Two Groups. Adv. Eng. Educ. 2016, 5, 1–20. [Google Scholar]
- Webster, D.R.; Majerich, D.M.; Luo, J. Flippin’ Fluid Mechanics—Quasi-experimental Pre-test and Post-test Comparison Using Two Groups. In Proceedings of the DFD14 Meeting of The American Physical Society, San Francisco, CA, USA, 23–25 November 2014. [Google Scholar]
- Wachs, F.L.; Fuqua, J.L.; Nissenson, P.M.; Shih, A.C.; Ramirez, M.P.; DaSilva, L.Q.; Nguyen, N.; Romero, C. Successfully Flipping a Fluid Mechanics Course Using Video Tutorials and Active Learning Strategies: Implementation and Assessment? In Proceedings of the 125th ASEE Annual Conference & Exhibition, Salt Lake City, UT, USA, 24–27 June 2018; Available online: https://www.asee.org/public/conferences/106/papers/23046/view (accessed on 8 July 2019).
- Pietrocola, M. Upgrading Physics Education to Meet the Needs of Society; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Kalman, C.S. Successful Science and Engineering Teaching: Theoretical and Learning Perspectives; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]
- Dori, Y.J.; Mevarech, Z.R.; Baker, D.R. Cognition, Metacognition and Culture in STEM Education: Leraning, Teaching and Assessment; Springer international Publishing: Cham, Switzerland, 2018. [Google Scholar]
- Pietrocola, M.; Gurgel, I. Crossing the Border of the Traditional Science Curriculum: Innovative Teaching in Basic Science; Sense Publishers: Rotterdam, The Netherlands, 2017. [Google Scholar]
- Clark, R.C.; Mayer, R.E. E-Learning and the Science of Instruction: Proven Guideline for Consumers and Designers of Multimedia Learning; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- De Silva, E. Cases on Research-Based Teaching Methods in Science Education; IGI Global: Hershey, PA, USA, 2014. [Google Scholar]

| Height (in meters) | T = (2 h/g)1/2 (s) | V (m/s) = gT |
|---|---|---|
| 1 | 0.45 | 4.4 |
| 2 | 0.64 | 6.3 |
| 3 | 0.78 | 7.6 |
| 5 | 1 | 9.8 |
| 10 | 1.43 | 14 |
| Targeted Concepts | |
|---|---|
| 3 Continuity; compressible 4 Bernoulli; incompressible 5 Boundary conditions 6 Momentum; incompressible 7 Pressure definition 8 Boundary layers; incompressible 9 Pascal’s Law 10 Manometry; compressible 11 Bernoulli; incompressible 12 Forces on submerged surface 13 Ideal Gas Law 14 Manometry; compressible 15 Shear stress; compressible 16 Boundary layers 17 Bernoulli; incompressible | 18 Manometry; compressible 19 Drag force; compressible 20 Boundary layer; compressible 21 Boundary layer; incompressible 22 Continuity; incompressible 23 Continuity/Bernoulli; incompressible 24 Boundary layer; compressible 25 Impulse-momentum; incompressible 26 Boundary layer; compressible 27 Continuity/Bernoulli; incompressible 28 Drag force; compressible 29 Drag force; compressible 30 Pressure measurement; compressible 31 Continuity/Temperature variations; compressible 32 Fluid properties (viscosity) |
| Targeted Concepts | |
|---|---|
| 3 Continuity; compressible 4 Bernoulli; incompressible 5 Boundary conditions for boundary layer 6 Momentum; incompressible, Euler 7 Pressure definition, statics 8 Viscous flow between flat-plates; incompressible 9 Pascal’s Law, statics 10 Manometry; compressible, Bernoulli 11 generalized Bernoulli; pressure loss in pipes 12 Forces on submerged surface 13 Ideal Gas Law 14 Manometry; statics 15 Shear stress 16 Flow between two flat-plates, velocity profile 17 Bernoulli; flow in a horizontal diffuser 18 Manometry; compressible, statics | 19 Laminar drag force over a flat-plate 20 Boundary layer; control volume approach 21 Flow between two moving flate-plates, velocity profile 22 Continuity; incompressible 23 Continuity/Bernoulli; vertical diffuser, incompressible 24 Boundary layer; velocity profile 25 Impulse-momentum; incompressible 26 Boundary layer and wall stress profile 27 Continuity/Bernoulli; vertical contraction, incompressible 28 Drag force of different profiles in air 29 Drag force; viscous drag 30 Pressure measurement; Prandtl/Pitot tube 31 Continuity/Temperature variations; compressible flow through a diffuser 32 Fluid properties (viscosity) |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huilier, D.G.F. Forty Years’ Experience in Teaching Fluid Mechanics at Strasbourg University. Fluids 2019, 4, 199. https://doi.org/10.3390/fluids4040199
Huilier DGF. Forty Years’ Experience in Teaching Fluid Mechanics at Strasbourg University. Fluids. 2019; 4(4):199. https://doi.org/10.3390/fluids4040199
Chicago/Turabian StyleHuilier, Daniel G. F. 2019. "Forty Years’ Experience in Teaching Fluid Mechanics at Strasbourg University" Fluids 4, no. 4: 199. https://doi.org/10.3390/fluids4040199
APA StyleHuilier, D. G. F. (2019). Forty Years’ Experience in Teaching Fluid Mechanics at Strasbourg University. Fluids, 4(4), 199. https://doi.org/10.3390/fluids4040199






