The Velocity Field Underneath a Breaking Rogue Wave: Laboratory Experiments Versus Numerical Simulations
Abstract
1. Introduction
2. Materials and Methods
2.1. Numerical Method
2.1.1. Higher Order Spectral Method (HOSM)
2.1.2. Level-Set Navier–Stokes (LS-NS)
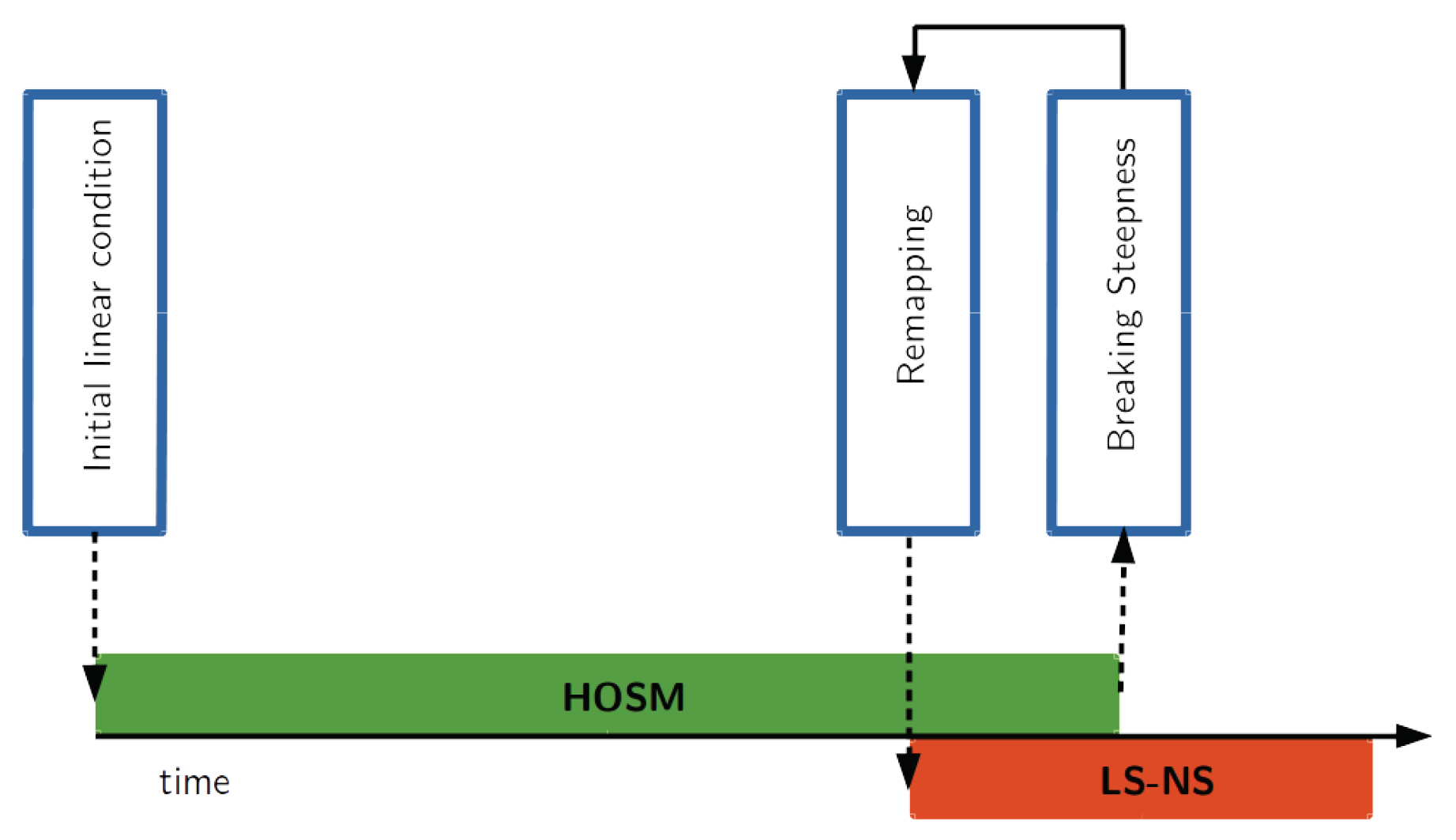
2.1.3. Coupling the HOSM and the LS-NS
- The HOSM surface elevation and potential at the final instant ( and ) are interpolated over a grid compatible with the resolution needed by the LS-NS simulation. This is about 400 elements per wavelength () [50]. A cubic spline with periodic conditions is used to resample the surface elevation and its potential.
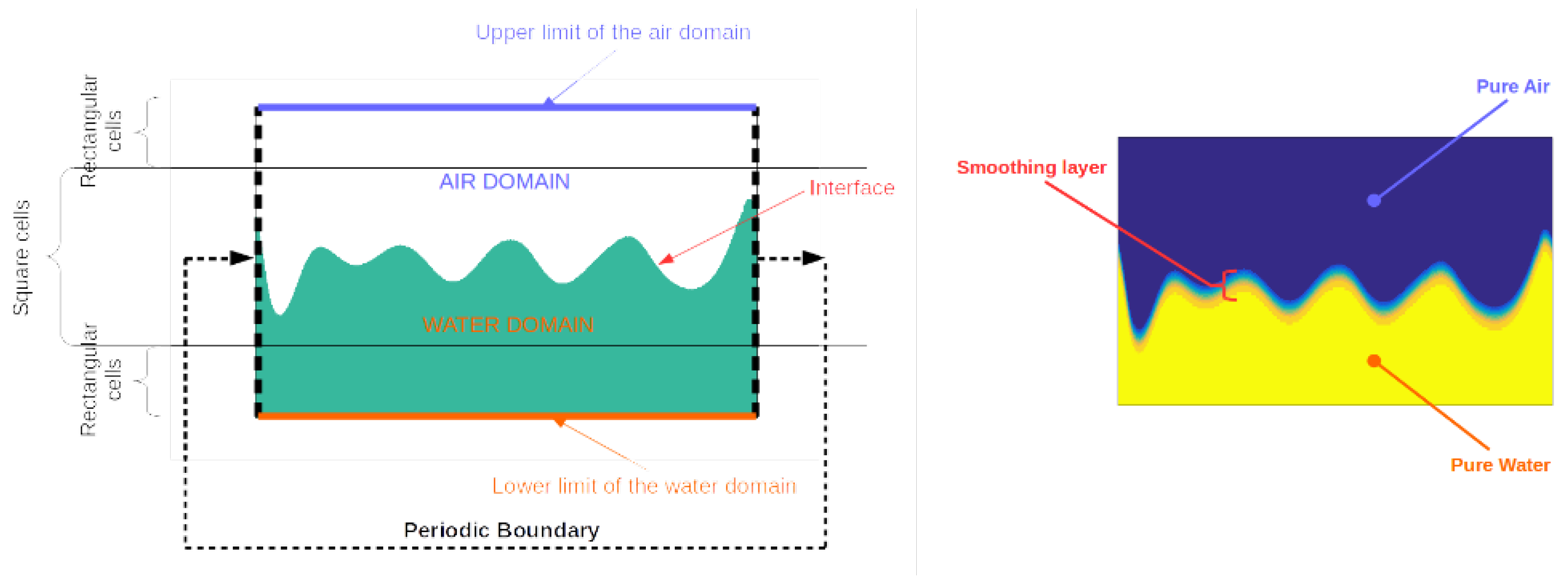
- Surface elevation and velocity potential are only defined at the surface. From the boundary value problem, defined on the contour, the potential at any point in the water domain is reconstructed by using boundary integral representation. The reconstruction is done numerically. The computational domain is discretised with square cells, i.e., dimension in the vertical axis is equal to the horizontal dimension, for . Out of this layer the vertical dimension is stretched logarithmically, i.e., rectangular cells (see Figure 2). A no slip boundary condition is used to limit the computational domain in .
- To obtain the velocity components in the water domain the spatial derivatives of the potential are computed using a second order finite difference scheme. The value at the centre of the cell, , is computed using the four points at . denotes the dimension of the cell.
- The boundary value problem is formulated also for the air domain. The boundary of the air domain are the air-water interface (at the bottom), and the arbitrarily chosen limit of the computational domain at the top (indicated in blue in Figure 2). At the free surface the continuity on the normal velocity is enforced providing the necessary Neumann condition for the solution of the boundary value problem. The velocity field in the air is then computed adopting the same methodology used for the water side (point 2. and 3.).
- The signed distance function d is initialised. This is needed for the initialisation of the density distribution in the Level-Set technique. The distance is measured from each grid node to the closest segment defined by two successive points on the resampled free surface. The distance is positive if the grid node is in water, negative in the air side. The Point in Polygon algorithm is used to identify if a grid node belongs to the air or the water side of the domain.
- At the interface between the two fluids (air and water), the velocity component tangential to the free surface has a jump. The discontinuity is consistent with the potential flow theory (no stress condition at the interface) but it does not apply to the two fluid approach. The jump is smoothed by gradually varying the fluid properties (density and viscosity) across the interface. Spurious component that are generated in this layer (∼5 cells, see Figure 2) because of the baroclinic variation of the velocity and of the spreading of the surface tension forces are not propagated in the rest of the domain because the density is reinitialised at each step.
3. Results
3.1. Numerical Simulations
3.1.1. Set-Up and Initial Conditions
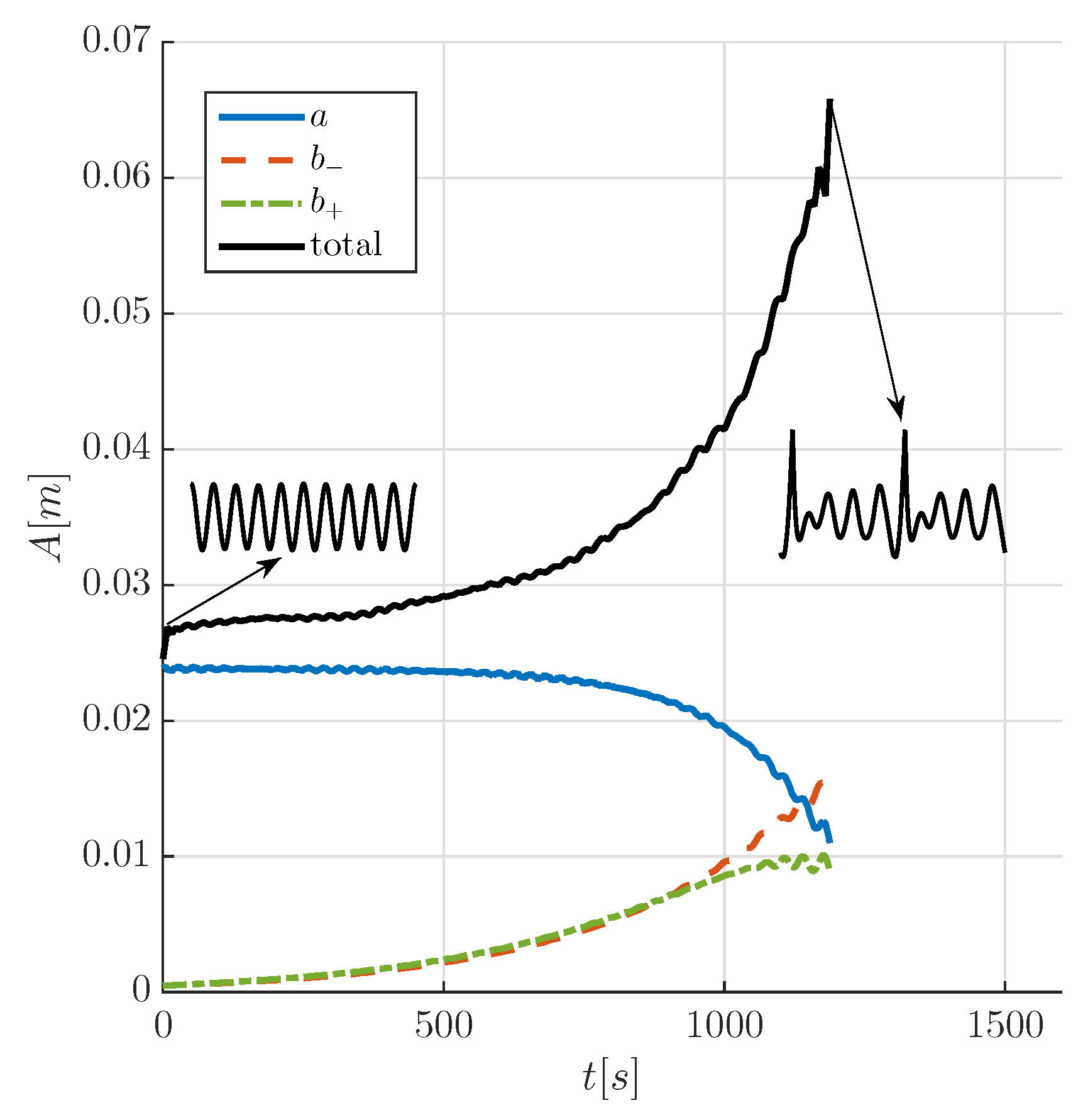
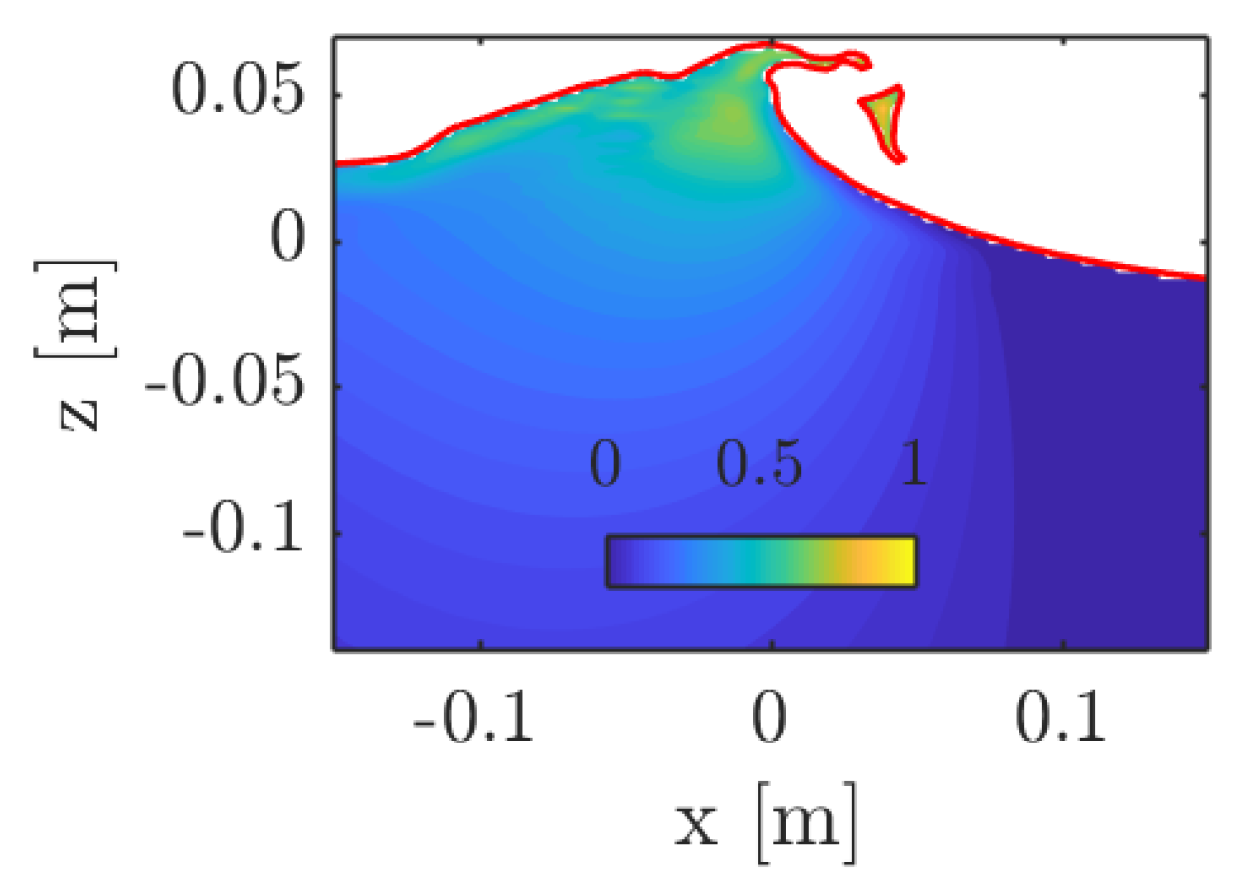
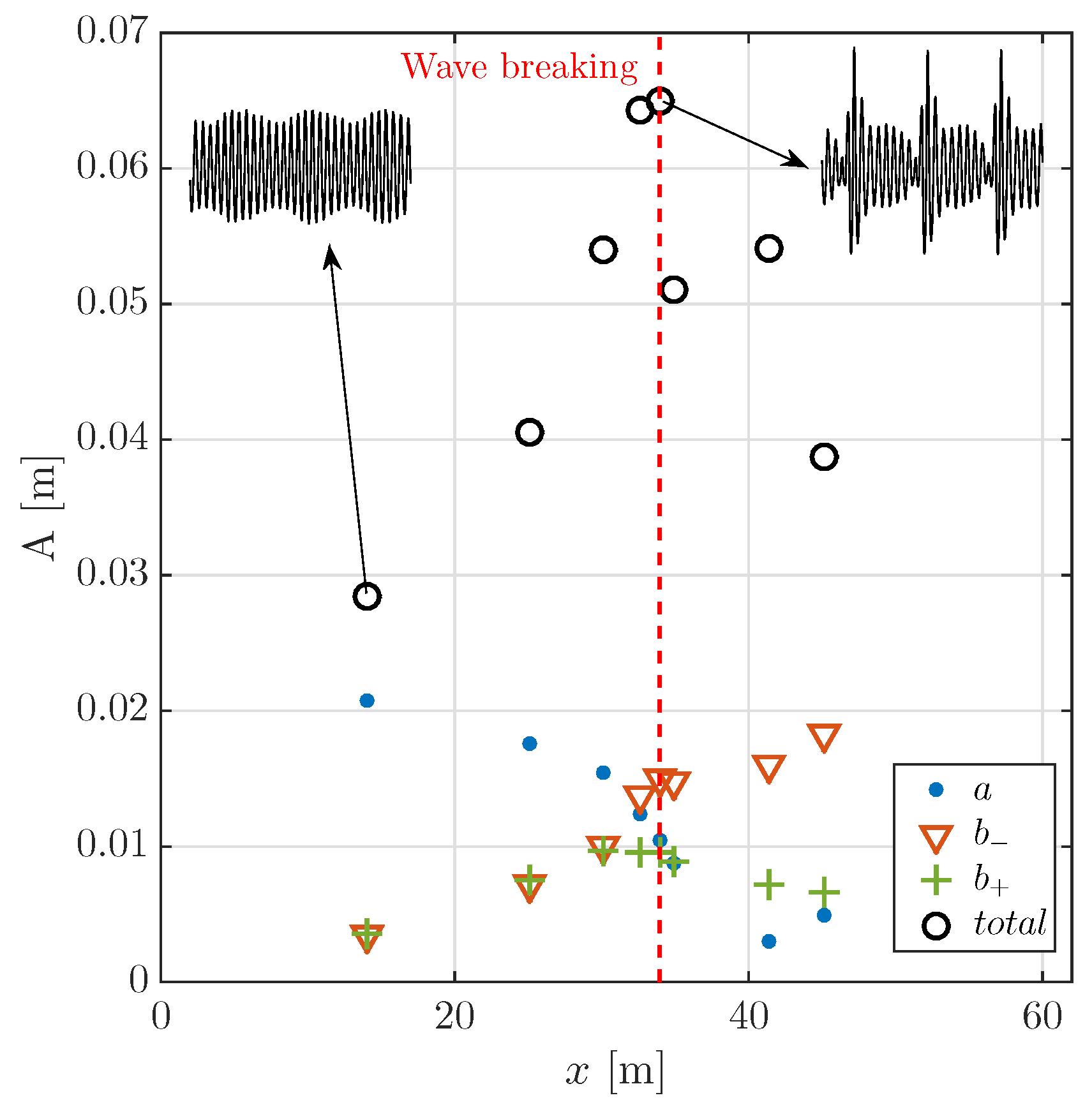
3.1.2. Wave Evolution
3.2. Laboratory Experiment
3.2.1. Set-Up and Initial Conditions
3.2.2. Wave Evolution
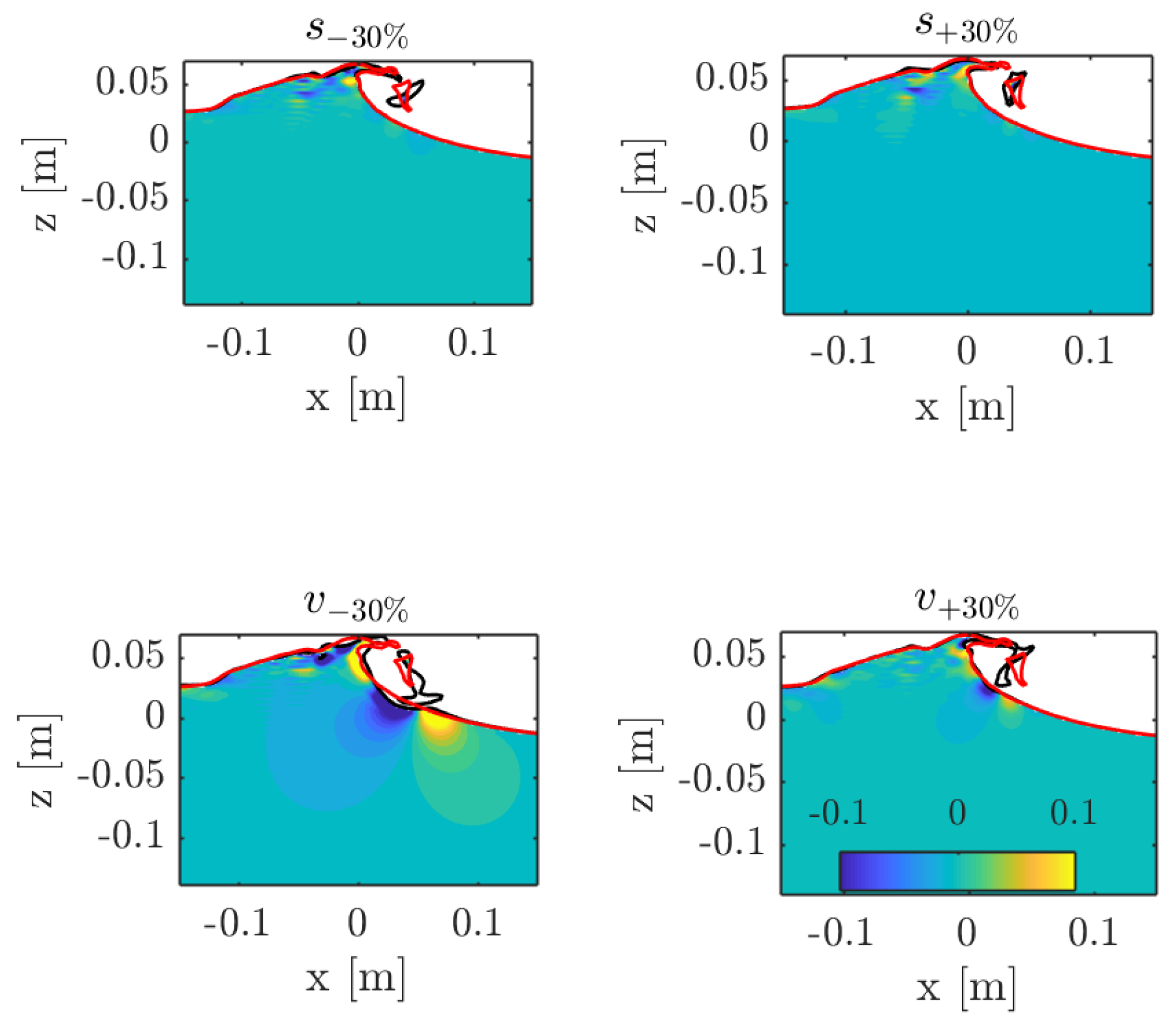
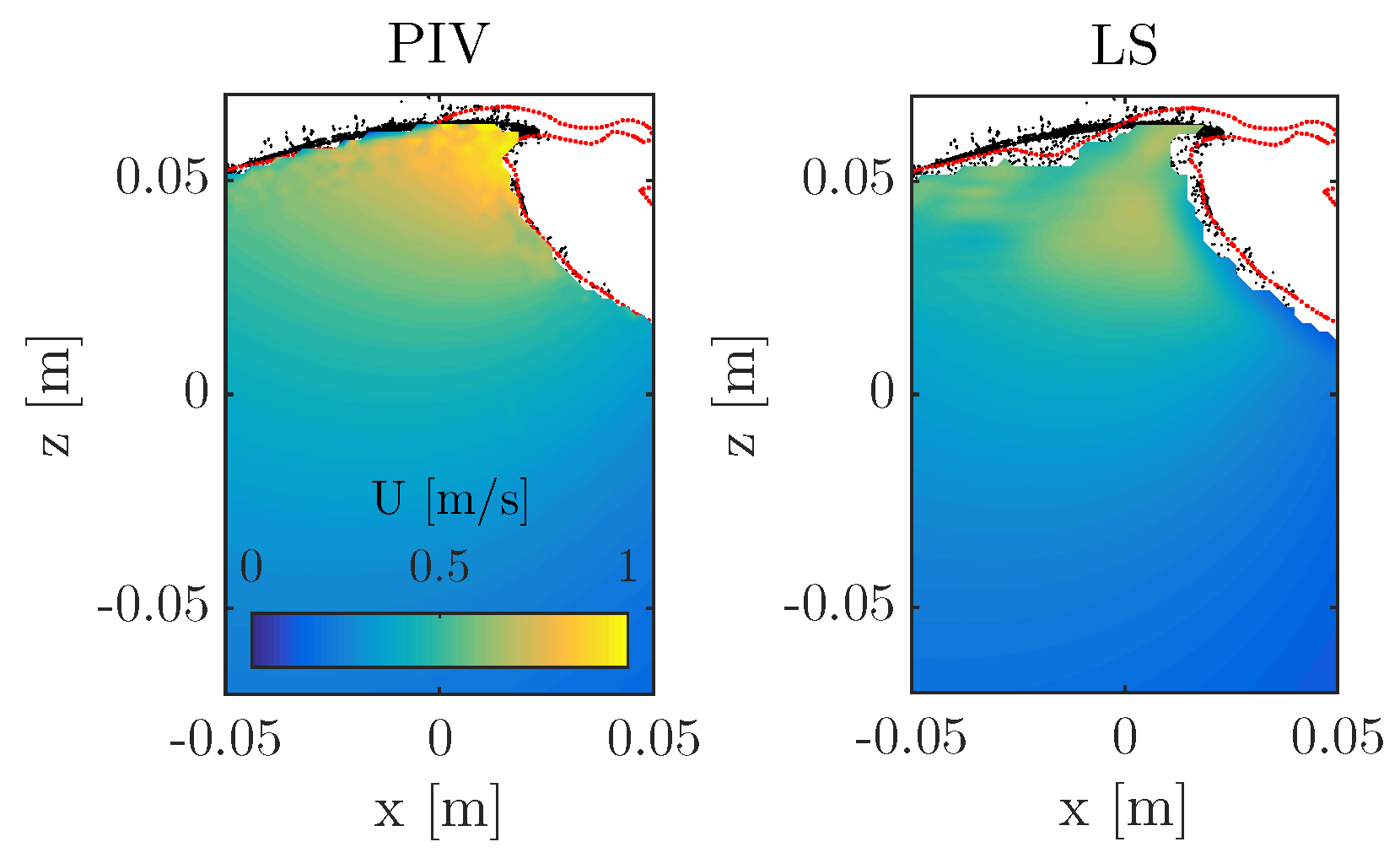
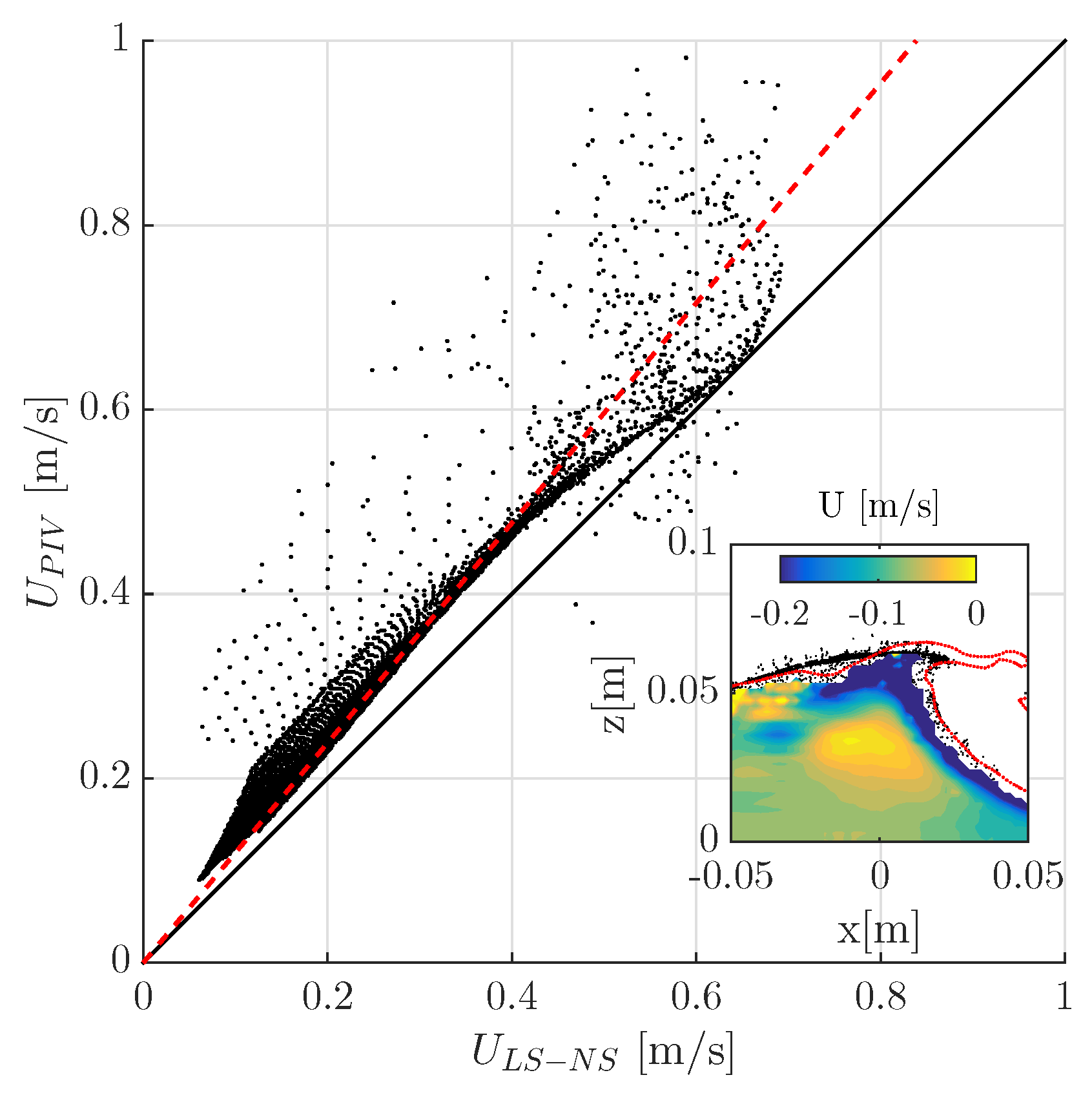
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bitner-Gregersen, E.; Toffoli, A. Occurrence of rogue sea states and consequences for marine structures. Ocean Dyn. 2014, 64, 1457–1468. [Google Scholar] [CrossRef]
- Liu, P. A chronology of freauqe wave encounters. Geofizika 2007, 24, 57–70. [Google Scholar]
- Nikolkina, I.; Didenkulova, I. Rogue waves in 2006–2010. Nat. Hazards Earth Syst. Sci. 2011, 11, 2913–2924. [Google Scholar] [CrossRef]
- Cavaleri, L.; Bertotti, L.; Torrisi, L.; Bitner-Gregersen, E.; Serio, M.; Onorato, M. Rogue waves in crossing seas: The Louis Majesty accident. J. Geophys. Res. Ocean. 2012, 117. [Google Scholar] [CrossRef]
- Longuet-Higgins, M. Breaking waves in deep or shallow water. In Proceedings of the 10th Conference on Naval Hydrodynamics, Cambridge, MA, USA, 24–28 June 1974; Volume 597. [Google Scholar]
- Tromans, P.; Anaturk, A.; Hagemeijer, P. A new model for the kinematics of large ocean waves-application as a design wave. In Proceedings of the First International Offshore and Polar Engineering Conference, Edinburgh, UK, 11–16 August 1991. [Google Scholar]
- Faltinsen, O. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Cambridge, UK, 1993; Volume 1. [Google Scholar]
- Clauss, G.; Klein, M. The New Year Wave in a seakeeping basin: Generation, propagation, kinematics and dynamics. Ocean Eng. 2011, 38, 1624–1639. [Google Scholar] [CrossRef]
- Onorato, M.; Proment, D.; Clauss, G.; Klein, M. Rogue waves: From nonlinear Schrödinger breather solutions to sea-keeping test. PLoS ONE 2013, 8, e54629. [Google Scholar] [CrossRef]
- Zhang, H.; Guedes Soares, C. Ship responses to abnormal waves simulated by the Nonlinear Schrödinger Equation. Ocean Eng. 2016. [Google Scholar] [CrossRef]
- Alberello, A.; Chabchoub, A.; Babanin, A.; Monty, J.; Lee, J.; Elsnab, J.; Bitner-Gregersen, E.; Toffoli, A. The Velocity Field Underneath Linear and Nonlinear Breaking Rogue Waves. In Proceedings of the ASME 2016 35th International Conference on Offshore Mechanics and Arctic Engineering, Busan, Korea, 19–24 June 2016. [Google Scholar]
- Alberello, A.; Chabchoub, A.; Monty, J.P.; Nelli, F.; Lee, J.H.; Elsnab, J.; Toffoli, A. An experimental comparison of velocities underneath focussed breaking waves. Ocean Eng. 2018, 155, 201–210. [Google Scholar] [CrossRef]
- Chaplin, J.; Rainey, R.; Yemm, R. Ringing of a vertical cylinder in waves. J. Fluid Mech. 1997, 350, 119–147. [Google Scholar] [CrossRef]
- Grue, J. On four highly nonlinear phenomena in wave theory and marine hydrodynamics. Appl. Ocean Res. 2002, 24, 261–274. [Google Scholar] [CrossRef]
- Wienke, J.; Oumeraci, H. Breaking wave impact force on a vertical and inclined slender pile—Theoretical and large-scale model investigations. Coast. Eng. 2005, 52, 435–462. [Google Scholar] [CrossRef]
- Morison, J.; Johnson, J.; Schaaf, S. The force exerted by surface waves on piles. J. Pet. Technol. 1950, 2, 149–154. [Google Scholar] [CrossRef]
- Goda, Y. Random Seas and Design of Maritime Structures; World Scientific: London, UK, 2010. [Google Scholar]
- Alberello, A.; Chabchoub, A.; Gramstad, O.; Babanin, A.V.; Toffoli, A. Non-Gaussian properties of second-order wave orbital velocity. Coast. Eng. 2016, 110, 42–49. [Google Scholar] [CrossRef]
- Grue, J.; Clamond, D.; Huseby, M.; Jensen, A. Kinematics of extreme waves in deep water. Appl. Ocean Res. 2003, 25, 355–366. [Google Scholar] [CrossRef]
- Grue, J.; Jensen, A. Experimental velocities and accelerations in very steep wave events in deep water. Eur. J. Mech. B Fluids 2006, 25, 554–564. [Google Scholar] [CrossRef]
- Alberello, A.; Pakodzi, C.; Nelli, F.; Bitner-Gregersen, E.M.; Toffoli, A. Three dimensional velocity field underneath a breaking rogue wave. In Proceedings of the ASME 2017 36th International Conference on Ocean, Offshore and Arctic Engineering, Trondheim, Norway, 25–30 June 2017. [Google Scholar]
- Lee, J.H.; Monty, J.P.; Elsnab, J.; Toffoli, A.; Babanin, A.V.; Alberello, A. Estimation of Kinetic Energy Dissipation from Breaking Waves in the Wave Crest Region. J. Phys. Oceanogr. 2017, 47, 1145–1150. [Google Scholar] [CrossRef]
- Donelan, M.; Anctil, F.; Doering, J. A simple method for calculating the velocity field beneath irregular waves. Coast. Eng. 1992, 16, 399–424. [Google Scholar] [CrossRef]
- Stansberg, C.; Gudmestad, O.; Haver, S. Kinematics under extreme waves. J. Offshore Mech. Arct. Eng. 2006, 130, 021010. [Google Scholar] [CrossRef]
- Iafrati, A. Numerical study of the effects of the breaking intensity on wave breaking flows. J. Fluid Mech. 2009, 622, 371–411. [Google Scholar] [CrossRef]
- Jacobsen, N.; Fuhrman, D.; Fredsøe, J. A Wave Generation Toolbox for the Open-Source CFD Library: OpenFOAM®. Int. J. Numerl. Meth. Fluids 2012, 70, 1073–1088. [Google Scholar] [CrossRef]
- Higuera, P.; Lara, J.; Losada, I. Simulating coastal engineering processes with OpenFOAM. Coast. Eng. 2013, 71, 119–134. [Google Scholar] [CrossRef]
- Alagan Chella, M.; Bihs, H.; Myrhaug, D.; Muskulus, M. Hydrodynamic characteristics and geometric properties of plunging and spilling breakers over impermeable slopes. Ocean Model. 2016, 103, 53–72. [Google Scholar] [CrossRef]
- Popinet, S. Gerris: A tree-based adaptive solver for the incompressible Euler equations in complex geometries. J. Comput. Phys. 2003, 190, 572–600. [Google Scholar] [CrossRef]
- Hirt, C.; Nichols, B. Volume of Fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Sussman, M.; Smereka, P.; Osher, S. A level set approach for computing solutions to incompressible two-phase flow. J. Comput. Phys. 1994, 114, 146–159. [Google Scholar] [CrossRef]
- Vogt, M.; Larsson, L. Level set methods for predicting viscous free surface flows. In Proceedings of the 7th International Conference on Numerical Ship Hydrodynamics, Nantes, France, 19–22 July 1999. [Google Scholar]
- Banner, M.; Peirson, W. Wave breaking onset and strength for two-dimensional deep-water wave groups. J. Fluid Mech. 2007, 585, 93–115. [Google Scholar] [CrossRef]
- Iafrati, A.; Babanin, A.; Onorato, M. Modulational instability, wave breaking, and formation of large-scale dipoles in the atmosphere. Phys. Rev. Lett. 2013, 110, 184504. [Google Scholar] [CrossRef]
- Iafrati, A.; Babanin, A.; Onorato, M. Modeling of ocean–atmosphere interaction phenomena during the breaking of modulated wave trains. J. Comput. Phys. 2014, 271, 151–171. [Google Scholar] [CrossRef]
- Perić, R.; Hoffmann, N.; Chabchoub, A. Initial wave breaking dynamics of Peregrine-type rogue waves: A numerical and experimental study. Eur. J. Mech. B Fluids 2015, 49, 71–76. [Google Scholar] [CrossRef]
- Vyzikas, T.; Deshoulières, S.; Giroux, O.; Barton, M.; Greaves, D. Numerical study of fixed Oscillating Water Column with RANS-type two-phase CFD model. Renew. Energy 2016. [Google Scholar] [CrossRef]
- Dommermuth, D.G.; Yue, D.K.P.; Lin, W.M.; Rapp, R.J.; Chan, E.S.; Melville, W.K. Deep-water plunging breakers: A comparison between potential theory and experiments. J. Fluid Mech. 1988, 189, 423–442. [Google Scholar] [CrossRef]
- Skyner, D. A comparison of numerical predictions and experimental measurements of the internal kinematics of a deep-water plunging wave. J. Fluid Mech. 1996, 315, 51–64. [Google Scholar] [CrossRef]
- Emarat, N.; Forehand, D.I.; Christensen, E.D.; Greated, C.A. Experimental and numerical investigation of the internal kinematics of a surf-zone plunging breaker. Eur. J. Mech. B Fluids 2012, 32, 1–16. [Google Scholar] [CrossRef]
- Iafrati, A.; De Vita, F.; Toffoli, A.; Alberello, A. Strongly nonlinear phenomena in water waves. Trans. SNAME 2015, 123, 17–38. [Google Scholar]
- Iafrati, A. Energy dissipation mechanisms in wave breaking processes: Spilling and highly aerated plunging breaking events. J. Geophys. Res. Ocean. 2011, 116. [Google Scholar] [CrossRef]
- West, B.; Brueckner, K.; Janda, R.; Milder, D.; Milton, R. A new numerical method for surface hydrodynamics. J. Geophys. Res. Ocean. 1987, 92, 11803–11824. [Google Scholar] [CrossRef]
- Dommermuth, D.; Yue, D. A high-order spectral method for the study of nonlinear gravity waves. J. Fluid Mech. 1987, 184, 267–288. [Google Scholar] [CrossRef]
- Toffoli, A.; Bitner-Gregersen, E.; Onorato, M.; Babanin, A. Wave crest and trough distributions in a broad-banded directional wave field. Ocean Eng. 2008, 35, 1784–1792. [Google Scholar] [CrossRef]
- Toffoli, A.; Benoit, M.; Onorato, M.; Bitner-Gregersen, E. The effect of third-order nonlinearity on statistical properties of random directional waves in finite depth. Nonlinear Process. Geophys. 2009, 16, 131–139. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.; Lewy, H. On the partial difference equations of mathematical physics. IBM J. Res. Dev. 1967, 11, 215–234. [Google Scholar] [CrossRef]
- Iafrati, A.; Di Mascio, A.; Campana, E. A level set technique applied to unsteady free surface flows. Int. J. Numer. Methods Fluids 2001, 35, 281–297. [Google Scholar] [CrossRef]
- Iafrati, A.; Campana, E. Free-surface fluctuations behind microbreakers: Space–time behaviour and subsurface flow field. J. Fluid Mech. 2005, 529, 311–347. [Google Scholar] [CrossRef]
- Babanin, A. Breaking and Dissipation of Ocean Surface Waves; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Alberello, A.; Onorato, M.; Frascoli, F.; Toffoli, A. Observation of turbulence and intermittency in wave-induced oscillatory flows. Wave Motion 2019, 84, 81–89. [Google Scholar] [CrossRef]
- Benjamin, T.; Feir, J. The disintegration of wave trains on deep water Part 1. Theory. J. Fluid Mech. 1967, 27, 417–430. [Google Scholar] [CrossRef]
- De Vita, F.; Verzicco, R.; Iafrati, A. Breaking of modulated wave groups: Kinematics and energy dissipation processes. J. Fluid Mech. 2018, 855, 267–298. [Google Scholar] [CrossRef]
- Iafrati, A.; Vita, F.D.; Verzicco, R. Effects of the wind on the breaking of modulated wave trains. Eur. J. Mech. B Fluids 2019, 73, 6–23. [Google Scholar] [CrossRef]
- Tulin, M.; Waseda, T. Laboratory observations of wave group evolution, including breaking effects. J. Fluid Mech. 1999, 378, 197–232. [Google Scholar] [CrossRef]
- Janssen, P. Nonlinear four-wave interactions and freak waves. J. Phys. Oceanogr. 2003, 33, 863–884. [Google Scholar] [CrossRef]
- Onorato, M.; Osborne, A.; Serio, M.; Cavaleri, L.; Brandini, C.; Stansberg, C. Observation of strongly non-Gaussian statistics for random sea surface gravity waves in wave flume experiments. Phys. Rev. E 2004, 70, 067302. [Google Scholar] [CrossRef]
- Ducrozet, G.; Bonnefoy, F.; Ferrant, P. On the equivalence of unidirectional rogue waves detected in periodic simulations and reproduced in numerical wave tanks. Ocean Eng. 2016, 117, 346–358. [Google Scholar] [CrossRef]
- Liu, X.; Duncan, J. The effects of surfactants on spilling breaking waves. Nature 2003, 421, 520–523. [Google Scholar] [CrossRef]
- Thielicke, W.; Stamhuis, E. PIVlab–Towards user-friendly, affordable and accurate digital particle image velocimetry in MATLAB. J. Open Res. Softw. 2014, 2, e30. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alberello, A.; Iafrati, A. The Velocity Field Underneath a Breaking Rogue Wave: Laboratory Experiments Versus Numerical Simulations. Fluids 2019, 4, 68. https://doi.org/10.3390/fluids4020068
Alberello A, Iafrati A. The Velocity Field Underneath a Breaking Rogue Wave: Laboratory Experiments Versus Numerical Simulations. Fluids. 2019; 4(2):68. https://doi.org/10.3390/fluids4020068
Chicago/Turabian StyleAlberello, Alberto, and Alessandro Iafrati. 2019. "The Velocity Field Underneath a Breaking Rogue Wave: Laboratory Experiments Versus Numerical Simulations" Fluids 4, no. 2: 68. https://doi.org/10.3390/fluids4020068
APA StyleAlberello, A., & Iafrati, A. (2019). The Velocity Field Underneath a Breaking Rogue Wave: Laboratory Experiments Versus Numerical Simulations. Fluids, 4(2), 68. https://doi.org/10.3390/fluids4020068




