Microstreaming and Its Role in Applications: A Mini-Review
Abstract
1. Introduction
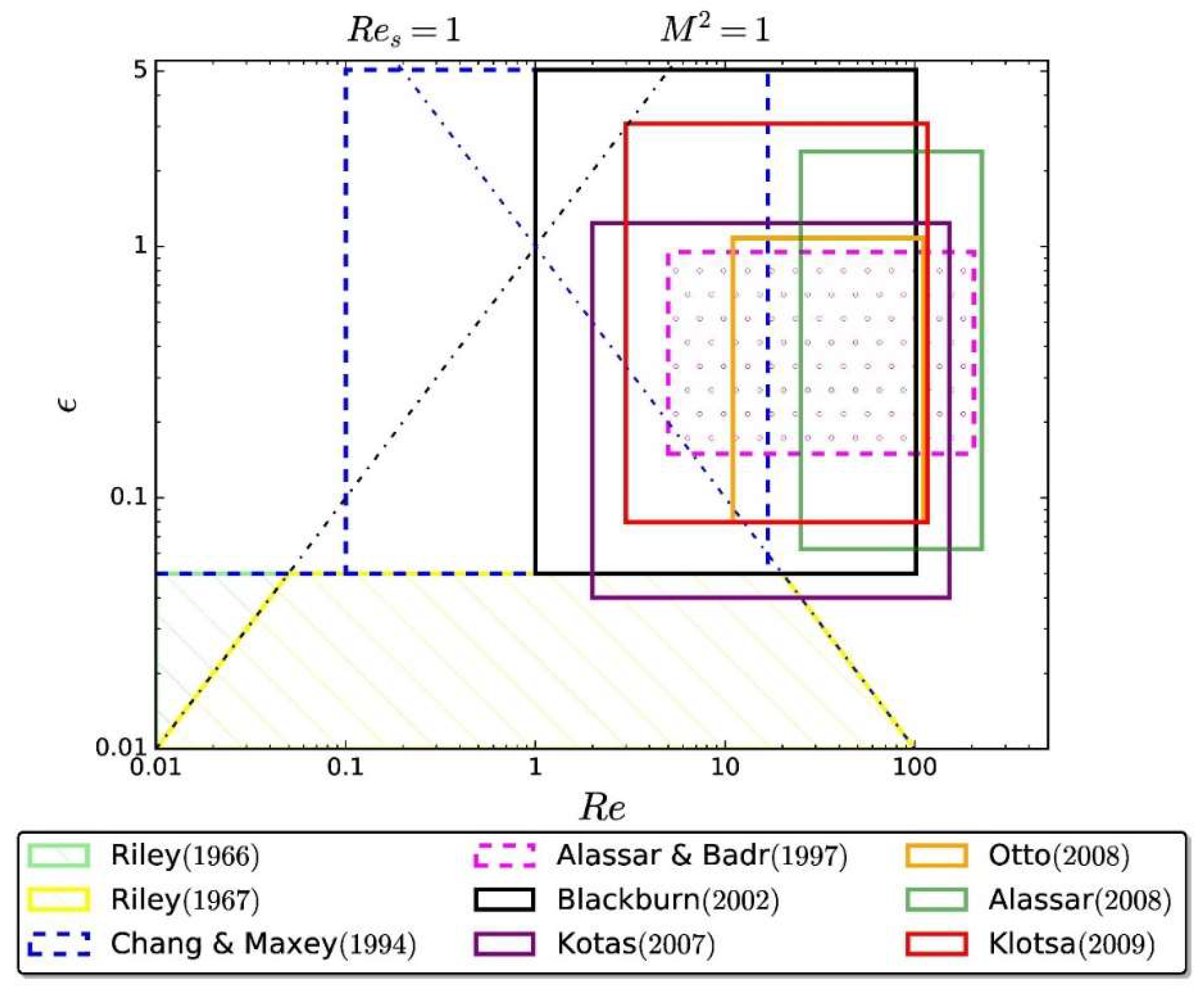
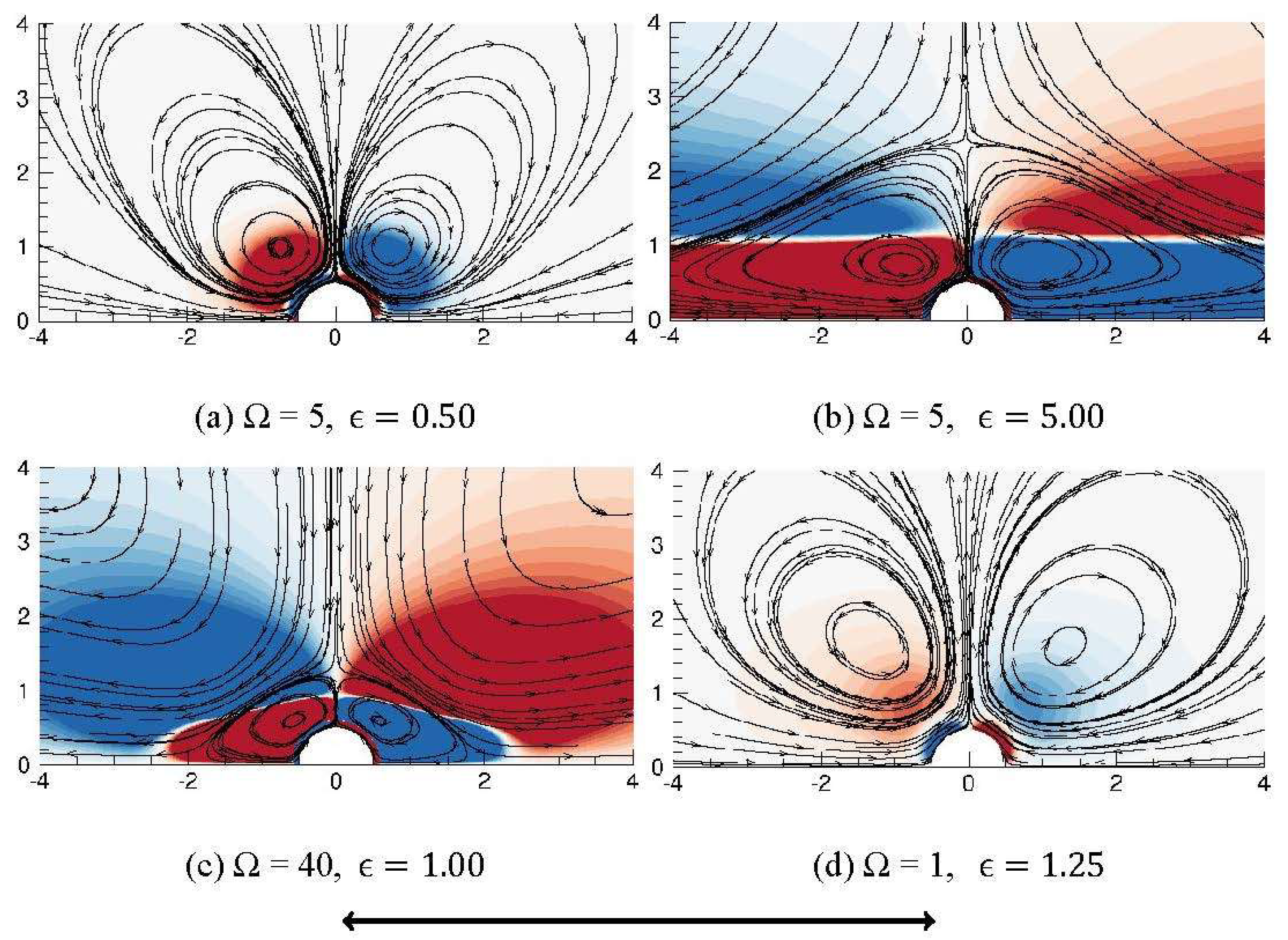
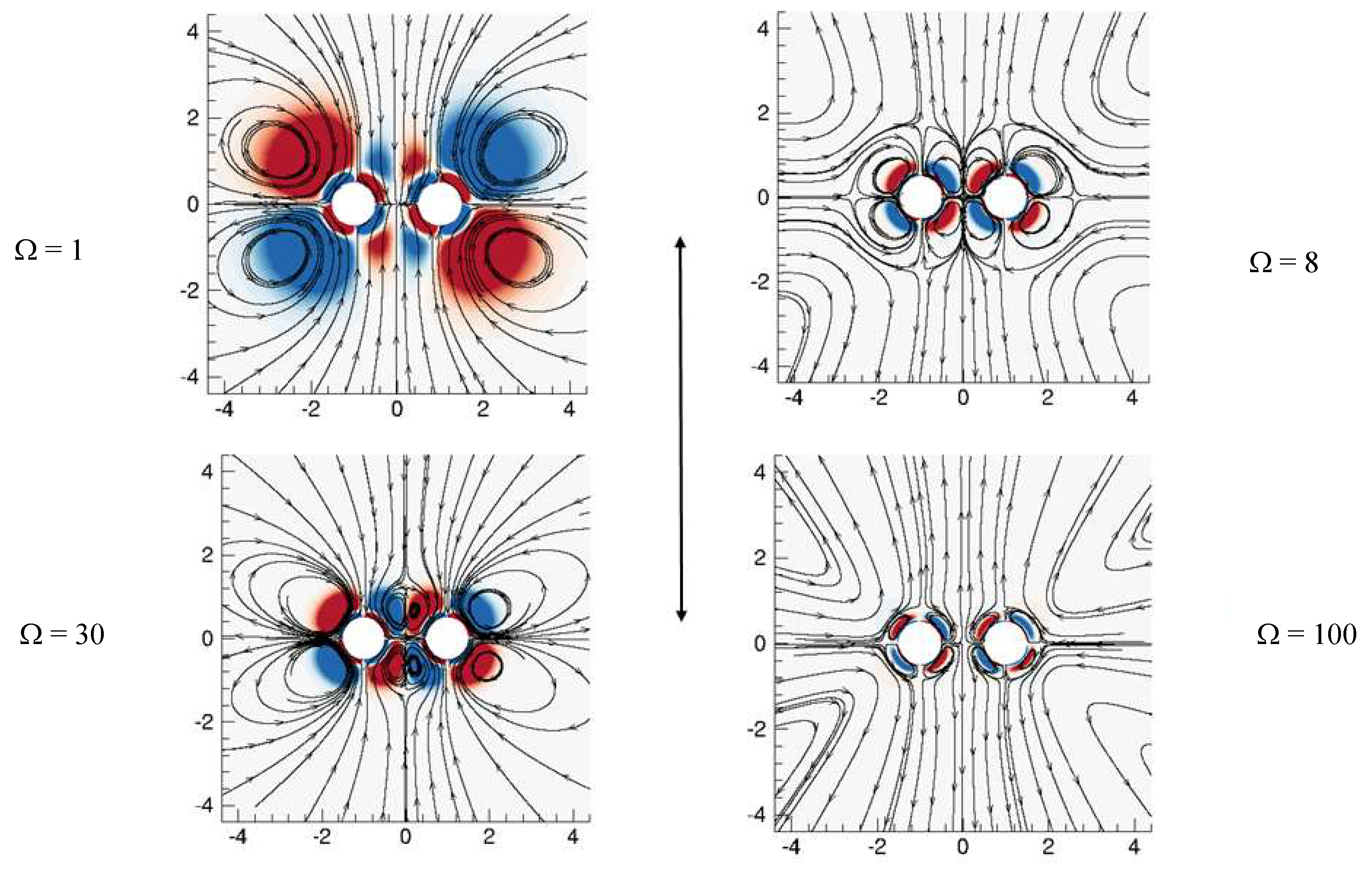
Numerical Origin of Microstreaming
2. Role of Microstreaming in Applications—Recent Developments
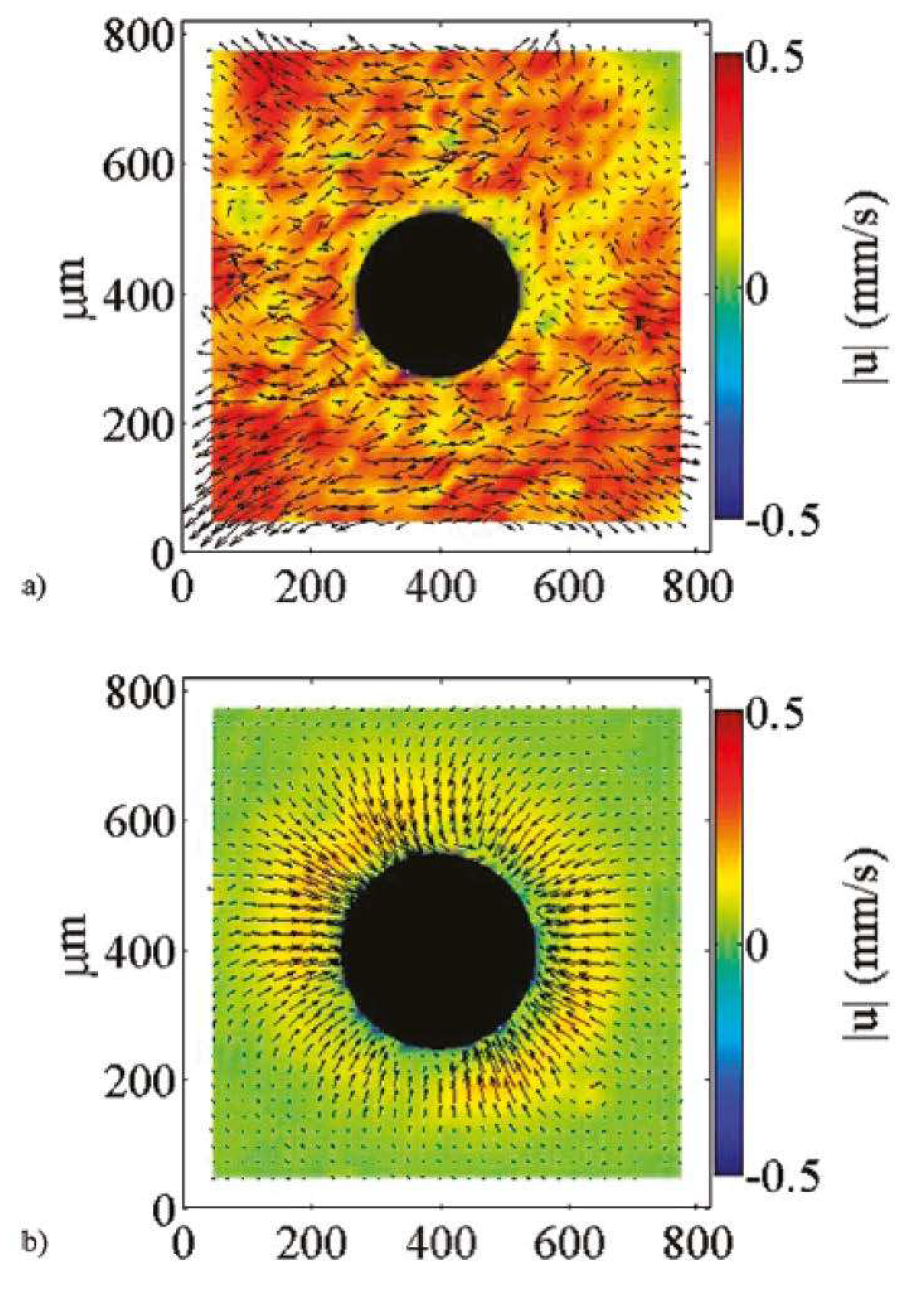
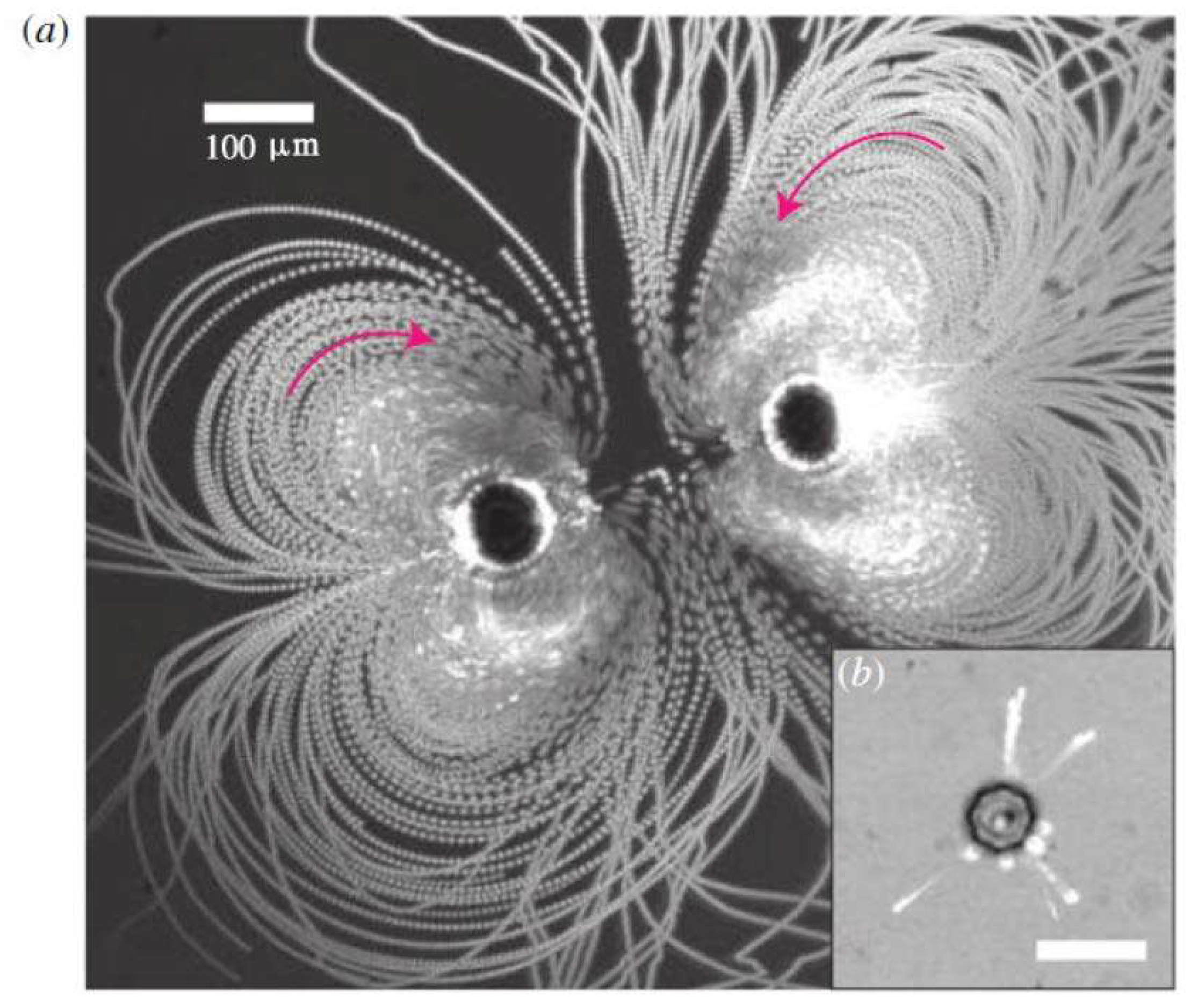
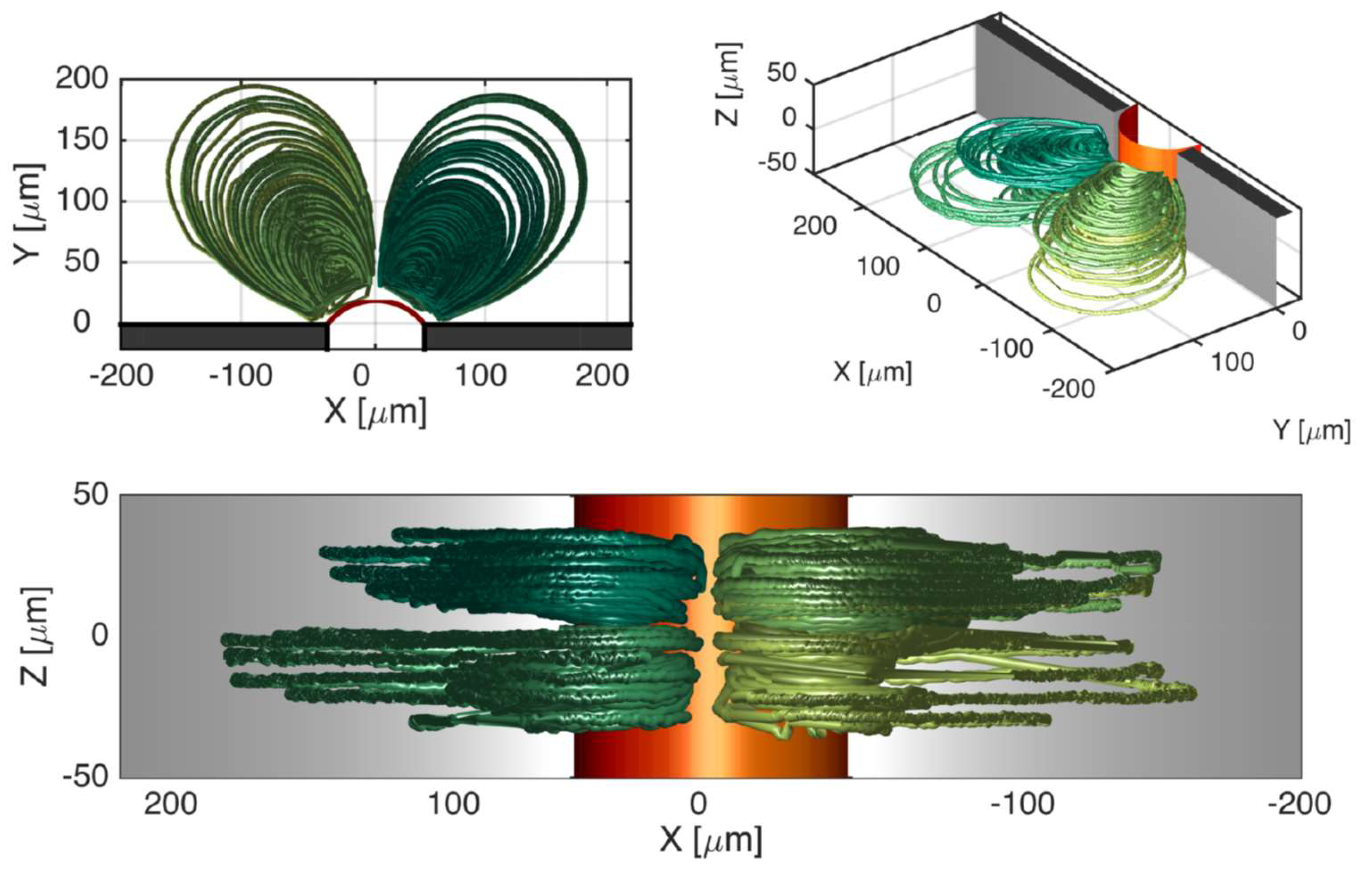
2.1. Cavitation Microstreaming
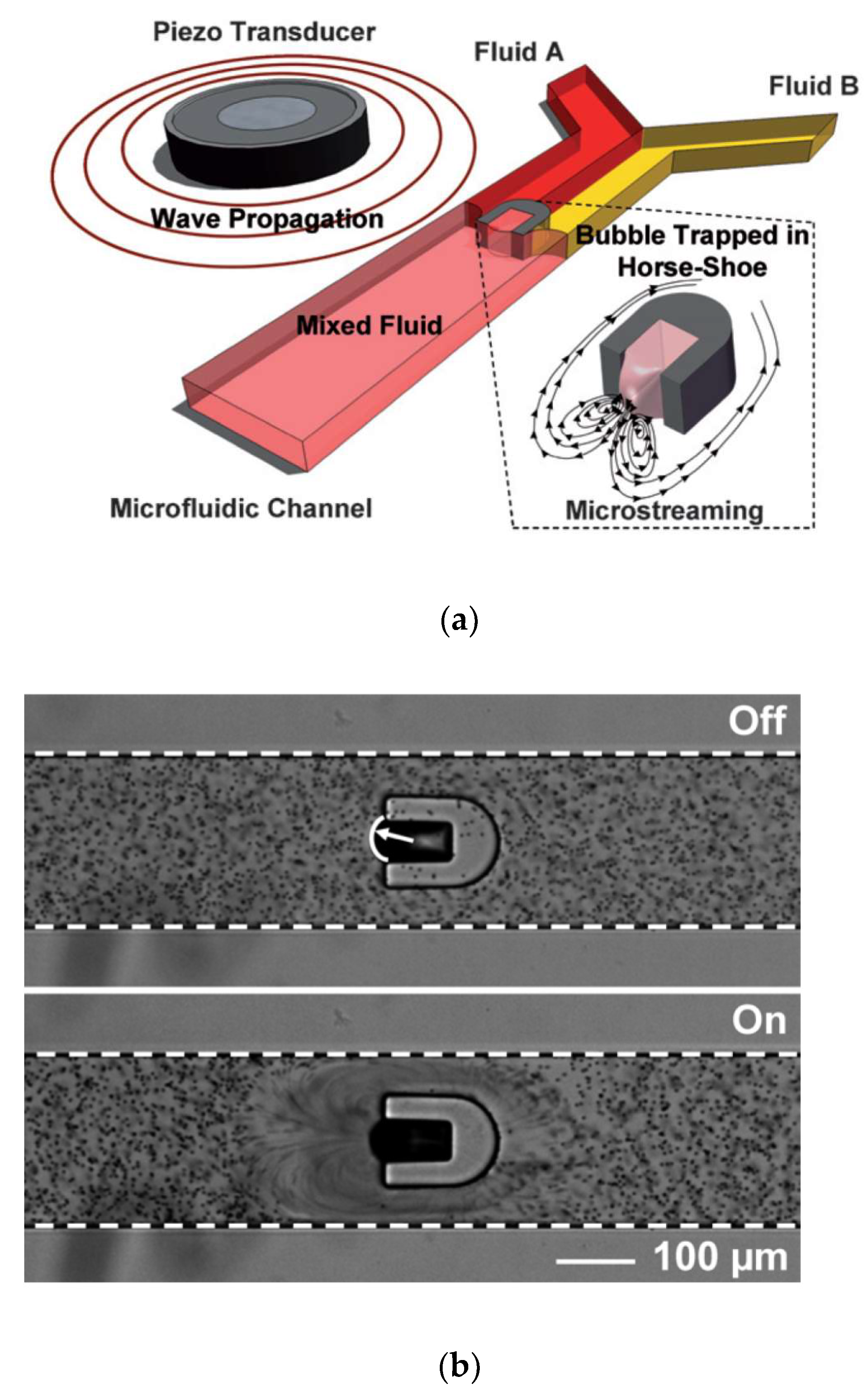
2.2. Microstreaming in Microfluidic Applications
2.2.1. Particle Separation and Manipulation
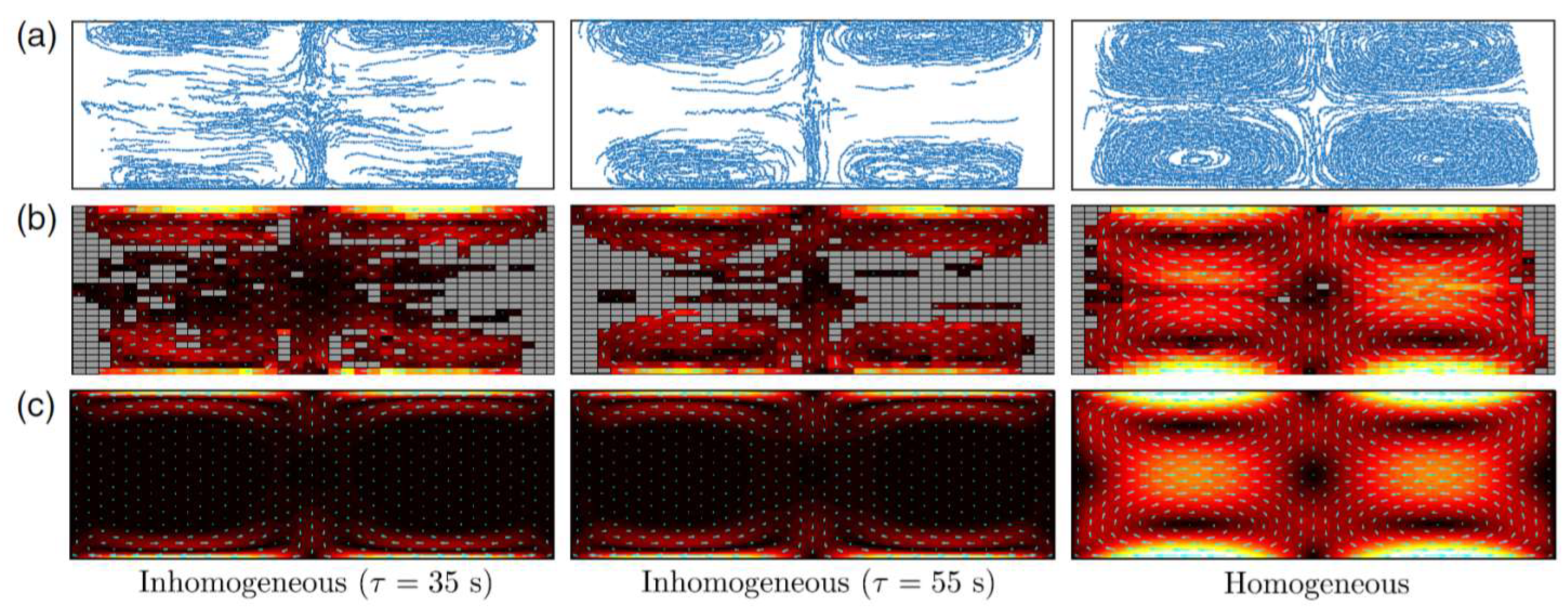
2.2.2. Mixing in Microfluidic Systems
3. Future Directions and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rayleigh, L. On the circulation of air observed in Kundt’s tubes and on some allied acoustical problems. Philos. Trans. R. Soc. 1884, 175, 1–21. [Google Scholar] [CrossRef]
- Faraday, M., XVII. On a peculiar class of acoustical figures; and on certain forms assumed by groups of particles upon vibrating elastic surfaces. Philos. Trans. R. Soc. 1831, 121, 299–340. [Google Scholar] [CrossRef]
- Chladni, E.F.F. Entdeckungen über die Theorie des Klanges; Zentralantiquariat der DDR: Leipzig, Germany, 1787. [Google Scholar]
- Dvořák, V. Ueber die akustische anziehung und abstossung. Ann. Phys. 1876, 233, 42–73. [Google Scholar] [CrossRef]
- Rayleigh, J.W.S. The Theory of Sound; Macmillan: London, UK, 2015; Volume 1. [Google Scholar]
- Schlichting, H. Boundary-Layer Theory; McGraw-Hill: New York, NY, USA, 1955. [Google Scholar]
- Stuart, J. Double boundary layers in oscillatory viscous flow. J. Fluid Mech. 1966, 24, 673–687. [Google Scholar] [CrossRef]
- Lighthill, J. Acoustic streaming. J. Sound Vibr. 1978, 61, 391–418. [Google Scholar] [CrossRef]
- Riley, N. Steady streaming. Annu. Rev. Fluid Mech. 2001, 33, 43–65. [Google Scholar] [CrossRef]
- Nyborg, W.L. Acoustic streaming due to attenuated plane waves. J. Acoust. Soc. Am. 1953, 25, 68–75. [Google Scholar] [CrossRef]
- Meissner, A. Uber piezo-elektrische kristalle bei hoch-frequenz. Z. Tekh. Fiz. 1926, 7, 585. [Google Scholar]
- Walker, J.; Allen, C. Sonic wind and static pressure in intense sound fields. J. Acoust. Soc. Am. 1950, 22, 680–681. [Google Scholar] [CrossRef]
- Eckart, C. Vortices and Streams Caused by Sound Waves. Phys. Rev. 1948, 73, 68–76. [Google Scholar] [CrossRef]
- Riley, N. Oscillatory viscous flows. Review and extension. IMA J. Appl. Math. 1967, 3, 419–434. [Google Scholar] [CrossRef]
- Riley, N. Acoustic streaming. Theor. Comput. Fluid Dyn. 1998, 10, 349–356. [Google Scholar] [CrossRef]
- Yeo, L.Y.; Friend, J.R. Surface acoustic wave microfluidics. Annu. Rev. Fluid Mech. 2014, 46, 379–406. [Google Scholar] [CrossRef]
- Friend, J.; Yeo, L.Y. Microscale acoustofluidics: Microfluidics driven via acoustics and ultrasonics. Rev. Mod. Phys. 2011, 83, 647. [Google Scholar] [CrossRef]
- Wiklund, M.; Green, R.; Ohlin, M. Acoustofluidics 14: Applications of acoustic streaming in microfluidic devices. Lab Chip 2012, 12, 2438–2451. [Google Scholar] [CrossRef] [PubMed]
- Riley, N. On a sphere oscillating in a viscous fluid. Q. J. Mech. Appl. Math. 1966, 19, 461–472. [Google Scholar] [CrossRef]
- Chang, E.J.; Maxey, M.R. Unsteady flow about a sphere at low to moderate Reynolds number. Part 1. Oscillatory motion. J. Fluid Mech. 1994, 277, 347–379. [Google Scholar] [CrossRef]
- Alassar, R.; Badr, H. Oscillating viscous flow over a sphere. Comput. Fluids 1997, 26, 661–682. [Google Scholar] [CrossRef]
- Blackburn, H.M. Mass and momentum transport from a sphere in steady and oscillatory flows. Phys. Fluids 2002, 14, 3997–4011. [Google Scholar] [CrossRef]
- Kotas, C.W.; Yoda, M.; Rogers, P.H. Visualization of steady streaming near oscillating spheroids. Exp. Fluids 2007, 42, 111–121. [Google Scholar] [CrossRef]
- Otto, F.; Riegler, E.K.; Voth, G.A. Measurements of the steady streaming flow around oscillating spheres using three dimensional particle tracking velocimetry. Phys. Fluids 2008, 20, 093304. [Google Scholar] [CrossRef]
- Alassar, R.S. Acoustic streaming on spheres. Int. J. Non-Linear Mech. 2008, 43, 892–897. [Google Scholar] [CrossRef]
- Klotsa, D.; Swift, M.R.; Bowley, R.; King, P. Interaction of spheres in oscillatory fluid flows. Phys. Rev. E 2007, 76, 056314. [Google Scholar] [CrossRef] [PubMed]
- Jalal, J. Interaction of Spherical Particles Owing to Steady Streaming Induced by Ultrasound. Ph.D. Thesis, Swinburne University of Technology, Melbourne, Victoria, March 2018. [Google Scholar]
- Tho, P.; Manasseh, R.; Ooi, A. Cavitation microstreaming patterns in single and multiple bubble systems. J. Fluid Mech. 2007, 576, 191–233. [Google Scholar] [CrossRef]
- Leong, T.; Collis, J.; Manasseh, R.; Ooi, A.; Novell, A.; Bouakaz, A.; Ashokkumar, M.; Kentish, S. The role of surfactant headgroup, chain length, and cavitation microstreaming on the growth of bubbles by rectified diffusion. J. Phys. Chem. C 2011, 115, 24310–24316. [Google Scholar] [CrossRef]
- Leong, T.; Wu, S.; Kentish, S.; Ashokkumar, M. Growth of bubbles by rectified diffusion in aqueous surfactant solutions. J. Phys. Chem. C 2010, 114, 20141–20145. [Google Scholar] [CrossRef]
- Church, C.C. A method to account for acoustic microstreaming when predicting bubble growth rates produced by rectified diffusion. J. Acoust. Soc. Am. 1988, 84, 1758–1764. [Google Scholar] [CrossRef] [PubMed]
- Gould, R.K. Rectified diffusion in presence of, and absence of, acoustic streaming. J. Acoust. Soc. Am. 1974, 56, 1740–1746. [Google Scholar] [CrossRef]
- Marmottant, P.; Versluis, M.; de Jong, N.; Hilgenfeldt, S.; Lohse, D. High-speed imaging of an ultrasound-driven bubble in contact with a wall: “Narcissus” effect and resolved acoustic streaming. Exp. Fluids 2006, 41, 147–153. [Google Scholar] [CrossRef]
- Mekki-Berrada, F.; Combriat, T.; Thibault, P.; Marmottant, P. Interactions enhance the acoustic streaming around flattened microfluidic bubbles. J. Fluid Mech. 2016, 797, 851–873. [Google Scholar] [CrossRef]
- Uemura, Y.; Sasaki, K.; Minami, K.; Sato, T.; Choi, P.-K.; Takeuchi, S. Observation of cavitation bubbles and acoustic streaming in high intensity ultrasound fields. Jpn. J. Appl. Phys. 2015, 54, 07HB05. [Google Scholar] [CrossRef]
- Slama, R.B.H.; Gilles, B.; Chiekh, M.B.; Béra, J.-C. PIV for the characterization of focused field induced acoustic streaming: Seeding particle choice evaluation. Ultrasonics 2017, 76, 217–226. [Google Scholar] [CrossRef] [PubMed]
- Gale, G.W.; Busnaina, A.A. Roles of cavitation and acoustic streaming in megasonic cleaning. Part. Sci. Technol. 1999, 17, 229–238. [Google Scholar] [CrossRef]
- Leong, T.; Johansson, L.; Mawson, R.; McArthur, S.L.; Manasseh, R.; Juliano, P. Ultrasonically enhanced fractionation of milk fat in a litre-scale prototype vessel. Ultrason. Sonochem. 2016, 28, 118–129. [Google Scholar] [CrossRef] [PubMed]
- Hagsäter, S.M.; Jensen, T.G.; Bruus, H.; Kutter, J.P. Acoustic resonances in microfluidic chips: Full-image micro-PIV experiments and numerical simulations. Lab Chip 2007, 7, 1336–1344. [Google Scholar] [CrossRef] [PubMed]
- Castro, A.; Hoyos, M. Study of the onset of the acoustic streaming in parallel plate resonators with pulse ultrasound. Ultrasonics 2016, 66, 166–171. [Google Scholar] [CrossRef] [PubMed]
- Devendran, C.; Gralinski, I.; Neild, A. Separation of particles using acoustic streaming and radiation forces in an open microfluidic channel. Microfluid Nanofluid 2014, 17, 879–890. [Google Scholar] [CrossRef]
- Ahmed, D.; Mao, X.; Shi, J.; Juluri, B.K.; Huang, T.J. A millisecond micromixer via single-bubble-based acoustic streaming. Lab Chip 2009, 9, 2738–2741. [Google Scholar] [CrossRef] [PubMed]
- Louisnard, O. A viable method to predict acoustic streaming in presence of cavitation. Ultrason. Sonochem. 2017, 35, 518–524. [Google Scholar] [CrossRef] [PubMed]
- Karlsen, J.T.; Qiu, W.; Augustsson, P.; Bruus, H. Acoustic streaming and its suppression in inhomogeneous fluids. Phys. Rev. Lett. 2018, 120, 054501. [Google Scholar] [CrossRef] [PubMed]
- Marin, A.; Rossi, M.; Rallabandi, B.; Wang, C.; Hilgenfeldt, S.; Kähler, C.J. Three-dimensional phenomena in microbubble acoustic streaming. Phys. Rev. Appl. 2015, 3, 041001. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jalal, J.; Leong, T.S.H. Microstreaming and Its Role in Applications: A Mini-Review. Fluids 2018, 3, 93. https://doi.org/10.3390/fluids3040093
Jalal J, Leong TSH. Microstreaming and Its Role in Applications: A Mini-Review. Fluids. 2018; 3(4):93. https://doi.org/10.3390/fluids3040093
Chicago/Turabian StyleJalal, Javeria, and Thomas S. H. Leong. 2018. "Microstreaming and Its Role in Applications: A Mini-Review" Fluids 3, no. 4: 93. https://doi.org/10.3390/fluids3040093
APA StyleJalal, J., & Leong, T. S. H. (2018). Microstreaming and Its Role in Applications: A Mini-Review. Fluids, 3(4), 93. https://doi.org/10.3390/fluids3040093



