Numerical Investigation of Cylindrical Water Droplets Subjected to Air Shock Loading at a High Weber Number
Abstract
1. Introduction
2. Two-Phase Flow Simulation
2.1. Governing Equations
2.2. Computational Model
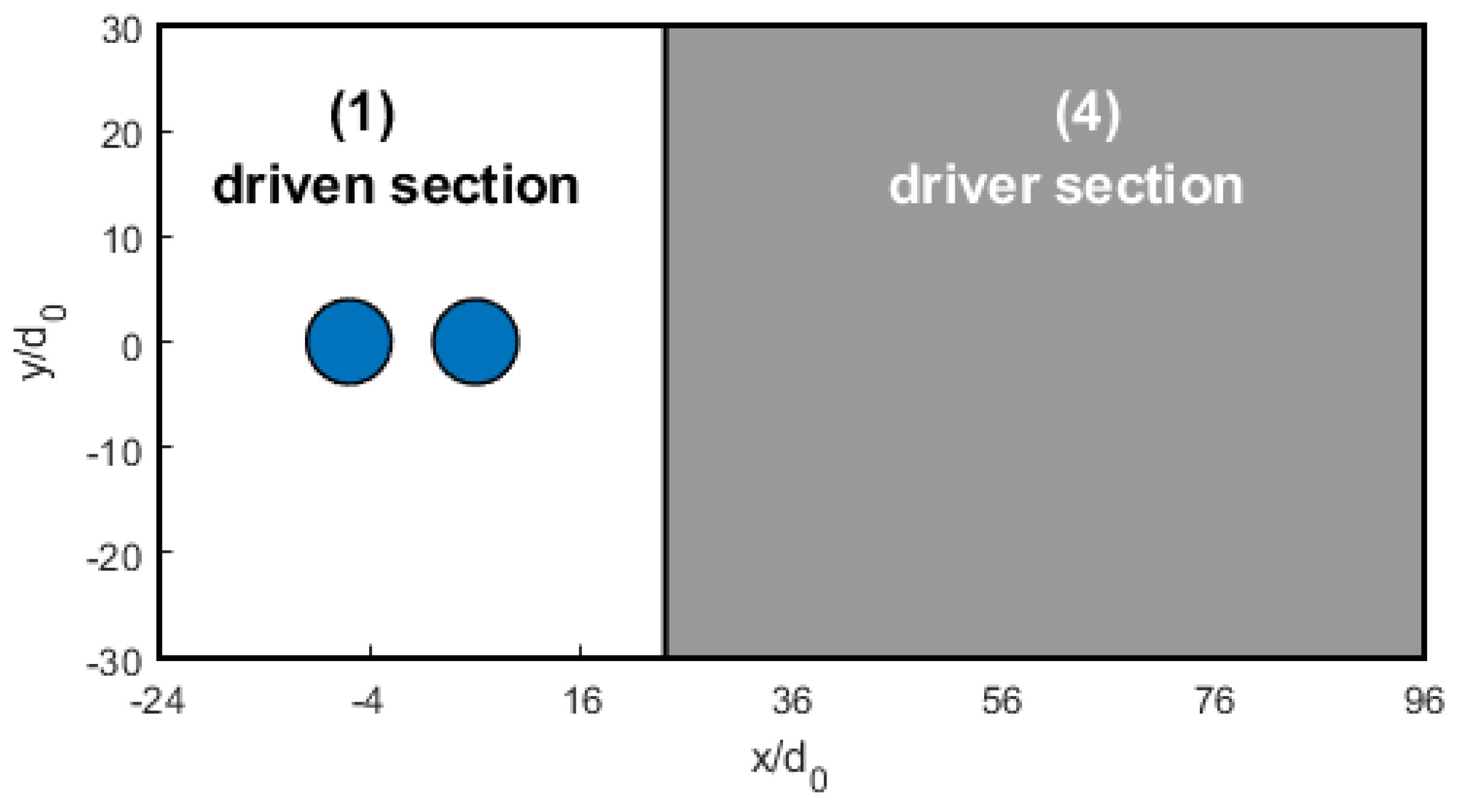
2.3. Case Study
3. Numerical Method
4. Results
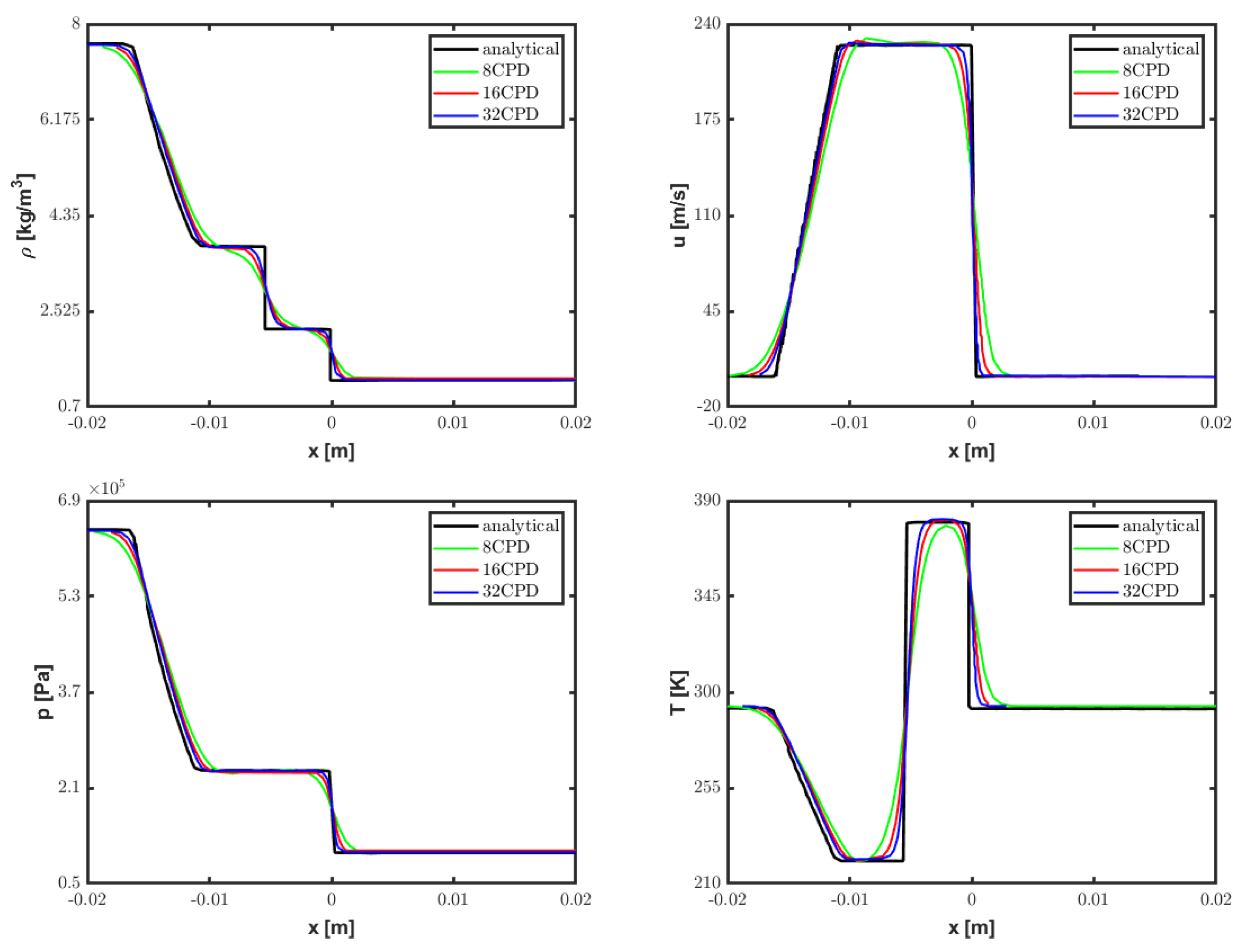
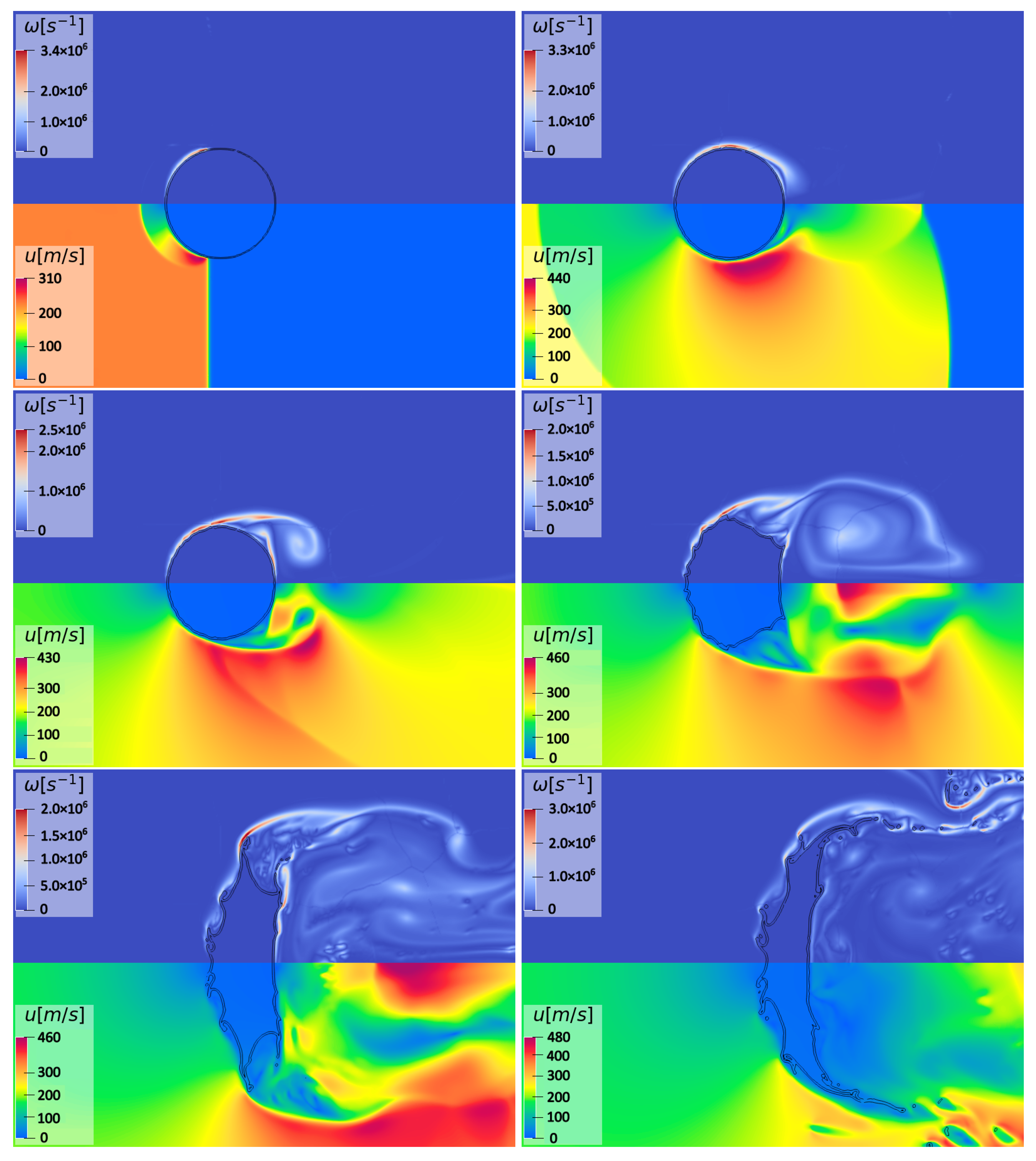
4.1. Shock-Tube Flow
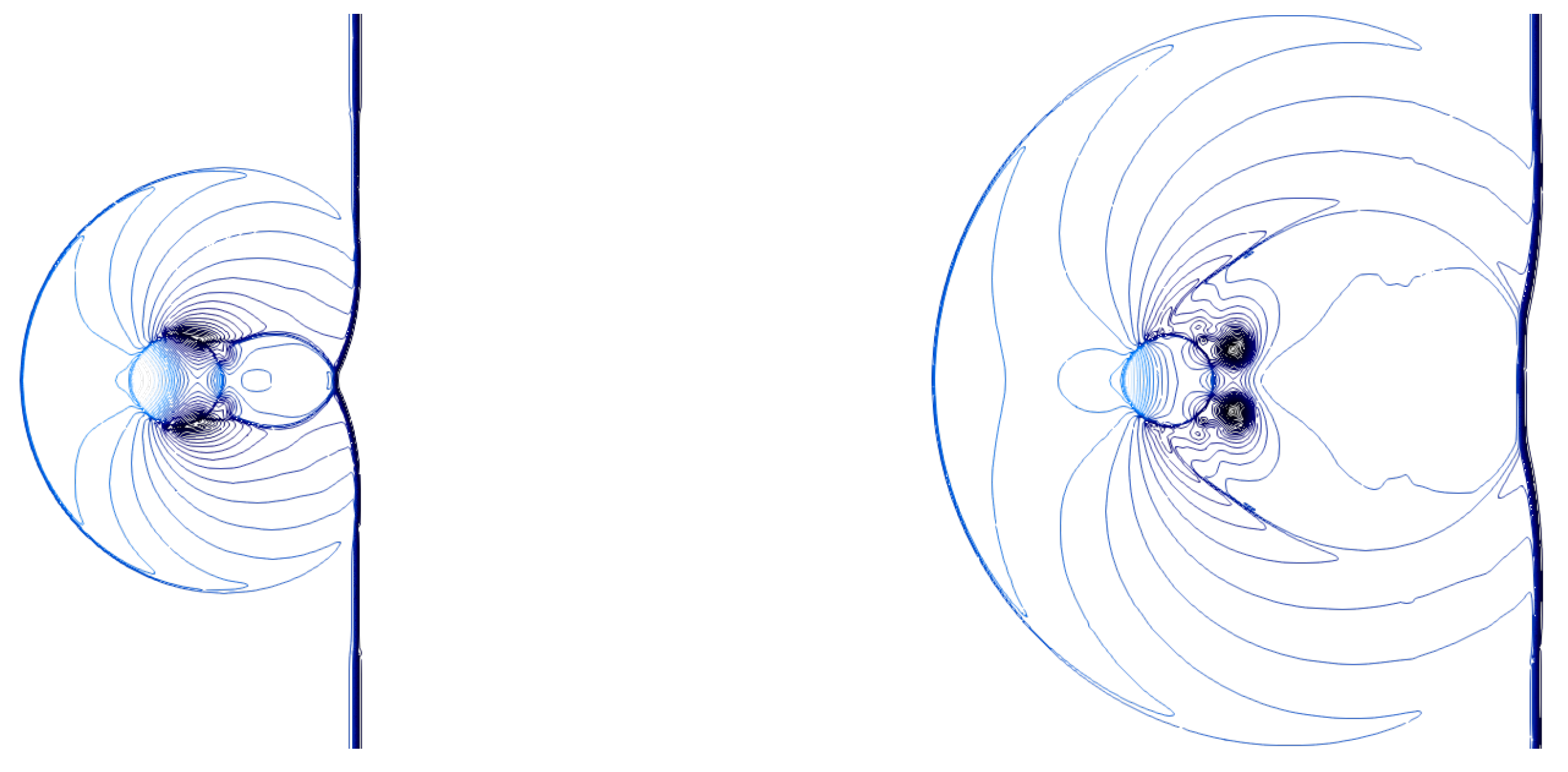
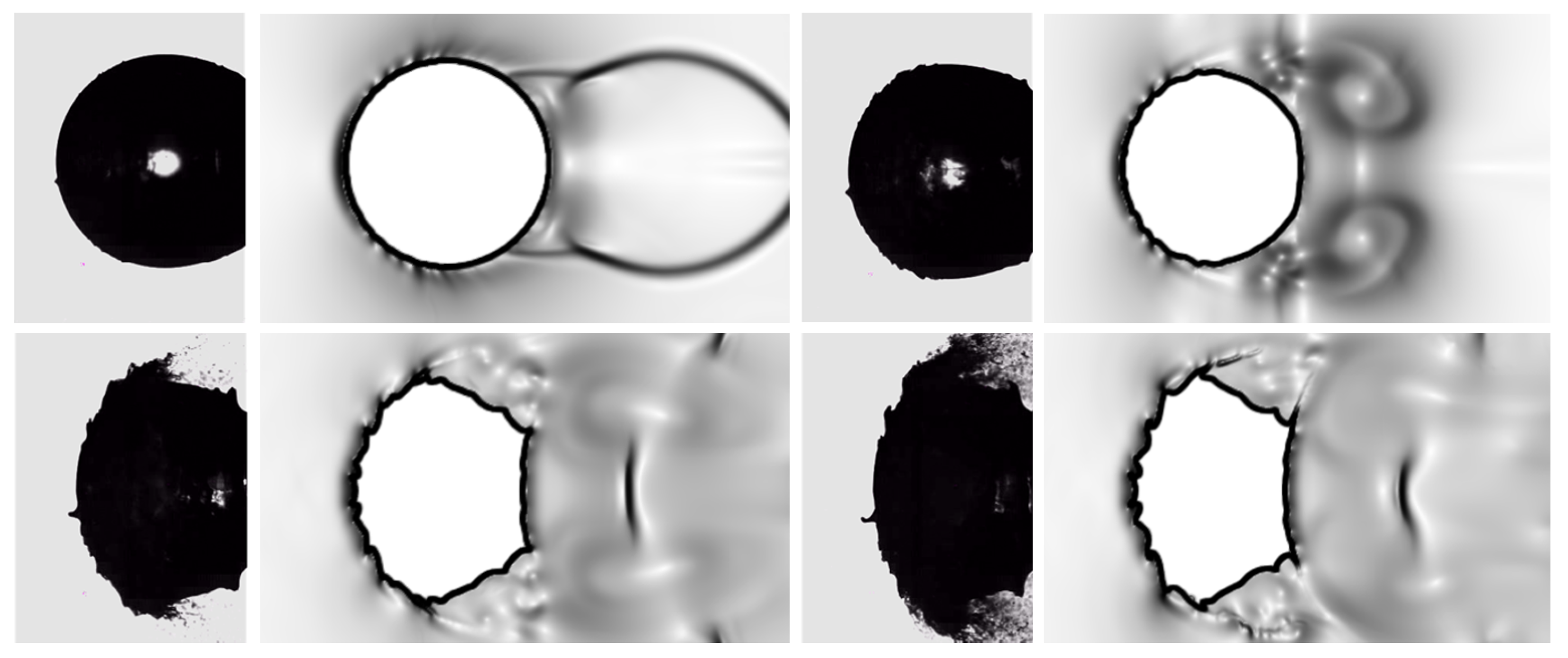
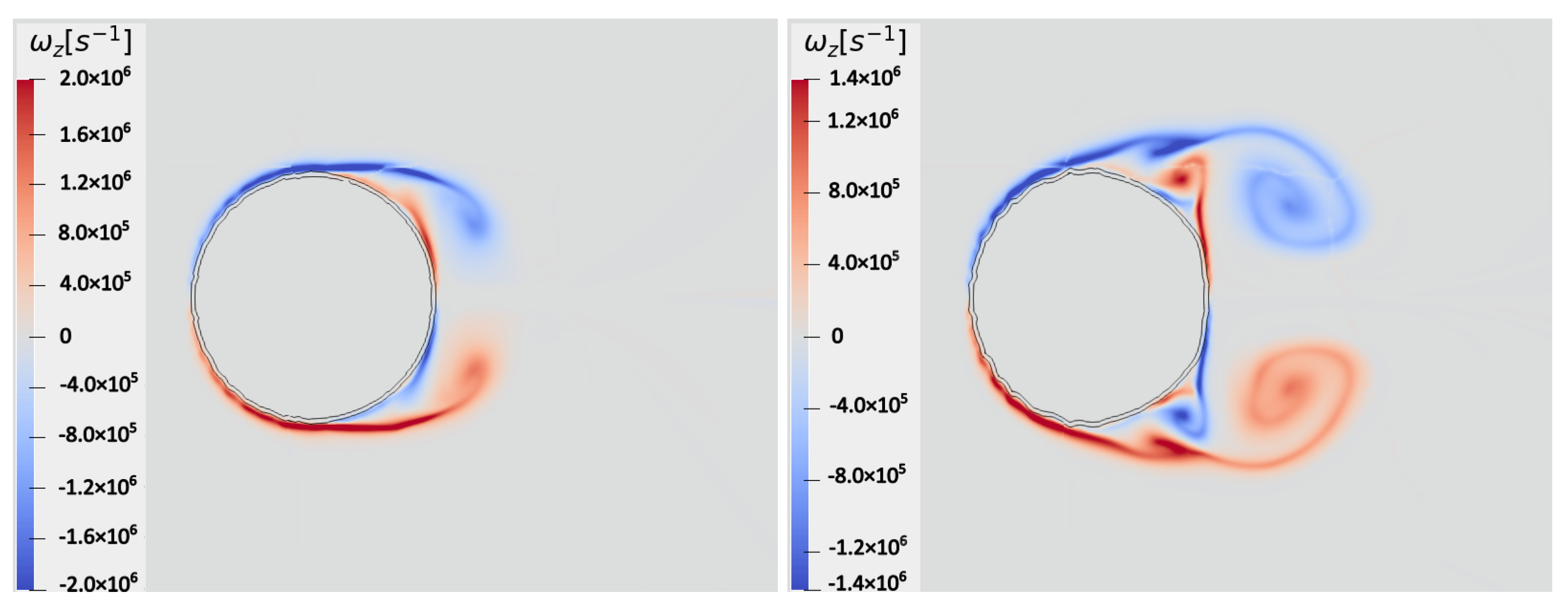
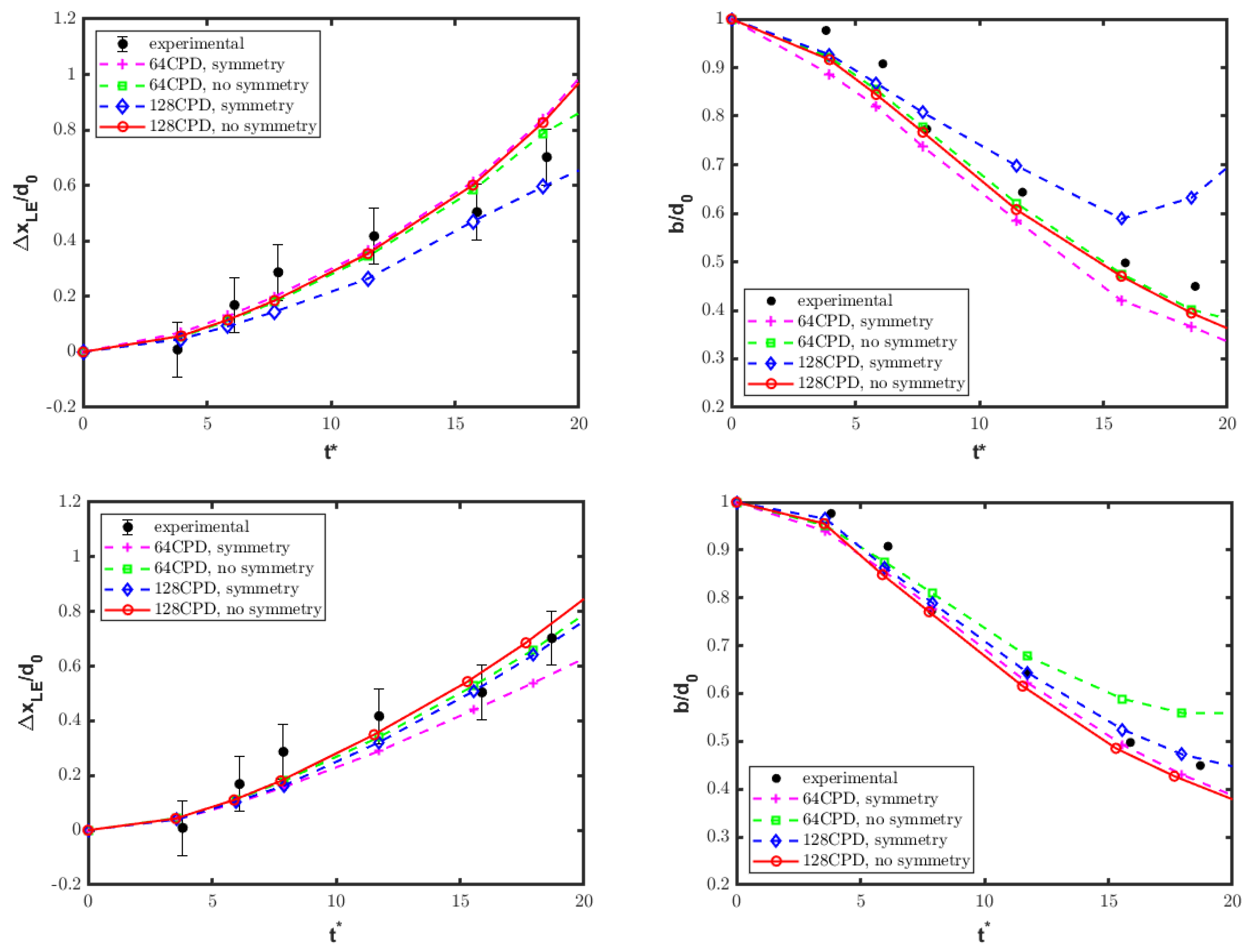
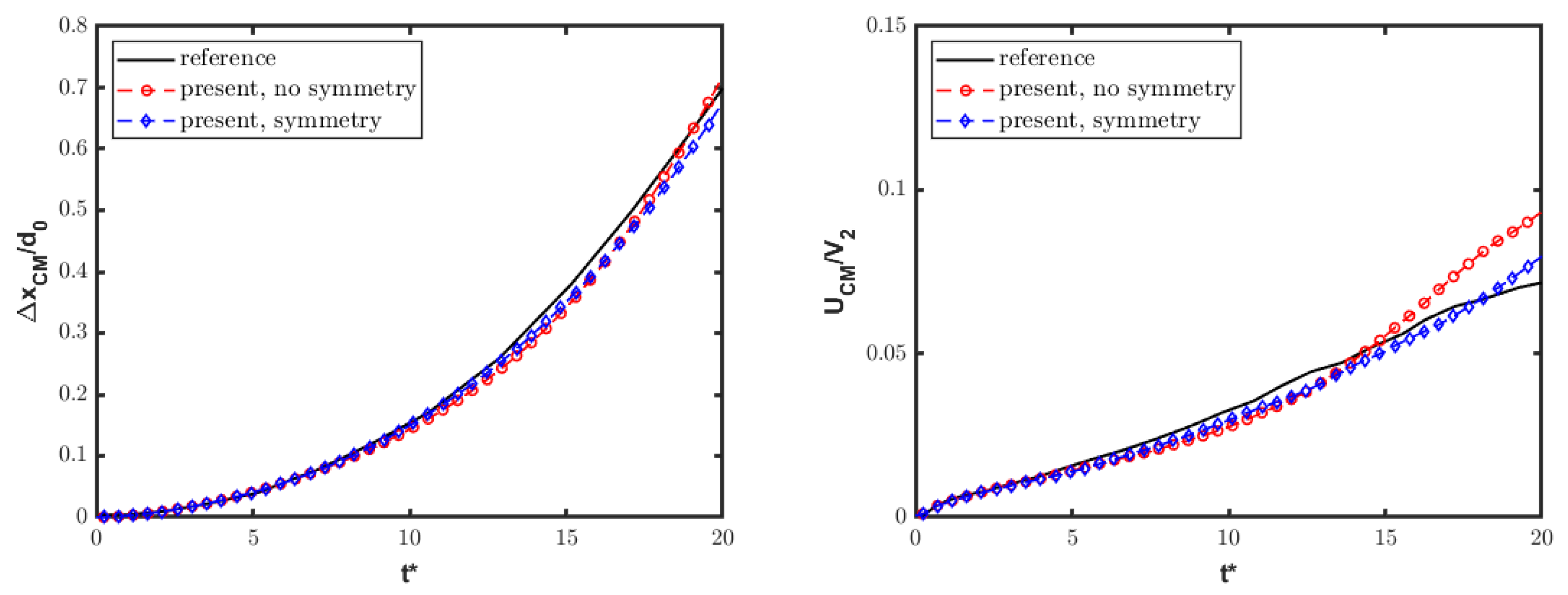
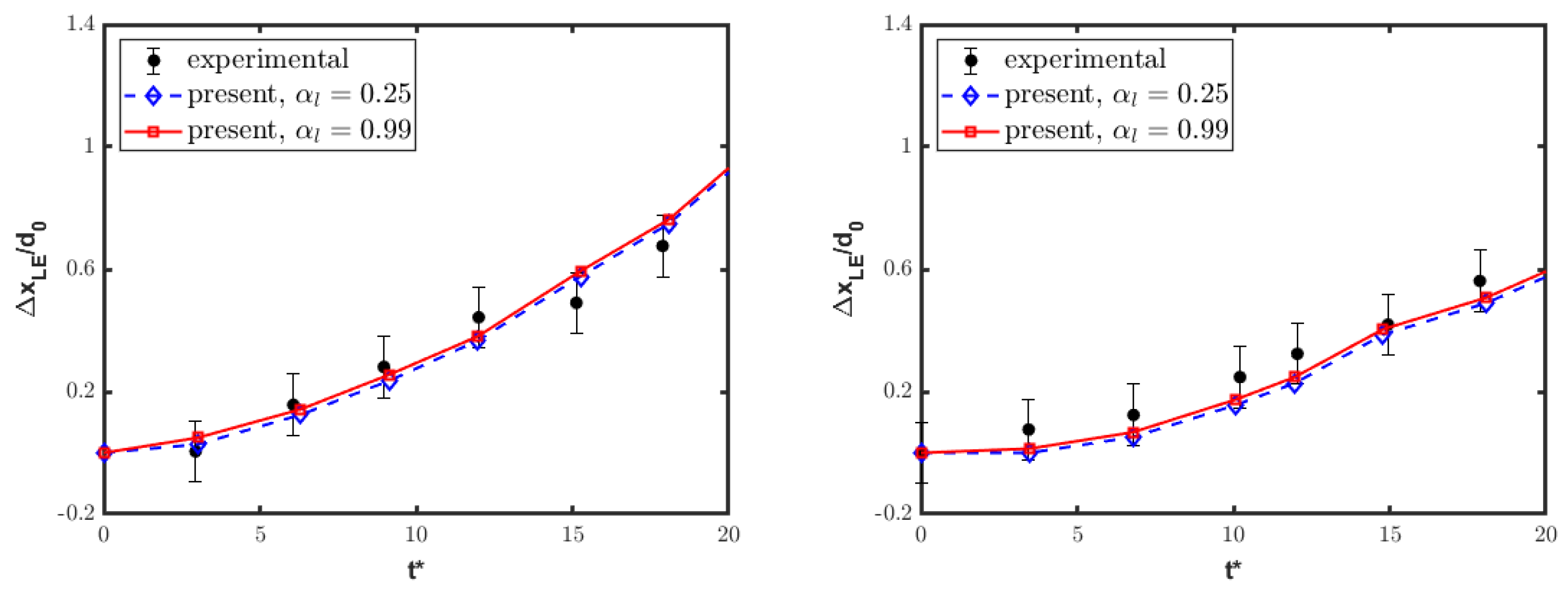
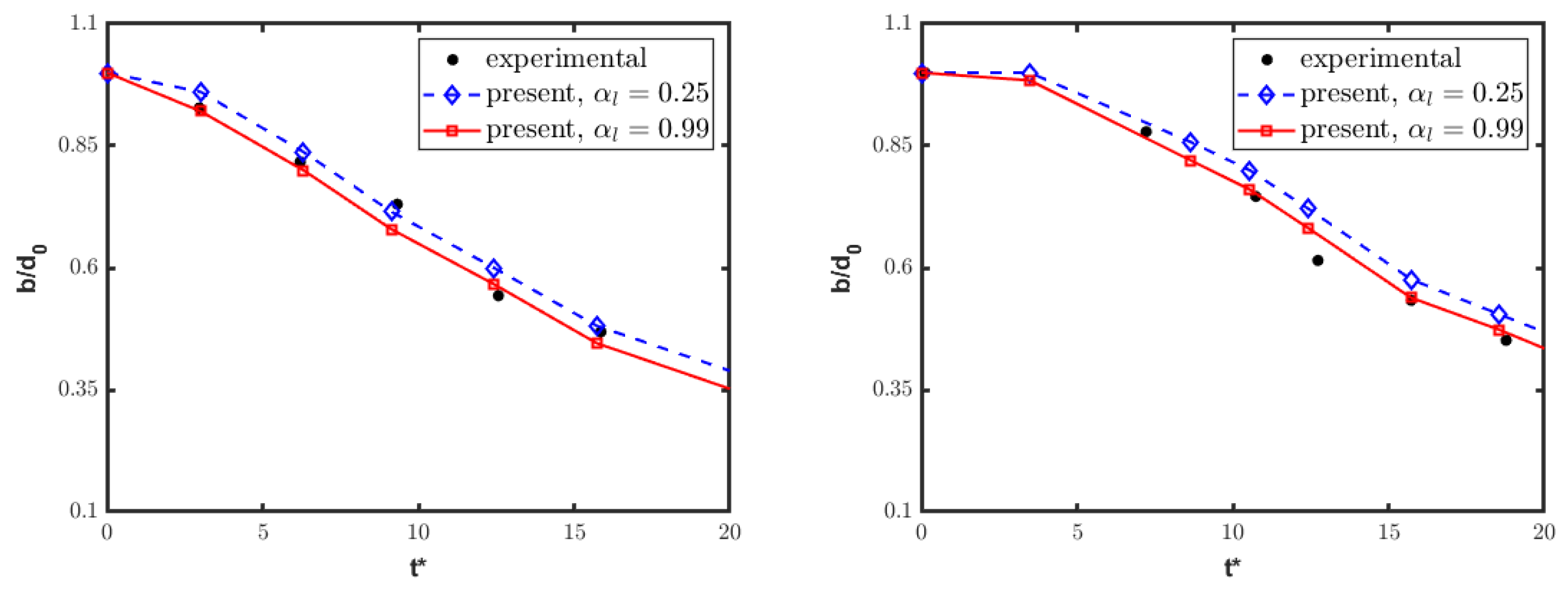
4.2. Single-Column Configuration
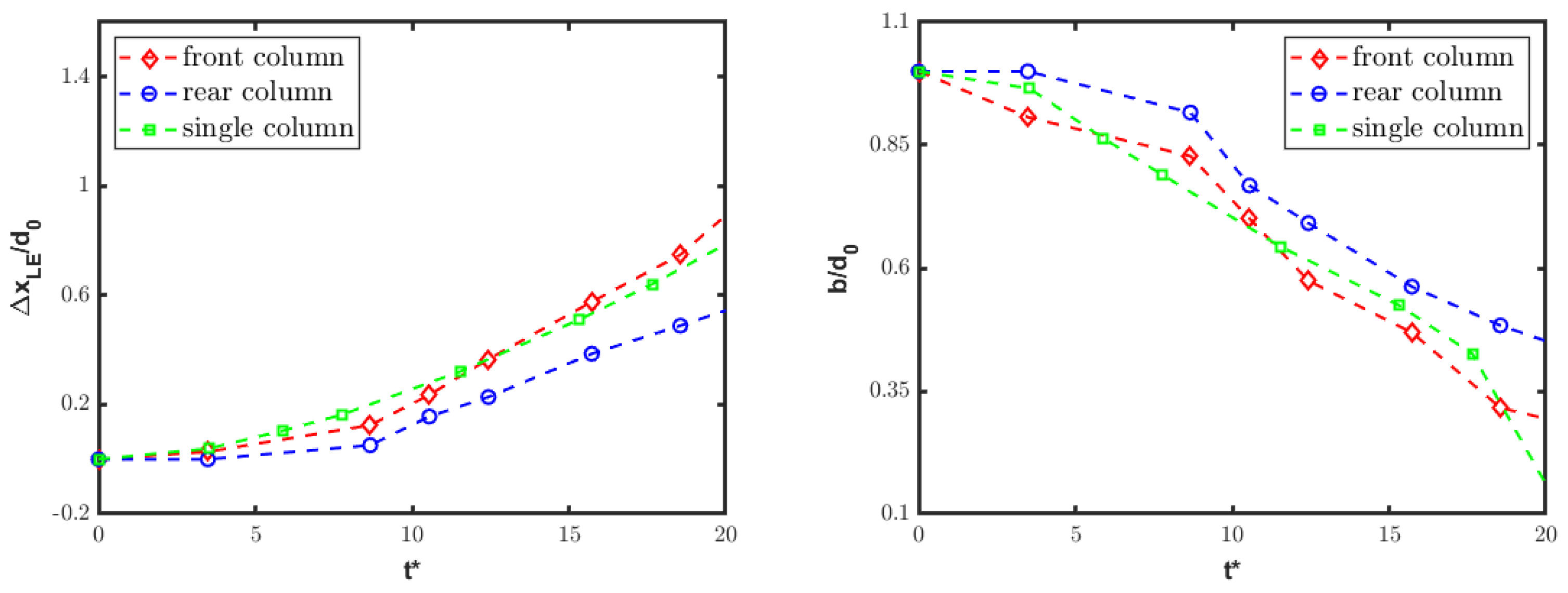
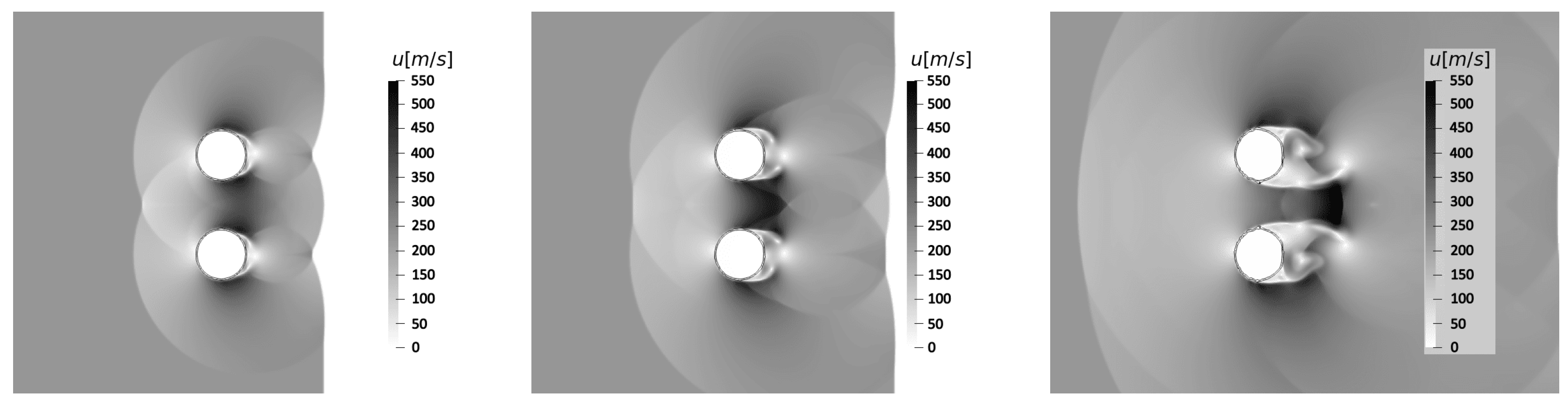
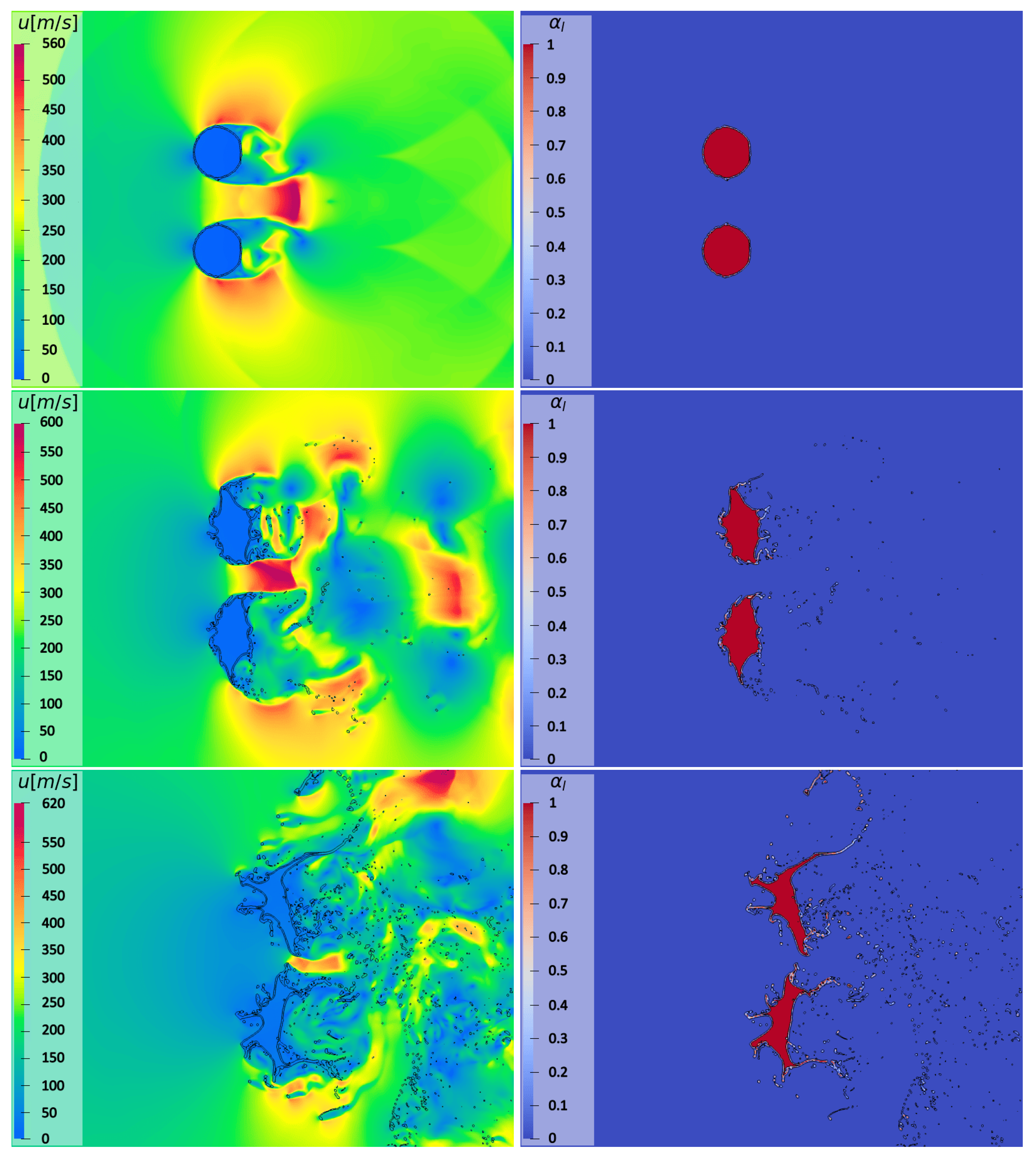
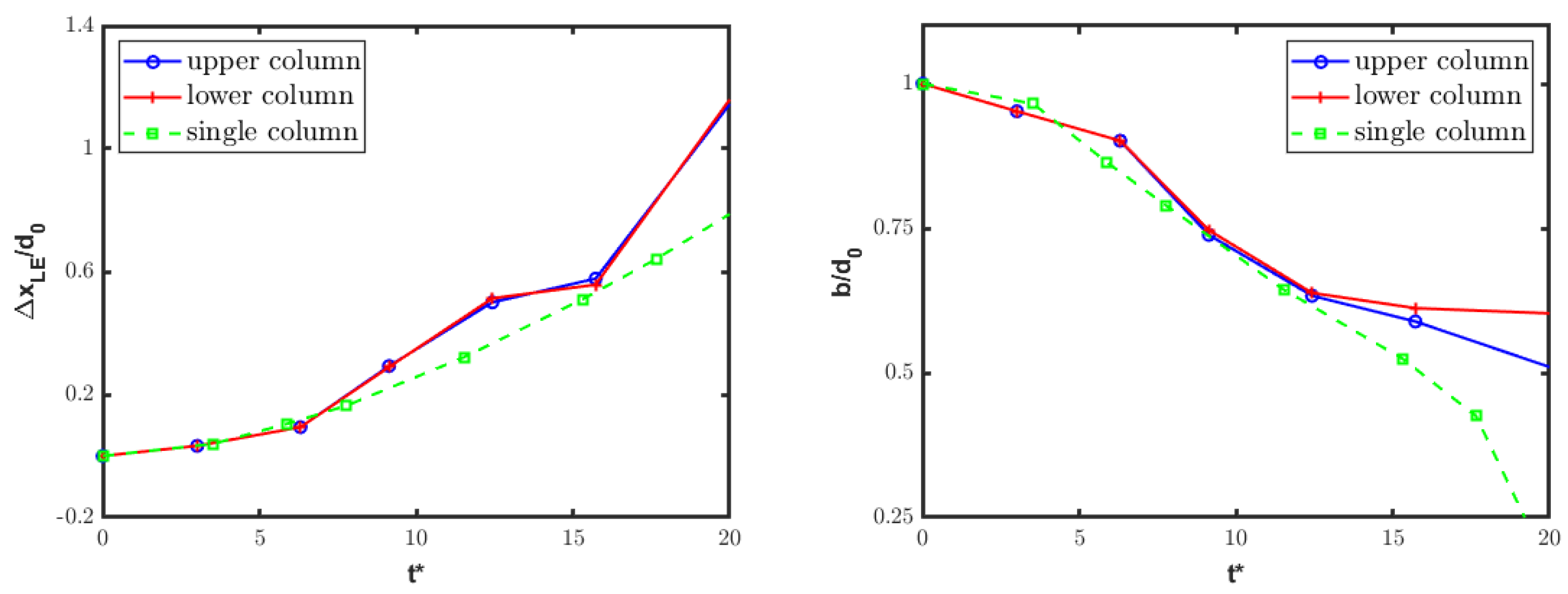
4.3. Tandem-Column Configurations
4.3.1. Streamwise Disposition
4.3.2. Spanwise Disposition
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACID | acoustically conservative interface discretization |
| CFD | computational fluid dynamics |
| CM | center-of-mass |
| CPD | cells-per-diameter |
| DW | diffracted wave |
| FV | finite volume (method) |
| HSZ | high-speed zone |
| KNP | Kurganov–Noelle–Petrova (scheme) |
| PIMPLE | pressure implicit method (for) pressure-linked equations |
| RT | Rayleigh–Taylor (instability) |
| RTP | Rayleigh–Taylor piercing |
| RW | reflected wave |
| SIE | shear-induced entrainment |
| TP | triple point |
| VOF | volume-of-fluid (method) |
| Nomenclature | |
| b | column streamwise extent |
| initial column diameter | |
| E | total energy (per unit mass) |
| numerical Schlieren constant | |
| K | interface compression coefficient |
| molar mass | |
| shock Mach number |
| Ohnesorge number | |
| p | mixture pressure |
| R | gas constant |
| non-dimensional time | |
| instant of the shock impact | |
| T | mixture temperature |
| mixture velocity vector | |
| shock front velocity | |
| Weber number | |
| cylinder leading edge position | |
| Z | acoustic impedance |
| volume fraction of liquid phase | |
| compression ratio | |
| specific heat ratio | |
| dynamic viscosity | |
| mixture density | |
| surface tension | |
| viscous stress tensor | |
| numerical Schlieren function | |
| computational domain |
References
- Villermaux, E. Fragmentation. Annu. Rev. Fluid Mech. 2007, 39, 419–446. [Google Scholar]
- Rajamanickam, K.; Basu, S. On the dynamics of vortex–droplet interactions, dispersion and breakup in a coaxial swirling flow. J. Fluid Mech. 2017, 827, 572–613. [Google Scholar]
- Liu, N.; Wang, Z.; Mingbo, S.; Wang, H.; Wang, B. Numerical simulation of liquid droplet breakup in supersonic flows. Acta Astronaut. 2018, 145, 116–130. [Google Scholar]
- Meng, J.C.; Colonius, T. Numerical simulations of the early stages of high-speed droplet breakup. Shock Waves 2015, 25, 399–414. [Google Scholar]
- Guildenbecher, D.R.; López-Rivera, C.; Sojka, P.E. Secondary atomization. Exp. Fluids 2009, 45, 371–402. [Google Scholar]
- Theofanous, T.G.; Li, G.J. On the physics of aerobreakup. Phys. Fluids 2008, 20, 052103. [Google Scholar]
- Theofanous, T.G. Aerobreakup of Newtonian and Viscoelastic Liquids. Annu. Rev. Fluid Mech. 2011, 43, 661–690. [Google Scholar]
- Theofanous, T.G.; Mitkin, V.V.; Ng, C.L.; Chang, C.-H.; Deng, X.; Sushchikh, S. The physics of aerobreakup. II. Viscous liquids. Phys. Fluids 2012, 24, 022104. [Google Scholar]
- Gelfand, B.E. Droplet breakup phenomena in flows with velocity lag. Progr. Energy Combust. Sci. 1996, 22, 201–265. [Google Scholar]
- Igra, D.; Takayama, K. Investigation of aerodynamic breakup of a cylindrical water droplet. At. Sprays 2001, 11, 167–185. [Google Scholar]
- Igra, D.; Takayama, K. Numerical simulation of shock wave interaction with a water column. Shock Waves 2001, 11, 219–228. [Google Scholar]
- Sembian, S.; Liverts, M.; Tillmark, N.; Apazidis, N. Plane shock wave interaction with a cylindrical water column. Phys. Fluids 2016, 28, 056102. [Google Scholar]
- Biasiori-Poulanges, L.; Schmidmayer, K. A phenomenological analysis of droplet shock-induced cavitation using a multiphase modeling approach. Phys. Fluids 2023, 35, 013312. [Google Scholar]
- Igra, D.; Ogawa, T.; Takayama, K. A parametric study of water column deformation resulting from shock wave loading. At. Sprays 2002, 12, 577–591. [Google Scholar]
- Igra, D.; Sun, M. Shock-Water Column Interaction, from Initial Impact to Fragmentation Onset. AIAA J. 2010, 48, 2763–2771. [Google Scholar]
- Xiong, T.; Shao, C.; Luo, K. Exploration of shock—Droplet interaction based on high-fidelity simulation and improved theoretical model. J. Fluid Mech. 2024, 988, A46. [Google Scholar]
- Xu, S.; Fan, W.; Wu, W.; Wen, H.; Wang, B. Analysis of wave converging phenomena inside the shocked two-dimensional cylindrical water column. J. Fluid Mech. 2023, 964, A12. [Google Scholar]
- Xiang, G.; Wang, B. Numerical study of a planar shock interacting with a cylindrical water column embedded with an air cavity. J. Fluid Mech. 2017, 825, 825–852. [Google Scholar]
- Kaiser, J.W.J.; Winter, J.M.; Adami, S.; Adams, N.A. Investigation of interface deformation dynamics during high-Weber number cylindrical droplet breakup. Int. J. Multiph. Flow 2020, 132, 103409. [Google Scholar]
- Igra, D.; Takayama, K. Experimental investigation of two cylindrical water columns subjected to planar shock wave loading. J. Fluids Eng. 2003, 125, 325–331. [Google Scholar]
- Chen, H.; Liang, S.M. Flow visualization of shock/water column interactions. Shock Waves 2008, 17, 309–321. [Google Scholar]
- Coralic, V.; Colonius, T. Finite-volume WENO scheme for viscous compressible multicomponent flows. J. Comput. Phys. 2014, 274, 95–121. [Google Scholar] [PubMed]
- Denner, F.; Xiao, C.-N.; van Wachem, B.G.M. Pressure-based algorithm for compressible interfacial flows with acoustically-conservative interface discretisation. J. Comput. Phys. 2018, 367, 192–234. [Google Scholar]
- Zhang, X.; Pirker, S.; Saeedipour, M. Numerical investigation of particle motion at the steel–slag interface in continuous casting using VOF method and dynamic overset grids. Exp. Comput. Multiph. Flow 2023, 5, 178–192. [Google Scholar]
- Kraposhin, M.V.; Kukharskii, A.V.; Korchagova, V.N.; Shevelev, A.A. An extension of the all-Mach number pressure-based solution framework for numerical modelling of two-phase flows with interface. Ind. Process. Technol. 2022, 166, 6–27. [Google Scholar]
- Kapila, A.K.; Menikoff, R.; Bdzil, J.B.; Son, S.F.; Stewart, D.S. Two-phase modeling of deflagration-to-detonation transition in granular materials: Reduced equations. Phys. Fluids 2001, 13, 3002–3024. [Google Scholar]
- Baer, M.R.; Nunziato, J.W. A two-phase mixture theory for the deflagration-to-detonation transition in reactive granular materials. Int. J. Multiph. Flow 1986, 12, 861–889. [Google Scholar]
- Saurel, R.; Pantano, C. Diffuse-Interface Capturing Methods for Compressible Two-Phase Flows. Annu. Rev. Fluid Mech. 2018, 50, 105–130. [Google Scholar]
- Zlotnik, A.; Lomonosov, T. On a doubly reduced model for dynamics of heterogeneous mixtures of stiffened gases, its regularizations and their implementations. Chaos 2023, 33, 113128. [Google Scholar]
- Rossano, V.; De Stefano, G. Computational evaluation of shock wave interaction with a cylindrical water column. Appl. Sci. 2021, 11, 4934. [Google Scholar] [CrossRef]
- Rossano, V.; Cittadini, A.; De Stefano, G. Computational evaluation of shock wave interaction with a liquid droplet. Appl. Sci. 2022, 12, 1349. [Google Scholar] [CrossRef]
- Schmidmayer, K.; Biasiori-Poulanges, L. Geometry effects on the droplet shock-induced cavitation. Phys. Fluids 2023, 35, 063315. [Google Scholar]
- Denaro, F.M.; De Stefano, G. A new development of the dynamic procedure in large-eddy simulation based on a Finite Volume integral approach. Application to stratified turbulence. Theoret. Comput. Fluid Dyn. 2011, 25, 315–355. [Google Scholar]
- Kraposhin, M. Available Solvers with Hybrid Approximation. GitHub Repository. 2022. Available online: https://github.com/mkraposhin/hybridCentralSolvers (accessed on 5 November 2024).
- Kurganov, A.; Tadmor, E. New high-resolution central schemes for nonlinear conservation laws and convection-diffusion equations. J. Comput. Phys. 2000, 160, 241–282. [Google Scholar]
- Yang, H.; Peng, J. Numerical study of the shear-thinning effect on the interaction between a normal shock wave and a cylindrical liquid column. Phys. Fluids 2019, 31, 043101. [Google Scholar]
- Sod, G.A. A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws. J. Comput. Phys. 1978, 27, 1–31. [Google Scholar]
- Johnsen, E. Numerical simulations of non-spherical bubble collapse. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2007. [Google Scholar]
- Sharma, S.; Singh, A.P.; Rao, S.S.; Kumar, A.; Basu, S. Shock induced aerobreakup of a droplet. J. Fluid Mech. 2021, 929, A27. [Google Scholar]
- Fujisawa, K. Onset and evolution of counter-rotating baroclinic vortex pair in shock-induced aerobreakup of droplets. Prog. Nucl. Energy 2022, 152, 104343. [Google Scholar]
- Hong, Z.-Y.; Song, Y.; Wang, R.; Ma, Z.-Q.; Ma, D.-J.; Wang, P. Deformation and mutual influence of two cylindrical water columns in tandem subjected to shock wave. Chin. Phys. B 2024, 33, 084702. [Google Scholar]
- Rossano, V.; De Stefano, G. Hybrid VOF–Lagrangian CFD modeling of droplet aerobreakup. Appl. Sci. 2022, 12, 8302. [Google Scholar] [CrossRef]
- Zhu, W.; Zhao, N.; Jia, X.; Chen, X.; Zheng, H. Effect of airflow pressure on the droplet breakup in the shear breakup regime. Phys. Fluids 2021, 33, 053309. [Google Scholar] [CrossRef]
- Meng, J.C.; Colonius, T. Numerical simulation of the aerobreakup of a water droplet. J. Fluid Mech. 2018, 835, 1108–1135. [Google Scholar] [CrossRef]
- Rossano, V.; De Stefano, G. Scale-resolving simulation of shock-induced aerobreakup of water droplet. Computation 2024, 12, 71. [Google Scholar] [CrossRef]
- Rossano, V.; De Stefano, G. Large-eddy simulation of droplet deformation and fragmentation under shock wave impact. Appl. Sci. 2025, 15, 1233. [Google Scholar] [CrossRef]



| Boundary | p | T | u | |
|---|---|---|---|---|
| Driver section side | zeroGradient | zeroGradient | fixedValue | fixedValue |
| Driven section side | zeroGradient | zeroGradient | zeroGradient | zeroGradient |
| Lateral sides | zeroGradient | zeroGradient | slip | zeroGradient |
| Parameter | Symbol | Value |
|---|---|---|
| Driven section pressure | 101.3 | |
| Driven section density | 1.204 | |
| Driver section pressure | 640 | |
| Driver section density | 7.61 | |
| Temperature | 293.15 | |
| Velocity | 0 |
| Parameter | Symbol | Value |
|---|---|---|
| Pressure | 238.1 | |
| Density | 2.18 | |
| Temperature | 381.1 | |
| Velocity | 225.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taglialatela, F.E.; De Stefano, G. Numerical Investigation of Cylindrical Water Droplets Subjected to Air Shock Loading at a High Weber Number. Fluids 2025, 10, 81. https://doi.org/10.3390/fluids10040081
Taglialatela FE, De Stefano G. Numerical Investigation of Cylindrical Water Droplets Subjected to Air Shock Loading at a High Weber Number. Fluids. 2025; 10(4):81. https://doi.org/10.3390/fluids10040081
Chicago/Turabian StyleTaglialatela, F. Edoardo, and Giuliano De Stefano. 2025. "Numerical Investigation of Cylindrical Water Droplets Subjected to Air Shock Loading at a High Weber Number" Fluids 10, no. 4: 81. https://doi.org/10.3390/fluids10040081
APA StyleTaglialatela, F. E., & De Stefano, G. (2025). Numerical Investigation of Cylindrical Water Droplets Subjected to Air Shock Loading at a High Weber Number. Fluids, 10(4), 81. https://doi.org/10.3390/fluids10040081







