Numerical Investigation of NASA SC (2)-0714 Airfoil Icing in a Supersonic Flow
Abstract
1. Introduction
2. Computational Approach
2.1. Equations for Aerodynamic Flow and Turbulence
2.2. Equations for Motion of Liquid Droplet as a Continuous Medium in a Gas Flow
2.3. Equations for Water Film Motion over Solid Surface and Compatibility Relations
2.4. Model Surface Motions
3. Numerical Simulation
- -
- The first stage models the viscous compressible flow using the Reynolds-averaged Navier–Stokes equations. Turbulent flows are incorporated using the equations of the k-ω SST model. At the same stage, the motion of liquid droplets in the form of a continuous medium is simulated using the Euler equation system. The continuum droplets are assumed to have no effect on the gas flow and to have a size of 20 µm [3];
- -
- The second stage models the motion of the water film on the solid surface using the results of the first stage;
- -
- The third stage involves deformation of the computational model surface at ice accretion locations. Numerical discretization on the equations is performed by the finite volume method on arbitrary unstructured grids, which is a specific feature of numerical discretization of the equations.
4. Result and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bogatkin, O.G. Fundamentals of Aviation Meteorology: A Textbook; Publishing House of RGGMU: St. Petersburg, Russia, 2009. [Google Scholar]
- Callaghan, E.E.; Serafini, J.S. Analytical Investigation of Icing Limit for Diamond-Shaped Airfoil in Transonic and Supersonic Flow; NACA TN 2861; NACA Tech: Washington, DC, USA, 1953. [Google Scholar]
- Federal Aviation Authority (FAA). Airworthness Standards: Transport Category Airplanes, CFR Title 14, Part 25. 2025. Available online: https://www.ecfr.gov/current/title-14/chapter-I/subchapter-C/part-25 (accessed on 25 May 2025).
- Suhanov, D.B.; Serebryakov, L.I.; Radchenko, P.A.; Strijhak, S.V. To the Problem of Selecting the Anti-Icing System for the Swept Wing of Supersonic Flight Demonstrator. In Recent Developments in High-Speed Transport; Strelets, D.Y., Korsun, O.N., Eds.; Springer Aerospace Technology; Springer: Singapore, 2023. [Google Scholar] [CrossRef]
- Demidov, A.I.; Shishelova, T.I. Problem of aircraft icing and applied methods of combating it. Int. J. Experiment. Educ. 2014, 8, 88–89. [Google Scholar]
- Bragg, M.B.; Paraschivoiu, I.; Saeed, F. Aircraft Icing; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Lei, Z.-J.; Zha, G.-C. Lift Enhancement of Supersonic Thin Airfoil at Low Speed by Co-Flow Jet Active Flow Control. In Proceedings of the AIAA AVIATION, Virtual, 2–6 August 2021. [Google Scholar] [CrossRef]
- Welge, H.; Nelson, C.; Bonet, J. Supersonic vehicle systems for the 2020 to 2035 timeframe. In Proceedings of the 28th AIAA Applied Aerodynamics Conference, Chicago, IL, USA, 28 June–1 July 2010; p. 4930. [Google Scholar]
- Yousuf, A.B.; Kamal, T.M.B. Study of the Aerodynamic Characteristics of a Supercritical Airfoil under Supersonic Flow. In Proceedings of the International Conference on Mechanical, Industrial and Materials Engineering 2022 (ICMIME 2022), Rajshahi, Bangladesh, 20–22 December 2022. [Google Scholar]
- Kozelkov, A.; Kurkin, A.; Kurulin, V.; Plygunova, K.; Krutyakova, O. Validation of the LOGOS Software Package Methods for the Numerical Simulation of Cavitational Flows. Fluids 2023, 8, 104. [Google Scholar] [CrossRef]
- Sarazov, A.V.; Kozelkov, A.S.; Strelets, D.Y.; Zhuchkov, R.N. Modeling Object Motion on Arbitrary Unstructured Grids Using an Invariant Principle of Computational Domain Topology: Key Features. Symmetry 2023, 15, 2081. [Google Scholar] [CrossRef]
- Kozelkov, A.S.; Struchkov, A.V.; Strelets, D.Y. Two Methods to Improve the Efficiency of Supersonic Flow Simulation on Unstructured Grids. Fluids 2022, 7, 136. [Google Scholar] [CrossRef]
- Fletcher, C.A.J. Computational Techniques for Fluid Dynamics; Springer: Berlin, Germany, 1991. [Google Scholar]
- Kim, J.W.; Dennis, P.G.; Sankar, L.N.; Kreeger, R.E. Ice Accretion Modeling using an Eulerian Approach for Droplet Impingement. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. AIAA 2013-0246. [Google Scholar]
- Norde, E. Eulerian Method for Ice Crystal Icing in Turbofan Engines. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2017. [Google Scholar] [CrossRef]
- Bourgault, Y.; Beaugendre, H.; Habashi, W.G. Development of a Shallow-Water Icing Model in FENSAP-ICE. J. Aircr. 2000, 37, 640–646. [Google Scholar] [CrossRef]
- Uyttersprot, L. Inverse Distance Weighting Mesh Deformation. A Robust and Efficient Method for Unstructured Meshes. Master’s Thesis, Department of Aerodynamics, Delft University of Technology, Delft, The Netherlands, 12 February 2014; p. 177. [Google Scholar]
- Kozelkov, A.S.; Galanov, N.G.; Semenov, I.V.; Zhuchkov, R.N.; Strelets, D.Y. Computational Investigation of the Water Droplet Effects on Shapes of Ice on Airfoils. Aerospace 2023, 10, 906. [Google Scholar] [CrossRef]
- Kozelkov, A.; Galanov, N. Consideration of surface roughness when modeling icing processes. Ecol. Syst. Devices 2024, 10, 58–69. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Peric, M. Computational Method for Fluid Dynamics; Springer: New York, NY, USA, 2002. [Google Scholar]
- Hirsch, C. Computational Methods for Inviscid and Viscous Flows. In Numerical Computation of Internal and External Flows; Butterworth-Heinemann: Oxford, UK, 1990; Volume 2. [Google Scholar]
- Jasak, H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flow; Department of Mechanical Engineering, Imperial College of Science: London, UK, 1996. [Google Scholar]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with SST turbulence model. Turbul. Heat Mass 2003, 4, 625–632. [Google Scholar]
- Luke, E.; Collins, E.; Blades, E. A fast mesh deformation method using explicit interpolation. J. Comput. Phys. 2012, 231, 586–601. [Google Scholar] [CrossRef]
- Xu, X.; Liu, D.-W.; Chen, D.-H.; Wei, Z.; Wang, Y.-J. Investigation on Improved Correlation of CFD and EFD for Supercritical Airfoil. Res. J. Appl. Sci. Eng. Technol. 2014, 7, 1007–1011. [Google Scholar] [CrossRef]
- Harris, C.D. NASA Supercritical Airfoils, NASA TP 2969, 1990. Airfoil Coordinates. Airfoil Tools. Available online: http://airfoiltools.com/airfoil/details?airfoil=sc20714-il (accessed on 26 March 2025).

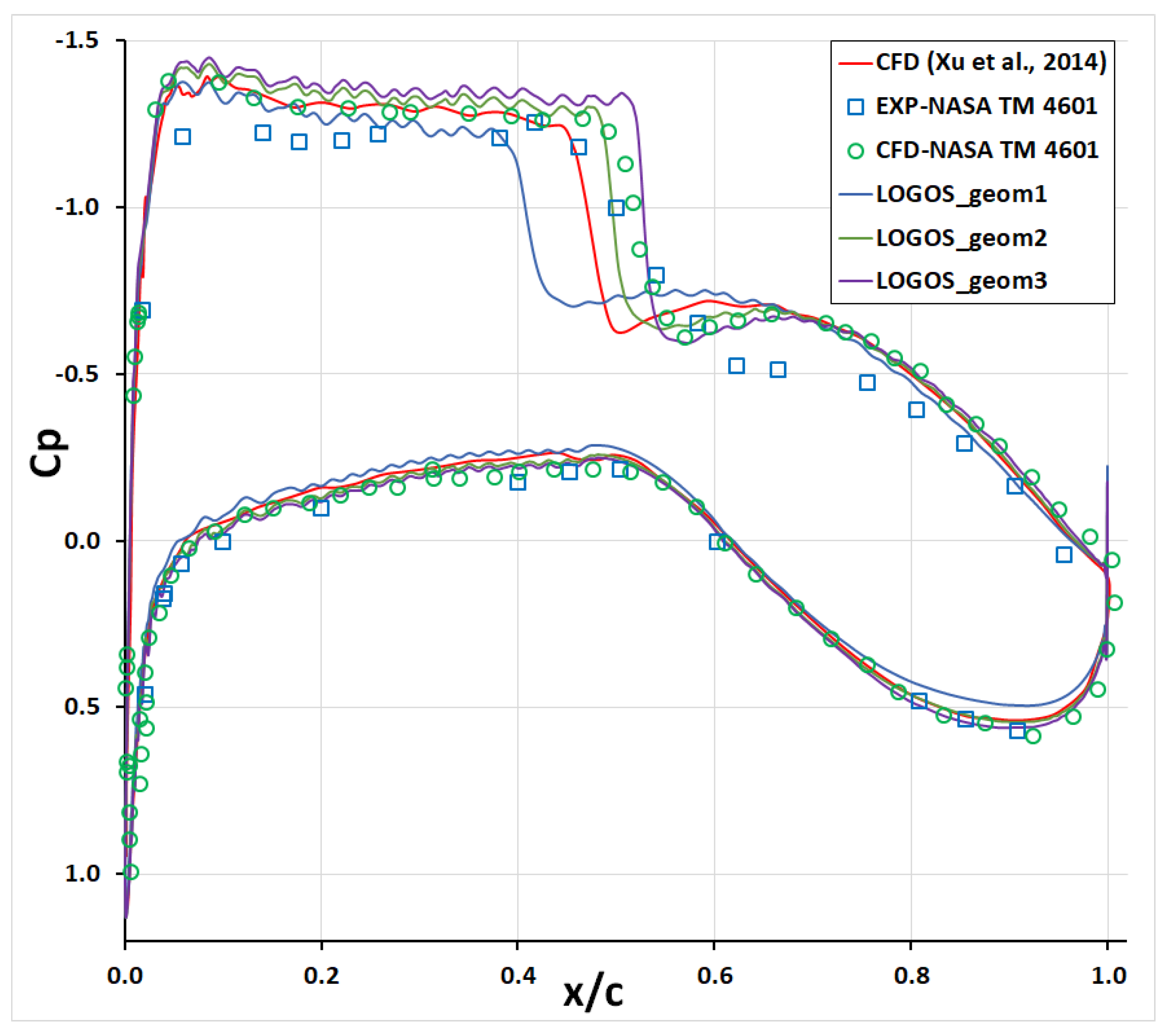
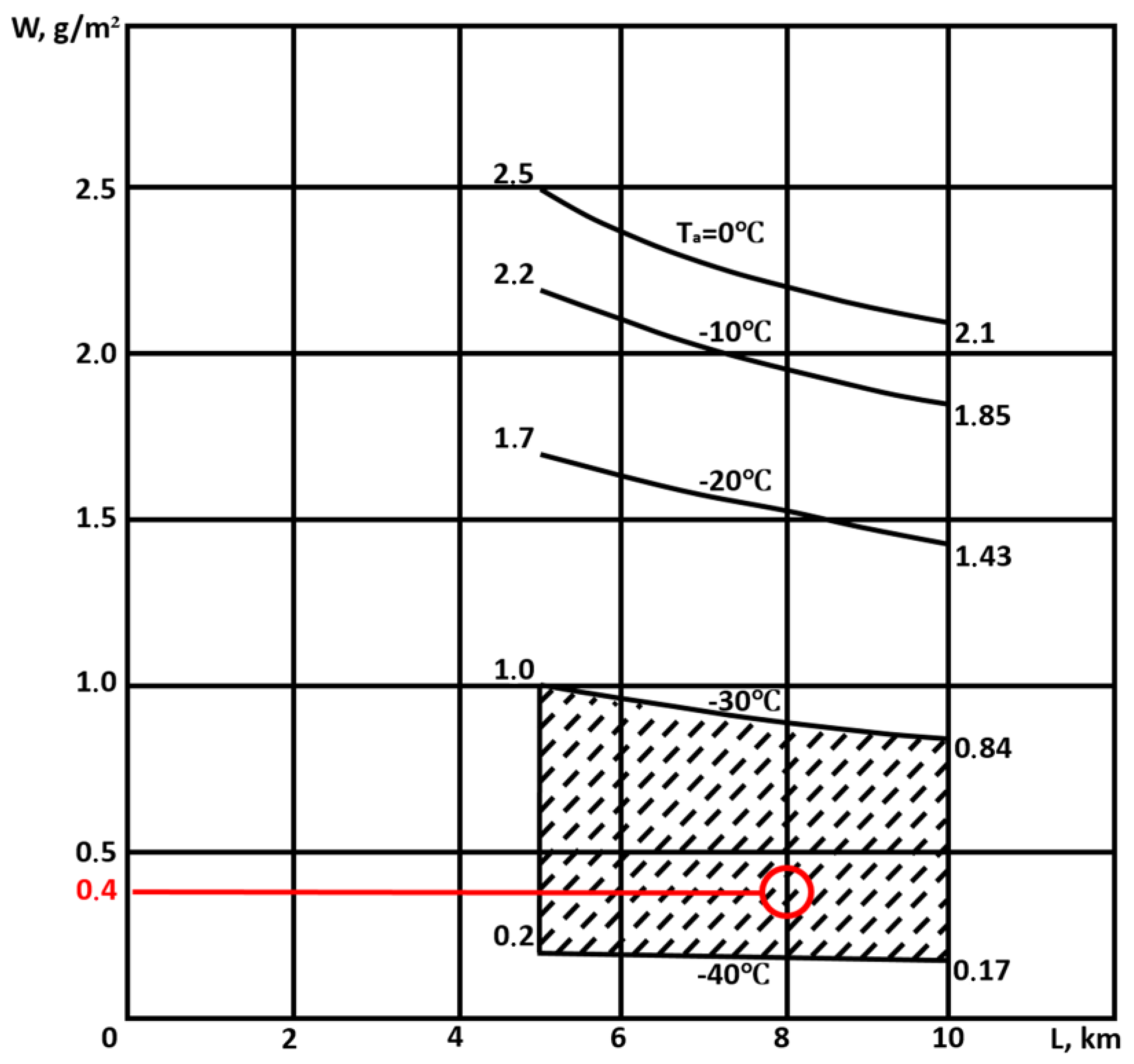
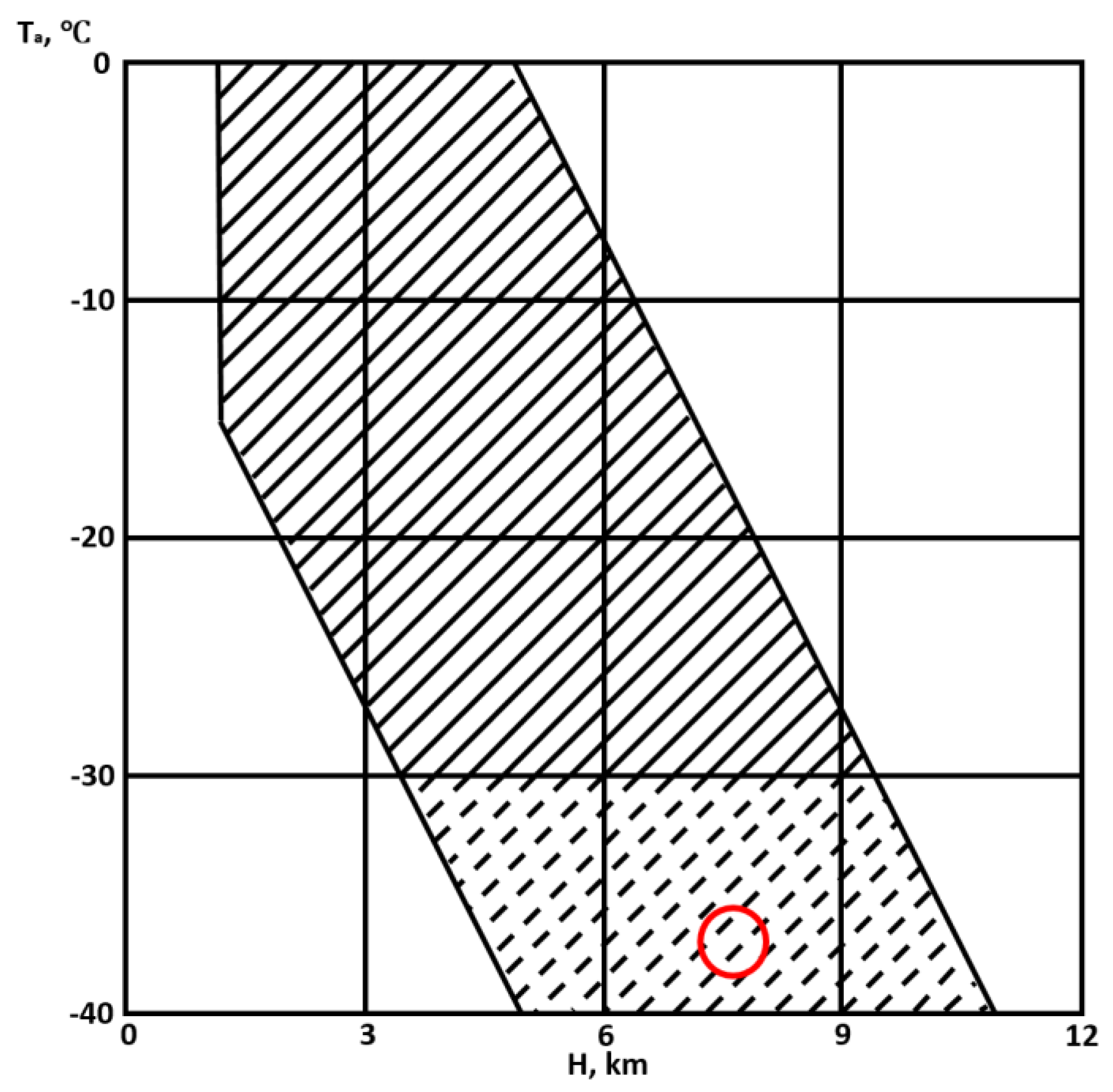

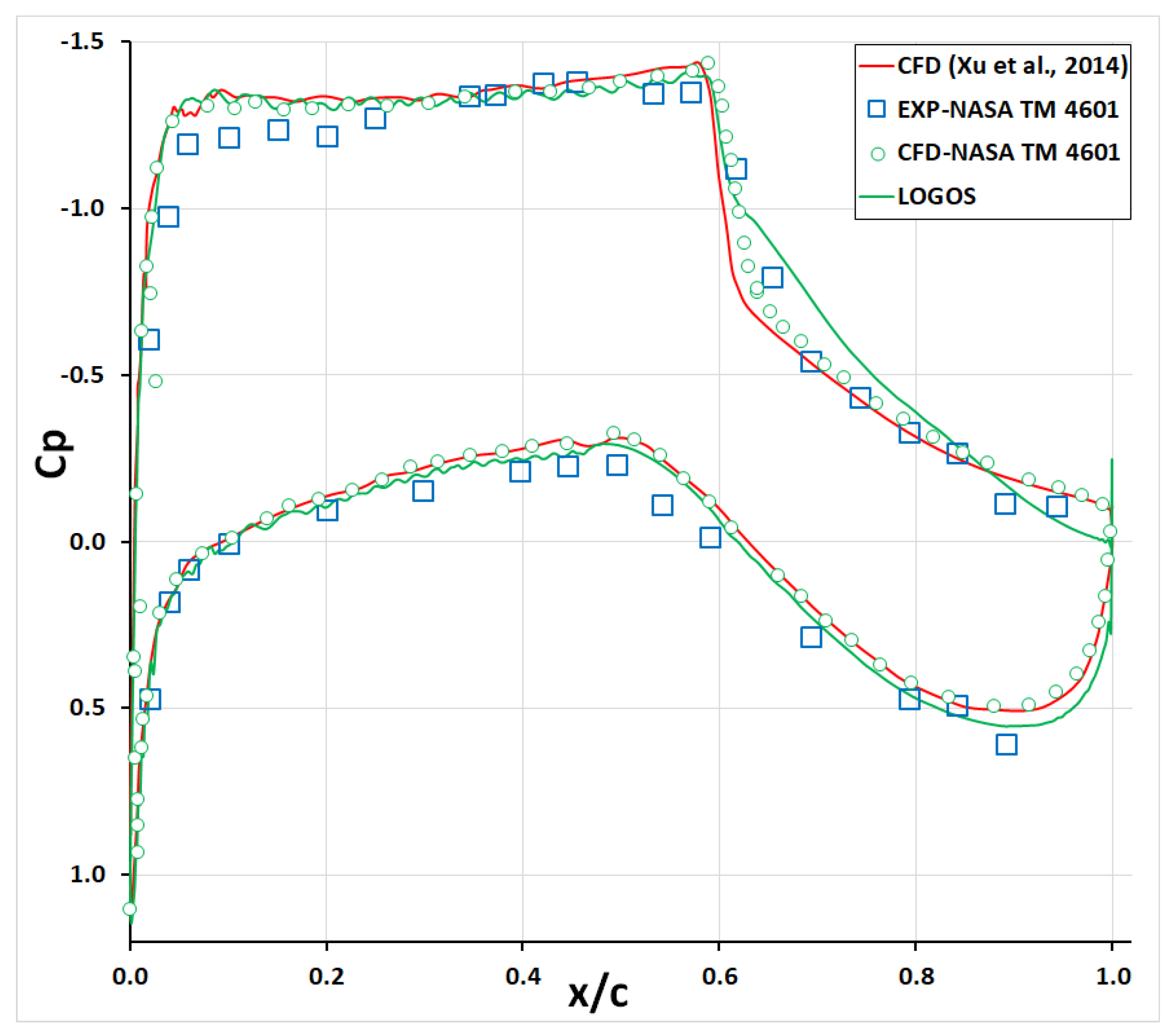

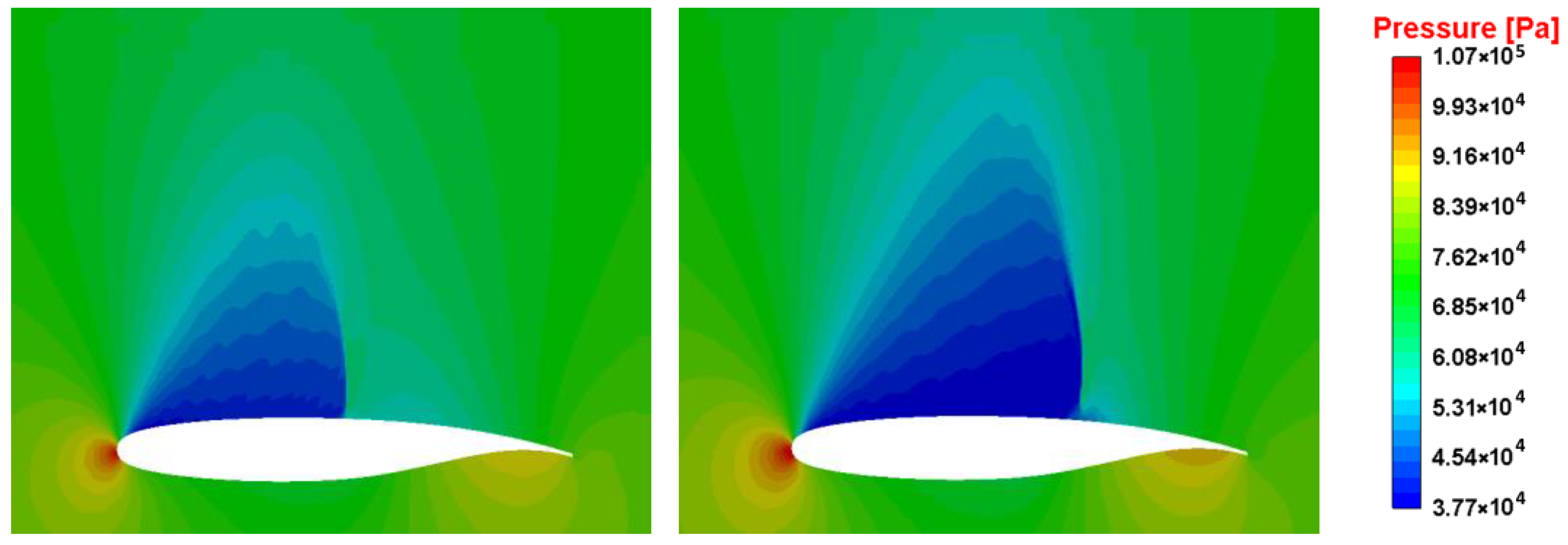
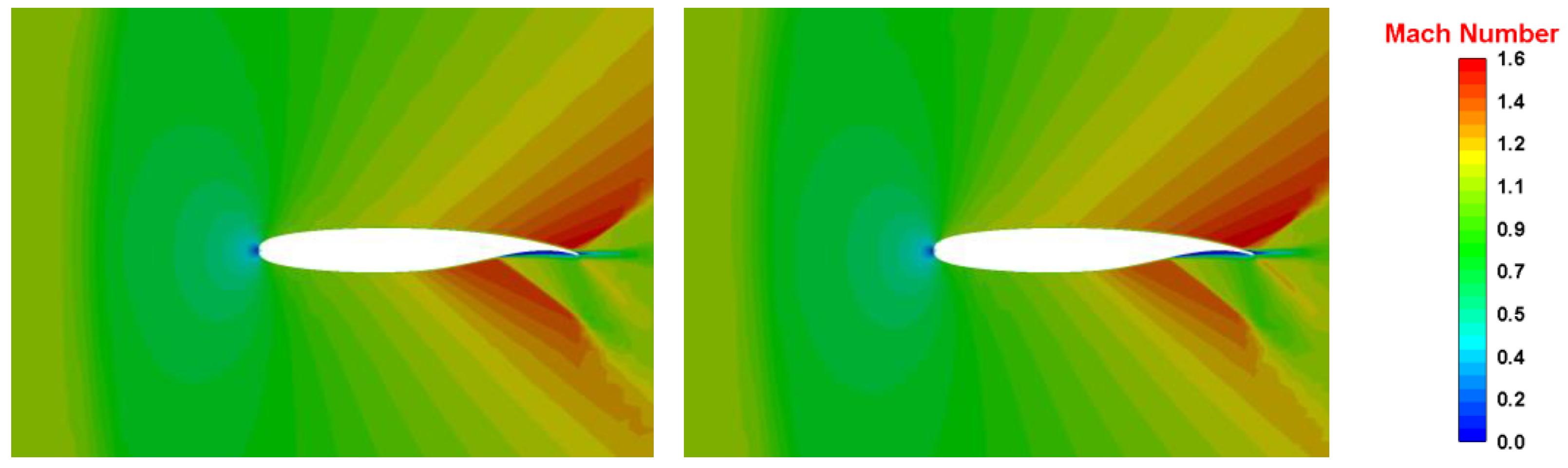

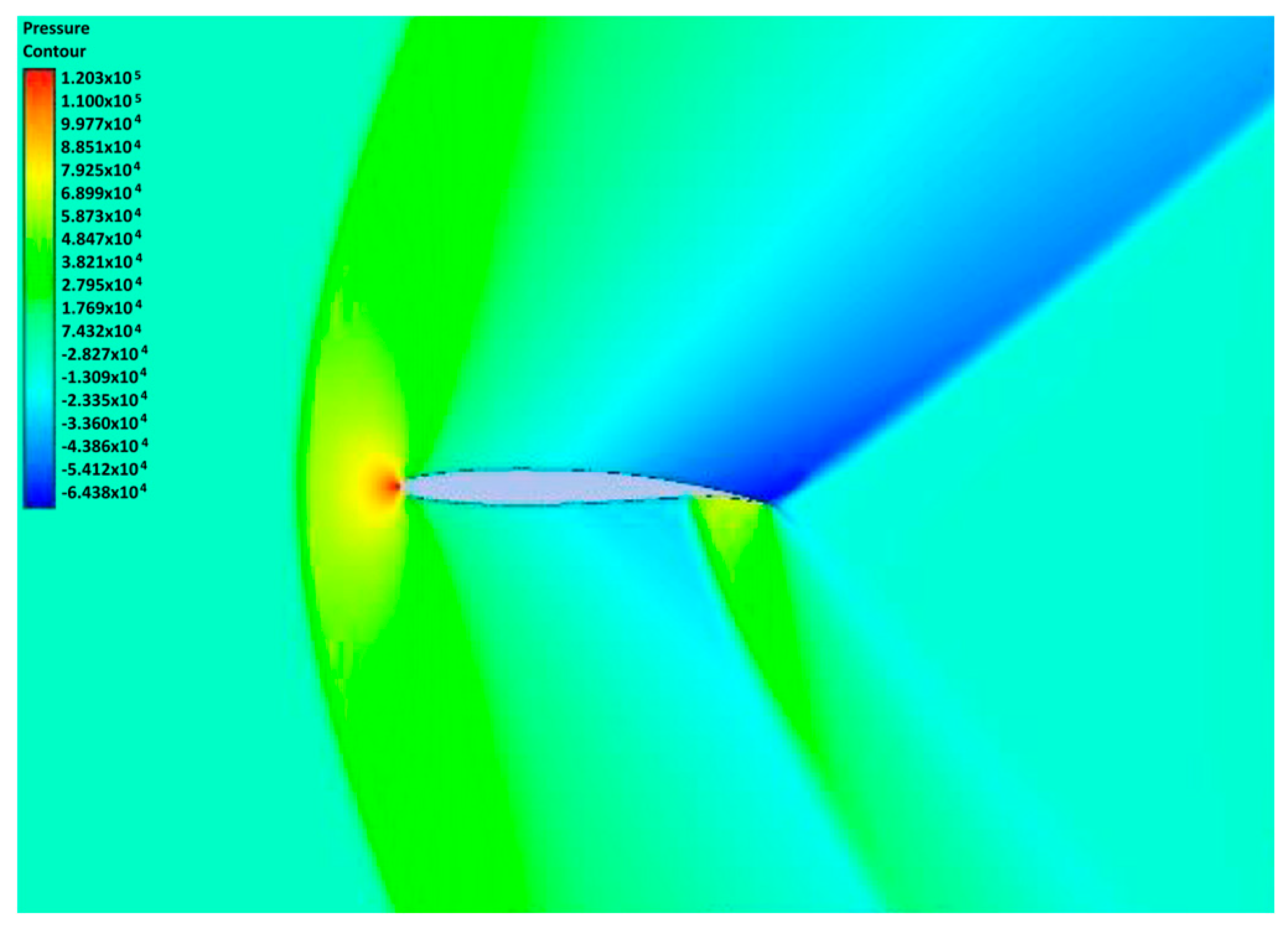

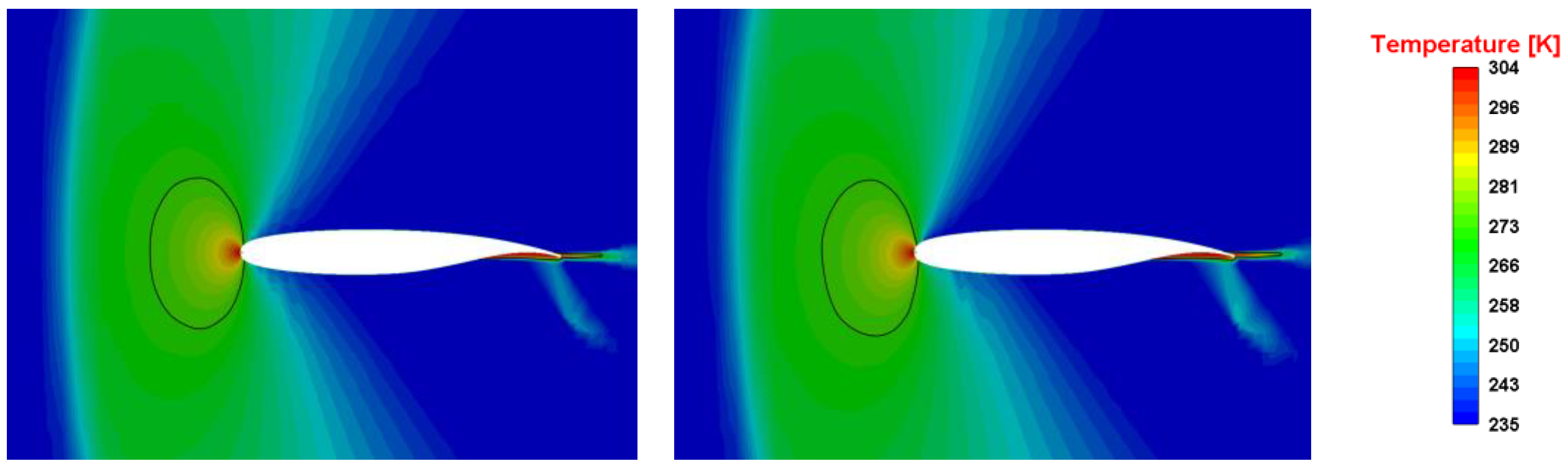
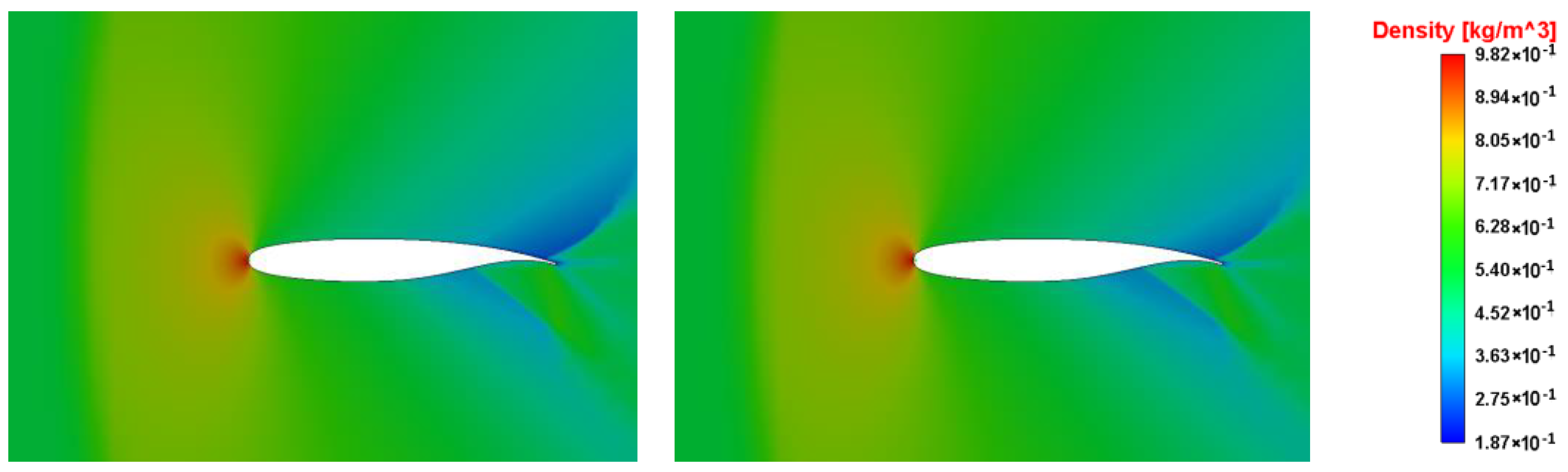
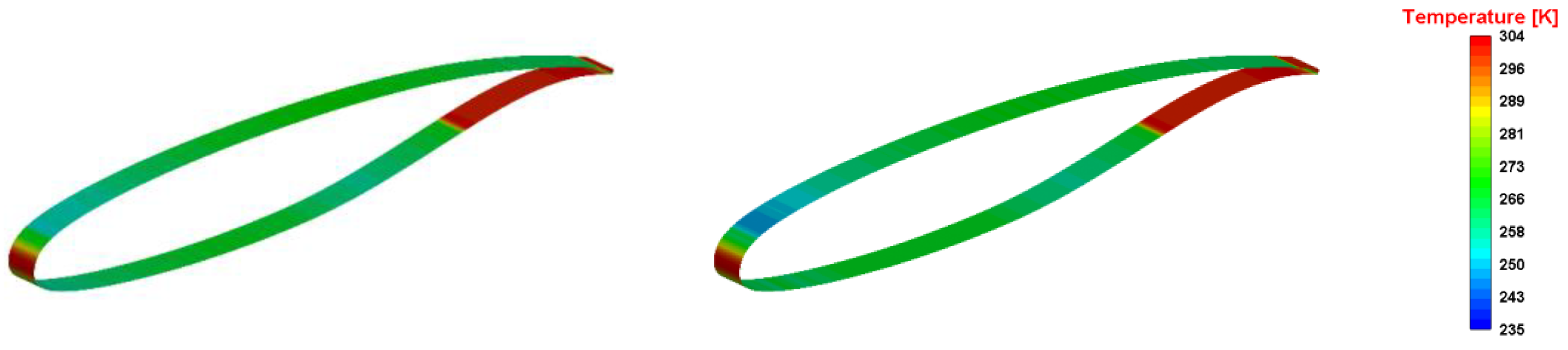




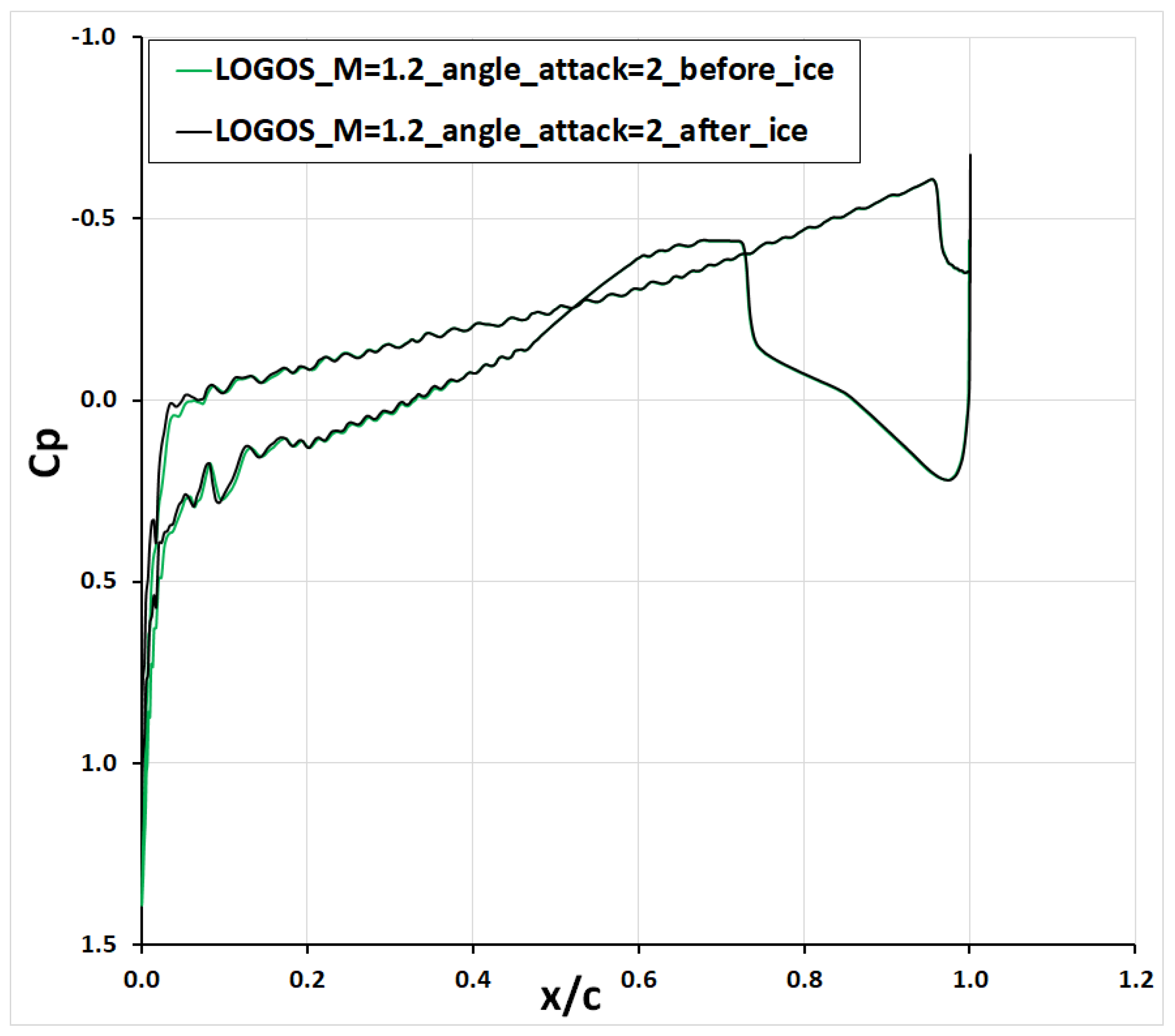
| Cases | Mach Number | Temperature Air, °K | Pressure Air, Pa | Angle of Attack α, ° |
|---|---|---|---|---|
| 1 | 0.7055 | 249.18 | 75.95 | 0.5202 |
| 2 | 0.74 | 249.18 | 75.95 | 2 |
| 3 | 1.2 | 246.25 | 35.65 | 0.5202 |
| 4 | 1.2 | 246.25 | 35.65 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kozelkov, A.; Galanov, N.; Kurkin, A. Numerical Investigation of NASA SC (2)-0714 Airfoil Icing in a Supersonic Flow. Fluids 2025, 10, 260. https://doi.org/10.3390/fluids10100260
Kozelkov A, Galanov N, Kurkin A. Numerical Investigation of NASA SC (2)-0714 Airfoil Icing in a Supersonic Flow. Fluids. 2025; 10(10):260. https://doi.org/10.3390/fluids10100260
Chicago/Turabian StyleKozelkov, Andrey, Nikolay Galanov, and Andrey Kurkin. 2025. "Numerical Investigation of NASA SC (2)-0714 Airfoil Icing in a Supersonic Flow" Fluids 10, no. 10: 260. https://doi.org/10.3390/fluids10100260
APA StyleKozelkov, A., Galanov, N., & Kurkin, A. (2025). Numerical Investigation of NASA SC (2)-0714 Airfoil Icing in a Supersonic Flow. Fluids, 10(10), 260. https://doi.org/10.3390/fluids10100260








