Rheology of Gels and Yielding Liquids
Abstract
:1. Introduction
- -
- To propose an unambiguous and unequivocal classification of gels and related materials based on rheological arguments;
- -
- To summarize the results of studies of yielding liquids published during the last few years;
- -
- To discuss some typical errors, difficulties, and wrong interpretations of experimental data in the studies of yielding liquids.
- -
- Gels are solid bodies incapable of irreversible deformations;
- -
- Yielding liquids are materials that can be in a solid-like state but, under some threshold conditions, can transfer to a liquid state;
- -
- A gel-like state is the solid-like state of a yielding liquid.
2. Gels and Gel-like States
2.1. Formation of a Gel
2.2. Rheology of Gels
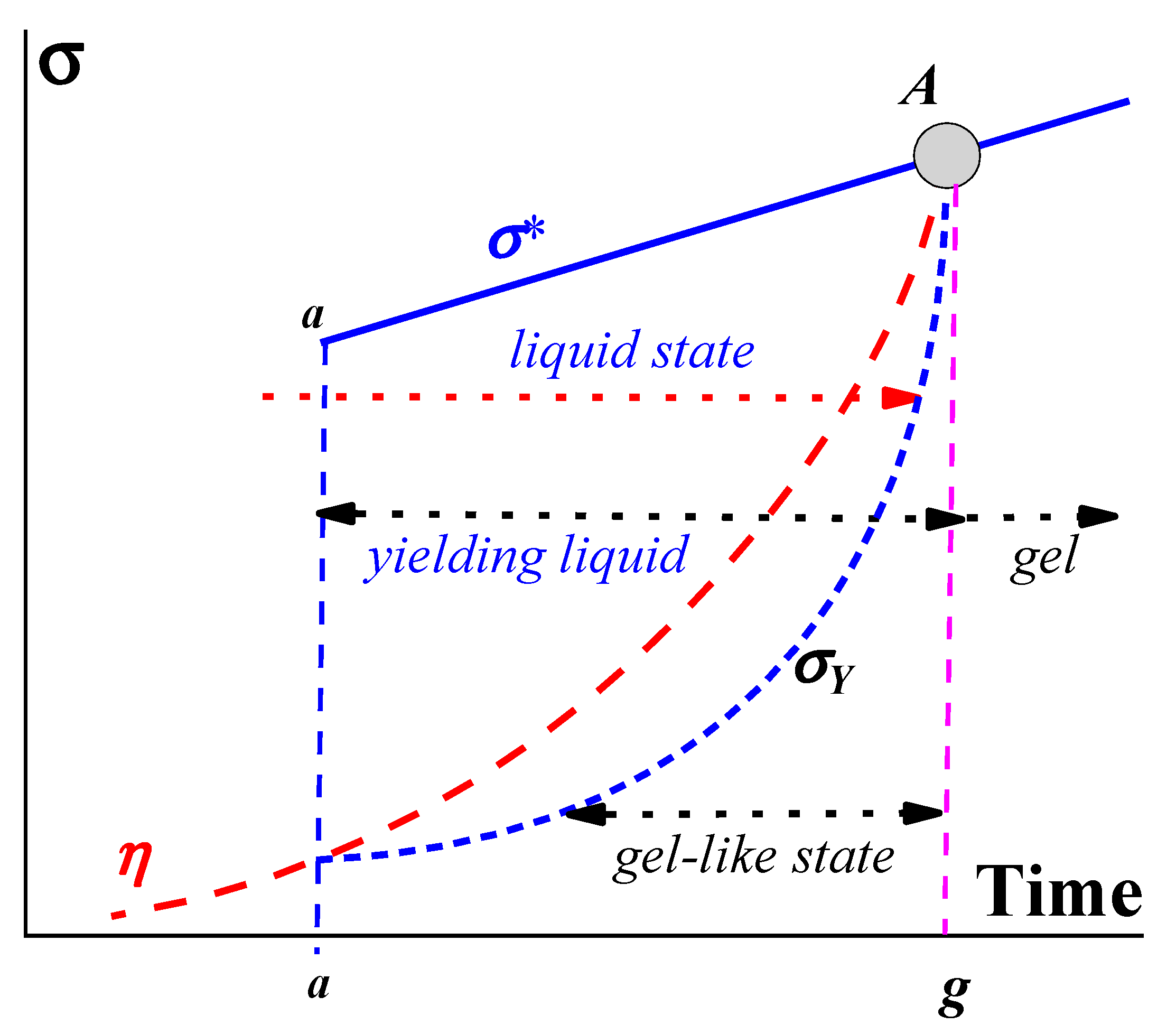
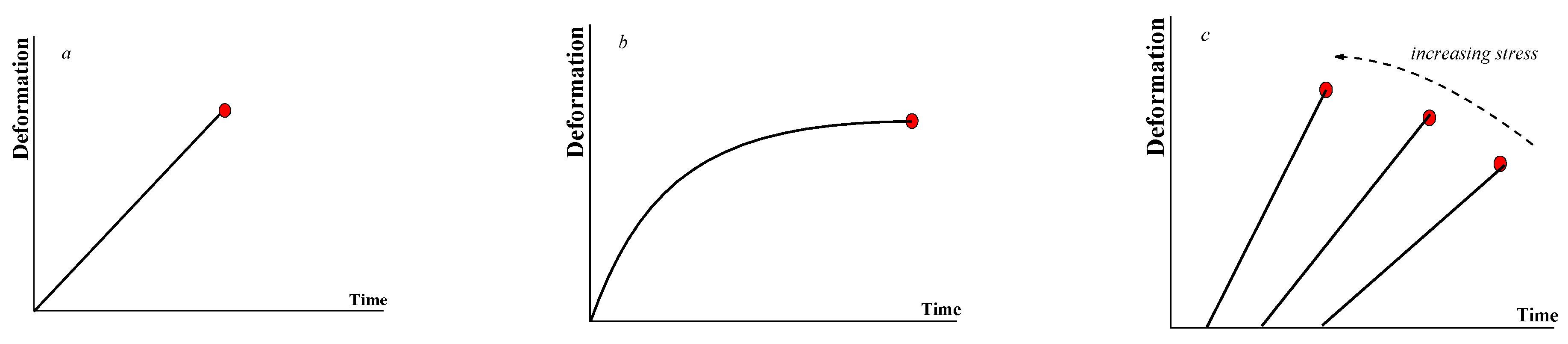
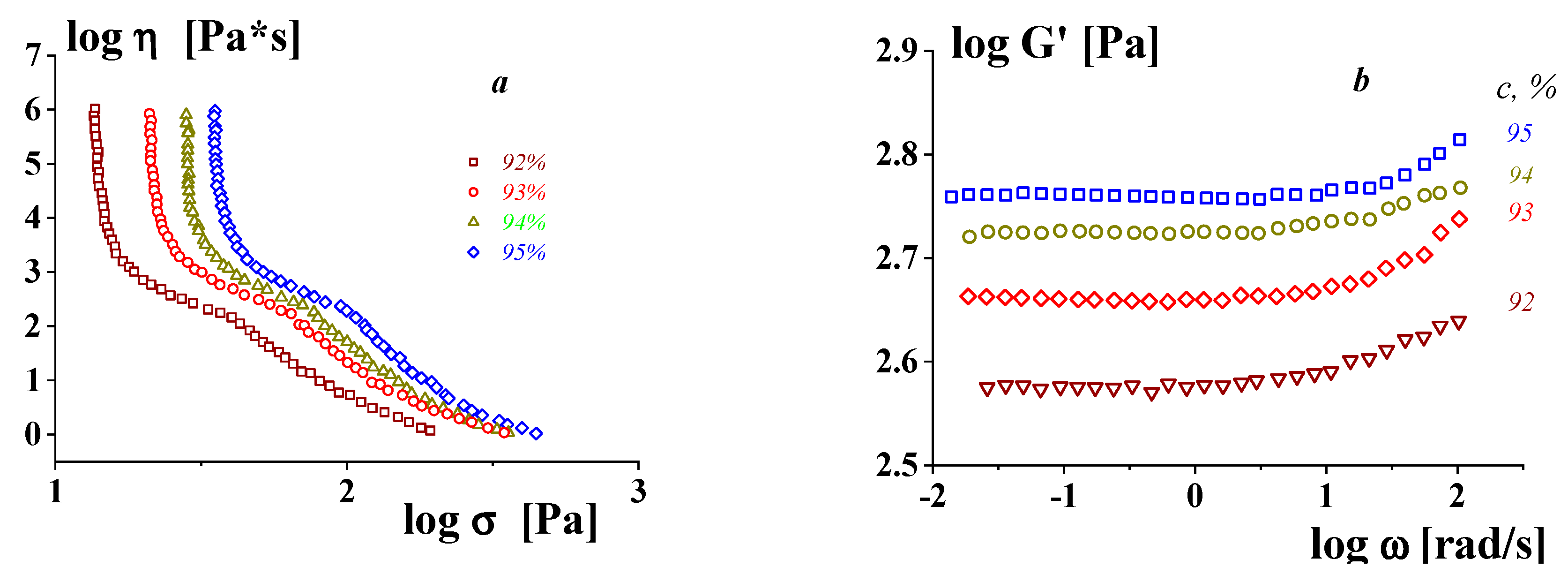
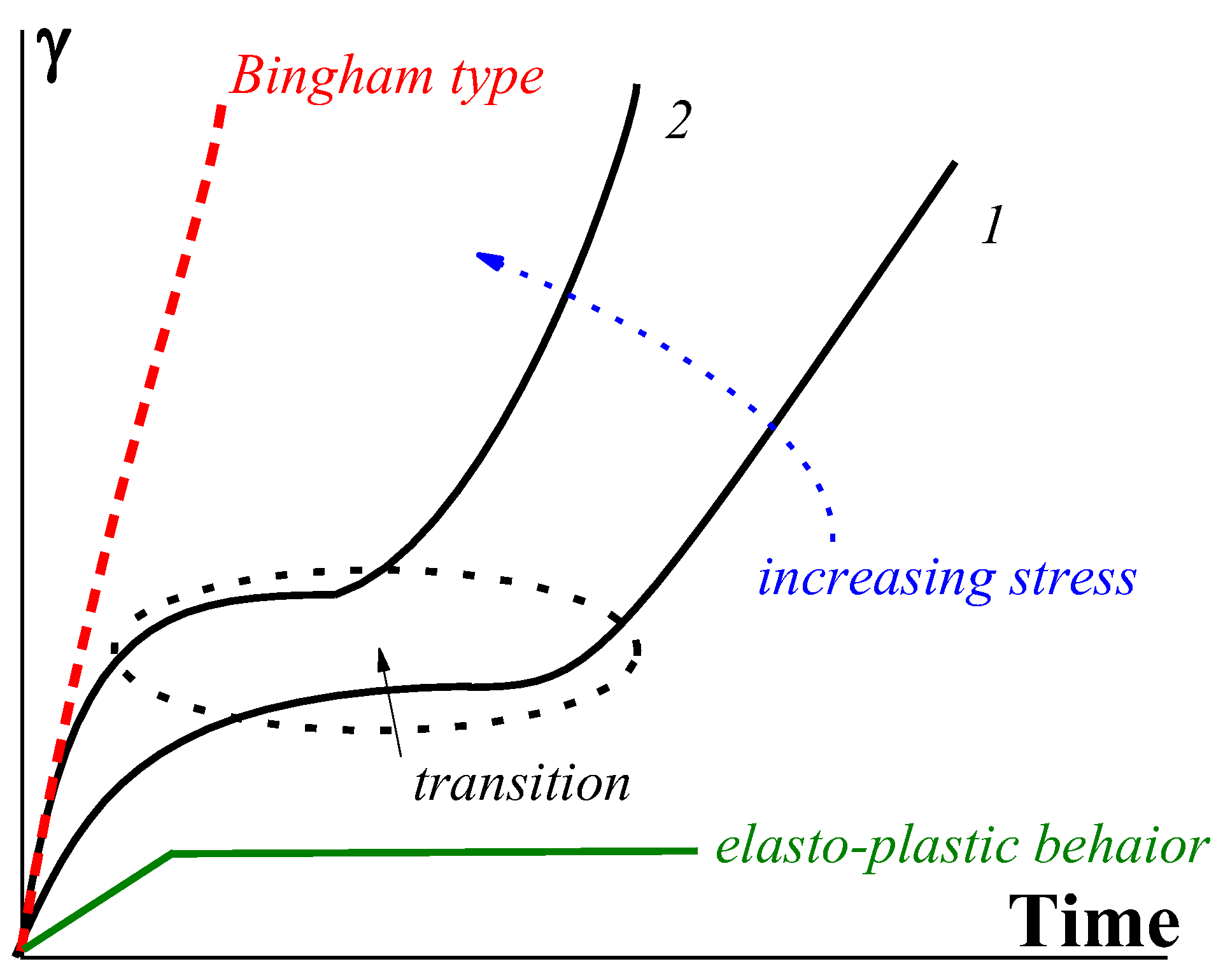
2.3. Yielding Materials (Liquids)
3. On the Yield Stress in Soft Matter
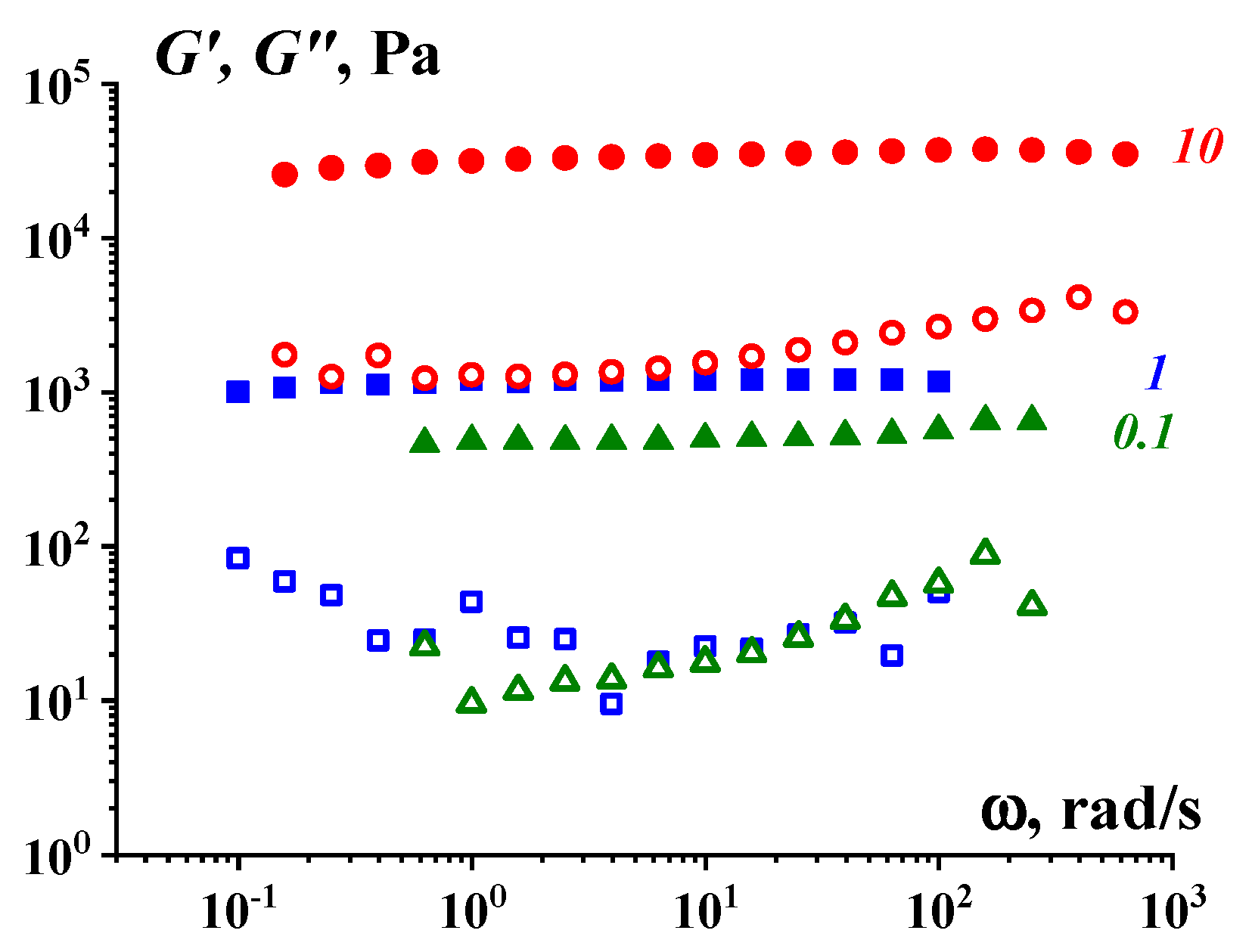
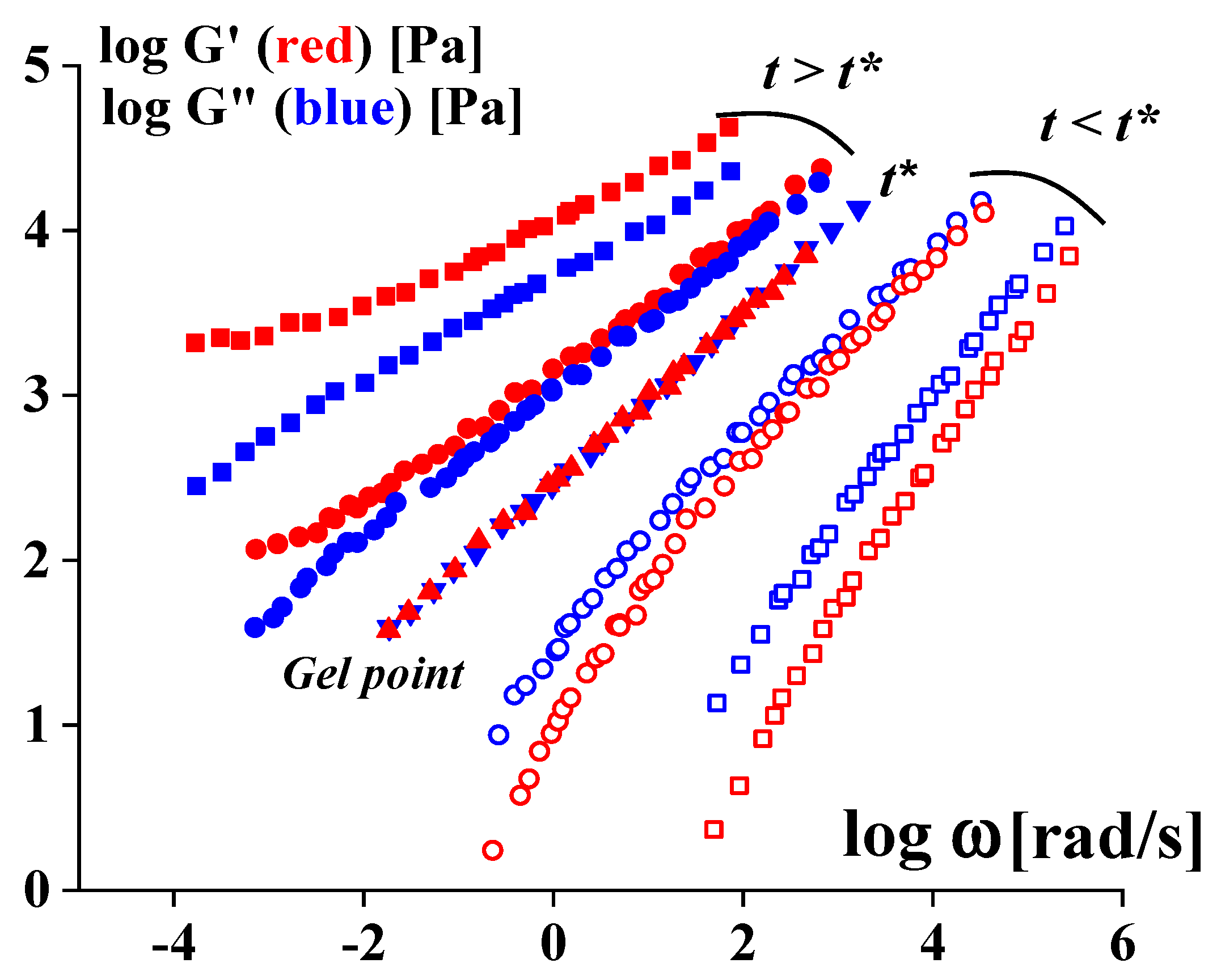
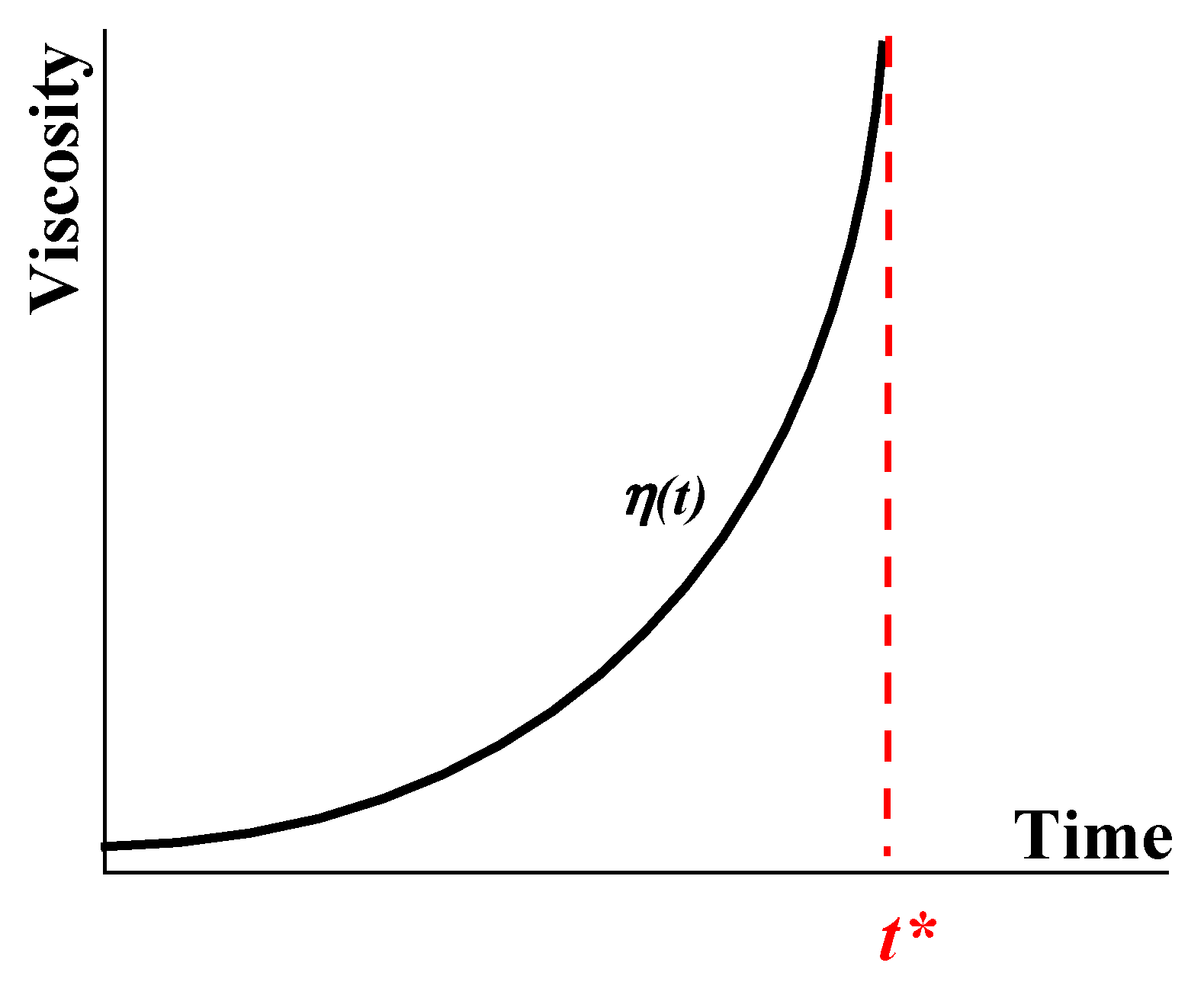
4. Sol–Gel Transition
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- de Gennes, P.G. Soft matter (Nobel lecture). Angew. Chem. Int. Ed. Engl. 1992, 31, 842–845. [Google Scholar] [CrossRef]
- van der Sman, R.G.M. Soft matter approaches to food structuring. Adv. Colloid Interface Sci. 2012, 176–177, 18–30. [Google Scholar] [CrossRef] [PubMed]
- de Souza Mendes, P.R.; Thompson, R.L. Time-dependent yield stress materials. Curr. Opin. Colloid Interface Sci. 2019, 43, 15–25. [Google Scholar] [CrossRef]
- de Souza Mendes, P.R. Thixotropic elasto-viscoplastic model for structured fluids. Soft Matter 2011, 7, 2471–2483. [Google Scholar] [CrossRef]
- de Souza Mandes, P.R.; Thomspon, R.L. A unified approach to model elasto-viscoplastic thixotropic yield-stress materials and apparent yield-stress fluids. Rheol. Acta 2013, 52, 673–694. [Google Scholar] [CrossRef]
- Overlez, G.; Barral, K.; Coussot, P. Three-dimensional jamming and flows of soft glassy materials. Nat. Mater. 2010, 9, 115–119. [Google Scholar] [CrossRef]
- Coussot, P.; Rogers, S.A. Oldroyd’s model and the foundation of modern rheology of yield stress fluids. J. Non-Newton. Fluid Mech. 2021, 295, 104604. [Google Scholar] [CrossRef]
- Armstrong, M.; Pincot, A.; Jariwala, S.; Horner, J.; Wagner, N.; Beris, A. Tensorial formulations for improved thixotropic viscoelastic modeling of human blood. J. Rheol. 2022, 66, 327–347. [Google Scholar] [CrossRef]
- Gopalakrishnan, A.; Shankarappa, S.A.; Rajanikant, G.K. Hydrogel scaffolds: Towards restitution of ischemic stroke-injured brain. Transl. Stroke Res. 2019, 10, 1–18. [Google Scholar] [CrossRef]
- Papkov, S.P. Studneobraznoe Sostoyanie Polimerov [Gel-Like State of Polymers]; Khimiya: Moscow, Russia, 1974. (In Russian) [Google Scholar]
- Vermonden, T.; Klumperman, B. The past, present and future of hydrogels. Eur. Polym. J. 2015, 72, 341–342. [Google Scholar] [CrossRef]
- Landrum, B.J.; Russel, W.; Zia, R.N. Delayed yield in colloidal gels: Creep, flow, and re-entrant solid regimes. J. Rheol. 2016, 60, 783–807. [Google Scholar] [CrossRef]
- Eberle, A.P.R.; Wagner, N.J.; Castaneda-Priego, R. Dynamical arrest transition in nanoparticle dispersions with short-range interactions. Phys. Rev. Lett. 2011, 106, 105704. [Google Scholar] [CrossRef] [PubMed]
- Zaccarelli, E. Colloidal gels: Equilibrium and non-equilibrium routes. J. Phys. Condens. Matter 2007, 19, 323101. [Google Scholar] [CrossRef]
- Emenike, E.C.; Adeleke, J.; Iwuozor, K.O.; Ogunniyi, S.; Abeyanju, C.A.; Amusa, V.T.; Okoro, H.K.; Adeniyi, A.G. Adsorption of crude oil from aqueous solution: A review. J. Water Process Eng. 2022, 50, 103330. [Google Scholar] [CrossRef]
- Asadizadeh, S.; Ayatollahi, S.; ZareNezhad, B. Fabrication of a highly efficient new nanocomposite polymer gel for controlling the excess water production in petroleum reservoirs and increasing the performance of enhanced oil recovery processes. Chin. J. Chem. Eng. 2021, 32, 385–392. [Google Scholar] [CrossRef]
- Kang, W.; Kang, X.; Lashari, Z.A.; Li, Z.; Zhou, B.; Yang, H.; Sarsenbekuly, B.; Aidarova, S. Progress of polymer gels for conformance control in oilfield. Adv. Colloid Interface Sci. 2021, 289, 102363. [Google Scholar] [CrossRef]
- Ni, F.; Xiao, P.; Zhang, C.; Chen, T. Hygroscopic polymer gels toward atmospheric moisture exploitations for energy management and freshwater generation. Matter 2022, 5, 2624–2658. [Google Scholar] [CrossRef]
- Ghosh, D.; Roy, S.G.; De, P. Amino acid-based polymeric gel network and its application in different fields. J. Indian Chem. Soc. 2022, 99, 100366. [Google Scholar] [CrossRef]
- Yuan, Z.; Ding, J.; Zhang, Y.; Huang, B.; Song, Z.; Meng, X.; Ma, X.; Gong, X.; Huang, Z.; Ma, S.; et al. Components, mechanisms and applications of stimuli-responsive polymer gels. Eur. Polym. J. 2022, 177, 111473. [Google Scholar] [CrossRef]
- Ahmed, K.; Shiblee, N.I. 4D printing of gels and soft materials. In Additive Manufacturing Materials and Technologies, Smart Materials in Additive Manufacturing; Bodaghi, M., Zolfagharian, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 265–295. ISBN 9780128240823. [Google Scholar] [CrossRef]
- Cui, L.; Guo, J.; Meng, Z. A review on food-grade-polymer-based O/W emulsion gels: Stabilization mechanism and 3D printing application. Food Hydrocoll. 2023, 139, 108588. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, K.; Qian, H.; Ramachandran, B.; Jiang, F. The advances of characterization and evaluation methods for the compatibility and assembly structure stability of food soft matter. Trends Food Sci. Technol. 2021, 112, 753–763. [Google Scholar] [CrossRef]
- Carvalho, C.; Mansur, H.S.; Leonel, A.G.; Mansur, A.A.P.; Lobato, Z.I.P. Soft matter polysaccharide-based hydrogels as versatile bioengineered platforms for brain tissue repair and regeneration. Int. J. Biol. Macromol. 2021, 182, 1091–1111. [Google Scholar] [CrossRef] [PubMed]
- Ivan’kova, E.; Egorov, V.; Marokhin, V.; Myasnilova, L.; Boiko, Y.; Radovanova, E. Fundamental structural and kinetic principals of high strength UHMWPE fibers production by gel-technology. Polymers 2022, 14, 4771. [Google Scholar] [CrossRef] [PubMed]
- Tsyurupa, M.P.; Blinnilova, Z.K.; Pavlova, L.A.; Pastukhov, A.V.; Davankov, V.A. Hypercrosslinked polystyrene: Half a century from a non-trivial idea to industrial implementation. Lab. Prod. 2020, 1, 86–96. [Google Scholar] [CrossRef]
- Li, L.; Guo, J.; Kang, C. LCST-UCST Transition Property of a Novel Retarding Swelling and Thermosensitive Particle Gel. Materials 2023, 16, 2761. [Google Scholar] [CrossRef]
- Chen, H.; Qiu, X.; Xia, T.; Li, Q.; Wen, Z.; Huang, B.; Li, Y. Mesoporous Materials Make Hydrogels More Powerful in Biomedicine. Gels 2023, 9, 207. [Google Scholar] [CrossRef] [PubMed]
- Foegeding, E.A. Rheology and sensory texture of biopolymer gels. Curr. Opin. Colloid Interface Sci. 2007, 12, 242–250. [Google Scholar] [CrossRef]
- Moosavian, H.; Tang, T. Statistical mechanics of coil–rod structure in biopolymer gels. J. Mech. Phys. Solids 2023, 175, 105272. [Google Scholar] [CrossRef]
- Liu, D.; Song, K.; Chen, W.; Chen, J.; Sun, G.; Li, L. Review: Current progresses of small-angle neutron scattering on soft-matters investigation. Nucl. Anal. 2022, 1, 100011. [Google Scholar] [CrossRef]
- Rebry, F.; Declerck, A.; Ratzsch, K.-F.; Wilhelm, M.; Dewettinck, K.; Van der Meeren, P. Rheo-NMR to investigate fat crystallization under shear. Curr. Res. Food Sci. 2021, 4, 414–420. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, K.; Li, H.; Yuan, C.; Zhu, X.; Huang, H.; Wang, Y.; Su, L.; Fang, Y. In situ observation of sol-gel transition of agarose aqueous solution by fluorescence measurement. Inter. J. Biol. Macromol. 2018, 112, 803–808. [Google Scholar] [CrossRef] [PubMed]
- Bharati, A.; Hudson, S.D.; Weigandt, K.M. Poiseuille and extensional flow small-angle scattering for developing structure–rheology relationships in soft matter systems. Curr. Opin. Colloid Interface Sci. 2019, 42, 137–146. [Google Scholar] [CrossRef]
- Makshakova, N.; Zuev, Y.F. Interaction-Induced Structural Transformations in Polysaccharide and Protein-Polysaccharide Gels as Functional Basis for Novel Soft-Matter: A Case of Carrageenans. Gels 2022, 8, 287. [Google Scholar] [CrossRef] [PubMed]
- Osad, Y.; Kajiwara, K. (Eds.) Gels Handbook; Academixc Press: San Diego, CA, USA, 2001. [Google Scholar] [CrossRef]
- Malkin, Y.; Petrie, C.J.S. Some conditions for rupture of polymeric liquids in extension. J. Rheol. 1997, 41, 1–25. [Google Scholar] [CrossRef]
- Boukany, P.E.; Wang, S.-Q.; Wang, X. Step shear of entangled linear polymer melts: New experimental evidence for elastic yielding. Macromolecules 2009, 42, 6261–6269. [Google Scholar] [CrossRef]
- Huang, Q.; Hassager, O. Polymer liquids fracture like solids. Soft Matter 2017, 13, 3470–3474. [Google Scholar] [CrossRef] [PubMed]
- Berret, J.-F.; Séréro, Y. Evidence of shear-induced fluid fracture in telechelic polymer networks. Phys. Rev. Lett. 2001, 87, 048303. [Google Scholar] [CrossRef]
- Leocmach, M.; Perge, C.; Divoux, T.; Manneville, S. Creep and Fracture of a Protein Gel under Stress. Phys. Rev. Lett. 2014, 113, 038303. [Google Scholar] [CrossRef]
- Skrzeszewska, P.J.; Sprakel, J.; de Wolf, F.A.; Fokkink, R.; Stuart, M.A.C.; der Gucht, J. Fracture and Self-Healing in a Well-Defined Self-Assembled Polymer Network. Macromolecules 2010, 43, 3542–3548. [Google Scholar] [CrossRef]
- Zhurkov, S.N. Kinetic concept of the strength of solids. Int. J. Fract. 1984, 26, 295. [Google Scholar] [CrossRef]
- Ligoure, C.; Mora, S. Fractures in complex fluids: The case of transient networks. Rheol. Acta 2013, 52, 91–114. [Google Scholar] [CrossRef]
- Poole, R.J. The Deborah and Weissenberg numbers. Br. Soc. 2012, 53, 32–39. [Google Scholar]
- Ghebremedhin, M.; Seiffert, S.; Vilgis, T.A. Physics of agarose fluid gels: Rheological properties and microstructure. Curr. Res. Food Sci. 2021, 4, 436–448. [Google Scholar] [CrossRef] [PubMed]
- Derkach, S.; Zhabyko, I.; Voron, N.; Maklakova, A.; Dyakina, T. Stability and the rheological properties of concentrated emulsions containing gelatin/k-carrageenan polyelectrolyte complexes. Colloids Surf. A Physicochem. Eng. Asp. 2015, 483, 216–223. [Google Scholar] [CrossRef]
- Makarova, A.O.; Derkach, S.R.; Kadyirov, A.I.; Ziganshina, S.A.; Kazantseva, M.A.; Zueva, O.S.; Gubaidullin, A.T.; Zuev, Y.F. Supramolecular structure and mechanical properties of κ-carrageenan-gelatin gels. Polymers 2022, 14, 4347. [Google Scholar] [CrossRef] [PubMed]
- Du, L.; Meng, Z. Oleofoams and emulsion foams stabilized by sodium stearoyl lactylate: Insight into their relations based on microstructure, rheology and tribology. Food Hydrocoll. 2023, 137, 108317. [Google Scholar] [CrossRef]
- Malafronte, L.; Yilmaz-Turan, S.; Dahl, L.; Vilaplana, F.; Lopez-Sanchez, P. Shear and extensional rheological properties of whole grain rye and oat aqueous suspensions. Food Hydrocoll. 2023, 137, 108319. [Google Scholar] [CrossRef]
- Amorim, P.A.; D’Ávila, M.A.; Anand, R.; Moldenaers, P.; Van Puyvelde, P.; Bloemen, V. Insights on shear rheology of inks for extrusion-based 3D bioprinting. Bioprinting 2021, 22, e00129. [Google Scholar] [CrossRef]
- Patel, P.; Mujmer, K.; Aswal, V.K.; Gupta, S.; Thareja, P. Structure, rheology, and 3D printing of salt-induced κ-carrageenan gels. Mater. Today Commun. 2023, 35, 105807. [Google Scholar] [CrossRef]
- Baby, D.K. Chapter 9—Rheology of Hydrogels. In Micro and Nano Technologies, Rheology of Polymer Blends and Nanocomposites; Thomas, S., Sarathchandran, C., Chandran, N., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 193–204. ISBN 9780128169575. [Google Scholar] [CrossRef]
- Sangroniz, L.; Fernández, M.; Santamaria, A. Polymers and rheology: A tale of give and take. Polymer 2023, 271, 125811. [Google Scholar] [CrossRef]
- Vlassopoulos, D.; Cloitre, M. Tunable rheology of dense soft deformable colloids. Curr. Opin. Colloid Interface Sci. 2014, 19, 561–574. [Google Scholar] [CrossRef]
- Negi, S.; Redmon, C.G.; Ramakrishnan, S.; Osuji, C.O. Viscoelasticity of a colloidal gel during dynamical arrest: Evolution through the critical gel and comparison with a soft colloidal glass. J. Rheol. 2014, 58, 1557–1579. [Google Scholar] [CrossRef]
- Lerouge, S.; Berret, J.-F. Shear-induced transitions and instabilities in surfactant wormlike micelles. Adv. Polym. Sci. 2010, 230, 1–71. [Google Scholar] [CrossRef]
- Moud, A.A.; Moud, A.A. Flow and assembly of cellulose nanocrystals (CNC): A bottom-up perspective—A review. Int. J. Biol. Macromol. 2023, 232, 123391. [Google Scholar] [CrossRef] [PubMed]
- Mitishita, R.S.; Elfring, G.J.; Frigaard, I.A. Turbulent drag reduction of viscoelastic wormlike micellar gels. J. Non-Newton. Fluid Mech. 2022, 301, 104724. [Google Scholar] [CrossRef]
- Bao, X.-N.; Zhang, W.-D.; Gang, H.-Z.; Yang, S.-Z.; Li, Y.-C.; Mu, B.-Z. Formation of viscoelastic micellar solutions by a novel cationic surfactant and anionic salt system. Colloids Surf. A Physicochem. Eng. Asp. 2021, 611, 125795. [Google Scholar] [CrossRef]
- Giustiniani, A.; Ilyas, M.; Indei, T.; Gong, J.P. Relaxation mechanisms in hydrogels with uniaxially oriented lamellar bilayers. Polymer 2023, 267, 125686. [Google Scholar] [CrossRef]
- Carrillo-Navas, H.; Hernández-Jaimes, C.; Utrilla-Coello, R.G.; Meraz, M.; Vernon-Carter, E.J.; Alvarez-Ramirez, J. Viscoelastic relaxation spectra of some native starch gels. Food Hydrocoll. 2014, 37, 25–33. [Google Scholar] [CrossRef]
- Masalova, I.; Malkin, A.Y. The engineering rheology of liquid explosives as highly concentrated emulsions. Chem. Eng. Res. Des. 2013, 91, 204–210. [Google Scholar] [CrossRef]
- Ilyin, S.O.; Arinina, M.P.; Malkin, A.Y.; Kulichikhin, V.G. Sol-gel transition and rheological properties of silica nanoparticle dispersions. Colloid J. 2016, 78, 608–615. [Google Scholar] [CrossRef]
- Derkach, S.R.; Voron’ko, N.G.; Kuchina, Y.A.; Kolotova, D.S.; Gordeeva, A.M.; Faizullin, D.A.; Gusev, Y.A.; Zuev, Y.F.; Makshakova, O.N. Molecular structure and properties of κ-carrageenan-gelatin gels. Carbohydr. Polym. 2018, 197, 66–74. [Google Scholar] [CrossRef] [PubMed]
- Rehbinder, P.A.; Abdraghimova, L.A.; Serb-Serbina, N.N. Elasto-viscous properties of thixotropic structures of bentonite in aqueous suspensions. Kolloid. J. 1955, 17, 184–190. (In Russian) [Google Scholar]
- Stokes, J.R.; Telford, J.H.; Williamson, A.-M. The flowability of ice suspension. J. Rheol. 2005, 49, 139–148. [Google Scholar] [CrossRef]
- Zhang, K.-M.; Xu, M.-X.; Hao, X.; Zhao, H.-R. Peculiarities of rheological behavior of highly concentrated water-in-oil emulsion: The role of droplet size, surfactant, oil and ammonium nitrate content. J. Mol. Liq. 2018, 272, 539–547. [Google Scholar] [CrossRef]
- Pal, R. Rheology of high internal phase ratio emulsions. Food Hydrocoll. 2006, 20, 997–1005. [Google Scholar] [CrossRef]
- Shakeel, A.; Kirichek, A.; Chassagne, C. Rheology and yielding transitions in mixed kaolinite/bentonite suspensions. Appl. Clay Sci. 2021, 211, 106206. [Google Scholar] [CrossRef]
- Kim, M.; Kim, S.; Han, N.; Lee, S.; Kim, H. Understanding viscoelastic behavior of hybrid nanocellulose film based on rheological and electrostatic observation in blended suspension. Carbohydr. Polym. 2023, 300, 120218. [Google Scholar] [CrossRef] [PubMed]
- Borah, P.K.; Yakubov, G.E.; Duary, R.K. Rheology, microstructure and diffusion in soft gelatin nanocomposites packed with anionic nanogels. Food Struct. 2021, 30, 100216. [Google Scholar] [CrossRef]
- Masalova, I.; Taylor, M.; Kharatiyan, E.; Malkin, A.Y. Rheopexy in highly concentrated emulsions. J. Rheol. 2005, 49, 839–849. [Google Scholar] [CrossRef]
- Choi, J.; Armstrong, M.; Rogers, S.A. The role of elasticity in thixotropy: Transient elastic stress. Phys. Fluids 2021, 33, 033112. [Google Scholar] [CrossRef]
- Møller, P.C.F.; Fall, A.; Bonn, D. Origin of apparent viscosity in yield stress fluids below yielding. Europlast. Lett. 2009, 87, 38004. [Google Scholar] [CrossRef]
- Dinkgreve, M.; Fazilati, M.; Denn, M.M.; Bonn, D. Carbopol: From a simple to a thixotropic yield stress. J. Rheol. 2018, 62, 773–780. [Google Scholar] [CrossRef]
- Graziano, R.; Preziosi, V.; Uva, D.; Tomaiuolo, G.; Mohebbi, B.; Claussen, J.; Guido, S. The microstructure of Carbopol in water under static and flow conditions and its effect on the yield stress. J. Colloid Interface Sci. 2021, 582, 1067–1074. [Google Scholar] [CrossRef]
- Donley, G.J.; de Bruyn, J.R.; McKinley, G.H.; Rogers, S.A. Time-resolved dynamics of the yielding transition in soft materials. J. Non-Newton. Fluid Mech. 2019, 264, 117–134. [Google Scholar] [CrossRef]
- Jaworski, Z.; Spychaj, T.; Story, A.; Story, G. Carbomer microgels as model yield-stress fluids. Rev. Chem. Eng. 2021, 38, 1–39. [Google Scholar] [CrossRef]
- Bonn, D. Yield stress fluids slowly yield to analysis. Science 2009, 324, 1401–1402. [Google Scholar] [CrossRef] [PubMed]
- Cerbino, R.; Trappe, V. Introduction to viscoelasticity and plasticity, and their relation to the underlying microscopic dynamics in soft matter systems. Phys. A Stat. Mech. Its Appl. 2023, 9, 128653. [Google Scholar] [CrossRef]
- Nicolas, A.; Ferrero, E.E.; Martens, K.; Barrat, J.-L. Deformation and flow of amorphous solids: Insights from elastoplastic models. Rev. Modern Phys. 2018, 90, 045006. [Google Scholar] [CrossRef]
- Ghosh, A.; Budrikis, Z.; Chikkadi, V.; Sellerio, A.L.; Zapperi, S.; Schall, P. Direct observation of percolation in the yielding transition of colloidal glasses. Phys. Rev. Lett. 2017, 118, 148001. [Google Scholar] [CrossRef]
- Donley, G.J.; Singh, P.K.; Shetty, A.; Rogers, S.A. Elucidating the G″ overshoot in soft materials with a yield transition via a time-resolved experimental strain decomposition. Proc. Natl. Acad. Sci. USA 2020, 117, 21945–21952. [Google Scholar] [CrossRef]
- Edera, P.; Brizioli, M.; Zanchetta, G.; Petekidis, G.; Giavazzi, F.; Cerbino, R. Deformation profiles and microscopic dynamics of complex fluids during oscillatory shear experiments. Soft Matter 2021, 17, 8553–8566. [Google Scholar] [CrossRef]
- de Cagny, H.; Fazilati, M.; Habibi, M.; Denn, M.M.; Bonn, D. The yield normal stress. J. Rheol. 2019, 63, 285–290. [Google Scholar] [CrossRef]
- Geffrault, A.; Bessaies-Bey, H.; Roussel, N.; Coussot, P. Instant yield stress measurement from falling drop size: The “syringe test”. J. Rheol. 2023, 67, 305–314. [Google Scholar] [CrossRef]
- Barnes, H.A.; Walters, K. The yield stress myth? Rheol. Acta 1985, 24, 323–326. [Google Scholar] [CrossRef]
- Barnes, H.A. The yield stress myth? Paper—25 years on. Appl. Rheol. 2007, 17, 43110-1–43110-5. [Google Scholar] [CrossRef]
- Bingham, E.C. An investigation of the laws of plastic flow. Bull. Bur. Stand. 1916, 13, 309–353. [Google Scholar] [CrossRef]
- Goh, R.; Leong, Y.-K.; Lehane, B. Bentonite slurries—Zeta potential, yield stress, adsorbed additive and time-dependent behaviour. Rheol. Acta 2011, 50, 29–38. [Google Scholar] [CrossRef]
- Abend, S.; Lagaly, G. Sol–gel transitions of sodium montmorillonite dispersions. Appl. Clay Sci. 2000, 16, 201–227. [Google Scholar] [CrossRef]
- He, F.; Xue, B.; Lei, Q.; Liu, Y.; Zhao, X.; Yin, J. Influence of molecular weight on electro-responsive electrorheological effect of poly(ionic liquid)s: Rheology and dielectric spectroscopy analysis. Polymer 2021, 234, 124241. [Google Scholar] [CrossRef]
- Coussot, P. Yield stress fluid flows: A review of experimental data. J. Non-Newton. Fluid Mech. 2014, 211, 31–49. [Google Scholar] [CrossRef]
- Uman, S.; Dhand, A.; Burdick, J.A. Recent advances in shear-thinning and self-healing hydrogels for biomedical applications. J. Appl. Polym. Sci. 2020, 137, 48668. [Google Scholar] [CrossRef]
- Belyaeva, A.A.; Tretyakov, I.V.; Kireynov, A.V.; Nashchekina, Y.A.; Solodilov, V.I.; Korzhikova-Vlakh, E.G.; Morozova, S.M. Fibrillar biocompatible colloidal gels based on cellulose nanocrystals and poly(N-isopropylacrylamide) for direct ink writing. J. Colloid Interface Sci. 2023, 635, 348–357. [Google Scholar] [CrossRef]
- Song, Y.; Kim, B.; Park, J.D.; Lee, D. Probing metal-carboxylate interactions in cellulose nanofibrils-based hydrogels using nonlinear oscillatory rheology. Carbohydr. Polym. 2023, 300, 120262. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Song, K.; Zhang, D.; Ren, B.; Sole-Gras, M.; Huang, Y.; Yin, J. Embedded extrusion printing in yield-stress-fluid baths. Matter 2022, 5, 3775–3806. [Google Scholar] [CrossRef]
- Mistry, S.; Fuhrmann, P.L.; de Vries, A.; Karshafian, R.; Rousseau, D. Structure-rheology relationship in monoolein liquid crystals. J. Colloid Interface Sci. B 2023, 630, 878–887. [Google Scholar] [CrossRef]
- Shahnazian, H.; Odenbach, S. Yield stress in ferrofluids? Int. J. Mod. Phys. B 2007, 21, 4806–4812. [Google Scholar] [CrossRef]
- Li, Z.; Li, D.; Dong, J.; Yao, J.; Chen, Y. Parallel superposition rheology on the yielding behaviors of ferrofluids. J. Magn. Magn. Mater. 2021, 539, 168279. [Google Scholar] [CrossRef]
- De Vicente, J.; Klingenberg, D.J.; Hidalgo-Alvarez, R. Magnetorheological fluids: A review. Soft Matter 2011, 7, 3701. [Google Scholar] [CrossRef]
- Frigaard, I.A.; Paso, K.G.; de Souza Mendes, P.R. Bingham’s model in the oil and gas industry. Rheol. Acta 2017, 56, 259–282. [Google Scholar] [CrossRef]
- Zhou, Z.; Solomon, M.J.; Scales, P.J.; Boger, D.V. The yield stress of concentrated flocculated suspensions of size distributed particles. J. Rheol. 1999, 43, 651–700. [Google Scholar] [CrossRef]
- Malkin, Y. Rheology of filled polymers. Adv. Polym. Sci. 1990, 96, 69–97. [Google Scholar] [CrossRef]
- Malkin, A.Y.; Isayev, A. Rheology: Concepts, Methods, Applications, 4th ed.; Chemtec Publishing: Toronto, ON, Canada, 2022; ISBN 9781927885932. [Google Scholar]
- Malkin, Y.; Ilyin, S.O.; Roumyantseva, T.B.; Kulichikhin, V.G. Rheological evidence of gel formation in dilute poly(acrylnitrile) solutions. Macromolecules 2013, 46, 257–266. [Google Scholar] [CrossRef]
- O’Shea, J.-P.; Tallon, C. Yield stress behaviour of concentrated silica suspensions with temperature-responsive polymers. Colloids Surf. A Physicochem. Eng. Asp. 2011, 385, 40–46. [Google Scholar] [CrossRef]
- Ilyin, S.; Roumyantseva, T.; Spiridonova, V.; Frenkin, E.; Malkin, A.; Kulichikhin, V. Gels of cysteine/Ag-based dilute colloid systems and their rheological properties. Soft Matter 2011, 7, 9090–9103. [Google Scholar] [CrossRef]
- Adachi, Y.; Kawashima, Y.T.; Ghazali, M.E.B. Rheology and sedimentation of aqueous suspension of Na-montmorillonite in the very dilute domain. KONA Powder Part. J. 2020, 37, 145–165. [Google Scholar] [CrossRef]
- Terech, P.; Friol, S. Rheometry of an androstanol steroid derivative paramagnetic organogel. Methodology for a comparison with a fatty acid organogel. Tetrahedron 2007, 63, 7366–7374. [Google Scholar] [CrossRef]
- Patel, R.; Babaahmadi, M.; Lesaffer, A.; Dewettinck, K. Rheological profiling of organogels prepared at critical gelling concentrations of natural waxes in a triacylglycerol solvent. J. Agric. Food Chem. 2015, 63, 4862–4869. [Google Scholar] [CrossRef]
- Malkin, Y.; Kulichikhin, V.; Ilyin, S. A modern look on yield stress fluids. Rheol. Acta 2017, 56, 177–188. [Google Scholar] [CrossRef]
- Bonn, D.; Denn, M.M.; Berthier, L.; Divoux, T.; Manneville, S. Yield stress materials in soft condensed matter. Rev. Mod. Phys. 2017, 89, 035005. [Google Scholar] [CrossRef]
- Bhattacharyya, T.; Jacob, A.R.; Petekidis, G.; Joshi, Y.M. On the nature of flow curve and categorization of thixotropic yield stress materials. J. Rheol. 2023, 67, 461–477. [Google Scholar] [CrossRef]
- Malkin, Y.; Sabsai, O.Y.; Verbitskaya, E.A.; Zolotarev, V.A.; Vinogradov, G.V. Time effects in transition through the yield stress for disperse systems. Kolloid. J. 1976, 38, 181–182. (In Russian) [Google Scholar]
- Caton, F.; Baravian, C. Plastic behavior of some yield stress fluids: From creep to long-time yield. Rheol. Acta 2008, 47, 601–607. [Google Scholar] [CrossRef]
- Møller, P.C.F.; Mewis, J.; Bonn, D. Yield stress and thixotropy: On the difficulty of measuring yield stresses in practice. Soft Matter 2006, 2, 274–283. [Google Scholar] [CrossRef] [PubMed]
- Moller, P.; Fall, A.; Chikkad, V.; Derks, D.; Bonn, D. An attempt to categorize yield stress fluid behavior. Philos. Trans. R. Soc. A 2009, 367, 5139–5155. [Google Scholar] [CrossRef]
- Uhlherr, P.H.T.; Guo, J.; Tio, C.; Zhang, X.-M.; Zhou, J.Z.-Q.; Fang, T.-M. The shear-induced solid–liquid transition in yield stress materials with chemically different structures. J. Non-Newton. Fluid Mech. 2005, 125, 101–119. [Google Scholar] [CrossRef]
- Liu, H.; Lu, Y.; Zhang, J. A comprehensive investigation of the viscoelasticity and time-dependent yielding transition of waxy crude oils. J. Rheol. 2018, 62, 527–541. [Google Scholar] [CrossRef]
- Poling-Skutvik, R.; McEvoy, E.; Shenoy, V.; Osuji, C.O. Yielding and bifurcated aging in nanofibrillar networks. Phys. Rev. Mater. 2020, 4, 102601. [Google Scholar] [CrossRef]
- Malkin, Y. Oil as an object of rheology. Pet. Chem. 2019, 59, 1092–1107. [Google Scholar] [CrossRef]
- Liu, W.-W.; Peng, J.; Zhu, K.-Q.; Zhang, J.-J. A microstructural criterion for yielding: Linking thixotropy and the yield stress. Rheol. Acta 2016, 55, 957–968. [Google Scholar] [CrossRef]
- Larson, R.G.; Wei, Y. A review of thixotropy and its rheological modeling. J. Rheol. 2019, 63, 477–501. [Google Scholar] [CrossRef]
- Geri, M.; Venkatesan, R.; Sambath, K.; McKinley, G.H. Thermokinematic memory and the thixotropic elasto-viscoplasticity of waxy crude oils. J. Rheol. 2017, 61, 427–454. [Google Scholar] [CrossRef]
- Dimitriou, J.; McKinley, G.H.; Venkatesan, R. Rheo-PIV analysis of the yielding and flow of model waxy crude oils. Energy Fuels 2011, 25, 3040–3052. [Google Scholar] [CrossRef]
- Wei, Y.F.; Solomon, M.J.; Larson, R.G. A multimode structural kinetics constitutive equation for the transient rheology of thixotropic elasto-viscoplastic fluids. J. Rheol. 2018, 62, 321–342. [Google Scholar] [CrossRef]
- Agarwal, M.; Joshi, Y.M. Signatures of physical aging and thixotropy in aqueous dispersion of carbopol. Phys. Fluids 2019, 31, 063107. [Google Scholar] [CrossRef]
- Nicolai, T. Gelation of food protein-protein mixtures. Adv. Colloid Interface Sci. 2019, 270, 147–164. [Google Scholar] [CrossRef]
- Vilgis, T.A. Gels: Model systems for soft matter food physics. Curr. Opin. Food Sci. 2015, 3, 71–84. [Google Scholar] [CrossRef]
- Derkach, S.; Voron’ko, N.; Sokolan, N. The rheology of hydrogels based on chitosan–gelatin (bio)polyelectrolyte complexes. J. Dispers. Sci. Technol. 2017, 38, 1427–1434. [Google Scholar] [CrossRef]
- Derkach, S.R.; Kolotova, D.S.; Voron’ko, N.G.; Obluchinskaya, E.D.; Malkin, Y.A. Rheological Properties of Fish Gelatin Modified with Sodium Alginate. Polymers 2021, 13, 743. [Google Scholar] [CrossRef]
- Barnes, H.A. The yield stress—A review or ‘panta roi’—Everything flows? J. Non-Newton. Fluid Mech. 1999, 81, 133–178. [Google Scholar] [CrossRef]
- Agarwal, M.; Sharma, S.; Shankar, V.; Joshi, Y.M. Distinguishing thixotropy from viscoelasticity. J. Rheol. 2021, 65, 663–680. [Google Scholar] [CrossRef]
- Sun, G.; Zhang, G.J. Structural breakdown and recovery of waxy crude oil emulsion gels. Rheol. Acta 2015, 54, 817–829. [Google Scholar] [CrossRef]
- Dimitriou, J.; McKinley, G.H. A comprehensive constitutive law for waxy crude oil: A thixotropic yield stress fluid. Soft Matter 2014, 10, 6619–6644. [Google Scholar] [CrossRef] [PubMed]
- Abedi, B.; Rodrigues, E.C.; de Souza Mendes, P.R. Irreversible time dependence of gelled waxy crude oils: Flow experiments and modeling. J. Rheol. 2020, 64, 1237–1250. [Google Scholar] [CrossRef]
- de Souza Mendes, P.R.; Abedi, B.; Thompson, R.L. Constructing a thixotropy model from rheological experiments. J. Non-Newton. Fluid Mech. 2018, 261, 1–8. [Google Scholar] [CrossRef]
- Wei, Y.; Solomon, M.J.; Larson, R.G. Letter to the Editor: Modeling the nonmonotonic time-dependence of viscosity bifurcation in thixotropic yield-stress fluids. J. Rheol. 2019, 63, 673–675. [Google Scholar] [CrossRef]
- Teoman, B.; Marron, G.; Potanin, A. Rheological characterization of flow inception of thixotropic yield stress fluids using vane and T-bar geometries. Rheol. Acta 2021, 60, 531–542. [Google Scholar] [CrossRef]
- Lin, Y.-J.; Horner, J.; Illie, B.; Lynch, M.L.; Furst, E.M.; Wagner, N.J. Molecular engineering of thixotropic, sprayable fluids with yield stress using associating polysaccharides. J. Colloid Interface Sci. 2020, 580, 264–274. [Google Scholar] [CrossRef]
- Varchanis, S.G.; Makrigiorgos, G.; Moschopoulos, P.; Dimakopoulos, Y.; Tsamopoulos, J. Modeling the rheology of thixotropic elasto-visco-plastic materials. J. Rheol. 2016, 63, 609–639. [Google Scholar] [CrossRef]
- Barnes, H.A. Thixotropy—A review. J. Non-Newton. Fluid Mech. 1997, 70, 1–33. [Google Scholar] [CrossRef]
- Serial, M.R.; Bonn, D.; Huppertz, T.; Dijksman, J.A.; van der Gucht, J.; van Duynhoven, J.P.M.; Terenzi, C. Nonlocal effects in the shear banding of a thixotropic yield stress fluid. Phys. Rev. Fluids 2021, 6, 113301. [Google Scholar] [CrossRef]
- Fall, A.; Paredes, J.; Bonn, D. Yielding and Shear Banding in Soft Glassy Materials. Phys. Rev. Lett. 2010, 105, 225502. [Google Scholar] [CrossRef] [PubMed]
- Masalova, I.; Malkin, A.Y.; Foudazi, R. Yield stress of emulsions and suspensions as measured in steady shearing and in oscillations. Appl. Rheol. 2008, 18, 44790-1–44790-8. [Google Scholar] [CrossRef]
- Jamali, S.; McKinley, G.H.; Armstrong, R.C. Microstructural Rearrangements and their Rheological Implications in a Model Thixotropic Elastoviscoplastic Fluid. Phys. Rev. Lett. 2017, 118, 048003. [Google Scholar] [CrossRef]
- Coussot, P.; Nguyen, Q.D.; Huynh, H.T.; Bonn, D. Viscosity bifurcation in thixotropic, yielding fluids. J. Rheol. 2002, 46, 573–589. [Google Scholar] [CrossRef]
- da Silva, J.A.L.; Coutinho, J.A.P. Dynamic rheological analysis of the gelation behaviour of waxy crude oils. Rheol. Acta 2004, 43, 433–441. [Google Scholar] [CrossRef]
- Visintin, R.F.G.; Lapasin, R.; Vignati, E.; D’Antona, P.; Lockhart, T.P. Rheological behavior and structural interpretation of waxy crude oil gels. Langmuir 2005, 21, 6240–6249. [Google Scholar] [CrossRef] [PubMed]
- Kané, M.; Djabourov, M.; Volle, J.L. Rheology and structure of waxy crude oils in quiescent and under shearing conditions. Fuel Energy 2005, 46, 1591–1605. [Google Scholar] [CrossRef]
- Derkach, S.R.; Ilyin, S.O.; Maklakova, A.A.; Kulichikhin, V.G.; Malkin, A.Y. The rheology of gelatin hydrogels modified by k-carrageenan. LWT-Food Sci. Technol. 2015, 63, 612–619. [Google Scholar] [CrossRef]
- Dinkgreve, M.; Paredes, J.; Denn, M.M.; Bonn, D. On different ways of measuring “the” yield stress. J. Non-Newton. Fluid Mech. 2016, 238, 233–241. [Google Scholar] [CrossRef]
- Kamari, K.M.; Donley, G.J.; Rao, R.; Grillet, A.M.; Roberts, C.; Shetty., A.; Simon, A.; Rogers, S.A. Understanding the transient large amplitude oscillatory shear behavior of yield stress fluids. J. Rheol. 2023, 67, 331–352. [Google Scholar] [CrossRef]
- Dinkgreve, M.; Denn, M.M.; Bonn, D. “Everything flows?”: Elastic effects on startup flows of yield-stress fluids. Rheol. Acta 2017, 56, 189–194. [Google Scholar] [CrossRef]
- Loppinet, B.; Stiakakis, E.; Vlassopoulos, D.; Fytas, G.; Roovers, J. Reversible Thermal Gelation in Star Polymers: An Alternative Route to Jamming of Soft Matter. Macromolecules 2001, 34, 8216–8223. [Google Scholar] [CrossRef]
- Sasaki, T.; Tsuzuki, Y.; Nakane, T. A Dynamically Correlated Network Model for the Collective Dynamics in Glass-Forming Molecular Liquids and Polymers. Polymers 2021, 13, 3424. [Google Scholar] [CrossRef]
- Malkin, Y. Why does the viscosity of waxy oil decrease with the decrease in the cooling rate? A model. Thermochim. Acta 2016, 624, 82–85. [Google Scholar] [CrossRef]
- Legnani, A.; Santos, T.G.M.; Andrade, D.E.V.; Negrão, C.O.R. Waxy oils: Deformation-dependent materials. J. Non-Newton. Fluid Mech. 2020, 285, 104378. [Google Scholar] [CrossRef]
- Magda, J.J.; El-Gendy, H.; Oh, K.; Deo, M.D.; Montesi, A.; Venkatesan, R. Time-dependent rheology of a model waxy crude oil with relevance to gelled pipeline restart. Energy Fuels 2009, 23, 1311–1315. [Google Scholar] [CrossRef]
- Abivin, P.; Taylor, S.D.; Freed, D. Thermal behavior and viscoelasticity of heavy oils. Energy Fuels 2012, 26, 3448–3461. [Google Scholar] [CrossRef]
- Jia, B.; Zhang, J. Yield Behavior of Waxy Crude Gel: Effect of isothermal structure development before prior applied stress. Ind. Eng. Chem Res. 2012, 51, 10977–10982. [Google Scholar] [CrossRef]
- Teng, H.; Zhang, J. Modeling the thixotropic behavior of waxy crude. Ind. Eng. Chem. Res. 2013, 52, 8079–8089. [Google Scholar] [CrossRef]
- Van Der Geest, C.; Guersoni, V.C.B.; Merino-Garcia, D.; Bannwart, A.C. A modified elasto-viscoplastic thixotropic model for two commercial gelled waxy crude oils. Rheol. Acta 2015, 54, 545–561. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, J.; Lu, Y. Yielding characterization of waxy gels by energy dissipation. Rheol. Acta 2018, 57, 473–480. [Google Scholar] [CrossRef]
- Ahmadpour, A.; Sadeghy, K.; Maddah-Sadatieh, S.-R. The effect of a variable plastic viscosity on the restart problem of pipelines filled with gelled waxy crude oils. J. Non-Newton. Fluid Mech. 2014, 205, 16–27. [Google Scholar] [CrossRef]
- Mendes, R.; Vinay, G.; Ovarlez, G.; Coussot, P. Modeling the rheological behavior of waxy crude oils as a function of flow and temperature history. J. Rheol. 2015, 59, 703–732. [Google Scholar] [CrossRef]
- Mendes, R.; Vinay, G.; Coussot, P. Yield stress and minimum pressure for simulating the flow restart of a waxy crude oil pipeline. Energy Fuels 2017, 31, 395–407. [Google Scholar] [CrossRef]
- Chala, G.T.; Sulaiman, S.A.; Japper-Jaafar, A. Flow start-up and transportation of waxy crude oil in pipelines-A review. J. Non-Newton. Fluid Mech. 2018, 251, 69–87. [Google Scholar] [CrossRef]
- Diba, M.; Wang, H.; Kodger, T.E.; Parsa, S.; Leeuwenburgh, S.C.G. Highly Elastic and Self-Healing Composite Colloidal Gels. Adv. Mater. 2017, 29, 1604672. [Google Scholar] [CrossRef] [PubMed]
- Mitsoulis, E.; Tsamopoulos, J. Numerical simulations of complex yield-stress fluid flows. Rheol. Acta 2017, 56, 231–258. [Google Scholar] [CrossRef]
- Saramito, P.; Wachs, A. Progress in numerical simulation of yield stress fluid flows. Rheol. Acta 2017, 56, 211–230. [Google Scholar] [CrossRef]
- Fernandes, R.R.; Turezo, G.; Andrade, D.E.V.; Franco, A.T.; Negrão, C.O.R. Are the rheological properties of water-based and synthetic drilling fluids obtained by the Fann 35A viscometer reliable? J. Pet. Sci. Eng. 2019, 177, 872–879. [Google Scholar] [CrossRef]
- Winter, H.H. Can the gel point of a cross-linking polymer be detected by the G′–G″ crossover? Polym. Eng. Sci. 1987, 27, 1698–1702. [Google Scholar] [CrossRef]
- Winter, H.H.; Chambon, F. Analysis of Linear Viscoelasticity of a Crosslinking Polymer at the Gel Point. J. Rheol. 1986, 30, 367–382. [Google Scholar] [CrossRef]
- Nijenhuis, K.T.; Winter, H.H. Mechanical properties at the gel point of a crystallizing poly(vinyl chloride) solution. Macromolecules 1989, 21, 411–414. [Google Scholar] [CrossRef]
- Nishinary, K. Rheological and DSC study of sol-gel transition in aqueous dispersions of industrially important polymers and colloids. Colloid Polym. Sci. 1997, 275, 1097–1107. [Google Scholar] [CrossRef]
- Zhao, Y.; Cao, Y.; Yang, Y.; Wu, C. Rheological Study of the Sol-Gel Transition of Hybrid Gels. Macromolecules 2003, 36, 855–859. [Google Scholar] [CrossRef]
- Liu, X.; Qian, L.; Shu, T.; Tong, Z. Rheology characterization of sol–gel transition in aqueous alginate solutions induced by calcium cations through in situ release. Polymer 2003, 44, 407–412. [Google Scholar] [CrossRef]
- Winter, H.H.; Mours, M. Rheology of polymers near liquid-Solid transitions. Adv. Polym. Sci. 1997, 134, 165–234. [Google Scholar] [CrossRef]
- Muthukumar, M. Screening effect on viscoelasticity near the gel point. Macromolecules 1989, 22, 4656–4658. [Google Scholar] [CrossRef]
- Jatav, S.; Joshi, Y.M. Phase behavior of aqueous suspension of laponite: New insights with microscopic evidence. Langmuir 2017, 33, 2370–2377. [Google Scholar] [CrossRef]
- Li, L. Thermal gelation of methylcellulose in water: Scaling and thermos reversibility. Macromolecules 2002, 35, 5990–5998. [Google Scholar] [CrossRef]
- Bouthier, L.-V.; Gibaud, T. Three length-scales colloidal gels: The clusters of clusters versus the interpenetrating clusters approach. J. Rheol. 2023, 67, 621–633. [Google Scholar] [CrossRef]
- Li, B.; Guo, Y.; Steeman, P.; Bulters, M.; Yu, W. Shear-induced breakdown and agglomeration in nanoparticles filled polymer: The shift of phase boundary and kinetics. J. Rheol. 2021, 65, 291–309. [Google Scholar] [CrossRef]
- Cho, J.; Heuzey, M.-C. Dynamic scaling for gelation of a thermosensitive chitosan-β-glycerophosphate hydrogel. Colloid Polym. Sci. 2008, 286, 427–434. [Google Scholar] [CrossRef]
- Suman, K.; Joshi, Y.M. On the universality of the scaling relations during sol-gel transition. J. Rheol. 2020, 64, 863–877. [Google Scholar] [CrossRef]
- Indei, T. Rheological study of transient networks with junctions of limited multiplicity. II. Sol/gel transition and rheology. J. Chem. Phys. 2007, 127, 144905. [Google Scholar] [CrossRef]
- Karagöz, İ.; Tuna, Ö. Effect of melt temperature on product properties of injection-molded high-density polyethylene. Polym. Bull. 2021, 78, 6073–6091. [Google Scholar] [CrossRef]
- Bovas, B.C.; Karunamoorthy, L.; Chuan, F.B. Effect of extrusion process melt temperature on polyurethane catheter surfaces. Mater. Manuf. Process. 2018, 33, 180–185. [Google Scholar] [CrossRef]
- Djabjurov, V.; Leblond, J.; Papon, P. Gelation of aqueous gelatin solutions II: Rheology of the sol-gel transition. J. Phys. Fr. 1988, 49, 333–343. [Google Scholar] [CrossRef]
- Zhou, S.; Zhou, Q.; Lu, C.; Zhang, Z.; Ren, L. Design and preparation of 3D printing intelligent poly N,N-dimethylacrylamide hydrogel actuators. e-Polymers 2020, 20, 273–281. [Google Scholar] [CrossRef]
- Choudhary, S.; White, J.C.; Stoppel, W.L.; Roberts, S.C.; Bhatia, S.R. Gelation behavior of polysaccharide-based interpenetrating polymer network (IPN) hydrogels. Rheol. Acta 2011, 50, 39–52. [Google Scholar] [CrossRef]
- Zhu, X.; Yang, Y.; Zheng, Z.; Xiang, B.; Cui, X. Multiwave rheology and dynamic light scattering characterizations for a two-step sol-gel transition of tetraethoxysilane hydrolysis and condensation. J. Sol-Gel Sci. Technol. 2018, 88, 255–262. [Google Scholar] [CrossRef]
- Xu, Z.; Raphaelides, S.N. A dynamic U-tube rheometer of novel design for the study of weak gels and foams. Rheol. Acta 2005, 45, 77–82. [Google Scholar] [CrossRef]
- Malkin, Y.; Begishev, V.P.; Mansurov, V.A. Determining the dynamic characteristics of polymeric materials by non-sinusoidal vibrations technique. Vysokomol. Coedineniya Seriya A 1984, 26, 869–871. (In Russian) [Google Scholar] [CrossRef]
- Kudryavstev, P. Investigation of the sol-gel transition by rheological methods. WSEAS Trans. Heat Mass Transf. 2018, 13, 66–75. [Google Scholar]
- Varchanis, S.; Haward, S.J.; Hopkins, C.C.; Syrakos, A.; Shen, A.Q.; Dimakopoulos, Y.; Tsamopoulos, J. Transition between solid and liquid state of yield-stress fluids under purely extensional deformations. Appl. Phys. Sci. 2020, 117, 12611–12617. [Google Scholar] [CrossRef] [PubMed]
- Geffrault, A.; Bessaies-Bey, H.; Roussel, N.; Coussot, P. Extensional gravity-rheometry (EGR) for yield stress fluids. J. Rheol. 2021, 65, 887–901. [Google Scholar] [CrossRef]
- Wainewright, W. Physical tests for gelatin and gelatin products. In The Science and Technology of Gelatin; Ward, A.G., Courts, A., Eds.; Academic Press: London, UK; New York, NY, USA; San Francisco, CA, USA, 1977; pp. 507–534. [Google Scholar]
- Suryaningrum, T.D.; Utomo, B.S.D. Instructions for Seaweed Analysis and Results Processed; Center for Product Processing Resilience and Socio-Economic Fisheries and Marine: Jakarta, Indonesia, 2002. [Google Scholar]
- Oishi, M.; Martins, F.P.; Thompson, R.L. The “avalanche effect” of an elasto-viscoplastic thixotropic material on an inclined plane. J. Non-Newton. Fluid Mech. 2017, 247, 165–177. [Google Scholar] [CrossRef]
- Fu, Y.; Ren, P.; Wang, F.; Liang, M.; Hu, W.; Zhou, N.; Lu, Z.; Zhang, T. Mussel-inspired hybrid network hydrogel for continuous adhesion in water. Mater. Chem. B 2020, 8, 2148–2154. [Google Scholar] [CrossRef]
- Desai, M.S.; Chen, M.; Hing, F.; Honga, J.; Lee, J.H.; Wu, Y.; Lee, S.W. Catechol Functionalized Elastin-like Polypeptides as Tissue Adhesives. Biomacromolecules 2020, 21, 2938–2948. [Google Scholar] [CrossRef]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malkin, A.Y.; Derkach, S.R.; Kulichikhin, V.G. Rheology of Gels and Yielding Liquids. Gels 2023, 9, 715. https://doi.org/10.3390/gels9090715
Malkin AY, Derkach SR, Kulichikhin VG. Rheology of Gels and Yielding Liquids. Gels. 2023; 9(9):715. https://doi.org/10.3390/gels9090715
Chicago/Turabian StyleMalkin, Alexander Ya., Svetlana R. Derkach, and Valery G. Kulichikhin. 2023. "Rheology of Gels and Yielding Liquids" Gels 9, no. 9: 715. https://doi.org/10.3390/gels9090715
APA StyleMalkin, A. Y., Derkach, S. R., & Kulichikhin, V. G. (2023). Rheology of Gels and Yielding Liquids. Gels, 9(9), 715. https://doi.org/10.3390/gels9090715









