Portable Quartz Crystal Resonator Sensor for Characterising the Gelation Kinetics and Viscoelastic Properties of Hydrogels
Abstract
1. Introduction
2. Results
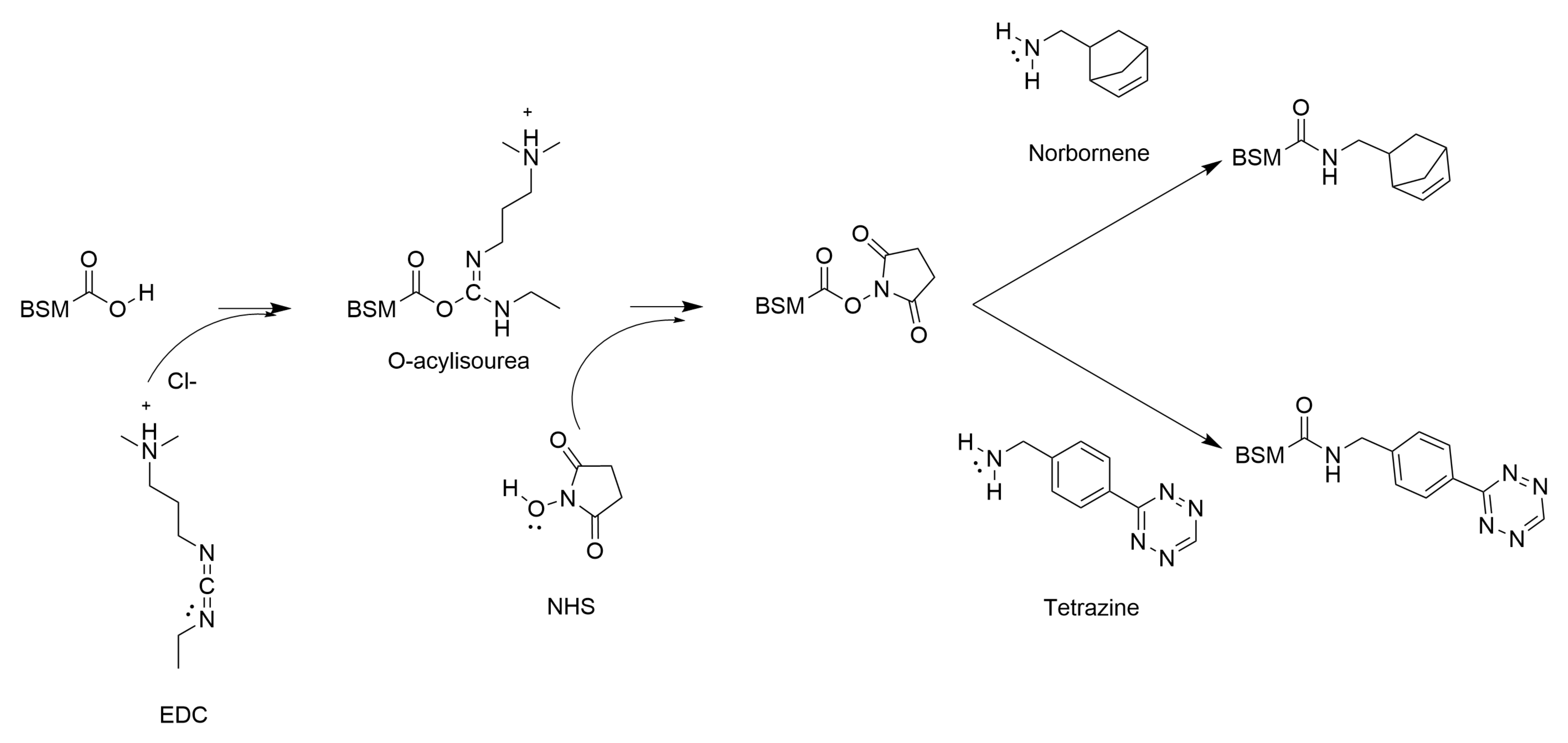
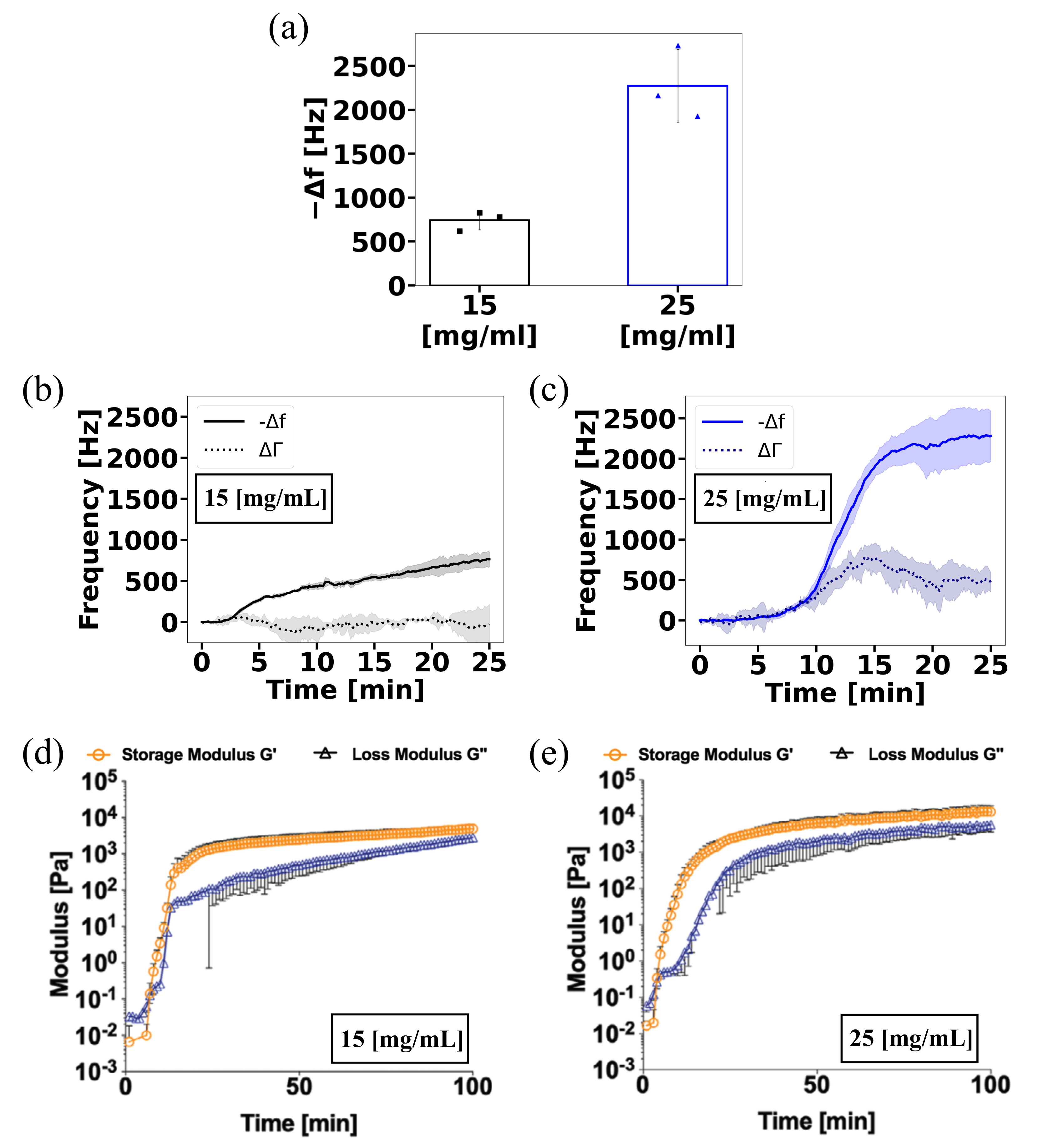
2.1. QCR Can Measure the Gelation Kinetics of Covalently Crosslinked Hydrogels
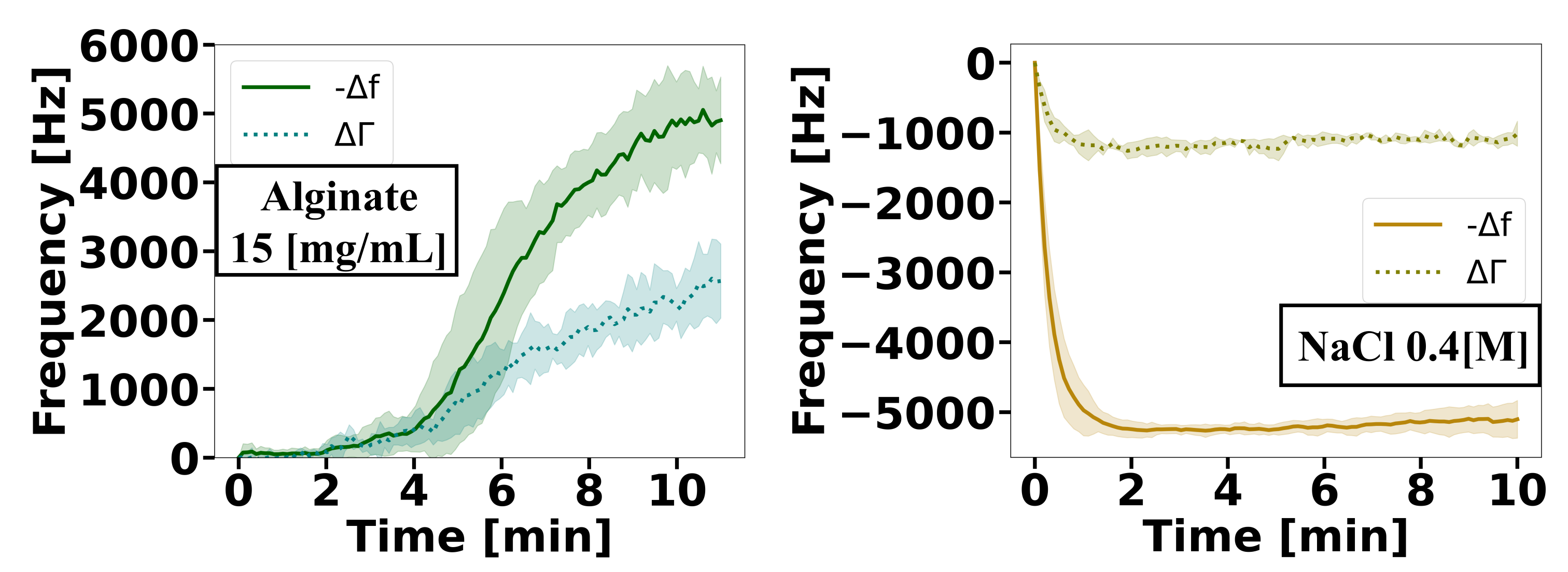
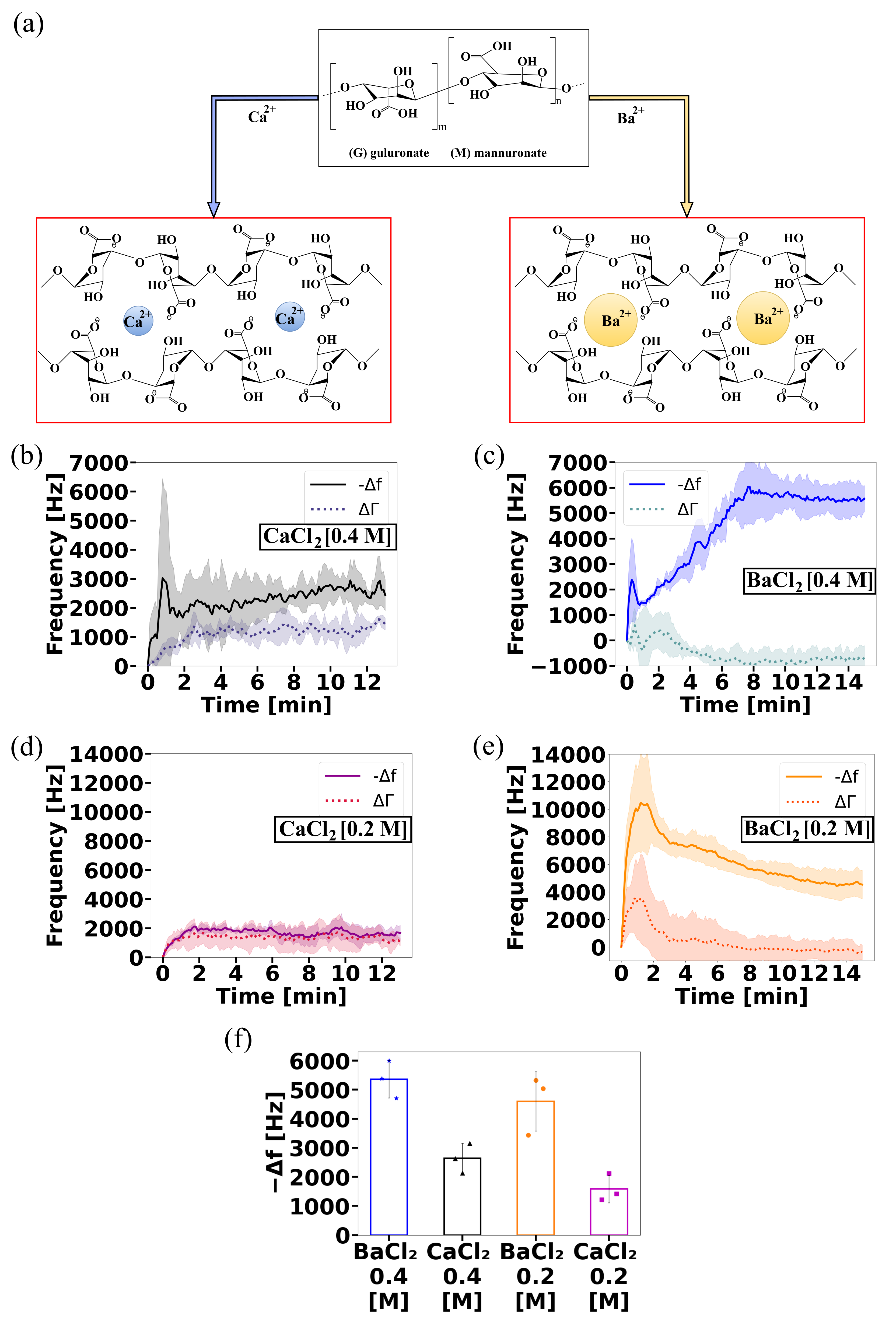
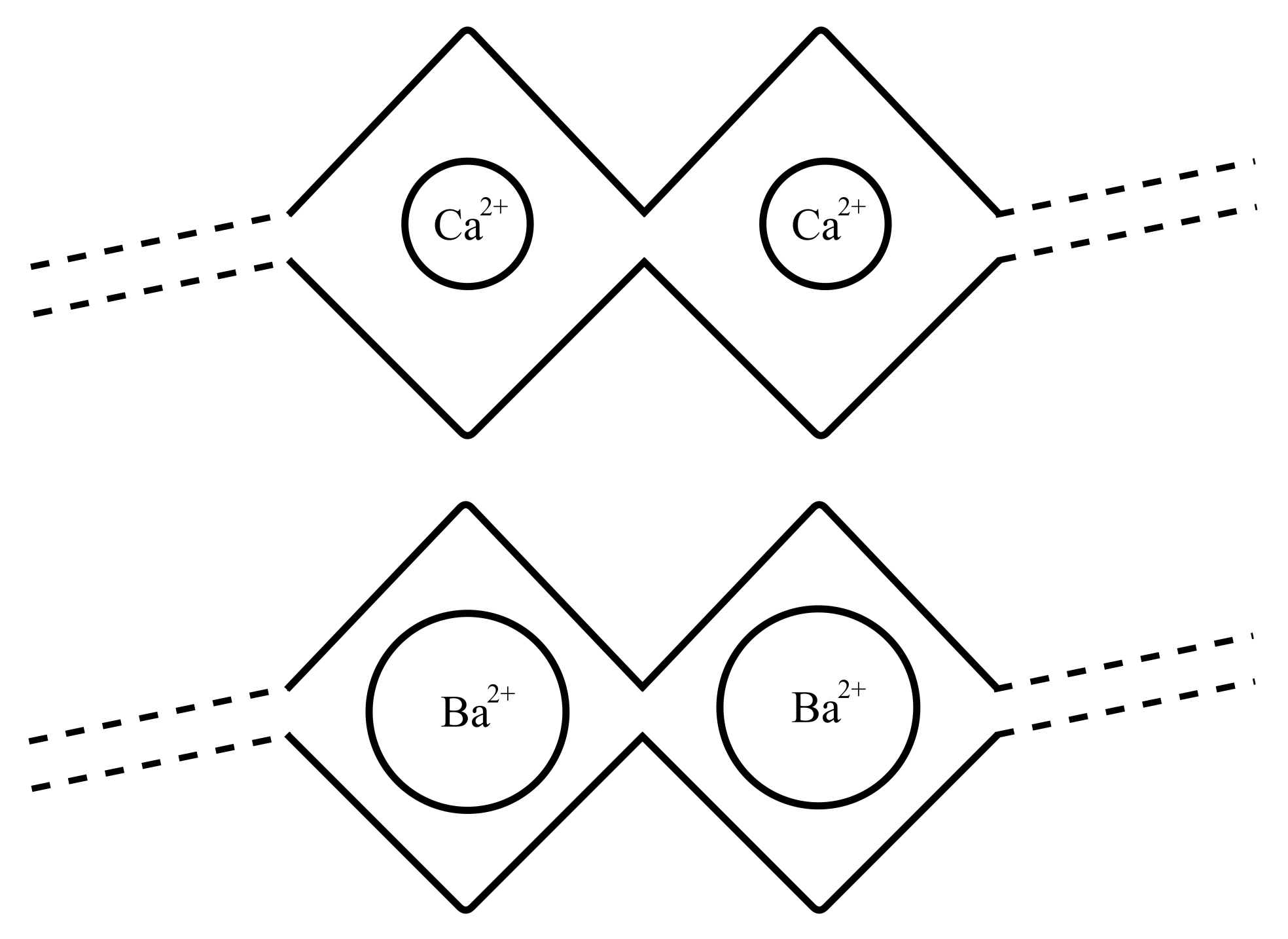
2.2. QCR Can Measure the Gelation Kinetics of Physically Crosslinked Alginate Hydrogels
3. Conclusions
4. Materials and Methods
4.1. Covalently Crosslinked Mucin Hydrogels
4.2. Physically Crosslinked Alginate Hydrogels
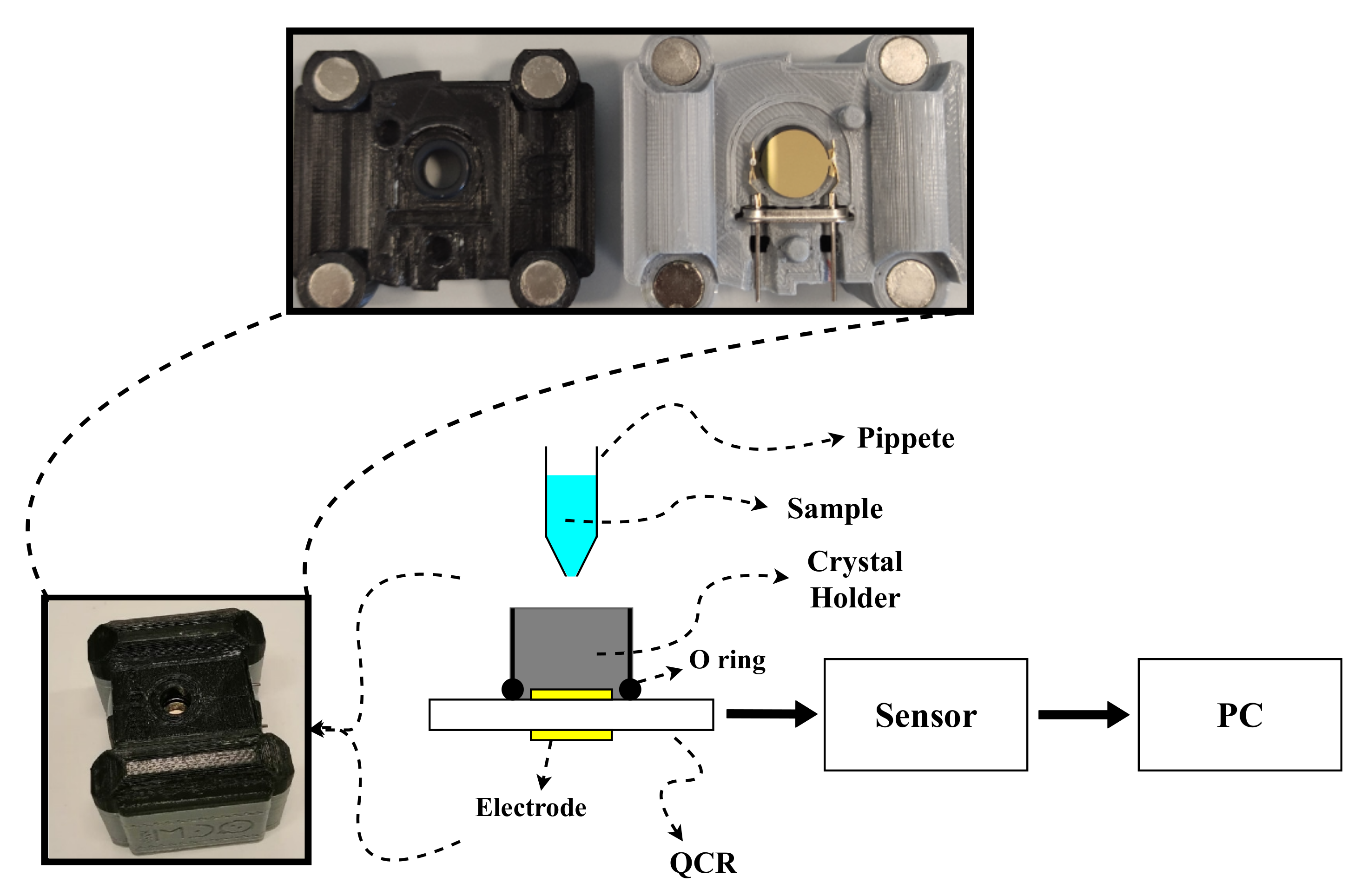
4.3. QCR Sensor
4.4. Experimental Setup
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A



References
- Deligkaris, K.; Tadele, T.S.; Olthuis, W.; van den Berg, A. Hydrogel-based devices for biomedical applications. Sens. Actuators B Chem. 2010, 147, 765–774. [Google Scholar] [CrossRef]
- Alonso, J.M.; Del Olmo, J.A.; Gonzalez, R.P.; Saez-martinez, V. Injectable hydrogels: From laboratory to industrialization. Polymers 2021, 13, 650. [Google Scholar] [CrossRef] [PubMed]
- Yan, H.; Melin, M.; Jiang, K.; Trossbach, M.; Badadamath, B.; Langer, K.; Winkeljann, B.; Lieleg, O.; Hong, J.; Joensson, H.N.; et al. Immune-Modulating Mucin Hydrogel Microdroplets for the Encapsulation of Cell and Microtissue. Adv. Funct. Mater. 2021, 31, 2105967. [Google Scholar] [CrossRef]
- Moeinzadeh, S.; Jabbari, E. Gelation characteristics, physico-mechanical properties and degradation kinetics of micellar hydrogels. Eur. Polym. J. 2015, 72, 566–576. [Google Scholar] [CrossRef] [PubMed]
- Chung, Y.M.; Simmons, K.L.; Gutowska, A.; Jeong, B. Sol-Gel transition temperature of PLGA-g-PEG aqueous solutions. Biomacromolecules 2002, 3, 511–516. [Google Scholar] [CrossRef]
- Van Vlierberghe, S.; Dubruel, P.; Schacht, E. Biopolymer-Based Hydrogels As Scaffolds for Tissue Engineering Applications: A Review. Biomacromolecules 2011, 12, 1387–1408. [Google Scholar] [CrossRef]
- Yang, J.A.; Yeom, J.; Hwang, B.W.; Hoffman, A.S.; Hahn, S.K. In situ-forming injectable hydrogels for regenerative medicine. Prog. Polym. Sci. 2014, 39, 1973–1986. [Google Scholar] [CrossRef]
- Shields, C.W., IV; Wang, L.L.W.; Evans, M.A.; Mitragotri, S. Materials for Immunotherapy. Adv. Mater. 2020, 32, 1901633. [Google Scholar] [CrossRef]
- Chen, Z.; Klein, T.; Murray, R.Z.; Crawford, R.; Chang, J.; Wu, C.; Xiao, Y. Osteoimmunomodulation for the development of advanced bone biomaterials. Mater. Today 2016, 19, 304–321. [Google Scholar] [CrossRef]
- Dingal, P.C.D.P.; Discher, D.E. Material control of stem cell differentiation: Challenges in nano-characterization. Curr. Opin. Biotechnol. 2014, 28, 46–50. [Google Scholar] [CrossRef]
- Zhao, Y.; Yan, H.; Qiao, S.; Zhang, L.; Wang, T.; Meng, Q.; Chen, X.; Lin, F.H.; Guo, K.; Li, C.; et al. Hydrogels bearing bioengineered mimetic embryonic microenvironments for tumor reversion. J. Mater. Chem. B 2016, 4, 6183–6191. [Google Scholar] [CrossRef] [PubMed]
- Ehre, C.; Worthington, E.N.; Liesman, R.M.; Grubb, B.R.; Barbier, D.; O’Neal, W.K.; Sallenave, J.M.; Pickles, R.J.; Boucher, R.C. Overexpressing mouse model demonstrates the protective role of Muc5ac in the lungs. Proc. Natl. Acad. Sci. USA 2012, 109, 16528–16533. [Google Scholar] [CrossRef] [PubMed]
- Sheng, Y.H.; Lourie, R.; Lindén, S.K.; Jeffery, P.L.; Roche, D.; Tran, T.V.; Png, C.W.; Waterhouse, N.; Sutton, P.; Florin, T.H.J.; et al. The MUC13 cell-surface mucin protects against intestinal inflammation by inhibiting epithelial cell apoptosis. Gut 2011, 60, 1661–1670. [Google Scholar] [CrossRef]
- Becher, N.; Waldorf, K.A.; Hein, M.; Uldbjerg, N. The cervical mucus plug: Structured review of the literature. Acta Obstet. Et Gynecol. Scand. 2009, 88, 502–513. [Google Scholar] [CrossRef] [PubMed]
- Damiano, J.; Bardin, T. Synovial fluid. In EMC-Rhumatologie-Orthopedie; Elsevier: Amsterdam, The Netherlands, 2004; Volume 1, pp. 2–16. [Google Scholar] [CrossRef]
- Yan, H.; Hjorth, M.; Winkeljann, B.; Dobryden, I.; Lieleg, O.; Crouzier, T. Glyco-Modification of Mucin Hydrogels to Investigate Their Immune Activity. ACS Appl. Mater. Interfaces 2020, 12, 19324–19336. [Google Scholar] [CrossRef] [PubMed]
- Łabowska, M.B.; Cierluk, K.; Jankowska, A.M.; Kulbacka, J.; Detyna, J.; Michalak, I. A review on the adaption of alginate-gelatin hydrogels for 3D cultures and bioprinting. Materials 2021, 14, 858. [Google Scholar] [CrossRef]
- Zuidema, J.M.; Rivet, C.J.; Gilbert, R.J.; Morrison, F.A. A protocol for rheological characterization of hydrogels for tissue engineering strategies. J. Biomed. Mater. Res.—Part B Appl. Biomater. 2014, 102, 1063–1073. [Google Scholar] [CrossRef]
- Kretschmer, M.; Ceña-Diez, R.; Butnarasu, C.; Silveira, V.; Dobryden, I.; Visentin, S.; Berglund, P.; Sönnerborg, A.; Lieleg, O.; Crouzier, T.; et al. Synthetic Mucin Gels with Self-Healing Properties Augment Lubricity and Inhibit HIV-1 and HSV-2 Transmission. Adv. Sci. 2022, 2203898. [Google Scholar] [CrossRef]
- Martin, S.J.; Granstaff, V.E.; Frye, G.C. Characterization of a Quartz Crystal Microbalance with Simultaneous Mass and Liquid Loading. Anal. Chem. 1991, 63, 2272–2281. [Google Scholar] [CrossRef]
- Huang, X.; Bai, Q.; Hu, J.; Hou, D. A practical model of quartz crystal microbalance in actual applications. Sensors 2017, 17, 1785. [Google Scholar] [CrossRef]
- Fort, A.; Panzardi, E.; Vignoli, V.; Tani, M.; Landi, E.; Mugnaini, M.; Vaccarella, P. An adaptive measurement system for the simultaneous evaluation of frequency shift and series resistance of QCM in liquid. Sensors 2021, 21, 678. [Google Scholar] [CrossRef] [PubMed]
- Kittle, J.; Levin, J.; Levin, N. Water content of polyelectrolyte multilayer films measured by quartz crystal microbalance and deuterium oxide exchange. Sensors 2021, 21, 771. [Google Scholar] [CrossRef] [PubMed]
- Ahumada, L.A.C.; González, M.X.R.; Sandoval, O.L.H.; Olmedo, J.J.S. Evaluation of hyaluronic acid dilutions at different concentrations using a quartz crystal resonator (QCR) for the potential diagnosis of arthritic diseases. Sensors 2016, 16, 1956. [Google Scholar] [CrossRef] [PubMed]
- Miranda-Martínez, A.; Rivera-González, M.X.; Zeinoun, M.; Carvajal-Ahumada, L.A.; Serrano-Olmedo, J.J. Viscosity measurement sensor: A prototype for a novel medical diagnostic method based on quartz crystal resonator. Sensors 2021, 21, 2743. [Google Scholar] [CrossRef] [PubMed]
- Tan, F.; Qiu, D.Y.; Guo, L.P.; Ye, P.; Zeng, H.; Jiang, J.; Tang, Y.; Zhang, Y.C. Separate density and viscosity measurements of unknown liquid using quartz crystal microbalance. AIP Adv. 2016, 6, 095313. [Google Scholar] [CrossRef]
- Sadman, K.; Wiener, C.G.; Weiss, R.A.; White, C.C.; Shull, K.R.; Vogt, B.D. Quantitative Rheometry of Thin Soft Materials Using the Quartz Crystal Microbalance with Dissipation. Anal. Chem. 2018, 90, 4079–4088. [Google Scholar] [CrossRef]
- Yan, H.; Seignez, C.; Hjorth, M.; Winkeljann, B.; Blakeley, M.; Lieleg, O.; Phillipson, M.; Crouzier, T. Immune-Informed Mucin Hydrogels Evade Fibrotic Foreign Body Response In Vivo. Adv. Funct. Mater. 2019, 29, 1902581. [Google Scholar] [CrossRef]
- Bierhalz, A.C.K.; da Silva, M.A.; Braga, M.E.M.; Sousa, H.J.C.; Kieckbusch, T.G. Effect of calcium and/or barium crosslinking on the physical and antimicrobial properties of natamycin-loaded alginate films. LWT—Food Sci. Technol. 2014, 57, 494–501. [Google Scholar] [CrossRef]
- Vanýsek, P. Ionic Conductivity and Diffusion at Infinite Dilution, Handbook of Chemistry and Physics, 83rd ed.; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Johannsmann, D. The quartz crystal microbalance in soft matter research. Soft and Biological Matter; Springer: Gewerbestrasse, Switzerland, 2015; pp. 191–204. [Google Scholar] [CrossRef]
- Alizadeh Sardroud, H.; Nemati, S.; Baradar Khoshfetrat, A.; Nabavinia, M.; Beygi Khosrowshahi, Y. Barium-cross-linked alginate-gelatine microcapsule as a potential platform for stem cell production and modular tissue formation. J. Microencapsul. 2017, 34, 488–497. [Google Scholar] [CrossRef]
- Carvajal Ahumada, L.A.; Peña Pérez, N.; Herrera Sandoval, O.L.; del Pozo Guerrero, F.; Serrano Olmedo, J.J. A new way to find dielectric properties of liquid sample using the quartz crystal resonator (QCR). Sens. Actuators A Phys. 2016, 239, 153–160. [Google Scholar] [CrossRef]
- Sauerbrey, G. Verwendung von Schwingquarzen zur Wägung dünner Schichten und zur Mikrowägung. Z. Für Phys. 1959, 155, 206–222. [Google Scholar] [CrossRef]
- Keiji Kanazawa, K.; Gordon, J.G. The oscillation frequency of a quartz resonator in contact with liquid. Anal. Chim. Acta 1985, 175, 99–105. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miranda-Martínez, A.; Yan, H.; Silveira, V.; Serrano-Olmedo, J.J.; Crouzier, T. Portable Quartz Crystal Resonator Sensor for Characterising the Gelation Kinetics and Viscoelastic Properties of Hydrogels. Gels 2022, 8, 718. https://doi.org/10.3390/gels8110718
Miranda-Martínez A, Yan H, Silveira V, Serrano-Olmedo JJ, Crouzier T. Portable Quartz Crystal Resonator Sensor for Characterising the Gelation Kinetics and Viscoelastic Properties of Hydrogels. Gels. 2022; 8(11):718. https://doi.org/10.3390/gels8110718
Chicago/Turabian StyleMiranda-Martínez, Andrés, Hongji Yan, Valentin Silveira, José Javier Serrano-Olmedo, and Thomas Crouzier. 2022. "Portable Quartz Crystal Resonator Sensor for Characterising the Gelation Kinetics and Viscoelastic Properties of Hydrogels" Gels 8, no. 11: 718. https://doi.org/10.3390/gels8110718
APA StyleMiranda-Martínez, A., Yan, H., Silveira, V., Serrano-Olmedo, J. J., & Crouzier, T. (2022). Portable Quartz Crystal Resonator Sensor for Characterising the Gelation Kinetics and Viscoelastic Properties of Hydrogels. Gels, 8(11), 718. https://doi.org/10.3390/gels8110718






