Whole Three-Dimensional Dosimetry of Carbon Ion Beams with an MRI-Based Nanocomposite Fricke Gel Dosimeter Using Rapid T1 Mapping Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Gel Preparation
2.2. Irradiation
2.3. MRI Measurements
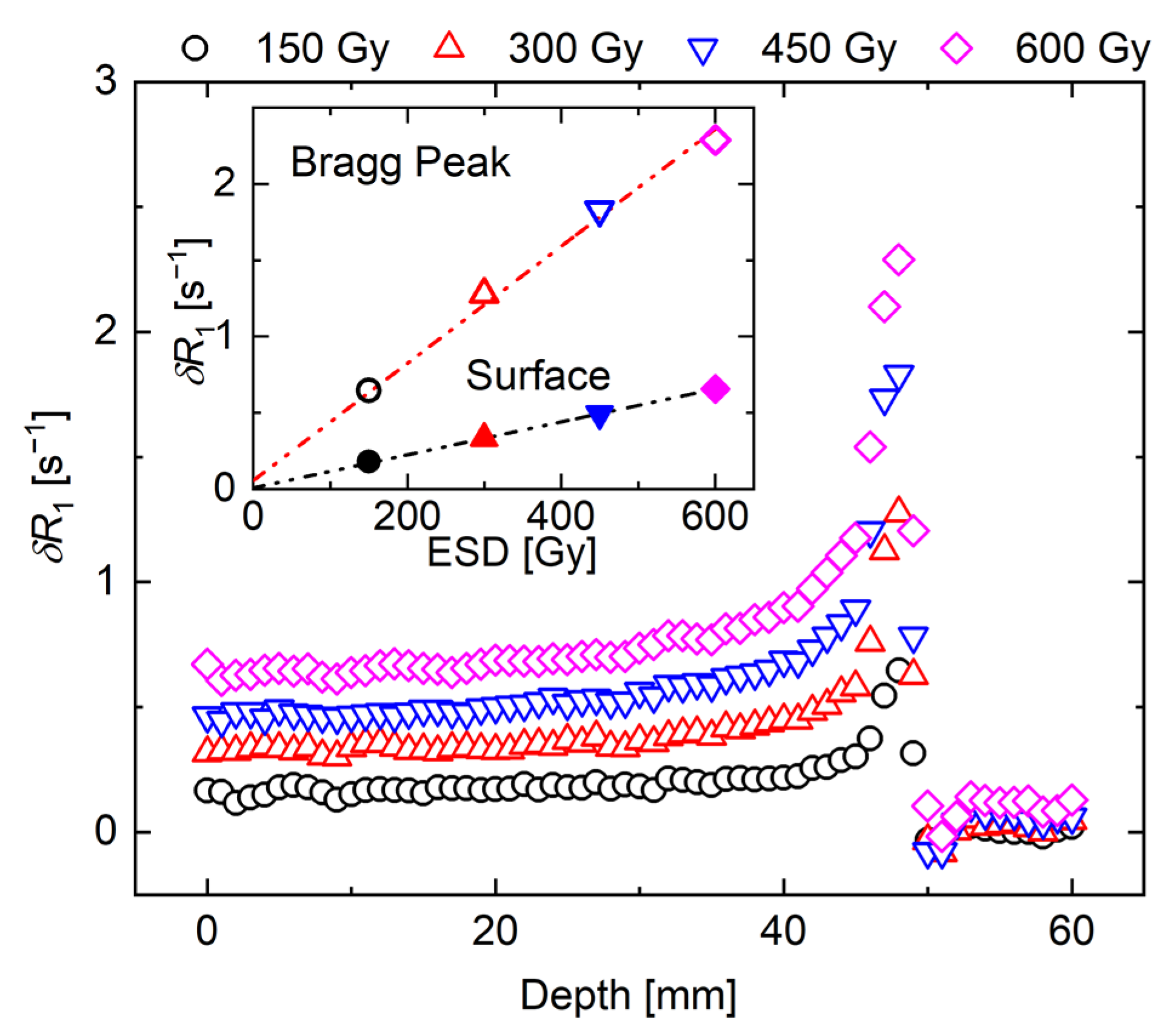
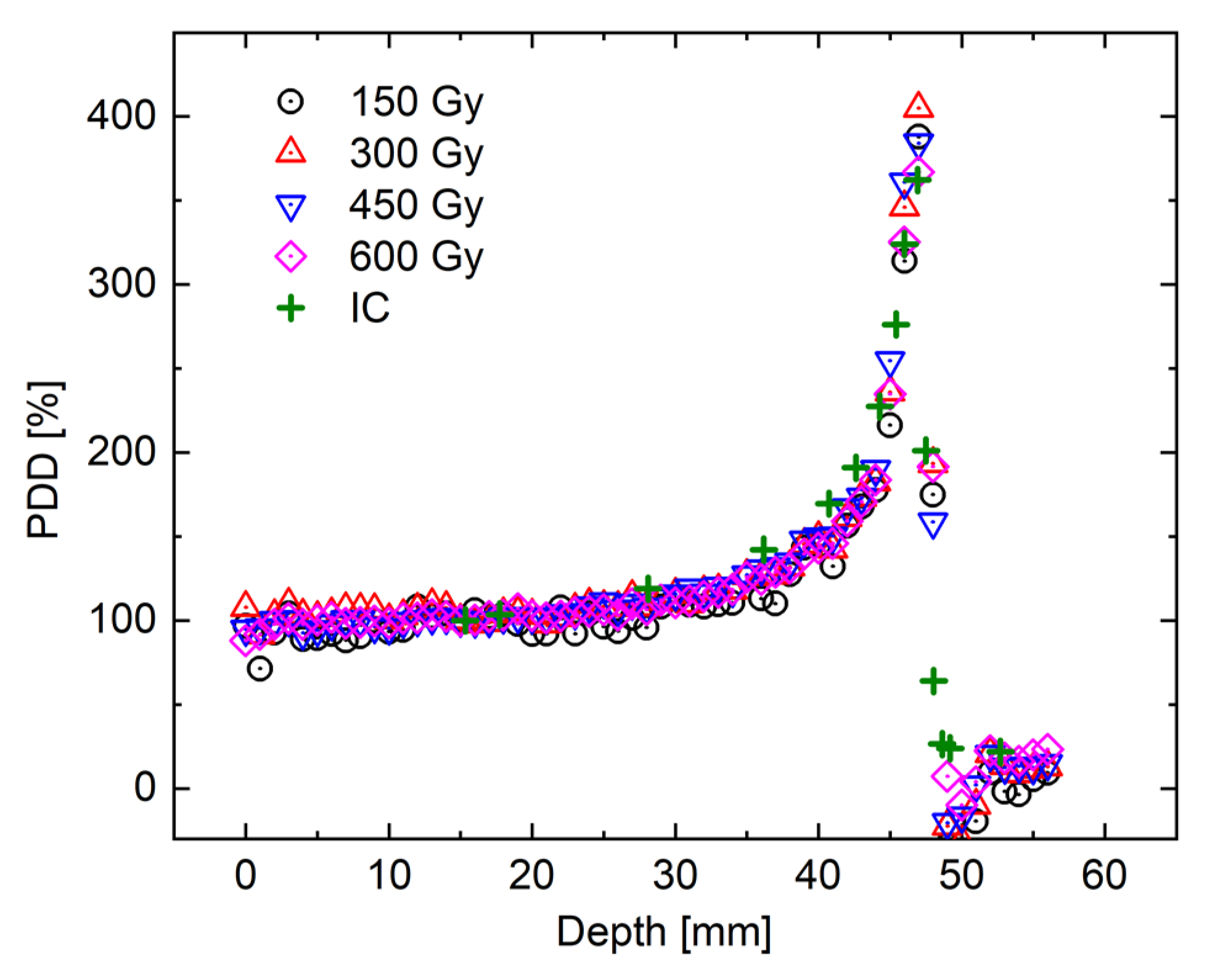
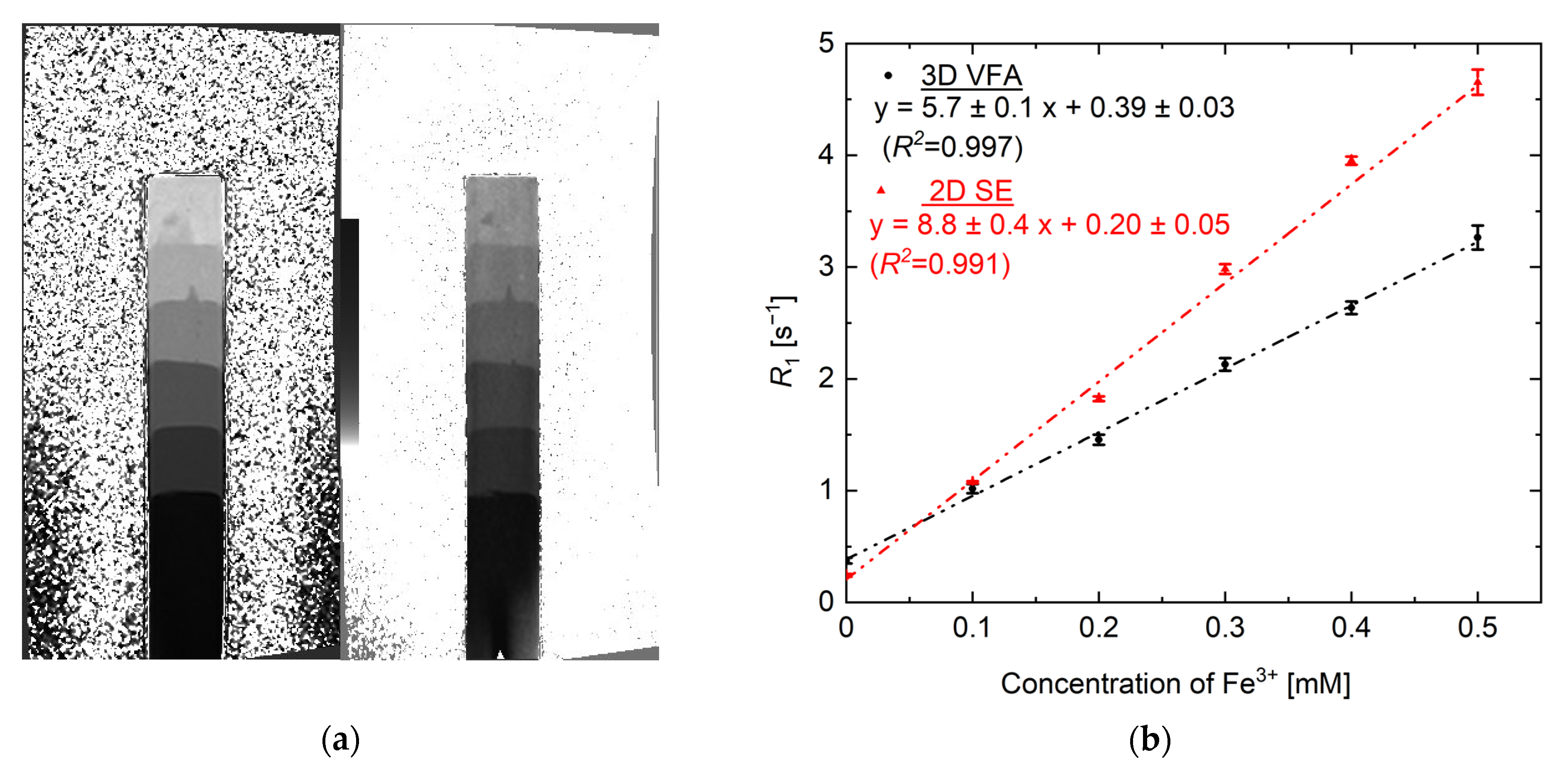
3. Results and Discussion
3.1. Whole R1 Distribution of NC-FG Using VFA Methods
3.2. R1 vs. [Fe3+] Calibration Curve Using VFA and SE Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Schardt, D.; Elsaesser, T.; Schulz-Ertner, D. Heavy-ion tumor therapy: Physical and radiobiological benefits. Rev. Mod. Phys. 2010, 82, 383–425. [Google Scholar] [CrossRef]
- Fukumura, A.; Tsujii, H.; Kamada, T.; Baba, M.; Tsuji, H.; Kato, S.; Yamada, S.; Yasuda, S.; Yanagi, T.; Kato, H.; et al. Carbon-ion radiotherapy: Clinical aspects and related dosimetry. Radiat. Prot. Dosim. 2009, 137, 149–155. [Google Scholar] [CrossRef]
- Schardt, D. Tumor therapy with high-energy carbon ion beams. Nucl. Phys. A 2007, 787, 633–641. [Google Scholar] [CrossRef]
- Debus, J.; Haberer, T.; Schulz-Ertner, D.; Jäkel, O.; Wenz, F.; Enghardt, W.; Schlegel, W.; Kraft, G.; Wannenmacher, M. Fractionated carbon ion irradiation of skull base tumors at GSI. First clinical results and future perspective. Strahlenther. Onkol. 2000, 176, 211–216. [Google Scholar] [CrossRef]
- Hara, Y.; Furukawa, T.; Mizushima, K.; Inaniwa, T.; Saotome, N.; Tansho, R.; Saraya, Y.; Shirai, T.; Noda, K. Commissioning of full energy scanning irradiation with carbon-ion beams ranging from 55.6 to 430 MeV/u at the NIRS-HIMAC. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2017, 406, 343–346. [Google Scholar] [CrossRef]
- Karger, C.P.; Jäkel, O.; Palmans, H.; Kanai, T. Dosimetry for ion beam radiotherapy. Phys. Med. Biol. 2010, 55, R193–R234. [Google Scholar] [CrossRef] [PubMed]
- Gillin, M.T.; Sahoo, N.; Bues, M.; Ciangaru, G.; Sawakuchi, G.; Poenisch, F.; Arjomandy, B.; Martin, C.; Titt, U.; Suzuki, K.; et al. Commissioning of the discrete spot scanning proton beam delivery system at the University of Texas M.D. Anderson Cancer Center, Proton Therapy Center, Houston. Med. Phys. 2009, 37, 154–163. [Google Scholar] [CrossRef] [PubMed]
- IAEA. Absorbed Dose Determination in External Beam Radiotherapy; International Atomic Energy Agency: Vienna, Austria, 2000. [Google Scholar]
- Li, Y.; Zhu, R.X.; Sahoo, N.; Anand, A.; Zhang, X. Beyond Gaussians: A study of single-spot modeling for scanning proton dose calculation. Phys. Med. Biol. 2012, 57, 983–997. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hara, Y.; Furukawa, T.; Mizushima, K.; Takeshita, E.; Shirai, T.; Noda, K. Application of radiochromic film for quality assurance in the heavy-ion beam scanning irradiation system at HIMAC. Nucl. Instrum. Methods Phys. Res. Sect. B 2014, 331, 253–256. [Google Scholar] [CrossRef]
- Spielberger, B.; Scholz, M.; Krämer, M.; Kraft, G. Experimental investigations of the response of films to heavy-ion irradiation. Phys. Med. Biol. 2001, 46, 2889–2897. [Google Scholar] [CrossRef] [PubMed]
- Castriconi, R.; Ciocca, M.; Mirandola, A.; Sini, C.; Broggi, S.; Schwarz, M.; Fracchiolla, F.; Martišíková, M.; Aricò, G.; Mettivier, G.; et al. Dose–response of EBT3 radiochromic films to proton and carbon ion clinical beams. Phys. Med. Biol. 2017, 62, 377–393. [Google Scholar] [CrossRef]
- Maeyama, T.; Hase, S. Nanoclay gel-based radio-fluorogenic gel dosimeters using various fluorescence probes. Radiat. Phys. Chem. 2018, 151, 42–46. [Google Scholar] [CrossRef]
- Maeyama, T.; Ishida, Y.; Kudo, Y.; Fukasaku, K.; Ishikawa, K.L.; Fukunishi, N. Polymer gel dosimeter with AQUAJOINT® as hydrogel matrix. Radiat. Phys. Chem. 2018, 146, 121–125. [Google Scholar] [CrossRef]
- Maeyama, T.; Kato, A.; Mochizuki, A.; Sato, N.; Watanabe, Y.; Mizukami, S. Dose-rate-independent and diffusion-free nanoclay-based radio-fluorogenic gel dosimeter. Sens. Actuators A Phys. 2019, 298, 111435. [Google Scholar] [CrossRef]
- Watanabe, Y.; Mizukami, S.; Eguchi, K.; Maeyama, T.; Hayashi, S.-I.; Muraishi, H.; Terazaki, T.; Gomi, T. Dose distribution verification in high-dose-rate brachytherapy using a highly sensitive normoxic N-vinylpyrrolidone polymer gel dosimeter. Phys. Med. 2019, 57, 72–79. [Google Scholar] [CrossRef]
- Watanabe, Y.; Maeyama, T.; Mochizuki, A.; Mizukami, S.; Hayashi, S.-I.; Terazaki, T.; Muraishi, H.; Takei, H.; Gomi, T.; Shimono, T. Verification of dose distribution in high-dose-rate brachytherapy using a nanoclay-based radio-fluorogenic gel dosimeter. Phys. Med. Biol. 2020, 65, 175008. [Google Scholar] [CrossRef]
- Tachibana, H.; Watanabe, Y.; Mizukami, S.; Maeyama, T.; Terazaki, T.; Uehara, R.; Akimoto, T. End-to-end delivery quality assurance of computed tomography–based high-dose-rate brachytherapy using a gel dosimeter. Brachytherapy 2020, 19, 362–371. [Google Scholar] [CrossRef] [PubMed]
- Mochizuki, A.; Maeyama, T.; Watanabe, Y.; Mizukami, S. Sensitivity enhancement of DHR123 radio-fluorogenic nanoclay gel dosimeter by incorporating surfactants and halogenides. RSC Adv. 2020, 10, 28798–28806. [Google Scholar] [CrossRef]
- Maeyama, T.; Yoshida, K.; Watanabe, Y.; Inui, H. Improvement of light stability of DHR123 radio fluorogenic nano clay gel dosimeter by incorporating a new dispersant. J. Photochem. Photobiol. A Chem. 2021, 418, 113423. [Google Scholar] [CrossRef]
- Ono, K.; Fujino, K.; Kurihara, R.; Hayashi, S.; Akagi, Y.; Hirokawa, Y. Three-dimensional Winston–Lutz test using reusable polyvinyl alcohol-iodide (PVA-I) radiochromic gel dosimeter. Phys. Med. Biol. 2021, 66, 205001. [Google Scholar] [CrossRef]
- MacDougall, N.D.; Pitchford, W.G.; Smith, M.A. A systematic review of the precision and accuracy of dose measurements in photon radiotherapy using polymer and Fricke MRI gel dosimetry. Phys. Med. Biol. 2002, 47, R107–R121. [Google Scholar] [CrossRef]
- Dudek, M.; Piotrowski, M.; Maras, P.; Jaszczak, M.; Kozicki, M. Anisotropic diffusion of Fe ions in Fricke-XO-Pluronic F-127 and Fricke-XO-gelatine 3D radiotherapy dosimeters. Phys. Med. Biol. 2021, 66, 155005. [Google Scholar] [CrossRef] [PubMed]
- De Oliveira, L.N.; Nascimento, E.O.D.; Caldas, L.V.E. New Fricke Xylenol Liquid detector doped with methylene blue (FXL-mblue) irradiated with red LED light. J. Lumin. 2021, 230, 117730. [Google Scholar] [CrossRef]
- Baldock, C.; de Deene, Y.; Doran, S.; Ibbott, G.; Jirasek, A.; Lepage, M.; McAuley, K.B.; Oldham, M.; Schreiner, L.J. Polymer gel dosimetry. Phys. Med. Biol. 2010, 55, R1–R63. [Google Scholar] [CrossRef]
- Eyadeh, M.M.; Smadi, S.A.; Rabaeh, K.A.; Oglat, A.A.; Diamond, K.R. Effect of lithium chloride inorganic salt on the performance of N-(Hydroxymethyl)acrylamide polymer-gel dosimeter in radiation therapy. J. Radioanal. Nucl. Chem. 2021, 330, 1255–1261. [Google Scholar] [CrossRef]
- Rabaeh, K.A.; Hammoudeh, I.M.E.; Oglat, A.A.; Eyadeh, M.M.; Abdel-Qader, A.J.; Aldweri, F.M.; Awad, S.I. Polymer gel containing N,N′-methylene-bis-acrylamide (BIS) as a single monomer for radiotherapy dosimetry. Radiat. Phys. Chem. 2021, 187, 109522. [Google Scholar] [CrossRef]
- Ramm, U.; Weber, U.; Bock, M.; Krämer, M.; Bankamp, A.; Damrau, M.; Thilmann, C.; Böttcher, H.D.; Schad, L.R.; Kraft, G. Three-dimensional BANGTMgel dosimetry in conformal carbon ion radiotherapy. Phys. Med. Biol. 2000, 45, N95–N102. [Google Scholar] [CrossRef]
- Ramm, U.; Moog, J.; Spielberger, B.; Bankamp, A.; Bottcher, H.-D.; Kraft, G. Investigations of dose response of BANG® polymer-gels to carbon ion irradiation. Radiother. Oncol. 2004, 73, S99–S101. [Google Scholar] [CrossRef]
- Kantemiris, I.; Petrokokkinos, L.; Angelopoulos, A.; Bassler, N.; Seimenis, I.; Karaiskos, P. Carbon beam dosimetry using VIP polymer gel and MRI. J. Phys. Conf. Ser. 2009, 164, 012055. [Google Scholar] [CrossRef] [Green Version]
- Maeyama, T.; Fukunishi, N.; Ishikawa, K.L.; Furuta, T.; Fukasaku, K.; Takagi, S.; Noda, S.; Himeno, R.; Fukuda, S. Radiological characteristics of MRI-based VIP polymer gel under carbon beam irradiation. Radiat. Phys. Chem. 2015, 107, 7–11. [Google Scholar] [CrossRef]
- Maeyama, T.; Fukunishi, N.; Ishikawa, K.L.; Furuta, T.; Fukasaku, K.; Takagi, S.; Noda, S.; Himeno, R.; Fukuda, S. A diffusion-free and linear-energy-transfer-independent nanocomposite Fricke gel dosimeter. Radiat. Phys. Chem. 2014, 96, 92–96. [Google Scholar] [CrossRef]
- Maeyama, T.; Fukunishi, N.; Ishikawa, K.L.; Fukasaku, K.; Fukuda, S. Radiological properties of nanocomposite Fricke gel dosimeters for heavy ion beams. J. Radiat. Res. 2016, 57, 318–324. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maeyama, T.; Fukunishi, N.; Ishikawa, K.L.; Fukasaku, K.; Fukuda, S. Organic-Gelatin-Free Nanocomposite Fricke Gel Dosimeter. J. Phys. Chem. B 2017, 121, 4238–4246. [Google Scholar] [CrossRef] [PubMed]
- De Deene, Y.; Jirasek, A. Uncertainty in 3D gel dosimetry. J. Phys. Conf. Ser. 2015, 573, 012008. [Google Scholar] [CrossRef]
- Vandecasteele, J.; de Deene, Y. On the validity of 3D polymer gel dosimetry: III. MRI-related error sources. Phys. Med. Biol. 2012, 58, 63–85. [Google Scholar] [CrossRef]
- Papoutsaki, M.-V.; Pappas, E.; Papadakis, A.E.; Varveris, C.; Damilakis, J.; Maris, T.G. Polymer gel dosimetry utilizing a 2D (SE) and a 2D (HASTE) multiple echo sequences. J. Phys. Conf. Ser. 2013, 444, 012088. [Google Scholar] [CrossRef] [Green Version]
- Cho, N.-Y.; Huang, S.-C.; Chung, W.-Y.; Guo, W.-Y.; Chu, W.-C. Isotropic three-dimensional MRI-Fricke-infused gel dosimetry. Med Phys. 2013, 40, 052101. [Google Scholar] [CrossRef] [PubMed]
- Asena, A.; Kairn, T.; Crowe, S.B.; Smith, S.T.; Trapp, J.V. PAGAT gel dosimeters for dose distribution measurements in the vicinity of high-density implants: A preliminary study. J. Phys. Conf. Ser. 2015, 573, 012061. [Google Scholar] [CrossRef] [Green Version]
- Massillon-Jl, G.; Minniti, R.; Mitch, M.G.; Maryanski, M.J.; Soares, C.G. The use of gel dosimetry to measure the 3D dose distribution of a90Sr/90Y intravascular brachytherapy seed. Phys. Med. Biol. 2009, 54, 1661–1672. [Google Scholar] [CrossRef] [Green Version]
- Vedelago, J.; Obando, D.C.; Malano, F.; Conejeros, R.; Figueroa, R.; Garcia, D.; González, G.; Romero, M.; Santibañez, M.; Strumia, M.; et al. Fricke and polymer gel 2D dosimetry validation using Monte Carlo simulation. Radiat. Meas. 2016, 91, 54–64. [Google Scholar] [CrossRef] [Green Version]
- Wuu, C.-S.; Xu, Y. Three-dimensional dose verification for intensity modulated radiation therapy using optical CT based polymer gel dosimetry. Med. Phys. 2006, 33, 1412–1419. [Google Scholar] [CrossRef] [PubMed]
- Marrale, M.; D’Errico, F. Hydrogels for Three-Dimensional Ionizing-Radiation Dosimetry. Gels 2021, 7, 74. [Google Scholar] [CrossRef]
- Wang, H.Z.; Riederer, S.J.; Lee, J.N. Optimizing the precision in T1 relaxation estimation using limited flip angles. Magn. Reson. Med. 1987, 5, 399–416. [Google Scholar] [CrossRef]
- Deoni, S.C.; Rutt, B.K.; Peters, T.M. Rapid combinedT1 andT2 mapping using gradient recalled acquisition in the steady state. Magn. Reson. Med. 2003, 49, 515–526. [Google Scholar] [CrossRef]
- Crawley, A.P.; Henkelman, R.M. A comparison of one-shot and recovery methods in T1 imaging. Magn. Reson. Med. 1988, 7, 23–34. [Google Scholar] [CrossRef]
- Haase, A. Snapshot flash mri. applications to t1, t2, and chemical-shift imaging. Magn. Reson. Med. 1990, 13, 77–89. [Google Scholar] [CrossRef] [PubMed]
- Look, D.C.; Locker, D.R. Time Saving in Measurement of NMR and EPR Relaxation Times. Rev. Sci. Instrum. 1970, 41, 250–251. [Google Scholar] [CrossRef] [Green Version]
- Christensen, K.A.; Grant, D.M.; Schulman, E.M.; Walling, C. Optimal determination of relaxation times of fourier transform nuclear magnetic resonance. Determination of spin-lattice relaxation times in chemically polarized species. J. Phys. Chem. 1974, 78, 1971–1977. [Google Scholar] [CrossRef]
- Minohara, S.; Fukuda, S.; Kanematsu, N.; Takei, Y.; Furukawa, T.; Inaniwa, T.; Matsufuji, N.; Mori, S.; Noda, K. Recent Innovations in Carbon-Ion Radiotherapy. J. Radiat. Res. 2010, 51, 385–392. [Google Scholar] [CrossRef] [Green Version]
- Kanai, T.; Fukumura, A.; Kusano, Y.; Shimbo, M.; Nishio, T. Cross-calibration of ionization chambers in proton and carbon beams. Phys. Med. Biol. 2004, 49, 771–781. [Google Scholar] [CrossRef] [PubMed]
- Torikoshi, M.; Minohara, S.; Kanematsu, N.; Komori, M.; Kanazawa, M.; Noda, K.; Miyahara, N.; Itoh, H.; Endo, M.; Kanai, T. Irradiation System for HIMAC. J. Radiat. Res. 2007, 48, A15–A25. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kanai, T.; Endo, M.; Minohara, S.; Miyahara, N.; Koyama-Ito, H.; Tomura, H.; Matsufuji, N.; Futami, Y.; Fukumura, A.; Hiraoka, T.; et al. Biophysical characteristics of HIMAC clinical irradiation system for heavy-ion radiation therapy. Int. J. Radiat. Oncol. 1999, 44, 201–210. [Google Scholar] [CrossRef]
- Cheng, H.-L.M.; Wright, G.A. Rapid high-resolutionT1 mapping by variable flip angles: Accurate and precise measurements in the presence of radiofrequency field inhomogeneity. Magn. Reson. Med. 2006, 55, 566–574. [Google Scholar] [CrossRef] [PubMed]
- Zur, Y.; Stokar, S.; Bendel, P. An analysis of fast imaging sequences with steady-state transverse magnetization refocusing. Magn. Reson. Med. 1988, 6, 175–193. [Google Scholar] [CrossRef]
- Wolf, M.; de Boer, A.; Sharma, K.; Boor, P.; Leiner, T.; Sunder-Plassmann, G.; Moser, E.; Caroli, A.; Jerome, N.P. Magnetic resonance imaging T1- and T2-mapping to assess renal structure and function: A systematic review and statement paper. Nephrol. Dial. Transplant. 2018, 33, ii41–ii50. [Google Scholar] [CrossRef] [Green Version]
- Calhoun, P.S.; Kuszyk, B.S.; Heath, D.G.; Carley, J.C.; Fishman, E.K. Three-dimensional Volume Rendering of Spiral CT Data: Theory and Method. Radiographics 1999, 19, 745–764. [Google Scholar] [CrossRef] [Green Version]
- Suit, H.; DeLaney, T.; Goldberg, S.; Paganetti, H.; Clasie, B.; Gerweck, L.; Niemierko, A.; Hall, E.; Flanz, J.; Hallman, J.; et al. Proton vs carbon ion beams in the definitive radiation treatment of cancer patients. Radiother. Oncol. 2010, 95, 3–22. [Google Scholar] [CrossRef]
- Curtis, S.B. The New Particles and Their Application in Medicine; Springer: Boston, MA, USA, 1980; pp. 5–25. [Google Scholar]
- Furuta, T.; Sato, T. Medical application of particle and heavy ion transport code system PHITS. Radiol. Phys. Technol. 2021, 14, 215–225. [Google Scholar] [CrossRef]
- Furuta, T.; Maeyama, T.; Ishikawa, K.L.; Fukunishi, N.; Fukasaku, K.; Takagi, S.; Noda, S.; Himeno, R.; Hayashi, S. Comparison between Monte Carlo simulation and measurement with a 3D polymer gel dosimeter for dose distributions in biological samples. Phys. Med. Biol. 2015, 60, 6531–6546. [Google Scholar] [CrossRef]
- Sato, T.; Iwamoto, Y.; Hashimoto, S.; Ogawa, T.; Furuta, T.; Abe, S.-I.; Kai, T.; Tsai, P.-E.; Matsuda, N.; Iwase, H.; et al. Features of Particle and Heavy Ion Transport code System (PHITS) version 3.02. J. Nucl. Sci. Technol. 2018, 55, 684–690. [Google Scholar] [CrossRef] [Green Version]
- Gallagher, T.A.; Nemeth, A.J.; Hacein-Bey, L. An Introduction to the Fourier Transform: Relationship to MRI. Am. J. Roentgenol. 2008, 190, 1396–1405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pusey, E.; Lufkin, R.B.; Brown, R.K.; Solomon, M.A.; Stark, D.D.; Tarr, R.W.; Hanafee, W.N. Magnetic resonance imaging artifacts: Mechanism and clinical significance. Radiographics 1986, 6, 891–911. [Google Scholar] [CrossRef] [Green Version]
- Czervionke, L.F.; Czervionke, J.M.; Daniels, D.L.; Haughton, V.M. Characteristic features of MR truncation artifacts. Am. J. Roentgenol. 1988, 151, 1219–1228. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kanai, T.; Furusawa, Y.; Fukutsu, K.; Itsukaichi, H.; Eguchi-Kasai, K.; Ohara, H. Irradiation of Mixed Beam and Design of Spread-Out Bragg Peak for Heavy-Ion Radiotherapy. Radiat. Res. 1997, 147, 78. [Google Scholar] [CrossRef] [PubMed]
- De Deene, Y.; de Wagter, C.; van Duyse, B.; Derycke, S.; Mersseman, B.; de Gersem, W.; Voet, T.; Achten, E.; de Neve, W. Validation of MR-based polymer gel dosimetry as a preclinical three-dimensional verification tool in conformal radiotherapy. Magn. Reson. Med. 2000, 43, 116–125. [Google Scholar] [CrossRef]


| Gel Sample | Ion Beam | Reference | |
|---|---|---|---|
| Method | VFA | VFA | SE Method |
| TR (ms) | 15 | 15 | 500, 3000 |
| TE (ms) | 3.38 | 3.38 | 2.57 |
| FA (°) | 7 and 36 | 7 and 36 | |
| FOV (mm) | 256 × 256 | 256 × 128 | 256 × 128 |
| Matrix | 256 × 256 | 256 × 128 | 256 × 128 |
| ST (mm) | 1 | 0.5 | 5 |
| Ns | 40 | 40 | 1 |
| BW (Hz/pixel) | 130 | 130 | 250 |
| NEX | 4 | 2 | 1 |
| Scan time (s) | 1219 | 614 | 444 (63 + 381) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mizukami, S.; Watanabe, Y.; Mizoguchi, T.; Gomi, T.; Hara, H.; Takei, H.; Fukunishi, N.; Ishikawa, K.L.; Fukuda, S.; Maeyama, T. Whole Three-Dimensional Dosimetry of Carbon Ion Beams with an MRI-Based Nanocomposite Fricke Gel Dosimeter Using Rapid T1 Mapping Method. Gels 2021, 7, 233. https://doi.org/10.3390/gels7040233
Mizukami S, Watanabe Y, Mizoguchi T, Gomi T, Hara H, Takei H, Fukunishi N, Ishikawa KL, Fukuda S, Maeyama T. Whole Three-Dimensional Dosimetry of Carbon Ion Beams with an MRI-Based Nanocomposite Fricke Gel Dosimeter Using Rapid T1 Mapping Method. Gels. 2021; 7(4):233. https://doi.org/10.3390/gels7040233
Chicago/Turabian StyleMizukami, Shinya, Yusuke Watanabe, Takahiro Mizoguchi, Tsutomu Gomi, Hidetake Hara, Hideyuki Takei, Nobuhisa Fukunishi, Kenichi L. Ishikawa, Shigekazu Fukuda, and Takuya Maeyama. 2021. "Whole Three-Dimensional Dosimetry of Carbon Ion Beams with an MRI-Based Nanocomposite Fricke Gel Dosimeter Using Rapid T1 Mapping Method" Gels 7, no. 4: 233. https://doi.org/10.3390/gels7040233
APA StyleMizukami, S., Watanabe, Y., Mizoguchi, T., Gomi, T., Hara, H., Takei, H., Fukunishi, N., Ishikawa, K. L., Fukuda, S., & Maeyama, T. (2021). Whole Three-Dimensional Dosimetry of Carbon Ion Beams with an MRI-Based Nanocomposite Fricke Gel Dosimeter Using Rapid T1 Mapping Method. Gels, 7(4), 233. https://doi.org/10.3390/gels7040233






