Evaluation of Mesh Size in Model Polymer Networks Consisting of Tetra-Arm and Linear Poly(ethylene glycol)s
Abstract
:1. Introduction
2. Theoretical
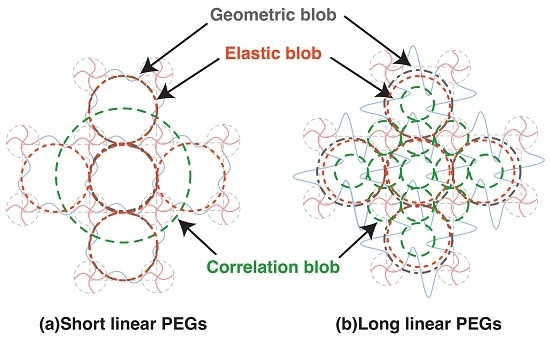
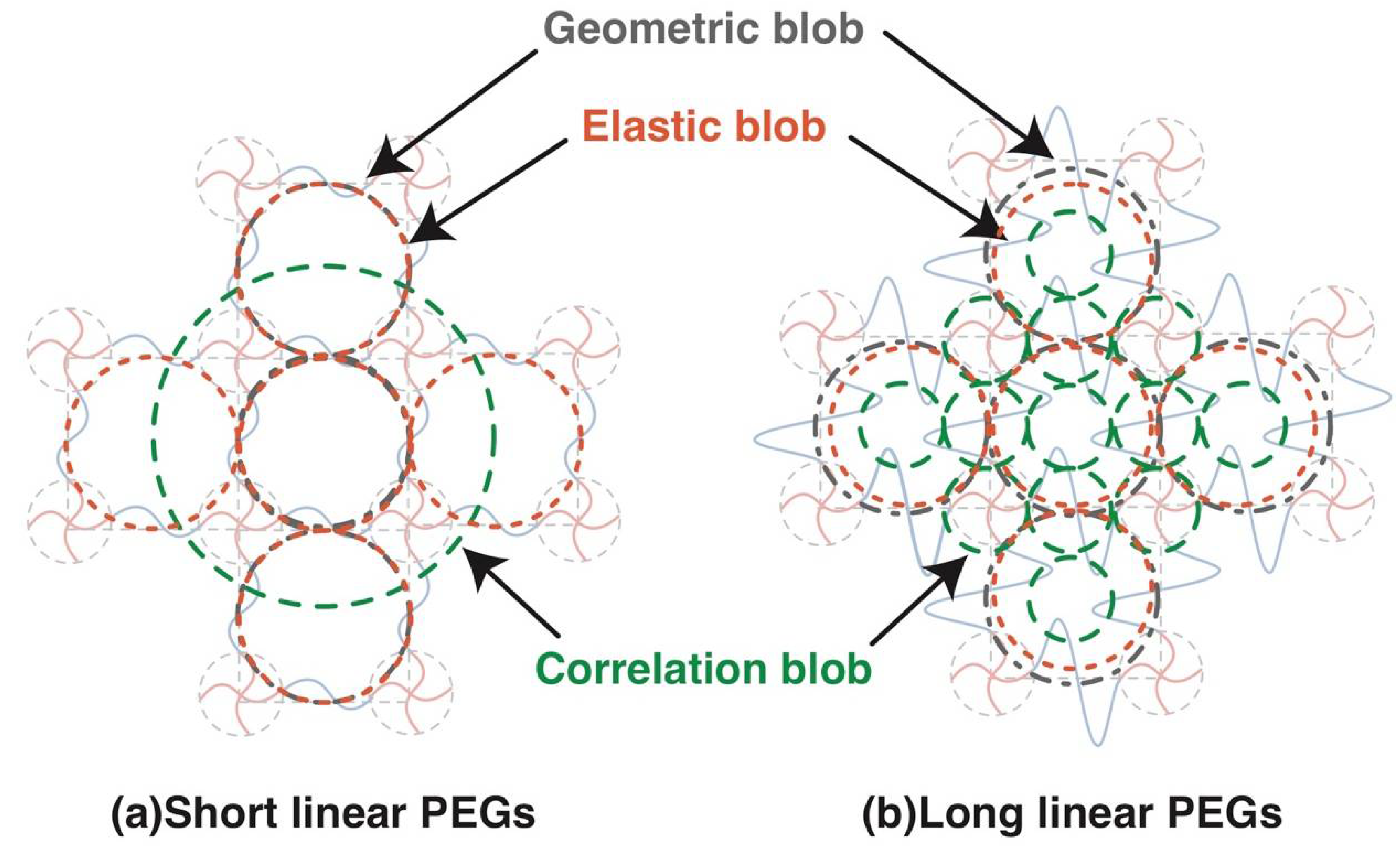
2.1. Geometric Blob
2.2. Elastic Blob
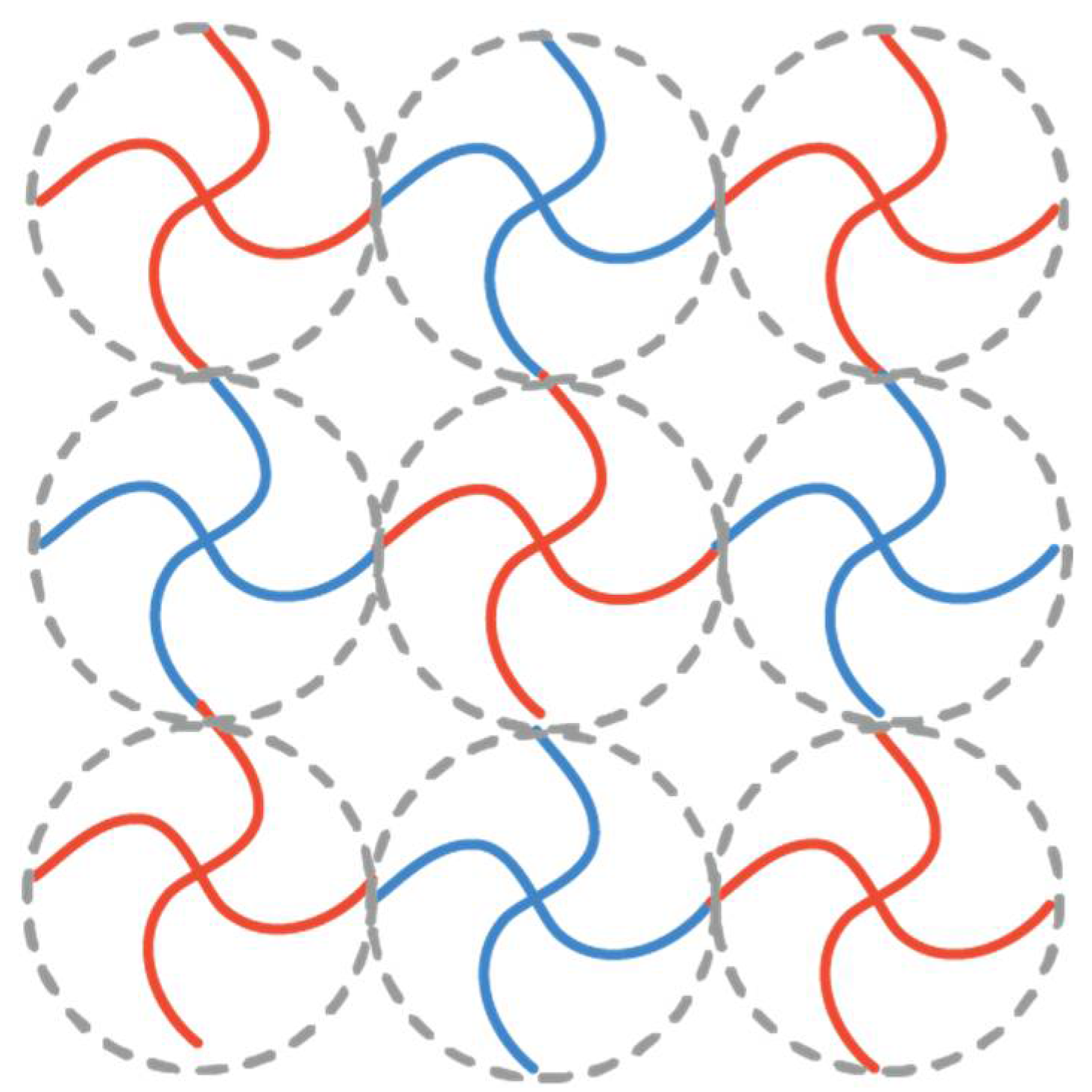
2.3. Correlation Blob
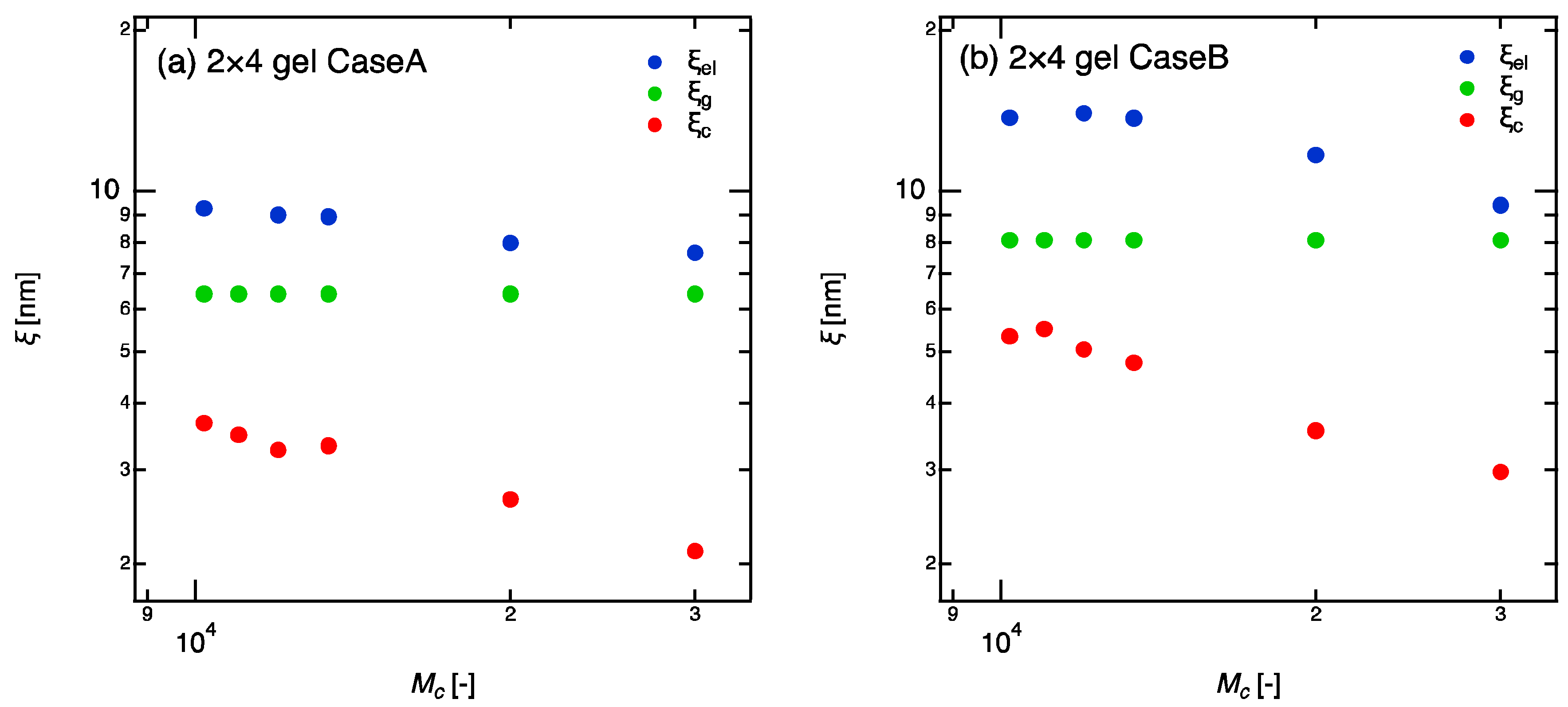
3. Results and Discussion
4. Experimental
4.1. Sample Preparation
4.2. Dynamic Light-Scattering Measurements
4.3. Rheological Measurements
5. Conclusions
- (1)
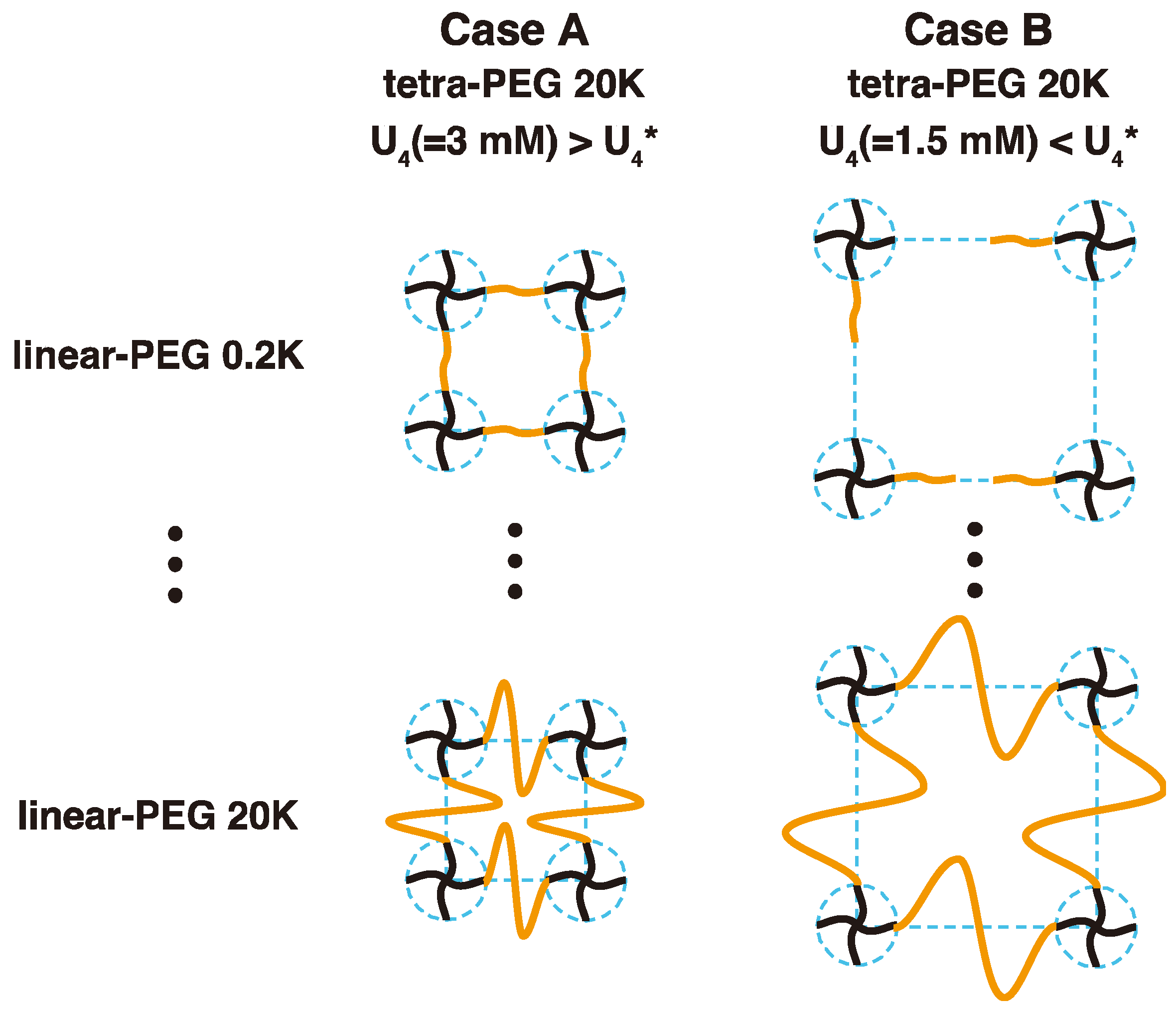
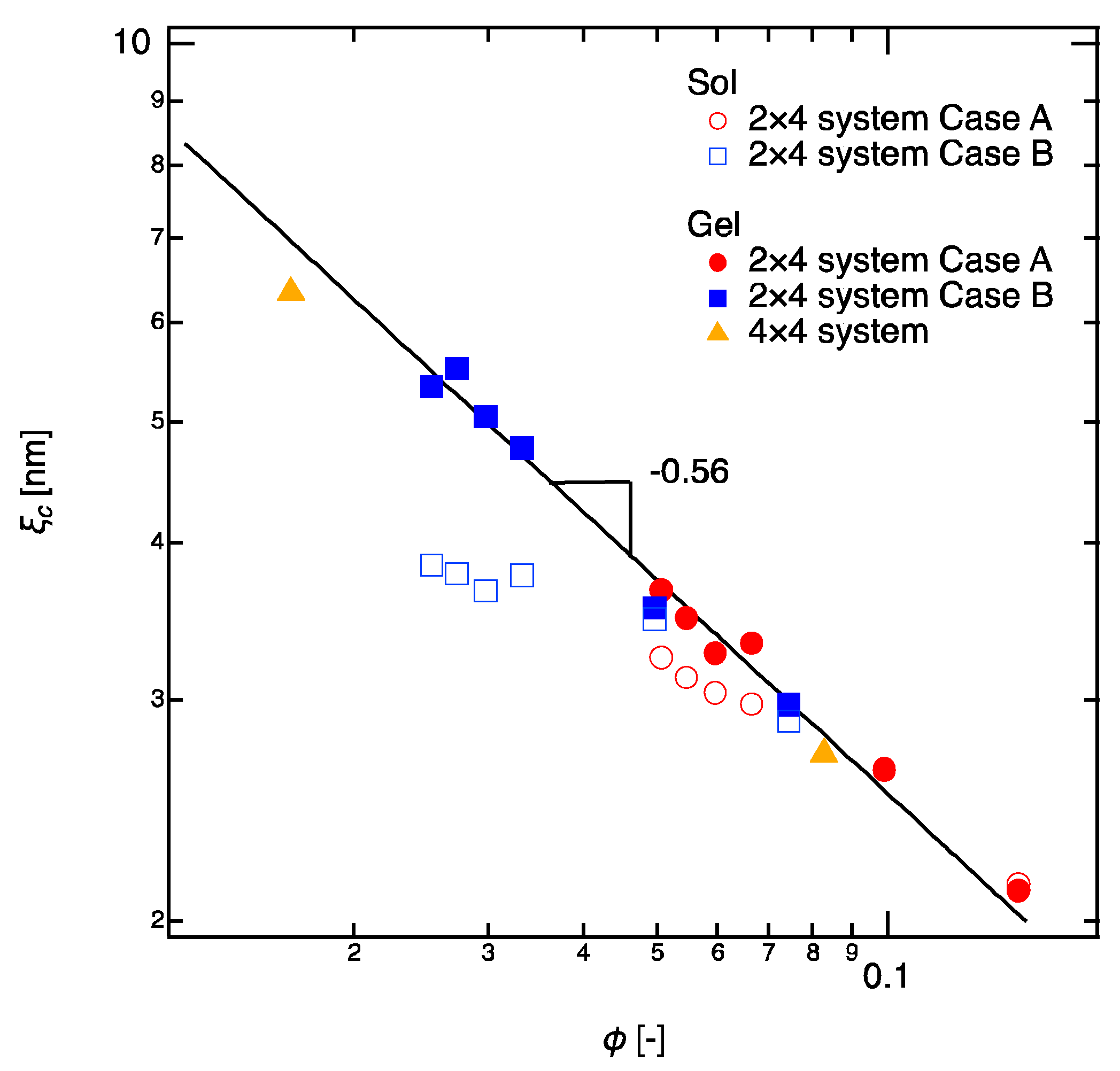
- The concentration dependence of the correlation length, , is independent of the molecular weight and the completeness of the network structure, and follows the well-known scaling law, . The gels essentially possess the semidilute correlations, which is irrelevant to the network structure.
- (2)
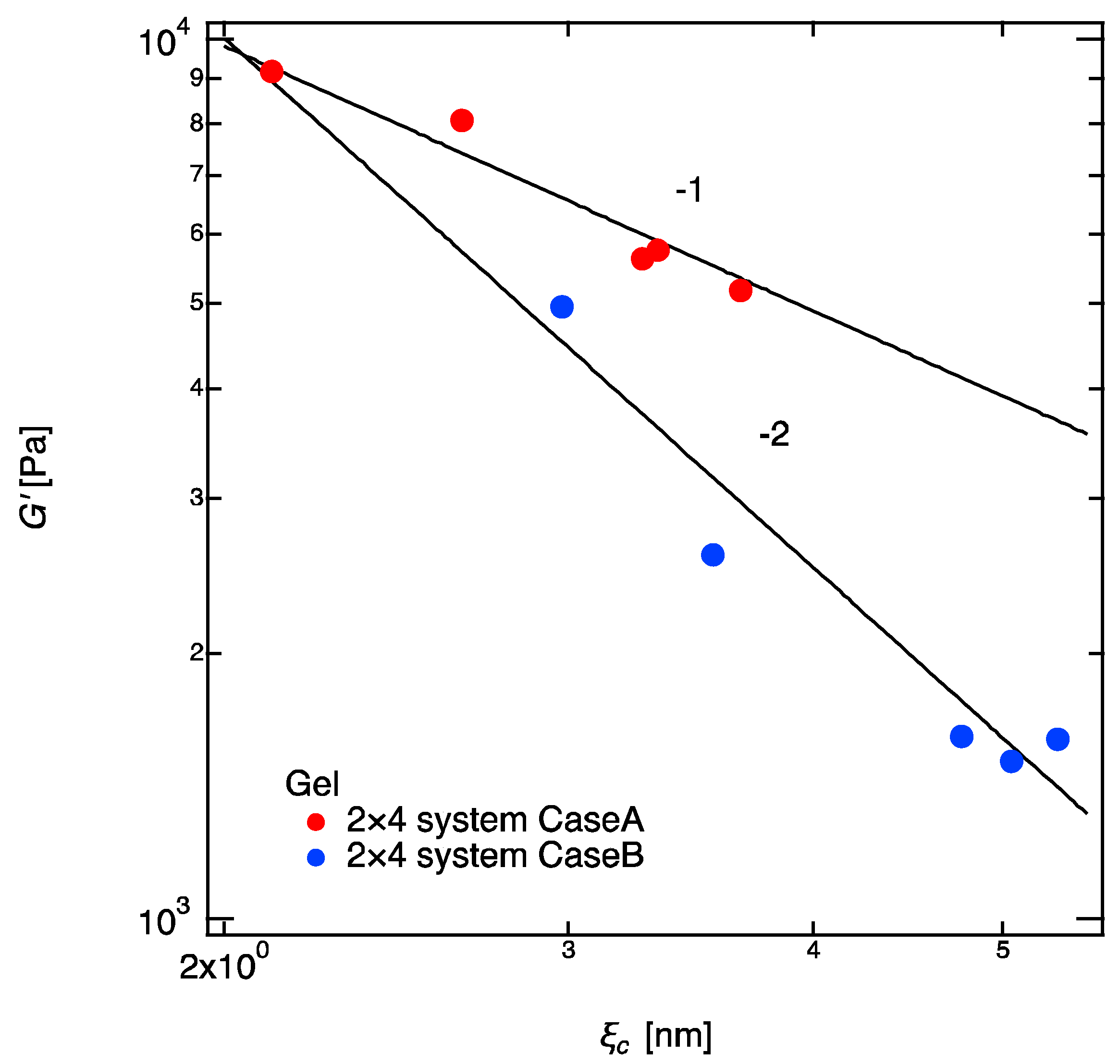
- In contrast to the correlation length, the mechanical properties, i.e., the elastic modulus, depend strongly on the completeness of the networks, and two different scaling relations were found.
- (3)
- The correlation blob is definitely not the mesh size in polymer gels, although it is often referred to as the mesh size in polymer networks. The elastic blob is, by definition, close to the mesh size. However, it is found that the molecular weight between crosslinkers brings a complicated effect in estimation of the mesh size.
- (4)
- An interesting correlation was found for the first time between and , depending on the complete/incompleteness of the networks, and , respectively, for the complete networks and incomplete networks. The Pincus blob may be a clue for explanation of these correlations.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Miller, D.R.; Macosko, C.W. A New Derivation of Post Gel Properties of Network Polymers. Macromolecules 1976, 9, 206–211. [Google Scholar] [CrossRef]
- Nishi, K.; Chijiishi, M.; Katsumoto, Y.; Nakao, T.; Fujii, K.; Chung, U.I.; Noguchi, H.; Sakai, T.; Shibayama, M. Rubber elasticity for incomplete polymer networks. J. Chem. Phys. 2012, 137, 224903. [Google Scholar] [CrossRef] [PubMed]
- De Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Oikawa, H.; Murakami, K. Dynamic light scattering of swollen rubber vulcanizates and the swelling mechanism. Macromolecules 1991, 24, 1117–1122. [Google Scholar] [CrossRef]
- Sakai, T.; Kurakazu, M.; Akagi, Y.; Shibayama, M.; Chung, U.-I. Effect of swelling and deswelling on the elasticity of polymer networks in the dilute to semi-dilute region. Soft Matter 2012, 8, 2730–2736. [Google Scholar] [CrossRef]
- Rüchel, R.; Brager, M.D. Scanning electron microscopic observations of polyacrylamide gels. Anal. Biochem. 1975, 68, 415–428. [Google Scholar] [CrossRef]
- Marmorat, C.; Arinstein, A.; Koifman, N.; Talmon, Y.; Zussman, E.; Rafailovich, M. Cryo-Imaging of Hydrogels Supermolecular Structure. Sci. Rep. 2016, 6, 25495. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, T. Collapse of Gels and the Critical Endpoint. Phys. Rev. Lett. 1978, 40, 820–823. [Google Scholar] [CrossRef]
- Shibayama, M.; Tanaka, T. Volume Phase-Transition and Related Phenomena of Polymer Gels. Adv. Polym. Sci. 1993, 109, 1–62. [Google Scholar] [CrossRef]
- Tanaka, T.; Sato, E.; Hirokawa, Y.; Hirotsu, S.; Peetermans, J. Critical kinetics of volume phase transition of gels. Phys. Rev. Lett. 1985, 55, 2455–2458. [Google Scholar] [CrossRef] [PubMed]
- Shibayama, M.; Tanaka, T.; Han, C.C. Small angle neutron scattering study on poly(N-isopropyl acrylamide) gels near their volume-phase transition temperature. J. Chem. Phys. 1992, 97, 6829–6841. [Google Scholar] [CrossRef]
- Pincus, P. Excluded Volume Effects and Stretched Polymer Chains. Macromolecules 1976, 9, 386–388. [Google Scholar] [CrossRef]
- Shibayama, M.; Norisuye, T.; Nomura, S. Cross-link Density Dependence of Spatial Inhomogeneities and Dynamic Fluctuations of Poly(N-isopropylacrylamide) Gels. Macromolecules 1996, 29, 8746–8750. [Google Scholar] [CrossRef]
- Watanabe, N.; Li, X.; Shibayama, M. Probe Diffusion during Sol–Gel Transition of a Radical Polymerization System Using Isorefractive Dynamic Light Scattering. Macromolecules 2017, 50, 9726–9733. [Google Scholar] [CrossRef]
- Sakai, T.; Matsunaga, T.; Yamamoto, Y.; Ito, C.; Yoshida, R.; Suzuki, S.; Sasaki, N.; Shibayama, M.; Chung, U.-I. Design and Fabrication of a High-Strength Hydrogel with Ideally Homogeneous Network Structure from Tetrahedron-like Macromonomers. Macromolecules 2008, 41, 5379–5384. [Google Scholar] [CrossRef]
- Matsunaga, T.; Asai, H.; Akagi, Y.; Sakai, T.; Chung, U.-I.; Shibayama, M. SANS Studies on Tetra-PEG Gel under Uniaxial Deformation. Macromolecules 2011, 44, 1203–1210. [Google Scholar] [CrossRef]
- Akagi, Y.; Gong, J.P.; Chung, U.-I.; Sakai, T. Transition between Phantom and Affine Network Model Observed in Polymer Gels with Controlled Network Structure. Macromolecules 2013, 46, 1035–1040. [Google Scholar] [CrossRef]
- Matsunaga, T.; Sakai, T.; Akagi, Y.; Chung, U.-I.; Shibayama, M. SANS and SLS Studies on Tetra-Arm PEG Gels in As-Prepared and Swollen States. Macromolecules 2009, 42, 6245–6252. [Google Scholar] [CrossRef]
- Kurakazu, M.; Katashima, T.; Chijiishi, M.; Nishi, K.; Akagi, Y.; Matsunaga, T.; Shibayama, M.; Chung, U.-I.; Sakai, T. Evaluation of Gelation Kinetics of Tetra-PEG Gel. Macromolecules 2010, 43, 3935–3940. [Google Scholar] [CrossRef]
- Li, X.; Tsutsui, Y.; Matsunaga, T.; Shibayama, M.; Chung, U.-I.; Sakai, T. Precise Control and Prediction of Hydrogel Degradation Behavior. Macromolecules 2011, 44, 3567–3571. [Google Scholar] [CrossRef]
- Katashima, T.; Urayama, K.; Chung, U.-I.; Sakai, T. Strain energy density function of a near-ideal polymer network estimated by biaxial deformation of Tetra-PEG gel. Soft Matter 2012, 8, 8217–8222. [Google Scholar] [CrossRef]
- Li, X.; Khairulina, K.; Chung, U.-I.; Sakai, T. Electrophoretic Mobility of Double-Stranded DNA in Polymer Solutions and Gels with Tuned Structures. Macromolecules 2014, 47, 3582–3586. [Google Scholar] [CrossRef]
- Nishi, K.; Fujii, K.; Katsumoto, Y.; Sakai, T.; Shibayama, M. Kinetic Aspect on Gelation Mechanism of Tetra-PEG Hydrogel. Macromolecules 2014, 47, 3274–3281. [Google Scholar] [CrossRef]
- Li, X.; Kondo, S.; Chung, U.-I.; Sakai, T. Degradation Behavior of Polymer Gels Caused by Nonspecific Cleavages of Network Strands. Chem. Mater. 2014, 26, 5352–5357. [Google Scholar] [CrossRef]
- Kamata, H.; Akagi, Y.; Kayasuga-Kariya, Y.; Chung, U.I.; Sakai, T. “Nonswellable” Hydrogel Without Mechanical Hysteresis. Science 2014, 343, 873–875. [Google Scholar] [CrossRef] [PubMed]
- Kondo, S.; Hiroi, T.; Han, Y.S.; Kim, T.H.; Shibayama, M.; Chung, U.I.; Sakai, T. Reliable Hydrogel with Mechanical “Fuse Link” in an Aqueous Environment. Adv. Mater. 2015, 27, 7407–7411. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Watanabe, N.; Sakai, T.; Shibayama, M. Probe Diffusion of Sol–Gel Transition in an Isorefractive Polymer Solution. Macromolecules 2017, 50, 2916–2922. [Google Scholar] [CrossRef]
- Li, X.; Hirosawa, K.; Sakai, T.; Gilbert, E.P.; Shibayama, M. SANS Study on Critical Polymer Clusters of Tetra-Functional Polymers. Macromolecules 2017, 50, 3655–3661. [Google Scholar] [CrossRef]
- Kondo, S.; Chung, U.-I.; Sakai, T. Effect of prepolymer architecture on the network structure formed by AB-type crosslink-coupling. Polym. J. 2013, 46, 14–20. [Google Scholar] [CrossRef]
- Kondo, S.; Sakurai, H.; Chung, U.-I.; Sakai, T. Mechanical Properties of Polymer Gels with Bimodal Distribution in Strand Length. Macromolecules 2013, 46, 7027–7033. [Google Scholar] [CrossRef]
- Nishi, K.; Noguchi, H.; Sakai, T.; Shibayama, M. Rubber elasticity for percolation network consisting of Gaussian chains. J. Chem. Phys. 2015, 143, 184905. [Google Scholar] [CrossRef] [PubMed]
- Pusey, P.N.; Van Megen, W. Dynamic light scattering by non-ergodic media. Phys. A Stat. Mech. Appl. 1989, 157, 705–741. [Google Scholar] [CrossRef]
- Joosten, J.G.H.; McCarthy, J.L.; Pusey, P.N. Dynamic and static light scattering by aqueous polyacrylamide gels. Macromolecules 1991, 24, 6690–6699. [Google Scholar] [CrossRef]
- Rubinstein, M.; Colby, R.H. Polymer Physics; OUP Oxford: Oxford, UK, 2003. [Google Scholar]
- Lange, F.; Schwenke, K.; Kurakazu, M.; Akagi, Y.; Chung, U.-I.; Lang, M.; Sommer, J.-U.; Sakai, T.; Saalwächter, K. Connectivity and Structural Defects in Model Hydrogels: A Combined Proton NMR and Monte Carlo Simulation Study. Macromolecules 2011, 44, 9666–9674. [Google Scholar] [CrossRef]
- Katashima, T.; Asai, M.; Urayama, K.; Chung, U.-I.; Sakai, T. Mechanical properties of tetra-PEG gels with supercoiled network structure. J. Chem. Phys. 2014, 140, 074902–074910. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsuji, Y.; Li, X.; Shibayama, M. Evaluation of Mesh Size in Model Polymer Networks Consisting of Tetra-Arm and Linear Poly(ethylene glycol)s. Gels 2018, 4, 50. https://doi.org/10.3390/gels4020050
Tsuji Y, Li X, Shibayama M. Evaluation of Mesh Size in Model Polymer Networks Consisting of Tetra-Arm and Linear Poly(ethylene glycol)s. Gels. 2018; 4(2):50. https://doi.org/10.3390/gels4020050
Chicago/Turabian StyleTsuji, Yui, Xiang Li, and Mitsuhiro Shibayama. 2018. "Evaluation of Mesh Size in Model Polymer Networks Consisting of Tetra-Arm and Linear Poly(ethylene glycol)s" Gels 4, no. 2: 50. https://doi.org/10.3390/gels4020050
APA StyleTsuji, Y., Li, X., & Shibayama, M. (2018). Evaluation of Mesh Size in Model Polymer Networks Consisting of Tetra-Arm and Linear Poly(ethylene glycol)s. Gels, 4(2), 50. https://doi.org/10.3390/gels4020050