1. Introduction
There are many water-soluble polymers distributed throughout the natural world. Some of these can be synthesized artificially, while others solely originate from biological systems. Since water-soluble polymers are environmentally sustainable, they are widely used in science, technology and even in our day-to-day lives. The phase behavior and the phase transition of polymer solution play important roles in the fabrication processes of polymeric materials. Therefore, it may be important to obtain information on the phase structure of the water-soluble polymer in the solution state for the effective fabrication of many practical commodities. In this paper, we report on the phase behaviors of gelatin, water and poly(ethylene glycol) (PEG) in a system.
Gelatin is a typical protein derived from collagen in the skin and bones of animals. It is well known that the aqueous solution of gelatin shows sol-gel transition. The gel of gelatin is widely used in food, and hence, the sol-gel transition of gelatin solution has been studied in detail thus far [
1,
2,
3]. On the other hand, PEG is also well known as a neutral water-soluble polymer. The polymer and its oligomers interact with proteins, and hence, they are used as precipitating agents of protein in protein crystallography. The phase diagram of the aqueous PEG system has been also studied [
4]. It is clarified that the aqueous PEG solution shows the phase separation only at very higher temperature regions rather than the room temperature region.
It has been reported that the phase separation becomes obvious when methanol is added to the aqueous solution of gelatin as the third component of the system [
5]. Although the results are not systematic, it was also reported that the aqueous gelatin solution shows phase separation when a trace amount of large-molecular-weight PEG is added to the solution [
6]. Therefore, the ternary system of the aqueous gelatin with PEG has attracted much attention since these studies, and then, many more studies have been done, especially in pharmaceutical science [
7,
8,
9,
10,
11]. However, the systematic study of the phase behaviors of the ternary system of gelatin, water and PEG has yet to be done.
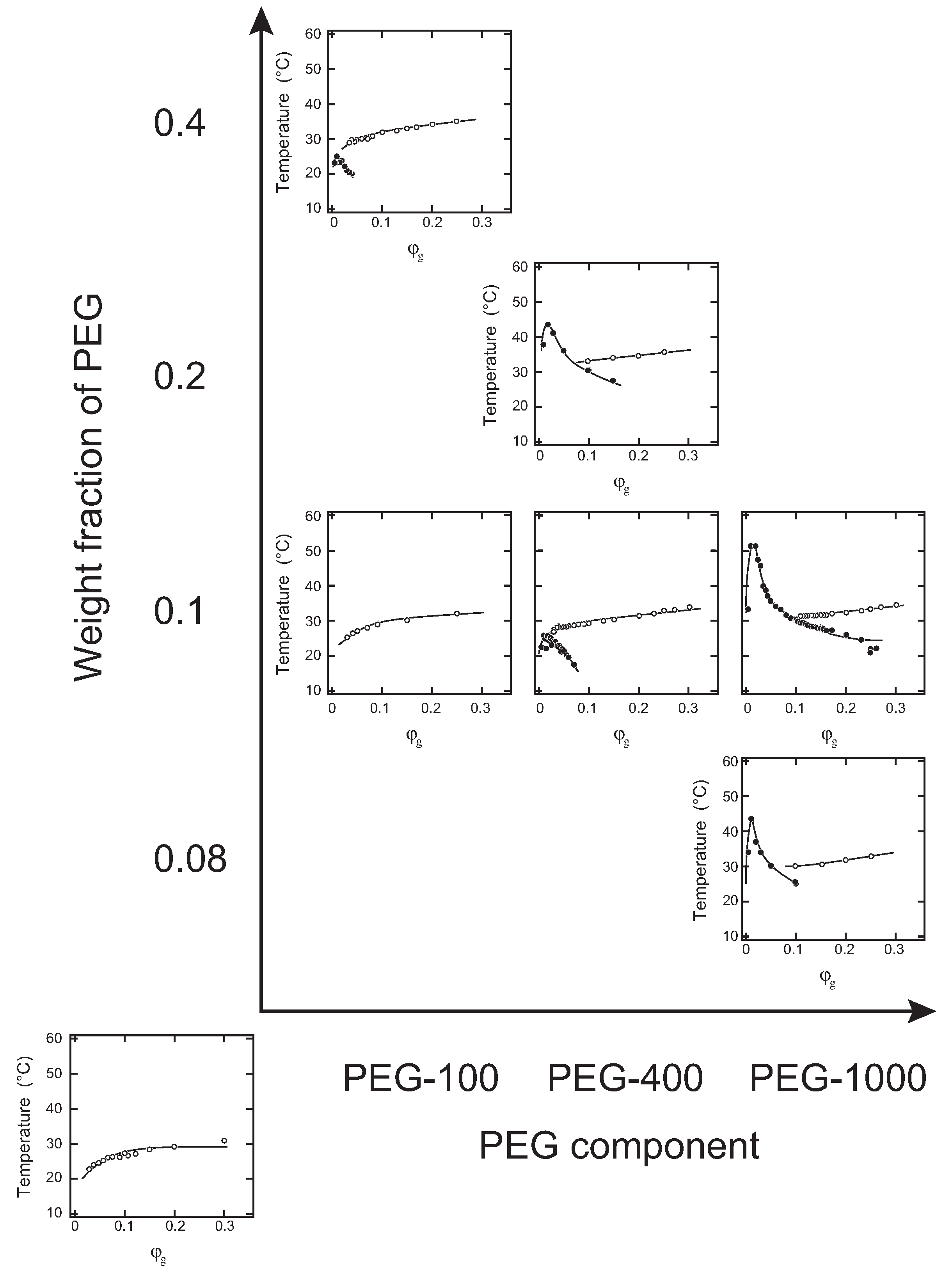
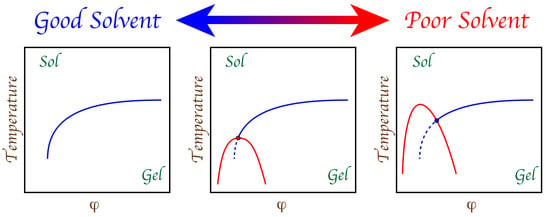
Here, we report on the systematic study of the phase behaviors in the ternary system of gelatin, water and PEG. A typical phase diagram of the system has been described in the previous report [
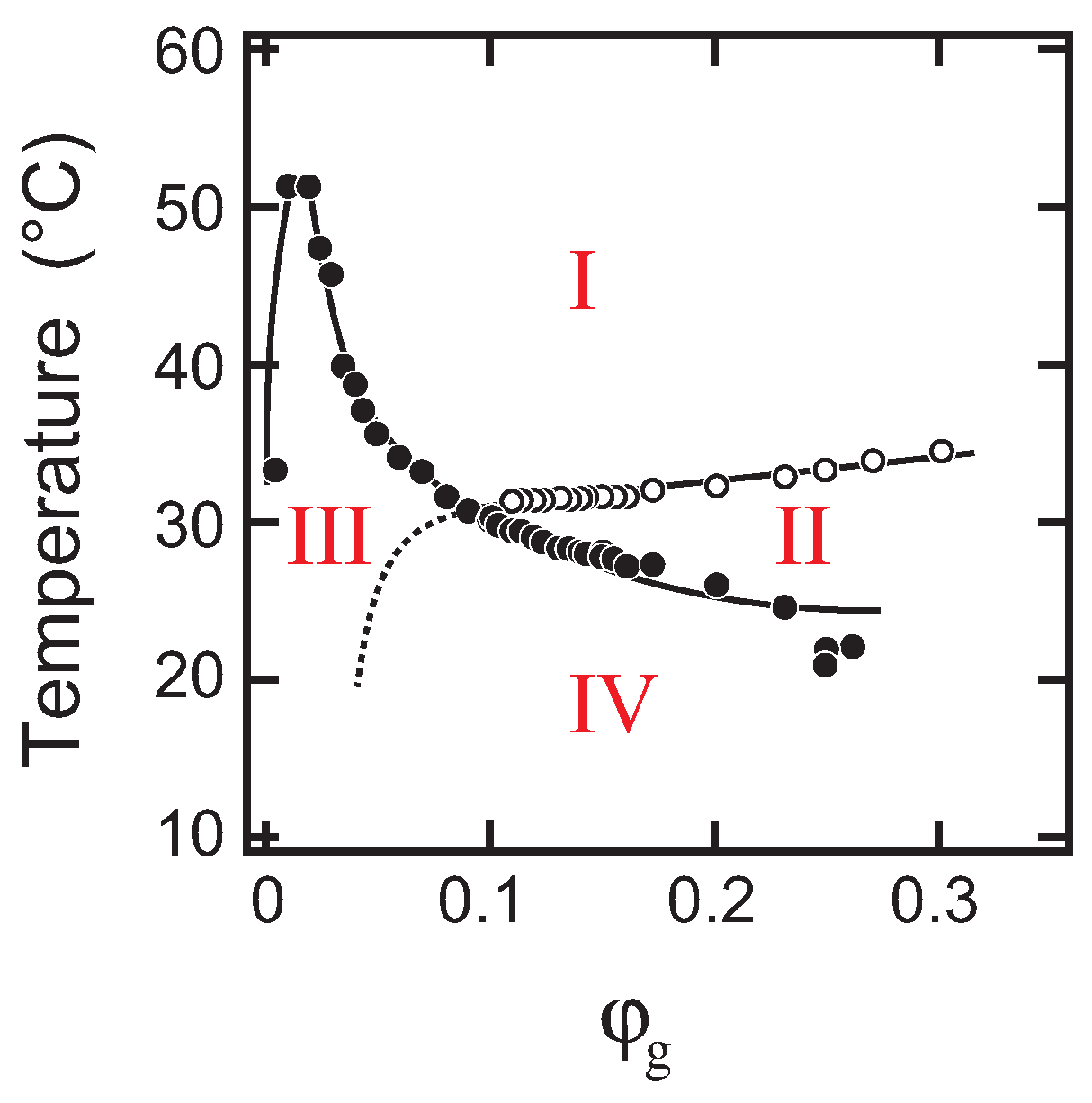
12]. The key point of the previous study is the choice of PEG. We choose the oligomers of PEG with various molecular weights in this study. As such, the weight fraction of PEG oligomer can be changed widely, and hence, the overall aspects of the phase behaviors of the ternary system of gelatin, water and PEG were revealed. In this study, the concentration range of PEG in the system was changed widely to obtain the phase diagram of the system in the entire parameter space. The phase separation of the solution was observed in addition to the sol-gel transition of the solution in the ternary system. It was found that two phase transition lines of the phase separation and the sol-gel transition cross in the
phase space, where
T and
represent the temperature and the weight fraction of gelatin, respectively. Therefore, the phase space of the ternary system is typically divided into four regions corresponding to the definite phases. The phase transitions were investigated mainly by the microscopic observations in the previous study. Thus, the light-scattering measurements were taken to clarify the characteristics of the phase transitions between these four phases in this study.
3. Discussion
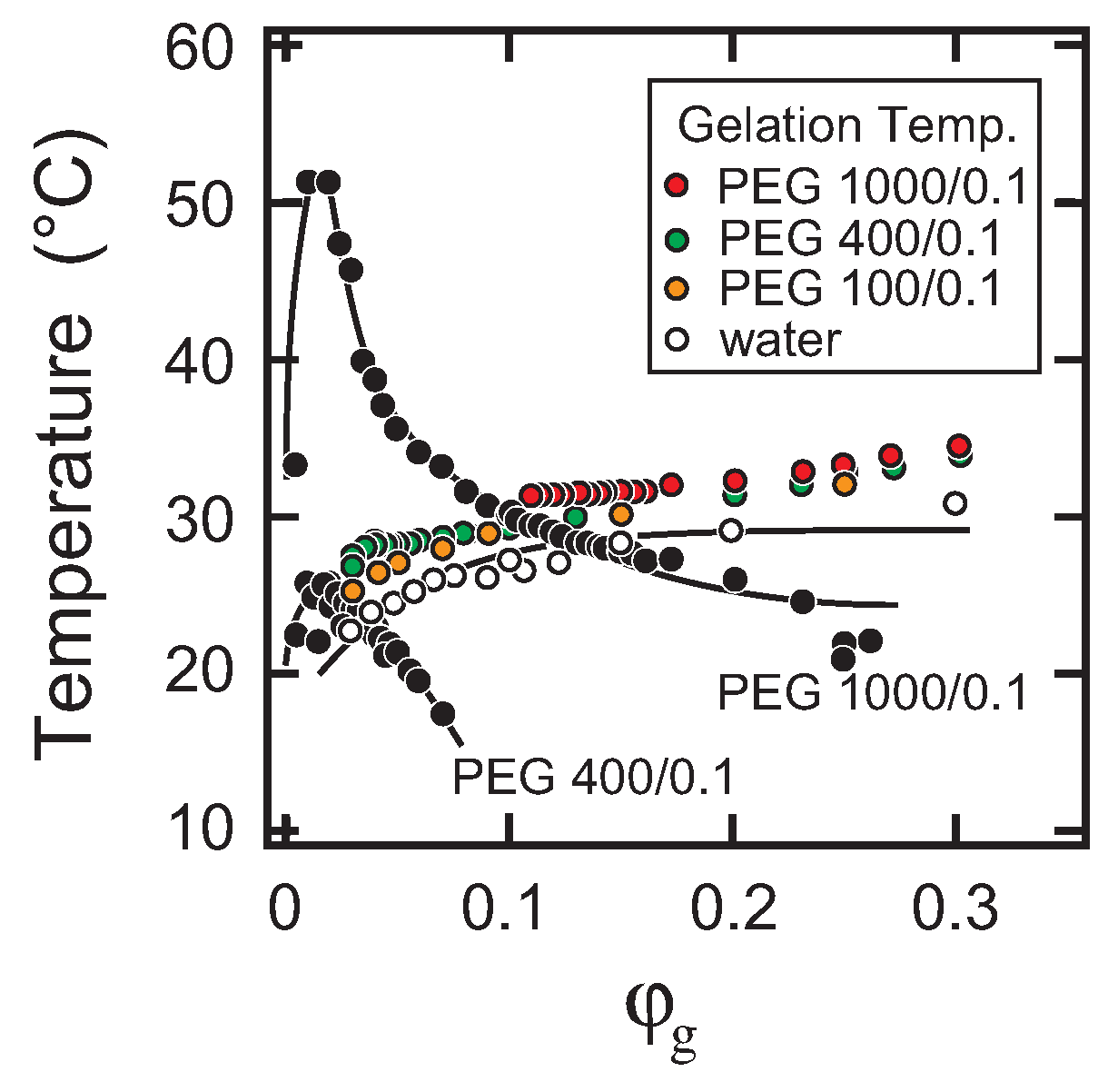
In this study, the interaction between gelatin and PEG was viewed in the form of a phase diagram of the ternary system. It was found from the phase diagrams that the two transitions of the phase separation and the sol-gel transition appear in the
phase space in the ternary system of gelatin, water and PEG oligomer. The relative position of the phase separation line and the sol-gel transition line was found to depend both on the concentration and the molecular weight of PEG oligomer. The results indicate that the addition of PEG into the aqueous solution of gelatin deteriorates the quality of the solvent as has been observed in the ternary system of gelatin, water and methanol [
5]. The phase behaviors of the present ternary system that are shown in
Figure 1 are essentially in agreement with the site-bond correlated-percolation theory of the polymer gelation [
19,
20].
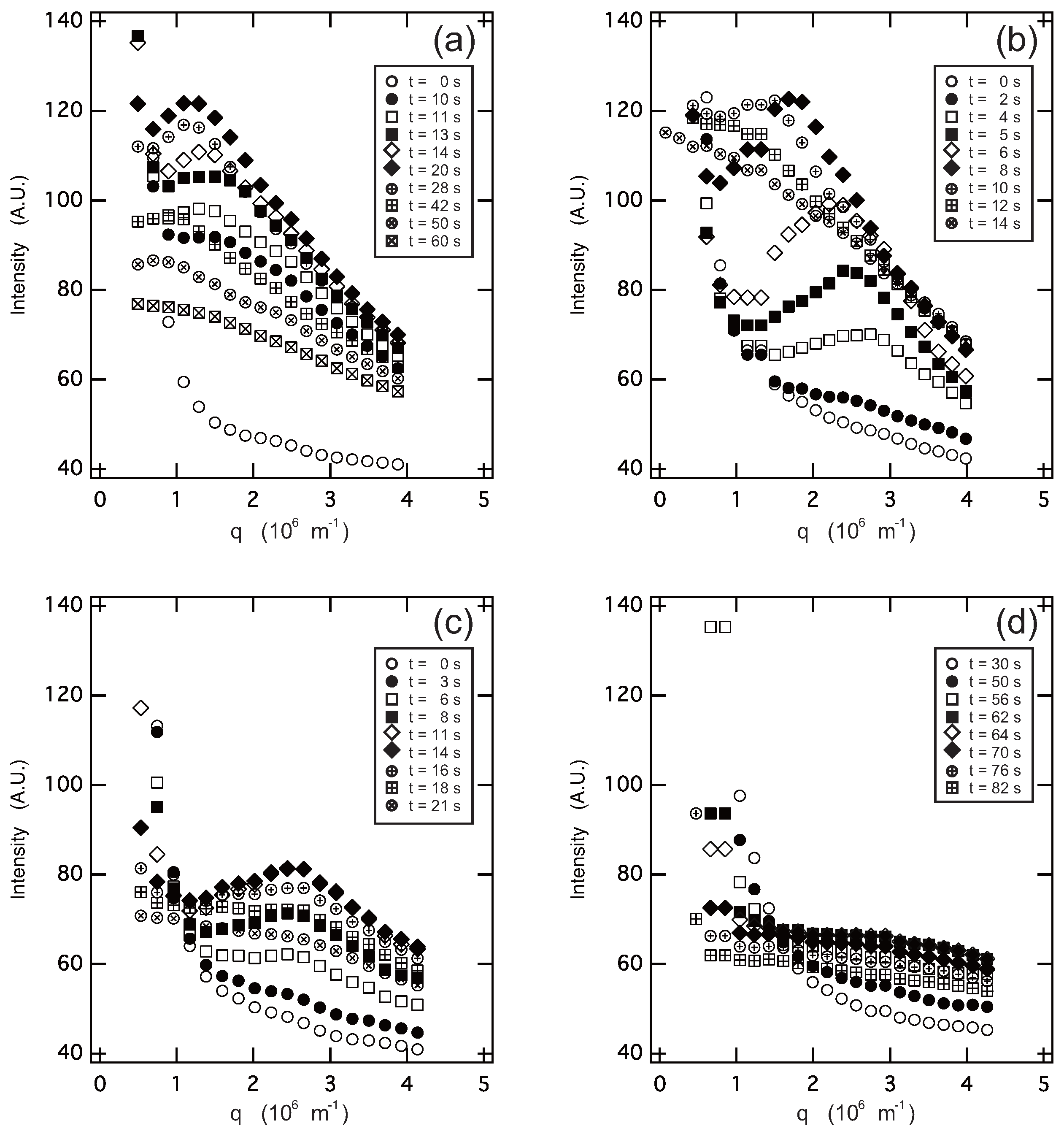
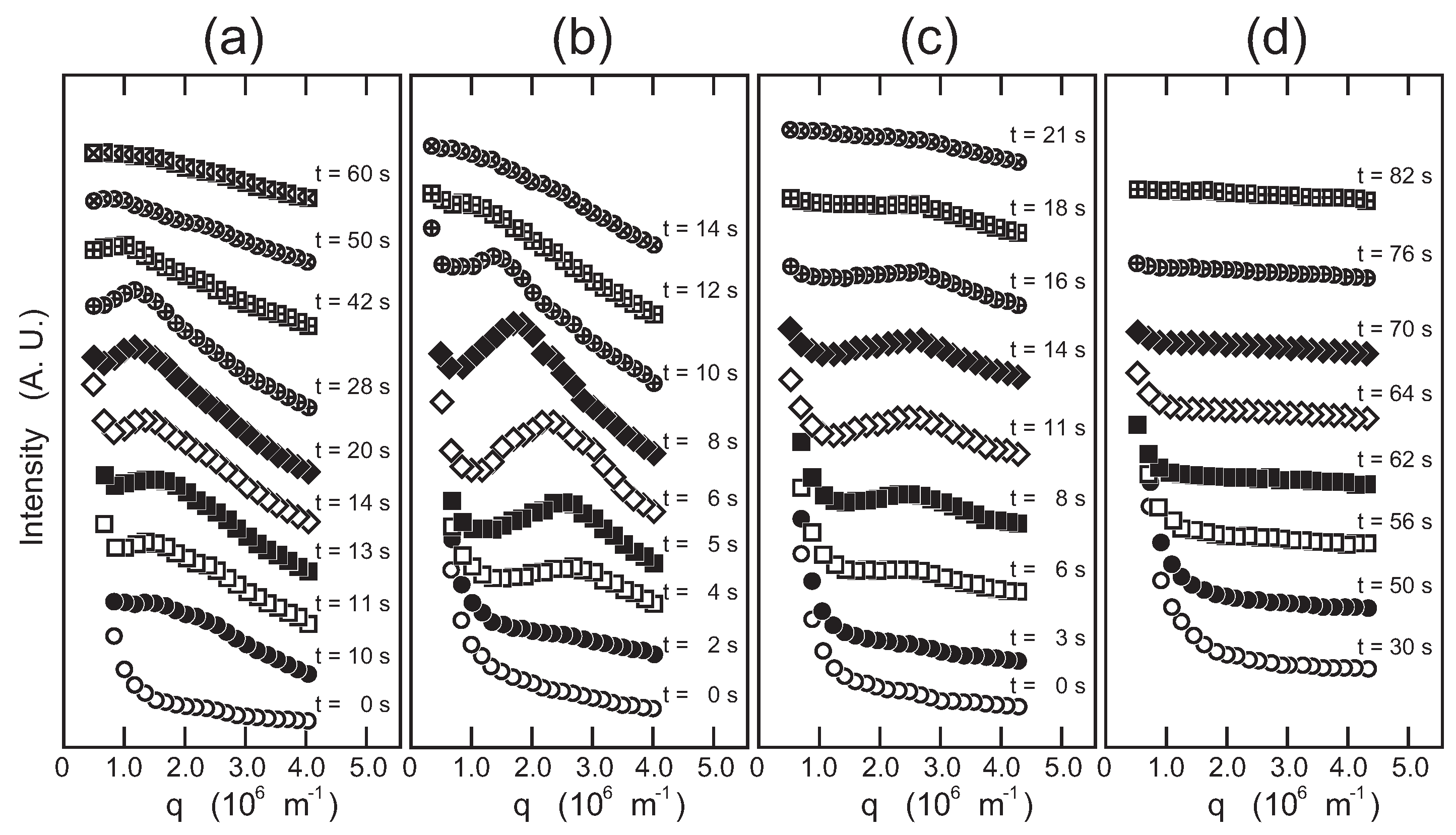
The time evolution of the light-scattering profiles from the solution shown in
Figure 4 and
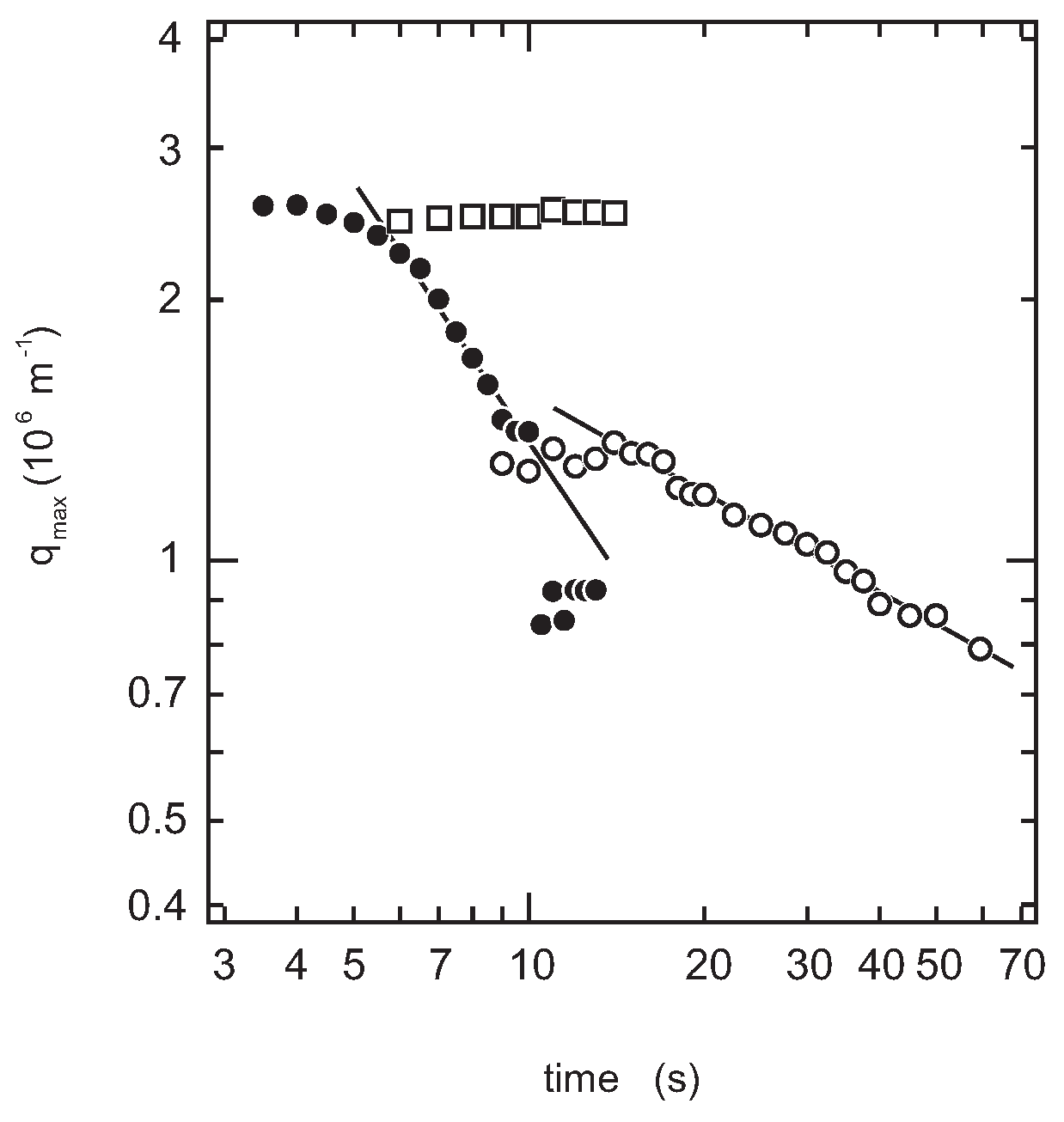
Figure 5 indicates that the spinodal decomposition plays essential roles in the quench processes of the system. Therefore, the time evolution of the magnitude of the scattering vector at the maximum that appears in the scattering profile,
, is shown in
Figure 7. The reciprocal of
is the measure of the correlation length,
, over which the density fluctuation of the spinodal decomposition correlates. The least squares analysis of the results shown in
Figure 7 yields the following.
The late stage behavior of the
system is close to the typical behavior of the simple liquid-liquid phase separation,
, where
[
21]. Since the sol-gel transition temperature is quite similar to that of aqueous gelatin solution without PEG, as shown in
Figure 2, the PEG addition might not have affected the gelation of gelatin via triple-helix formation at this concentration of PEG oligomer. In contrast to the dilute system, it is clearly observed that the phase separation is much accelerated in the dense system of
, where
. In this accelerated phase separation, the following two factors are considered: (i) the attractive interaction due to the gelation and (ii) viscoelastic phase separation. Such acceleration of the phase separation has been studied theoretically, as well as experimentally so far [
22,
23,
24,
25,
26,
27]. Since the sol-gel transition temperature was slightly above 30
C, entanglement of the polymers might contribute to the elastic nature of the system and bring viscoelastic phase separation. Such viscoelastic phase separation is expected to be observed by adding much longer PEG [
6]. Besides, the previous studies suggest that the viscoelastic phase separation is strongly affected by the experimental conditions such as the cooling rate and the shear rate, so detailed and precise experiments are required for the full understanding of the viscoelastic phase separation in this system [
28,
29,
30]. Such studies are now in progress and will be reported elsewhere.
On the other hand, the phase transition in the
system is completely different from that of the previous two systems as shown in
Figure 4,
Figure 5 and
Figure 7,
. It is clear from
Figure 3 that the phase separation line is buried in the gel phase in this system. Therefore, the quench depth is deeper for the gelation than that of phase separation, and hence, the gelation proceeds faster. The density fluctuation of the spinodal decomposition appears in the system; however, it cannot grow beyond the size of the polymer network of the gel. Then, the density fluctuations are spontaneously pinned into the polymer network of the gel in the intermediate stage. Finally, the density fluctuations once pinned in the polymer network of the gel are smeared out by the cross-linking reaction. The spontaneous pinning of the density fluctuations was reported in the late stage of the spinodal decomposition in the polymer mixture and the gelation process of agarose solution [
18,
31]. We, then, carried out the double quench experiment to clarify the competition of the gelation and the phase separation in the
system. The transparent gel was formed in the first quench process from Region I to II. The double quench process, therefore, corresponds to the case where the gelation reaction proceeds much earlier than the phase separation. It is clear that the time evolution of the light-scattering profile does not show any characteristic behavior, and only the turbidity of the gel increases after the second quench process as shown in
Figure 4d,
Figure 5d, and
Figure 6. Although the polymer network of the gel is formed, the phase separation can occur in the system. This further suggests that the phase separation and the sol-gel transition are independent phenomena under the present experimental conditions. The results are what would be expected from the site-bond correlated-percolation model of the polymer gelation. Since the phase separation occurs in the polymer network of the gel, the phase separation is restricted to the microscopic scale by the polymer network of the gel, which prevents the divergence of the density fluctuations. Such a phase separation has been called microphase separation so far. The microphase separation within the gel is also expected in the equivalent phase diagram of the gelling system [
32]. The phase boundary that separates Phases II and IV, which is drawn as the extrapolation of the phase separation line in the lower concentration region in
Figure 3, should be recognized as the microphase separation line in the homogeneous gel. The physical meaning of the phase separation line changes at the cross-over point of the sol-gel transition line and the phase separation line.
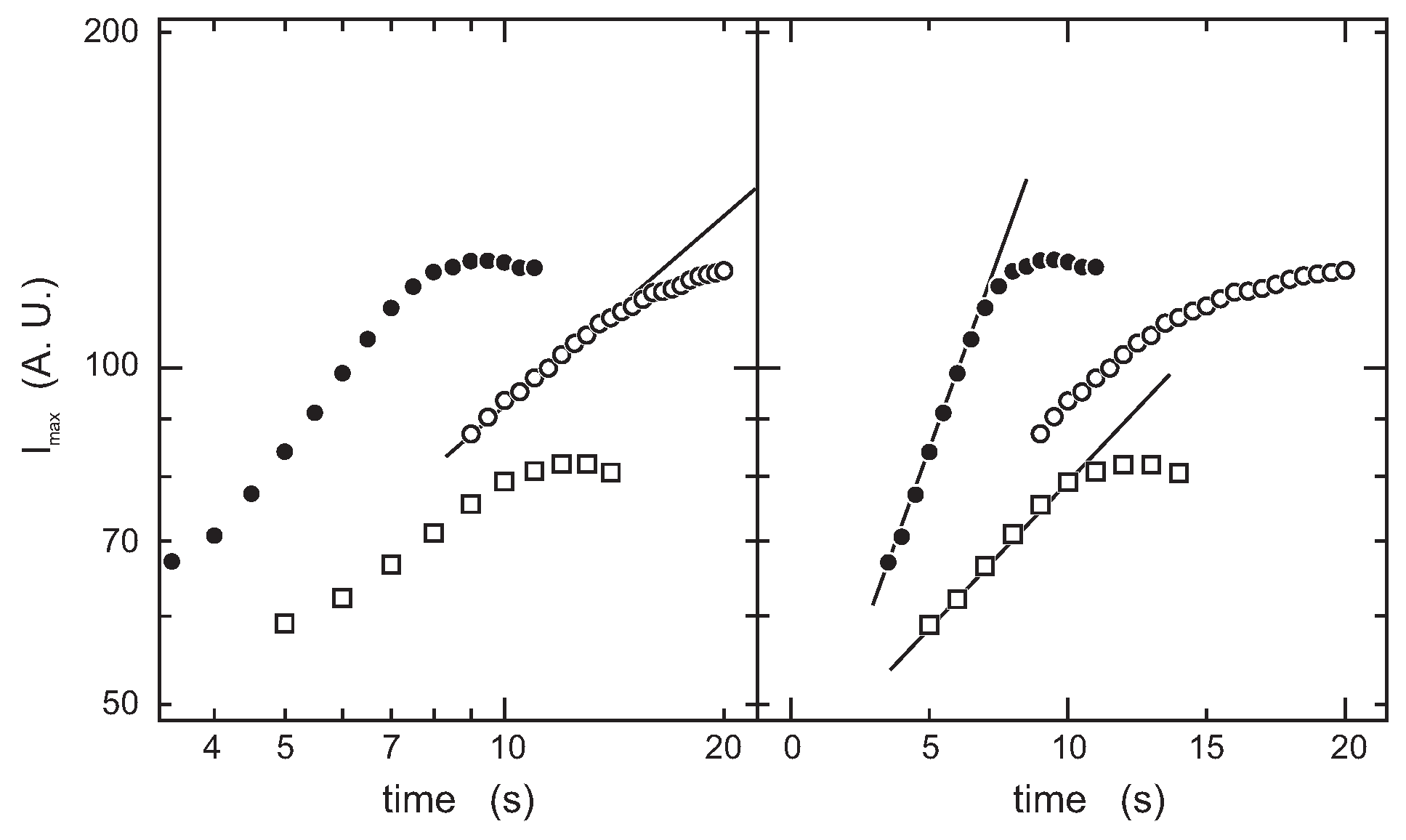
The time evolution of the scattering light intensity from the system is also discussed together with the time evolution of
in the dynamics of the phase separation. The scattering light intensity at the position of the maximum,
, is shown as a function of time,
t, in the double and semilogarithmic plot in
Figure 8. Two kinds of time evolution are observed in this system depending on the weight fraction of gelatin. The time evolution of the scattered light intensity in the
system in the time region around 10 s seems to be expressed by a power law relationship
with
, as shown in the double logarithmic plot in
Figure 8. On the other hand,
increases with an exponential-like growth in the
and
systems, as shown in the semilogarithmic plot of
Figure 8. Since the time interval of the measurement is limited, we do not strongly claim the above results. It is, however, worth noting here that the time evolution in the spinodal decomposition process is divided into an early and a late stage, and the scattering light intensity increases as a function of time with an exponential-like growth in the very early stage of decomposition. The time interval of the measurements in the
and
systems may correspond to the very early stage of the spinodal decomposition. The results may be natural since the gelation reaction accelerates the spinodal decomposition in these two systems. The power law relationship for the
system may also suggest the presence of the scaling relation,
[
31]. The detailed discussion of these results requires further precise experimental studies of the system.
4. Conclusions
The phase behaviors of the ternary system of gelatin, water and PEG oligomer are studied as a function of the weight fraction of gelatin and the weight fraction and molecular weight of PEG oligomer. In addition to the sol-gel transition line, the phase separation line appears in the lower concentration region of the phase diagram when PEG oligomer coexists in the aqueous gelatin solution. The phase separation line is shifted to the higher temperature region upon increasing the concentration and/or the molecular weight of PEG oligomer. The phase behaviors of the system observed under present experimental conditions are well explainable by the site-bond correlated-percolation model of the polymer gelation. Since the phase separation line and the sol-gel transition line cross over in the phase space of , the phase space is typically divided into four regions. The regions thus appearing in the phase space correspond to the definite phases: one-phase sol, one-phase gel, two-phase sol and two-phase gel.
The transitions between these phases in a system with PEG-1000 at a weight fraction of 0.1 are studied by the light-scattering method. The light-scattering profile from the quenched sample solution shows a maximum at a certain magnitude of the scattering vector, . Both the time evolution of the magnitude of and the scattering intensity at the maximum, , are analyzed.
The time evolutions of and for the system of show the typical behaviors that correspond to the simple spinodal decomposition of the liquid-liquid phase separation process. The results are consistent with the previous optical microscope observations.
The similar behaviors of and in the system are observed for the system. The results suggest that the spinodal decomposition also plays a role in the phase transition of this system. However, and change much earlier and faster than in the system, suggesting the acceleration of the spinodal decomposition. Two reasons are considered for the acceleration of the spinodal decomposition. One is the attractive interaction due to the gelation, and the other is the effects of the viscoelastic phase separation.
In contrast to the above two systems, the time evolution of is completely altered from the simple spinodal decomposition in the single quench process of the system. The results indicate that the sol-gel transition plays a dominant role in all of the transition behaviors. The stepwise quench experiments are done to separate the effects of the sol-gel transition and the phase separation. The results indicate that the phase separation occurs even in the polymer network of the gel. However, the phase separation is limited to a microscopic scale because of the presence of the polymer network of the gel. The results suggest that the phase separation line, when it appears in the gel phase, should be regarded as the microphase separation line.
5. Materials and Methods
Gelatin (Type-B, alkali-treated gelatin, No. 1040781000, Merck, Darmstadt, Germany, M. W. ) was obtained from Merck and used as obtained. The average molecular weight of gelatin was determined by gel permeation chromatography.
The oligomers of PEG, namely diethylene glycol (M. W. = 106, PEG-100), triethylene glycol (M. W. = 150, PEG-150) and tetraethylene glycol (M. W. = 194, PEG-200) were obtained from Wako Pure Chemical Industry (Osaka, Japan). The polymers of PEG at M. W. ∼ 400 (PEG-400) and PEG at M. W. ∼ 1000 (PEG-1000), were obtained from Nichiyu Corporation (Tokyo, Japan) and Sanyo Chemical Industry (Kyoto, Japan), respectively.These oligomers and polymers are also used as obtained.
Firstly, water and ethylene glycols were mixed at the desired ratio to make the mixed solvent of gelatin. After ethylene glycol is dissolved completely into water, the calculated amount of gelatin was added into the mixture of water and ethylene glycol. The solutions thus made are heated up to 60
C to dissolve the gelatin. The obtained solution was transferred into a temperature-controlled bath at a temperature of 60
C, and then, the temperature is lowered at a rate of 10
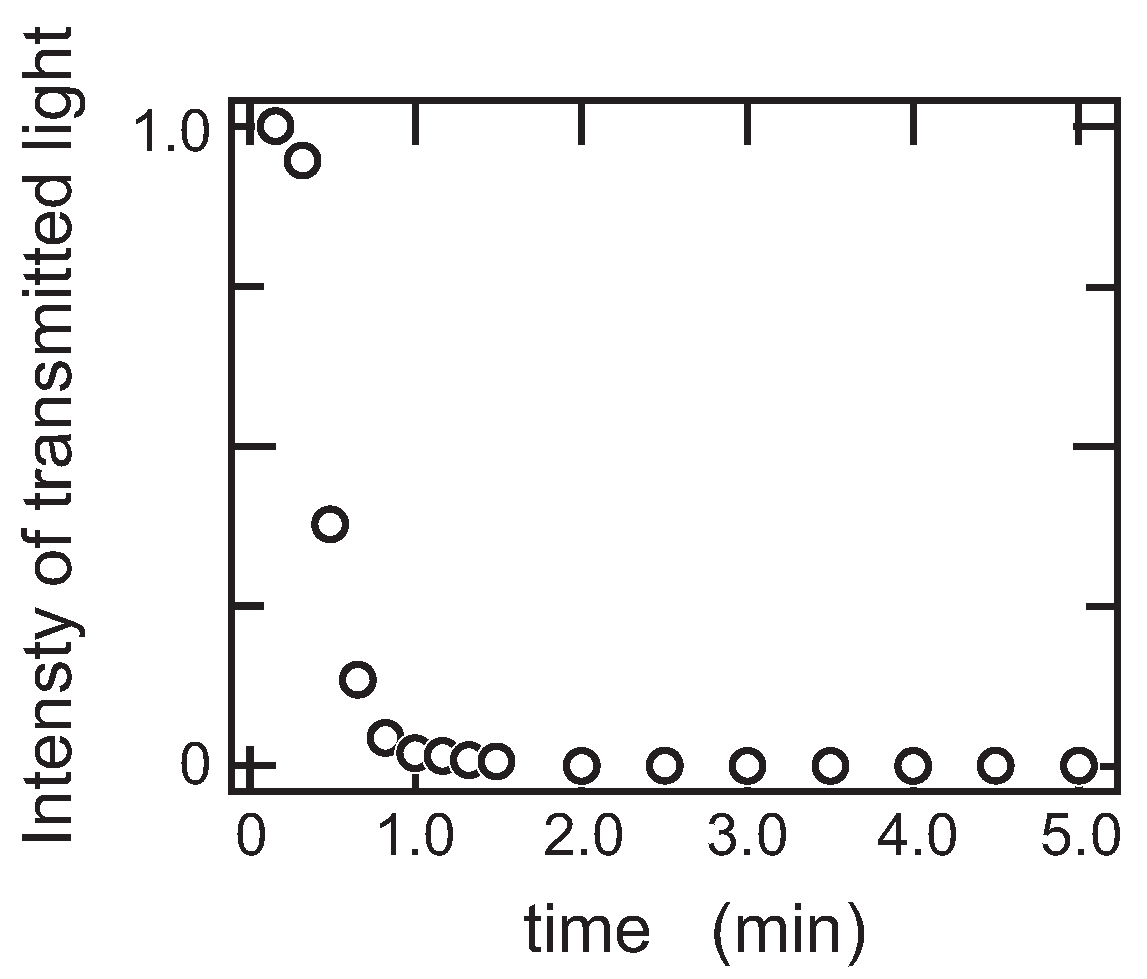
C/h. The solution became opaque near the phase separation temperature. The opaqueness of the solution near the phase separation temperature is caused by the structure change and the formation of the phase-separated droplets by the aggregation of polymers. It has been clarified that the cloud point temperature of the polymer solution practically coincides with the phase separation temperature within an accuracy of a few millidegrees [
33,
34]. Therefore, the cloud point temperature, which is determined by visual inspection, is assigned as the phase separation temperature in this study. The accuracy of the phase separation temperature thus determined was already confirmed by comparing the data with the light-scattering measurement and the turbidity measurement in previous studies [
11,
12]. The turbidity of the solution was also measured as a function of the temperature if necessary for the cross-check of the phase separation temperature. After the determination of the phase separation temperature, the solution is kept at 15
C for 12 h to ensure the gelation. The gelation temperature was determined in this heating process by the falling ball method using a Teflon ball with a wait of 16 mg. Firstly, the Teflon ball was placed on the surface of the gel. The heating rate was chosen as 5
C/h. The gelation temperature was determined as that at which the ball on the surface of the gel falls into the solution. In this method, the applied stress due to the ball is balanced with the elasticity of the polymer network of the gel. However, the elasticity due to the polymer network diminishes when the system attains the sol-gel transition temperature. The ball falls into the gel when the stress due to the ball overcomes the elasticity of the polymer network. Therefore, the gelation temperature that is determined by the falling ball method corresponds to the fracture temperature of the polymer network of the gel. Although the elastic modulus is not measured, the falling ball method is one of the rheological methods. The weight of the ball should be as small as possible to determine the correct gelation temperature.
It is well known that gelatin is easily degraded by the autocatalysis reaction in the solution state. Thus, it is not favorable to expose gelatin solution to a higher temperature. The cooling rate to determine the phase separation temperature was 10
C/h, taking into account that the degradation of gelatin should be avoided. Conversely, the slower heating rate was chosen for the exact determination of the gelation temperature by the falling ball method. The phase diagram obtained here, therefore, did not represent an equilibrium state since the cooling rate was rather high. It was, however, sufficient for the present purpose because the phase separation in the liquid state occurs rather quickly. In addition, the thermal hysteresis is not significant in the case of gelatin gel. Further details were given in the previous report [
12].
The small angle laser light-scattering measurements were taken using a homemade apparatus. The details of the apparatus are given in [
35]. Our apparatus consists of a He-Ne laser (JDSU Uniphase, Milpitas, CA, USA; 8 mW,
= 632.8 nm) and the one-dimensional detector (Hamamatsu, Japan; S3901-512Q; 512 channels, 50
m width/channel). The distance between the sample and the detector was changed from about 2 to 30 cm by a one-dimensional translator. Multiple scattering from the sample virtually dominates in the strongly-opalescent region. Such effects are crucial in the detailed discussion near the critical point. In the present system, however, the strong opalescence becomes dominant only in the late stage of the spinodal decomposition. For the present system, a suitable way of minimizing the effects of the multiple scattering is to suppress it by shortening the optical path length in the cell and to work at a larger wavelength because the scattering intensity is proportional to
. The sample gel was, therefore, prepared in the optical cell of a thickness from 1 to 10 mm, depending on the opacity of the gel. The scattering data were obtained by a computer system. The scattering profiles from the gels thus obtained are expressed as a function of the scattering vector,
, where
n,
and
are the refractive index, the scattering angle and the wave length of the incident light [
36].