A Simple Method of Interpretating the Effects of Electric Charges on the Volume Phase Transition of Thermosensitive Gels
Abstract
1. Introduction
2. The Swelling Equations of Gels
2.1. The Elastic Free Energy of Gels Gelas
2.2. Uncharged Gels (Δμwion = 0)
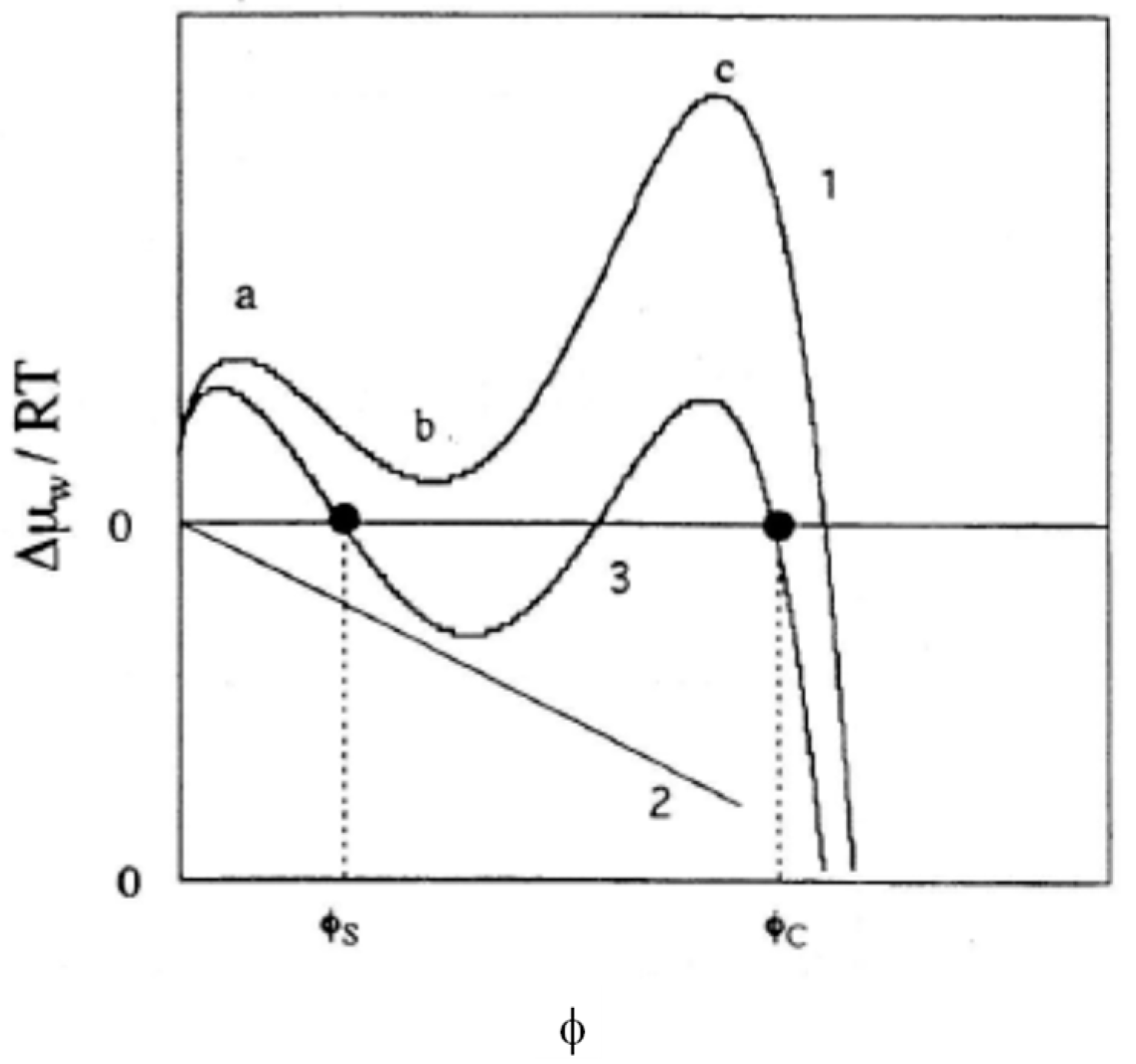
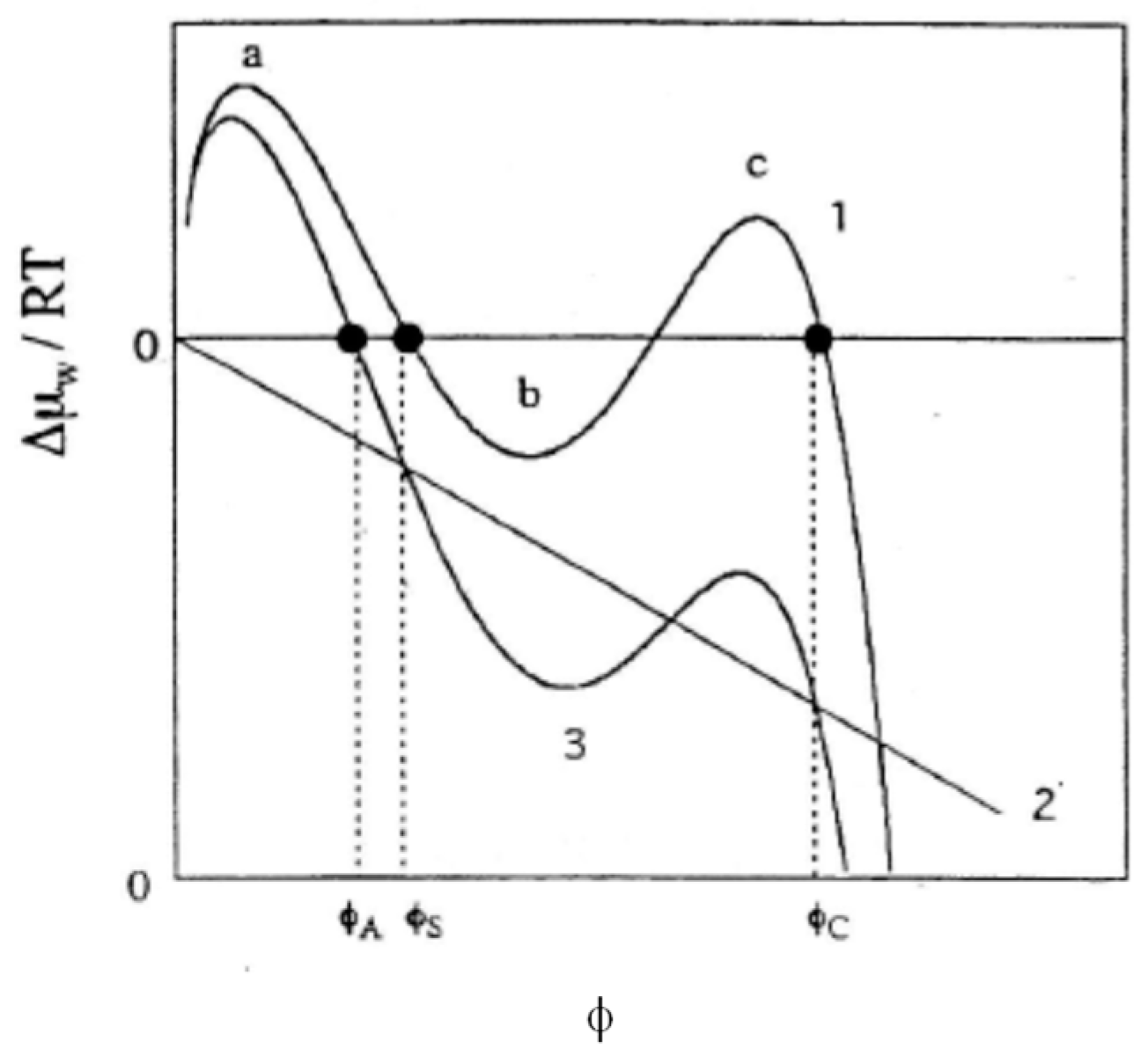
3. Effects of Electric Charge on the Swelling Behavior of Gels
- Contribution from the mixing with counterions.
- Effects on Gelas (introduction of electric charges generally makes polymer chains stiffer).
- Introduction of ionic groups is nothing more than the introduction of different chemical species into polymer chains. Accordingly, two (or more) kinds of χ parameters are required to describe the polymer-solvent interactions. When a kind of average χ parameter is introduced, it may significantly differ from that for the parent non-ionic polymer.
Osmotic Pressure of Small Ions
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Dušek, K.; Patterson, D. Transition in Swollen Polymer Networks Induced by Intramolecular Condensation. J. Polym. Sci. A-2 1968, 6, 1209–1216. [Google Scholar] [CrossRef]
- Tanaka, T. Collapse of Gels and the Critical Endpoint. Phys. Rev. Lett. 1978, 40, 820–823. [Google Scholar] [CrossRef]
- Ilavsky, M.; Hrouz, J.; Ulbrich, K. Phase transition in swollen gels: 3. The Temperature Collapse and Mechanical Behaviour of poly(N,N-diethylacrylamide) Networks in Water. Polym. Bull. 1982, 7, 107–113. [Google Scholar] [CrossRef]
- Ilavsky, M.; Hrouz, J.; Havlicek, I. Phase transition in swollen gels: 7. Effect of charge concentration on the temperature collapse of poly(N,N-diethylacrylamide) networks in water. Polymer 1982, 7, 1514–1518. [Google Scholar] [CrossRef]
- Hirokawa, Y.; Tanaka, T. Volume Phase Transition in a Non-ionic Gel. J. Chem. Phys. 1984, 81, 6379–6380. [Google Scholar] [CrossRef]
- Hirotsu, S.; Hirokawa, Y.; Tanaka, T. Volume-phase transitions of ionized N-isopropylacrylamide gels. J. Chem. Phys. 1987, 87, 1392–1395. [Google Scholar] [CrossRef]
- Beltran, S.; Hooper, H.H.; Blanch, H.W.; Prausnitz, J.M. Swelling equilibria for ionized temperature-sensitive gels in water and in aqueous salt solutions. J. Chem. Phys. 1990, 92, 2061–2066. [Google Scholar] [CrossRef][Green Version]
- Karbarz, M.; Pulka, K.; Misicka, A.; Stojek, Z. pH and Temperature-Sensitive N-isopropylacrylamide Ampholytic Networks Incorporating l-Lysine. Langmuir 2006, 22, 7843–7847. [Google Scholar] [CrossRef] [PubMed]
- Kawasaki, H.; Sasaki, S.; Maeda, H. Effect of Introduced Electric Charge on the Volume Phase Transition of N-isopropylacrylamide Gels. J. Phys. Chem. B 1997, 101, 4184–4187. [Google Scholar] [CrossRef]
- Kawasaki, H.; Sasaki, S.; Maeda, H. Effect of pH on the Volume Phase Transition of Copolymer Gels of N-isopropylacrylamide and Sodium Acrylate. J. Phys. Chem. B 1997, 101, 5089–5092. [Google Scholar] [CrossRef]
- Erman, B.; Flory, P.J. Critical Phenomena and Transitions in Swollen Polymer Networks and in Linear Macromolecules. Macromolecules 1986, 19, 2342–2353. [Google Scholar] [CrossRef]
- Alexandrowicz, Z. Calculation of the Thermodynamic Properties of Polyelectrolytes in the Presence of Salt. J. Polym. Sci. 1962, 56, 97–114. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maeda, H.; Sasaki, S.; Kawasaki, H.; Kakehashi, R. A Simple Method of Interpretating the Effects of Electric Charges on the Volume Phase Transition of Thermosensitive Gels. Gels 2018, 4, 24. https://doi.org/10.3390/gels4010024
Maeda H, Sasaki S, Kawasaki H, Kakehashi R. A Simple Method of Interpretating the Effects of Electric Charges on the Volume Phase Transition of Thermosensitive Gels. Gels. 2018; 4(1):24. https://doi.org/10.3390/gels4010024
Chicago/Turabian StyleMaeda, Hiroshi, Shigeo Sasaki, Hideya Kawasaki, and Rie Kakehashi. 2018. "A Simple Method of Interpretating the Effects of Electric Charges on the Volume Phase Transition of Thermosensitive Gels" Gels 4, no. 1: 24. https://doi.org/10.3390/gels4010024
APA StyleMaeda, H., Sasaki, S., Kawasaki, H., & Kakehashi, R. (2018). A Simple Method of Interpretating the Effects of Electric Charges on the Volume Phase Transition of Thermosensitive Gels. Gels, 4(1), 24. https://doi.org/10.3390/gels4010024






