Hydrogels in Simulated Microgravity: Thermodynamics at Play
Abstract
1. Introduction
2. Hydrogel in Normal Gravity and SMG
2.1. Normal Gravity
2.1.1. Structural and Crosslinking Mechanisms
2.1.2. Fluid Behavior and Its Impact on Hydrogel Properties
2.1.3. Hydration and Swelling Behavior
2.1.4. Mechanical Stability and Degradation
2.1.5. Mathematical Modeling of Hydrogel Behavior in Normal Gravity
Swelling Kinetics
Mass Transport Models
2.2. Simulated Microgravity
2.2.1. Structural and Crosslinking Mechanisms
2.2.2. Fluid Behavior and Its Impact on Hydrogel Properties
2.2.3. Hydration and Swelling Behavior
2.2.4. Mechanical Stability and Degradation
2.2.5. Hydrogel Behavior in Normal Gravity vs. Simulated Microgravity
2.2.6. Mathematical Modeling of Hydrogel Behavior in SMG
Swelling Kinetics
Mass Transport Models
Phase Transition Predictions
3. Thermodynamic Principles in Hydrogel Behavior in Normal Gravity
3.1. Swelling Behavior and Thermodynamic Potentials
3.2. Pressure Variations, Mechanical Stability, and Entropy-Driven Interactions
3.3. Osmotic Pressure, Ionic Transport, and Crosslinking Efficiency
3.4. Generating Energy Through Nanofluidic Systems
3.5. Temperature Gradients, Phase Behavior, and Biomedical Applications
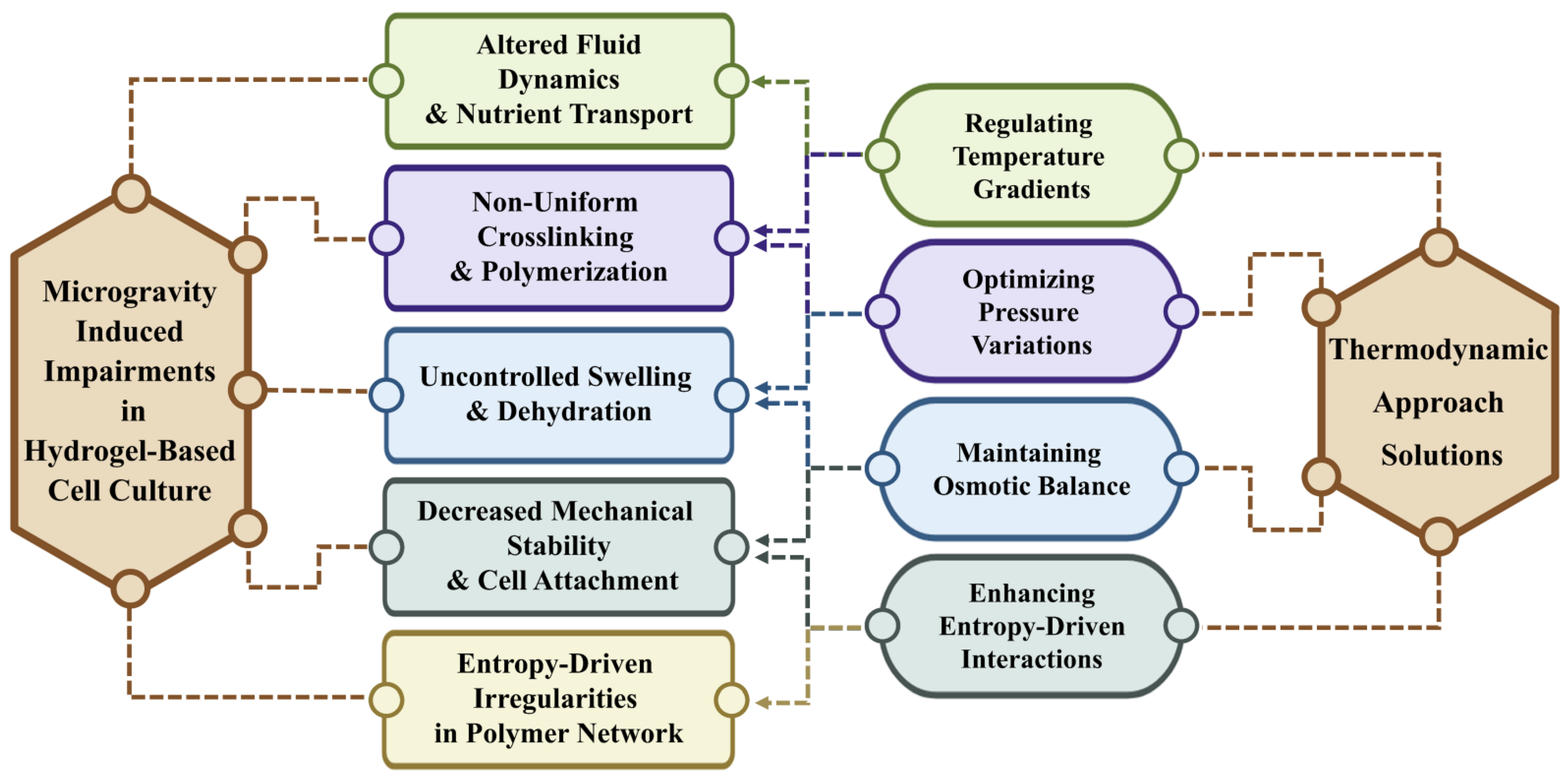
4. Thermodynamic Principles in Hydrogel Structure Under SMG
4.1. Temperature Gradients and Hydrogel Behavior
4.2. Pressure Variations and Mechanical Stability
4.3. Osmotic Balance and Cellular Microenvironments
4.4. Entropy-Driven Interactions and Polymer Network Dynamics
4.5. Thermodynamics as a Framework for Standardizing Hydrogel Behavior in Microgravity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mišković, V.; Greco, I.; Minetti, C.; Cialdai, F.; Monici, M.; Gazzi, A.; Marcellino, J.; Samad, Y.A.; Delogu, L.G.; Ferrari, A.C.; et al. Hydrogel mechanical properties in altered gravity. Npj Microgravity 2024, 10, 83. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.; Duan, X.; Lei, X. 3D cell culture model: From ground experiment to microgravity study. Front. Bioeng. Biotechnol. 2023, 11, 1136583. [Google Scholar] [CrossRef] [PubMed]
- Hicks, J.; Olson, M.; Mitchell, C.; Juran, C.M.; Paul, A.M. The Impact of Microgravity on Immunological States. Immunohorizons 2023, 7, 670–682. [Google Scholar]
- Bizzarri, M.; Monici, M.; van Loon, J.J.W.A. How Microgravity Affects the Biology of Living Systems. BioMed Res. Int. 2015, 2015, 1–4. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, W.; Zhao, S.; Zhao, Y.; Dai, J. Advances in Microgravity Directed Tissue Engineering. Adv. Healthc. Mater. 2023, 12, 2202768. [Google Scholar] [CrossRef]
- Ho, T.-C.; Chang, C.-C.; Chan, H.-P.; Chung, T.-W.; Shu, C.-W.; Chuang, K.-P.; Duh, T.-H.; Yang, M.-H.; Tyan, Y.-C. Hydrogels: Properties and Applications in Biomedicine. Molecules 2022, 27, 2902. [Google Scholar] [CrossRef]
- Li, J.; Mooney, D.J. Designing hydrogels for controlled drug delivery. Nat. Rev. Mater. 2016, 1, 16071. [Google Scholar] [CrossRef]
- Vailati, A.; Bataller, H.; Bou-Ali, M.M.; Carpineti, M.; Cerbino, R.; Croccolo, F.; Egelhaaf, S.U.; Giavazzi, F.; Giraudet, C.; Guevara-Carrion, G.; et al. Diffusion in liquid mixtures. Npj Microgravity 2023, 9, 1. [Google Scholar] [CrossRef]
- Oliveira, J.M.; Carvalho, L.; Silva-Correia, J.; Vieira, S.; Majchrzak, M.; Lukomska, B.; Stanaszek, L.; Strymecka, P.; Malysz-Cymborska, I.; Golubczyk, D.; et al. Hydrogel-based scaffolds to support intrathecal stem cell transplantation as a gateway to the spinal cord: Clinical needs, biomaterials, and imaging technologies. Npj Regen. Med. 2018, 3, 8. [Google Scholar] [CrossRef]
- Kapałczyńska, M.; Kolenda, T.; Przybyła, W.; Zajączkowska, M.; Teresiak, A.; Filas, V.; Ibbs, M.; Bliźniak, R.; Łuczewski, Ł.; Lamperska, K. 2D and 3D cell cultures–a comparison of different types of cancer cell cultures. Arch. Med. Sci. 2018, 14, 910–919. [Google Scholar] [CrossRef]
- Jensen, C.; Teng, Y. Is It Time to Start Transitioning From 2D to 3D Cell Culture? Front. Mol. Biosci. 2020, 7, 33. [Google Scholar] [CrossRef] [PubMed]
- Mironov, V.; Visconti, R.P.; Kasyanov, V.; Forgacs, G.; Drake, C.J.; Markwald, R.R. Organ printing: Tissue spheroids as building blocks. Biomaterials 2009, 30, 2164–2174. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Lian, M.; Wu, Q.; Qiao, Z.; Sun, B.; Dai, K. Effect of Pore Size on Cell Behavior Using Melt Electrowritten Scaffolds. Front. Bioeng. Biotechnol. 2021, 9, 629270. [Google Scholar] [CrossRef] [PubMed]
- Annabi, N.; Nichol, J.W.; Zhong, X.; Ji, C.; Koshy, S.; Khademhosseini, A.; Dehghani, F. Controlling the Porosity and Microarchitecture of Hydrogels for Tissue Engineering. Tissue Eng. Part B Rev. 2010, 16, 371–383. [Google Scholar] [CrossRef]
- Van Den Nieuwenhof, D.W.A.; Moroni, L.; Chou, J.; Hinkelbein, J. Cellular response in three-dimensional spheroids and tissues exposed to real and simulated microgravity: A narrative review. Npj Microgravity 2024, 10, 102. [Google Scholar] [CrossRef]
- Aleshcheva, G.; Bauer, J.; Hemmersbach, R.; Slumstrup, L.; Wehland, M.; Infanger, M.; Grimm, D. Scaffold-free Tissue Formation Under Real and Simulated Microgravity Conditions. Basic Clin. Pharmacol. Toxicol. 2016, 119, 26–33. [Google Scholar] [CrossRef]
- Li, C.; Ouyang, L.; Pence, I.J.; Moore, A.C.; Lin, Y.; Winter, C.W.; Armstrong, J.P.K.; Stevens, M.M. Buoyancy-Driven Gradients for Biomaterial Fabrication and Tissue Engineering. Adv. Mater. 2019, 31, 1900291. [Google Scholar] [CrossRef]
- Nie, H.-Y.; Ge, J.; Liu, K.-G.; Yue, Y.; Li, H.; Lin, H.-G.; Yan, H.-F.; Zhang, T.; Sun, H.-W.; Yang, J.-W.; et al. The effects of microgravity on stem cells and the new insights it brings to tissue engineering and regenerative medicine. Life Sci. Space Res. 2024, 41, 1–17. [Google Scholar] [CrossRef]
- Chen, G. Thermodynamics of hydrogels for applications in atmospheric water harvesting, evaporation, and desalination. Phys. Chem. Chem. Phys. 2022, 24, 12329–12345. [Google Scholar] [CrossRef]
- Hoffman, A.S. Hydrogels for biomedical applications. Adv. Drug Deliv. Rev. 2012, 64, 18–23. [Google Scholar] [CrossRef]
- Herrmann, A.; Haag, R.; Schedler, U. Hydrogels and Their Role in Biosensing Applications. Adv. Healthc. Mater. 2021, 10, 2100062. [Google Scholar] [CrossRef] [PubMed]
- Koetting, M.C.; Peters, J.T.; Steichen, S.D.; Peppas, N.A. Stimulus-responsive hydrogels: Theory, modern advances, and applications. Mater. Sci. Eng. R Rep. 2015, 93, 1–49. [Google Scholar] [CrossRef] [PubMed]
- Pojman, J.A.; Bessonov, N.; Volpert, V.; Paley, M. Miscible Fluids in Microgravity (MFMG): A zero-upmass investigation on the International Space Station. Microgravity Sci. Technol. 2007, 19, 33–41. [Google Scholar] [CrossRef]
- Klein, M.; Teichert, W. The Dynamic Behaviour of Fluids in Microgravity. ESA Bull. 1995, 85, 38–40. [Google Scholar]
- Vernerey, F.J.; Sridhar, S.L.; Muralidharan, A.; Bryant, S.J. Mechanics of 3D Cell–Hydrogel Interactions: Experiments, Models, and Mechanisms. Chem. Rev. 2021, 121, 11085–11148. [Google Scholar] [CrossRef]
- Vashist, A.; Ahmad, S. Hydrogels in Tissue Engineering: Scope and Applications. Curr. Pharm. Biotechnol. 2015, 16, 606–620. [Google Scholar] [CrossRef]
- Prot, V.; Sveinsson, H.M.; Gawel, K.; Gao, M.; Skalleruda, B.; Stokke, B.T. Swelling of a hemi-ellipsoidal ionic hydrogel for determination of material properties of deposited thin polymer films: An inverse finite element approach. Soft Matter 2013, 9, 5815–5827. [Google Scholar] [CrossRef]
- Zhao, X. Multifunctional Hydrogel Properties and Their Biomedical Applications. Chem. Rev. 2019, 119, 5261–5315. [Google Scholar]
- Van Vlierberghe, S.; Dubruel, P.; Schacht, E. Biopolymer-Based Hydrogels As Scaffolds for Tissue Engineering Applications: A Review. Biomacromolecules 2011, 12, 1387–1408. [Google Scholar] [CrossRef]
- Chaudhuri, O.; Gu, L.; Klumpers, D.; Darnell, M.; Bencherif, S.A.; Weaver, J.C.; Huebsch, N.; Lee, H.-P.; Lippens, E.; Duda, G.N.; et al. Hydrogels with tunable stress relaxation regulate stem cell fate and activity. Nat. Mater. 2016, 15, 326–334. [Google Scholar] [CrossRef]
- Ganji, F.; Vasheghani-Farahani, S.; Vasheghani-Farahani, E. Theoretical Description of Hydrogel Swelling: A Review. Iran. Polym. J. 2010, 19, 375–398. [Google Scholar]
- Caccavo, D. An overview on the mathematical modeling of hydrogels’ behavior for drug delivery systems. Int. J. Pharm. 2019, 560, 175–190. [Google Scholar] [CrossRef] [PubMed]
- Van Ombergen, A.; Chalupa-Gantner, F.; Chansoria, P.; Colosimo, B.M.; Costantini, M.; Domingos, M.; Dufour, A.; De Maria, C.; Groll, J.; Jungst, T.; et al. 3D Bioprinting in Microgravity: Opportunities, Challenges, and Possible Applications in Space. Adv. Healthc. Mater. 2023, 12, 2300443. [Google Scholar] [CrossRef] [PubMed]
- Briskman, V.A.; Kostarev, K.G.; Yudina, T.M.; Kondyurin, A.V.; Leontyev, V.B.; Levkovich, M.G.; Mashinsky, A.L.; Nechitailo, G.S. Polymerization in microgravity as a new process in space technology. Acta Astronaut. 2001, 48, 169–180. [Google Scholar] [CrossRef]
- Downey, J.P.; Pojman, J.A. (Eds.) Polymer Research in Microgravity: Polymerization and Processing. In ACS Symposium Series; American Chemical Society: Washington, DC, USA, 2001; Volume 793. [Google Scholar] [CrossRef]
- Peromingo, C.; Sánchez, P.S.; Gligor, D.; Bello, A.; Rodríguez, J. Sloshing reduction in microgravity with passive baffles: Design, performance, and supplemental thermocapillary control. Phys. Fluids 2023, 35, 112108. [Google Scholar] [CrossRef]
- Smirnova, M.N.; Nikitin, V.F.; Skryleva, E.I.; Weisman, Y.G. Capillary driven fluid flows in microgravity. Acta Astronaut. 2023, 204, 892–899. [Google Scholar] [CrossRef]
- Bronowicki, P.; Canfield, P.; Grah, A.; Dreyer, M. Free surfaces in open capillary channels—Parallel plates. Phys. Fluids 2015, 27, 012106. [Google Scholar] [CrossRef]
- Elele, E.; Shen, Y.; Tang, J.; Lei, Q.; Khusid, B. Single-bubble water boiling on small heater under Earth’s and low gravity. Npj Microgravity 2018, 4, 21. [Google Scholar] [CrossRef]
- Hovestreijdt, J. The influence of the surface tension difference on the boiling of mixtures. Chem. Eng. Sci. 1963, 18, 631–639. [Google Scholar] [CrossRef]
- Ashtaputrey, P.; Ashtaputrey, S. STUDY OF SWELLING BEHAVIOR AND DETERMINATION OF SWELLING PARAMETERS OF SPHERICAL HYDROGELS IN WATER. J. Drug Deliv. Ther. 2018, 8, 218–222. [Google Scholar] [CrossRef]
- Ehrenhofer, A.; Elstner, M.; Wallmersperger, T. Normalization of hydrogel swelling behavior for sensoric and actuatoric applications. Sens. Actuators B Chem. 2018, 255, 1343–1353. [Google Scholar] [CrossRef]
- Plummer, A.; Adkins, C.; Louf, J.-F.; Košmrlj, A.; Datta, S.S. Obstructed swelling and fracture of hydrogels. Soft Matter 2024, 20, 1425–1437. [Google Scholar] [CrossRef] [PubMed]
- Žuržul, N.; Ilseng, A.; Prot, V.E.; Sveinsson, H.M.; Skallerud, B.H.; Stokke, B.T. Donnan Contribution and Specific Ion Effects in Swelling of Cationic Hydrogels are Additive: Combined High-Resolution Experiments and Finite Element Modeling. Gels 2020, 6, 31. [Google Scholar] [CrossRef]
- Radstake, W.E.; Gautam, K.; Miranda, S.; Vermeesen, R.; Tabury, K.; Rehnberg, E.; Buset, J.; Janssen, A.; Leysen, L.; Neefs, M.; et al. The Effects of Combined Exposure to Simulated Microgravity, Ionizing Radiation, and Cortisol on the In Vitro Wound Healing Process. Cells 2023, 12, 246. [Google Scholar] [CrossRef]
- Wei, F.; Flowerdew, K.; Kinzel, M.; Perotti, L.E.; Asiatico, J.; Omer, M.; Hovell, C.; Reumers, V.; Coathup, M.J. Changes in interstitial fluid flow, mass transport and the bone cell response in microgravity and normogravity. Bone Res. 2022, 10, 65. [Google Scholar] [CrossRef]
- Setapa, A.; Ahmad, N.; Mahali, S.M.; Amin, M.C.I.M. Mathematical Model for Estimating Parameters of Swelling Drug Delivery Devices in a Two-Phase Release. Polymers 2020, 12, 2921. [Google Scholar] [CrossRef]
- Blanco, A.; González, G.; Casanova, E.; Pirela, M.E.; Briceño, A. Mathematical Modeling of Hydrogels Swelling Based on the Finite Element Method. Appl. Math. 2013, 4, 161–170. [Google Scholar] [CrossRef]
- Romain, M.; Cai, S.; Hong, W.; Zhao, X.; Lapusta, Y.; Suo, Z. A theory of constrained swelling of a pH-sensitive hydrogel. Soft Matter 2010, 6, 784–793. [Google Scholar]
- Kyoo, K.M. Rui Huang A Variational Approach and Finite Element Implementation for Swelling of Polymeric Hydrogels Under Geometric Constraints. J. Appl. Mech. 2010, 77, 061004. [Google Scholar]
- De Piano, R.; Caccavo, D.; Barba, A.A.; Lamberti, G. Swelling Behavior of Anionic Hydrogels: Experiments and Modeling. Gels 2024, 10, 813. [Google Scholar] [CrossRef]
- Klouda, L.; Mikos, A.G. Thermoresponsive hydrogels in biomedical applications. Eur. J. Pharm. Biopharm. 2008, 68, 34–45. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Liu, Y.; Fu, W.; Yao, M.; Ding, Z.; Xuan, J.; Li, D.; Wang, S.; Xia, Y.; Cao, M. Poly(N-isopropylacrylamide)-Based Thermoresponsive Composite Hydrogels for Biomedical Applications. Polymers 2020, 12, 580. [Google Scholar] [CrossRef]
- Zhou, Y.; Jin, L. Mechanics Underpinning Phase Separation of Hydrogels. Macromolecules 2023, 56, 426–439. [Google Scholar] [CrossRef] [PubMed]
- Abbott, S. PolymerSwelling. Available online: https://www.stevenabbott.co.uk/practical-solubility/polymer-swelling.php (accessed on 1 April 2025).
- Rizwan, M.; Yahya, R.; Hassan, A.; Yar, M.; Azzahari, A.D.; Selvanathan, V.; Sonsudin, F.; Abouloula, C.N. pH Sensitive Hydrogels in Drug Delivery: Brief History, Properties, Swelling, and Release Mechanism, Material Selection and Applications. Polymers 2017, 9, 137. [Google Scholar] [CrossRef]
- Mohan, B.; Singh, K.; Ahmadov, E.; Pombeiro, A.J.L.; Ren, P. Harvesting sustainable osmotic energy: The art of nanofluidic hydrogel membranes. J. Energy Chem. 2025, 105, 577–594. [Google Scholar] [CrossRef]
- Tanaka, K.; Nishimura, N.; Kawai, Y. Adaptation to microgravity, deconditioning, and countermeasures. J. Physiol. Sci. 2017, 67, 271–281. [Google Scholar] [CrossRef]
- Buravkova, L.; Larina, I.; Andreeva, E.; Grigoriev, A. Microgravity Effects on the Matrisome. Cells 2021, 10, 2226. [Google Scholar] [CrossRef]
- Jeyaraman, M.; Ramasubramanian, S.; Yadav, S.; Jeyaraman, N. Exploring New Horizons: Advancements in Cartilage Tissue Engineering Under Space Microgravity. Cureus 2024, 16, e66224. [Google Scholar] [CrossRef]
- Loo, S.; Vásquez, L.; Athanassiou, A.; Fragouli, D. Polymeric Hydrogels—A Promising Platform in Enhancing Water Security for a Sustainable Future. Adv. Mater. Interfaces 2021, 8, 2100580. [Google Scholar] [CrossRef]
- Kong, V.A.; Staunton, T.A.; Laaser, J.E. Effect of Cross-Link Homogeneity on the High-Strain Behavior of Elastic Polymer Networks. Macromolecules 2024, 57, 4670–4679. [Google Scholar] [CrossRef]
- Thang, N.H.; Chien, T.B.; Cuong, D.X. Polymer-Based Hydrogels Applied in Drug Delivery: An Overview. Gels 2023, 9, 523. [Google Scholar] [CrossRef] [PubMed]

| Aspect | Normal Gravity (1 g) | Simulated Microgravity (μg) |
|---|---|---|
| Crosslinking Mechanisms | Crosslinking polymers of hydrogels exist in many forms, such as chemical covalent bonds, and physical bonds, such as ionic and hydrogen bonds. These mechanisms are affected by sedimentation due to gravitational forces and natural convection, which may lead to anisotropy [22]. | The microgravity environment results in a lack of natural convection and removes the driving force for sedimentation, resulting in more uniform crosslinking of polymers. This is especially so in the physically bonded polymer crosslinks. The result is improved strength and rigidity, but at the cost of flexibility [13]. |
| Fluid Behavior | Under normal gravity, buoyancy drives the transport process within the hydrogel. Phase separation also occurs during swelling in the polymer network. This can result in uneven solute distribution [22]. | In the absence of gravity and capillary forces, surface tension effects will be dominant. This results in larger, more stable bubbles and homogeneous mixtures, leading to increased fatigue resistance and reduced swelling behavior [23,24]. |
| Swelling Behavior | The swelling behavior of a hydrogel will be anisotropic as it attempts to reach equilibrium due to the forces of gravity and capillary action [24]. | Without the forces of gravity and capillary action acting on the hydrogel, the material will exhibit much more uniform swelling behavior. The advantages of uniform swelling are a more stable structure and minimized stress points [24]. |
| Mechanical Stability | Due to the composition of hydrogels, they exhibit mechanical properties of both viscous and elastic materials. Under a stressor such as the force of gravity, the material undergoes fatigue and creep [22]. | With minimal external stresses, the hydrogel can experience increased amounts of swelling while potentially experiencing higher stability through less fatigue/creep. |
| Degradation | Degradation of a hydrogel involves change in properties due to breakdown of the polymer structure. This is often achieved through the diffusion of an enzyme into the material. In a normal gravity environment, this diffusion can be uneven, resulting in a comparably uneven breakdown [22]. | In SMG, a more uniform degradation can be expected, potentially slowing the overall process. This is beneficial because it leads to a predictable loss of mechanical properties and a controlled release rate. |
| Thermodynamic Parameter | Normal Gravity (1 g) | Microgravity (µg) |
|---|---|---|
| Temperature Gradients | Heat Transfer: Natural convection facilitates uniform heat distribution within hydrogels, promoting consistent crosslinking and mechanical properties. Thermal Conductivity: Standard temperature regulation ensures well-defined sol–gel transitions and polymer relaxation [52]. | Heat Transfer: Absence of convection leads to reliance on conduction and radiation for heat transfer, potentially causing non-uniform temperature distribution. Thermal Conductivity: Altered thermal properties may affect hydrogel stability and performance. Phase Transition: It can be concluded that reduced gravity conditions may shift sol–gel transition thresholds and hydrogel response times. |
| Pressure Variations | Hydrostatic Pressure: Standard atmospheric pressure maintains typical swelling ratios and mechanical stability. Mechanical Properties: Hydrogels exhibit predictable compressive strengths suitable for load-bearing applications [61]. Network Stability: Consistent pressure conditions support uniform polymer crosslinking and mechanical resilience [62]. | Hydrostatic Pressure: Reduced pressure can lead to increased swelling, altering pore size and mechanical strength. Mechanical Properties: Changes in pressure may affect the structural integrity of hydrogels in microgravity environments. Network Stability: Variations in mechanical load distribution can cause unpredictable deformations in hydrogels [63]. |
| Osmotic Balance | Solvent Movement: Gravity-driven convection aids in maintaining osmotic equilibrium. Swelling Behavior: Controlled osmotic pressure supports stable swelling and deswelling cycles. Ion Transport prevents pH fluctuations [58]. Water-structuring ions enhance hydrogen bonding and reduce swelling, while water-disrupting ions weaken hydrogen bonds and increase swelling [44]. Osmotic energy harvesting creates an electric current through concentration differences [57]. | Solvent Movement: Lack of convection may disrupt osmotic balance, uneven swelling, and dehydration. Swelling Behavior: Altered osmotic conditions can affect hydrogel performance in microgravity. Ion Transport: Reduced buoyancy-driven mixing may lead to heterogeneous ion distributions [58]. Microgravity can encourage water to move to a higher concentration, yielding higher energy from osmotic energy harvesting [57]. |
| Entropy-Driven Interactions | Polymer Chain Dynamics: Entropy influences polymer flexibility and network rearrangements, affecting hydrogel elasticity and resilience. Molecular Diffusion: Standard diffusion rates facilitate predictable drug release profiles. Phase Separation: Thermodynamic stability ensures proper distribution of polymer chains, avoiding microstructural defects [44,55]. In situ delivery, an entropy-driven reaction, uses the heat-activated phase behavior of thermoresponsive hydrogels to tailor materials for specific biomedical applications, including drug delivery [5]. | Polymer Chain Dynamics: Microgravity may prevent polymer relaxation and hydrogel mechanical properties. Molecular Diffusion: Changes in diffusion rates could affect nutrient transport within hydrogels. Phase Separation: Lack of gravity-driven segregation results in more homogeneous hydrogel structures [44,55]. |
| pH | Acidic hydrogels shrink at low pH and swell at high pH. Basic hydrogels swell at low pH and shrink at a high pH [56]. | The effect of pH on swelling is unchanged by microgravity [56]. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sepahvandi, A.; Johnson, J.; Arasan, A.; Cataldo, R.; Ghoreishian, S.M. Hydrogels in Simulated Microgravity: Thermodynamics at Play. Gels 2025, 11, 342. https://doi.org/10.3390/gels11050342
Sepahvandi A, Johnson J, Arasan A, Cataldo R, Ghoreishian SM. Hydrogels in Simulated Microgravity: Thermodynamics at Play. Gels. 2025; 11(5):342. https://doi.org/10.3390/gels11050342
Chicago/Turabian StyleSepahvandi, Azadeh, Joseph Johnson, Ava Arasan, Ryan Cataldo, and Seyed Majid Ghoreishian. 2025. "Hydrogels in Simulated Microgravity: Thermodynamics at Play" Gels 11, no. 5: 342. https://doi.org/10.3390/gels11050342
APA StyleSepahvandi, A., Johnson, J., Arasan, A., Cataldo, R., & Ghoreishian, S. M. (2025). Hydrogels in Simulated Microgravity: Thermodynamics at Play. Gels, 11(5), 342. https://doi.org/10.3390/gels11050342









