Early-Warning System for Antimicrobial Resistance in Campylobacter in the Broiler Production Chain from High-Level Indicators—A Graph-Based Machine Learning and Bayesian Approach
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Description and Preparation
2.1.1. Indicator Data
2.1.2. AMR Data and Processing
2.1.3. Feature Engineering and Data Preparation
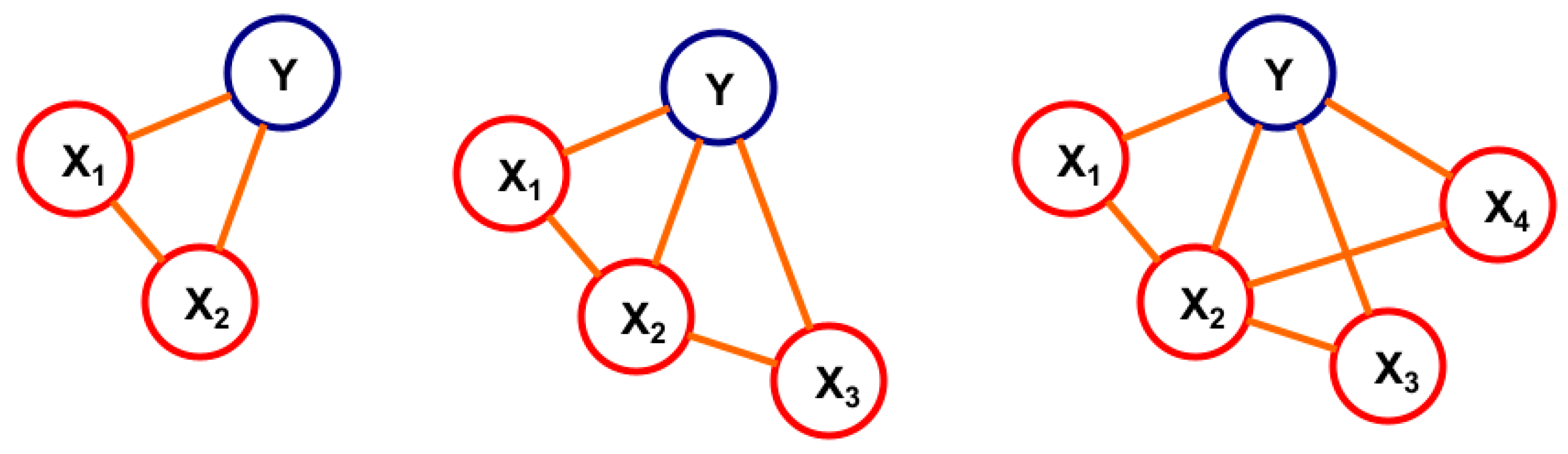
2.1.4. Variable Selection for BN
2.2. A Multi-Method Analytical Approach: From Exploratory Machine Learning to Probabilistic Graphical Models for AMR Profiling
2.2.1. Exploratory Classification (Machine Learning)
2.2.2. Generalized Naive Bayes Approach
2.2.3. Bayesian Network (BN)
2.2.4. Analysis of Multi-Step Network Pathways
3. Results
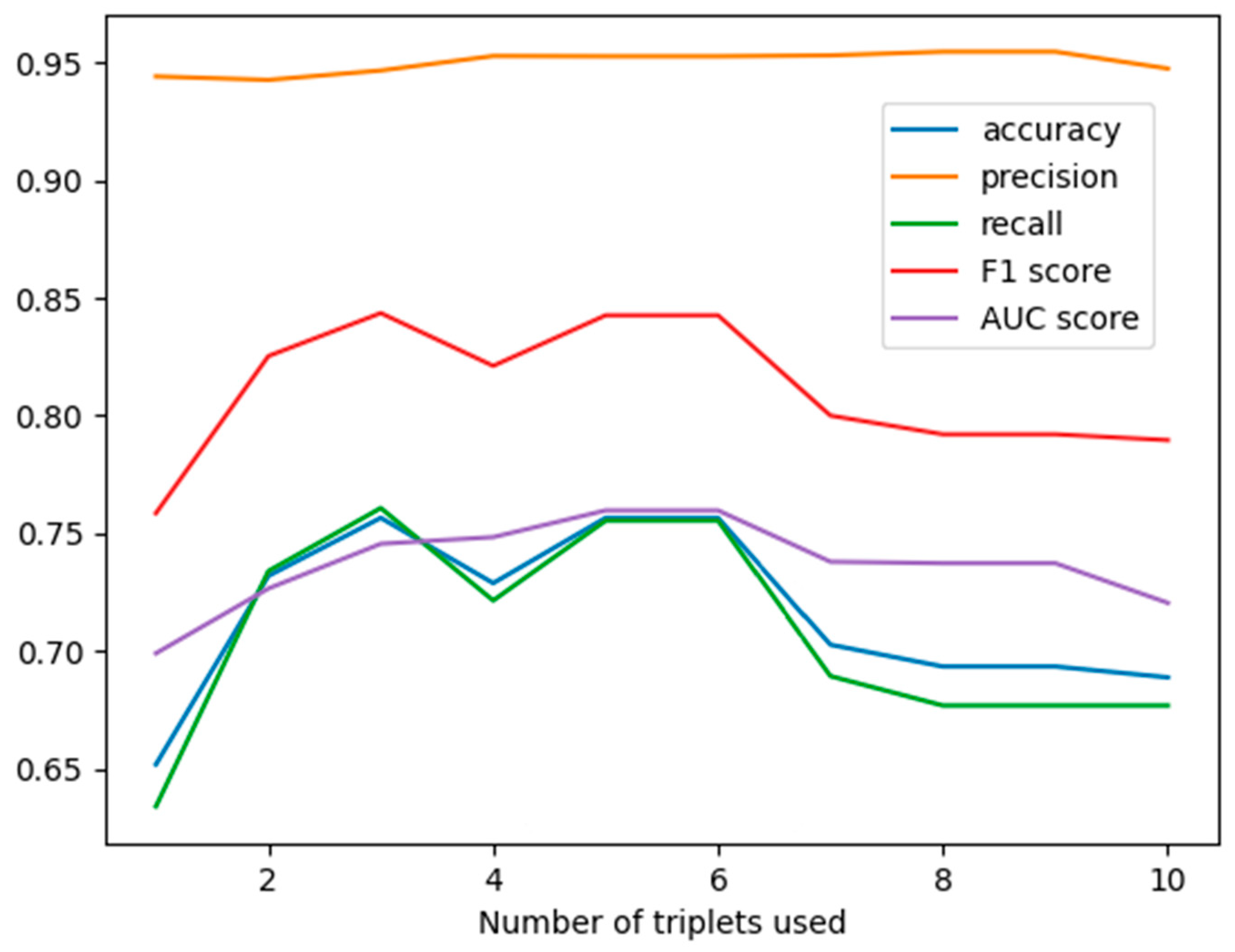
3.1. The Results by Applying GNB
3.2. Results of Bayesian Network Analysis
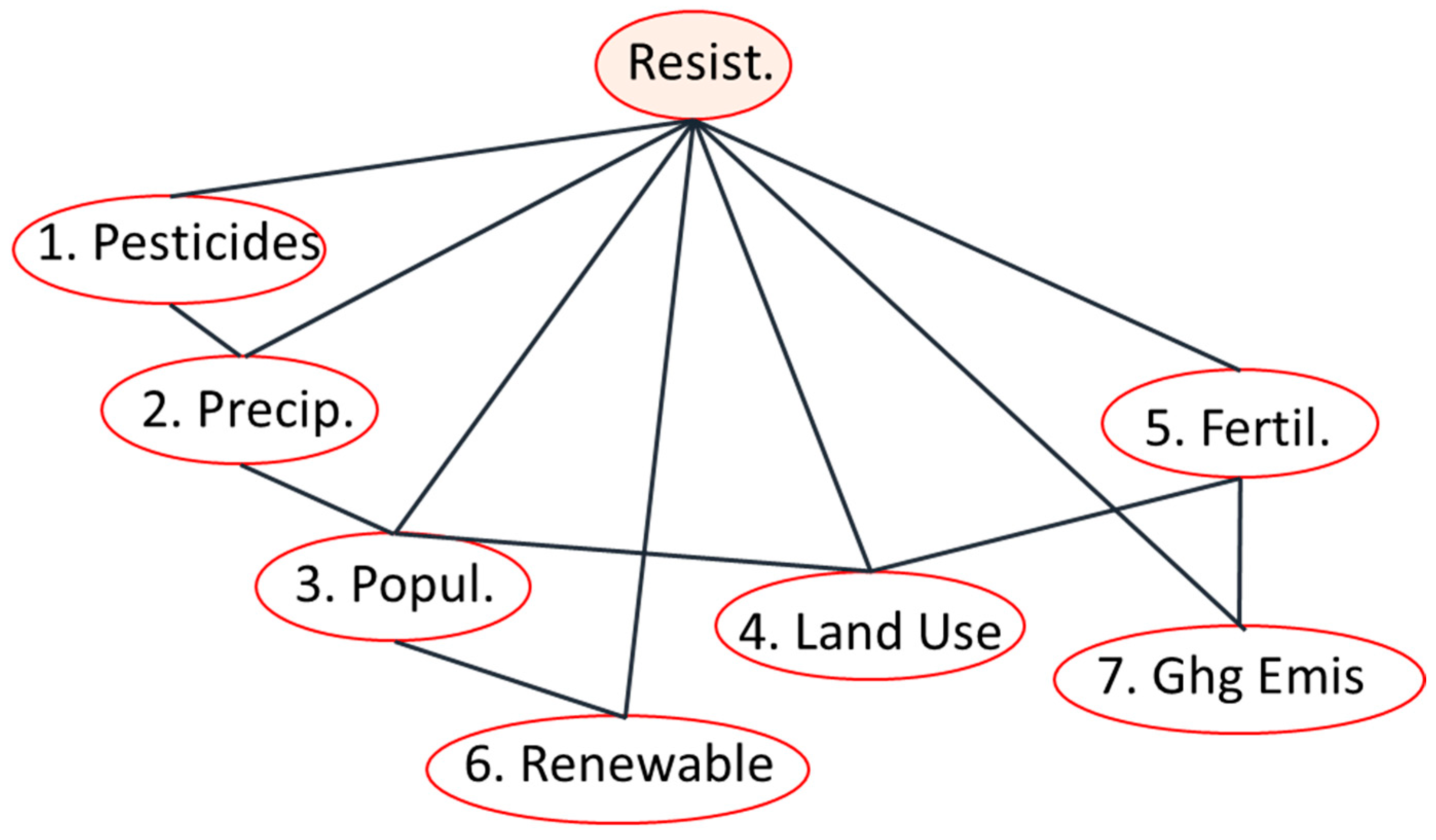
3.2.1. Structure Learning and Robustness of the Bayesian Network Analysis
3.2.2. Conditional Probability Distributions (CPDs) and Predictive Insights
3.2.3. Network-Wide Associations with AMR: Complex Pathways and Environmental Context
4. Discussion
4.1. Limitations and Future Research
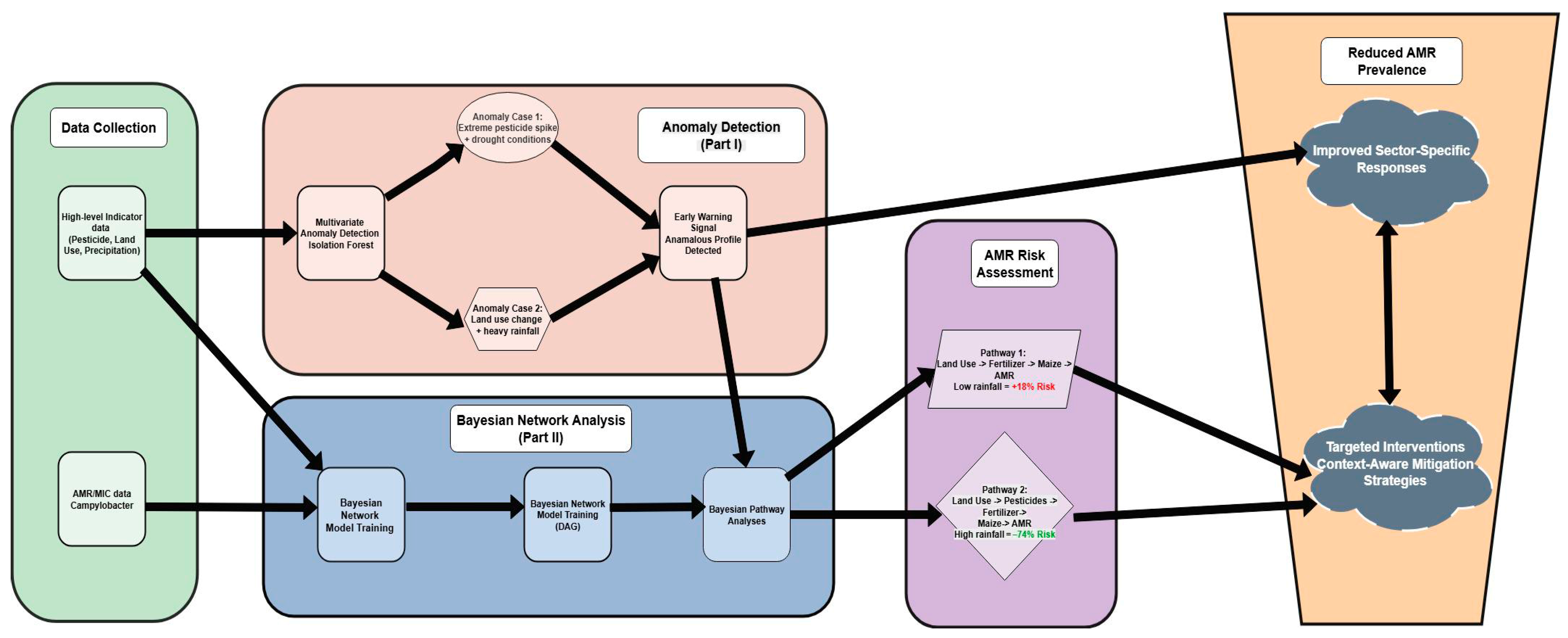
4.2. Towards a Proactive Early-Warning System for AMR Surveillance
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AMR | Antimicrobial resistance |
| ARG | Antimicrobial resistance gene |
| AUC | Area under the curve |
| BIC | Bayesian information criterion |
| BN | Bayesian network |
| CFU | Colony forming unit |
| CPD | Conditional probability distribution |
| EFSA | European Food Safety Authority |
| ECOFF | Epidemiological cut-off |
| EUCAST | European Committee on Antimicrobial Susceptibility Testing |
| FAOSTAT | Food and Agriculture Organization Statistical Database |
| F1-score | F-measure (harmonic mean of precision and recall) |
| GNB | Generalized naive Bayes |
| HPC | Hill climbing (algorithm) |
| KL Divergence | Kullback–Leibler divergence |
| KSVC | Kernel support vector classification |
| MIC | Minimum inhibitory concentration |
| ML | Machine learning |
| PGM | Probabilistic graphical model |
| ROC | Receiver operating characteristic |
| SMOTE | Synthetic minority over-sampling technique |
| XGBoost | Extreme gradient boosting |
References
- Wang, X.; Bouzembrak, Y.; Lansink, A.O.; van der Fels-Klerx, H.J. Application of Machine Learning to the Monitoring and Prediction of Food Safety: A Review. Compr. Rev. Food Sci. Food Saf. 2022, 21, 416–434. [Google Scholar] [CrossRef]
- Deng, X.; Cao, S.; Horn, A.L. Emerging Applications of Machine Learning in Food Safety. Annu. Rev. Food Sci. Technol. 2021, 12, 513–538. [Google Scholar] [CrossRef]
- Peters, D.P.C.; McVey, D.S.; Elias, E.H.; Pelzel-McCluskey, A.M.; Derner, J.D.; Burruss, N.D.; Schrader, T.S.; Yao, J.; Pauszek, S.J.; Lombard, J.; et al. Big Data–Model Integration and AI for Vector-Borne Disease Prediction. Ecosphere 2020, 11, e03157. [Google Scholar] [CrossRef]
- Du, H.; Zhao, Y.; Zhao, J.; Xu, S.; Lin, X.; Chen, Y.; Gardner, L.M.; Yang, H. ‘Frank’ Advancing Real-Time Infectious Disease Forecasting Using Large Language Models. Nat. Comput. Sci. 2025, 5, 467–480. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, M.; Long, S.W.; McDermott, P.F.; Olsen, R.J.; Olson, R.; Stevens, R.L.; Tyson, G.H.; Zhao, S.; Davis, J.J. Using Machine Learning To Predict Antimicrobial MICs and Associated Genomic Features for Nontyphoidal Salmonella. J. Clin. Microbiol. 2019, 57, e01260-18. [Google Scholar] [CrossRef] [PubMed]
- Maguire, F.; Rehman, M.A.; Carrillo, C.; Diarra, M.S.; Beiko, R.G. Identification of Primary Antimicrobial Resistance Drivers in Agricultural Nontyphoidal Salmonella Enterica Serovars by Using Machine Learning. mSystems 2019, 4, 10.1128/msystems.00211-19. [Google Scholar] [CrossRef]
- Resci, I.; Zavatta, L.; Piva, S.; Mondo, E.; Albertazzi, S.; Nanetti, A.; Bortolotti, L.; Cilia, G. Predictive Statistical Models for Monitoring Antimicrobial Resistance Spread in the Environment Using Apis mellifera (L. 1758) Colonies. Environ. Res. 2024, 248, 118365. [Google Scholar] [CrossRef]
- Collignon, P.; Beggs, J.J.; Walsh, T.R.; Gandra, S.; Laxminarayan, R. Anthropological and Socioeconomic Factors Contributing to Global Antimicrobial Resistance: A Univariate and Multivariable Analysis. Lancet Planet. Health 2018, 2, e398–e405. [Google Scholar] [CrossRef]
- Kim, J.I.; Maguire, F.; Tsang, K.K.; Gouliouris, T.; Peacock, S.J.; McAllister, T.A.; McArthur, A.G.; Beiko, R.G. Machine Learning for Antimicrobial Resistance Prediction: Current Practice, Limitations, and Clinical Perspective. Clin. Microbiol. Rev. 2022, 35, e00179-21. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2013; ISBN 978-1-4398-4095-5. [Google Scholar]
- Kaakoush, N.O.; Castaño-Rodríguez, N.; Mitchell, H.M.; Man, S.M. Global Epidemiology of Campylobacter Infection. Clin. Microbiol. Rev. 2015, 28, 687–720. [Google Scholar] [CrossRef]
- Igwaran, A.; Okoh, A.I. Human Campylobacteriosis: A Public Health Concern of Global Importance. Heliyon 2019, 5, e02814. [Google Scholar] [CrossRef]
- Myintzaw, P.; Jaiswal, A.K.; Jaiswal, S. A Review on Campylobacteriosis Associated with Poultry Meat Consumption. Food Rev. Int. 2023, 39, 2107–2121. [Google Scholar] [CrossRef]
- European Food Safety Authority (EFSA); European Centre for Disease Prevention and Control (ECDC). The European Union One Health 2023 Zoonoses report. EFSA J. 2024, 22, e9106. Available online: https://efsa.onlinelibrary.wiley.com/doi/full/10.2903/j.efsa.2024.9106 (accessed on 4 September 2025). [PubMed]
- Sproston, E.L.; Wimalarathna, H.M.L.; Sheppard, S.K. Trends in Fluoroquinolone Resistance in Campylobacter. Microb. Genom. 2018, 4, e000198. [Google Scholar] [CrossRef] [PubMed]
- Signorini, M.L.; Rossler, E.; Díaz David, D.C.; Olivero, C.R.; Romero-Scharpen, A.; Soto, L.P.; Astesana, D.M.; Berisvil, A.P.; Zimmermann, J.A.; Fusari, M.L.; et al. Antimicrobial Resistance of Thermotolerant Campylobacter Species Isolated from Humans, Food-Producing Animals, and Products of Animal Origin: A Worldwide Meta-Analysis. Microb. Drug Resist. 2018, 24, 1174–1190. [Google Scholar] [CrossRef] [PubMed]
- Van Boeckel, T.P.; Brower, C.; Gilbert, M.; Grenfell, B.T.; Levin, S.A.; Robinson, T.P.; Teillant, A.; Laxminarayan, R. Global Trends in Antimicrobial Use in Food Animals. Proc. Natl. Acad. Sci. USA 2015, 112, 5649–5654. [Google Scholar] [CrossRef]
- Wieczorek, K.; Osek, J. Antimicrobial Resistance Mechanisms among Campylobacter. Biomed. Res. Int. 2013, 2013, 340605. [Google Scholar] [CrossRef]
- EFSA Panel on Biological Hazards (BIOHAZ); Koutsoumanis, K.; Allende, A.; Alvarez-Ordóñez, A.; Bolton, D.; Bover-Cid, S.; Davies, R.; De Cesare, A.; Herman, L.; Hilbert, F.; et al. Update and Review of Control Options for Campylobacter in Broilers at Primary Production. EFSA J. 2020, 18, e06090. [Google Scholar] [CrossRef]
- Dai, L.; Sahin, O.; Grover, M.; Zhang, Q. New and Alternative Strategies for the Prevention, Control, and Treatment of Antibiotic-Resistant Campylobacter. Transl. Res. 2020, 223, 76–88. [Google Scholar] [CrossRef]
- European Food Safety Authority. European Centre for Disease Prevention and Control The European Union Summary Report on Antimicrobial Resistance in Zoonotic and Indicator Bacteria from Humans, Animals and Food in 2022–2023. EFSA J. 2025, 23, e9237. [Google Scholar] [CrossRef]
- Robinson, T.P.; Bu, D.P.; Carrique-Mas, J.; Fèvre, E.M.; Gilbert, M.; Grace, D.; Hay, S.I.; Jiwakanon, J.; Kakkar, M.; Kariuki, S.; et al. Antibiotic Resistance Is the Quintessential One Health Issue. Trans. R Soc. Trop. Med. Hyg. 2016, 110, 377–380. [Google Scholar] [CrossRef] [PubMed]
- McEwen, S.A.; Collignon, P.J. Antimicrobial Resistance: A One Health Perspective. Microbiol. Spectr. 2018, 6, 10.1128/microbiolspec.arba-0009–2017. [Google Scholar] [CrossRef] [PubMed]
- Berendonk, T.U.; Manaia, C.M.; Merlin, C.; Fatta-Kassinos, D.; Cytryn, E.; Walsh, F.; Bürgmann, H.; Sørum, H.; Norström, M.; Pons, M.-N.; et al. Tackling Antibiotic Resistance: The Environmental Framework. Nat. Rev. Microbiol. 2015, 13, 310–317. [Google Scholar] [CrossRef] [PubMed]
- Csorba, S.; Vribék, K.; Farkas, M.; Süth, M.; Strang, O.; Zentai, A.; Farkas, Z. Data-Driven Early Warning Approach for Antimicrobial Resistance Prediction–Anomaly Detection Based on High-Level Indicators. Vet. Sci. 2025, 12, 935. [Google Scholar] [CrossRef]
- Zhang, Y.; Kuang, F.; Liu, C.; Ma, K.; Liu, T.; Zhao, M.; Lv, G.; Huang, H. Contamination and Health Risk Assessment of Multiple Mycotoxins in Edible and Medicinal Plants. Toxins 2023, 15, 209. [Google Scholar] [CrossRef]
- Sible, C.N.; Kent, A.D.; Margenot, A.J.; Below, F.E. Long-Term Continuous Maize: Impacts on the Soil Microbiome and Implications for Residue Management. Soil Sci. Soc. Am. J. 2024, 88, 1109–1126. [Google Scholar] [CrossRef]
- Wang, P.; Xie, W.; Ding, L.; Zhuo, Y.; Gao, Y.; Li, J.; Zhao, L. Effects of Maize–Crop Rotation on Soil Physicochemical Properties, Enzyme Activities, Microbial Biomass and Microbial Community Structure in Southwest China. Microorganisms 2023, 11, 2621. [Google Scholar] [CrossRef]
- Yang, T.; Lupwayi, N.; Marc, S.-A.; Siddique, K.H.M.; Bainard, L.D. Anthropogenic Drivers of Soil Microbial Communities and Impacts on Soil Biological Functions in Agroecosystems. Glob. Ecol. Conserv. 2021, 27, e01521. [Google Scholar] [CrossRef]
- Kurenbach, B.; Marjoshi, D.; Amábile-Cuevas, C.F.; Ferguson, G.C.; Godsoe, W.; Gibson, P.; Heinemann, J.A. Sublethal Exposure to Commercial Formulations of the Herbicides Dicamba, 2,4-Dichlorophenoxyacetic Acid, and Glyphosate Cause Changes in Antibiotic Susceptibility in Escherichia Coli and Salmonella Enterica Serovar Typhimurium. mBio 2015, 6, 10.1128/mbio.00009-15. [Google Scholar] [CrossRef]
- Qiu, D.; Ke, M.; Zhang, Q.; Zhang, F.; Lu, T.; Sun, L.; Qian, H. Response of Microbial Antibiotic Resistance to Pesticides: An Emerging Health Threat. Sci. Total Environ. 2022, 850, 158057. [Google Scholar] [CrossRef]
- MacFadden, D.R.; McGough, S.F.; Fisman, D.; Santillana, M.; Brownstein, J.S. Antibiotic Resistance Increases with Local Temperature. Nat. Clim. Change 2018, 8, 510–514. [Google Scholar] [CrossRef]
- Burnham, J.P. Climate Change and Antibiotic Resistance: A Deadly Combination. Ther. Adv. Infect. Dis. 2021, 8, 2049936121991374. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Chen, X.; Jin, J.; Guo, B.; Qiu, G.; Wang, X.; Zhou, H.; Li, H. Effects of Nitrogen Fertilization on Antibiotic Resistance Gene Spread from Soil to Floodwater in Paddy Fields. Environ. Res. 2025, 274, 121345. [Google Scholar] [CrossRef] [PubMed]
- Leonard, A.F.C.; Zhang, L.; Balfour, A.J.; Garside, R.; Gaze, W.H. Human Recreational Exposure to Antibiotic Resistant Bacteria in Coastal Bathing Waters. Environ. Int. 2015, 82, 92–100. [Google Scholar] [CrossRef] [PubMed]
- Grenni, P.; Ancona, V.; Barra Caracciolo, A. Ecological Effects of Antibiotics on Natural Ecosystems: A Review. Microchem. J. 2018, 136, 25–39. [Google Scholar] [CrossRef]
- Fu, C.; Qin, Y.; Xiang, Q.; Qiao, M.; Zhu, Y. pH Drives the Spatial Variation of Antibiotic Resistance Gene Profiles in Riparian Soils at a Watershed Scale. Environ. Pollut. 2023, 326, 121486. [Google Scholar] [CrossRef]
- Tilman, D.; Balzer, C.; Hill, J.; Befort, B.L. Global Food Demand and the Sustainable Intensification of Agriculture. Proc. Natl. Acad. Sci. USA 2011, 108, 20260–20264. [Google Scholar] [CrossRef]
- van Buuren, S.; Groothuis-Oudshoorn, K. Mice: Multivariate Imputation by Chained Equations in R. J. Stat. Softw. 2011, 45, 1–67. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Szántai, T.; Kovács, E. Hypergraphs as a Mean of Discovering the Dependence Structure of a Discrete Multivariate Probability Distribution. Ann. Oper. Res. 2012, 193, 71–90. [Google Scholar] [CrossRef]
- Kovács, E.A.; Ország, A.; Pfeifer, D.; Benczúr, A. Generalized Naive Bayes. arXiv 2024, arXiv:2408.15923. [Google Scholar] [CrossRef]
- Jensen, F.V.; Nielsen, T.D. Bayesian Networks and Decision Graphs, 2nd ed.; Information Science and Statistics; Springer: New York, NY, USA, 2007; ISBN 978-0-387-68281-5. [Google Scholar]
- Ankan, A.; Textor, J. Pgmpy: A Python Toolkit for Bayesian Networks. J. Mach. Learn. Res. 2023, 25, 1–8. [Google Scholar]
- Toklu-Alicli, B.; Durmus, T.; Bozkurt, M. The Impact of Global Climate Change on Marine Zooplankton. In Ecological Dynamics in the Face of Climate Change; Dogruoz Gungor, N., Arslan Aydogdu, E.O., Eds.; Nobel Tip Kitabevleri: Istanbul, Turkey, 2024; pp. 119–131. ISBN 978-605-335-925-8. [Google Scholar]
- Wang, L.; Gu, X.; Hui, K.; Yu, T.; Yuan, Y.; Chen, G.; Tan, W. Interactions between Antibiotic Resistance Genes and Soil Environmental Factors: Coupling, Antagonism, and Synergism. Emerg. Contam. 2025, 11, 100578. [Google Scholar] [CrossRef]
- Li, X.; Bickel, S.; Wicaksono, W.A.; Lin, X.; Berg, G.; Zhu, Y. Unraveling Antibiotic Resistance Dynamics at the Soil–Plant Interface under Climate Change for One Health. One Health Adv. 2025, 3, 16. [Google Scholar] [CrossRef]
- Jori, F.; Hernandez-Jover, M.; Magouras, I.; Dürr, S.; Brookes, V.J. Wildlife–Livestock Interactions in Animal Production Systems: What Are the Biosecurity and Health Implications? Anim. Fron. 2021, 11, 8–19. [Google Scholar] [CrossRef]
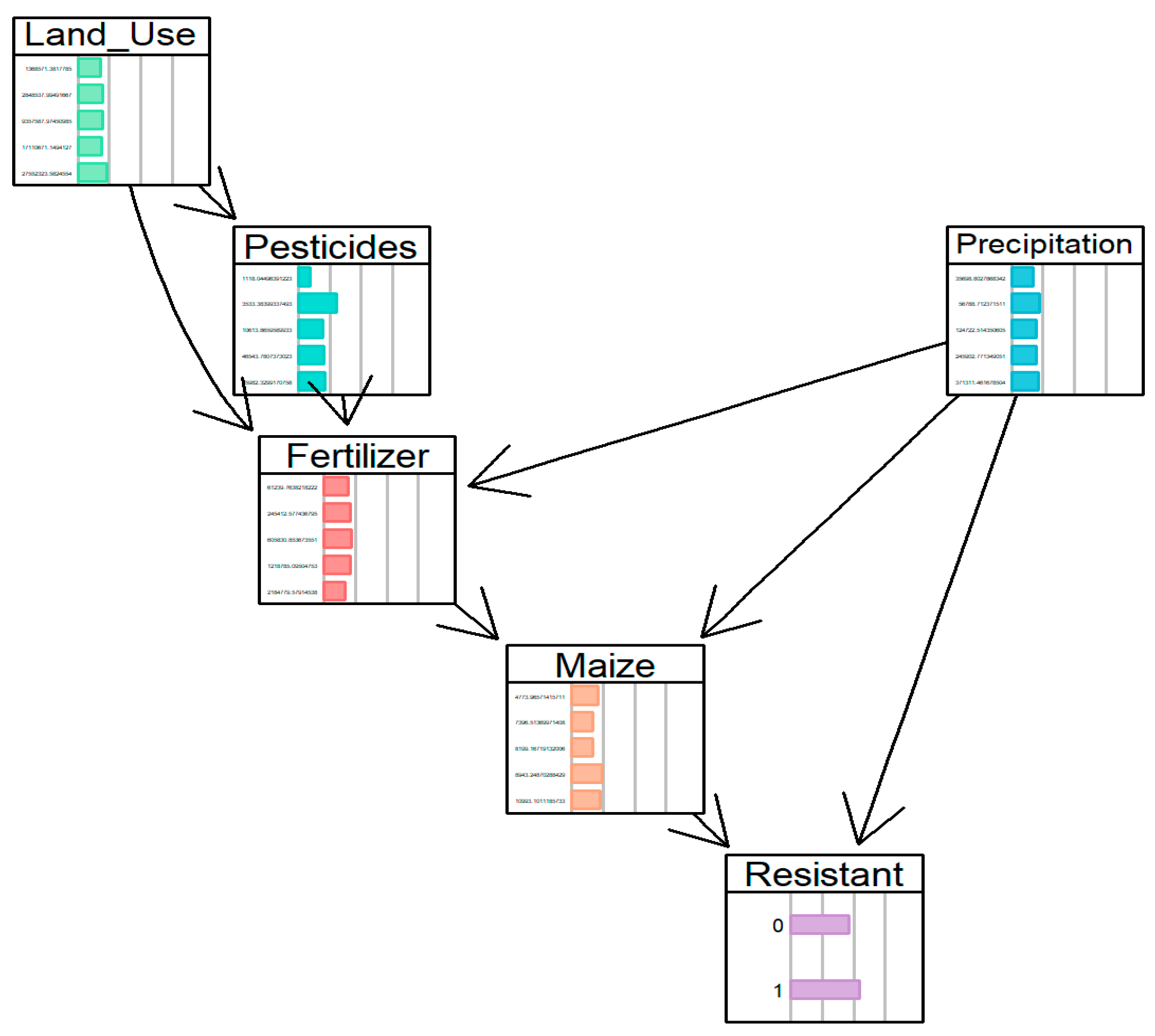
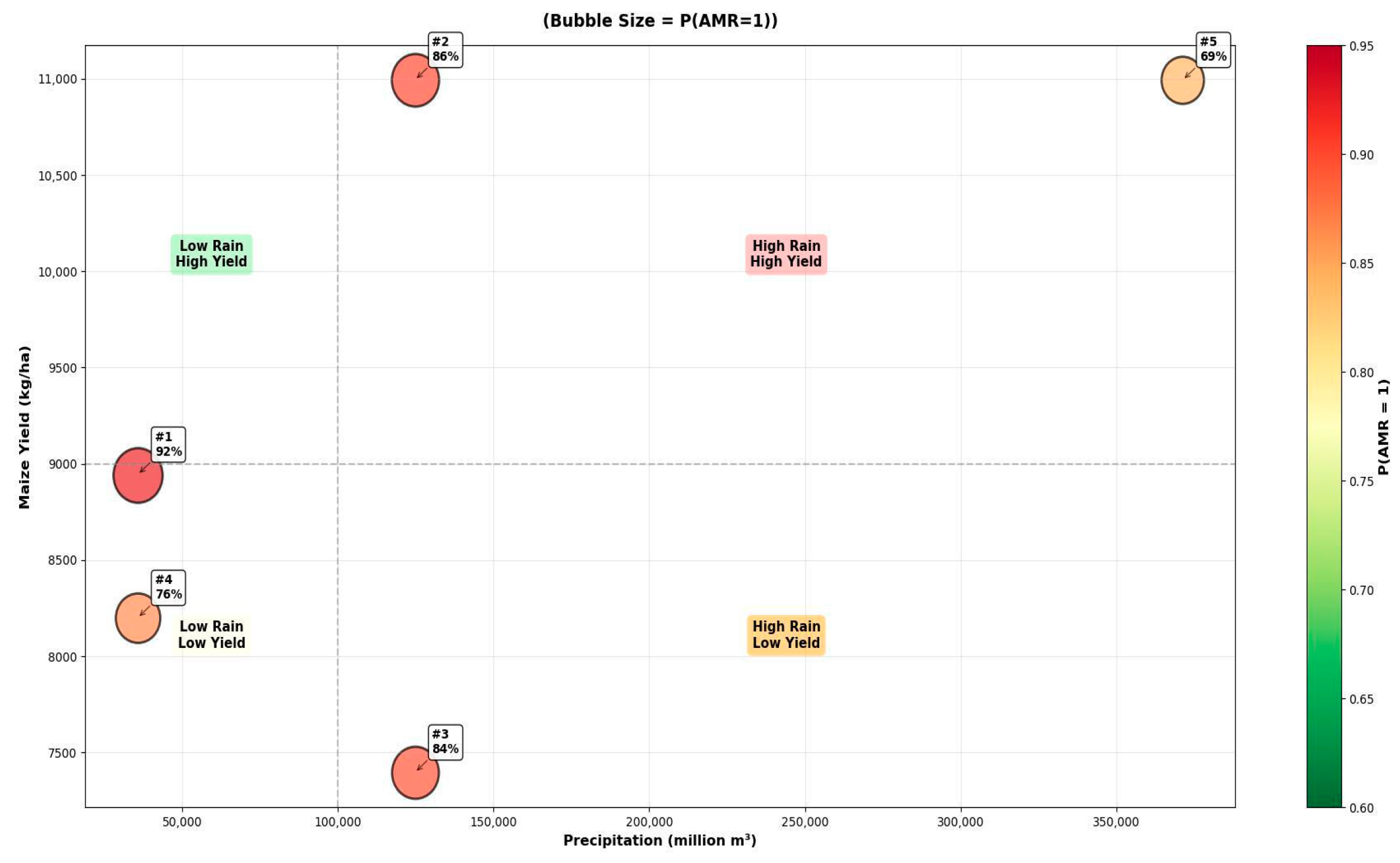
| Rank | P (Resistant = 1) | Maize Yield (kg/ha) | Precipitation (Million m3) | Interpreted AMR Pathway |
|---|---|---|---|---|
| 1 | 0.925 | Moderate–High (8943) | Low (35,698) | Selection Pressure in Water-Stressed Environments |
| 2 | 0.856 | High (10,993) | High (124,722) | Runoff-Mediated Dissemination |
| 3 | 0.840 | Low (7396) | High (124,722) | Environmental Spread Independent of Yield |
| 4 | 0.757 | Medium (8199) | Low (35,698) | Baseline Agricultural Selection Pressure |
| 5 | 0.687 | High (10,993) | Very High (371,311) | Saturated System with High Dissemination |
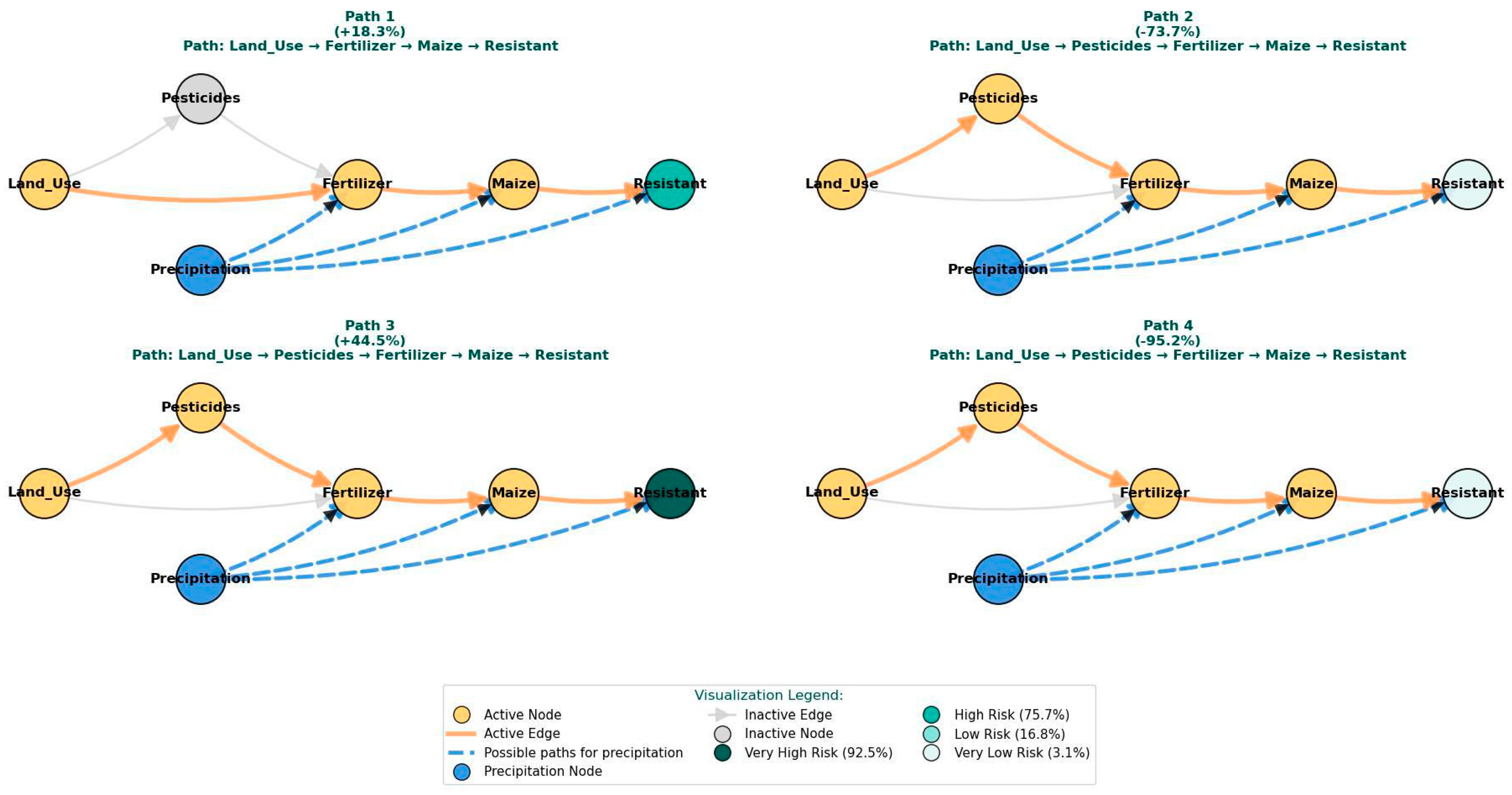
| Pathway | Land Use Intervention | Key Effects | Precipitation Role |
|---|---|---|---|
| Baseline | - | - | - |
| Path 1 | 1.37 M→2.85 M | Fert: 61 K→245 K Maize: 5 K→8 K | Low precipitation enables selection pressure |
| Path 2 | 2.85 M→9.36 M | Pest: 4 K→11 K Fert: 245 K→606 K Maize: 8 K→11 K | High precipitation drives runoff-mediated dilution |
| Path 3 | 9.36 M→17.11 M | Pest: 11 K→47 K Fert: 606 K→1.22 M Maize: 11 K→9 K | Moderate precipitation optimizes environmental persistence |
| Path 4 | 17.11 M→27.55 M | Pest: 47 K→66 K Fert: 1.22 M→2.18 M Maize: 9 K→7 K | Very high precipitation causes system flushing and dilution |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Csorba, S.; Vribék, K.; Farkas, M.; Kovács, E.A.; Pfeifer, D.; Süth, M.; Strang, O.; Zentai, A.; Farkas, Z. Early-Warning System for Antimicrobial Resistance in Campylobacter in the Broiler Production Chain from High-Level Indicators—A Graph-Based Machine Learning and Bayesian Approach. Vet. Sci. 2025, 12, 1080. https://doi.org/10.3390/vetsci12111080
Csorba S, Vribék K, Farkas M, Kovács EA, Pfeifer D, Süth M, Strang O, Zentai A, Farkas Z. Early-Warning System for Antimicrobial Resistance in Campylobacter in the Broiler Production Chain from High-Level Indicators—A Graph-Based Machine Learning and Bayesian Approach. Veterinary Sciences. 2025; 12(11):1080. https://doi.org/10.3390/vetsci12111080
Chicago/Turabian StyleCsorba, Szilveszter, Krisztián Vribék, Máté Farkas, Edith Alice Kovács, Dániel Pfeifer, Miklós Süth, Orsolya Strang, Andrea Zentai, and Zsuzsa Farkas. 2025. "Early-Warning System for Antimicrobial Resistance in Campylobacter in the Broiler Production Chain from High-Level Indicators—A Graph-Based Machine Learning and Bayesian Approach" Veterinary Sciences 12, no. 11: 1080. https://doi.org/10.3390/vetsci12111080
APA StyleCsorba, S., Vribék, K., Farkas, M., Kovács, E. A., Pfeifer, D., Süth, M., Strang, O., Zentai, A., & Farkas, Z. (2025). Early-Warning System for Antimicrobial Resistance in Campylobacter in the Broiler Production Chain from High-Level Indicators—A Graph-Based Machine Learning and Bayesian Approach. Veterinary Sciences, 12(11), 1080. https://doi.org/10.3390/vetsci12111080






