Genomic Selection for Economic Traits in Inner Mongolia Cashmere Goats by Integrating GWAS Prior Information
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Source of Experimental Animals
2.2. Sources of Phenotypic and Genotypic Data
2.3. Model for Genomic Selection by Integrating Prior GWAS Information
2.4. Evaluation for Accuracy of Genomic Breeding Value
3. Results
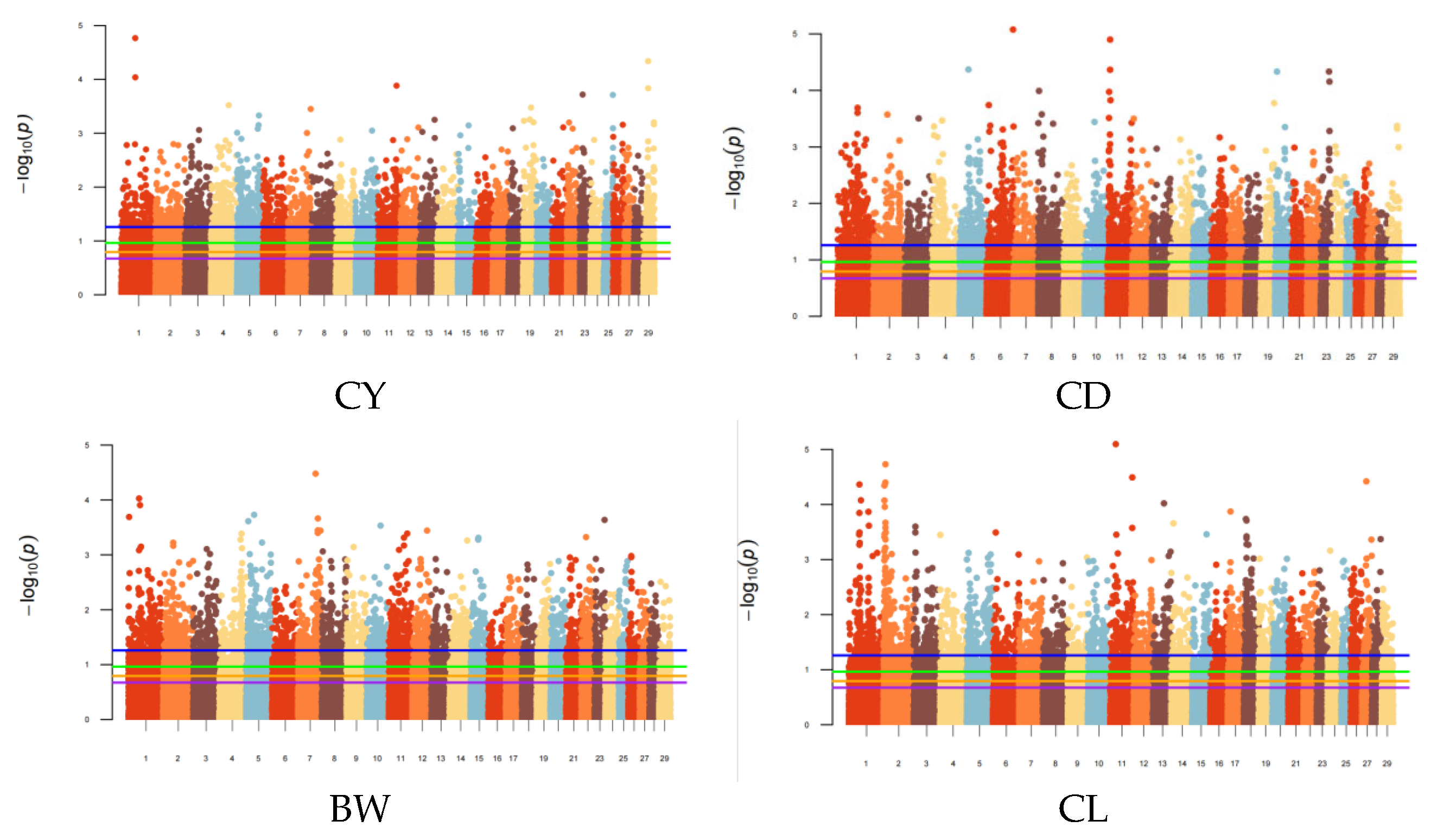
3.1. Statistics of Significant SNPs Based on Different Prior Marker Information
3.2. Estimation of Variance Components and Genetic Parameters for Economic Traits Based on Prior Marker Information
3.2.1. Estimation of Variance Components and Genetic Parameters for Cashmere Yield Based on Prior Marker Information
3.2.2. Estimation of Variance Components and Genetic Parameters for Cashmere Diameter Based on Prior Marker Information
3.2.3. Estimation of Variance Components and Genetic Parameters for Body Weight Based on Prior Marker Information
3.2.4. Estimation of Variance Components and Genetic Parameters for Cashmere Length Based on Prior Marker Information
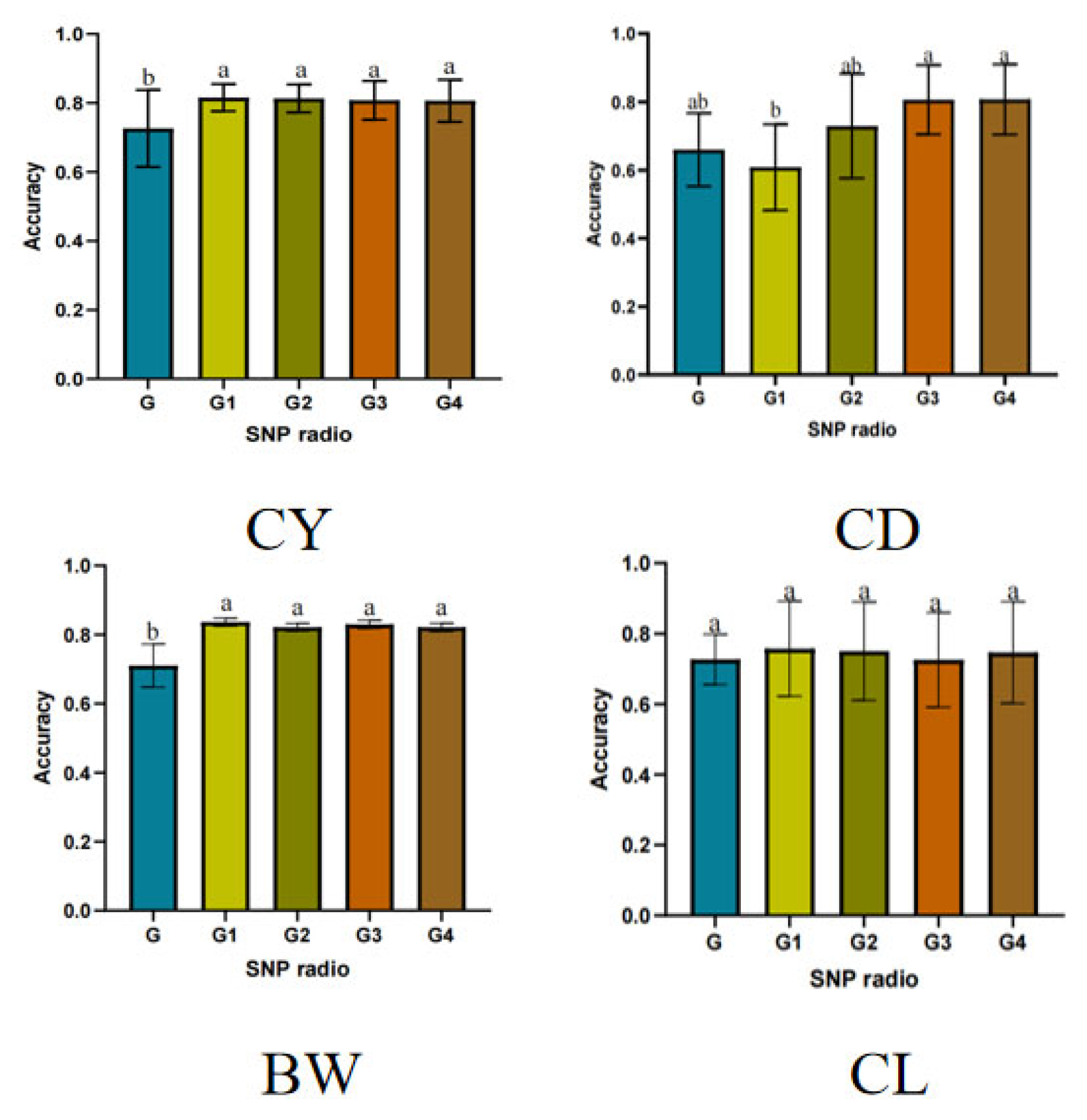
3.3. Evaluation of Genomic Prediction Accuracy for Economic Traits Based on Prior Marker Information
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IMCGs | Inner Mongolia cashmere goats |
| GWAS | Genome-Wide Association Study |
| SNP | single nucleotide polymorphism |
| CY | cashmere yield |
| CD | cashmere diameter |
| BW | body weight |
| CL | cashmere length |
| GEBV | Genomic Estimated Breeding Value |
| GS | Genomic Selection |
References
- Rong, Y.; Wang, X.; Na, Q.; Ao, X.; Xia, Q.; Guo, F.; Han, M.; Ma, R.; Sahng, F.; Liu, Y.; et al. Genome-wide association study for cashmere traits in Inner Mongolia cashmere goat population reveals new candidate genes and haplotypes. BMC Genom. 2024, 25, 658. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.Y.; Xu, Q.; He, Y.X.; Xi, H.J.; Liu, Y.F.; Zhang, T.; Li, J.; Zhang, Y.; Wang, R.; Lv, Q.; et al. Comparison of genomic prediction methods for early growth traits of Inner Mongolia cashmere goats based on multi trait models. Yi Chuan 2024, 46, 421–430. [Google Scholar] [CrossRef] [PubMed]
- Schneider, H.; Heise, J.; Tetens, J.; Thaller, G.; Wellmann, R.; Bennewitz, J. Genomic dominance variance analysis of health and milk production traits in German Holstein cattle. J. Anim. Breed. Genet. 2023, 140, 390–399. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Baccino, C.A.; Lourenco, D.A.L.; Miller, S.P.; Cantet, R.J.C.; Vitezica, Z.G. Estimating dominance genetic variances for growth traits in American Angus males using genomic models. J. Anim. Sci. 2020, 98, skz384. [Google Scholar] [CrossRef]
- Alipanah, M.; Roudbari, Z.; Momen, M.; Esmailizadeh, A. Impact of inclusion non-additive effects on genome-wide association and variance’s components in Scottish black sheep. Anim. Biotechnol. 2023, 34, 3765–3773. [Google Scholar] [CrossRef]
- Li, M.; Hall, T.; MacHugh, D.E.; Chen, L.; Garrick, D.; Wang, L.; Zhao, F. A novel machine learning approach for effectively capturing nonadditive effects in genomic prediction. Brief. Bioinform. 2024, 26, bbae683. [Google Scholar] [CrossRef]
- Mohammadpanah, M.; Ayatollahi Mehrgardi, A.; Gilbert, H.; Larzul, C.; Mercat, M.J.; Esmailizadeh, A.; Momen, M.; Tusell, L. Genic and non-genic SNP contributions to additive and dominance genetic effects in purebred and crossbred pig traits. Sci. Rep. 2022, 12, 3795. [Google Scholar] [CrossRef]
- Srihi, H.; Noguera, J.L.; Topayan, V.; Martín de Hijas, M.; Ibañez-Escriche, N.; Casellas, J.; Vázquez-Gómez, M.; Martínez-Castillero, M.; Rosas, J.P.; Varona, L. Additive and Dominance Genomic Analysis for Litter Size in Purebred and Crossbred Iberian Pigs. Genes 2021, 13, 12. [Google Scholar] [CrossRef]
- Bhuiyan, M.S.A.; Kim, Y.K.; Lee, D.H.; Chung, Y.; Lee, D.J.; Kang, J.M.; Lee, S. Evaluation of non-additive genetic effects on carcass and meat quality traits in Korean Hanwoo cattle using genomic models. Animal 2024, 18, 101152. [Google Scholar] [CrossRef]
- Sadeghi, S.A.T.; Rokouei, M.; Valleh, M.V.; Abbasi, M.A.; Faraji-Arough, H. Estimation of additive and non-additive genetic variance component for growth traits in Adani goats. Trop. Anim. Health Prod. 2020, 52, 733–742. [Google Scholar] [CrossRef]
- Mei, Q.; Vitezica, Z.G.; Li, J.; Zhao, S.; Legarra, A.; Xiang, T. Impacts of additive, dominance, and inbreeding depression effects on genomic evaluation by combining two SNP chips in Canadian Yorkshire pigs bred in China. Genet. Sel. Evol. 2022, 54, 69. [Google Scholar] [CrossRef]
- Gebreyesus, G.; Bovenhuis, H.; Lund, M.S.; Poulsen, N.A.; Sun, D.; Buitenhuis, B. Reliability of genomic prediction for milk fatty acid composition by using a multi-population reference and incorporating GWAS results. Genet. Sel. Evol. 2019, 51, 16. [Google Scholar] [CrossRef] [PubMed]
- van den Berg, I.; Boichard, D.; Lund, M.S. Sequence variants selected from a multi-breed GWAS can improve the reliability of genomic predictions in dairy cattle. Genet. Sel. Evol. 2016, 48, 83. [Google Scholar] [CrossRef]
- van den Berg, I.; Ho, P.N.; Nguyen, T.V.; Haile-Mariam, M.; MacLeod, I.M.; Beatson, P.R.; O’connor, E.; Pryce, J.E. GWAS and genomic prediction of milk urea nitrogen in Australian and New Zealand dairy cattle. Genet. Sel. Evol. 2022, 54, 15. [Google Scholar] [CrossRef] [PubMed]
- Gao, N.; Li, J.; He, J.; Xiao, G.; Luo, Y.; Zhang, H.; Chen, H.; Zhang, Z. Improving accuracy of genomic prediction by genetic architecture based priors in a Bayesian model. BMC Genet. 2015, 16, 120. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.; Zhang, W.; Gao, N.; Wei, C.; Wu, X.; Si, J.; Gao, Y.; Li, J.; Yin, T.; Zhang, Z. Integrating large-scale meta-analysis of genome-wide association studies improve the genomic prediction accuracy for combined pig populations. J. Anim. Breed. Genet. 2025, 142, 223–236. [Google Scholar] [CrossRef]
- Haque, M.A.; Jang, E.B.; Lee, H.D.; Shin, D.H.; Jang, J.H.; Kim, J.J. Performance of weighted genomic BLUP and Bayesian methods for Hanwoo carcass traits. Trop. Anim. Health Prod. 2025, 57, 38. [Google Scholar] [CrossRef]
- Xu, Q. Genome-Wide Association Study and Design of a Low-Density SNP Chip for Important Traits in Inner Mongolia Cashmere Goats. Ph.D. Thesis, Inner Mongolia Agricultural University, Hohhot, China, 2024. [Google Scholar]
- Wang, F. Design of a Goat SNP Chip and Genome-Wide Association Study and Genomic Selection of Important Economic Traits in Inner Mongolia Cashmere Goats. Ph.D. Thesis, Inner Mongolia Agricultural University, Hohhot, China, 2021. [Google Scholar]
- Vanraden, P.M. Efficient methods to compute genomic predictions. J. Dairy Sci. 2008, 91, 4414–4423. [Google Scholar] [CrossRef]
- Vitezica, Z.G.; Varona, L.; Legarra, A. On the additive and dominant variance and covariance of individuals within the genomic selection scope. Genetics 2013, 195, 1223–1230. [Google Scholar] [CrossRef]
- McHugh, M.L. Multiple comparison analysis testing in ANOVA. Biochem. Med. 2011, 21, 203–209. [Google Scholar] [CrossRef]
- Berkman, S.J.; Roscoe, E.M.; Bourret, J.C. Comparing self-directed methods for training staff to create graphs using Graphpad Prism. J. Appl. Behav. Anal. 2019, 52, 188–204. [Google Scholar] [CrossRef]
- Nani, J.P.; Rezende, F.M.; Peñagaricano, F. Predicting male fertility in dairy cattle using markers with large effect and functional annotation data. BMC Genom. 2019, 20, 258. [Google Scholar] [CrossRef]
- Gao, N.; Teng, J.; Ye, S.; Yuan, X.; Huang, S.; Zhang, H.; Zhang, X.; Li, J.; Zhang, Z. Genomic Prediction of Complex Phenotypes Using Genic Similarity Based Relatedness Matrix. Front. Genet. 2018, 9, 364. [Google Scholar] [CrossRef]
- Ni, G.; Cavero, D.; Fangmann, A.; Erbe, M.; Simianer, H. Whole-genome sequence-based genomic prediction in laying chickens with different genomic relationship matrices to account for genetic architecture. Genet. Sel. Evol. 2017, 49, 8. [Google Scholar] [CrossRef]
- Song, H.; Hu, H. Strategies to improve the accuracy and reduce costs of genomic prediction in aquaculture species. Evol. Appl. 2022, 15, 578–590. [Google Scholar] [CrossRef] [PubMed]
- Li, C. Construction and Application of a Genomic Selection Comprehensive Breeding Index for Plateau Merino Sheep. Ph.D. Thesis, Chinese Academy of Agricultural Sciences, Beijing, China, 2024. [Google Scholar]
- Yiga-Kibuuka, J.; Raphaka, K.; Monau, P.I.; Nsoso, S.J. Preliminary outcomes on phenotypic and genetic parameter estimates for body weight of indigenous Tswana goats in Botswana. Trop. Anim. Health Prod. 2024, 56, 333. [Google Scholar] [CrossRef] [PubMed]
- Li, W.H.; Li, G.Y.; Zhang, J.; Wang, X.J.; Zhang, A.W.; Zhao, J.T.; Wang, L.J.; Yang, J.F.; Luo, T.Z.; Shen, K.Z. Estimates of (co)variance components and phenotypic and genetic parameters of growth traits and wool traits in Alpine Merino sheep. J. Anim. Breed. Genet. 2022, 139, 351–365. [Google Scholar] [CrossRef]
- Ramos, Z.; Garrick, D.J.; Blair, H.T.; De Barbieri, I.; Ciappesoni, G.; Montossi, F.; Kenyon, P.R. Genetic and phenotypic relationships between ewe reproductive performance and wool and growth traits in Uruguayan Ultrafine Merino sheep. J. Anim. Sci. 2023, 101, skad071. [Google Scholar] [CrossRef]
- Ahmad, S.F.; Khan, N.N.; Chakraborty, D.; Rather, M.A.; Shanaz, S.; Alam, S.; Ganai, N.A. Estimation of (Co)Variance components and genetic parameters of fibre traits in Rambouillet sheep using multi-trait analysis. Trop. Anim. Health Prod. 2021, 53, 190. [Google Scholar] [CrossRef]
- Xi, H.J.; Li, J.Q.; Zhang, Y.J.; Wang, R.; Lv, Q.; Mei, B.; Wang, N.; Su, R.; Wang, Z. Effects of dominance on the accuracy of breeding value estimation for cashmere yield and cashmere fiber diameter in Inner Mongolia cashmere goats. Acta Vet. Zootech. Sin. 2025, 56, 571–581. [Google Scholar]
- Zhang, Y.; Zhuang, Z.; Liu, Y.; Huang, J.; Luan, M.; Zhao, X.; Dong, L.; Ye, J.; Yang, M.; Zheng, E.; et al. Genomic prediction based on preselected single-nucleotide polymorphisms from genome-wide association study and imputed whole-genome sequence data annotation for growth traits in Duroc pigs. Evol. Appl. 2024, 17, e13651. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhang, Y.; Zhou, F.; Yao, Z.; Zhan, Y.; Fan, Z.; Meng, X.; Zhang, Z.; Liu, L.; Yang, J.; et al. Increased Accuracy of Genomic Prediction Using Preselected SNPs from GWAS with Imputed Whole-Genome Sequence Data in Pigs. Animals 2023, 13, 3871. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Li, C.; Li, J.; Zhang, R.; An, X.; Yuan, C.; Guo, T.; Yue, Y. Genomic Selection for Weaning Weight in Alpine Merino Sheep Based on GWAS Prior Marker Information. Animals 2024, 14, 1904. [Google Scholar] [CrossRef] [PubMed]
- Mehrban, H.; Naserkheil, M.; Lee, D.H.; Cho, C.; Choi, T.; Park, M.; Ibáñez-Escriche, N. Genomic Prediction Using Alternative Strategies of Weighted Single-Step Genomic BLUP for Yearling Weight and Carcass Traits in Hanwoo Beef Cattle. Genes 2021, 12, 266. [Google Scholar] [CrossRef]
- de Las Heras-Saldana, S.; Lopez, B.I.; Moghaddar, N.; Park, W.; Park, J.E.; Chung, K.Y.; Lim, D.; Lee, S.H.; Shin, D.; van der Werf, J.H.J. Use of gene expression and whole-genome sequence information to improve the accuracy of genomic prediction for carcass traits in Hanwoo cattle. Genet. Sel. Evol. 2020, 52, 54. [Google Scholar] [CrossRef]
- Xu, L.; Gao, N.; Wang, Z.; Xu, L.; Liu, Y.; Chen, Y.; Xu, L.; Gao, X.; Zhang, L.; Gao, H.; et al. Incorporating Genome Annotation Into Genomic Prediction for Carcass Traits in Chinese Simmental Beef Cattle. Front. Genet. 2020, 11, 481. [Google Scholar] [CrossRef]
- Gao, N.; Martini, J.W.R.; Zhang, Z.; Yuan, X.; Zhang, H.; Simianer, H.; Li, J. Incorporating Gene Annotation into Genomic Prediction of Complex Phenotypes. Genetics 2017, 207, 489–501. [Google Scholar] [CrossRef]
- Wei, C.; Chang, C.; Zhang, W.; Ren, D.; Cai, X.; Zhou, T.; Shi, S.; Wu, X.; Si, J.; Yuan, X.; et al. Preselecting Variants from Large-Scale Genome-Wide Association Study Meta-Analyses Increases the Genomic Prediction Accuracy of Growth and Carcass Traits in Large White Pigs. Animals 2023, 13, 3746. [Google Scholar] [CrossRef]
- Ye, S.; Li, J.; Zhang, Z. Multi-omics-data-assisted genomic feature markers preselection improves the accuracy of genomic prediction. J. Anim. Sci. Biotechnol. 2020, 11, 109. [Google Scholar] [CrossRef]
- Shi, H.; Geng, H.; Yang, B.; Yin, Z.; Liu, Y. Integrating QTL and expression QTL of PigGTEx to improve the accuracy of genomic prediction for small population in Yorkshire pigs. Anim. Genet. 2025, 56, e70001. [Google Scholar] [CrossRef]
| Prior Marker Information | Matrix | r | τ | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Top 5% | G | 7684.90 | 2679.40 | 2639.60 | 25,396.30 | 0.200 ± 0.03 | 0.070 ± 0.01 | 0.339 | |
| G1 | 9064.44 | 1943.28 | 9.88 × 10−4 | 26,416.63 | 0.242 ± 0.05 | 0.052 ± 0.01 | 0.294 | 0.64 | |
| G2 | 6324.64 | 1.02 × 10−3 | 7542.55 | 27,746.20 | 0.152 ± 0.02 | 2.45 × 10−8 ± 0.00 | 0.333 | 0.36 | |
| Gt | 9672.55 | 2049.59 | 4.40 × 10−7 | 26,699.68 | 0.252 ± 0.04 | 0.053 ± 0.01 | 0.305 | ||
| Top 10% | G1 | 9670.59 | 1893.72 | 9.93 × 10−4 | 26,450.71 | 0.254 ± 0.04 | 0.050 ± 0.01 | 0.304 | 0.68 |
| G2 | 5490.67 | 1.77 × 10−3 | 8298.26 | 27,730.98 | 0.132 ± 0.02 | 4.26 × 10−8 ± 0.00 | 0.332 | 0.32 | |
| Gt | 10,288.58 | 2062.71 | 3.44 × 10−7 | 26,781.20 | 0.263 ± 0.03 | 0.053 ± 0.01 | 0.316 | ||
| Top 15% | G1 | 9929.96 | 2130.17 | 4.51 × 10−4 | 26,562.58 | 0.257 ± 0.04 | 0.055 ± 0.01 | 0.312 | 0.70 |
| G2 | 5049.34 | 1.20 × 10−3 | 8714.02 | 27,722.05 | 0.122 ± 0.01 | 2.89 × 10−8 ± 0.00 | 0.332 | 0.30 | |
| Gt | 10,453.66 | 2356.57 | 3.37 × 10−7 | 26,885.58 | 0.263 ± 0.03 | 0.059 ± 0.02 | 0.323 | ||
| Top 20% | G1 | 10,324.52 | 2208.65 | 4.93 × 10−4 | 26,710.11 | 0.263 ± 0.03 | 0.056 ± 0.02 | 0.319 | 0.71 |
| G2 | 5049.34 | 8.44 × 10−4 | 8714.02 | 27,722.05 | 0.121 ± 0.02 | 2.03 × 10−8 ± 0.00 | 0.332 | 0.29 | |
| Gt | 10,704.93 | 2511.09 | 4.03 × 10−7 | 27,012.14 | 0.266 ± 0.04 | 0.062 ± 0.02 | 0.329 |
| Prior Marker Information | Matrix | r | τ | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Top 5% | G | 0.145 | 0.013 | 0.027 | 0.317 | 0.290 ± 0.03 | 0.026 ± 0.01 | 0.368 | |
| G1 | 0.145 | 1.98 × 10−7 | 5.33 × 10−7 | 0.309 | 0.319 ± 0.05 | 4.37 × 10−7 ± 0.00 | 0.319 | 0.47 | |
| G2 | 0.124 | 0.038 | 0.036 | 0.338 | 0.231 ± 0.03 | 0.071 ± 0.02 | 0.369 | 0.53 | |
| Gt | 0.161 | 3.87 × 10−7 | 4.71 × 10−8 | 0.381 | 0.297 ± 0.02 | 7.14 × 10−7 ± 0.00 | 0.297 | ||
| Top 10% | G1 | 0.153 | 1.00 × 10−7 | 1.99 × 10−7 | 0.303 | 0.336 ± 0.04 | 2.19 × 10−7 ± 0.00 | 0.336 | 0.51 |
| G2 | 0.107 | 0.038 | 0.051 | 0.338 | 0.200 ± 0.01 | 0.071 ± 0.01 | 0.367 | 0.49 | |
| Gt | 0.316 | 4.60 × 10−7 | 1.30 × 10−5 | 0.228 | 0.580 ± 0.06 | 8.46 × 10−7 ± 0.00 | 0.581 | ||
| Top 15% | G1 | 0.161 | 1.02 × 10−7 | 1.03 × 10−7 | 0.303 | 0.346 ± 0.03 | 2.20 × 10−7 ± 0.01 | 0.347 | 0.55 |
| G2 | 0.094 | 0.040 | 0.060 | 0.338 | 0.177 ± 0.02 | 0.075 ± 0.02 | 0.365 | 0.45 | |
| Gt | 0.181 | 1.02 × 10−7 | 3.60 × 10−7 | 0.313 | 0.362 ± 0.03 | 2.06 × 10−7 ± 0.00 | 0.366 | ||
| Top 20% | G1 | 0.167 | 1.95 × 10−7 | 4.87 × 10−7 | 0.304 | 0.354 ± 0.04 | 4.14 × 10−7 ± 0.00 | 0.355 | 0.57 |
| G2 | 0.086 | 0.039 | 0.068 | 0.338 | 0.162 ± 0.01 | 0.073 ± 0.03 | 0.363 | 0.43 | |
| Gt | 0.187 | 1.70 × 10−7 | 3.73 × 10−7 | 0.315 | 0.367 ± 0.03 | 3.39 × 10−7 ± 0.00 | 0.373 |
| Prior Marker Information | Matrix | r | τ | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Top 5% | G | 3.13 | 0.16 | 4.14 | 10.82 | 0.171 ± 0.01 | 0.009 ± 0.01 | 0.407 | |
| G1 | 8.66 | 0.02 | 3.18 | 17.27 | 0.297 ± 0.03 | 6.85 × 10−4 ± 0.00 | 0.407 | 0.76 | |
| G2 | 2.38 | 0.35 | 10.31 | 17.12 | 0.079 ± 0.01 | 0.012 ± 0.01 | 0.432 | 0.24 | |
| Gt | 8.96 | 1.99 × 10−6 | 3.22 | 17.23 | 0.305 ± 0.03 | 6.77 × 10−8 ± 0.00 | 0.414 | ||
| Top 10% | G1 | 9.47 | 1.70 × 10−7 | 2.49 | 17.29 | 0.324 ± 0.04 | 5.81 × 10−9 ± 0.00 | 0.409 | 0.79 |
| G2 | 2.06 | 0.39 | 10.59 | 17.12 | 0.068 ± 0.01 | 0.013 ± 0.01 | 0.432 | 0.21 | |
| Gt | 9.56 | 1.17 × 10−6 | 2.83 | 17.24 | 0.323 ± 0.05 | 3.95 × 10−8 ± 0.00 | 0.418 | ||
| Top 15% | G1 | 9.96 | 7.13 × 10−7 | 2.36 | 17.27 | 0.337 ± 0.06 | 2.41 × 10−8 ± 0.00 | 0.416 | 0.81 |
| G2 | 1.85 | 0.43 | 10.75 | 17.11 | 0.061 ± 0.01 | 0.014 ± 0.01 | 0.432 | 0.19 | |
| Gt | 9.90 | 6.31 × 10−7 | 2.85 | 17.22 | 0.330 ± 0.05 | 2.11 × 10−8 ± 0.00 | 0.425 | ||
| Top 20% | G1 | 10.03 | 5.53 × 10−7 | 2.63 | 17.25 | 0.335 ± 0.05 | 1.85 × 10−8 ± 0.00 | 0.423 | 0.82 |
| G2 | 1.73 | 0.51 | 10.80 | 17.11 | 0.057 ± 0.01 | 0.017 ± 0.01 | 0.433 | 0.18 | |
| Gt | 9.83 | 3.36 × 10−7 | 3.23 | 17.21 | 0.324 ± 0.04 | 1.11 × 10−8 ± 0.00 | 0.431 |
| Prior Marker Information | Matrix | r | τ | ||||
|---|---|---|---|---|---|---|---|
| Top 5% | G | 0.092 | 0.0001 | 0.908 | 0.092 ± 0.01 | 0.092 | |
| G1 | 0.108 | 5.87 × 10−8 | 0.922 | 0.105 ± 0.02 | 0.105 | 0.66 | |
| G2 | 0.055 | 0.050 | 0.979 | 0.051 ± 0.01 | 0.097 | 0.34 | |
| Gt | 0.112 | 3.79 × 10−6 | 0.928 | 0.108 ± 0.03 | 0.108 | ||
| Top 10% | G1 | 0.112 | 4.87 × 10−8 | 0.922 | 0.108 ± 0.03 | 0.108 | 0.73 |
| G2 | 0.042 | 0.063 | 0.979 | 0.038 ± 0.01 | 0.097 | 0.27 | |
| Gt | 0.117 | 8.15 × 10−6 | 0.928 | 0.112 ± 0.02 | 0.112 | ||
| Top 15% | G1 | 0.116 | 4.79 × 10−8 | 0.925 | 0.111 ± 0.02 | 0.111 | 0.77 |
| G2 | 0.035 | 0.069 | 0.979 | 0.032 ± 0.01 | 0.096 | 0.23 | |
| Gt | 0.112 | 5.99 × 10−6 | 0.930 | 0.107 ± 0.02 | 0.107 | ||
| Top 20% | G1 | 0.120 | 4.71 × 10−8 | 0.927 | 0.114 ± 0.03 | 0.115 | 0.80 |
| G2 | 0.030 | 0.074 | 0.979 | 0.028 ± 0.01 | 0.092 | 0.20 | |
| Gt | 0.123 | 8.67 × 10−6 | 0.932 | 0.117 ± 0.03 | 0.105 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xi, H.; Xu, Q.; Yao, H.; Shen, Z.; Zhou, B.; Lv, Q.; Li, J.; Wang, R.; Zhang, Y.; Su, R.; et al. Genomic Selection for Economic Traits in Inner Mongolia Cashmere Goats by Integrating GWAS Prior Information. Vet. Sci. 2025, 12, 996. https://doi.org/10.3390/vetsci12100996
Xi H, Xu Q, Yao H, Shen Z, Zhou B, Lv Q, Li J, Wang R, Zhang Y, Su R, et al. Genomic Selection for Economic Traits in Inner Mongolia Cashmere Goats by Integrating GWAS Prior Information. Veterinary Sciences. 2025; 12(10):996. https://doi.org/10.3390/vetsci12100996
Chicago/Turabian StyleXi, Haijiao, Qi Xu, Huanfeng Yao, Zihao Shen, Bohan Zhou, Qi Lv, Jinquan Li, Ruijun Wang, Yanjun Zhang, Rui Su, and et al. 2025. "Genomic Selection for Economic Traits in Inner Mongolia Cashmere Goats by Integrating GWAS Prior Information" Veterinary Sciences 12, no. 10: 996. https://doi.org/10.3390/vetsci12100996
APA StyleXi, H., Xu, Q., Yao, H., Shen, Z., Zhou, B., Lv, Q., Li, J., Wang, R., Zhang, Y., Su, R., & Wang, Z. (2025). Genomic Selection for Economic Traits in Inner Mongolia Cashmere Goats by Integrating GWAS Prior Information. Veterinary Sciences, 12(10), 996. https://doi.org/10.3390/vetsci12100996






