Forecasting Daily COVID-19 Case Counts Using Aggregate Mobility Statistics
Abstract
1. Introduction
2. Related Work
3. Background and Preliminary Analysis
3.1. Data Sources
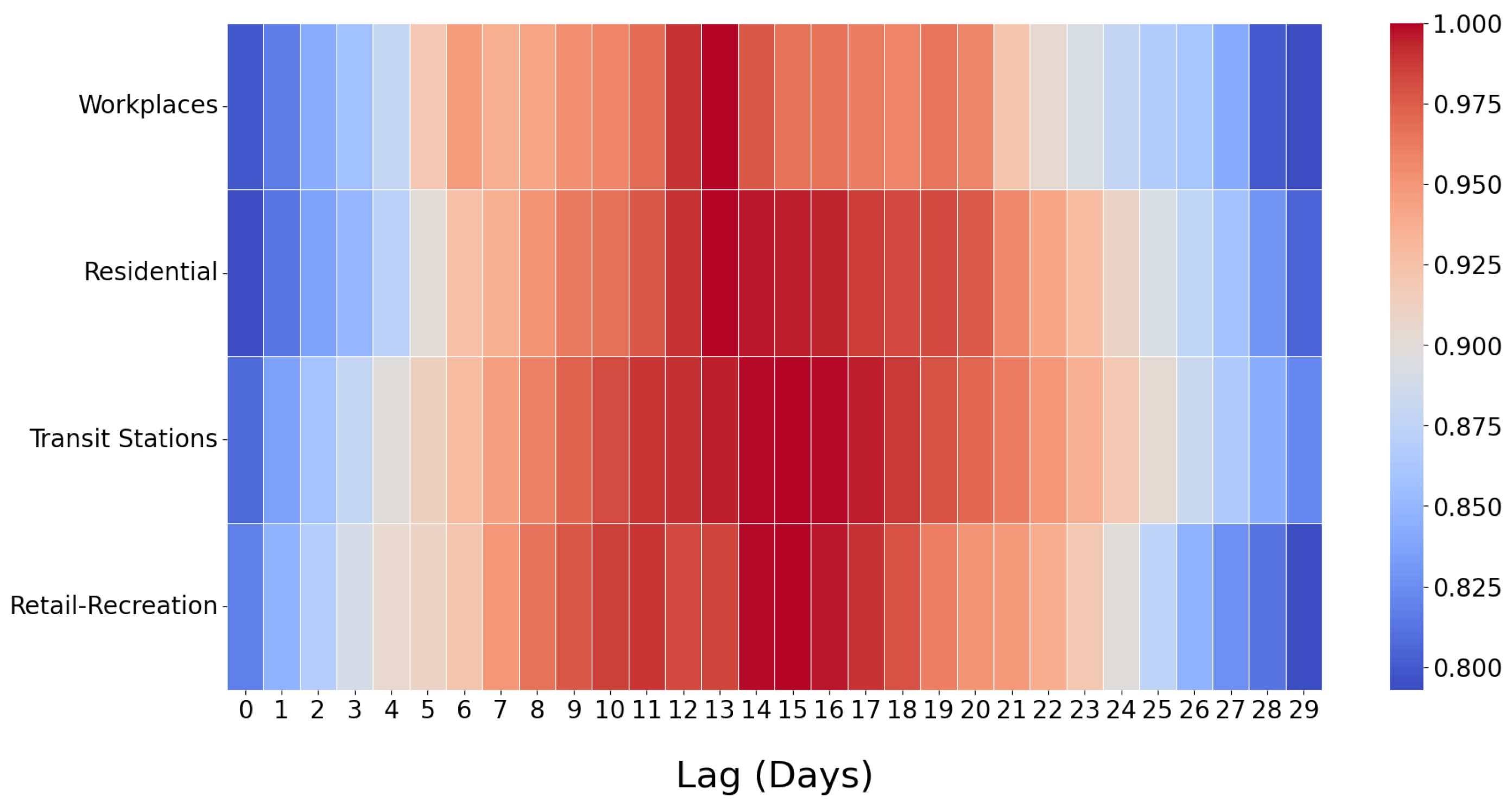
3.2. Time-Lagged Cross-Correlation Analysis
4. Forecasting Methodology
4.1. Moving Average for
4.2. Time Intervals
4.3. Feature Extraction and Selection
| Algorithm 1: Custom search algorithm to construct best model |
 |
4.4. Regression
4.5. Cross-Validation and Evaluation Setup
5. Results and Discussion
5.1. Comparison of Actual versus Predicted Case Counts
5.2. Forecasting Accuracy
5.3. Impact of Window Size w
5.4. Comparison of Regression Types
5.5. Analysis of Feature Sets
5.6. Analysis of Forecasting Bias
5.7. Runtime Performance and Overhead
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
| 1 | https://movement.uber.com/?lang=en-US, accessed on 15 September 2022 |
| 2 | https://covid19.apple.com/mobility, accessed on 15 September 2022 |
References
- WHO. WHO Director-General’s Opening Remarks at the Media Briefing on COVID-19. 2020. Available online: https://www.who.int/director-general/speeches/detail/who-director-general-s-opening-remarks-at-the-media-briefing-on-covid-19—11-march-2020 (accessed on 15 September 2022).
- WHO. WHO Coronavirus (COVID-19) Dashboard 2022. Available online: https://covid19.who.int/ (accessed on 15 September 2022).
- Google. COVID-19 Community Mobility Reports. 2020. Available online: https://www.google.com/covid19/mobility/ (accessed on 15 September 2022).
- Aktay, A.; Bavadekar, S.; Cossoul, G.; Davis, J.; Desfontaines, D.; Fabrikant, A.; Gabrilovich, E.; Gadepalli, K.; Gipson, B.; Guevara, M.; et al. Google COVID-19 community mobility reports: Anonymization process description (version 1.1). arXiv 2020, arXiv:2004.04145. [Google Scholar]
- Alessandretti, L. What human mobility data tell us about COVID-19 spread. Nat. Rev. Phys. 2022, 4, 12–13. [Google Scholar] [CrossRef]
- Zhang, C.; Qian, L.X.; Hu, J.Q. COVID-19 pandemic with human mobility across countries. J. Oper. Res. Soc. China 2021, 9, 229–244. [Google Scholar] [CrossRef]
- Du, B.; Zhao, Z.; Zhao, J.; Yu, L.; Sun, L.; Lv, W. Modelling the epidemic dynamics of COVID-19 with consideration of human mobility. Int. J. Data Sci. Anal. 2021, 12, 369–382. [Google Scholar] [CrossRef]
- Sulyok, M.; Walker, M. Community movement and COVID-19: A global study using Google’s Community Mobility Reports. Epidemiol. Infect. 2020, 148, 1–9. [Google Scholar] [CrossRef]
- Xiong, C.; Hu, S.; Yang, M.; Luo, W.; Zhang, L. Mobile device data reveal the dynamics in a positive relationship between human mobility and COVID-19 infections. Proc. Natl. Acad. Sci. USA 2020, 117, 27087–27089. [Google Scholar] [CrossRef]
- Yilmazkuday, H. Stay-at-home works to fight against COVID-19: International evidence from Google mobility data. J. Hum. Behav. Soc. Environ. 2021, 31, 210–220. [Google Scholar] [CrossRef]
- Tian, H.; Liu, Y.; Li, Y.; Wu, C.H.; Chen, B.; Kraemer, M.U.; Li, B.; Cai, J.; Xu, B.; Yang, Q.; et al. An investigation of transmission control measures during the first 50 days of the COVID-19 epidemic in China. Science 2020, 368, 638–642. [Google Scholar] [CrossRef]
- Kraemer, M.U.; Yang, C.H.; Gutierrez, B.; Wu, C.H.; Klein, B.; Pigott, D.M.; Du Plessis, L.; Faria, N.R.; Li, R.; Hanage, W.P.; et al. The effect of human mobility and control measures on the COVID-19 epidemic in China. Science 2020, 368, 493–497. [Google Scholar] [CrossRef]
- Chang, S.L.; Harding, N.; Zachreson, C.; Cliff, O.M.; Prokopenko, M. Modelling transmission and control of the COVID-19 pandemic in Australia. Nat. Commun. 2020, 11, 5710. [Google Scholar] [CrossRef]
- Li, Y.; Li, M.; Rice, M.; Zhang, H.; Sha, D.; Li, M.; Su, Y.; Yang, C. The impact of policy measures on human mobility, COVID-19 cases, and mortality in the US: A spatiotemporal perspective. Int. J. Environ. Res. Public Health 2021, 18, 996. [Google Scholar] [CrossRef]
- Wellenius, G.A.; Vispute, S.; Espinosa, V.; Fabrikant, A.; Tsai, T.C.; Hennessy, J.; Dai, A.; Williams, B.; Gadepalli, K.; Boulanger, A.; et al. Impacts of social distancing policies on mobility and COVID-19 case growth in the US. Nat. Commun. 2021, 12, 3118. [Google Scholar] [CrossRef]
- Zhou, Y.; Xu, R.; Hu, D.; Yue, Y.; Li, Q.; Xia, J. Effects of human mobility restrictions on the spread of COVID-19 in Shenzhen, China: A modelling study using mobile phone data. Lancet Digit. Health 2020, 2, e417–e424. [Google Scholar] [CrossRef]
- Nouvellet, P.; Bhatia, S.; Cori, A.; Ainslie, K.E.; Baguelin, M.; Bhatt, S.; Boonyasiri, A.; Brazeau, N.F.; Cattarino, L.; Cooper, L.V.; et al. Reduction in mobility and COVID-19 transmission. Nat. Commun. 2021, 12, 1090. [Google Scholar] [CrossRef]
- Xi, W.; Pei, T.; Liu, Q.; Song, C.; Liu, Y.; Chen, X.; Ma, J.; Zhang, Z. Quantifying the time-lag effects of human mobility on the COVID-19 transmission: A multi-city study in China. IEEE Access 2020, 8, 216752–216761. [Google Scholar] [CrossRef]
- Ilin, C.; Annan-Phan, S.; Tai, X.H.; Mehra, S.; Hsiang, S.; Blumenstock, J.E. Public mobility data enables COVID-19 forecasting and management at local and global scales. Sci. Rep. 2021, 11, 13531. [Google Scholar] [CrossRef]
- Rostami-Tabar, B.; Rendon-Sanchez, J.F. Forecasting COVID-19 daily cases using phone call data. Appl. Soft Comput. 2021, 100, 106932. [Google Scholar] [CrossRef]
- Liu, D.; Clemente, L.; Poirier, C.; Ding, X.; Chinazzi, M.; Davis, J.T.; Vespignani, A.; Santillana, M. A machine learning methodology for real-time forecasting of the 2019-2020 COVID-19 outbreak using Internet searches, news alerts, and estimates from mechanistic models. arXiv 2020, arXiv:2004.04019. [Google Scholar]
- Athanasios, A.; Irini, F.; Tasioulis, T.; Konstantinos, K. Prediction of the effective reproduction number of COVID-19 in Greece: A machine learning approach using Google mobility data. medRxiv 2021. [Google Scholar] [CrossRef]
- Wang, P.; Zheng, X.; Ai, G.; Liu, D.; Zhu, B. Time series prediction for the epidemic trends of COVID-19 using the improved LSTM deep learning method: Case studies in Russia, Peru and Iran. Chaos Solitons Fractals 2020, 140, 110214. [Google Scholar] [CrossRef]
- Luo, J.; Zhang, Z.; Fu, Y.; Rao, F. Time series prediction of COVID-19 transmission in America using LSTM and XGBoost algorithms. Results Phys. 2021, 27, 104462. [Google Scholar] [CrossRef]
- Auliya, S.F.; Wulandari, N. The Impact of Mobility Patterns on the Spread of the COVID-19 in Indonesia. J. Inf. Syst. Eng. Bus. Intell. 2021, 7, 31–41. [Google Scholar] [CrossRef]
- Awwad, F.A.; Mohamoud, M.A.; Abonazel, M.R. Estimating COVID-19 cases in Makkah region of Saudi Arabia: Space-time ARIMA modeling. PLoS ONE 2021, 16, e0250149. [Google Scholar] [CrossRef]
- de Araujo Morais, L.R.; da Silva Gomes, G.S. Forecasting daily Covid-19 cases in the world with a hybrid ARIMA and neural network model. Appl. Soft Comput. 2022, 126, 109315. [Google Scholar] [CrossRef]
- Schwabe, A.; Persson, J.; Feuerriegel, S. Predicting COVID-19 spread from large-scale mobility data. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Singapore, 14–18 August 2021; pp. 3531–3539. [Google Scholar]
- Wang, H.; Yamamoto, N. Using a partial differential equation with Google Mobility data to predict COVID-19 in Arizona. arXiv 2020, arXiv:2006.16928. [Google Scholar] [CrossRef]
- Li, R.Q.; Song, Y.R.; Jiang, G.P. Prediction of epidemics dynamics on networks with partial differential equations: A case study for COVID-19 in China. Chin. Phys. B 2021, 30, 120202. [Google Scholar] [CrossRef]
- Sun, D.; Duan, L.; Xiong, J.; Wang, D. Modeling and forecasting the spread tendency of the COVID-19 in China. Adv. Differ. Equ. 2020, 2020, 1–16. [Google Scholar] [CrossRef]
- Sarkar, K.; Khajanchi, S.; Nieto, J.J. Modeling and forecasting the COVID-19 pandemic in India. Chaos Solitons Fractals 2020, 139, 110049. [Google Scholar] [CrossRef]
- Zeng, Y.; Guo, X.; Deng, Q.; Luo, S.; Zhang, H. Forecasting of COVID-19: Spread with dynamic transmission rate. J. Saf. Sci. Resil. 2020, 1, 91–96. [Google Scholar] [CrossRef]
- Harjule, P.; Tiwari, V.; Kumar, A. Mathematical models to predict COVID-19 outbreak: An interim review. J. Interdiscip. Math. 2021, 24, 259–284. [Google Scholar] [CrossRef]
- Kumar, N.; Susan, S. Particle swarm optimization of partitions and fuzzy order for fuzzy time series forecasting of COVID-19. Appl. Soft Comput. 2021, 110, 107611. [Google Scholar] [CrossRef]
- Gomes, D.C.D.S.; Serra, G.L.D.O. Machine learning model for computational tracking and forecasting the COVID-19 dynamic propagation. IEEE J. Biomed. Health Inform. 2021, 25, 615–622. [Google Scholar] [CrossRef]
- Mileu, N.; Costa, N.M.; Costa, E.M.; Alves, A. Mobility and Dissemination of COVID-19 in Portugal: Correlations and Estimates from Google’s Mobility Data. Data 2022, 7, 107. [Google Scholar] [CrossRef]
- Kishore, K.; Jaswal, V.; Verma, M.; Koushal, V. Exploring the utility of Google mobility data during the COVID-19 pandemic in India: Digital epidemiological analysis. JMIR Public Health Surveill. 2021, 7, e29957. [Google Scholar] [CrossRef]
- World Health Organization. Coronavirus Disease 2019 (COVID-19) Situation Report 50. 2020. Available online: https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200310-sitrep-50-covid-19.pdf?sfvrsn=55e904fb_2 (accessed on 15 September 2022).
- Ritchie, H.; Mathieu, E.; Rodes-Guirao, L.; Appel, C.; Giattino, C.; Ortiz-Ospina, E.; Hasell, J.; Macdonald, B.; Beltekian, D.; Roser, M. Coronavirus Pandemic (COVID-19). Our World Data 2020. Available online: https://ourworldindata.org/coronavirus (accessed on 15 September 2022).
- Dong, E.; Du, H.; Gardner, L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect. Dis. 2020, 20, 533–534. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Routledge: Abingdon-on-Thames, UK, 2017. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2. [Google Scholar]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Drucker, H. Improving Regressors Using Boosting Techniques. In Proceedings of the International Conference on Machine Learning, Nashville, TN, USA, 8–12 July 1997; Volume 97, pp. 107–115. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. SIAM Rev. 2001, 43, 129–159. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Estimation of a Location Parameter. Ann. Math. Stat. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]







| Country | Time Interval | Country | Time Interval |
|---|---|---|---|
| Argentina | 03/04/2020– 18/12/2021 | Netherlands | 01/06/2020– 17/12/2021 |
| Austria | 03/03/2020– 14/12/2021 | Norway | 01/04/2020– 12/12/2021 |
| Canada | 12/03/2020– 17/12/2021 | Poland | 29/04/2020– 18/12/2021 |
| Denmark | 27/02/2020– 15/12/2021 | Portugal | 02/03/2020– 18/12/2021 |
| India | 24/04/2020– 18/12/2021 | Turkey | 25/11/2020– 08/11/2021 |
| Italy | 25/02/2020– 18/12/2021 | United Kingdom | 21/04/2020– 28/11/2021 |
| Japan | 02/04/2020– 18/12/2021 | - | - |
| Country | () | ||
|---|---|---|---|
| Argentina | 1401.15 | 41,080 | 3.41% |
| Austria | 389.06 | 15,809 | 2.46% |
| Canada | 719.59 | 11,381 | 6.32% |
| Denmark | 207.02 | 8773 | 2.36% |
| India | 3492.39 | 414,188 | 0.84% |
| Italy | 1108.03 | 40,902 | 2.71% |
| Japan | 270.15 | 25,992 | 1.04% |
| Netherlands | 515.97 | 23,714 | 2.18% |
| Norway | 193.20 | 7631 | 2.53% |
| Poland | 1457.33 | 35,253 | 4.13% |
| Portugal | 378.06 | 16,432 | 2.30% |
| Turkey | 369.41 | 63,082 | 1.99% |
| United Kingdom | 1929.96 | 68,053 | 2.84% |
| Country | |||
|---|---|---|---|
| Argentina | 4.18 | 2.99 | 2.09 |
| Austria | 5.09 | 4.12 | 2.53 |
| Canada | 7.13 | 4.49 | 3.51 |
| Denmark | 6.24 | 4.58 | 3.52 |
| India | 2.15 | 1.43 | 1.00 |
| Italy | 3.85 | 2.55 | 2.26 |
| Japan | 4.05 | 2.99 | 1.78 |
| Netherlands | 3.50 | 2.58 | 2.26 |
| Norway | 8.57 | 6.99 | 5.13 |
| Poland | 5.61 | 4.20 | 2.83 |
| Portugal | 6.57 | 4.93 | 3.68 |
| Turkey | 1.94 | 1.44 | 1.39 |
| United Kingdom | 3.72 | 2.58 | 2.21 |
| Regression Type | Countries |
|---|---|
| RANSAC | Argentina, Austria, Canada, Denmark, India, Italy, Japan, Norway, Poland |
| Ridge | Netherlands, Portugal, Turkey, United Kingdom |
| Country | Workplaces (WP) | Transit Stations (TS) | Residential (RS) | Retail and Recreation (RR) |
|---|---|---|---|---|
| Argentina | ✓ | ✓ | ||
| Austria | ✓ | ✓ | ||
| Canada | ✓ | ✓ | ||
| Denmark | ✓ | ✓ | ||
| India | ✓ | ✓ | ||
| Italy | ✓ | ✓ | ||
| Japan | ✓ | ✓ | ||
| Netherlands | ✓ | ✓ | ||
| Norway | ✓ | ✓ | ||
| Poland | ✓ | ✓ | ||
| Portugal | ✓ | ✓ | ||
| Turkey | ✓ | ✓ | ||
| United Kingdom | ✓ | ✓ |
| Regression Type or Method | Turkey | Netherlands | Italy |
|---|---|---|---|
| Linear | 0.15 | 0.20 | 0.25 |
| XGB | 1.72 | 3.16 | 3.59 |
| AdaBoost | 1.74 | 2.42 | 3.05 |
| Decision Tree | 0.19 | 0.20 | 0.29 |
| Gradient Boosting | 1.63 | 1.69 | 2.18 |
| Random Forest | 4.97 | 7.03 | 9.02 |
| Extra Trees | 4.01 | 5.64 | 7.47 |
| KNN | 0.26 | 0.38 | 0.45 |
| Ridge | 0.15 | 0.19 | 0.23 |
| Lasso | 0.24 | 0.26 | 0.31 |
| Huber | 0.34 | 0.36 | 0.39 |
| RANSAC | 0.51 | 0.63 | 0.71 |
| Algorithm 1 (total) | 2252.95 | 6293.88 | 7949.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boru, B.; Gursoy, M.E. Forecasting Daily COVID-19 Case Counts Using Aggregate Mobility Statistics. Data 2022, 7, 166. https://doi.org/10.3390/data7110166
Boru B, Gursoy ME. Forecasting Daily COVID-19 Case Counts Using Aggregate Mobility Statistics. Data. 2022; 7(11):166. https://doi.org/10.3390/data7110166
Chicago/Turabian StyleBoru, Bulut, and M. Emre Gursoy. 2022. "Forecasting Daily COVID-19 Case Counts Using Aggregate Mobility Statistics" Data 7, no. 11: 166. https://doi.org/10.3390/data7110166
APA StyleBoru, B., & Gursoy, M. E. (2022). Forecasting Daily COVID-19 Case Counts Using Aggregate Mobility Statistics. Data, 7(11), 166. https://doi.org/10.3390/data7110166








