Cryptocurrency Price Prediction with Convolutional Neural Network and Stacked Gated Recurrent Unit

Abstract

Virtual currencies have been declared as one of the financial assets that are widely recognized as exchange currencies. The cryptocurrency trades caught the attention of investors as cryptocurrencies can be considered as highly profitable investments. To optimize the profit of the cryptocurrency investments, accurate price prediction is essential. In view of the fact that the price prediction is a time series task, a hybrid deep learning model is proposed to predict the future price of the cryptocurrency. The hybrid model integrates a 1-dimensional convolutional neural network and stacked gated recurrent unit (1DCNN-GRU). Given the cryptocurrency price data over the time, the 1-dimensional convolutional neural network encodes the data into a high-level discriminative representation. Subsequently, the stacked gated recurrent unit captures the long-range dependencies of the representation. The proposed hybrid model was evaluated on three different cryptocurrency datasets, namely Bitcoin, Ethereum, and Ripple. Experimental results demonstrated that the proposed 1DCNN-GRU model outperformed the existing methods with the lowest RMSE values of 43.933 on the Bitcoin dataset, 3.511 on the Ethereum dataset, and 0.00128 on the Ripple dataset.

1. Introduction

Cryptocurrencies serve as a peer-to-peer digital currency where every detailed transaction occurs in a secured way. The transactions are further stored in a block, known as Blockchain. The security features made cryptocurrency a popular and well-known trading platform for investors. Cryptocurrencies have been growing dramatically, gaining popularity and capitalization. Bitcoin is the first decentralized cryptocurrency developed by Satoshi Nakamoto [1], and it has become the world’s most valuable cryptocurrency. With the vast transaction volume of cryptocurrencies, many types of currencies were introduced into the cryptography world. Some well-known cryptocurrencies are Ethereum and Ripple, among others.

This study focuses on cryptocurrency price prediction. The cryptocurrency price prediction is a time series problem that can be solved by using deep learning regression techniques. Although price prediction of cryptocurrency is challenging, developing cryptocurrency price prediction algorithms is worthwhile because it plays a vital role for cryptocurrency traders. Inspired by the success of deep learning regression models in a wide spectrum of applications, this paper proposes a hybrid regression model that amalgamates a 1-dimensional convolutional neural network (1DCNN) and a stacked gated recurrent unit (GRU), into the 1DCNN-GRU model for cryptocurrency price prediction. Three cryptocurrency historical price datasets are first collected from the cryptocurrency exchange website. Subsequently, the datasets are subjected to some data pre-processing, including normalization and missing value removal before passing into the 1DCNN-GRU model for representation learning and price prediction. The 1DCNN layer plays the role of extracting the salient features in the historical price data. The extracted features are then passed into the stacked GRU for temporal encoding where the long-range dependencies are captured. The temporal encoding is then leveraged for the cryptocurrency price prediction. The predicted price is compared against the real price and the root mean square error is computed. The main contributions of this paper are as follows.

• The cryptocurrency historical price data are acquired from the cryptocurrency exchange website. As the daily or hourly interval data are susceptible to information loss, this study leverages the one-minute interval data for more accurate price prediction.
• The feature scaling is performed on the cryptocurrency historical price data by normalization. In addition, the data is further pre-processed to remove the missing values that might affect model learning. The clean data are then partitioned into the training set and testing set for model learning and price prediction.
• A hybrid 1DCNN-GRU model is proposed for representation learning and cryptocurrency price prediction. The 1DCNN model encodes the prominent patterns in the historical price data, hence producing discriminative features to represent the historical price data. Thereafter, the stacked GRU model captures the long-range dependencies in the features, thus alleviating the gradient vanishing problems.

2. Related Works

This section describes some existing works in cryptocurrency price prediction. There are many deep learning models that are adopted for price prediction [2,3,4,5,6,7,8,9,10,11,12,13,14].

In early work, Sin et al. (2017) [15] proposed a forecasting algorithm that can be applied to different financial, engineering, and medical tasks. The algorithm integrated an artificial neural network (ANN) and a multilayer perceptron (MLP). From the experiments, the incorporation of MLP into ANN increased the Bitcoin price prediction accuracy from about 58% to 63%.

A deep learning algorithm, known as the Facebook Prophet for Bitcoin price prediction was adopted by Yenidogan et al. (2018) [16]. A three-fold splitting technique was conducted to provide optimum ratios for training, testing, and validation sets. The experimental results showed that the PROPHET algorithm outperformed the ARIMA algorithm, in which Prophet obtained a lower root mean square error (RMSE) of 652.18 compared to 817.01.

McNally et al. (2018) [17] leveraged several deep learning algorithms to predict the price of Bitcoin. In the early process, functional patterns were extracted from the data by feature engineering. The experimental results demonstrated that the long short-term memory (LSTM) model achieved the highest accuracy of 52.78% while recurrent neural networks (RNN) achieved the lowest accuracy of 5.45%.

Various regression techniques were presented by Phaladisailoed et al. (2018) [18] to predict Bitcoin prices by using Keras libraries and scikit-learn. The dataset was taken from Kaggle where it consists of one-minute interval data on the Bitcoin exchange website Bitstamp. The best results showed that R-Square of 99.2% was obtained by the LSTM and GRU models.

Jiang (2020) [19] proposed deep learning methods to forecast Bitcoin prices by gathering and reorganizing data on the Bitcoin price per minute to hours. The dataset was pre-processed, followed by mini-batch and min-max normalization before feeding it into the regression models. The work proposed a few deep learning networks such as MLP, RNN with the extension of LSTM, and GRU to predict future Bitcoin price. The experimental results showed that the MLP model, with the involvement of two layers of GRU achieved the best result, which had the minimal RMSE of 19.020.

Politis et al. (2021) [20] leveraged multiple deep learning models for predicting the price of Ethereum. Feature selection was performed to reduce the dataset complexity and anomalies. The ensemble model was implemented with the combination of LSTM, GRU and/or temporal convolutional networks (TCN). In the daily forecast experimental result, the ensemble model with LSTM, GRU, and Hybrid GRU-TCN had the best performance of 84.2% accuracy, whereas the LSTM-GRU model achieved the lowest RMSE of 8.6.

Another LSTM-GRU hybrid model was put forth by Tanwar et al. (2021) [21] for cryptocurrency price prediction. The work considered Bitcoin as the parent currency and captured the movement direction of Bitcoin price. Subsequently, the movement direction was utilized to predict the price of Litecoin and Zcash with the inter-dependency assumptions between Bitcoin-Litecoin and Bitcoin-Zcash. With a one-day window size, the LSTM-GRU model recorded a mean squared error (MSE) of 0.02038 for Litecoin and 0.00461 for Zcash.

Livieris et al. (2021) [22] proposed a multiple-input cryptocurrency deep learning model, also known as MICDL. The proposed approach utilized each cryptocurrency data as input in a convolutional layer, followed by a pooling layer and an LSTM layer. The classical structure of a deep learning neural network, such as a dense layer, batch normalization layer, dropout layer, and output layer were leveraged. The proposed CNN with an LSTM layer achieved 55.03% accuracy on the Bitcoin data, whereas accuracy of 51.51% was obtained for Ethereum data and 49.61% for Ripple data.

Zhang et al. (2021) [23] presented a weighted and attentive memory convolutional neural network (WAMC) for cryptocurrency price prediction. The model consists of a GRU to establish the attentive memory for each input sequence, a channel-wise weighting module to learn the interdependencies among several cryptocurrencies, and a CNN to extract local temporal features of the historical price data. The proposed WAMC recorded an RMSE of 9.70 for Ethereum and 1.37 for Bitcoin.

Jay et al. (2020) [24] devised stochastic neural networks for the price prediction of Bitcoin, Ethereum, and Litecoin. The work considered three factors, namely cryptocurrency exchange market statistics, blockchain data, and social sentiment as the neural networks’ input. In order to address the randomness in the factors, the stochastic layers were incorporated into the MLP and LSTM model. In comparison to the deterministic MLP and LSTM, the stochastic neural networks (MLP and LSTM) showed an average improvement of 4.84833% for Bitcoin, 4.15640% for Ethereum, and 4.74619% for Litecoin.

The price prediction of the same cryptocurrencies were performed by Sebastiao et al. (2021) [25]. The authors devised a few machine learning models, including linear models, random forest, and support vector machine to examine the predictability of the cryptocurrencies. The experimental results showed that the best results were achieved by the ensemble of linear models, random forest, and support vector machine on Ethereum prices, which was at 63.33% of win rates of the strategies. In another way, linear models achieved optimal RMSEs on forecasting Ethereum and Litecoin prices, which were only 6.85 and 8.14, whereas random forest achieved an RMSE of 5.77 on forecasting Bitcoin prices.

Saadah et al. (2020) [26] applied several machine learning and deep learning methods for predicting the price of Bitcoin, Ethereum, and Ripple. The methods include k-nearest neighbors, support vector machine, and LSTM. The experimental results demonstrated that the LSTM achieved the optimal RMSE for all three cryptocurrencies, with RMSE of 928.62 on Bitcoin, 11.69 on Ethereum, and 0.16 on Ripple.

Derbentsev et al. (2020) [27] implemented machine learning approaches, namely random forest and gradient boosting machine to forecast cryptocurrency prices. Three cryptocurrencies were used, i.e., Bitcoin, Ethereum, and Ripple. The experiments showed that gradient boosting machine is able to better forecast the price compared to random forest, in which RMSE of 263.34 was obtained on Bitcoin, 5.02 on Ethereum, and 0.92 on Ripple.

The summary of the existing works is presented in Table 1. Many existing works leveraged LSTM for price prediction, attributable to its gating mechanism that is able to capture the sequential and temporal information in the data. However, there might be noise or outliers in the raw historical price data; thus, this work first performs feature extraction by using 1DCNN to capture the salient features and suppress the noise in the data. Subsequently, GRU is leveraged to encode the long-range temporal information in the features. The details of the proposed hybrid model with 1DCNN and GRU are discussed in the next section.

Table 1. Summary of related works.

Paper	Best Method	Dataset	Results (Metric)
Sin et al. (2017) [15]	ANN + MLP	Bitcoin	63% (Accuracy)
Yenidogan et al. (2018) [16]	Facebook Prophet	Bitcoin	652.18 (RMSE)
McNally et al. (2018) [17]	LSTM	Bitcoin	52.78% (Accuracy)
Phaladisailoed et al. (2018) [18]	LSTM, GRU	Bitcoin	99.2% (R-Square)
Jiang (2020) [19]	MLP + GRU	Bitcoin	19.020 (RMSE)
Politis et al. (2021) [20]	LSTM-GRU	Bitcoin	8.6 (RMSE)
Tanwar et al. (2021) [21]	LSTM-GRU	Litecoin	0.02038 (MSE)
		Zcash	0.00461 (MSE)
Livieris et al. (2021) [22]	CNN + LSTM	Bitcoin	55.03% (Accuracy)
		Ethereum	51.51% (Accuracy)
		Ripple	49.61% (Accuracy)
Zhang et al. (2021) [23]	WAMC	Ethereum	9.70 (RMSE)
		Bitcoin	1.37 (RMSE)
Jay et al. (2020) [24]	Stochastic Neural Networks	Bitcoin	4.84833% (Improvement)
		Ethereum	4.15640% (Improvement)
		Litecoin	4.74619% (Improvement)
Sebastiao et al. (2021) [25]	Linear Models	Ethereum	6.85 (RMSE)
		Litecoin	8.14 (RMSE)
	Random Forest	Bitcoin	5.77 (RMSE)
Saadah et al. (2020) [26]	LSTM	Bitcoin	928.62 (RMSE)
		Ethereum	11.69 (RMSE)
		Ripple	0.16 (RMSE)
Derbentsev et al. (2020) [27]	Gradient Boosting Machine	Bitcoin	263.34 (RMSE)
		Ethereum	5.02 (RMSE)
		Ripple	0.92 (RMSE)

3. Cryptocurrency Price Prediction with 1-Dimensional Convolutional Neural Network and Stacked Gated Recurrent Unit (1DCNN-GRU)

This section details the proposed 1DCNN-GRU model for cryptocurrency price prediction. The historical price data of three cryptocurrencies are first acquired, namely Bitcoin, Ethereum, and Ripple. Subsequently, the collected data are pre-processed to clean missing values. Thereafter, the cleaned data are fed into the hybrid 1DCNN-GRU model for model learning and price prediction. Figure 1 illustrates the process flow of the cryptocurrency price prediction.

Figure 1. The process flow of the cryptocurrency price prediction.

3.1. Data Acquisition

Three datasets were used for the cryptocurrency price prediction, namely Bitcoin, Ethereum, and Ripple.

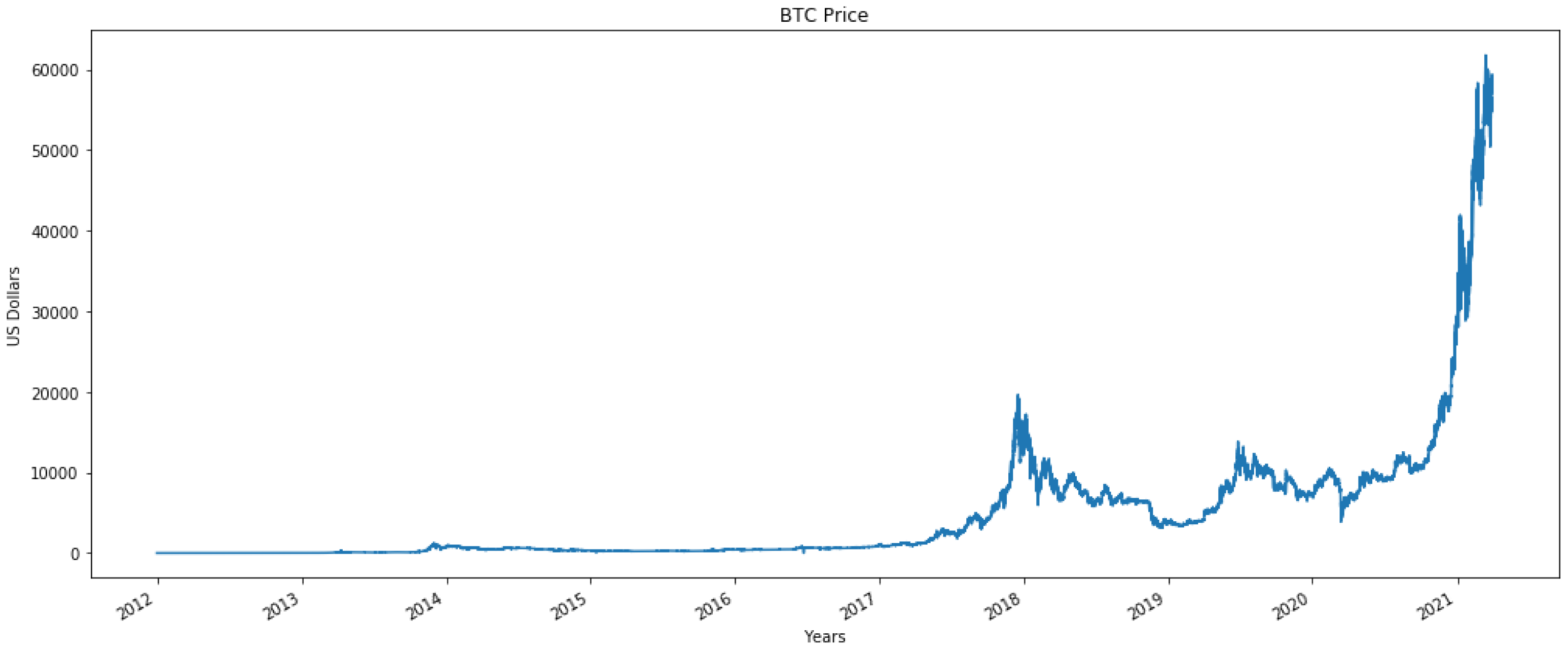
The Bitcoin historical data [28] were acquired from the Kaggle website. The provided one-minute interval data range from 1 January 2012 until 31 March 2021, which contain approximately 4.8 millions samples, including NaN values. Some columns in the data are open, high, low, close (OHLC) price, volume, and the weighted price. All the timestamps are in UNIX time. The NaN values indicate that no trade or activity happened at that time. Figure 2 visualizes the Bitcoin closing price for the years 2012 to 2021.

Figure 2. The historical price of Bitcoin (2012–2021).

The Ethereum historical data were collected from the Bitstamp exchange website. The data comprise around 396,403 samples at one-minute intervals. The Ethereum closing price of the year 2021 is shown in Figure 3.

Figure 3. The historical price of Ethereum (2021).

Ripple is another widely known cryptocurrency, which has slightly lower values compared to other cryptocurrencies. The Ripple historical data were also gathered from the Bitstamp exchange website. The historical data consist of around 396,403 samples, as displayed in Figure 4.

Figure 4. The historical price of Ripple (2021).

3.2. Data Pre-Processing

Some pre-processing steps are performed to clean the cryptocurrency historical data, including feature selection, timestamp conversion, missing values removal, train-test split, and min-max scaling normalization.

As each dataset consists of many features, this work only utilizes three features for price prediction, namely timestamp, date, and closing price. Subsequently, timestamp conversion is carried out where the timestamp in UNIX is converted into the YY:MM:DD date format. The zeros and NaNs are filtered out by dropping the associated rows. To avoid huge data losses and to provide more timely and detailed prediction, the samples are taken at one-min intervals. Due to the inconsistency of historical data and high sampling rates, the historical data of one week are used. With these settings, the number of samples is 10,797 for Bitcoin and 10,834 for both Ethereum and Ripple. The samples are further partitioned into six days for the training set and one day for the testing set. Apart from that, the features are subjected to min-max scaling normalization that transforms each feature into the range [0, 1]. The min-max scaling suppresses the effects of outliers while preserving the relationships among the data values. The min-max scaling is computed as

$$x_{\mathrm{norm}}=\frac{x-min\left(x\right)}{max\left(x\right)-min\left(x\right)}.$$

(1)

3.3. 1-Dimensional Convolutional Neural Network and Gated Recurrent Unit

In this work, a hybrid model that integrates 1DCNN and GRU is proposed for cryptocurrency price prediction. The architecture of the proposed 1DCNN-GRU model is depicted in Figure 5. The proposed 1DCNN-GRU comprises a 1D convolutional layer and two GRU layers with 256 units each.

Figure 5. The architecture of the proposed 1DCNN-GRU model.

The cryptocurrency historical price is a kind of time series data that captures the closing price over the time. Using the raw price data as the input might introduce noise and outliers, causing the regression model to learn on the insignificant data. Therefore, a 1DCNN is leveraged to extract the prominent patterns from the historical price data. In the 1-dimensional convolutional layer (Conv1D), the kernel slides along the temporal axis and encodes the price data into representative features. The Conv1D layer in the proposed model sets both kernel size and stride to 1; hence the convolution window will read one time step at one time. The Conv1D layer consists of 256 output filters in the convolution, thus producing 256-dimensional output space. The output of the Conv1D layer is passed into the subsequent GRU layer.

Two GRU layers are leveraged to encode the long-term dependencies of the extracted features. The ability of capturing long-term dependencies in GRU is attributable to the gating mechanisms. There are two gates in the GRU, namely update gate and reset gate. The update gate $z_t$ at time step t determines the information from the previous time steps to be passed to the future, defined as

$$z_t=\sigma \left(W^{\left(z\right)}{x}_t+U^{\left(z\right)}{h}_{t-1}\right),$$

(2)

where the weights $W^{\left(z\right)}$ and $U^{\left(z\right)}$ are multiplied with the input $x_t$ and hidden states $h_{t-1}$, respectively. The results of the multiplication are summed and passed into a sigmoid activation function to squash the values between 0 and 1.

The reset gate $r_t$ determines the past information to forget, where the computation is defined as

$$r_t=\sigma \left(W^{\left(r\right)}{x}_t+U^{\left(r\right)}{h}_{t-1}\right),$$

(3)

where the input $x_t$ and hidden states $h_{t-1}$ are multiplied with their corresponding weights $W^{\left(r\right)}$ and $U^{\left(r\right)}$. The sum of the results is likewise fed into a sigmoid activation function to limit the output to the range between 0 and 1.

A new memory content $h_t^{\prime }$ is then leveraged to store past information, defined as

$$h_t^{\prime }=tanh\left(W{x}_t+r_t\odot U{h}_{t-1}\right),$$

(4)

where ⊙ denotes the element-wise product. The new memory content is determined by first multiplying the input $x_t$ and hidden states $h_{t-1}$ with the corresponding weights W and U. Thereafter, the element-wise product of the reset gate $r_t$ and $U{h}_{t-1}$ is calculated. The product operation diminishes the information from the previous time step when the values of $r_t$ close to 0. Then, the sum of $W{x}_t$ and $r_t\odot U{h}_{t-1}$ is regulated by a tanh function to keep the output within −1 and 1.

Following that, the final memory at the current time step $h_t$ that determines the information to be passed to the next time step is calculated as

$$h_t=z_t\odot h_{t-1}+\left(1-z_t\right)\odot h_t^{\prime }.$$

(5)

Having $z_t$ values close to 1 will retain the majority of the previous information, whereas $z_t$ values close to 0 will keep the most part of the current information.

Lastly, the output from the GRU layers is passed into a dense layer with one hidden unit for price prediction. The layer-wise architecture of the proposed 1DCNN-GRU is presented in Table 2.

Table 2. The layer-wise architecture of the proposed 1DCNN-GRU model.

Layer	Configurations
Conv1D Layer	filters = 256, kernel_size = 1, strides = 1
GRU Layer	units = 256
GRU Layer	units = 256
Dense Layer	units = 1

4. Hyperparameter Tuning

A hyperparameter tuning by grid search is performed to determine the optimal settings of the 1DCNN-GRU model. The hyperparameters that are involved in the hyperparameter tuning are optimizer, activation function, and batch size. The optimizers play the role of optimizing the model learning process to ensure the model converges optimally. In this work, four optimizers are considered, namely Adam, SGD, Adamax, and RMSProp. The activation function is the function in the Conv1D layer and GRU layers that transforms the input, enabling the model to learn and perform more complex tasks. Five activation functions are explored, which are sigmoid, softmax, ReLU, tanh, and linear. The batch size defines the number of samples that is used for error gradient computation in each model weights update. The RMSE is adopted as the evaluation metric of the cryptocurrency price prediction models. The RMSE is the square root of the average squared distance between actual and predicted values, defined as

$$\mathrm{RMSE}=\sqrt{\frac{1}{n}\sum _{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2},$$

(6)

where n is the total number of predictions, y is the real price, and $\widehat{y}$ denotes the predicted price. The optimal settings are set to the hyperparameter values with the lowest RMSE.

Table 3 shows the experimental results of different hyperparameter values on the Bitcoin dataset. The lowest RMSE of 43.933 is obtained on the Bitcoin dataset when SGD optimizer, sigmoid activation function, and batch size of 16 are used. The experimental results on the Ethereum dataset are presented in Table 4. It is observed that the lowest RMSE of 3.511 is achieved with the Adamax optimizer, softmax activation function, and batch size of 32. As for the Ripple dataset, the lowest RMSE of 0.00128 is recorded when the Adam optimizer, softmax activation function, and batch size of 32 are set, as shown in Table 5. The experimental settings are given in Table 6.

Table 3. RMSE of 1DCNN-GRU with different hyperparameters on the Bitcoin dataset.

Hyperparameter		Batch Size
Optimizer	Activation	16	32	64	128
Adam	sigmoid	48.791	44.548	44.369	45.104
	softmax	44.085	44.260	44.056	44.025
	relu	44.250	44.445	44.050	44.170
	tanh	44.897	44.121	44.185	45.254
	linear	44.013	44.221	44.517	44.094
SGD	sigmoid	43.933	43.962	43.987	43.961
	softmax	-	-	-	-
	relu	44.045	44.395	44.211	44.167
	tanh	44.029	44.029	44.015	44.003
	linear	44.031	44.033	44.031	44.029
Adamax	sigmoid	44.434	44.898	44.105	44.562
	softmax	44.516	43.974	44.207	43.978
	relu	44.162	44.145	44.120	44.750
	tanh	44.147	44.843	44.527	44.074
	linear	46.624	45.204	44.515	44.048
RMSprop	sigmoid	49.824	44.495	47.559	44.995
	softmax	44.003	44.221	44.846	44.687
	relu	45.688	44.404	51.833	44.768
	tanh	44.854	44.940	44.353	44.812
	linear	44.620	44.131	44.108	44.182

Table 4. RMSE of 1DCNN-GRU with different hyperparameters on the Ethereum dataset.

Hyperparameter		Batch Size
Optimizer	Activation	16	32	64	128
Adam	sigmoid	3.807	3.617	3.556	3.576
	softmax	3.521	3.518	3.524	3.515
	relu	3.583	3.528	3.669	3.518
	tanh	3.729	3.529	3.579	3.556
	linear	3.515	3.559	3.519	3.677
SGD	sigmoid	3.528	3.524	3.516	3.514
	softmax	-	-	-	-
	relu	3.523	3.517	3.515	3.515
	tanh	3.518	3.515	3.516	3.516
	linear	3.515	3.515	3.516	3.515
Adamax	sigmoid	4.245	3.516	3.709	3.519
	softmax	3.526	3.511	3.515	3.514
	relu	3.546	3.624	3.609	3.516
	tanh	3.531	3.567	3.525	3.523
	linear	3.513	3.520	3.557	3.534
RMSprop	sigmoid	4.362	3.565	3.591	3.586
	softmax	3.517	3.580	3.717	3.592
	relu	3.636	3.630	3.515	3.534
	tanh	3.630	3.820	3.822	3.529
	linear	3.545	3.569	3.573	3.560

Table 5. RMSE of 1DCNN-GRU with different hyperparameters on the Ripple dataset.

Hyperparameter		Batch Size
Optimizer	Activation	16	32	64	128
Adam	sigmoid	0.00132	0.00129	0.00129	0.00132
	softmax	0.00129	0.00128	0.00129	0.00129
	relu	0.00131	0.00129	0.00131	0.00129
	tanh	0.00132	0.00129	0.00129	0.00129
	linear	0.00129	0.00130	0.00129	0.00129
SGD	sigmoid	0.01189	0.00129	0.00129	0.00129
	softmax	-	-	-	-
	relu	0.00129	0.00129	0.00129	0.00129
	tanh	0.00129	0.00129	0.00129	0.00129
	linear	0.00129	0.00129	0.00129	0.00129
Adamax	sigmoid	0.00129	0.00133	0.00130	0.00129
	softmax	0.00132	0.00130	0.00129	0.00129
	relu	0.00133	0.00129	0.00129	0.00129
	tanh	0.00129	0.00129	0.00129	0.00129
	linear	0.00144	0.00129	0.00130	0.00129
RMSprop	sigmoid	0.00131	0.00130	0.00134	0.00145
	softmax	0.00129	0.00129	0.00129	0. 00131
	relu	0.00134	0.00133	0.00129	0.00135
	tanh	0.00130	0.00130	0.00129	0.00139
	linear	0.00133	0.00131	0.00130	0.00134

Table 6. The experimental settings of the proposed 1DCNN-GRU model.

Dataset/Hyperparameter	Configurations
Bitcoin	optimizer = SGD, activation function = sigmoid, batch size = 16
Ethereum	optimizer = Adamax, activation function = softmax, batch size = 32
Ripple	optimizer = Adam, activation function = softmax, batch size = 32
Learning Rate	0.001
Training Epoch	150

5. Experimental Results and Analysis

In this section, the performance of the proposed 1DCNN-GRU model is compared with the existing prediction models. All models are trained on the same one-minute interval historical data.

Table 7 presents the comparison results of the methods on Bitcoin, Ethereum, and Ripple datasets. In general, the RMSE of all methods on the Bitcoin dataset is the highest, followed by the Ethereum dataset, and the Ripple dataset yields the lowest RMSE. This is due to the difference in the price where higher prices tend to result in higher RMSE.

Table 7. Experimental results on Bitcoin, Ethereum, and Ripple datasets.

Method	Root Mean Square Error (RMSE)
	Bitcoin	Ethereum	Ripple
ARIMA [17]	43.954	3.516	0.00129
Simple RNN [17]	44.003	3.517	0.00129
Facebook Prophet	805.169	157.046	0.05733
GRU [19]	43.998	3.512	0.00129
LSTM [26]	45.687	3.636	0.00130
CNN-LSTM [22]	47.537	3.516	0.00135
Bidirectional LSTM [22]	332.886	43.414	0.01499
XGBoost [29]	1477.181	101.361	0.01652
1DCNN-GRU (Proposed)	43.933	3.511	0.00128

The experimental results show that the proposed 1DCNN-GRU outshines the methods in comparison. The proposed 1DCNN-GRU model records an RMSE of 43.933 on the Bitcoin dataset, 3.511 on the Ethereum dataset, and 0.00128 on the Ripple dataset. Compared to the GRU model [19] alone, adding 1DCNN has reduced the RMSE on all datasets. This is attributable to 1DCNN that is able to learn local relationships and encode the cryptocurrency historical data into discriminative features. In doing so, the noise, outliers and insignificant data in the input are suppressed.

Apart from that, the proposed 1DCNN-GRU also showed much improvement in relation to the CNN-LSTM model [22]. The RMSE has reduced from 47.537 to 43.933 on the Bitcoin dataset, from 3.516 to 3.511 on the Ethereum dataset, and from 0.00135 to 0.00128 on the Ripple dataset. Both LSTM and GRU have their own strengths and perform well in different applications in which they utilize gating mechanisms to retain the historical information. In this application, the improvement corroborates the effectiveness of stacked GRU in capturing the long-range dependencies of the features, thus alleviating the vanishing gradient problems. The real and predicted prices of the Bitcoin, Ethereum, and Ripple are illustrated in Figure 6, Figure 7 and Figure 8, respectively.

Figure 6. The price prediction by 1DCNN-GRU model on the Bitcoin dataset.

Figure 7. The price prediction by 1DCNN-GRU model on the Ethereum dataset.

Figure 8. The price prediction by 1DCNN-GRU model on the Ripple dataset.

6. Conclusions

This paper presents a hybrid deep learning model that harnesses the strengths of 1DCNN and stacked GRU for cryptocurrency price prediction. The historical price of three cryptocurrencies are acquired, namely Bitcoin, Ethereum, and Ripple. The collected data are normalized and pre-processed to remove the missing values. Subsequently, the pre-processed data are passed into the hybrid 1DCNN-GRU model. The 1DCNN model transforms the price data into a discriminative representation that captures the significant patterns in the price data. Subsequently, the stacked GRU model encodes the long-range dependencies in the representation to mitigate past information loss problems. The gating mechanism of GRU determines the past and current information to be updated and reset, thus alleviating diminishing gradient problems. The experimental results demonstrate that the proposed 1DCNN-GRU outperforms the methods in comparison with the lowest RMSE values of 43.933 on the Bitcoin dataset, 3.511 on the Ethereum dataset, and 0.00128 on the Ripple dataset.

As a proof of concept and due to the limitations in computing resources, this study only utilizes the historical data for one week. Training the model on the cryptocurrency data for a longer time span should be able to further improve the generalization capability of the model. In addition to the closing price, other factors such as the seasonality trends, government policies and laws, social media, can also be considered as the input for price prediction model.