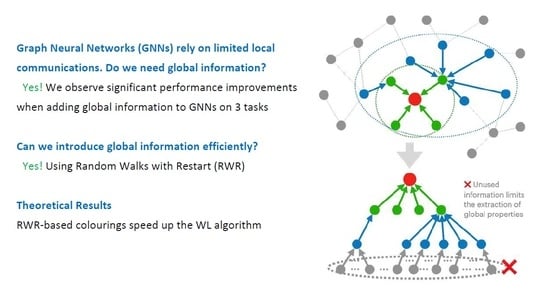
Appendix A. Proof of Proposition 1
Given a graph , we define its k-step RWR representation as the set of vectors , , where each entry describes the probability that an RWR of length k starting in v ends in u.
Proposition A1. Let and be two non-isomorphic graphs for which the 1-WL algorithm terminates with the correct answer after k iterations and starting from the labelling of all 1’s. Then, the k-step RWR representations of and are different.
Proof. Consider the WL algorithm with initial labeling given by all 1’s. It’s easy to see that (i) after k iterations the label of a node v corresponds to the information regarding the degree distribution of the neighborhood of distance from v and (ii) in iteration , the degrees of nodes at distance i from v are included in the label of v. In fact, after the first iteration, two nodes have the same colour if they have the same degree, as the colour of each node is given by the multiset of the colours of its neighbours (and we start with initial labeling given by all 1’s). After the second colour refinement iteration, two nodes have the same colour if they had the same colour after the first iteration (i.e., have the same degree), and the multisets containing the colours (degrees) of their neighbours are the same. In general, after the k-th iteration, two nodes have the same colour if they had the same colour in iteration , and the multiset containing the degrees of the neighbours at distance k is the same for the two nodes. Hence, two nodes that have different colours after a certain iteration will have different colours in all the successive iterations. Furthermore, the colour after the k-th iteration depends on the colour at the previous iteration (which “encodes” the distribution of degree of neighbours up to distance included), and the multiset of the degrees of neighbours at distance k.
Given two non-isomorphic graphs and , if the WL algorithm terminates with the correct answer starting from the all 1’s labelling in k iterations, it means that there is no matching between vertices in and vertices in such that matched vertices have the same degree distribution for neighborhoods at distance exactly k. Equivalently, any matching M that minimizes the number of matched vertices with different degree distribution has at least one such pair. Now consider one such matching M, and let and be vertices matched in M with different degree distributions for neighborhoods at distance exactly k. Since v and w have different degree distributions at distance k, the number of choices for paths of length k starting from v and w must be different (since the number of choices for the k-th edge on the path is different). Therefore, there must be at least a node and a node that are matched by M but for which the number of paths of length k from v to u is different from the number of paths of length k from w to z. Since is proportional to the number of paths of length k from v to u, we have that that is . Thus, the k-step RWR representation of and are different. □
Appendix B. Model Implementation Details
We present here a detailed description of the implementations of the models we use in our experimental section. Whenever possible, we started from the official implementation of the authors of each model.
Table A1 contains links to the implementations we used as a starting point for the code for our experiments.
Table A1.
Starting model implementations.
Table A1.
Starting model implementations.
With regard to the training procedure, we have that all models are trained with early stopping on the validation set (stopping the training if the validation loss does not decrease for a certain amount of epochs), and unless explicitly specified, we use Cross Entropy as loss function for all the classification tasks.
For the task of graph classification, we zero-pad the feature vectors of each node to make them all the same length when we inject structural information into the node feature vectors.
For the task of triangle counting, we follow [
32] and use the one-hot representation of node degrees as node feature vectors to impose some structural information in the network.
The experiments were run on a GPU cluster with 7 Nvidia 1080Ti, and on a CPU cluster (when the memory consumption was too big to fit in the GPUs) equipped with 8 cpus 12-Core Intel Xeon Gold 5118 @2.30 GHz, with 1.5 Tb of RAM.
In the rest of this section, we go through each model used in our experiments, specifying architecture, hyperparameters, and the position of the node embeddings used for RWRReg.
Appendix B.1. GCN (Node Classification)
We use a two layer architecture. The first layer outputs a 16-dimensional embedding vector for each node, and passes it through a ReLu activation, before applying dropout [
55], with probability
. The second layer outputs a
c-dimensional embedding vector for each node, where
c is the number of output classes and these vectors are passed through
Softmax to get the output probabilities for each class. An additional L2-loss is added with a balancing term of
. The model is trained using the Adam optimizer [
56] with a learning rate of 0.01.
We apply the RWRReg on the 16-dimensional node embeddings after the first layer.
Appendix B.2. GCN (Graph Classification)
We first have two GCN layers, each one generating a 128-dimensional embedding vector for each node. Then, we apply
max-pooling on the features of the nodes and pass the pooled 128-dimensional vector to a two-layer feed-forward neural network with 256 neurons at the first layer and
c at the last one, where
c is the number of output classes. A ReLu activation is applied in between the two feed-forward layers, and
Softmax is applied after the last layer. Dropout [
55] is applied in between the last GCN layer and the feed-forward layer, and in between the feedforward layers (after ReLu), in both cases with probability of 0.1. The model is trained using the Adam optimizer [
56] with a learning rate of 0.0005.
We apply the RWRReg on the 128-dimensional node embeddings after the last GCN layer.
Appendix B.3. GCN (Counting Triangles)
We first have three GCN layers, each one generating a 64-dimensional embedding vector for each node. Then, we apply
max-pooling on the features of the nodes and pass the pooled 64-dimensional vector to a one-layer feed-forward neural network with one neuron. Dropout [
55] is applied in between the last GCN layer and the feed-forward layer with probability of 0.1. The model is trained by minimizing the mean squared error (MSE) and is optimized using the Adam optimizer [
56] with a learning rate of 0.005.
We apply the RWRReg on the 64-dimensional node embeddings after the last GCN layer.
Appendix B.4. GraphSage
We use a two layer architecture. For Cora, we sample five nodes per-neighbourhood at the first layer and 5 at the second, while, on the other datasets, we sample 10 nodes per-neighbourhood at the first layer and 25 at the second. Both layers are composed of mean-aggregators (i.e., we take the mean of the feature vectors of the nodes in the sampled neighbourhood) that output a 128-dimensional embedding vector per node. After the second layer, these embeddings are multiplied by a learnable matrix with size , where c is the number of output classes, giving thus a c-dimensional vector per-node. These vectors are passed through Softmax to get the output probabilities for each class. The model is optimized using Stochastic Gradient Descent with a learning rate of 0.7.
We apply the RWRReg on the 128-dimensional node embeddings after the second aggregation layer.
Appendix B.5. GAT
We use a two layer architecture. The first layer uses an 8-headed attention mechanism that outputs an 8-dimensional embedding vector per-node. LeakyReLu is set with slope
. Dropout [
55] (with probability of 0.6) is applied after both layers. The second layer outputs a
c-dimensional vector for each node, where
c is the number of classes, and before passing each vector through
Softmax to obtain the output predictions, the vectors are passed through an Elu activation [
57]. An additional L2-loss is added with a balancing term of
. The model is optimized using Adam [
56] with a learning rate of 0.005.
We apply the RWRReg on the 8-dimensional node embeddings after the first attention layer. A particular note needs to be made for the training of GATs: we found that naively implementing the RWRReg term on the node embeddings in between two layers brings to an exploding loss as the RWRReg term grows exponentially at each epoch. We believe this happens because the attention mechanism in GATs allows the network to infer that certain close nodes, even 1-hop neighbours, might not be important to a specific node and so they should not be embedded close to each other. This clearly goes in contrast with the RWRReg loss, since 1-hop neighbours always have a high score. We solved this issue by using the attention weights to scale the RWR coefficients at each epoch (we make sure that gradients are not calculated for this operation as we only use them for scaling). This way, the RWRReg penalizations are in accordance with the attention mechanism, and are still encoding long-range dependencies.
Appendix B.6. DiffPool
We use a 1-pooling architecture. The initial node feature matrix is passed through two (one to obtain the assignment matrix and one for node embeddings) 3-layer GCN, where each layer outputs a 20-dimensional vector per-node. Pooling is then applied, where the number of clusters is set as 10% of the number of nodes in the graph, and then another 3-layer GCN is applied to the pooled node features. Batch normalization [
58] is added in between every GCN layer. The final graph embedding is passed through a 2-layer MLP with a final
Softmax activation. An additional L2-loss is added with a balancing term of
, together with two pooling-specific losses. The first enforces the intuition that nodes that are close to each other should be pooled together and is defined as:
, where
is the Frobenius norm, and
is the assignment matrix at layer
l. The second one encourages the cluster assignment to be close to a one-hot vector, and is defined as:
, where
H is the entropy function. However, in the implementation available online, the authors do not make use of these additional losses. We follow the latter implementation. The model is optimized using Adam [
56] with a learning rate of 0.001.
We apply the RWRReg on the 20-dimensional node embeddings after the first 3-layer GCN (before pooling). We tried applying it also after pooling on the coarsened graph, but the fact that this graph could change during training yields to poor results.
Appendix B.7. k-GNN
We use the hierarchical 1-2-3-GNN architecture (which is the one showing the highest empirical results). First, a 1-GNN is applied to obtain node embeddings, then these embeddings are used as initial values for the 2 GNN (1-2-GNN). The embeddings of the 2-GNN are then used as initial values for the 3-GNN (1-2-3-GNN). The 1-GNN applies three graph convolutions, while 2-GNN and the 3-GNN apply two graph convolutions. Each convolution outputs a 64-dimensional vector and is followed by an Elu activation [
57]. For each
k, node features are then globally averaged and the final vectors are concatenated and passed through a three layer MLP. The first layer outputs a 64-dimensional vector, while the second outputs a 3two-dimensional vector, and the third outputs a
c-dimensional vector, where
c is the number of output classes. To obtain the final output probabilities for each class,
log(Softmax) is applied, and the negative log likelihood is used as loss function. After the first and the second MLP layers an Elu activation [
57] is applied, furthermore, after the first MLP layer dropout [
55] is applied with probability 0.5. The model is optimized using Adam [
56] with a learning rate of 0.01, and a decaying learning rate schedule based on validation results (with minimum value of
).
We apply the RWRReg on the 64-dimensional node embeddings after the 1-GNN. We were not able to apply it also after the 2-GNN and the 3-GNN, as it would cause out-of-memory issues with our computing resources.
Appendix F. Empirical Analysis of the Random Walk with Restart Matrix
We now analyse the RWR matrix to justify the use of RWR for the encoding of global structural information. We consider the three node classification datasets (see
Section 5 of the paper), as this is the task with the largest input graphs, and hence where this kind of information seems more relevant.
We first consider the distribution of the RWR (we consider RWR, with a restart probability of
, as done for the experimental evaluation of our proposed technique) weights at different distances from a given node. In particular, for each node, we take the sum of the weights assigned to the 1-hop neighbours, the 2-hop neighbours, and so on. We then take the average, over all nodes, of the sum of the RWR weights at each hop. We discard nodes that belong to connected components with diameter
, and we only plot the values for the distances that have an average sum of weights higher than
. Plots are shown in
Figure A2. We notice that the RWR matrix contains information that goes beyond the immediate neighbourhood of a node. In fact, we see that approximately
of the weights are contained within the 6-hop neighbourhood, with a significant portion that is not contained in the 2-hop neighbourhood usually accessed by MPNN models.
Figure A2.
Average distribution of the RWR weights at different distances for the following node classification datasets: (a) Cora, (b) Pubmed, (c) Citeseer. Distance zero indicates the weight that a node assigns to itself.
Figure A2.
Average distribution of the RWR weights at different distances for the following node classification datasets: (a) Cora, (b) Pubmed, (c) Citeseer. Distance zero indicates the weight that a node assigns to itself.
Next, we analyse if RWR captures some non-trivial relationships between nodes. In particular, we investigate if there are nodes that are far from the starting node, but receive a higher weight than some closer nodes. To quantify this property, we use the Kendall Tau-b (We use the Tau-b version because the elements in the sequences we analyze are not all distinct) measure [
59]. In more detail, for each node
v, we consider the sequence
where the
i-th element is the weight that the RWR from node
v has assigned to node
i:
. We then define the sequence
such that
, where
dist(x, y) is the shortest path distance between node
x and node
y, and
is the node with the
j-th highest RWR weight in
. Intuitively, if the RWR matrix is not capable of capturing a non-trivial relationship, we would have that
is a sorted list (with repetitions). By comparing
with its sorted version with the Kendall Tau-b rank, we obtain a value between 1 and
, where 1 means that the two sequences are identical, and
means that one is the reverse of the other.
Table A4 presents the results, averaged over all nodes, on the node classification datasets. These results show that, while there is a strong relation between the information provided by RWR and the distance between nodes, there is information in the RWR that is not captured by shortest path distances.
Table A4.
Average and standard deviation, over all nodes, of Kendall Tau-b values measuring the non-trivial relationships between nodes captured by the RWR weights.
Table A4.
Average and standard deviation, over all nodes, of Kendall Tau-b values measuring the non-trivial relationships between nodes captured by the RWR weights.
| Dataset | Average Kendall Tau-b |
|---|
| Cora | |
| Pubmed | |
| Citeseer | |
As an example of the non-trivial relationships encoded by RWR,
Figure A3 presents a
sequence taken from a node in Cora. This sequence obtains a Kendall Tau-b value of
. We can observe that, for distances greater than 1, we already have some non-trivial relationships. In fact, we observe some nodes at distance 3 that receive a larger weight than nodes at distance 2. There are many other interesting non-trivial relationships; for example, we notice that some nodes at distance 7, and some at distance 11, obtain a higher weight than some nodes at distance 5.
Figure A3.
sequence for the 1000-th node in Cora.
Figure A3.
sequence for the 1000-th node in Cora.