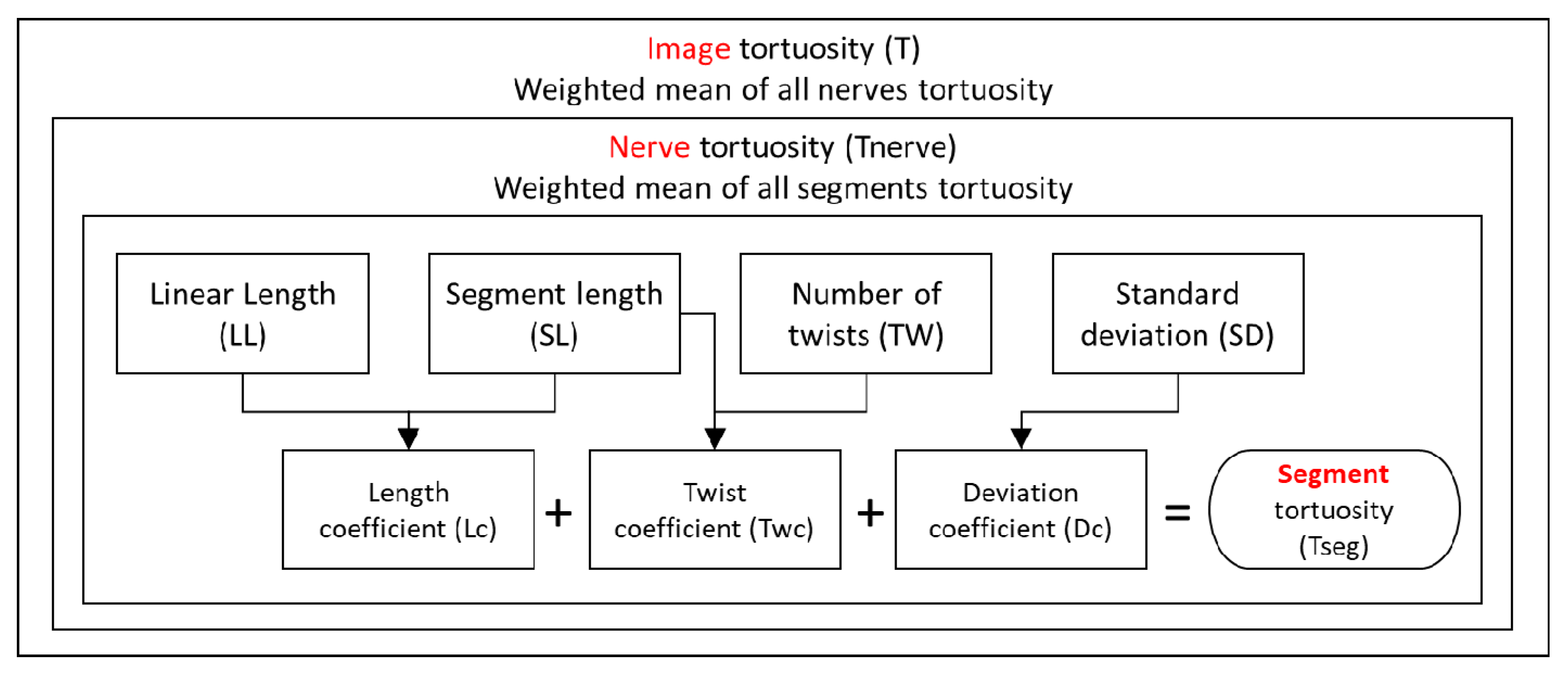
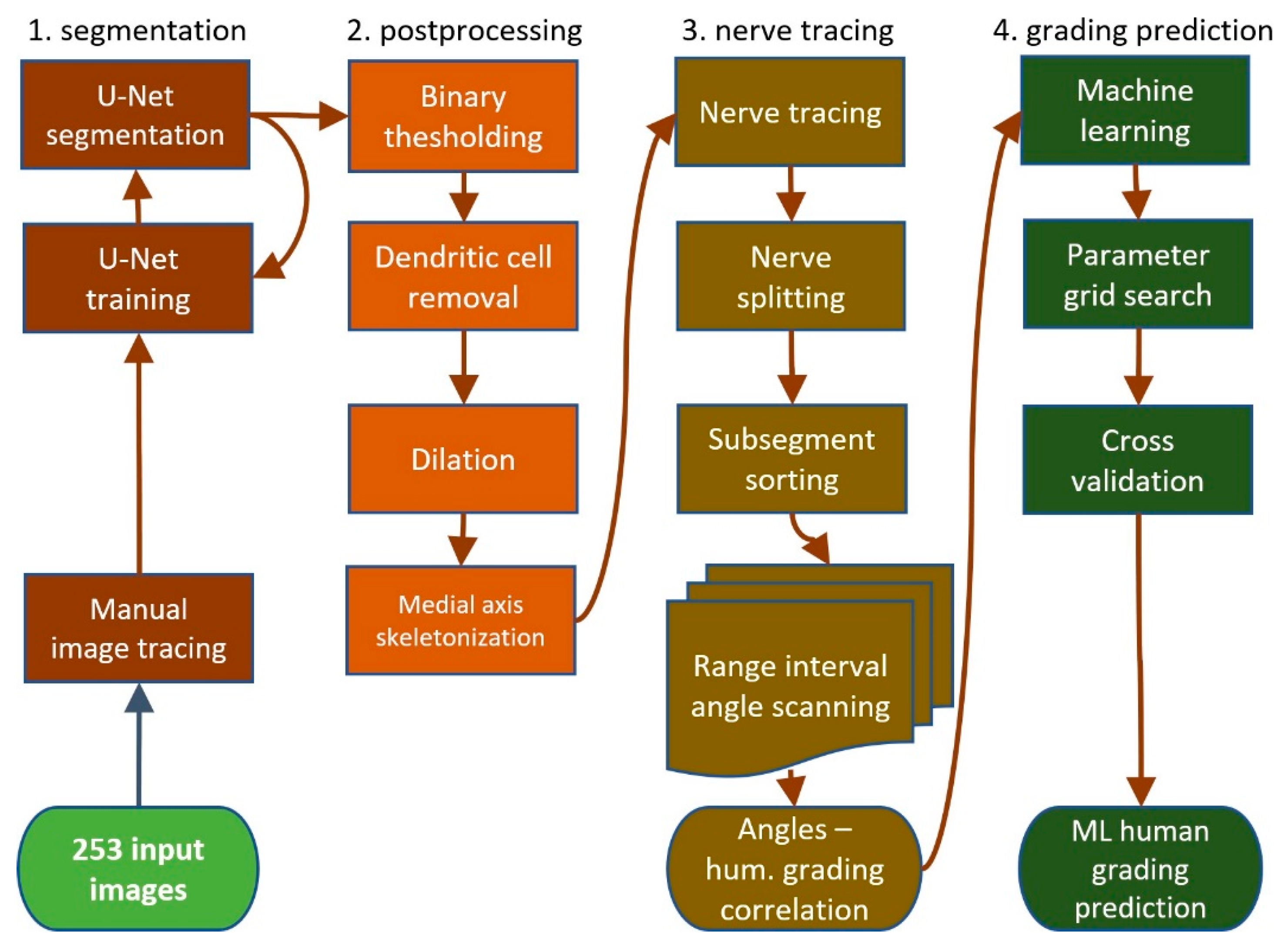
1. Introduction
Corneal nerve tortuosity is a morphological property which indicates the degree of curvature in nerves found in the sub-basal nerve plexus of the cornea. Nerves with low tortuosity (
Figure 1A) appear approximately straight, while high tortuosity nerves have many twists and are significantly curved (
Figure 1B).
Figure 1C shows other anomalies, such as washout, buckling and dendritic cells. Although these anomalies are not evaluated in the scope of this paper, they provide an enduring challenge to developing image analysis tools for clinical assessment of the cornea.
A major challenge for vision science is to estimate corneal nerve tortuosity from single images obtained by using in vivo confocal microscopy (IVCM) [
1]. Eyes are composed of two fused pieces, both the posterior and anterior components [
2]. The anterior component consists of the cornea, iris and lens. The cornea located at the front of human eyes is segmented into five layers [
3]. Schlemm (1831) [
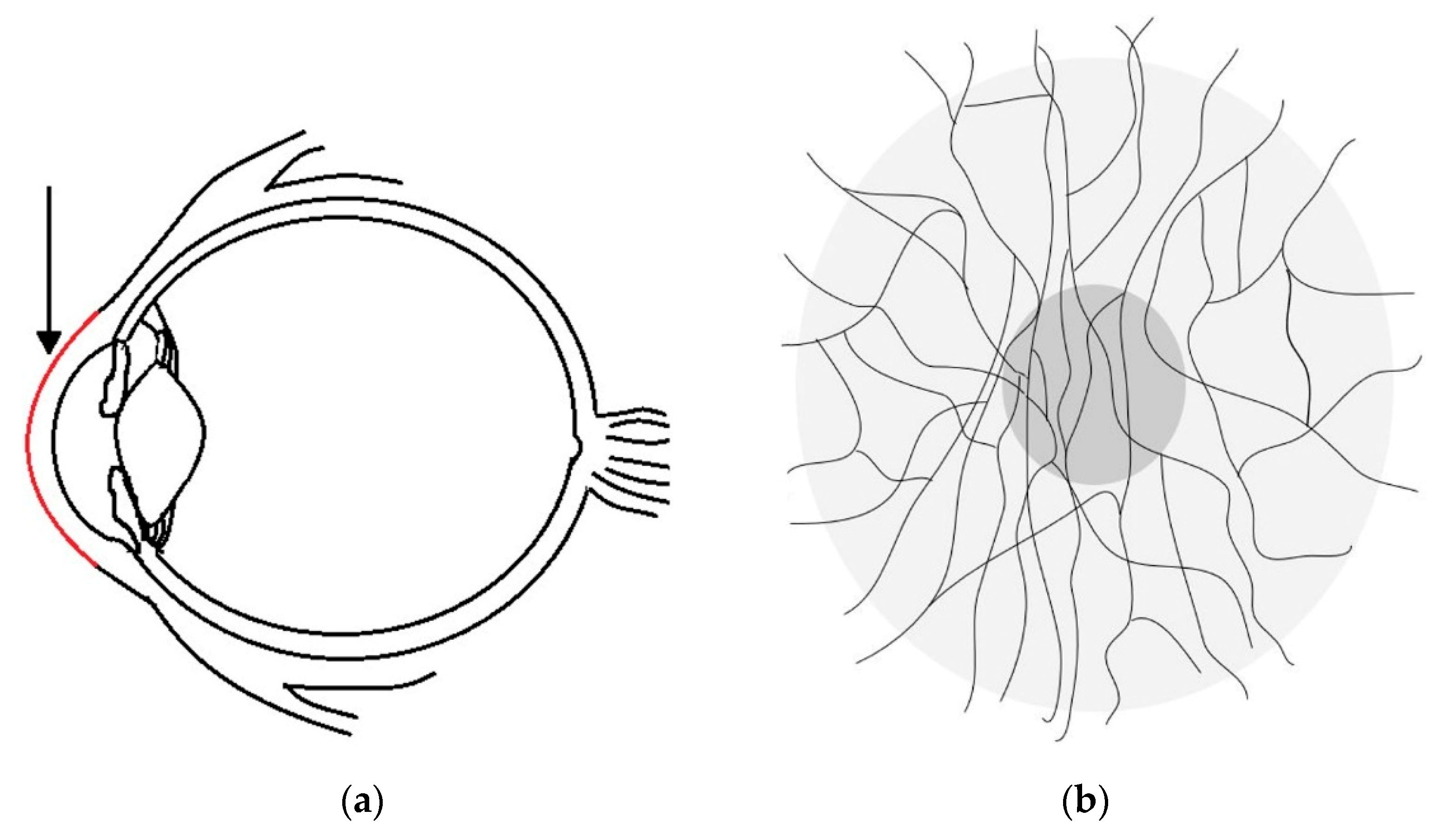
4] discovered nerves between the two outermost corneal layers; their location is illustrated in
Figure 2a,b (side view and front view). In the front view, the thin black lines show an approximate corneal nerve distribution of a healthy individual.
Eye diseases affect hundreds of millions of people worldwide [
5]. Historically, a connection between diseases and nerve dysfunction was established in 1864 [
6], but this research was not extended to corneal nerves until the late 20th century. In 2001, a breakthrough was achieved by Oliveria-Soto and Efron [
7], when they successfully applied IVCM to corneal nerve imaging. Only three years later, in 2004, the first automated system analysing corneal nerves was described by Kallinikos [
8]. Because corneal nerve tortuosity had been found to have a strong correlation with diabetic peripheral neuropathy and dry eye disease [
9], it implied that corneal tortuosity analysis could be helpful for early eye disease diagnosis.
In the ongoing work, Scarpa et al., contributed several algorithms for corneal nerve tortuosity evaluation and provided publicly available corneal image datasets [
10]. On the image acquisition side, Greenwald et al. [
11] reviewed how confocal microscopy was used for imaging corneal structure. Additionally, as of 2015, confocal microscopy was the most popular imaging device next to optical coherence tomography (OCT) [
12]. Among all the confocal microscopes, Tavakoli et al. [
13] noted that “only the Nidek Confoscan 4 and Heidelberg Retina Tomograph HRT III combined with Rostock Cornea Module were commercially available” in 2012. In 2017, a new Rostock Cornea Module with a resolution of 1536 by 1536 pixels became available [
14].
Despite the advances in image analysis, there has been no commonly agreed upon definition for corneal nerve tortuosity [
15]. Lagali et al. [
16] conducted experiments on expert graders with corneal nerve images. This investigation showed that a specific definition improves the agreement in tortuosity grading among experts. Specifically, the definition, “Grading only the most tortuous nerve in a given image,” results in the best intergrader repeatability [
16]. Kim and Markoulli [
15] compared different automated approaches for nerve analysis and produced tracing software to automatically segment contours in the corneal nerve and other medical applications.
Corneal nerve tortuosity could be graded into different levels linked to eye diseases [
8] and was relevant for clinical diagnosis and prevention. Several tortuosity grading scales coexisted with a large number of highly different levels (Resolution from 3 to 800), as compared in
Table 1. “Scale” represents the range of minimum to maximum “level,” and “interval” represents the increment (distance); i.e., for a scale from 1 to 10 there are 10 levels when only considering integers.
The most commonly used tortuosity grading method in the reviewed literature was manual grading; however, it was neither highly standardized nor free of problems. Manual grading was subjective, relied on the experience of the grader, and was difficult to compare and reproduce, as we show in the results section. It was therefore attractive to create a reliable automatic grading system for this measure.
1.1. Recent Work
Colonna et al. [
20] suggested in 2018 to use U-Net convolutional neural networks for corneal nerve segmentation. They achieved segmentation sensitivity that in some instances exceeded human capability while maintaining acceptable runtime. Hosseinaee et al., also proposed a segmentation algorithm to trace sub-basal corneal nerves for in vivo UHR-OCT images [
21] based on image contrast enhancement, thresholding and morphological operations.
In 2019, a study performed by Sturm et al. [
22] revealed that image quality changed the quantification of corneal nerve parameters. In an experiment, images of 75 participants were assessed by semiautomated software and three subjects. They found that lower image quality caused lower tortuosity parameters. Wang et al. [
23] created an architecture to evaluate optic nerve tortuosity using magnetic resonance imaging. They identified that optic nerve tortuosity may correlate with glaucoma. In summary, most reviewed recent publications focused on automatic cornea nerve segmentation but not on tortuosity estimations of the segmented nerves.
1.2. Purpose of This Work
The purpose of this study was to create a measure of tortuosity for normal healthy eyes that could then be used as a reference for future works on the diagnosis, detection and classification of eye diseases. We therefore sought to build automatic human corneal nerve tortuosity grading systems which may replace the time intensive and perceptually biased subjective tortuosity grading.
Our two primary research questions were: (i) How can we improve the corneal nerve tortuosity grading process? How are automated methods compared against subjective tortuosity gradings? and (ii) What is the ideal number of tortuosity grading levels?
3. Results
We compared four different tortuosity estimation methods: (i) a subjective grading baseline, (ii) an automated tortuosity estimation built on a previously published segmentation method, (iii) a completely new approach using segmentation and automatic tortuosity estimation and (iv) direct image classification using deep learning. We established a baseline accuracy for subjective corneal nerve tortuosity gradings. This baseline was created by re-grading the 253 IVCM images with two test subjects. Additionally, another informal experiment was conducted in which 10 experts were employed to grade the same four images. Two test subjects were asked to re-grade all 253 images on a scale from 0.1 to 1.0 in 10 steps. Both test subjects gave 70/253 (28%) images the same grading. Subject one graded the images on average 0.27 and subject two 0.36, respectively. The standard deviation between both gradings was 0.15 grades. Both subjects graded most images 0.3, but subject one graded 0.2 second most, and subject two graded images 0.4 second most, in line with subject two’s higher average gradings.
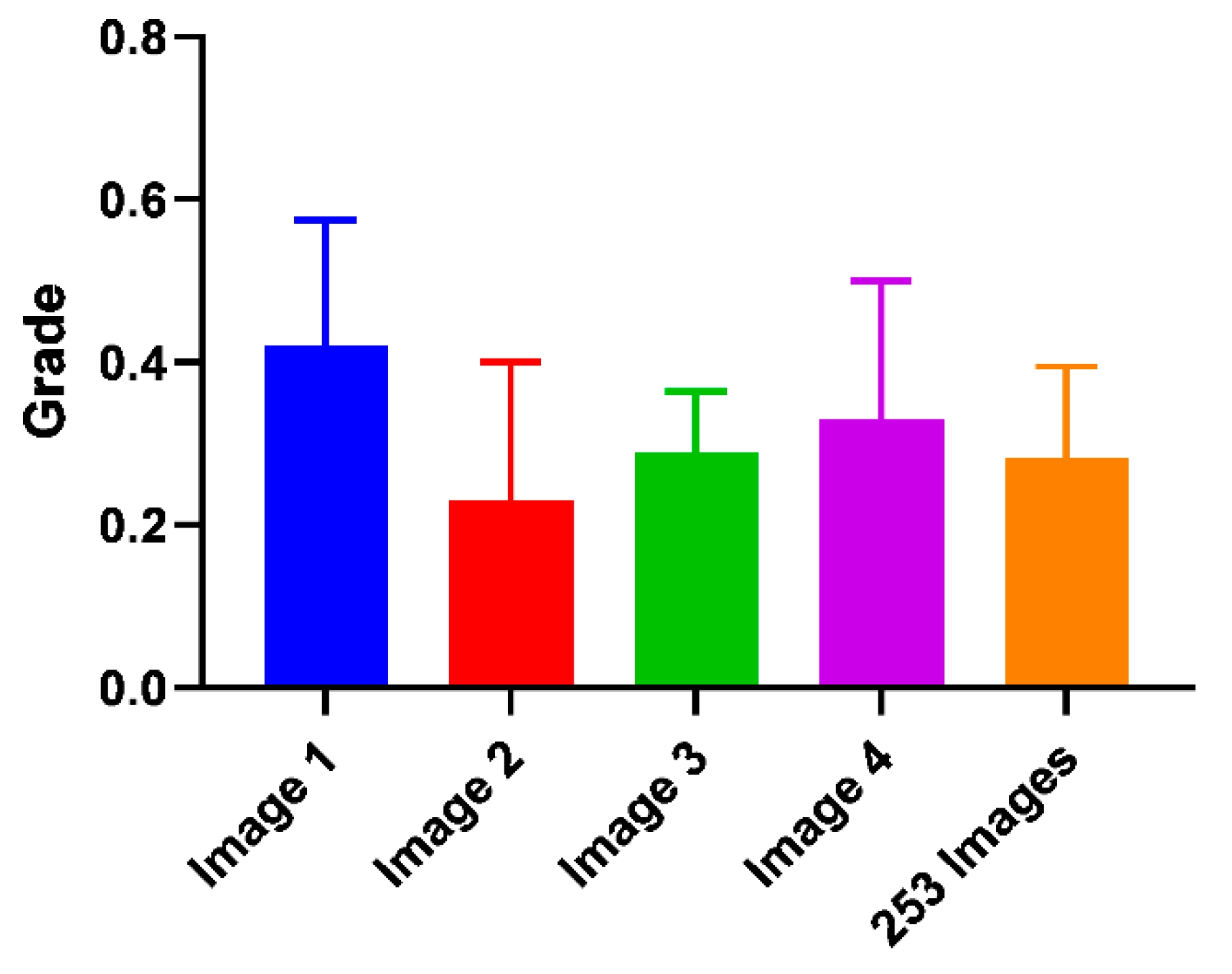
For the informal experiment, 10 experts in the clinical optometry domain were asked to grade four corneal nerve images (
Figure 12). Image four was the same as image one but had three outliers going against the dominant direction of the other nerves removed. The average grade for image one was 0.42, and for image four 0.33, there was a difference of 0.09. The standard deviation for images one to four from the subjective grading bias experiment was plotted below as well as the manual grading comparison between two test subjects:
The difference in the average grade of images one and four was 0.09 compared to the standard deviation of 0.15 and 0.17 for these classes.
The Cfibre tracing performance percentage varied from 35% to 110%. In general, Cfibre had an average positive tracing rate of approximately 80%. The images with uniform illumination and high nerve-background contrast showed a high positive tracing rate of 75%–80%. For images with high variation in illuminance and low contrast, it achieved a lower tracing rate of around 40%. Some images showed percentages greater than 100%; this was due to false tracing of noise as nerves. For example, for images containing dendritic cells, the positive tracing was about 85%; however, this included false positive tracing of dendritic cells as nerves. Similarly, for some images the tracing percentage exceeded 100% due to false tracing. About 80% of all images in our dataset had a tracing rate ranging between 70% and 100%. For 18% of all images the tracing percentage was below 70%, while for 6 images the tracing percentage was over 110%.
In some images, branches were traced but not completely and they were not connected to their respective parent nerves. Thus, they seemed to appear as two separate nerves rather than one single nerve with multiple branches. Cfibre recorded the highest accuracy compared to subjective grading for class 0.1 with an accuracy of approximately 53%. Thus, it meant that the Cfibre approach could calculate the tortuosity for low tortuosity nerves but had a low accuracy for high tortuosity. The skewed distribution could be explained by four potential image-based causes: over-segmentation, incorrect thresholding, lack of precise definition of tortuosity and human perception in manual grading. Rather than only relying on accuracy, we evaluated the results on three more relevant metrics; namely, precision, recall and f1-score (
Table 3). Precision was the ratio of correctly predicted images of all identified images of that class, and was around 0.34 for class 0.4 and 0.5–0.52 for class 0.6. Recall that the ratio of correctly predicted images to all images was between 0.34 for grades 0.3–0.5 and 0.56 for grade 0.1. Support was the number of samples in the respective class.
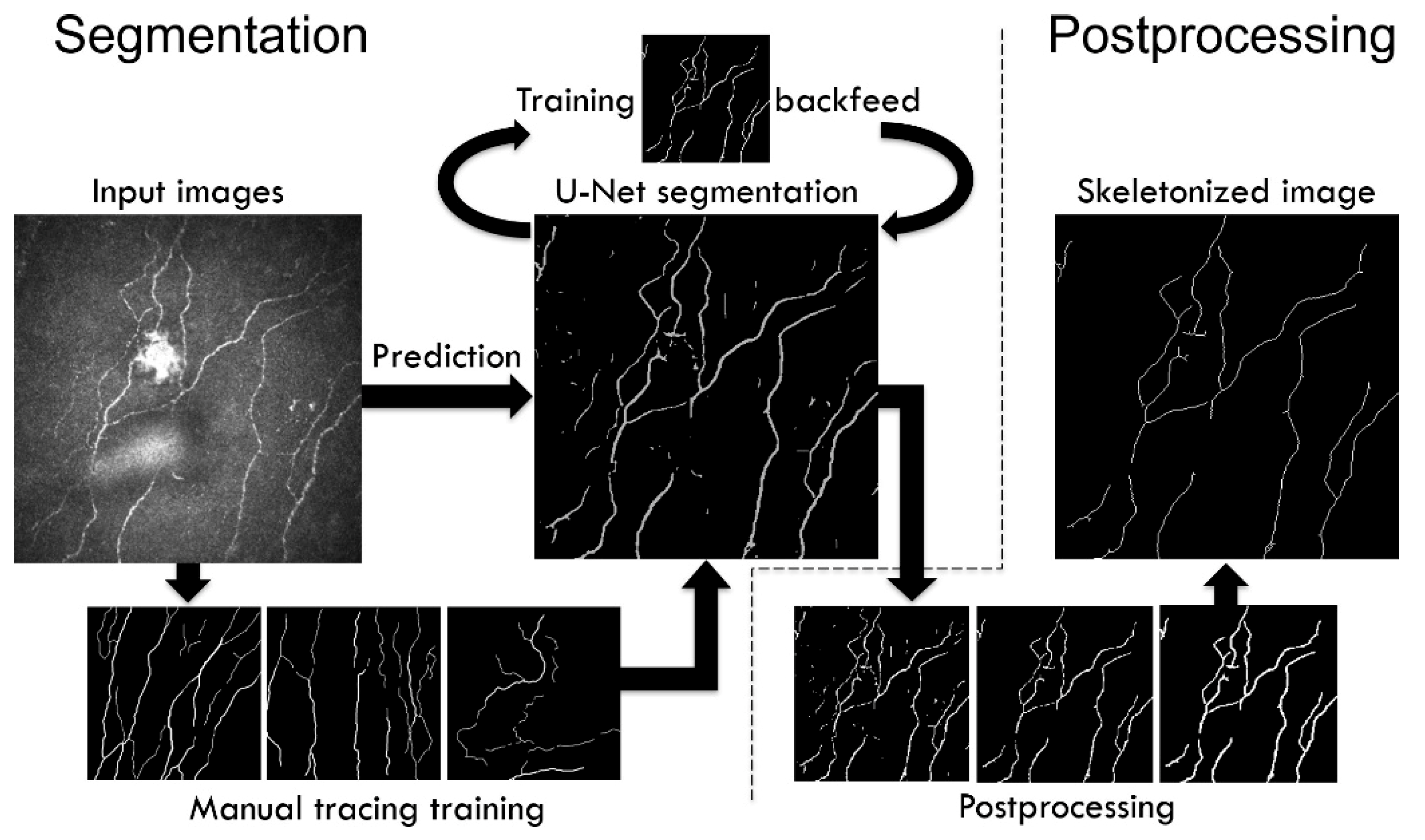
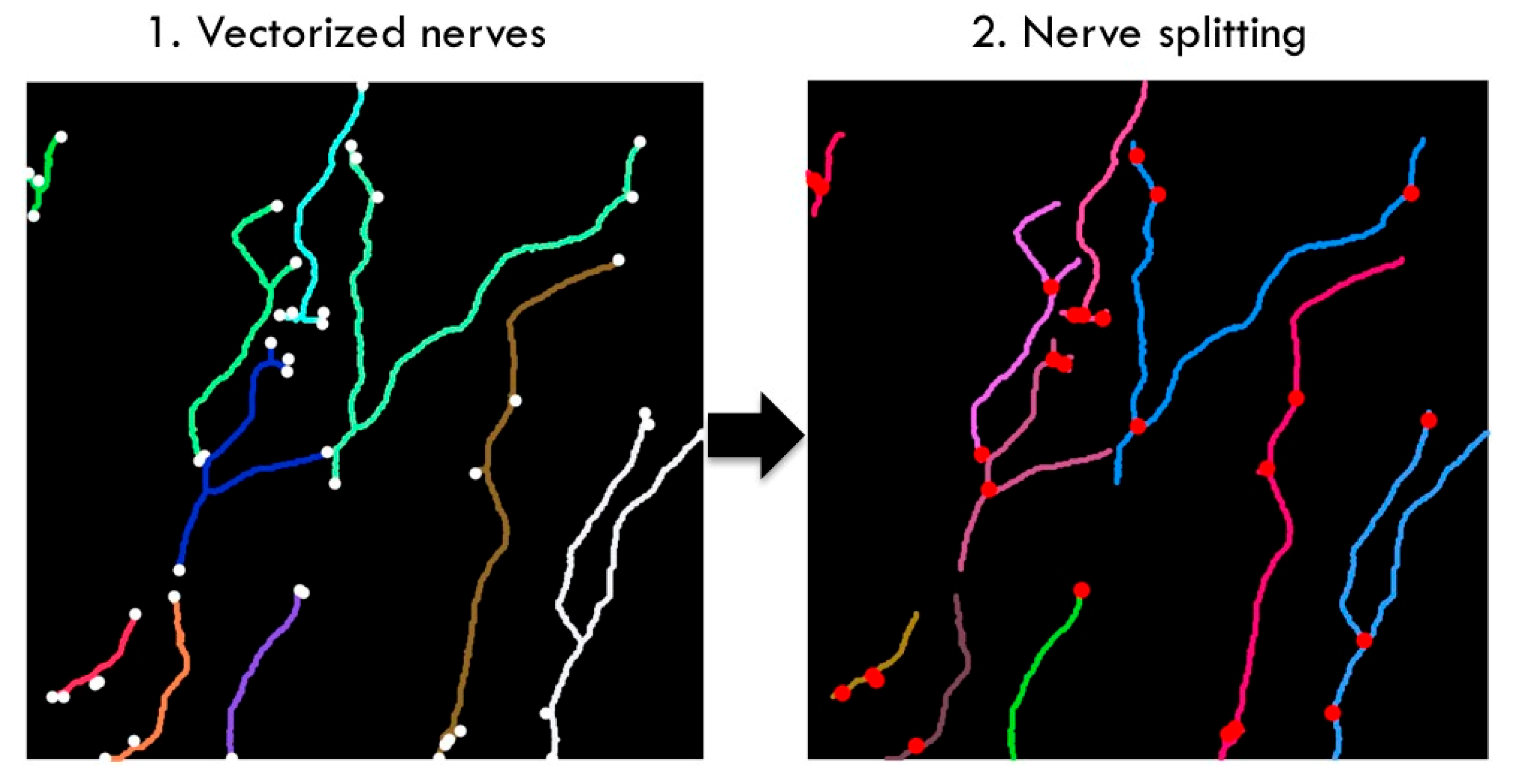
The first major intermediate result of the U-Net segmented adjacent angle detection method was the segmentation output of the U-Net and postprocessing. We assessed our segmentation performance by estimating the positive nerve tracing rate compared to manual nerve tracing for 20 random samples of our dataset. We particularly assessed segmentation performance regarding images with noise and anomalies. Some of these anomalies contained in IVCM images are buckling effects (
Figure 1 C3). These are caused by curvatures in the corneal surface due to applanation of the imaging device. From 20 random samples out of our dataset, we subjectively estimated the positive nerve tracing rate compared to manual tracing as better than 80% despite buckling effects. The lowest positive tracing performance compared to manual nerve tracing was observed for images with low contrast (lower than
Figure 6 left), which we estimated at ca. 60%. Although the true positive tracing performance was estimated to exceed 90% for images with many dendritic cells (
Figure 7 left), dendritic cells also led to an increase in false positive tracing rate.
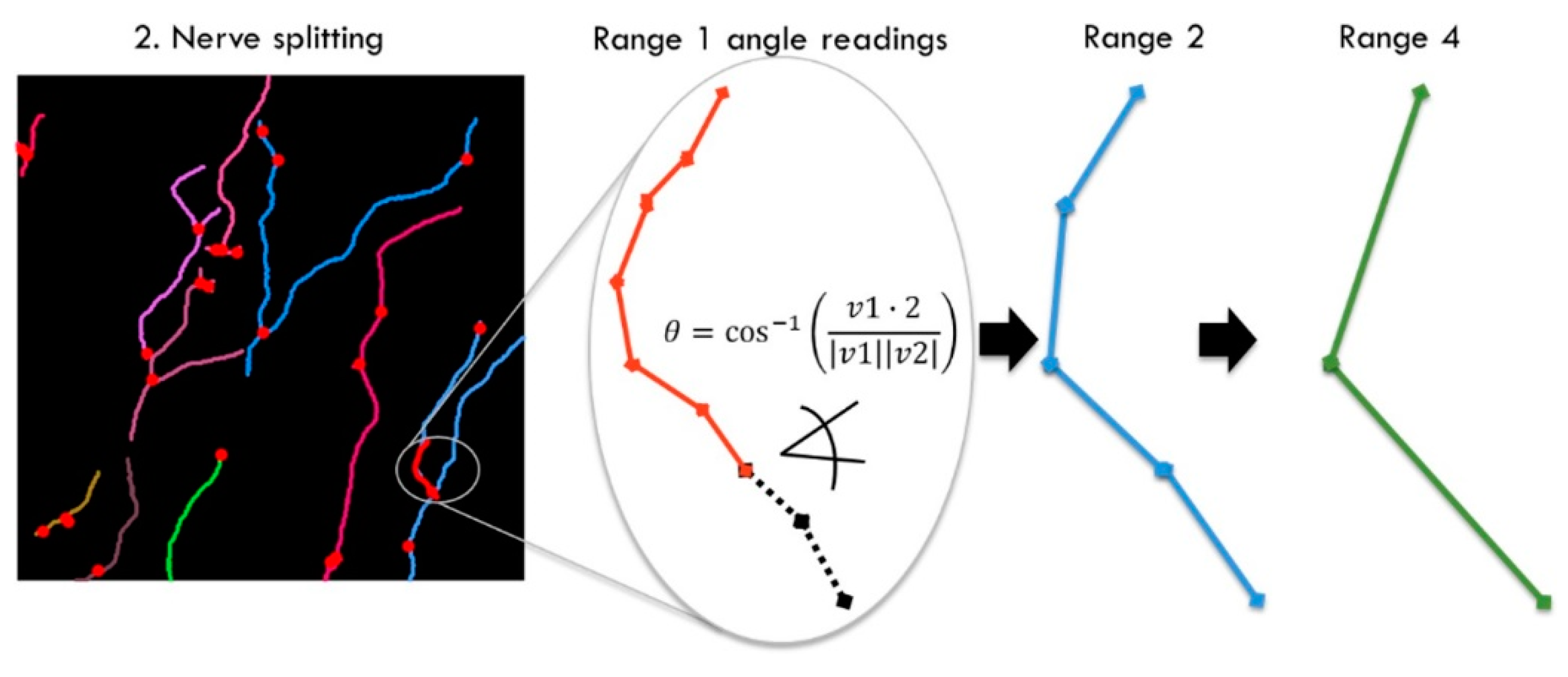
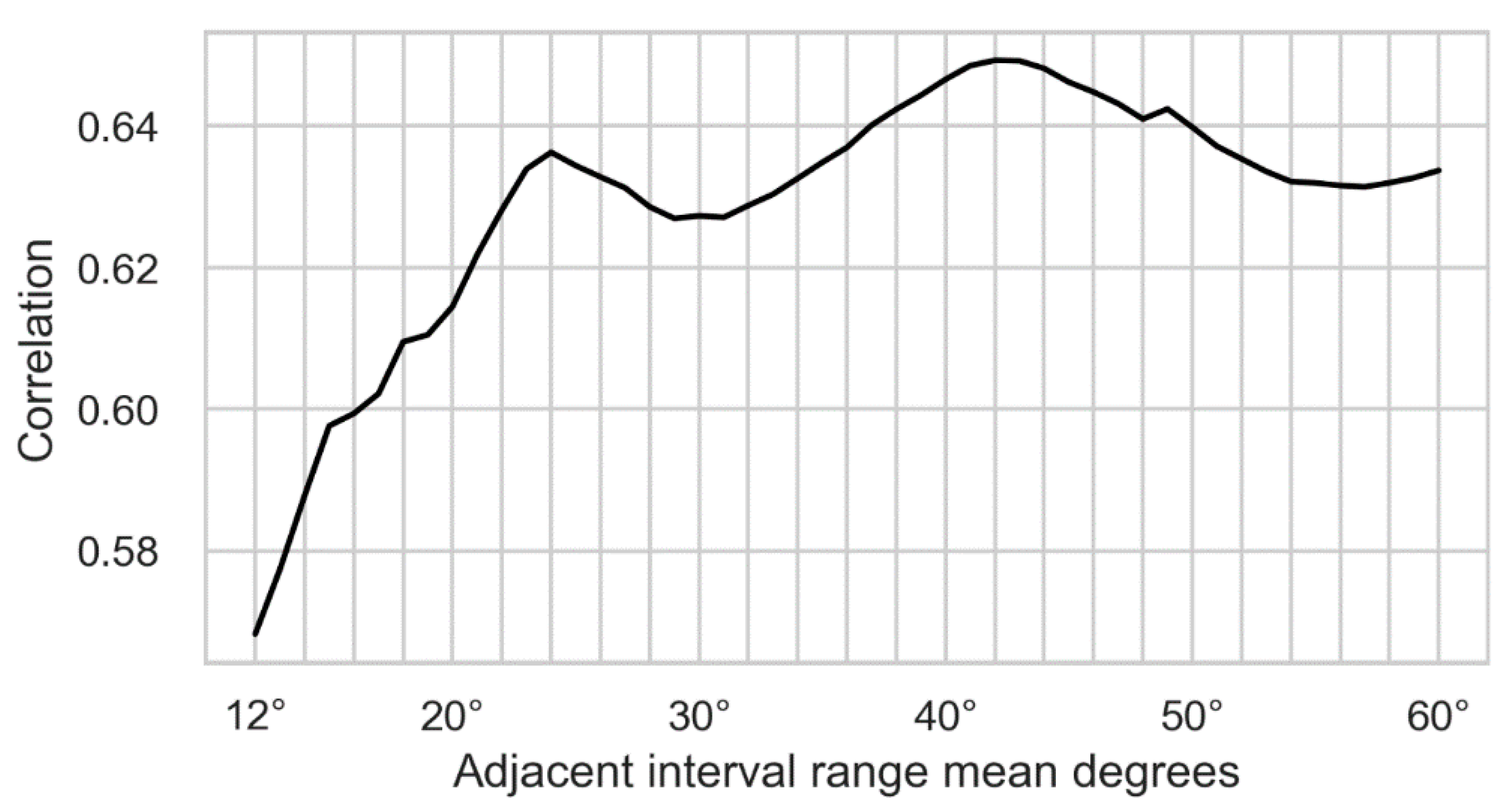
Initially, we recorded adjacent angles in a larger range, from 1–80, but then discarded ranges below 12 and above 60 for our dataset. Those ranges were removed for different reasons. For the prediction of subjective grading based on machine learning methods, it was required that the adjacent angles used for training showed a positive correlation with human grading. The adjacent angles were calculated for vectors on the raster given by the image pixels; therefore, the shorter the range, the fewer the possible discrete angles. This led to short ranges not exceeding a correlation significantly more than random chance, as can be observed by the correlation in
Figure 13 dropping towards randomness on the left. The highest correlation of the weighted angles was achieved for range 44 at ca. 0.65.
Since adjacent angles were always calculated between two nerve segments, it was required to have at least two such segments in the image. The longer the range, the fewer segments a nerve could be broken down into. Specifically, an adjacent angle calculation of range of 60 required at least two nerve segments of at least 60 pixels in length each. For our dataset, the highest range of 60 was determined empirically and the number of suitable nerves dropped off steeply around this range. In
Figure 13 the ranges are plotted on the x-axis and the correlation with human grading on the y-axis:
The number of vectors is dependent on the original image pixel grid, and therefore its resolution; they could also be converted into lengths. The microscope had a viewing area of 49 by 49 µm at a corresponding resolution of 384 by 384 pixels. To convert the vector range to µm, it had to be considered that a vector in parallel with the pixel grid had a smaller corresponding length than vectors of different orientation. The longest corresponding length resulted from vectors diagonal to the pixel grid with their equivalent length times √2 of those in parallel. A normal distribution of the nerve directions was assumed, and the length corrected on average between parallel and diagonal directions; this resulted in the following length correction factor:
With the correction factor Fn
correction, the nerve segment length that showed the maximum correlation with human grading could be calculated as follows:
The maximum correlated range equivalent was plotted in
Figure 14 to show the range in scale. Two highly correlated USAAD vector elements with an equivalent length of ≈6.8 µm are shown in the red circle.
Although the adjacent angles could be considered a corneal nerve tortuosity grading result, we also used the adjacent angles to predict a subjective grading using machine learning. The overall highest accuracy compared to subjective gradings of 41% was achieved with a multi-layer perceptron (MLP) classifier; its parameters were found by grid search. The parameters with the biggest effects were the hidden layer size and structure. The tolerance had to be increased to 0.0018 to ensure convergence. The overall accuracy could be increased to 43% by reducing the hidden layers to 1 × 120 instead of 2 × 60; however, this led to a very imbalanced prediction with accuracy of ca. 70% for class 0.1 and 0.6, but only random (20%) for class 0.3. The more balanced prediction of 2 × 60 layers was preferred and used in our final model. All results were 10x cross fold validated and the classification run 10× to average its results.
The overall accuracy (the ratio of correctly predicted images of all images) was 40%. Accuracy for the outermost classes 0.1 and 0.6 was highest, the prediction accuracy of all classes exceeded chance by at least 8%.
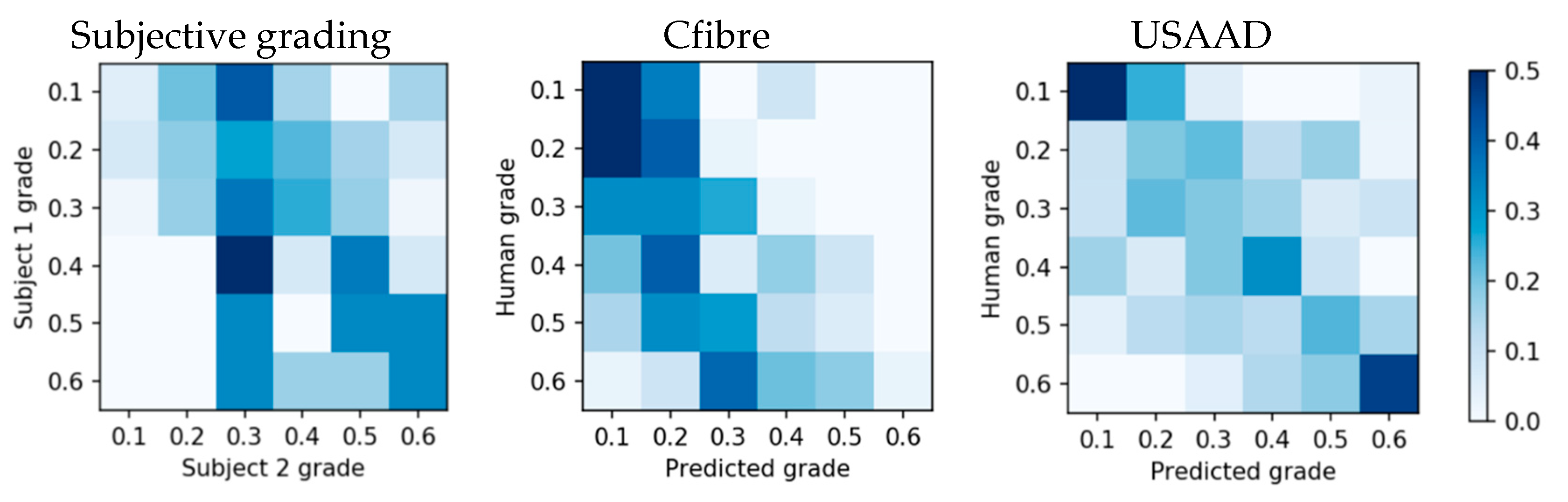
The subjective grading confusion matrix showed that the highest grading overlap was between grade 0.4 and 0.3 (
Figure 15 left), instead of on the same grade, and its accuracy did not exceed chance for all grades. Compared to subjective gradings, Cfibre (
Figure 14 center) showed high accuracy for images with low tortuosity, but lower accuracy with increasing tortuosity grade. No clear centreline is visible and accuracy did not exceed random for all grades. The centreline of the adjacent angle method (
Figure 15 right) was most visible and the prediction accuracy exceeded random for all grades.
Direct image classification accuracy with AlexNet and VGG-16 did not yield results exceeding chance for our balanced dataset. AlexNet predicted a tortuosity of 0.1 or 0.5 for all images, depending on random seed initialization. VGG-16 permanently predicted a tortuosity of 0.6 for all test images. We compared how accurately Cfibre, USAAD, AlexNet and VGG-16 predicted the rounded tortuosity gradings of our two subjective graders. We used the average F1 score, a measure for test accuracy considering both precision and recall. Our dataset was balanced; therefore, the F1 average scores did not have to consider weights for each class. The results are shown in
Table 4.
4. Discussion
Automatic curation of medical images has been in use in various domains of medical research [
29,
30]. In this research we show that automatic measurement of corneal nerve tortuosity is possible. We established a baseline for subjective corneal nerve tortuosity grading accuracy. For this task, two subjects received 13 images which were previously graded by an expert, two each of class 0.1–0.6. Only one image of class 0.7 was provided due to the limited availability of images in this grade. This was followed by each subject manually grading the 253 IVCM images on a scale of 0.1 to 1.0. Both test subjects’ gradings of our images were centred around class 0.3. The mean gradings were 0.27 and 0.36 respectively. The result showed both test subjects’ tortuosity grading maxima at 0.3. Randomly graded images collected of the eyes of the participants in this project supported this distribution; within 20 randomly graded images, none were more than 0.1 grades above or below 0.3. We measured a subjective grading normal deviation of 0.15 classes on a scale of 1.0 with 10 steps. This indicated that a subjective corneal nerve tortuosity grading scale of 10 steps was challenging, but not clearly an order of magnitude above what was possible.
For our informal experiment in which 10 experts each graded four images, we found that subjective gradings may have not been directly proportional to individual corneal nerve tortuosity. Our results indicated that outliers which strongly go against the otherwise dominant direction of the nerves may have swung subjective grading towards more tortuous. The mean grade for the image with the outliers removed was 0.09 lower on average in support of our hypothesis. However, the standard deviation of the manual gradings of these images by the 10 experts was relatively large (0.15 and 0.17) and not statistically significant. The standard deviations for the two unrelated images 2 and 3 were 0.17 and 0.07 respectively. For all subjective gradings, the standard deviation had always been between 0.07 and 0.17 relative to a scale of 0.1 to 1.0. This finding confirms that although 10 steps might be difficult to achieve by subjective grading, it is not too far off.
As evident from the results of the tortuosity estimation by Cfibre, we found that tortuosity estimates were highly skewed in favour of the first three grades. The reasons for this were assumed to be the following:
Over-segmentation because the nerves were broken into individual segments at the intersection points.
Human perception: The very fact that tortuosity gradings by subjects were partly influenced by their perception induced a lot of subjectivity, resulting in variation in the grading of the same image by different subjects. The image which may have been classified as 0.6 by one subject may have been graded as 0.3 by another.
There was no universally accepted scientific definition of tortuosity.
USAAD produced several results which could be interpreted as corneal nerve tortuosity gradings. The first result related to the raw angles in multiple ranges. Before the quadratic weight was added and before the angles were averaged, this was a raw and linear measurement of the angles of all the nerves in the images. However, as also mentioned in the Cfibre discussion, it was not defined at the time of writing which exact tortuosity parameters were required for eye disease detection and prevention. It was not possible to assess whether these results or subjective grading results may have done better in this regard.
Both Cfibre and USAAD predicted all images of the balanced dataset better than chance, ranging from slightly below 30% to over 50%, and therefore possibly even better than our two subjects. Corneal nerve tortuosity gradings were found to have several problems which should be addressed in future. The biggest issue was that the desired morphological corneal nerve parameters for medical applications were not exactly defined. The most commonly used method was a subjective assessment which appeared to include a high statistical error and systematic error in some cases.
Direct image classification with AlexNet and VGG-16 did not exceed random accuracy for our dataset. We expected that this was caused by at least two reasons. Deep learning accuracy typically increases with training sample quantity, and a minimum number of training samples is required to exceed random accuracy. Cho et al., analysed prediction accuracy dependence on training sample quantity by training a convolutional neural network on medical datasets [
31]. They used six classes of computed tomography images to train a GoogLeNet and systematically increased training dataset size, starting at five images per class. They exceeded random classification accuracy at 50 images per class.
We suspected that the second reason for not exceeding random accuracy with direct image classification was the similarity of the images in our dataset. Although we did not confirm this mathematically by, for example, calculating the Eucledian distance for the dataset by Cho et al., and ours, images in their dataset appear subjectively more dissimilar than ours; for example, a head CT image compared to a shoulder CT image.
The advantages of the proposed Cfibre and USAAD methods were that they were able to predict subjective grading with an accuracy better than chance for all classes. They outperformed direct image classification with AlexNet and VGG-16 for our dataset. Additionally, USAAD extracted raw tortuosity information from all nerves in a given image. These extracted short to long range angles were available for every nerve, which could be used for further medical analysis and development of a standardized corneal nerve tortuosity definition. We showed that these angles can be used to automatically predict subjective grading using machine learning.
We also identified disadvantages. Due to the limited availability of corneal nerve images, we could not show that our methods outperformed direct image classification for large datasets. The subjective tortuosity grading differed between two subjects; therefore, we suggest discussing and refining a standardized medical definition of corneal nerve tortuosity, for which our extracted raw angle data could be used.
5. Conclusions
Previous studies in the field have used tortuosity grading ranges that have been very limited [
19] or broad [
8]. Can the human visual system accurately differentiate between 0–8 levels in 0.01 intervals [
10] or even between 0–70 tortuosity coefficients in 0.01 intervals [
8]? We found slight variability in the frequency distribution of tortuosity ratings between graders using whole number intervals in our ten-point scale (1–10). However, the modal response was still centred around a value of three between graders. This would suggest that our 10-point scale was sufficient for characterising the shape of the true distribution in tortuosity parameters of corneal nerves imaged. The variability in uniformity of these estimates between graders would suggest that decimal-level sampling was not necessary for characterising the subjective estimation of these distributions. Indeed, if we were to use a three-point scale, we can expect there would have been greater correspondence in the distributions of subjective rating between our graders.
In our study, we used as many as 10 levels to observe some slight disintegration between these ratings. Although this range might seem large because it could be beyond the sampling resolution of the average subjective grader, it does offer added utility for future research. We found that the distribution of scores ranged up to six for our sample of images from normal healthy individuals. Based on previous research [
8], we would anticipate a 50% increase in the mean distribution of tortuosity coefficients in some clinical populations (e.g., controls versus those with severe diabetic neuropathy). The 10-level scale would offer the dynamic range to accommodate this increase above the baseline we report in the current study.
Our results indicated that human corneal nerves may have been centred and normally distributed around what we measured as grade 0.3, with very low and very high tortuosity grades being rare. Our automated methods, especially the adjacent angle method, created more reproducible results which may have already exceeded subjective gradings depending on which exact parameters are desired. We also developed an entirely new tortuosity grading method which can extract a lot of information from corneal nerve images or other biomedical images and may have exceeded the amount of extracted nerve information of previous methods, which we will analyse in future work. We established that a grading scale of 10 steps was likely on the upper end of subjective grading accuracy, but in the right order of magnitude. This range also appears to be close to ideal for the automated methods, as well as subjective grading with additional improvements.