A Python Algorithm for Shortest-Path River Network Distance Calculations Considering River Flow Direction
Abstract
1. Introduction
2. Description
2.1. Overview
2.2. Input Requirements
2.3. Network Requirement—Best Practices
- Delete duplicate nodes
- Delete duplicate geometries
- Correct or remove small and large overlapping lines
- Correct or remove geometries within other geometries
- Eliminate self-intersections and self-contacts
- Correct lineString overshoots, undershoots, and dangles
- Rivers and lakes represented by shorelines need to be “collapsed” and represented by a centerline, as a GIS network should be made with lineStrings only and not polygons or closed (self-contact) lineStrings
2.4. Network Requirements
- MultiLineStrings need to be converted to LineStrings.
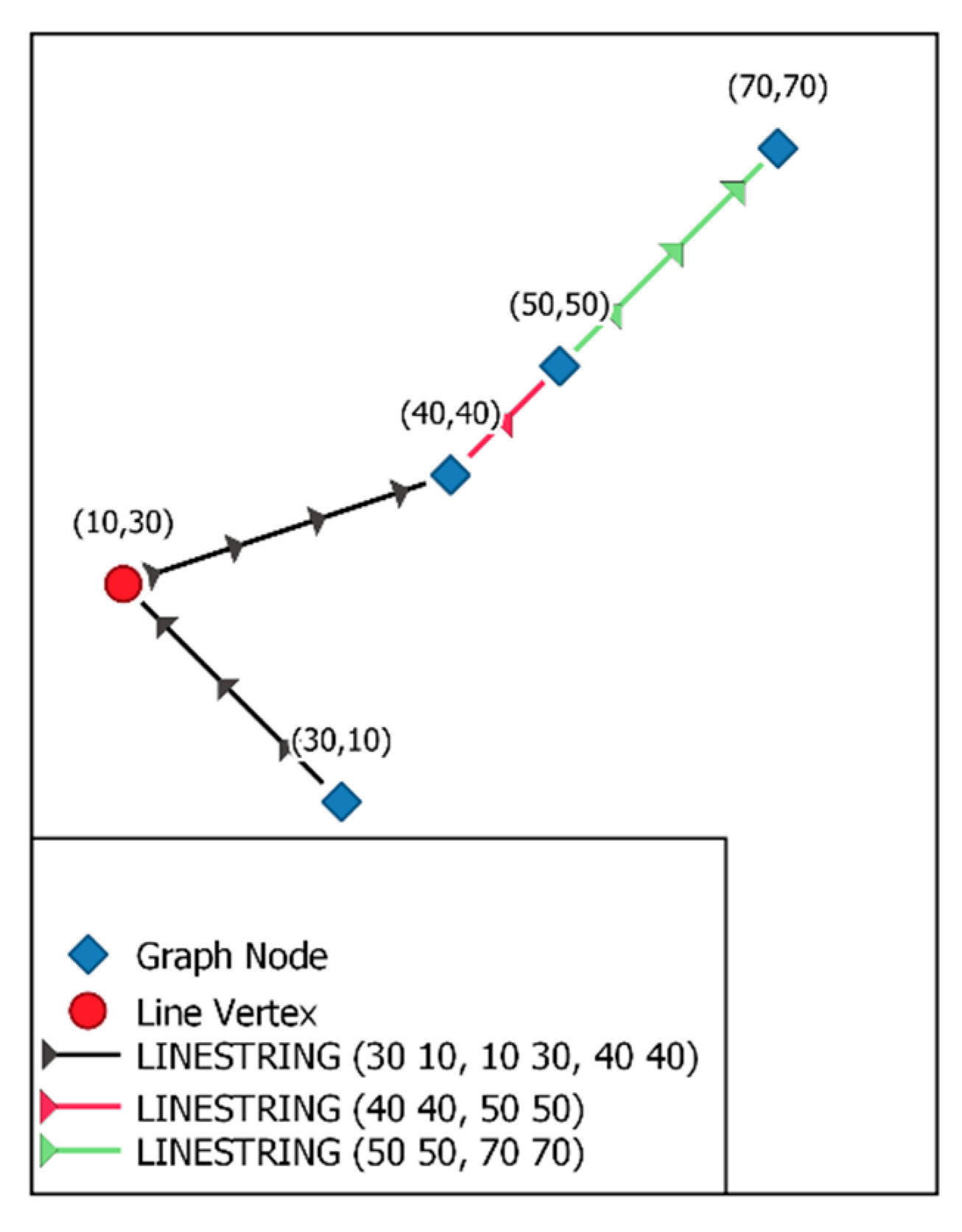
- LineString first or last vertex must snap (have identical coordinates) with the next object’s first or last vertex if they represent the same physical entity (river, lake…) or two physical entities that are connected. No error tolerance is built in the software.
- Lines must all be vectorized from upstream to downstream. When topography is complex, this can be facilitated by draping the two-dimensional (2D) shapefile on a DEM, such as the NASA DEMs (latest SRTMs) [31]. This adds the altitude value to the Z value for each lineString vertex. LineStrings can be automatically flipped (or reversed) if the last vertex Z is higher than the first vertex Z (vectorized going upstream). All of the lines must still be manually checked for errors and most GIS packages offer lineString reversal tools. In most GIS software, line direction can be visualized by adding a simple marker (like a triangle) to the line style. The triangle can be pointed in the vectorized direction. Every line’s last vertex needs to be snapped to the next line’s first vertex. If this is not the case, then it is assumed that the end of a stream has been reached, the water flow is reversed, or there is an error in the vectorization direction.
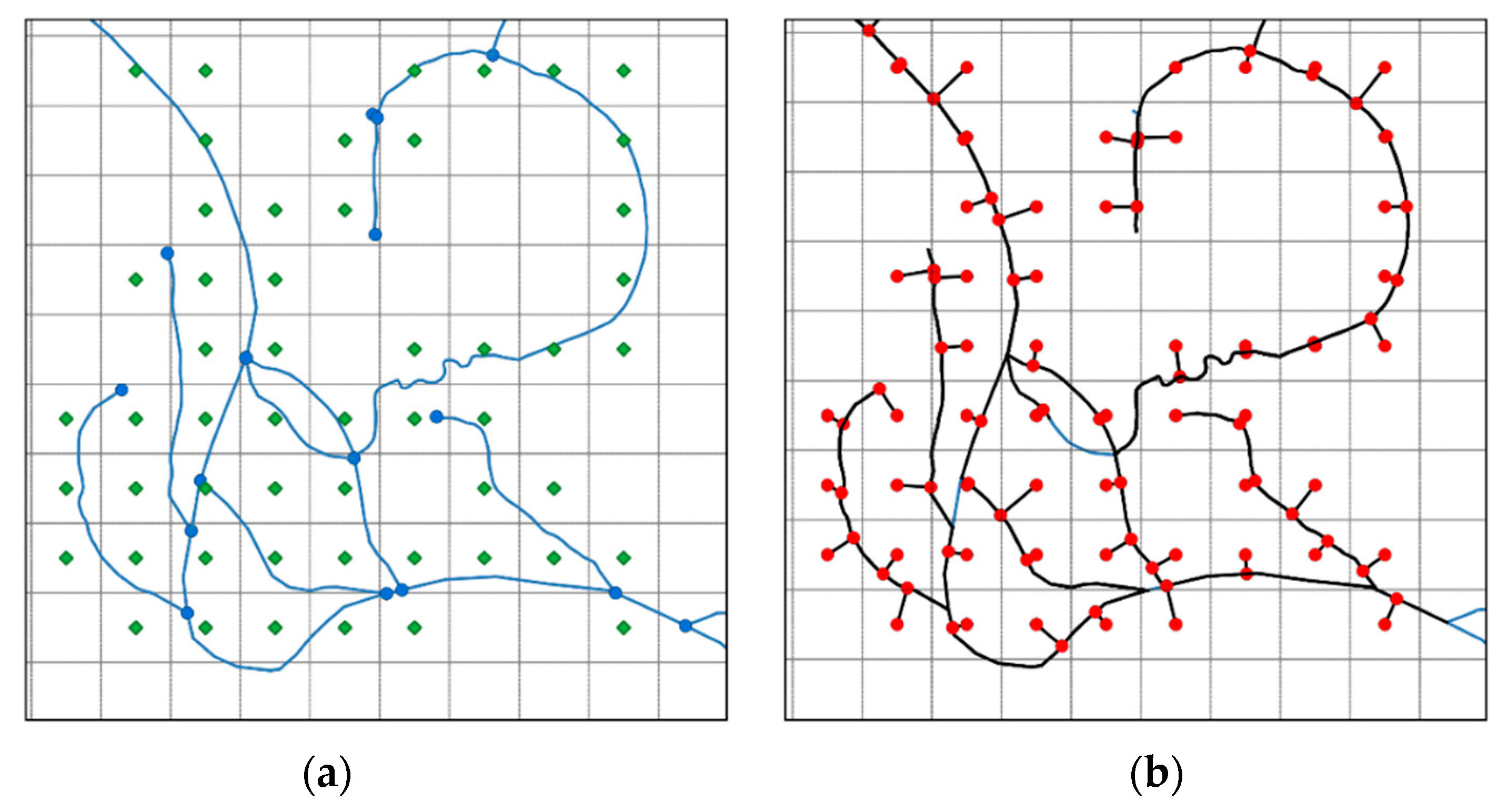
- Most importantly, users have a tendency to vectorize single entities while using a single line object (one road = one line) (or polygon) and to snap lines using middle vertices. This simplifies the database and the drawings. However, for a graph network analysis, the lines must be broken (or split) at each intersection and snapped to all other lines in that intersection. Tools, like “planarized” in ESRI ArcGIS or “v.clean” (break, snap) in QGIS, can help. In some cases, network segment areas also split where there is no intersection. Manipulations, like dissolve and merge, followed by a multipart to single part transformation, will reduce unnecessary splitting, but will, in the process, destroy the database. These manipulations may, in return, reduce the processing time if the GIS network is unnecessarily complex.
3. Methods and Implementation
3.1. Program Overview
- Package are imported
- User Input variables are defined
- Functions are defined
- Output directories are created. See create_directory() function.
- GeoPandas reads the input network shapefile using the read_shape_file_to_gpd_df() function.
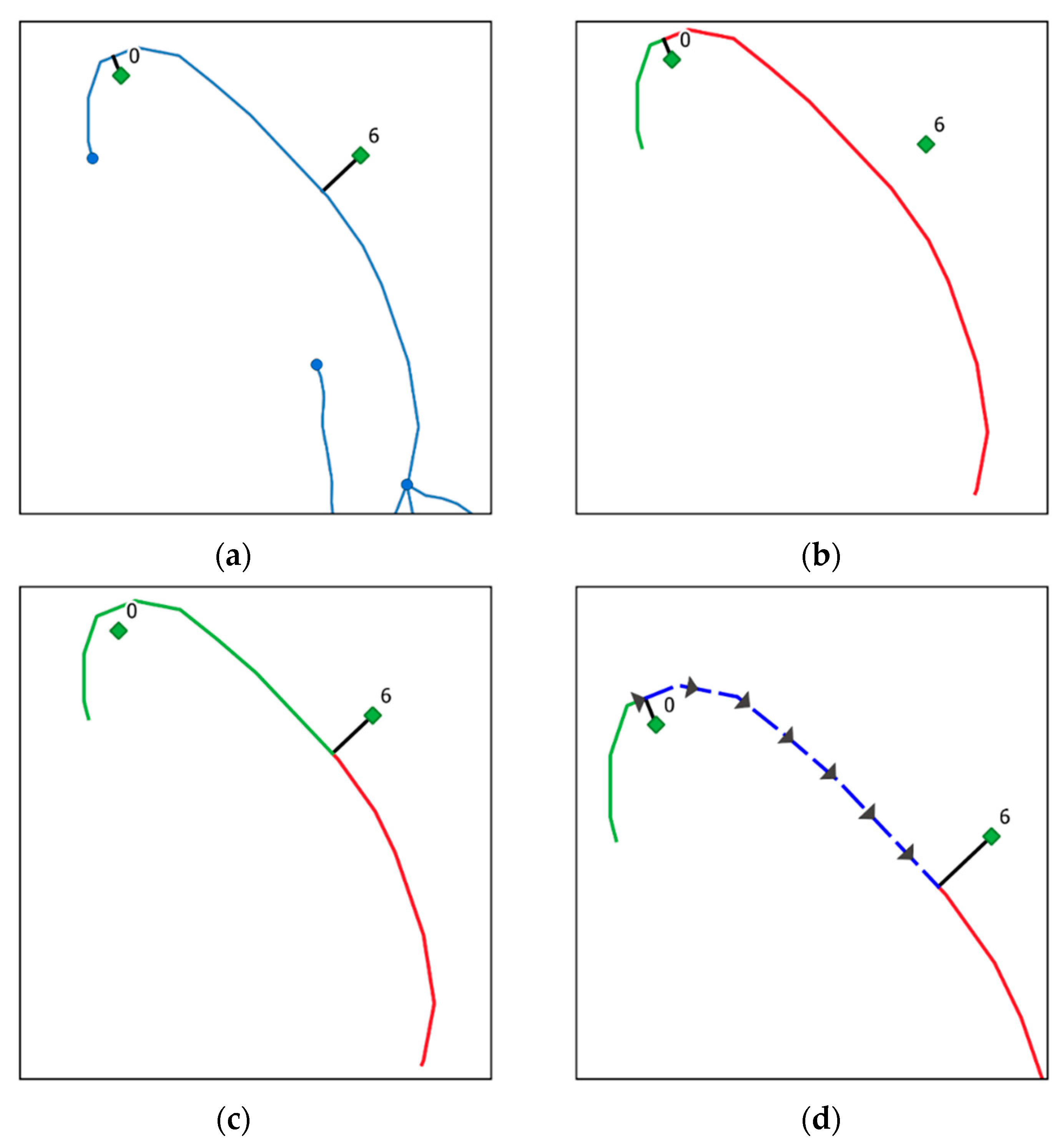
- NetworkX creates a DiGraph and the Graph with the GeoPandas DataFrame. See make_graph_from_gpd_df(). This function also creates a new GeoPandas DataFrame with parallel edges split in two as shown in Figure 2.
- Create a GeoPandas DataFrame for the input nodes using the read_shape_file_to_gpd_df() function.
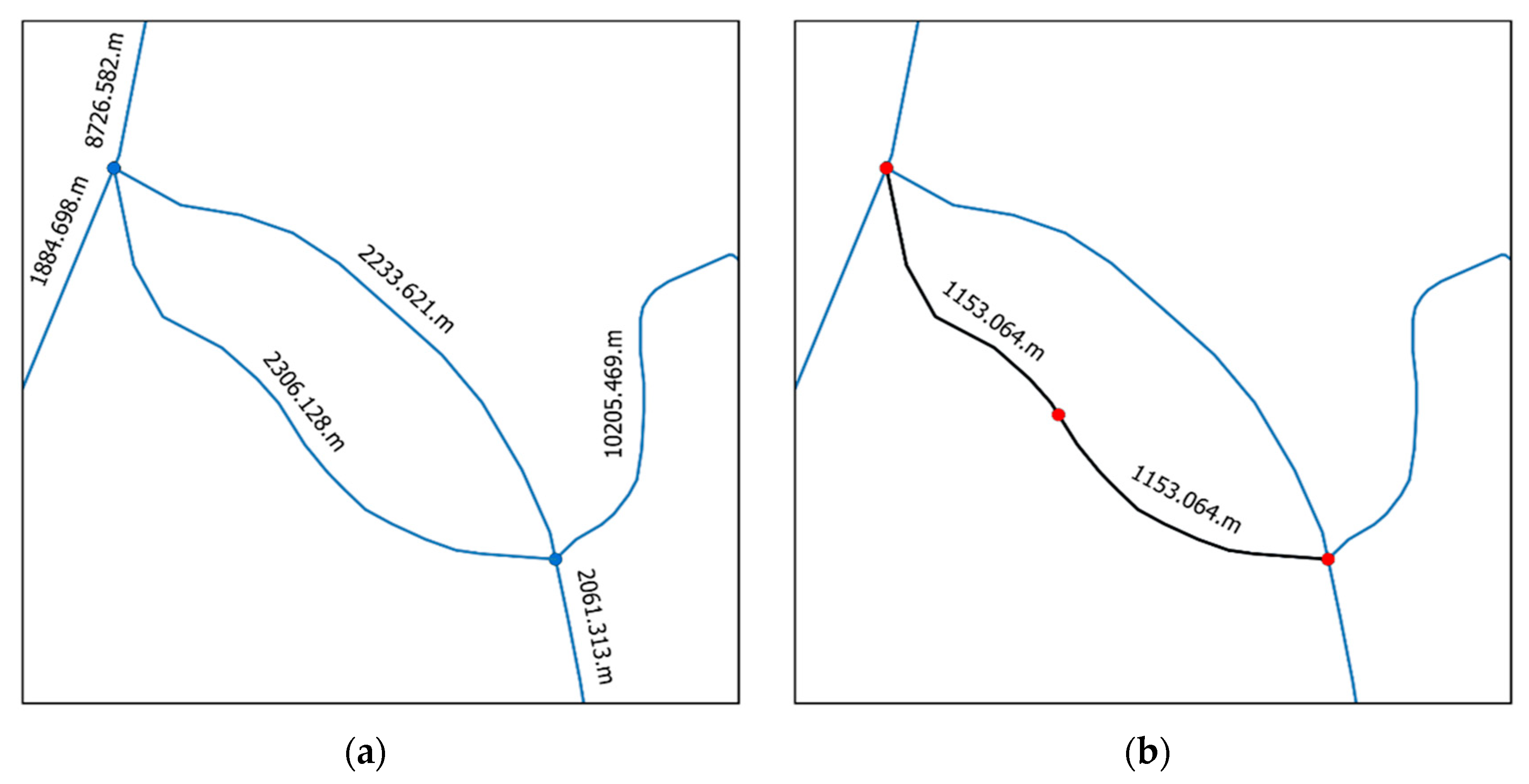
- Create a Python dictionary called NEW_EDGES_DCT that contains the new nodes and the new edges that will be added on the fly to the graph (Figure 3). The cartesian length of the line geometry found in the edge attribute is used to determine the length ratio of each segment if a river lineString must be split by the algorithm. This measure is planimetric in the spatial reference system (SRS) of this geometry, but it does not consider the ellipsoid. This ratio is then applied to the user’s given unit. If river line ab is split in two segments, ab1 and ab2, the “user” length of ab1 will be calculated with the Equation (1):User length ab1 = (planimetric length ab1/(planimetric length ab1 + planimetric length ab2)) * user length abThe tie_outside_node() function might take a long time to calculate, as it is not multithreaded. Python dictionaries can be saved to a file using the pickle_to_file() function.
- Checks the integrity between the network and graph and saves the graph to a file. Users can compare the Shapely python objects in a GIS: check_network_graph() function.
- Checks the integrity of the new nodes and new edges, saves these nodes and edges to a file. Users can compare in a GIS: save_new_edges_dct_to_csv() function.
- Makes an input list of all possible sources to target routes combinations (upper matrix only): upper_distance_matrix_route() function.
- List can be saved to file for inspection with pickle_to_file() function.
- The list from step 12 is split into chunks (according to the N_POINTS variable) and sent to the Python workers (threads)
- Sets up a pool of Python worker processes (multiprocessing threads).
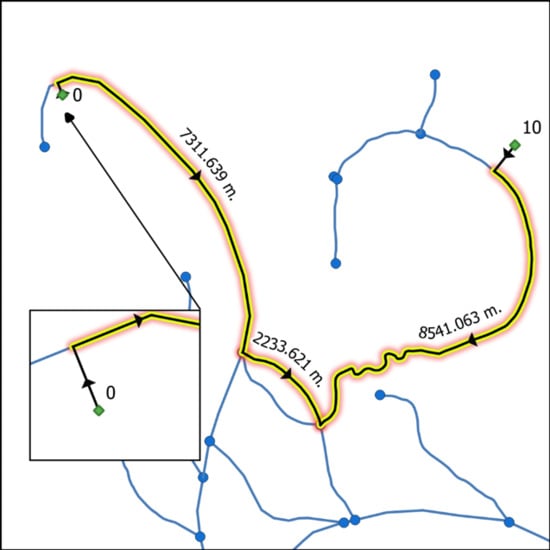
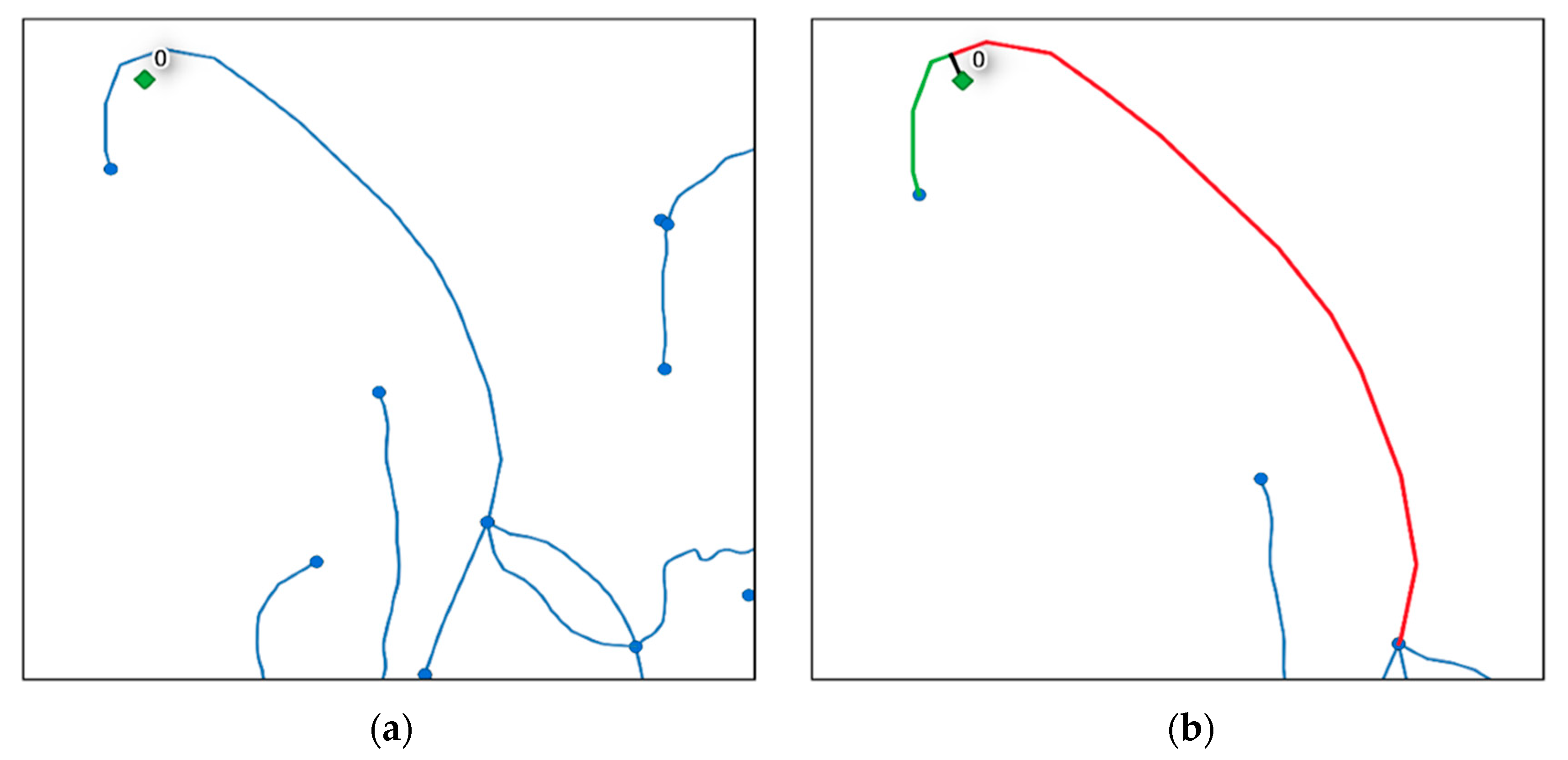
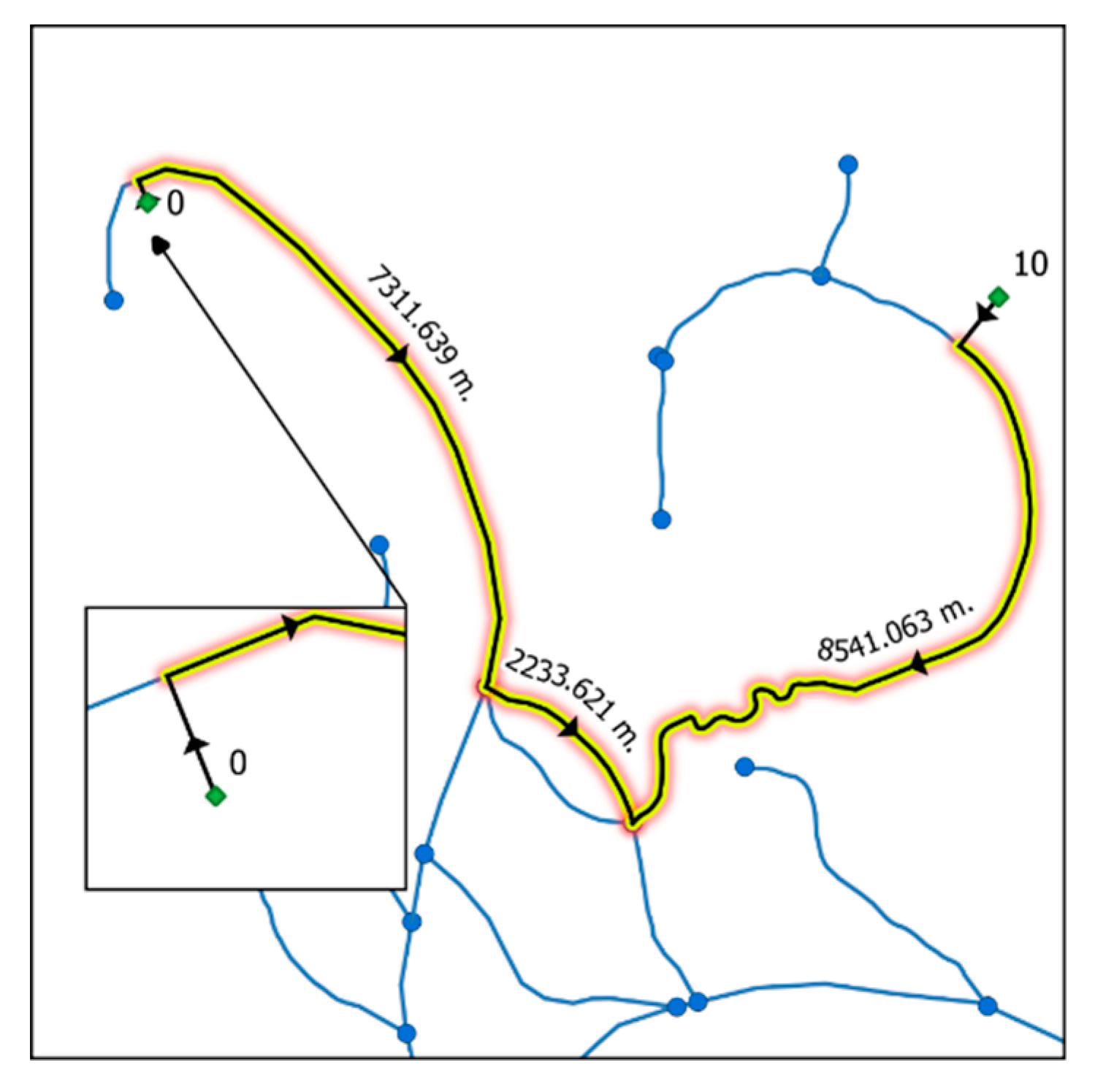
- Sends the list of routes to be calculated in chunks to a pool of workers while using the calculate_routes() function. When a route between a source node and target node is to be calculated, the first check to be done is to look up the NEW_EDGES_DCT dictionary to see if both CEs are connected to the same river segment (Figure 4a). A second verification is done to see whether the river segment is split twice by both CEs. If so, the river segment that is found between both CEs is re-split. Flow direction and total distance traveled are calculated without using the graphs (Figure 4). In all other cases, the source node and target node are inserted into the digraph and undirected graph along with accompanying edges (CEs and edges 0 and 1). The dijkstra_path (graph, source, target, [weight]) function is called and a shortest path is found. The algorithm returns a list of traveled nodes. The shortest path is calculated while using the undirected graph (Graph), while the directed graph (DiGraph) is only queried to see whether an edge is oriented downstream. As an example, if a river segment in edge (0,6) was vectorized from node 0 toward node 6, then edge (0,6) will be found in the DiGraph, but not edge (6,0). Therefore, if a route travels from node 6 to node 0, the traveler is moving upstream. Finally, each edge in the route is queried for its river flow direction and the distances are added to the upstream or downstream total distance. Before calculating the next route, all of the added edges and nodes are removed from the graphs.Optionally, the results can include the well-known-text geometry collection of the traveled route. As can be seen in Figure 5, this collection retains the vectorization directions of each line. Splitting the geometry from multiLineString to multiple lineStrings will permit a user to have access to individual features. The route contains the lines that are used to connect the source and target nodes to the GIS network. However, as can be seen in Figure 5, CEs are not used when calculating the distances. Only river distances are calculated.
- Each worker (thread) independently saves its own file results. Steps 15 and 16 are multithreaded, as can be seen in Figure 6.
3.2. Implementation Example
4. User Notes
4.1. Important Vocabulary and Concepts
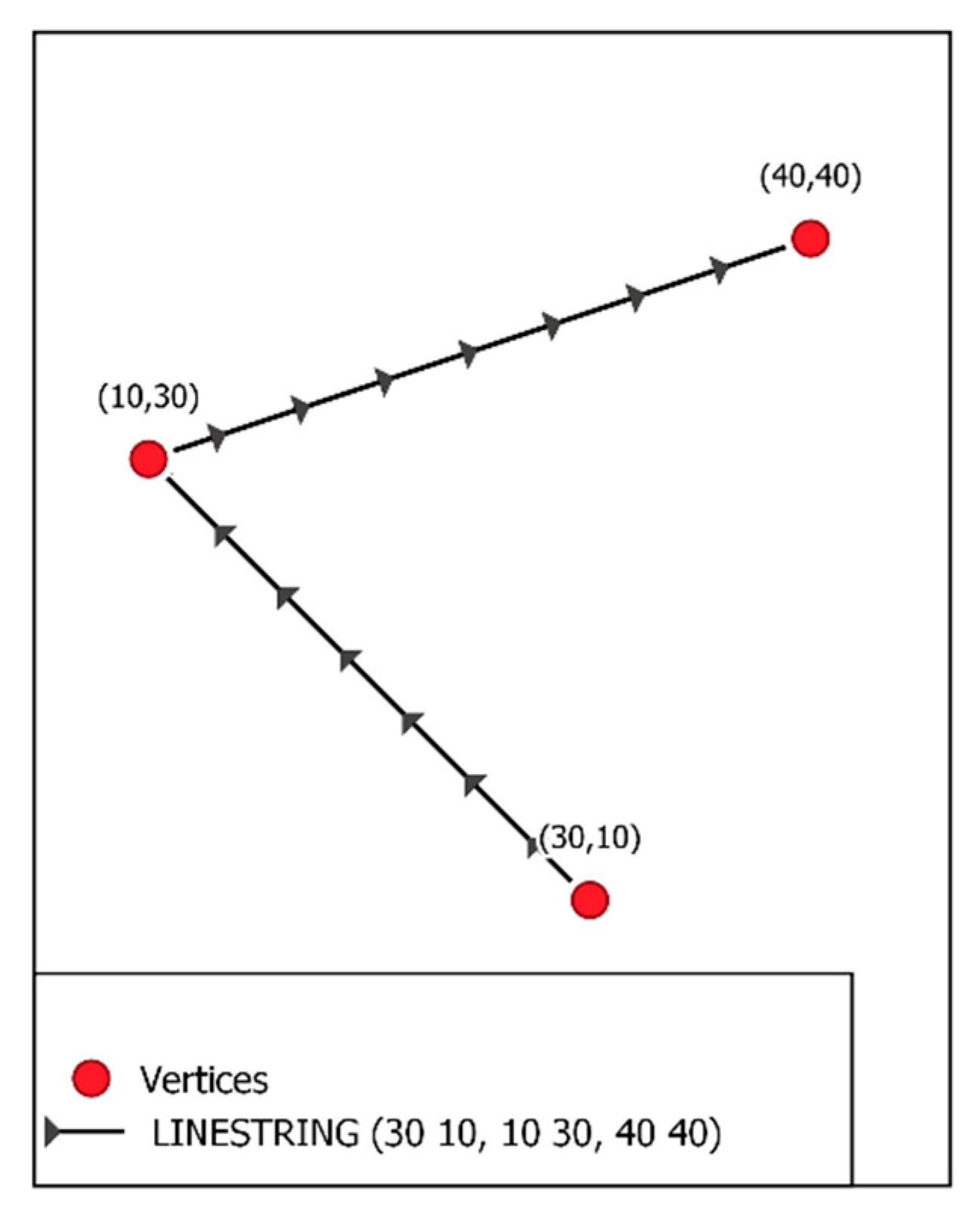
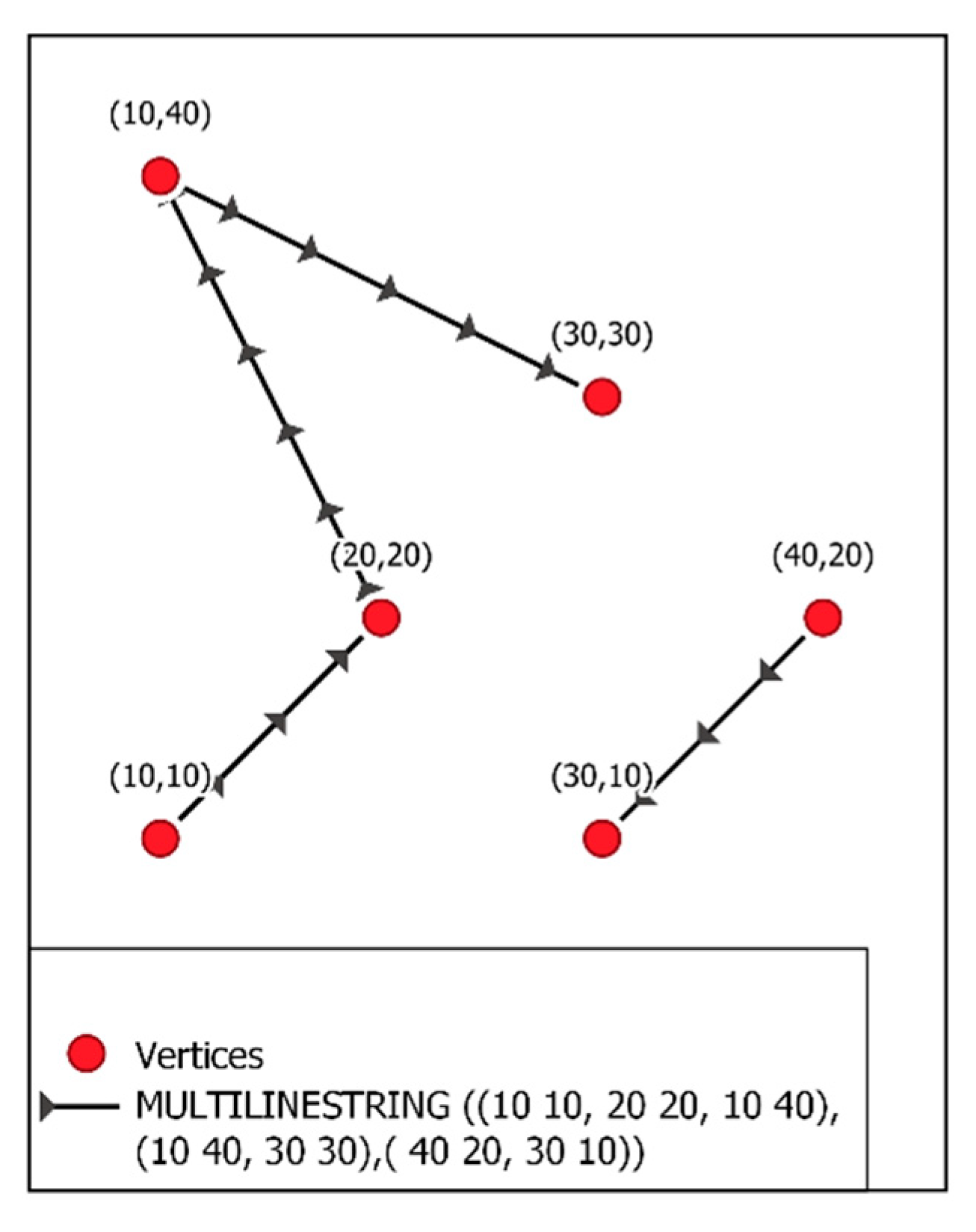
4.2. Creating a Graph with Geometric (Vector) Objects
4.3. Setting Up the Python Environment
- Pandas (0.24.2)
- Geopandas (0.4.1)
- NetworkX (2.3)
- Shapely (1.6.4)
4.4. Setting Up the User Input Variables
- INCLUDE_WKT_IN_ROUTES = False. If set to True, the program will add the nodes travelled list and well-known-text of routes in results. This will considerably slow down the program.
- BASIN = Name of the river basin. This will be used in the output file names.
- OUTPUT_FILE_MAIN_DIRECTORY = Complete path of the output file directory
- INPUT_NETWORK_FILE_SHP = Complete path for the input network.shp file
- INFILE_LENGTH = This is the name of length variable in the input network shapefile (network.shp).
- INPUT_ROUTES_SHP = Complete path to the node.shp file. This is the shapefile containing the source nodes that to be used as source and target nodes for the shortest path distances. If some of the nodes are already in the graph, they will need to be added to this file.
- THREADS = Number of Threads to be used to calculate routes (one per logical core). Keep one or two cores free.
- N_POINTS = The number of route calculations to send to each thread at a time. In order to speed up Python’s traditional slower speeds, the program is multithreaded with each thread solving a group of shortest paths (typically, one-million routes each). Output files are independently written by the threads and will contain the same number of routes.
- ROUTE_RESULT_DCT_MAX_SIZE = Number of shortest path results each thread must keep in memory before writing the results to the output files (typically 5000 to 10,000 results). A high number will increase memory usage, but decrease the number of disk writes.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- dos Santos, A.D.; Costa, L.; Braga, M.D.; Velloso, P.B.; Ghamri-Doudane, Y. Characterization of a delay and disruption tolerant network in the Amazon basin. Veh. Commun. 2016, 5, 35–43. [Google Scholar] [CrossRef]
- Salonen, M.; Toivonen, T.; Cohalan, J.M.; Coomes, O.T. Critical distances: Comparing measures of spatial accessibility in the riverine landscapes of Peruvian Amazonia. Appl. Geogr. 2012, 32, 501–513. [Google Scholar] [CrossRef]
- Tenkanen, H.; Salonen, M.; Lattu, M.; Toivonen, T. Seasonal fluctuation of riverine navigation and accessibility in Western Amazonia: An analysis combining a cost-efficient GPS-based observation system and interviews. Appl. Geogr. 2015, 63, 273–282. [Google Scholar] [CrossRef]
- Coomes, O.T.; Takasaki, Y.; Abizaid, C.; Arroyo-Mora, J.P. Environmental and market determinants of economic orientation among rain forest communities: Evidence from a large-scale survey in western Amazonia. Ecol. Econ. 2016, 129, 260–271. [Google Scholar] [CrossRef]
- Guagliardo, S.A.; Morrison, A.C.; Barboza, J.L.; Requena, E.; Astete, H.; Vazquez-Prokopec, G.; Kitron, U. River Boats Contribute to the Regional Spread of the Dengue Vector Aedes aegypti in the Peruvian Amazon. PLoS Negl. Trop. Dis. 2015, 9. [Google Scholar] [CrossRef] [PubMed]
- Parry, L.; Peres, C.A. Evaluating the use of local ecological knowledge to monitor hunted tropical-forest wildlife over large spatial scales. Ecol. Soc. 2015, 20. [Google Scholar] [CrossRef]
- Tregidgo, D.J.; Barlow, J.; Pompeu, P.S.; Rocha, M.D.; Parry, L. Rainforest metropolis casts 1,000-km defaunation shadow. Proc. Natl. Acad. Sci. USA 2017, 114, 8655–8659. [Google Scholar] [CrossRef]
- Apolinaire, E.; Bastourre, L. Nets and canoes: A network approach to the pre-Hispanic settlement system in the Upper Delta of the Parana River (Argentina). J. Anthropol. Archaeol. 2016, 44, 56–68. [Google Scholar] [CrossRef]
- Arias, L.; Barbieri, C.; Barreto, G.; Stoneking, M.; Pakendorf, B. High-resolution mitochondrial DNA analysis sheds light on human diversity, cultural interactions, and population mobility in Northwestern Amazonia. Am. J. Phys. Anthropol. 2018, 165, 238–255. [Google Scholar] [CrossRef]
- Ranacher, P.; van Gijin, R.; Derungs, C. Identifying probable pathways of language diffusion in South America. In Proceedings of the AGILE conference Wageningen, Wageningen, The Netherlands, 9–12 May 2017. [Google Scholar]
- Schillinger, K.; Lycett, S.J. The Flow of Culture: Assessing the Role of Rivers in the Inter-community Transmission of Material Traditions in the Upper Amazon. J. Archaeol. Method Theory 2019, 26, 135–154. [Google Scholar] [CrossRef]
- Loidl, M.; Wallentin, G.; Cyganski, R.; Graser, A.; Scholz, J.; Haslauer, E. GIS and Transport Modeling-Strengthening the Spatial Perspective. ISPRS Int. J. Geo-Inf. 2016, 5, 84. [Google Scholar] [CrossRef]
- Obe, R.O.; Hsu, L.S.; Sherman, G.E. PgRouting: A Practical Guide; Locate Press: Chugiak, AK, USA, 2017. [Google Scholar]
- Yang, C.W.; Raskin, R.; Goodchild, M.; Gahegan, M. Geospatial Cyberinfrastructure: Past, present and future. Comput. Environ. Urban Syst. 2010, 34, 264–277. [Google Scholar] [CrossRef]
- Nasri, M.I.; Bektas, T.; Laporte, G. Route and speed optimization for autonomous trucks. Comput. Oper. Res. 2018, 100, 89–101. [Google Scholar] [CrossRef]
- Schroder, M.; Cabral, P. Eco-friendly 3D-Routing: A GIS based 3D-Routing-Model to estimate and reduce CO2-emissions of distribution transports. Comput. Environ. Urban Syst. 2019, 73, 40–55. [Google Scholar] [CrossRef]
- Zeng, W.L.; Miwa, T.; Morikawa, T. Application of the support vector machine and heuristic k-shortest path algorithm to determine the most eco-friendly path with a travel time constraint. Transp. Res. Part D-Transp. Environ. 2017, 57, 458–473. [Google Scholar] [CrossRef]
- NetworkX. Software for Complex Networks. Available online: https://networkx.github.io (accessed on 9 November 2019).
- Dijkstra, E.W. A note on two problems in connection with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Gallo, G.; Pallottino, S. Shortest Path Algorithms. Ann. Oper. Res. 1988, 13, 1–79. [Google Scholar] [CrossRef]
- Ford, L.R., Jr. Network Flow Theory; The RAND Corporation: Santa Monica, CA, USA, 1956. [Google Scholar]
- Johnson, D.B. Efficient Algorithms for Shortest Paths in Sparse Networks. J. Assoc. Comput. Mach. 1977, 24, 1–13. [Google Scholar] [CrossRef]
- Floyd, R.W. Algorithm 97: Shortest Path. Commun. ACM 1962, 5, 345. [Google Scholar] [CrossRef]
- Ortega-Arranz, H.; Llanos, D.R.; Gonzalez-Escribano, A. The shortest-path problem. In Analysis and Comparison of Methods; Morgan&Claypool Publishers: San Rafael, CA, USA, 2015. [Google Scholar]
- Hart, E.P.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Telles, M. Python Power: The Comprehensive Guide; Thomson Course Technology: Boston, MA, USA, 2008. [Google Scholar]
- Muller, M.; Bernard, L.; Kadner, D. Moving code—Sharing geoprocessing logic on the Web. ISPRS J. Photogramm. Remote Sens. 2013, 83, 193–203. [Google Scholar] [CrossRef]
- Scheider, S.; Ballatore, A.; Lemmens, R. Finding and sharing GIS methods based on the questions they answer. Int. J. Digit. Earth 2019, 12, 594–613. [Google Scholar] [CrossRef]
- GeoPandas. Available online: http://geopandas.org (accessed on 9 November 2019).
- ESRI. ESRI Shapefile Technical Description an ESRI White Paper; ESRI: Redlands, CA, USA, 1998. [Google Scholar]
- Crippen, R.; Buckley, S.; Agram, P.; Belz, E.; Gurrola, E.; Hensley, S.; Kobrick, M.; Lavalle, M.; Martin, J.; Neumann, M.; et al. NASADEM Global Elevation Model: Methods and Progress. In XXIII ISPRS Congress, Commission IV; International Archives of the Photogrammetry Remote Sensing and Spatial Information Sciences; Halounova, L., Safar, V., Jiang, J., Olesovska, H., Dvoracek, P., Holland, D., Seredovich, V.A., Eds.; Copernicus Gesellschaft Mbh: Gottingen, Germany, 2016; pp. 125–128. [Google Scholar]
- Open Geospatial Consortium Inc. OpenGIS® Implementation Standard for Geographic Information—Simple Feature Access—Part 1: Common Architecture; Herring, J.R., Ed.; Open Geospatial Consortium Inc.: Wayland, MA, USA, 2011. [Google Scholar]
- Boeing, G. OSMnx: New methods for acquiring, constructing, analyzing, and visualizing complex street networks. Comput. Environ. Urban Syst. 2017, 65, 126–139. [Google Scholar] [CrossRef]
- Harary, F. Graph Theory; Addison-Wesley Publishing Co.: Reading, CA, USA, 1969. [Google Scholar]
- Toblerity/Shapely. Available online: https://github.com/Toblerity/Shapely (accessed on 9 November 2019).

| Basin Name | No. Graph Edges | No. Graph Nodes | No. Shortest Paths Calculated | Processing Time (min) | No. Shortest Paths/Minute |
|---|---|---|---|---|---|
| Napo | 4413 | 3978 | 134,783,571 | 5272 | 25,566 |
| Upper Ucayali | 4025 | 3832 | 115,254,153 | 3686 | 31,268 |
| Pastaza | 2605 | 2279 | 28,346,685 | 646 | 43,880 |
| Lower Ucayali | 1470 | 1329 | 28,527,681 | 336 | 84,904 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cadieux, N.; Kalacska, M.; Coomes, O.T.; Tanaka, M.; Takasaki, Y. A Python Algorithm for Shortest-Path River Network Distance Calculations Considering River Flow Direction. Data 2020, 5, 8. https://doi.org/10.3390/data5010008
Cadieux N, Kalacska M, Coomes OT, Tanaka M, Takasaki Y. A Python Algorithm for Shortest-Path River Network Distance Calculations Considering River Flow Direction. Data. 2020; 5(1):8. https://doi.org/10.3390/data5010008
Chicago/Turabian StyleCadieux, Nicolas, Margaret Kalacska, Oliver T. Coomes, Mari Tanaka, and Yoshito Takasaki. 2020. "A Python Algorithm for Shortest-Path River Network Distance Calculations Considering River Flow Direction" Data 5, no. 1: 8. https://doi.org/10.3390/data5010008
APA StyleCadieux, N., Kalacska, M., Coomes, O. T., Tanaka, M., & Takasaki, Y. (2020). A Python Algorithm for Shortest-Path River Network Distance Calculations Considering River Flow Direction. Data, 5(1), 8. https://doi.org/10.3390/data5010008