Predicting High-Risk Prostate Cancer Using Machine Learning Methods
Abstract
:1. Introduction
2. Literature Review
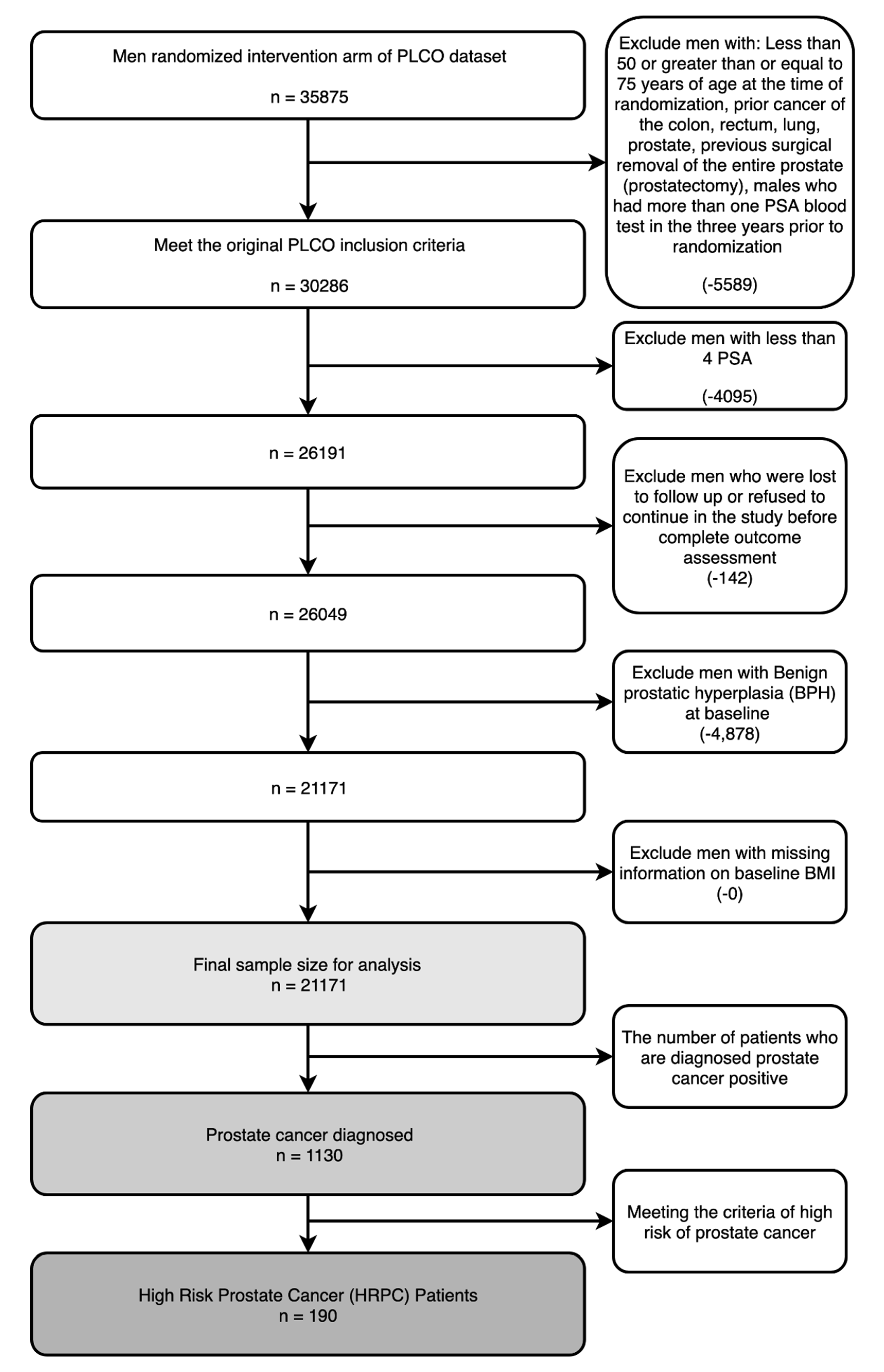
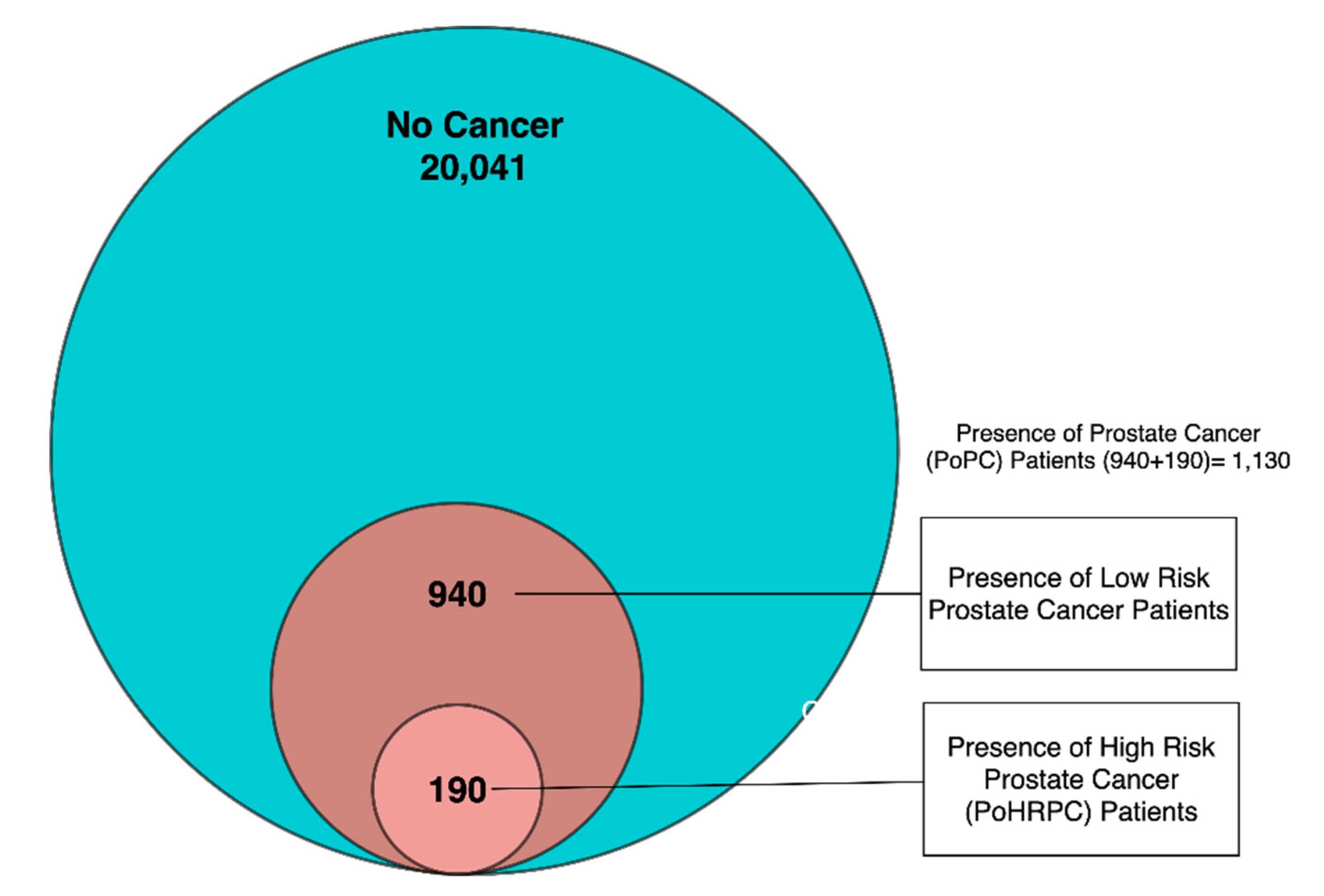
3. Data Description
4. Method
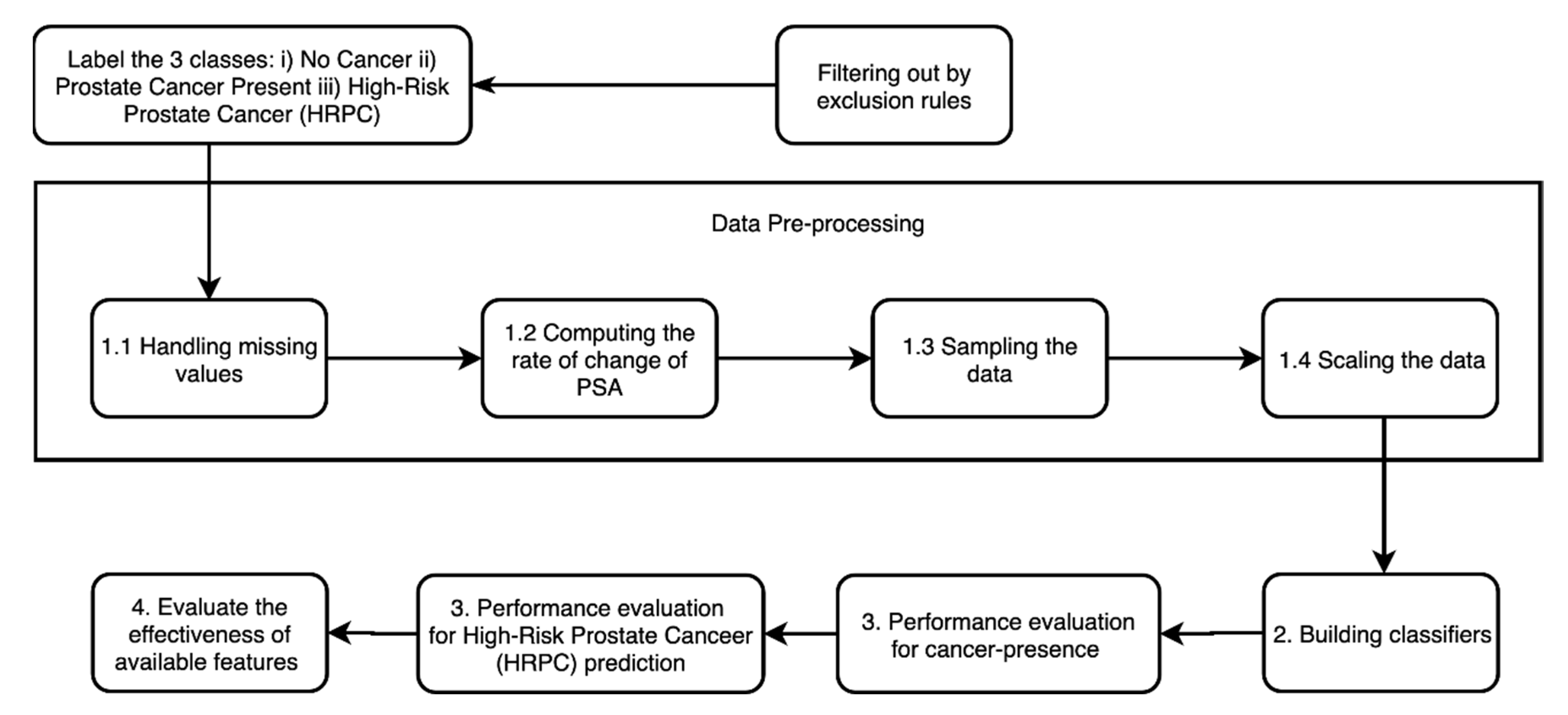
4.1. Data Preprocessing
4.1.1. Handling Missing Values
4.1.2. Calculation of Rate of Change
4.1.3. Data Imbalance Methods
4.1.4. Scaling/Normalization
4.2. Building Classifiers
4.3. Evaluating the Classifiers
4.4. Evaluating the Predictability of Features
5. Results
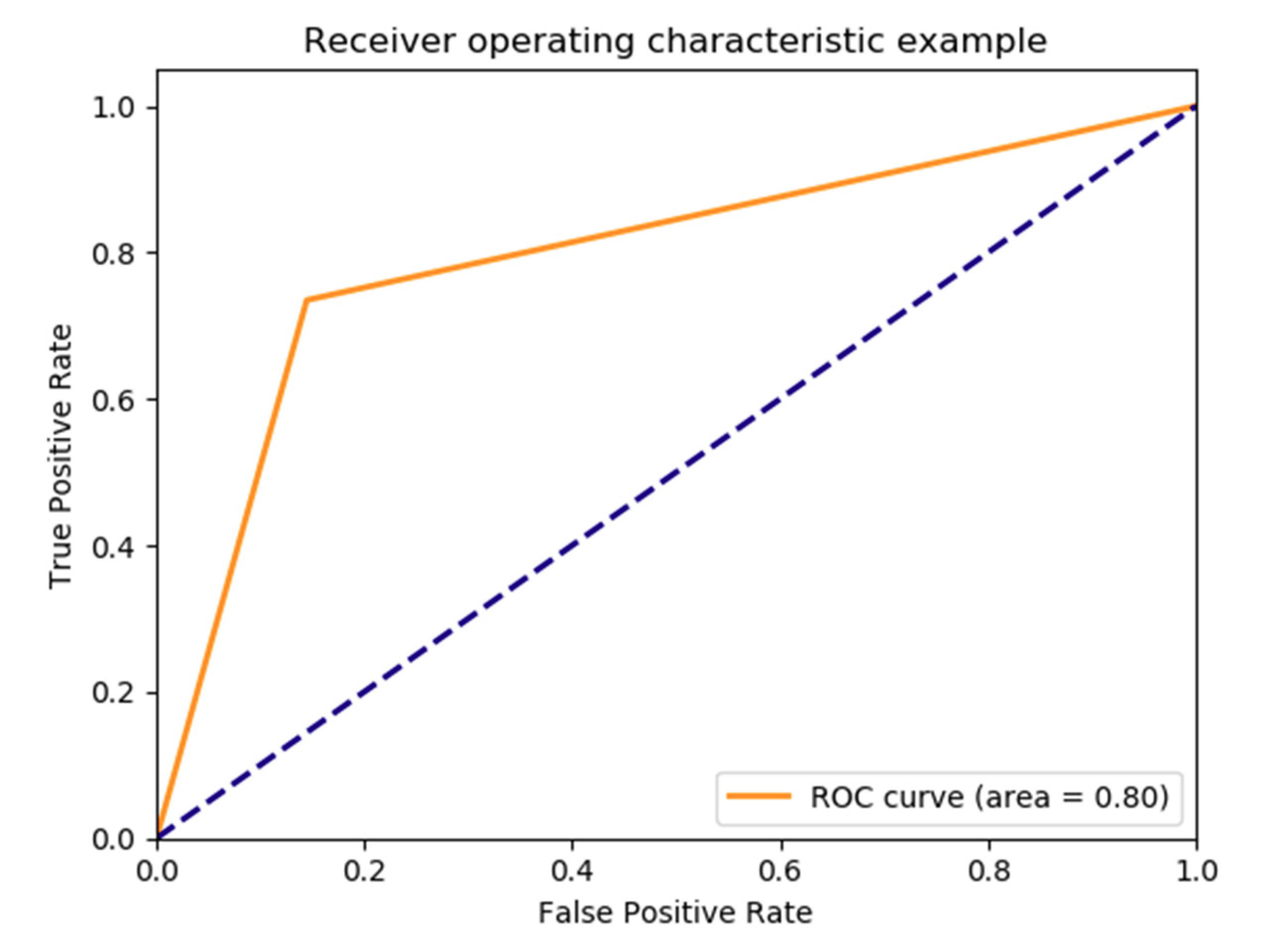
5.1. Result for PoPC Training and Test
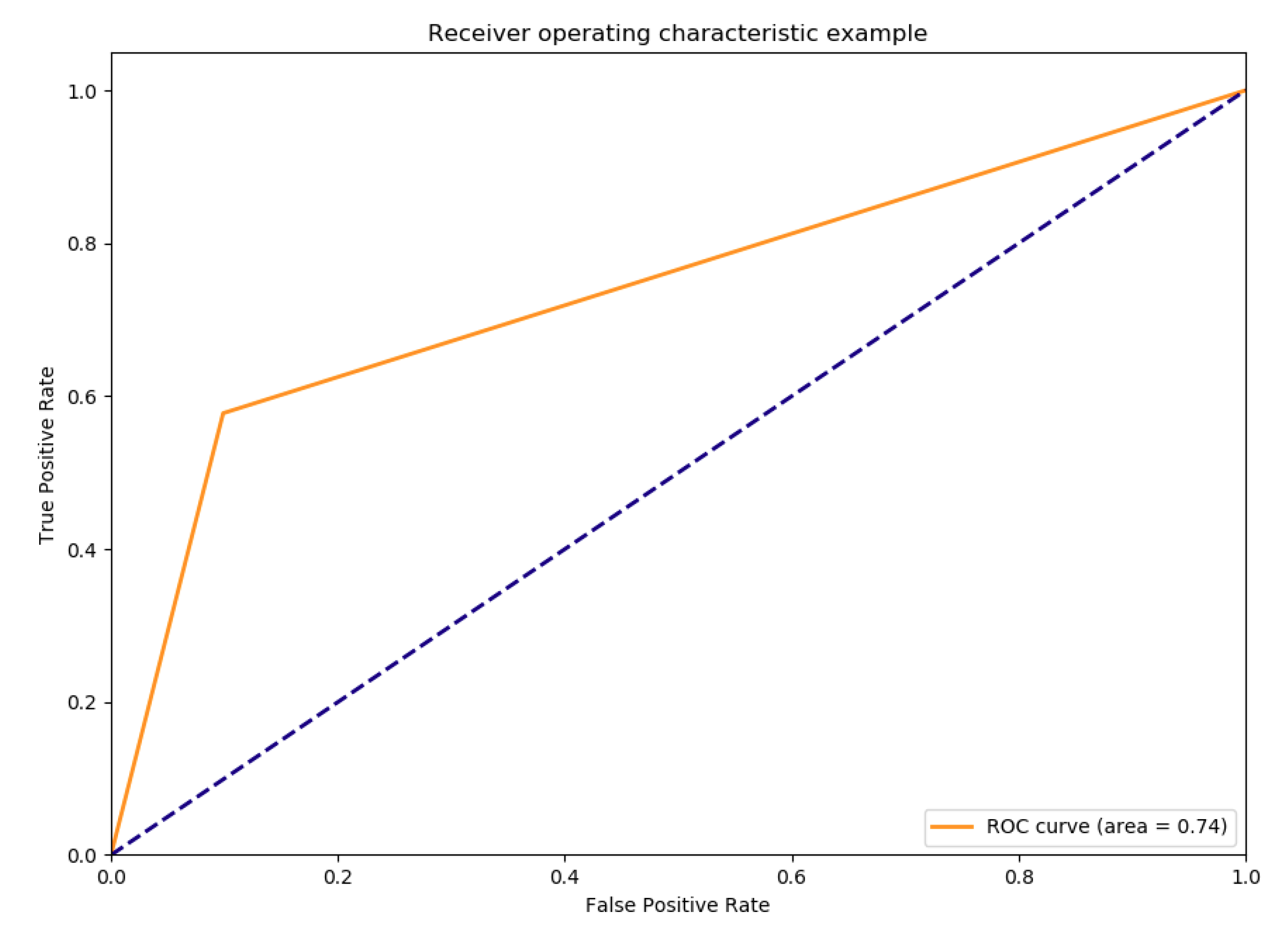
5.2. Result for PoHRPC Training and Test
5.3. Comparison of the Results with Related Work
6. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- U.S. Preventive Services Task Force. Final Update Summary: Prostate Cancer: Screening; U.S. Preventive Services Task Force: Rockville, MD, USA, 2018. [Google Scholar]
- Wang, G.; Teoh, J.Y.; Choi, K. Diagnosis of prostate cancer in a Chinese population by using machine learning methods. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 17–21 July 2018. [Google Scholar]
- Prostate-Specific Antigen (PSA) Test. [4/10/2019]. Available online: https://www.cancer.gov/types/prostate/psa-fact-sheet (accessed on 8 June 2019).
- Martin, R.M.; Donovan, J.L.; Turner, E.L.; Metcalfe, C.; Young, G.J.; Walsh, E.I.; Lane, J.A.; Noble, S.; Oliver, S.E.; Evans, S.; et al. Effect of a low-intensity PSA-based screening intervention on prostate cancer mortality: The CAP randomized clinical trialeffect of 1-time PSA screening on prostate cancer mortality effect of 1-time PSA screening on prostate cancer mortality. JAMA 2018, 319, 883–895. [Google Scholar] [CrossRef] [PubMed]
- Roland, M.; Neal, D.; Buckley, R. What should doctors say to men asking for a PSA test? BMJ 2018, 362, k3702. [Google Scholar] [CrossRef]
- Moyer, V.A.; U.S. Preventive Services Task Force. Screening for prostate cancer: U.S. Preventive services task force recommendation statement. Ann. Intern. Med. 2012, 157, 120–134. [Google Scholar] [PubMed]
- Auvinen, A.; Hakama, M. Cancer Screening: Theory and Applications. In International Encyclopedia of Public Health, 2nd ed.; Quah, S.R., Ed.; Academic Press: Oxford, UK, 2017; pp. 389–405. [Google Scholar]
- Negoita, S.; Feuer, E.J.; Mariotto, A.; Cronin, K.A.; Petkov, V.I.; Hussey, S.K.; Bernard, V.; Henley, S.J.; Anderson, R.N.; Fedewa, S. Annual report to the Nation on the status of cancer, part II: Recent changes in prostate cancer trends and disease characteristics. Cancer 2018, 124, 2801–2814. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, H.U.; Kirkham, A.; Arya, M.; Illing, R.; Freeman, A.; Allen, C.; Emberton, M. Is it time to consider a role for MRI before prostate biopsy? Nat. Rev. Clin. Oncol. 2009, 6, 197. [Google Scholar] [CrossRef] [PubMed]
- Lapa, P.; Goncales, I.; Rundo, L.; Casteli, M. Semantic learning machine improves the CNN-Based detection of prostate cancer in non-contrast-enhanced MRI. In Proceedings of the ACM Genetic and Evolutionary Computation Conference Companion, Prague, Czechia, 13–17 July 2019. [Google Scholar]
- Rundo, L.; Militello, C.; Russo, G.; Garufi, A.; Vitabile, S.; Gilardi, M.C.; Mauri, G. Automated prostate gland segmentation based on an unsupervised fuzzy C-means clustering technique using multispectral T1w and T2w MR imaging. Information 2017, 8, 49. [Google Scholar] [CrossRef]
- Shoaibi, A.; Rao, G.A.; Cai, B.; Rawl, J.; Haddock, K.S.; Hebert, J.R. Prostate specific antigen-growth curve model to predict high-risk prostate cancer. Prostate 2017, 77, 173–184. [Google Scholar] [CrossRef]
- Roffman, D.A.; Hart, G.R.; Leapman, M.S.; Yu, J.B.; Guo, F.L.; Deng, J. Development and validation of a multiparameterized artificial neural network for prostate cancer risk prediction and stratification. JCO Clin. Cancer Inf. 2018, 2, 1–10. [Google Scholar] [CrossRef]
- Lecarpentier, J.; Silvestri, V.; Kuchenbaecher, K.B.; Barrowdale, D.; Dennis, J.; McGuffog, L.; Soucy, P.; Leslie, G.; Rizzolo, P.; Navazio, A.S.; et al. Prediction of breast and prostate cancer risks in male BRCA1 and BRCA2 mutation carriers using polygenic risk scores. J. Clin. Oncol. 2017, 35, 2240. [Google Scholar]
- Vickers, A.J.; Cronin, A.M.; Aus, G.; Pihl, C.-G.; Becker, C.; Pettersson, K.; Scardino, P.T.; Hugosson, J.; Lilja, H. A panel of kallikrein markers can reduce unnecessary biopsy for prostate cancer: data from the European Randomized Study of Prostate Cancer Screening in Göteborg, Sweden. BMC Med. 2008, 6, 19. [Google Scholar] [CrossRef]
- Chang, A.J.; Autio, K.A.; Roach, M., 3rd; Scher, H.I. High-risk prostate cancer-classification and therapy. Nat. Rev. Clin. Oncol. 2014, 11, 308–323. [Google Scholar] [CrossRef] [PubMed]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michael, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. JMLR 2011, 12, 2825–2830. [Google Scholar]
- Ebenuwa, S.H.; Sharif, M.S.; Alazab, M.; Al-nemrat, A. Variance ranking attributes selection techniques for binary classification problem in imbalance data. IEEE Access 2019, 7, 24649–24666. [Google Scholar] [CrossRef]
- Imbalanced-Learn. 2016. Available online: https://imbalanced-learn.readthedocs.io/en/stable/index.html (accessed on 10 June 2019).
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Han, H.; Wang, W.-Y.; Mao, B.-H. Borderline-SMOTE: A New Over-Sampling Method in Imbalanced Data Sets Learning. In International Conference on Intelligent Computing; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Jeatrakul, P.; Wong, K.W.; Fung, C.C. Classification of imbalanced data by combining the complementary neural network and SMOTE algorithm. In International Conference on Neural Information Processing; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Tang, Y.; Zhang, Y.-Q.; Chawla, N.V.; Krasser, S. SVMs modeling for highly imbalanced classification. IEEE Trans. Syst. Man Cybern. Part B 2008, 39, 281–288. [Google Scholar] [CrossRef]
- Santos, M.; Soares, J.P.; Abreu, P.H.; Araujo, H.; Santos, J. Cross-validation for imbalanced datasets: Avoiding overoptimistic and overfitting approaches. IEEE Comput. Intell. Mag. 2018, 13, 59–76. [Google Scholar] [CrossRef]
- Brownlee, J. How to Train. a Final Machine Learning Model. 2017. Available online: https://machinelearningmastery.com/train-final-machine-learning-model/ (accessed on 26 May 2019).
- ROC Curve Analysis. 2016. Available online: https://www.medcalc.org/manual/roc-curves.php (accessed on 26 May 2019).
- Zhu, C.S.; Pinsky, P.F.; Kramer, B.S.; Prorok, P.C.; Purdue, M.P.; Berg, C.D.; Gohagan, J.K. The prostate, lung, colorectal, and ovarian cancer screening trial and its associated research resource. J. Natl. Cancer Inst. 2013, 105, 1684–1693. [Google Scholar] [CrossRef]
- Khushi, M.; Dean, I.M.; Teber, E.T.; Chircop, M.; Arhtur, J.W.; Flores-Rodriguez, N. Automated classification and characterization of the mitotic spindle following knockdown of a mitosis-related protein. BMC Bioinform. 2017, 18, 566. [Google Scholar] [CrossRef]
- Khushi, M.; Napier, C.E.; Smyth, C.M.; Reddel, R.R.; Arhtur, J.W. MatCol: A tool to measure fluorescence signal colocalisation in biological systems. Sci. Rep. 2017, 7, 8879. [Google Scholar] [CrossRef]
- Khushi, M.; Clarke, C.L.; Graham, J.D. Bioinformatic analysis of cis-regulatory interactions between progesterone and estrogen receptors in breast cancer. Peer J. 2014, 2, e654. [Google Scholar] [CrossRef] [Green Version]
- Di Zazzo, E.; Galasso, G.; Giovannelli, P.; Di Donato, M.; Di Santi, A.; Cernera, G.; Rossi, V.; Abbondanza, C.; Moncharmont, B.; Sinisi, A.A.; et al. Prostate cancer stem cells: the role of androgen and estrogen receptors. Oncotarget 2016, 7, 193–208. [Google Scholar] [CrossRef] [PubMed]
- Di Zazzo, E.; Galasso, G.; Giovannelli, P.; Di Donato, M.; Castoria, G. Estrogens and their receptors in prostate cancer: Therapeutic implications. Front. Oncol. 2018, 8, 2. [Google Scholar] [CrossRef] [PubMed]
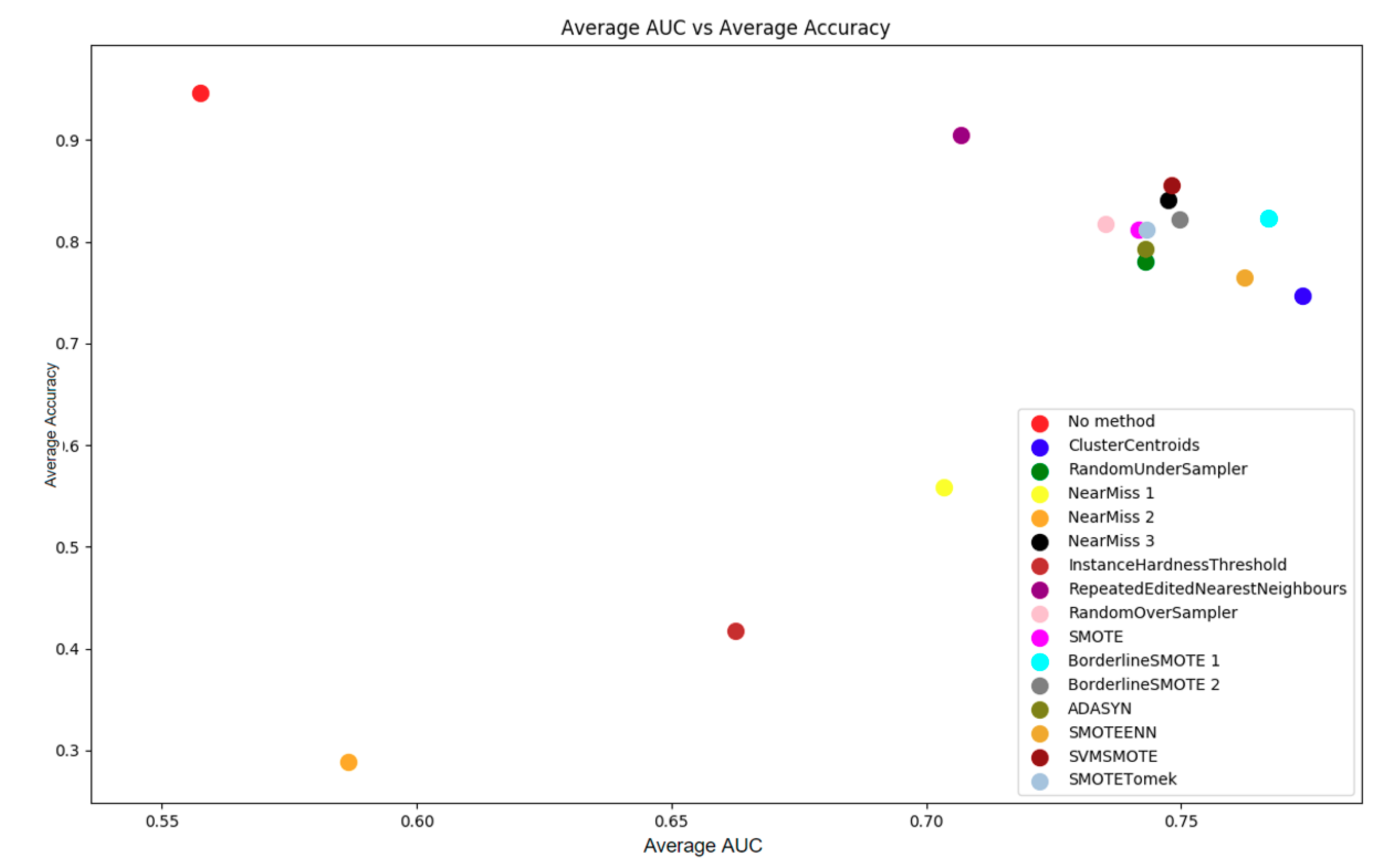

| No Method | CC | RUS | NM1 | NM2 | NM3 | |
| Avg Acc | 0.947 | 0.747 | 0.780 | 0.558 | 0.288 | 0.841 |
| Avg AUC | 0.558 | 0.774 | 0.743 | 0.703 | 0.587 | 0.747 |
| IHT | RENN | ROS | BS1 | BS2 | ADASYN | |
| Avg Acc | 0.417 | 0.905 | 0.818 | 0.823 | 0.822 | 0.794 |
| Avg AUC | 0.663 | 0.707 | 0.735 | 0.767 | 0.750 | 0.743 |
| SMOTE | SVMSMOTE | SMOTETomek | SMOTEENN | |||
| Avg Acc | 0.813 | 0.855 | 0.812 | 0.765 | ||
| Avg AUC | 0.742 | 0.748 | 0.743 | 0.765 |
| KN | SVM2 | QD | DT | RF | MLPC | ADA | |
|---|---|---|---|---|---|---|---|
| Holdout accuracy | 0.886 | 0.899 | 0.916 | 0.831 | 0.831 | 0.850 | 0.846 |
| Holdout auc-score | 0.683 | 0.653 | 0.577 | 0.777 | 0.772 | 0.791 | 0.777 |
| 10-fold cross validation accuracy | 0.876 (±0.009) | 0.894 (±0.013) | 0.919 (±0.009) | 0.838 (±0.023) | 0.835 (±0.024) | 0.845 (±0.015) | 0.843 (±0.014) |
| 10-fold cross validation auc | 0.674 (±0.038) | 0.662 (±0.049) | 0.575 (±0.049) | 0.778 (±0.030) | 0.771 (±0.024) | 0.771 (±0.037) | 0.776 (±0.028) |
| Disease Present | Disease Absent | |
|---|---|---|
| Predicted present | 208 | 725 |
| Predicted absent | 75 | 4285 |
| Evaluation | Value |
|---|---|
| Sensitivity | 0.735 |
| Specificity | 0.855 |
| PPV | 0.223 |
| NPV | 0.983 |
| F1 | 0.342 |
| AUC | Difference in AUC by Different Feature Set | |
|---|---|---|
| No exclusion (Same feature set as above model) | 0.791 | 0 |
| Recent ROC excluded | 0.767 | −0.024 |
| Overall ROC excluded | 0.787 | −0.004 |
| Overall ROC and Recent ROC excluded | 0.774 | −0.017 |
| Age added | 0.786 | −0.005 |
| BMI added | 0.792 | +0.001 |
| Age and BMI added | 0.786 | −0.005 |
| Filtered by race | 0.785 | −0.006 |
| KN | SVM2 | QD | DT | RF | MLPC | ADA | |
|---|---|---|---|---|---|---|---|
| Holdout accuracy | 0.979 | 0.926 | 0.930 | 0.906 | 0.930 | 0.905 | 0.929 |
| Holdout auc-score | 0.551 | 0.674 | 0.630 | 0.687 | 0.653 | 0.618 | 0.664 |
| 10-fold cross validation accuracy | 0.979 (±0.007) | 0.925 (±0.011) | 0.941 (±0.011) | 0.927 (±0.016) | 0.915 (±0.028) | 0.909 (±0.030) | 0.894 (±0.013) |
| 10-fold cross validation auc | 0.576 (±0.082) | 0.686 (±0.108) | 0.617 (±0.098) | 0.669 (±0.086) | 0.696 (±0.115) | 0.675 (±0.114) | 0.711 (±0.120) |
| Positive | Negative | |
|---|---|---|
| Predicted positive | 28 | 457 |
| Predicted negative | 17 | 4791 |
| Evaluation | Value |
|---|---|
| Sensitivity | 0.62 |
| Specificity | 0.913 |
| PPV | 0.057 |
| NPV | 0.996 |
| F1 | 0.106 |
| AUC | Difference in AUC by Different Feature Set | |
|---|---|---|
| No exclusion (Same feature set as above model) | 0.673 | 0 |
| Recent ROC excluded | 0.651 | −0.022 |
| Overall ROC excluded | 0.661 | −0.012 |
| Both Overall ROC and Recent ROC excluded | 0.643 | −0.03 |
| Age added | 0.711 | +0.038 |
| BMI added | 0.688 | +0.015 |
| Age and BMI added | 0.690 | +0.017 |
| Filtered by race | 0.669 | −0.004 |
| PoHRPC (ADABoost) | PoPC (ADABoost) | Wang et al. ANN on Training/Test Set from Same Dataset | Shoaibi et al. Validation | Roffman et al. ANN on Training/Test Set from Same Dataset | |
|---|---|---|---|---|---|
| Sensitivity | 0.62 | 0.735 | 0.9996 ± 0.0013 | 0.955 | 0.232 (0.195–0.269) |
| Specificity | 0.913 | 0.855 | 0.9035 ± 0.0163 | 0.852 | 0.894 (0.89–0.897) |
| NPV | 0.996 | 0.983 | |||
| PPV | 0. 057 | 0.223 | 0.265 (0.224–0.306) | ||
| Accuracy | 0.915 (±0.016) | 0.843 (±0.014) | 0.9527 ± 0.0079 | ||
| AUC | 0.711 (±0.120) | 0.776 (±0.028) | 0.9755 ± 0.0073 | 0.72 (0.70–0.75) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barlow, H.; Mao, S.; Khushi, M. Predicting High-Risk Prostate Cancer Using Machine Learning Methods. Data 2019, 4, 129. https://doi.org/10.3390/data4030129
Barlow H, Mao S, Khushi M. Predicting High-Risk Prostate Cancer Using Machine Learning Methods. Data. 2019; 4(3):129. https://doi.org/10.3390/data4030129
Chicago/Turabian StyleBarlow, Henry, Shunqi Mao, and Matloob Khushi. 2019. "Predicting High-Risk Prostate Cancer Using Machine Learning Methods" Data 4, no. 3: 129. https://doi.org/10.3390/data4030129
APA StyleBarlow, H., Mao, S., & Khushi, M. (2019). Predicting High-Risk Prostate Cancer Using Machine Learning Methods. Data, 4(3), 129. https://doi.org/10.3390/data4030129






