Need for Standardization and Systematization of Test Data for Job-Shop Scheduling
Abstract
:1. Introduction
2. Use of Test Models when Comparing Optimization Methods
2.1. The Job-Shop Scheduling Problem
2.2. Collections of JSP Test Data
- –
- http://jobshop.jjvh.nl/explanation.php by van Hoorn [30]
- –
- http://optimizizer.com/jobshop.php by Shylo [31]
- –
- https://github.com/tamy0612/JSPLIB by Tamura [32]
2.3. Design of Literature Analysis
2.4. Description of the Work Examined
3. Concepts for Differentiation and Systematization of Test Data
3.1. Structural Representation of Jobs and Tasks
3.2. Topology
3.3. Product Model Topologies
| Sequence: | A linear sequence of tasks in which a maximum of one predecessor and one successor exists for a node. |
| Splitting: | A completed task is followed up on by multiple other tasks. |
| Parallelism: | The coexistence of several simultaneous tasks, between an expanding and a merging tasks. |
| Merge: | The convergence of several tasks into one subsequent task. |
| Cycle: | One or more tasks may be performed repeatedly. |
| Optionality: | The existence of several, selectable successors of a task. This pattern corresponds to a logical OR operator. |
| Linear: | A linear production process can be represented by stringing together several sequences. |
| Parallel: | A process is split into two linear processes and reunited in a later work step. |
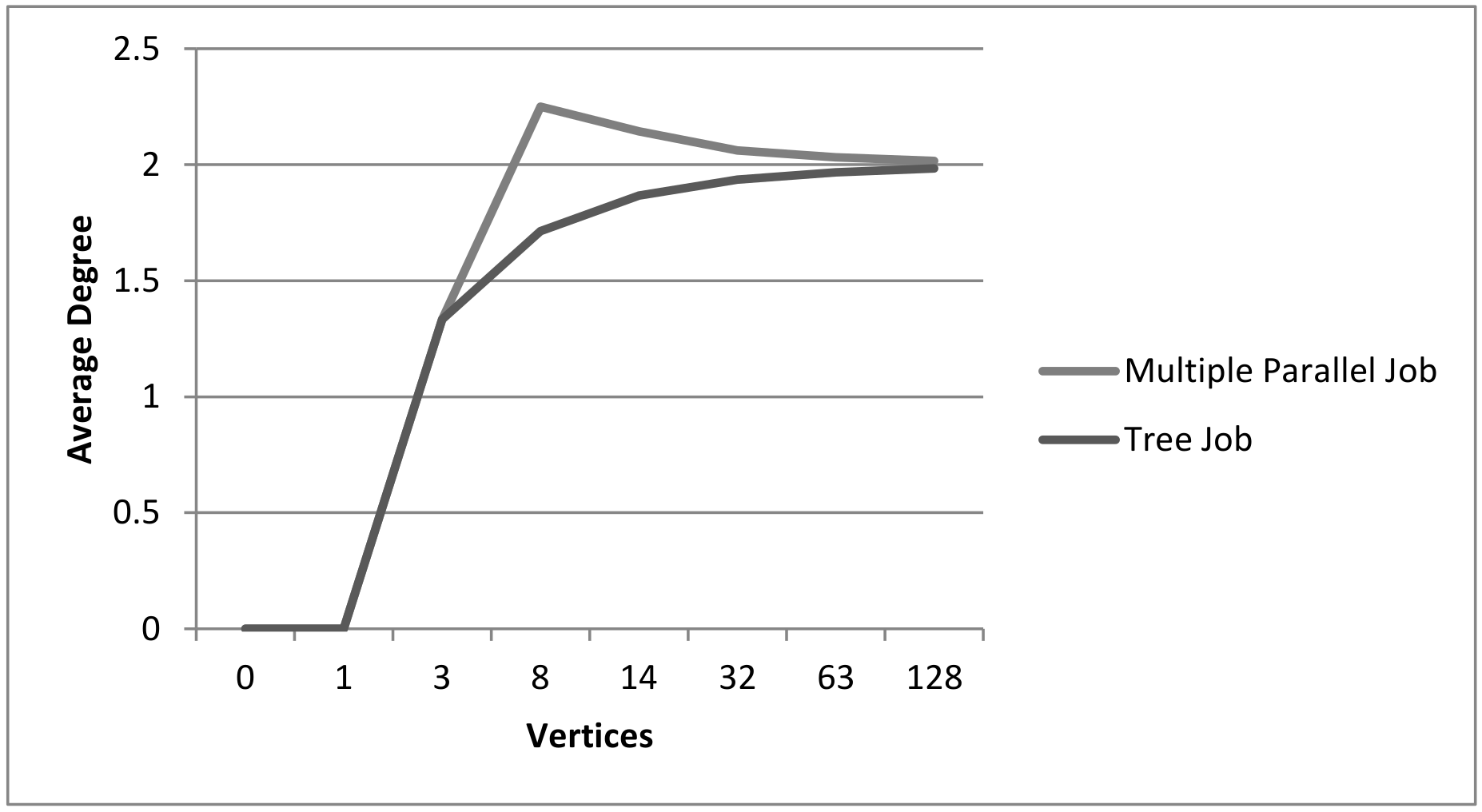
| Multiple Parallel: | The splitting of a process can also take place in more than two sub-sequences, which are merged again at a later point in time. The maximum number of sub-sequences running in parallel depends on the sum of the total number of tasks. |
| Ring: | If each task has exactly one predecessor and one successor, a sequential cycle is created that forms a ring. |
| Tree (splitting): | If the production process is split up after each work step, i.e., the number of tasks increases after each node, this model reflects an initial task with several end products. |
| Tree (merging): | This results in several initial tasks through a continuous combination of the production process, i.e., a reduction in the number of parallel sub-sequences, ultimately in a single final product. |
| Cycle: | Recurring tasks can also be present in every pattern presented so far. For example, in a linear sequence of tasks, one or more tasks may have to be performed repeatedly. There may also be additional tasks in a cycle (see Figure 3). |
| Option: | If not every task has to be performed for a product model, then the model contains options. Thus, in a split where at least one subsequent task is optional, parallelism does not have to follow. |
3.4. Complexity of Product Models
3.5. Metrics of Social Network Analysis
- Mean degree:
- Also called average degree, is a measure that reflects the interconnection of all nodes of a network by using the arithmetic mean. Here not only directionally connected nodes but all adjacent nodes are considered. The mean weighted degree differs from the mean degree: Its calculation only considers directed, connected nodes and not adjacents [77]:The mean degree is determined by the average of the degrees of the edges k, which is adjacent to the sum N of the nodes. This corresponds to dividing the double of the edge sum L by the sum of nodes N.
- Network diameter:
- Edge density:
- This is the ratio between the number of existing edges and the number of potentially possible directed or undirected edges in the network. The value is between 0 and 1 [80]. The edge density D can be represented by a division of the connections present in the network and the connections possible in the network (see formula 2):Here m denotes the number of edges and N the number of nodes in the network.
- Modularity:
- It describes the simplicity of breaking down a network into individual cliques. A high degree of modularity reflects the highly complex structure of the network [81]:The modularity Q is determined by the decomposition of the network into m cliques, the number of L edges, the number of edges between nodes of the s-th clique and the sum of degrees of nodes of the s-th clique [81].
- Strongly Connected Component:
- In a network, a strongly connected component is a group of nodes in which all nodes are directly or indirectly connected to each other. The length of the paths is not decisive here. In contrast to strongly connected components, the direction is not considered for weakly connected components [82]
- Mean path length:
3.6. Quantitative Systematization through Metrics
4. Obstacles Identified in Method Comparisons Carried Out
- Non-comparability of the search space implicitly predefined by the test data sets (complexity, location of good solutions).
- Incompleteness due to (un)consciously selected test scenarios.
- Non-differentiability due to missing characteristic descriptions for test models.
- Modeling effort.
- Illustrativeness of the scenarios represented by test data is too low and does not allow comparison between simulation and practical scenario.
- Inconsistent representation regarding denominators.
- Missing benchmark due to unknown optimal solution for a test scenario.
Non-Comparability
Incompleteness
Non-Differentiability
Modeling Effort
Illustrativeness
Inconsistent Representation
Missing Scale
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| JSP | Job-Shop Scheduling Problem |
| SNA | Social Network Analysis |
References
- Cheng, R.; Gen, M.; Tsujimura, Y. A Tutorial Survey of Job-Shop Scheduling Problems Using Genetic Algorithms—Representation. Comput. Ind. Eng. 1996, 30, 983–997. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Trubian, M. Applying Tabu Search to the Job-Shop Scheduling Problem. Ann. Oper. Res. 1993, 41, 231–252. [Google Scholar] [CrossRef]
- Fischäder, H.; Göhler, R.; Schneider, H.M. Maschinenbelegungsplanung in entkoppelten Produktionssystemen. productivITy 2017, 22, 1–20. [Google Scholar]
- Scharbrodt, M. Produktionsplanung in der Prozessindustrie: Modelle, Effziente Algorithmen und Umsetzung. Ph.D. Thesis, Technical University of Munich, Munich, Germany, October 2000. [Google Scholar]
- Carlier, J.; Pinson, E. An Algorithm for Solving the Job-Shop Problem. Manag. Sci. 1989, 35, 164–176. [Google Scholar] [CrossRef]
- Applegate, D.; Cook, W. A Computational Study of the Job-Shop Scheduling Problem. ORSA J. Comput. 1991, 3, 149–156. [Google Scholar] [CrossRef]
- Nakano, R.; Yamada, T. Conventional Genetic Algorithm for Job Shop Problems. In Proceedings of the 4th International Conference on Genetic Algorithms, San Diego, CA, USA, 13–16 July 1991; Volume 91, pp. 474–479. [Google Scholar]
- Nowicki, E.; Smutnicki, C. An Advanced Tabu Search Algorithm for the Job Shop Problem. J. Sched. 2005, 8, 145–159. [Google Scholar] [CrossRef]
- Van den Eynden, V.; Corti, L.; Wollard, M.; Bishop, L.; Horton, L. Managing and Sharing Data: A Best Practice Guide for Researchers, 3rd ed.; UK Data Archive University of Essex: Colchester, UK, 2011; OCLC: 727970452. [Google Scholar]
- Vahrenkamp, R. Produktionsmanagement, 6th ed.; Oldenbourg Verlag: Wien, Austria, 2008. [Google Scholar]
- Fischäder, H.; Göhler, R.; Schneider, H.M. Maschinenbelegungsplanung in Mehrstufigen Produktionssystemen. Ph.D. Thesis, Technische Universitat Ilmenau, Ilmenau, Germany, 2017. Volume 22. pp. 29–32. [Google Scholar]
- Henning, A. Praktische Job-Shop Scheduling-Probleme. Ph.D. Thesis, Friedrich Schiller University, Jena, Germany, August 2002. [Google Scholar]
- Käschel, J.; Teich, T. Reihenfolgeplanung in Produktionsnetzwerken. In IT-gestützte Betriebswirtschaftliche Entscheidungsprozesse; Jahnke, B., Wall, F., Eds.; Gabler Verlag: Wiesbaden, Germany, 2001; pp. 239–259. [Google Scholar]
- Pinedo, M. Scheduling: Theory, Algorithms, and Systems, 5th ed.; Springer: Berlin, Germany, 2016. [Google Scholar]
- Gronau, N.; Weber, E. Reihenfolgeplanung Im Zeitalter von Industrie 4.0. productivITy 2018, 23, 23–26. [Google Scholar] [CrossRef]
- Muth, J.F.; Thompson, G.L. Industrial Scheduling; Prentice Hall: Englewood Cliffs, NJ, USA, 1963. [Google Scholar]
- Baker, K.R. Introduction to Sequencing and Scheduling; Wiley: Hoboken, NJ, USA, 1974; Open Library ID: OL5047415M. [Google Scholar]
- Lenstra, J.K.; Rinnooy Kan, A.H.G.; Brucker, P. Complexity of Machine Scheduling Problems. In Studies in Integer Programming; Hammer, P.L., Johnson, E.L., Korte, B.H., Nemhauser, G.L., Eds.; Elsevier: Amsterdam, The Netherlands, 1977; Volume 1, pp. 343–362, Annals of Discrete Mathematics. [Google Scholar]
- Rinnooy Kan, A.H.G. Machine Scheduling Problems—Classification, Complexity and Computations; Springer US: New York, NY, USA, 1976; OCLC: 863792546. [Google Scholar]
- French, S. Sequencing and Scheduling: An Introduction to the Mathematics of the Job-Shop; Ellis Horwood Series in Mathematics and Its Applications; Wiley: Hoboken, NJ, USA, 1982. [Google Scholar]
- Conway, R.W.; Maxwell, W.L.; Miller, L.W. Theory of Scheduling; Courier Corporation: Washington, DC, USA, 1967. [Google Scholar]
- Dorndorf, U.; Pesch, E. Evolution Based Learning in a Job Shop Scheduling Environment. Comput. Oper. Res. 1995, 22, 25–40. [Google Scholar] [CrossRef]
- Jain, A.S.; Meeran, S. A State-of-the-Art Review of Job-Shop Scheduling Techniques; Technical Report; University of Dundee: Scotland, UK, 1998. [Google Scholar]
- Manne, A.S. On the Job-Shop Scheduling Problem. Oper. Res. 1960, 8, 219–223. [Google Scholar] [CrossRef]
- Barker, J.R.; McMahon, G.B. Scheduling the General Job-Shop. Manag. Sci. 1985, 31, 594–598. [Google Scholar] [CrossRef]
- Lawrence, S.R. Resource Constrained Project Scheduling: An Experimental Investigation of Heuristic Scheduling Techniques (Supplement); Graduate School of Industrial Administration, Carnegie-Mellon University: Pittsburgh, PA, USA, 1984. [Google Scholar]
- Adams, J.; Balas, E.; Zawack, D. The Shifting Bottleneck Procedure for Job Shop Scheduling. Manag. Sci. 1988, 34, 391–401. [Google Scholar] [CrossRef]
- Beasley, J.E. OR-Library: Distributing Test Problems by Electronic Mail. J. Oper. Res. Soc. 1990, 41, 1069–1072. [Google Scholar] [CrossRef]
- Beasley, J.E. OR-LIBRARY. 1990. Available online: http://people.brunel.ac.uk/ mastjjb/jeb/info.html (accessed on 1 December 2018).
- Van Hoorn, J. Job Shop Instances and Solutions. 2015. Available online: http://jobshop.jjvh.nl/ (accessed on 1 December 2018).
- Shylo, O. Job Shop Scheduling. 2018. Available online: http://optimizizer.com/jobshop.php (accessed on 1 December 2018).
- Tamura, Y. JSPLIB: Benchmark Instances for Job-Shop Scheduling Problem. 2018. Available online: https://github.com/tamy0612/JSPLIB (accessed on 1 December 2018).
- Staples, M.; Niazi, M. Experiences Using Systematic Review Guidelines. J. Syst. Softw. 2007, 80, 1425–1437. [Google Scholar] [CrossRef]
- Fisher, H.; Thompson, G.L. Probabilistic Learning Combinations of Local Job-Shop Scheduling Rules. In Industrial Scheduling; Muth, J.F., Thompson, G.L., Eds.; Prentice Hall: Upper Saddle River, NJ, USA, 1963; pp. 225–251. [Google Scholar]
- Giffler, B.; Thompson, G.L.; Van Ness, V. Numerical Experience with the Linear and Monte Carlo Algorithms for Solving Production Scheduling Problems. In Industrial Scheduling; Muth, J.F., Thompson, G.L., Eds.; Prentice Hall: Upper Saddle River, NJ, USA, 1963; pp. 21–38. [Google Scholar]
- Taillard, E. Benchmarks for Basic Scheduling Problems. Eur. J. Oper. Res. 1993, 64, 278–285. [Google Scholar] [CrossRef]
- Bierwirth, C. A Generalized Permutation Approach to Job Shop Scheduling with Genetic Algorithms. Oper.-Res.-Spektrum 1995, 17, 87–92. [Google Scholar] [CrossRef]
- Nowicki, E.; Smutnicki, C. A Fast Taboo Search Algorithm for the Job Shop Problem. Manag. Sci. 1996, 42, 797–813. [Google Scholar] [CrossRef]
- Vázquez, M.; Whitley, L.D. A Comparison of Genetic Algorithms for the Dynamic Job Shop Scheduling Problem. In Proceedings of the 2nd Annual Conference on Genetic and Evolutionary Computation, Las Vegas, NV, USA, 10–12 July 2000; Morgan Kaufmann Publishers Inc.: San Mateo, CA, USA, 2000; pp. 1011–1018. [Google Scholar]
- Bratley, P.; Florian, M.; Robillard, P. On Sequencing with Earliest Starts and Due Dates with Application to Computing Bounds for the (n/m/G/Fmax) Problem. Naval Res. Logist. Quart. 1973, 20, 57–67. [Google Scholar] [CrossRef]
- Brucker, P.; Jurisch, B.; Sievers, B. A Branch and Bound Algorithm for the Job-Shop Scheduling Problem. Discrete Appl. Math. 1994, 49, 107–127. [Google Scholar] [CrossRef]
- McMahon, G.; Florian, M. On Scheduling with Ready Times and Due Dates to Minimize Maximum Lateness. Oper. Res. 1975, 23, 475–482. [Google Scholar] [CrossRef]
- Lenstra, J.K. Sequencing by Enumerative Methods; Number 69 in Mathematical Centre Tract; Mathematisch Centrum: Amsterdam, The Netherlands, 1976; A Revision of Author’s Thesis, Mathematisch Centrum, Amsterdam. [Google Scholar]
- Carlier, J. Ordonnancements à Contraintes Disjonctives. Thèse de 3ème cycles. Ph.D. Thesis, Paris 6 University, Paris, France, November 1978. [Google Scholar]
- Kim, Y.D. A Comparison of Dispatching Rules for Job Shops with Multiple Identical Jobs and Alternative Routeings. Int. J. Prod. Res. 1990, 28, 953–962. [Google Scholar] [CrossRef]
- Nasr, N.; Elsayed, E.A. Job Shop Scheduling with Alternative Machines. Int. J. Prod. Res. 1990, 28, 1595–1609. [Google Scholar] [CrossRef]
- Storer, R.H.; Wu, S.D.; Vaccari, R. New Search Spaces for Sequencing Problems with Application to Job Shop Scheduling. Manag. Sci. 1992, 38, 1495–1509. [Google Scholar] [CrossRef]
- Yamada, T.; Nakano, R. A Genetic Algorithm Applicable to Large-Scale Job-Shop Problems. Parallel Proble. Solving Nat. 1992, 2, 283–292. [Google Scholar]
- Van Laarhoven, P.J.M.; Aarts, E.H.L.; Lenstra, J.K. Job Shop Scheduling by Simulated Annealing. Oper. Res. 1992, 40, 113–125. [Google Scholar] [CrossRef]
- Fang, H.L.; Ross, P.; Corne, D. A Promising Genetic Algorithm Approach to Job-Shop Scheduling, Re-Scheduling and Open-Shop Scheduling Problems. Available online: http://homepages.inf.ed.ac.uk/rbf/MY_DAI_OLD_FTP/rp623.pdf (accessed on 18 February 2019).
- Aarts, E.H.L.; Van Laarhoven, P.J.M.; Lenstra, J.K.; Ulder, N.L.J. A Computational Study of Local Search Algorithms for Job Shop Scheduling. ORSA J. Comput. 1994, 6, 118. [Google Scholar] [CrossRef]
- Aarts, E.H.L.; Van Laarhoven, P.J.M.; Ulder, N.L.J. Local-Search-Based Algorithms for Job Shop Scheduling; Working Paper; Eindhoven University of Technology: Eindhoven, The Netherlands, 1991. [Google Scholar]
- Demirkol, E.; Mehta, S.; Uzsoy, R. Benchmarks for Shop Scheduling Problems. Eur. J. Oper. Res. 1998, 109, 137–141. [Google Scholar] [CrossRef]
- Morton, T.E.; Pentico, D. Heuristic Scheduling Systems: With Applications to Production Systems and Project Management, 1st ed.; John Wiley and Sons: New York, NY, USA, 1993. [Google Scholar]
- Vázquez, M.; Whitley, L.D. A Comparison of Genetic Algorithms for the Static Job Shop Scheduling Problem; Parallel Problem Solving from Nature PPSN VI; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2000; pp. 303–312. [Google Scholar]
- Watson, J.P.; Barbulescu, L.; Howe, A.E.; Whitley, L.D. Algorithm Performance and Problem Structure for Flow-Shop Scheduling. In Proceedings of the AAAI-99 Proceedings, American Association for Artificial Intelligence, Orlando, FL, USA, 18–22 July 1999; pp. 688–695. [Google Scholar]
- Aiex, R.M.; Binato, S.; Resende, M.G.C. Parallel GRASP with Path-Relinking for Job Shop Scheduling. Parallel Comput. 2003, 29, 393–430. [Google Scholar] [CrossRef]
- Chong, C.S.; Sivakumar, A.I.; Low, M.Y.H.; Gay, K.L. A Bee Colony Optimization Algorithm to Job Shop Scheduling. In Proceedings of the 38th Conference on Winter Simulation. Winter Simulation Conference, Monterey, CA, USA, 3–6 December 2006; pp. 1954–1961. [Google Scholar]
- Özgüven, C.; Özbakır, L.; Yavuz, Y. Mathematical Models for Job-Shop Scheduling Problems with Routing and Process Plan Flexibility. Appl. Math. Modell. 2010, 34, 1539–1548. [Google Scholar] [CrossRef]
- Fattahi, P.; Mehrabad, M.S.; Jolai, F. Mathematical Modeling and Heuristic Approaches to Flexible Job Shop Scheduling Problems. J. Intell. Manuf. 2007, 18, 331–342. [Google Scholar] [CrossRef]
- Mousavi, S.; Zandieh, M.; Amiri, M. Comparisons of Bi-Objective Genetic Algorithms for Hybrid Flowshop Scheduling with Sequence-Dependent Setup Times. Int. J. Prod. Res. 2012, 50, 2570–2591. [Google Scholar] [CrossRef]
- Fisher, M.L. A Dual Algorithm for the One-Machine Scheduling Problem. Math. Programm. 1976, 11, 229–251. [Google Scholar] [CrossRef]
- Brandes, U. Graphentheorie. In Handbuch Netzwerkforschung; Stegbauer, C., Häußling, R., Eds.; VS Verlag für Sozialwissenschaften: Wiesbaden, Germany, 2010; pp. 345–353. [Google Scholar]
- Stegbauer, C.; Häussling, R. (Eds.) Netzwerkforschung. Handbuch Netzwerkforschung, 1st ed.; VS Verlag für Sozialwissenschaften: Wiesbaden, Germany, 2010; Volume 4. [Google Scholar]
- Bondy, J.A. Basic Graph Theory: Paths and Circuits. In Handbook of Combinatorics; Graham, R.L., Grötschel, M., Lovász, L., Eds.; MIT Press: Cambridge, MA, USA, 1995; Volume 1, pp. 3–110. [Google Scholar]
- Turau, V. Algorithmische Graphentheorie; Oldenbourg: Wien, Austria, 2009; OCLC: 467891833; 3, überarb, aufl. [Google Scholar]
- Lerner, J. Beziehungsmatrix. In Handbuch Netzwerkforschung; VS Verlag für Sozialwissenschaften: Wiesbaden, Germany, 2010; pp. 355–364. [Google Scholar]
- Kaderali, F.; Poguntke, W. Graphen Algorithmen Netze: Grundlagen und Anwendungen in der Nachrichtentechnik; Vieweg: Braunschweig, Germany, 1995. [Google Scholar]
- Hohberger, S.; Damlachi, H. Praxishandbuch Sanierung im Mittelstand; Springer Fachmedien: Wiesbaden, Germany, 2014. [Google Scholar]
- Pandya, K. Network Structure or Topology. Int. J. Adv. Res. Comput. Sci. Manag. Stud. 2013, 1, 22–27. [Google Scholar]
- Abts, D.; Mülder, W. Grundkurs Wirtschaftsinformatik: Eine Kompakte und Praxisorientierte Einführung, 9th ed.; Springer Vieweg: Berlin, Germany, 2002. [Google Scholar]
- Ernst, H.; Schmidt, J.; Beneken, G.H. Grundkurs Informatik: Grundlagen und Konzepte für die Erfolgreiche IT-Praxis; Eine Umfassende, Praxisorientierte Einführung, 5th ed.; Lehrbuch, Springer Vieweg: Berlin, Germany, 2015; OCLC: 907482533. [Google Scholar]
- Tanenbaum, A.S.; Wetherall, D.J. Computer Networks, 5th ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2011; OCLC: ocn660087726. [Google Scholar]
- Baumöl, U.; Ickler, H. Soziale Netzwerkanalyse. In Enzyklopädie der Wirtschaftsinformatik, 10th ed.; Gronau, N., Becker, J., Kliewer, N., Leimeister, J.M., Overhage, S., Eds.; GITO: Berlin, Germany, 2018. [Google Scholar]
- Stegbauer, C. Soziale Netzwerkanalyse. In Handbuch Medienpädagogik; VS Verlag für Sozialwissenschaften: Wiesbaden, Germany, 2008; pp. 166–172. [Google Scholar]
- Rürup, M.; Röbken, H.; Emmerich, M.; Dunkake, I. Netzwerke im Bildungswesen; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2015. [Google Scholar]
- Ayyappan, G.; Nalini, D.C.; Kumaravel, D.A. A Study on SNA: Measure Average Degree and Average Weighted Degree of Knowledge Diffusion in GEPHI. Indian J. Comput. Sci. Eng. (IJCSE) 2016, 7, 230–237. [Google Scholar]
- Bojic, I.; Lipic, T.; Podobnik, V. Bio-Inspired Clustering and Data Diffusion in Machine Social Networks. In Computational Social Networks; Abraham, A., Ed.; Springer: Berlin, Germany, 2012; pp. 51–79. [Google Scholar]
- Barabási, A.L.; Pósfai, M. Network Science; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Ghali, N.; Panda, M.; Hassanien, A.E.; Abraham, A.; Snasel, V. Social Networks Analysis: Tools, Measures and Visualization. In Computational Social Networks: Mining and Visualization; Abraham, A., Ed.; Springer: Berlin, Germany, 2012; pp. 3–23. [Google Scholar]
- Catanese, S.; De Meo, P.; Ferrara, E.; Fiumara, G.; Provetti, A. Extraction and Analysis of Facebook Friendship Relations. In Computational Social Networks: Mining and Visualization; Abraham, A., Ed.; Springer: Berlin, Germany, 2012; pp. 291–324. [Google Scholar]
- Easley, D.; Kleinberg, J. Networks, Crowds, and Markets: Reasoning about a Highly Connected World; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Wu, H.; Gu, X.; Zhao, Y. The Empirical Study of a Sna-Based Approach for Identifying KSC of Enterprise. Chem. Eng. Trans. 2015, 2, 1291–1296. [Google Scholar]
- Wiedenbeck, M.; Züll, C. Clusteranalyse. In Handbuch der Sozialwissenschaftlichen Datenanalyse, 1st ed.; Wolf, C., Best, H., Eds.; VS Verlag für Sozialwissenschaften: Wiesbaden, Germany, 2010; pp. 525–552. [Google Scholar]
- Bratley, P.; Fox, B.L.; Schrage, L.E. A Guide to Simulation, 2nd ed.; Springer: Berlin, Germany, 1987. [Google Scholar]
- Georgi, G. Job Shop Scheduling in der Produktion; Wirtschaftswissenschaftliche Beiträge; Physica-Verlag: Heidelberg, Germany, 1995; Volume 111. [Google Scholar]
- Van Hoorn, J. Jobshop Explanations. 2015. Available online: http://jobshop.jjvh.nl/explanation.php (accessed on 1 December 2018).
- Organisation for Economic Co-Operation and Development. OECD Principles and Guidelines for Access to Research Data from Public Funding; OECD Publishing: Paris, France, 2007. [Google Scholar]
- Nicol, A.; Caruso, J.; Archambault, E. Open Data Access Policies and Strategies in the European Research Area and Beyond; Technical Report RTD-B6-PP-2011-2; European Commission DG Research & Innovation: Brussels, Belgium, 2013. [Google Scholar]
- Mishra, S. (Ed.) Concepts of Openness and Open Access; United Nations Educational, Scientific and Cultural Organization: Paris, France, 2015. [Google Scholar]
| 1. | It was refered to the OR-Library. Primary sources were not mentioned. |
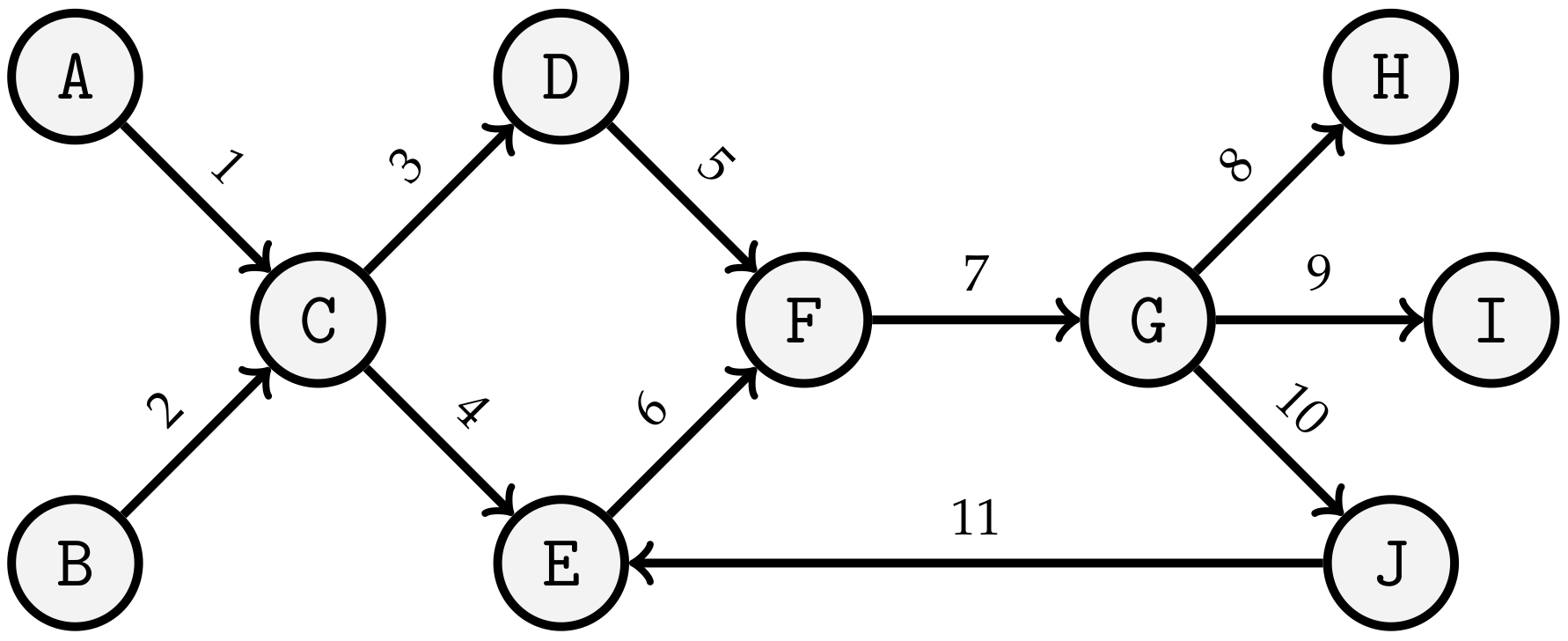

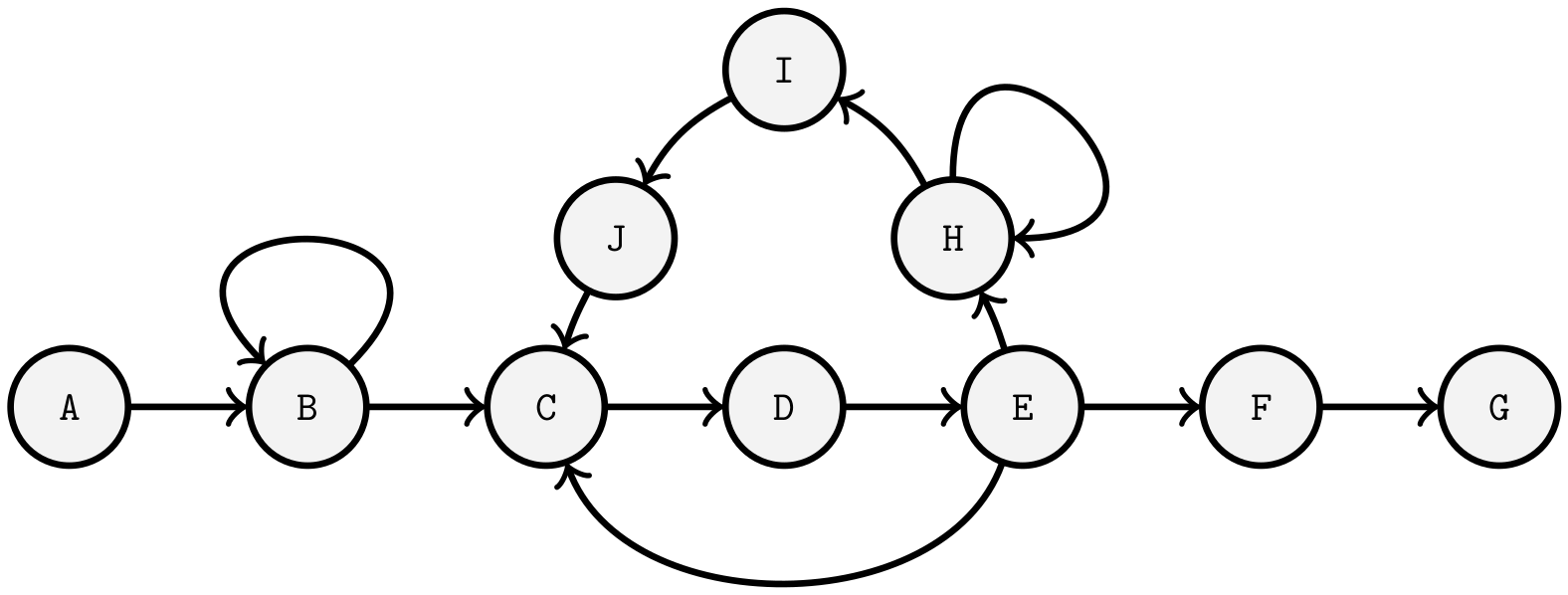


| Brucker et al. [41]—“A Branch and Bound Algorithm for the Job-Shop Scheduling Problem” [41] |
|---|
| Brucker et al. [41] describe in their work a developed algorithm to solve the known problem of the size from the work of Muth and Thompson [16] on a workstation in 16 minutes. It is stated that the algorithm—if used as a heuristic—is superior to the results of Adams et al. [27] in optimizing sequence problems up to a size of . Brucker et al. [41] present the details of their optimization method in detail and outline the basic idea of the Branch-and Bound method. The calculated results of 45 problems of different sizes are presented. The problems include between five and 15 machines and between 10 and 30 jobs. Three of these problems come from “Industrial Scheduling” by Muth and Thompson [16] and 42 were created by Adams et al. [27]. |
| Nowicki and Smutnicki [38]—“A Fast Taboo Search Algorithm for the Job Shop Problem” [38] |
|---|
| Nowicki and Smutnicki [38] present in “A Fast Taboo Search Algorithm for the Job Shop Problem” a taboo search algorithm, which pursues the goal to find the minimum lead time in workshop production. It was tested on a PC with up to 10 000 operations and solved a 10 × 10 serious problem in less than 30 s [38]. Therefore the algorithm TSAB was implemented in Pascal and C on an AT 386DX PC. It was then tested against the following problems. Three problems of Fisher and Thompson [34], abbreviated: FS1, FS2, FS3, with the sizes 6 × 6, 10 × 10 and 5 × 20 [34] as well as two problems with the size 10 × 10 of Adams et al. [27]. Furthermore, tests were performed on 40 problems with eight different sizes (10 × 10, 10 × 15, 10 × 20, 10 × 30, 5 × 10, 5 × 15, 5 × 20, 50 × 15) by Lawrence [26]. [26] was performed. Also 80 problems of Taillard [36] with eight different sizes (15 × 15, 15 × 20, 20 × 20, 15 × 30, 20 × 30, 15 × 50, 20 × 50, 20 × 100) were considered [38]. |
| Authors | Year | Algorithms | Plans/Problems | Machines | Jobs | Models Used | Sources Refered by Authors |
|---|---|---|---|---|---|---|---|
| Fisher and Thompson [34] | 1963 | 3 | 3 | 5–10 | 6–20 | ||
| Bratley et al. [40] | 1973 | 1 | N/A | 1 | 20–50 | randomly generated | |
| 2 | 80 | N/A | N/A | Conway et al. [21] | Conway et al. [21] | ||
| 2 | 3 | 5–10 | N/A | Fisher and Thompson [34] | Muth and Thompson [16] | ||
| McMahon and Florian [42] | 1975 | 1 | N/A | N/A | 20–50 | Bratley et al. [40] | Bratley et al. [40] |
| 2 | 3 | 5–10 | N/A | Fisher and Thompson [34] | Muth and Thompson [16] | ||
| Barker and McMahon [25] | 1985 | 1 | incomplete information | incomplete information | N/A | N/A | N/A |
| 1985 | 1 | 3 | 5–10 | N/A | Fisher and Thompson [34] | Muth and Thompson [16] | |
| Adams et al. [27] | 1988 | 2–3 | 9 + 21 | 10–15 | 10–50 | self-developed | |
| 2–3 | 1 | 5 | 4 | Lenstra [43] | Lenstra [43] | ||
| 2–3 | 3 | 5–10 | 6–20 | Fisher and Thompson [34] | Muth and Thompson [16] | ||
| 2–3 | 6 | 10 | 15–30 | Lawrence [26] | Lawrence [26] | ||
| Carlier and Pinson [5] | 1989 | 1 | approx. 150 | N/A | N/A | Fisher and Thompson [34], Carlier [44], randomly generated | Muth and Thompson [16], Carlier [44] |
| Kim [45] | 1990 | 29 | 150 | 10–25 | |||
| Nasr and Elsayed [46] | 1990 | 2 | 15 | N/A | N/A | N/A | N/A |
| Applegate and Cook [6] | 1991 | 1 | 3 | N/A | N/A | Fisher and Thompson [34] | Muth and Thompson [16] |
| 1 | 40 | N/A | N/A | Adams et al. [27] | Adams et al. [27] | ||
| 1 | 5 | N/A | N/A | Lawrence [26] | Lawrence [26] | ||
| 1 | 5 | N/A | N/A | Applegate and Cook [6], self-developed | |||
| Nakano and Yamada [7] | 1991 | 1(3) | 3 | 5–10 | 6–20 | Fisher and Thompson [34] | Muth and Thompson [16] |
| Storer et al. [47] | 1992 | 2(9) | 2 | 5–10 | 10–20 | Fisher and Thompson [34] | Muth and Thompson [16] |
| 2(9) | 20 | 10–15 | 20–50 | Storer et al. [47], self-developed | |||
| Yamada and Nakano [48] | 1992 | N/A (≥7) | 3 | 5–10 | 6–20 | Fisher and Thompson [34] | Muth and Thompson [16] |
| N/A (≥7) | 4 | 20 | 20 | self-developed | |||
| van Laarhoven et al. [49] | 1992 | 4 | 3 | 5–10 | 6–20 | Fisher and Thompson [34] | Fisher and Thompson [34] |
| 4 | 40 | 5–15 | 10–30 | Lawrence [26] | Lawrence [26] | ||
| Fang et al. [50] | 1993 | 1(3) | 2 | 5–10 | 10–20 | Fisher and Thompson [34] | Muth and Thompson [16] JSSP |
| 1(3) | 6 | 4–20 | 4–20 | [28] | [28] | ||
| Taillard [36] | 1993 | 1 | 80 | 15–20 | 15–100 | randomly generated | |
| 1 | 120 | 5–20 | 20–500 | randomly generated | |||
| 1 | 60 | 4–20 | 4–20 | randomly generated | |||
| Brucker et al. [41] | 1994 | 1 | 3 | 5–10 | 6–20 | Fisher and Thompson [34] | Muth and Thompson [16] |
| 1 | 42 | 5–15 | 10–30 | Adams et al. [27] | Adams et al. [27] | ||
| Aarts et al. [51] | 1994 | 7 | 3 | 5–10 | 6–20 | Fisher and Thompson [34] | Fisher and Thompson [34] |
| 7 | 40 | 5–15 | 10–30 | Lawrence [26] | Lawrence [26] | ||
| 2 | 3 | 15 | 20 | Adams et al. [27] | Applegate and Cook [6], Adams et al. [27] | ||
| 2 | 7 | 10–15 | 15–20 | Lawrence [26] | Applegate and Cook [6], Adams et al. [27] | ||
| Bierwirth [37] | 1995 | 9 | 2 | 5–10 | 10–20 | Fisher and Thompson [34] | Applegate and Cook [6] |
| 6 | 10 | 10–15 | 15–20 | Lawrence [26] | Applegate and Cook [6] | ||
| Dorndorf and Pesch [22] | 1995 | 6 | 3 | 5–10 | 6–20 | Fisher and Thompson [34] | Fisher and Thompson [34] |
| 6 | 105 (x5) | N/A | N/A | randomly generated | |||
| 6 | 35 | 5–15 | 10–20 | Lawrence [26] | Adams et al. [27], van Laarhoven et al. [49], Aarts et al. [52] | ||
| Nowicki and Smutnicki [38] | 1996 | 7 | 3 | 5–10 | 6–20 | Fisher and Thompson [34] | Fisher and Thompson [34], van Laarhoven et al. [49] |
| 7 | 2 | 10 | 10 | Adams et al. [27] | Adams et al. [27] | ||
| 7 | 40 | 5–15 | 10–30 | Lawrence [26] | Lawrence [26], van Laarhoven et al. [49] | ||
| 7 | 80 | 15–20 | 15–100 | Taillard [36] | Taillard [36] | ||
| 7 | 40 | 5–10 | 500–1000 | randomly generated | |||
| Demirkol et al. [53] | 1998 | N/A (≥3) | 600 | 15–20 | 20–50 | randomly generated | |
| Vázquez and Whitley [39] | 2000 | 6 | 12 | 3–8 | 10–50 | N/A | Morton and Pentico [54] |
| Vázquez and Whitley [55] | 2000 | 5 | 3 | 5–10 | 6–20 | Fisher and Thompson [34] | OR-Library1 |
| 5 | 4 | 20 | 20 | Yamada and Nakano [48] | OR-Library | ||
| 5 | 4 | 10–15 | 10–20 | Lawrence [26] | OR-Library | ||
| 5 | 10 | 20 | 30 | Taillard [36] | OR-Library | ||
| 4 | 16 | 10–20 | 10–20 | self-developed | [56] | ||
| Aiex et al. [57] | 2003 | 2 | 5 | 10–20 | 10–15 | Adams et al. [27] | [28] |
| 2 | 8 | 4–9 | 7–14 | Carlier [44] | [28] | ||
| 2 | 3 | 5–10 | 6–20 | Fisher and Thompson [34] | [28] | ||
| 2 | 10 | 10 | 10 | Applegate and Cook [6] | [28] | ||
| 2 | 40 | 5–15 | 10–30 | Lawrence [26] | [28] | ||
| Nowicki and Smutnicki [8] | 2005 | 4 | 3 | N/A | N/A | Fisher and Thompson [34] | Fisher and Thompson [34] |
| 4 | 40 | N/A | N/A | Lawrence [26] | Lawrence [26] | ||
| 4 | 5 | N/A | N/A | Adams et al. [27] | Adams et al. [27] | ||
| 4 | 10 | N/A | N/A | Applegate and Cook [6] | Applegate and Cook [6] | ||
| 4 | 4 | 20 | 20 | Yamada and Nakano [48] | Yamada and Nakano [48] | ||
| 4 | 20 | 10–15 | 20–50 | Storer et al. [47] | Storer et al. [47] | ||
| 4 | 80 | 15–20 | 15–100 | Taillard [36] | Taillard [36] | ||
| 4 | 80 | N/A | N/A | Demirkol et al. [53] | Demirkol et al. [53] | ||
| Chong et al. [58] | 2006 | 3 | 82 in total | 5–20 | 6–50 | ||
| 3 | 3 | N/A | N/A | Fisher and Thompson [34] | Fisher and Thompson [34] | ||
| 3 | 40 | N/A | N/A | Lawrence [26] | Lawrence [26] | ||
| 3 | 20 | N/A | N/A | Storer et al. [47] | Storer et al. [47] | ||
| 3 | 10 | N/A | N/A | Applegate and Cook [6] | Applegate and Cook [6] | ||
| 3 | 4 | N/A | N/A | Yamada and Nakano [48] | Yamada and Nakano [48] | ||
| 3 | 5 | N/A | N/A | Adams et al. [27] | Adams et al. [27] | ||
| Özgüven et al. [59] | 2010-06-01 | 2 | 20 | 2–8 | 2–12 | Fattahi et al. [60] | Fattahi et al. [60] |
| Mousavi et al. [61] | 2012-05-12 | 4 | N/A (≥15) | 1–10 | 15–40 | self-developed | Fisher [62] |
| Sequence | Splitting | Parallelism | Merge | Cycle | Optionality |
|---|---|---|---|---|---|
 |  |  |  |  |  |
| Linear | Parallel | Multiple-Parallel | Ring |
|---|---|---|---|
 |  |  |  |
| Tree (splitting) | Tree (merging) | Cycle | Option |
 |  |  |  |
| 3 Elements | 7 Elements | 15 Elements | |
|---|---|---|---|
| Topology |  |  |  |
| Possible combinations | 6 | 5040 | 1,307,674,368,000 |
| Valid serializations | 2 | 80 | 21,552,960 |
 | |||
 | … | … |
| 3 Elements | 7 Elements | 15 Elements | |
|---|---|---|---|
| Topologie |  | … | … |
| Possible combinations | 6 | 5040 | 1,307,674,368,000 |
| Possible combinations of linear model | 1 | 1 | 1 |
| Variants of linear model | 1 | 1 | 1 |
| Topology |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|
| Linear | Parallel | Multiple | Ring | Tree | Tree | Cycle | Option | |
| Parallel | (Splitting) | (Merging) | ||||||
| Metric | ||||||||
| Nodes | 15 | 14 | 14 | 15 | 15 | 15 | 14 | 14 |
| Edges | 14 | 14 | 15 | 15 | 14 | 14 | 16 | 16 |
| Average Degree | 1.867 | 2 | 2.143 | 2 | 1.867 | 1.867 | 2.286 | 2.286 |
| Average Weighted Degree | 0.933 | 1 | 1.071 | 1 | 0.933 | 0.933 | 1.143 | 1.143 |
| Network Diameter | 14 | 7 | 5 | 14 | 3 | 3 | 6 | 4 |
| Density (directed) | 0.067 | 0.077 | 0.082 | 0.071 | 0.067 | 0.067 | 0.088 | 0.088 |
| Density (undirected.) | 0.133 | 0.154 | 0.165 | 0.143 | 0.133 | 0.133 | 0.176 | 0.176 |
| Modularity | 0.513 | 0.449 | 0.393 | 0.48 | 0.513 | 0.513 | 0.393 | 0.375 |
| Weakly Conn. Components | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Strongly Conn. Components | 15 | 14 | 14 | 1 | 15 | 15 | 4 | 14 |
| Average Path Length | 5.333 | 2.927 | 2.209 | 7.5 | 1.824 | 1.824 | 3.153 | 2.122 |
| Topology |  |  |  |  |  |  |  |  |
|---|---|---|---|---|---|---|---|---|
| Linear | Parallel | Multiple | Ring | Tree | Tree | Cycle | Option | |
| Parallel | (Splitting) | (Merging) | ||||||
| Linear | ||||||||
| Avg. Wgt. Degree | < | < | < | = | = | < | < | |
| Network Diamater | > | > | = | > | > | > | > | |
| Str. Con. Comp. | = | = | > | = | = | > | = | |
| Avg. Path Length | > | > | < | > | > | > | > | |
| Parallel | ||||||||
| Avg. Wgt. Degree | > | < | = | > | > | < | < | |
| Network Diamater | < | > | < | > | > | > | > | |
| Str. Con. Comp. | = | = | > | = | = | > | = | |
| Avg. Path Length | < | > | < | > | > | ∼ | > | |
| Multiple Parallel | ||||||||
| Avg. Wgt. Degree | > | > | > | > | > | < | < | |
| Network Diamater | < | < | < | > | > | ∼ | ∼ | |
| Str. Con. Comp. | = | = | > | = | = | > | = | |
| Avg. Path Length | < | < | < | > | > | ∼ | ∼ | |
| Ring | ||||||||
| Avg. Wgt. Degree | > | = | < | > | > | < | < | |
| Network Diamater | = | > | > | > | > | > | > | |
| Str. Con. Comp. | < | < | < | < | < | < | < | |
| Avg. Path Length | > | > | > | > | > | > | > | |
| Splitting Tree | ||||||||
| Avg. Wgt. Degree | = | < | < | < | = | < | < | |
| Network Diamater | < | < | < | < | = | < | < | |
| Str. Con. Comp. | = | = | = | > | = | > | = | |
| Avg. Path Length | < | < | < | < | = | < | < | |
| Splitting Merging | ||||||||
| Avg. Wgt. Degree | = | < | < | < | = | < | < | |
| Network Diamater | < | < | < | < | = | < | < | |
| Str. Con. Comp. | = | = | = | > | = | > | = | |
| Avg. Path Length | < | < | < | < | = | < | < | |
| Cycle | ||||||||
| Avg. Wgt. Degree | > | > | > | > | > | > | ∼ | |
| Network Diamater | < | < | ∼ | < | > | > | ∼ | |
| Str. Con. Comp. | < | < | < | > | < | < | < | |
| Avg. Path Length | < | ∼ | ∼ | < | > | > | ∼ | |
| Option | ||||||||
| Avg. Wgt. Degree | > | > | > | > | > | > | ∼ | |
| Network Diamater | < | < | ∼ | < | > | > | ∼ | |
| Str. Con. Comp. | = | = | = | > | = | = | > | |
| Avg. Path Length | < | < | ∼ | < | > | > | ∼ |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weber, E.; Tiefenbacher, A.; Gronau, N. Need for Standardization and Systematization of Test Data for Job-Shop Scheduling. Data 2019, 4, 32. https://doi.org/10.3390/data4010032
Weber E, Tiefenbacher A, Gronau N. Need for Standardization and Systematization of Test Data for Job-Shop Scheduling. Data. 2019; 4(1):32. https://doi.org/10.3390/data4010032
Chicago/Turabian StyleWeber, Edzard, Anselm Tiefenbacher, and Norbert Gronau. 2019. "Need for Standardization and Systematization of Test Data for Job-Shop Scheduling" Data 4, no. 1: 32. https://doi.org/10.3390/data4010032
APA StyleWeber, E., Tiefenbacher, A., & Gronau, N. (2019). Need for Standardization and Systematization of Test Data for Job-Shop Scheduling. Data, 4(1), 32. https://doi.org/10.3390/data4010032




