Improving Urban Population Distribution Models with Very-High Resolution Satellite Information
Abstract
1. Introduction
2. Materials and Methods
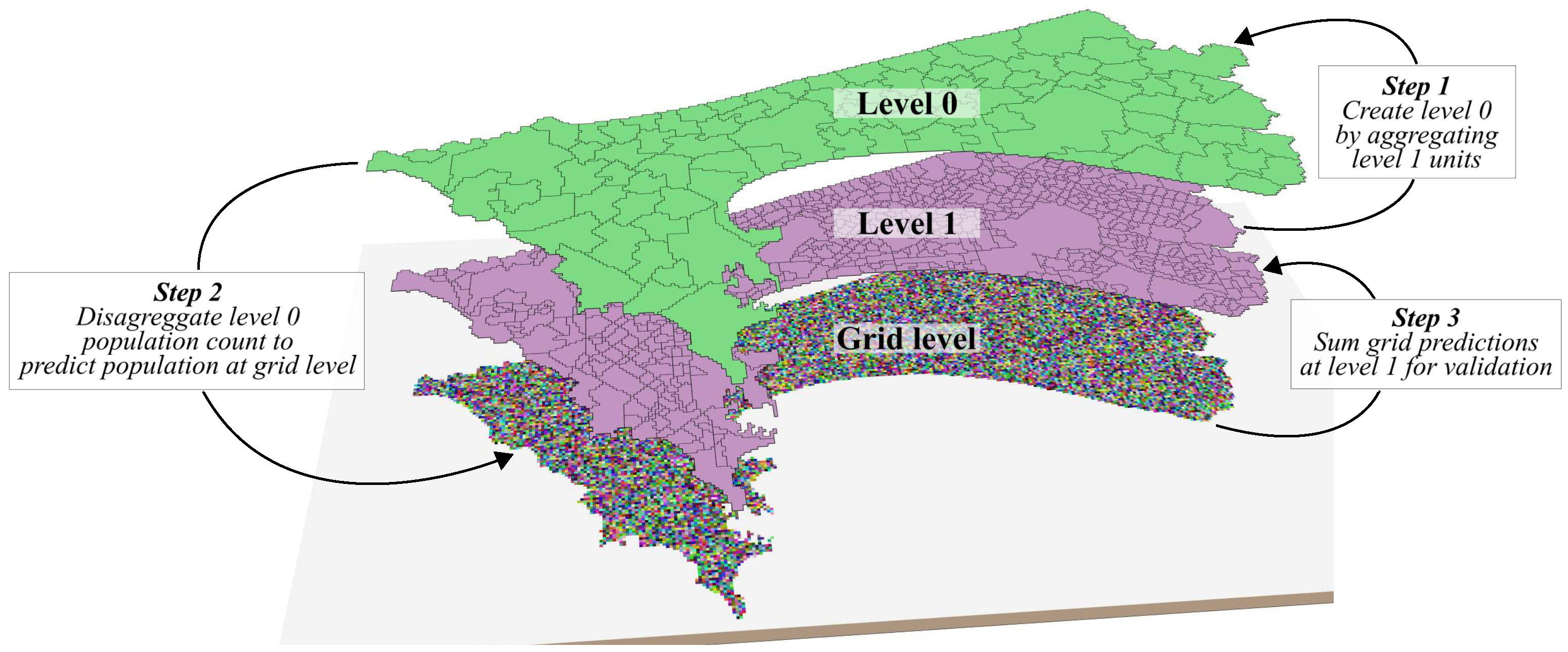
2.1. General Workflow
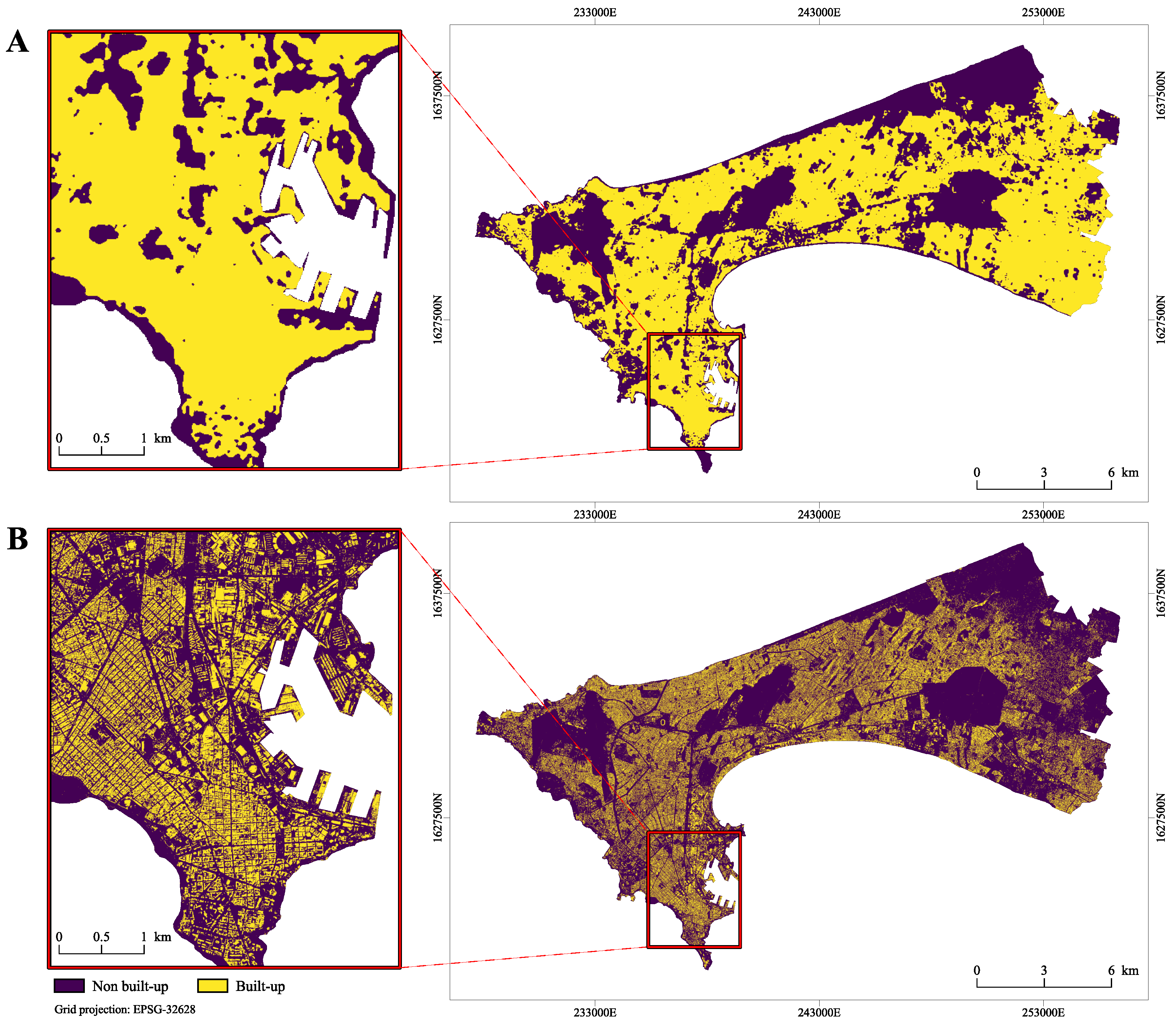
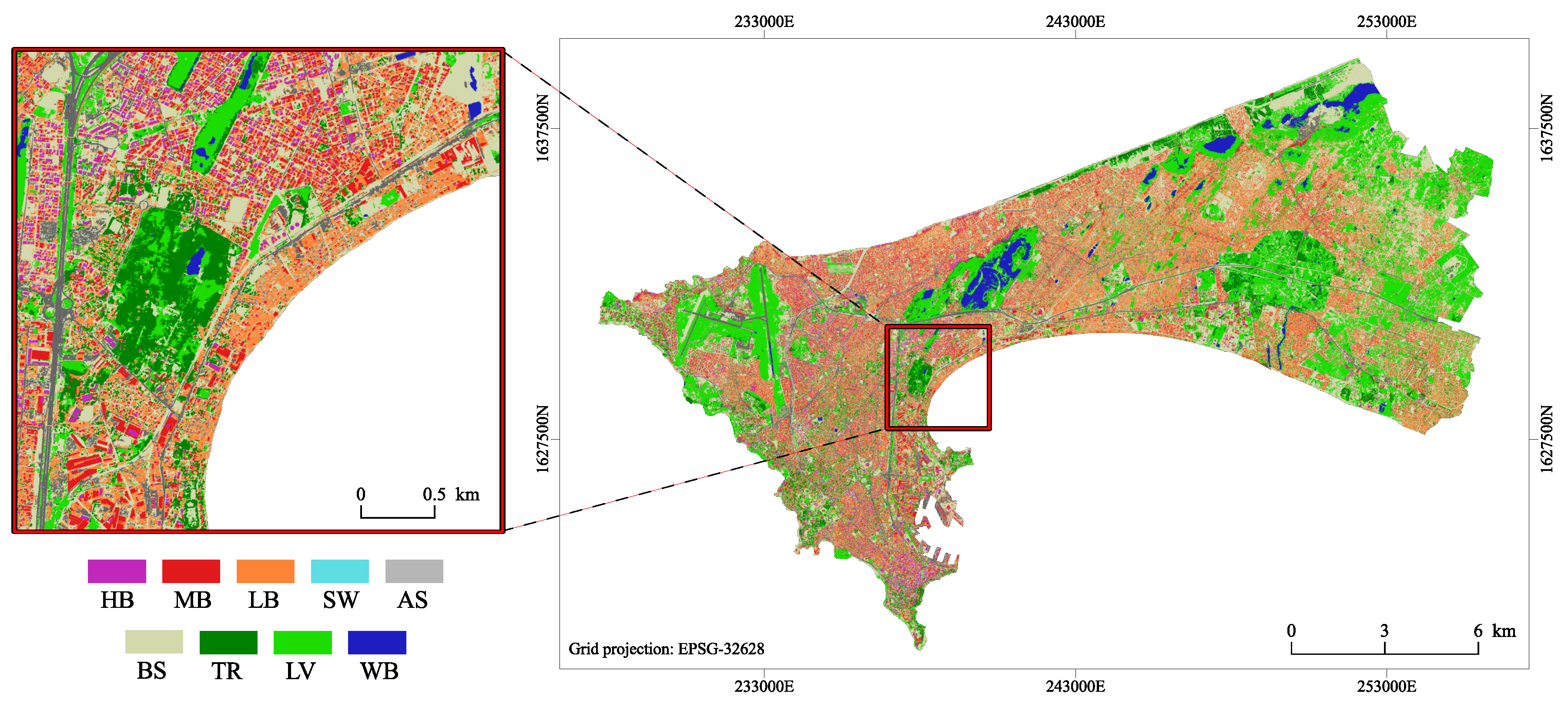
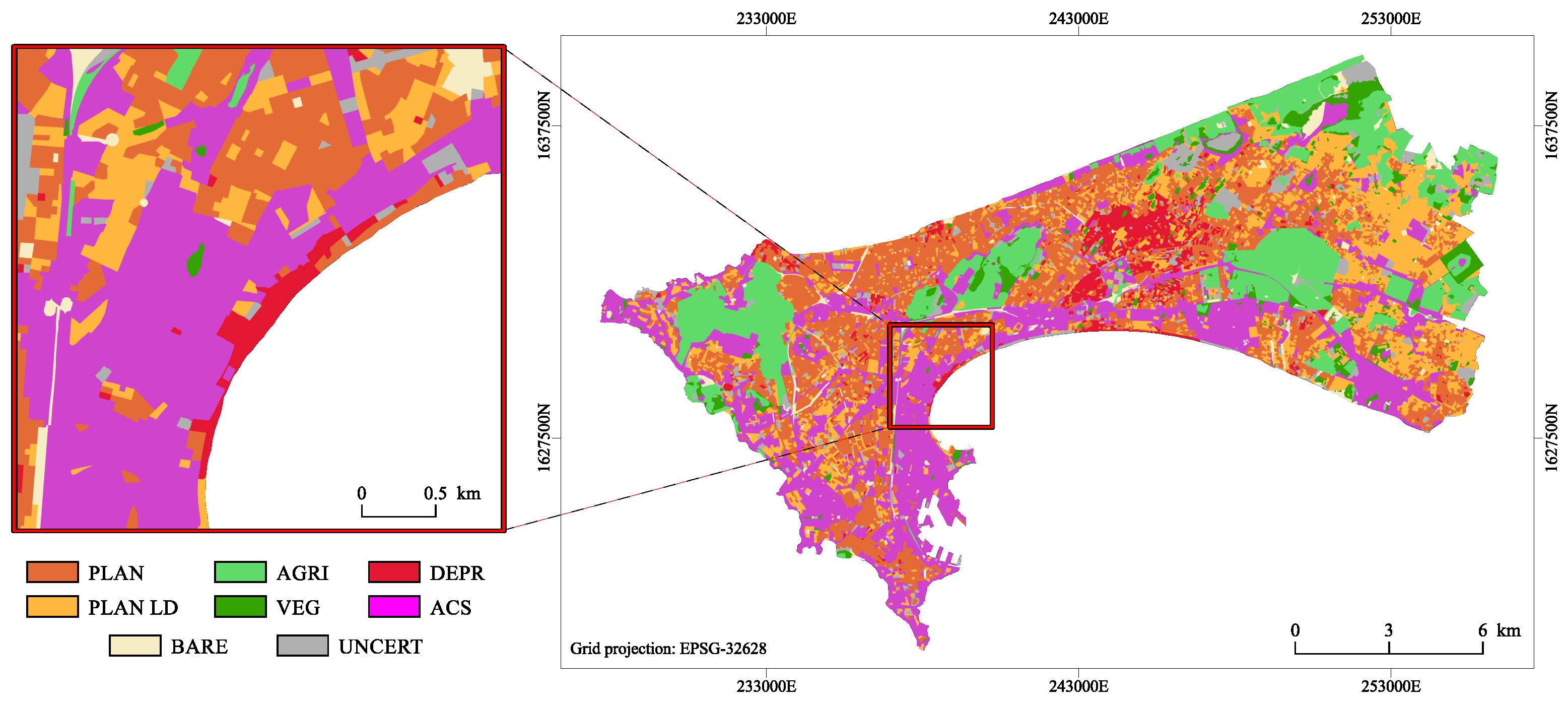
2.2. Remote Sensing Derived Data
2.3. Population Data
2.4. Creation of Validation and Training Levels
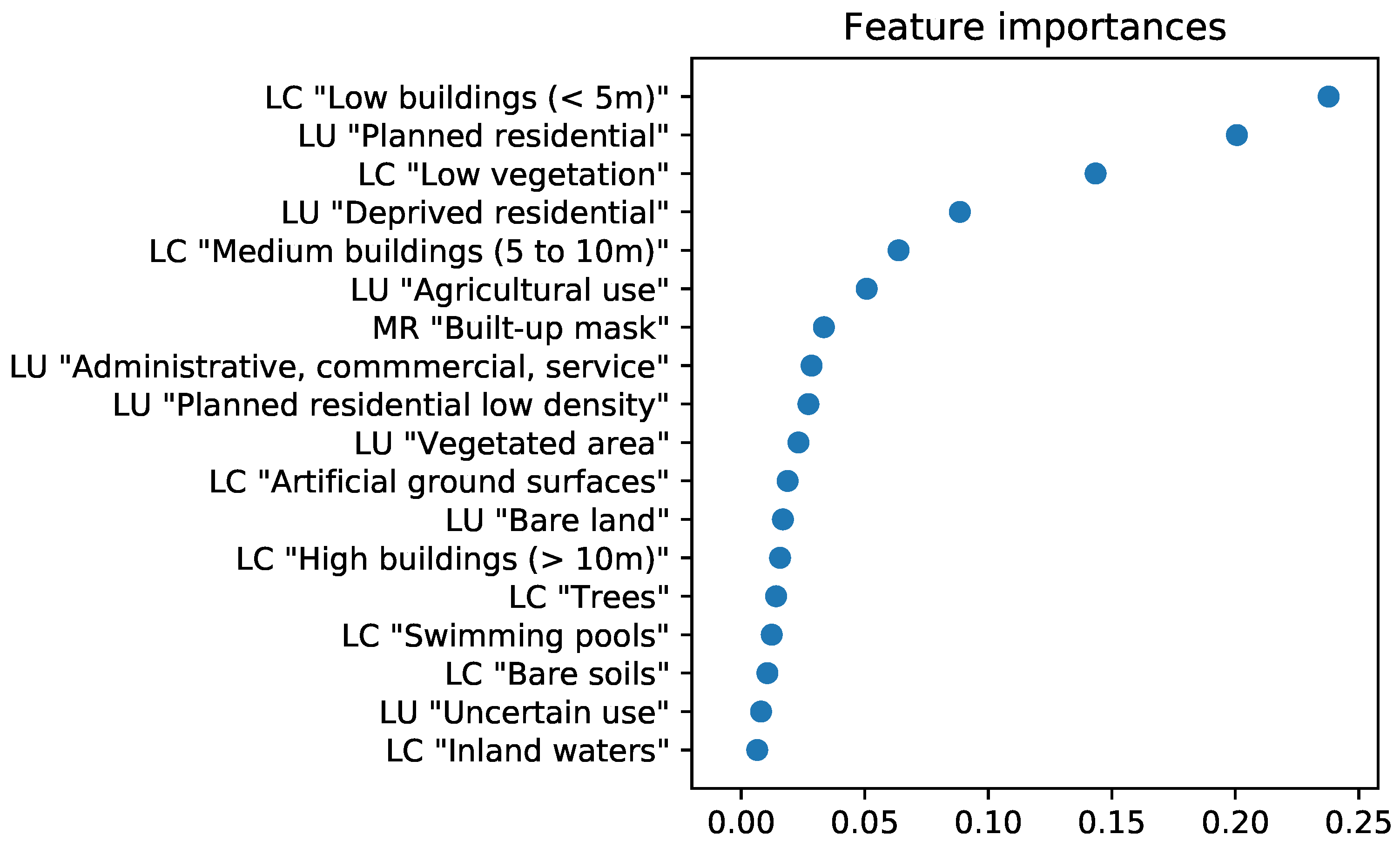
2.5. Analysis Design and Weighting Layer Creation
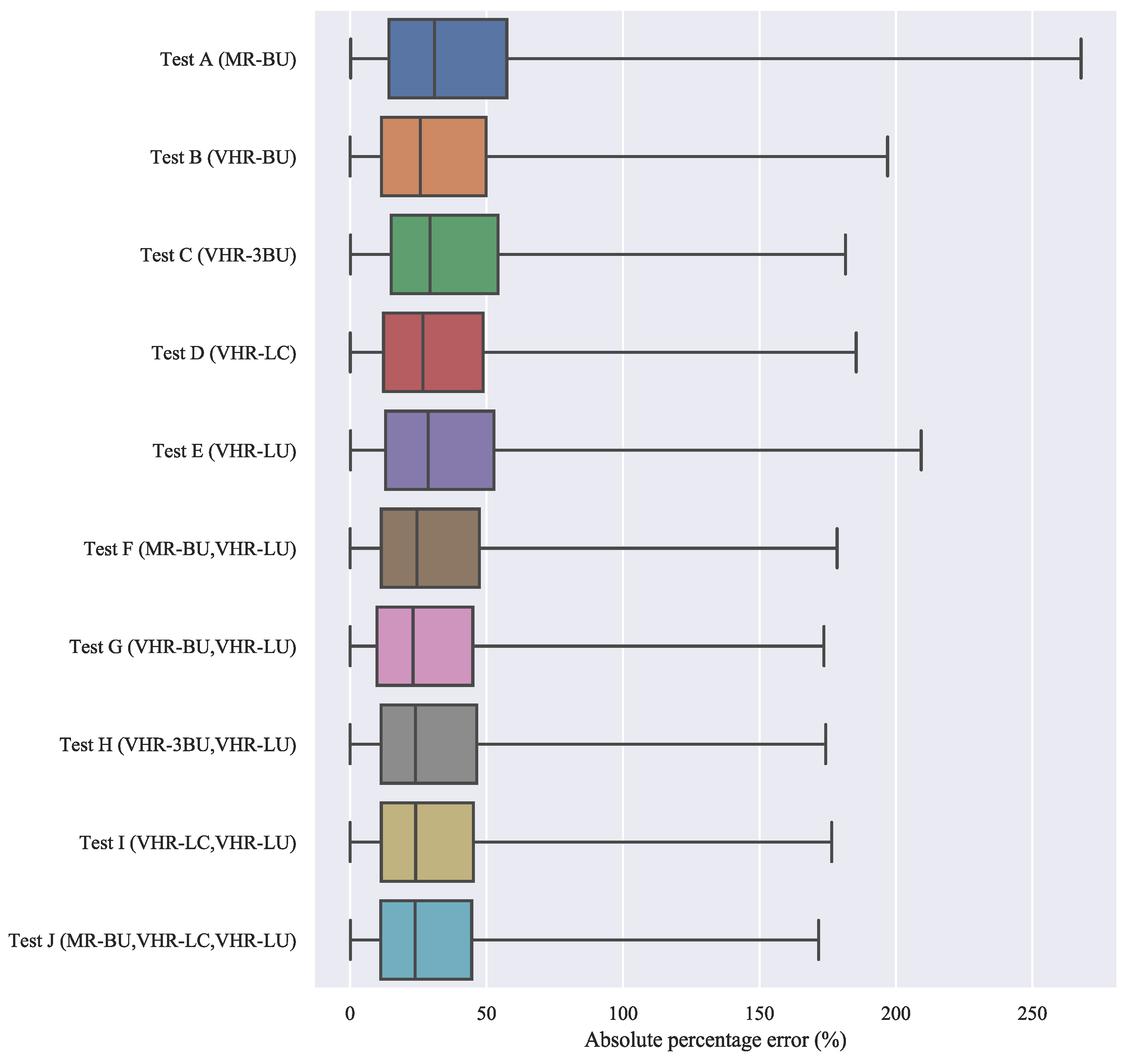
2.6. Validation Scheme
2.7. Software Environment and Computer Code Availability
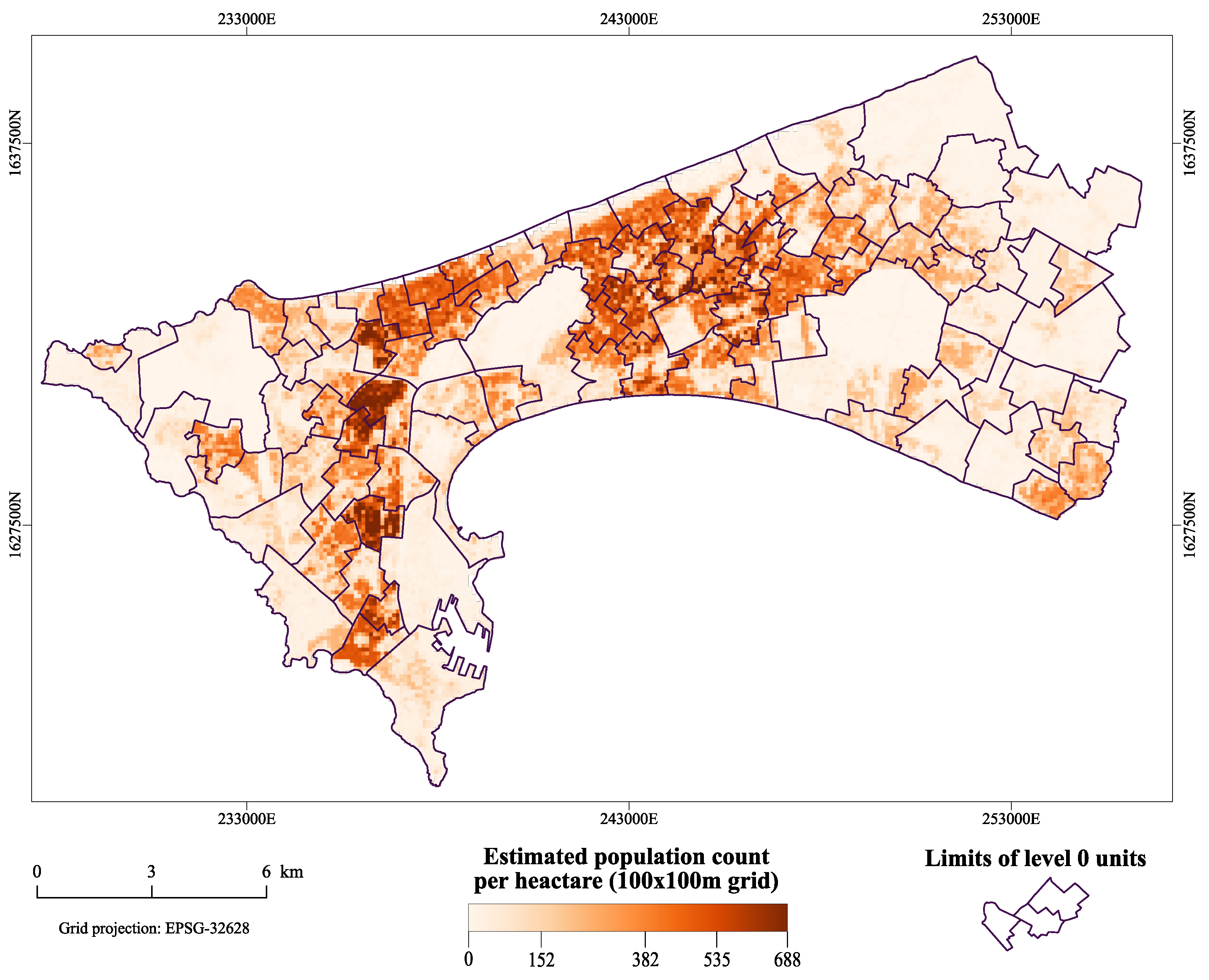
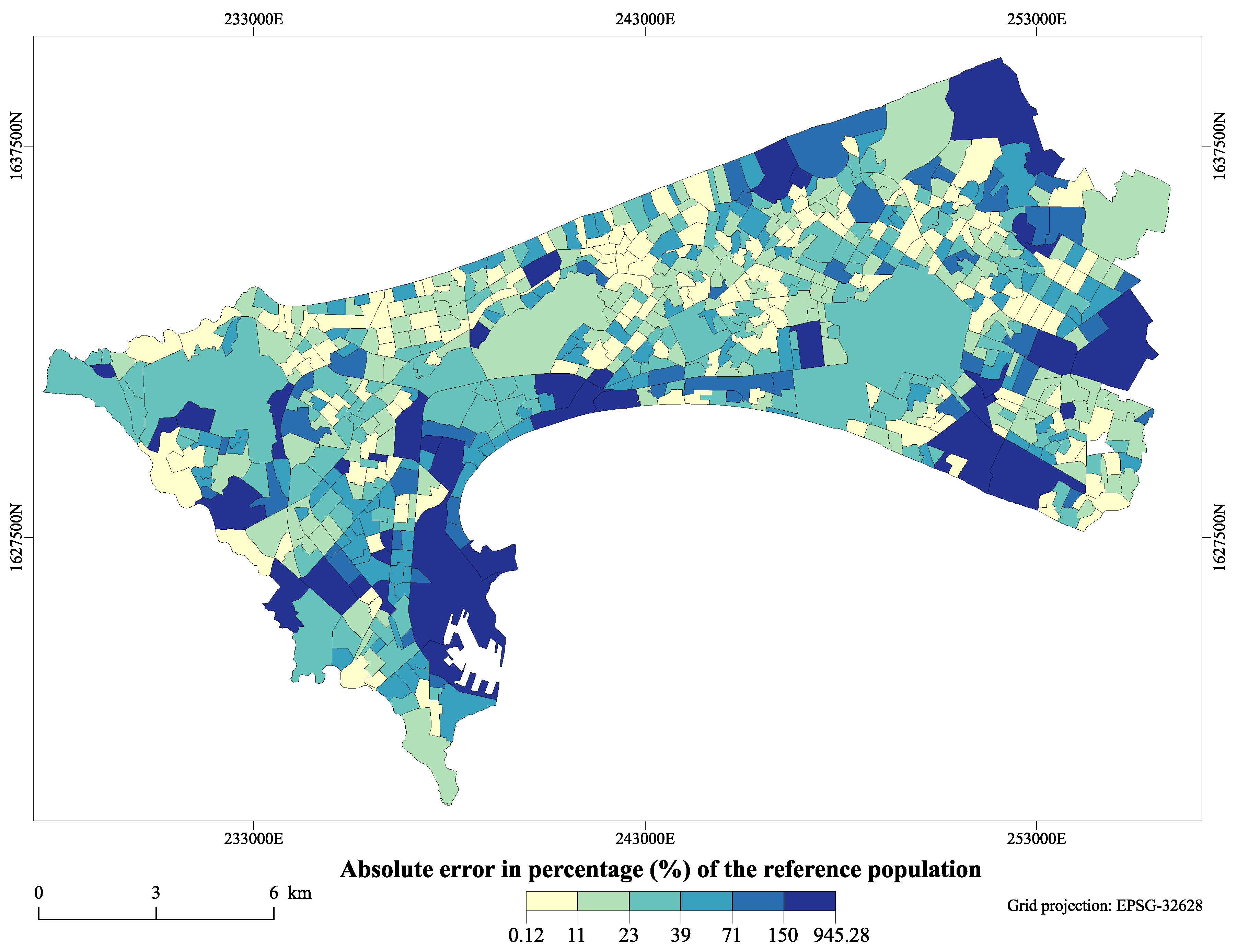
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- The MR built-up layer is available from https://doi.org/10.5281/zenodo.1450931.
- The VHR land-cover map is available from https://doi.org/10.5281/zenodo.1290799.
- The VHR land-use map is available from https://doi.org/10.5281/zenodo.1291388.
References
- UN DESA. World Urbanization Prospects: The 2018 Revision, Online Edition; United Nations Department of Economic and Social Affairs: New York, NY, USA, 2018. [Google Scholar]
- United Nations Human Settlements Programme (UN-Habitat). The State of African Cities, 2014: Re-Imagining Sustainable Urban Transitions; UN-Habitat: Nairobi, Kenya, 2014. [Google Scholar]
- Steiner, P.; Paulus, G. Dasymetric mapping for public health planning. In Proceedings of the 10th AGILE International Conference on Geographic Information Science, Aalborg, Denmark, 8–11 May 2007. [Google Scholar]
- Ehrlich, D.; Lang, S.; Laneve, G.; Mubareka, S.; Schneiderbauer, S.; Tiede, D. Can Earth Observation help to improve information on population? Indirect Population Estimations from EO Derived Geo-Spatial Data: Contribution from GMOSS. In Remote Sensing from Space: Supporting International Peace and Security; Springer: Dordrecht, The Netherlands, 2009; pp. 211–237. [Google Scholar]
- Su, M.D.; Lin, M.C.; Hsieh, H.I.; Tsai, B.W.; Lin, C.H. Multi-layer multi-class dasymetric mapping to estimate population distribution. Sci. Total Environ. 2010, 408, 4807–4816. [Google Scholar] [CrossRef] [PubMed]
- Wardrop, N.A.; Jochem, W.C.; Bird, T.J.; Chamberlain, H.R.; Clarke, D.; Kerr, D.; Bengtsson, L.; Juran, S.; Seaman, V.; Tatem, A.J. Spatially disaggregated population estimates in the absence of national population and housing census data. Proc. Natl. Acad. Sci. USA 2018, 115, 3529–3537. [Google Scholar] [CrossRef] [PubMed]
- Weber, E.M.; Seaman, V.Y.; Stewart, R.N.; Bird, T.J.; Tatem, A.J.; McKee, J.J.; Bhaduri, B.L.; Moehl, J.J.; Reith, A.E. Census-independent population mapping in northern Nigeria. Remote Sens. Environ. 2018, 204, 786–798. [Google Scholar] [CrossRef] [PubMed]
- United Nations Economic and Social Council. Report of the Inter-Agency and Expert Group on Sustainable Development Goal Indicators; United Nations Economic and Social Council: New York, NY, USA, 2016. [Google Scholar]
- Langford, M. Rapid facilitation of dasymetric-based population interpolation by means of raster pixel maps. Comput. Environ. Urban Syst. 2007, 31, 19–32. [Google Scholar] [CrossRef]
- Langford, M.; Unwin, D.J. Generating and mapping population density surfaces within a geographical information system. Cartogr. J. 1994, 31, 21–26. [Google Scholar] [CrossRef]
- Openshaw, S. The modifiable areal unit problem. Concepts Tech. Mod. Geogr. 1984, 38. [Google Scholar]
- Mennis, J. Generating Surface Models of Population Using Dasymetric Mapping. Prof. Geogr. 2003, 55, 31–42. [Google Scholar]
- Wu, S.; Qiu, X.; Wang, L. Population Estimation Methods in GIS and Remote Sensing: A Review. GISci. Remote Sens. 2005, 42, 80–96. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Stevens, F.R.; Gaughan, A.E.; Linard, C.; Tatem, A.J. Disaggregating census data for population mapping using random forests with remotely-sensed and other ancillary data. PLoS ONE 2015. [Google Scholar] [CrossRef]
- Nieves, J.J.; Stevens, F.R.; Gaughan, A.E.; Linard, C.; Sorichetta, A.; Hornby, G.; Patel, N.N.; Tatem, A.J. Examining the correlates and drivers of human population distributions across low- and middle-income countries. J. R. Soc. Interface 2017, 14, 20170401. [Google Scholar] [CrossRef] [PubMed]
- Tobler, W.R. Smooth pycnophylactic interpolation for geographical regions. J. Am. Stat. Assoc. 1979, 74, 519–530. [Google Scholar] [CrossRef] [PubMed]
- Forget, Y.; Shimoni, M.; Gilbert, M.; Linard, C. Complementarity Between Sentinel-1 and Landsat 8 Imagery for Built-Up Mapping in Sub-Saharan Africa. Preprints 2018. [Google Scholar] [CrossRef]
- Forget, Y.; Linard, C.; Gilbert, M. Automated supervised classification of Ouagadougou built-up areas in Landsat scenes using OpenStreetMap. In Proceedings of the 2017 Joint Urban Remote Sensing Event (JURSE), Dubai, UAE, 6–8 March 2017; pp. 1–4. [Google Scholar]
- Forget, Y.; Linard, C.; Gilbert, M.; Shimoni, M.; Lopez, J. Fusion Scheme for Automatic and Large-Scaled Built-up Mapping. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 2072–2075. [Google Scholar]
- Grippa, T.; Lennert, M.; Beaumont, B.; Vanhuysse, S.; Stephenne, N.; Wolff, E. An Open-Source Semi-Automated Processing Chain for Urban Object-Based Classification. Remote Sens. 2017, 9, 358. [Google Scholar] [CrossRef]
- Grippa, T.; Georganos, S.; Vanhuysse, S.; Lennert, M.; Wolff, E. A local segmentation parameter optimization approach for mapping heterogeneous urban environments using VHR imagery. In Remote Sensing Technologies and Applications in Urban Environments II; International Society for Optics and Photonics: Bellingham, WA, USA, 2017. [Google Scholar]
- Georganos, S.; Grippa, T.; Lennert, M.; Vanhuysse, S.; Wolff, E. SPUSPO: Spatially Partitioned Unsupervised Segmentation Parameter Optimization for efficiently segmenting large heterogeneous areas. In Proceedings of the 2017 Conference on Big Data from Space (BiDS’17), Toulouse, France, 28–30 November 2017. [Google Scholar]
- Brousse, O.; Georganos, S.; Demuzere, M.; Vanhuysse, S.; Wouters, H.; Wolff, E.; Linard, C.; van Lipzig, N.P.M.; Dujardin, S. Using Local Climate Zones in Sub-Saharan Africa to tackle urban health issues. Urban Clim. 2019, 27, 227–242. [Google Scholar] [CrossRef]
- Grippa, T.; Georganos, S.; Zarougui, S.; Bognounou, P.; Diboulo, E.; Forget, Y.; Lennert, M.; Vanhuysse, S.; Mboga, N.; Wolff, E. Mapping Urban Land Use at Street Block Level Using OpenStreetMap, Remote Sensing Data, and Spatial Metrics. ISPRS Int. J. Geo-Inf. 2018, 7, 246. [Google Scholar] [CrossRef]
- Agence Nationale de la Statistique et de la Démographie (ANSD). Rapport définitf du RGPHAE 2013; ANSD: Dakar, Senegal, 2013. [Google Scholar]
- Reed, F.; Gaughan, A.; Stevens, F.; Yetman, G.; Sorichetta, A.; Tatem, A. Gridded Population Maps Informed by Different Built Settlement Products. Data 2018, 3, 33. [Google Scholar] [CrossRef]
- Batista e Silva, F.; Gallego, J.; Lavalle, C. A high-resolution population grid map for Europe. J. Maps 2013, 9, 16–28. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Neteler, M.; Bowman, M.H.; Landa, M.; Metz, M. GRASS GIS: A multi-purpose open source GIS. Environ. Model. Softw. 2012, 31, 124–130. [Google Scholar] [CrossRef]
- Kluyver, T.; Ragan-Kelley, B.; Pérez, F.; Granger, B.; Bussonnier, M.; Frederic, J.; Kelley, K.; Hamrick, J.; Grout, J.; Corlay, S.; et al. Jupyter Notebooks—A publishing format for reproducible computational workflows. In Proceedings of the 20th International Conference on Electronic Publishing, Göttingen, Germany, 7–9 June 2016; pp. 87–90. [Google Scholar]
- Linard, C.; Tatem, A.J.; Gilbert, M. Modelling spatial patterns of urban growth in Africa. Appl. Geogr. 2013, 44, 23–32. [Google Scholar] [CrossRef] [PubMed]
- Box, G.E.P.; Hunter, J.S.; Hunter, W.G. Statistics for Experimenters: Design, Innovation, and Discovery, 2nd ed.; Wiley Series in Probability and Statistics; Wiley-Interscience: Hoboken, NJ, USA, 2005. [Google Scholar]
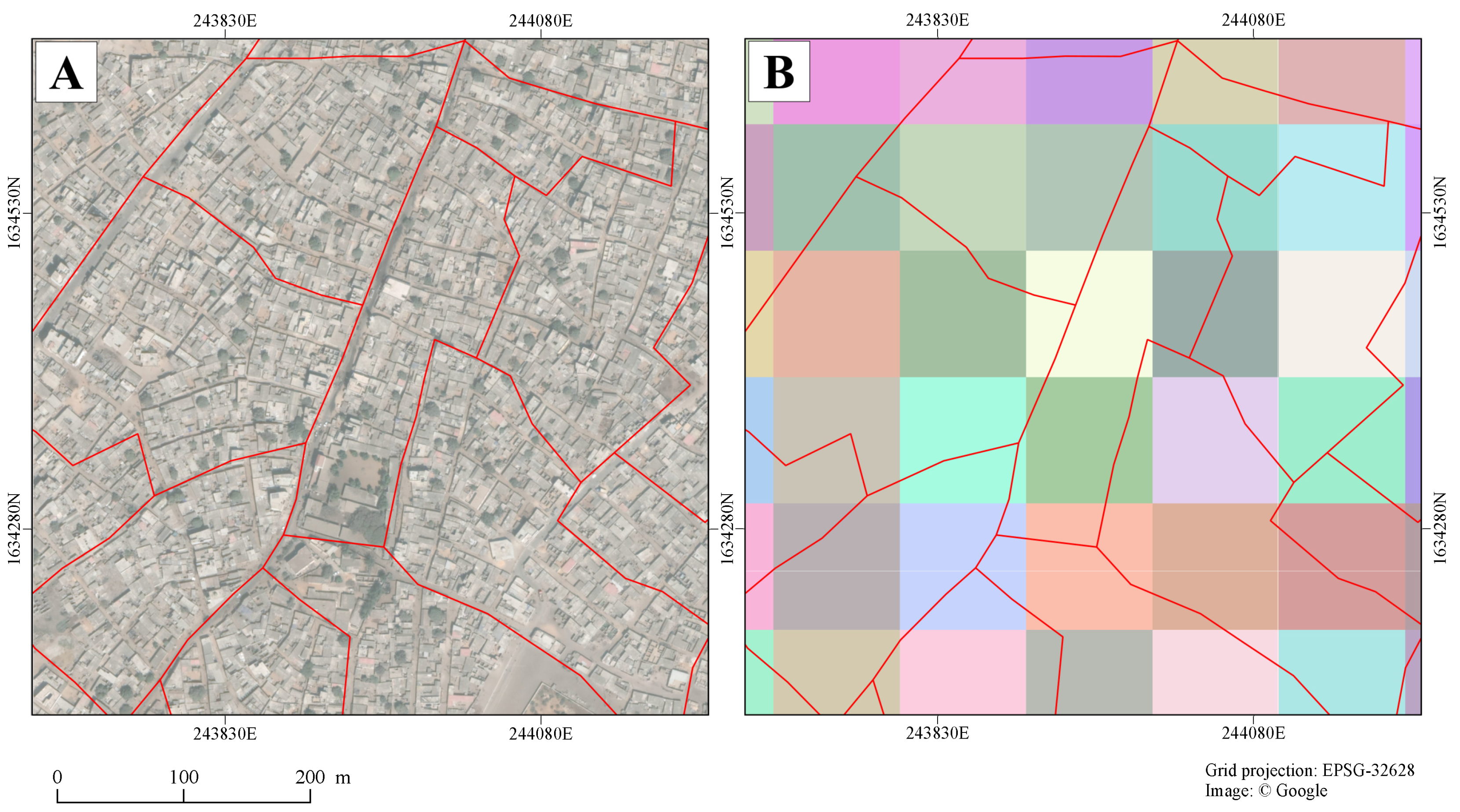
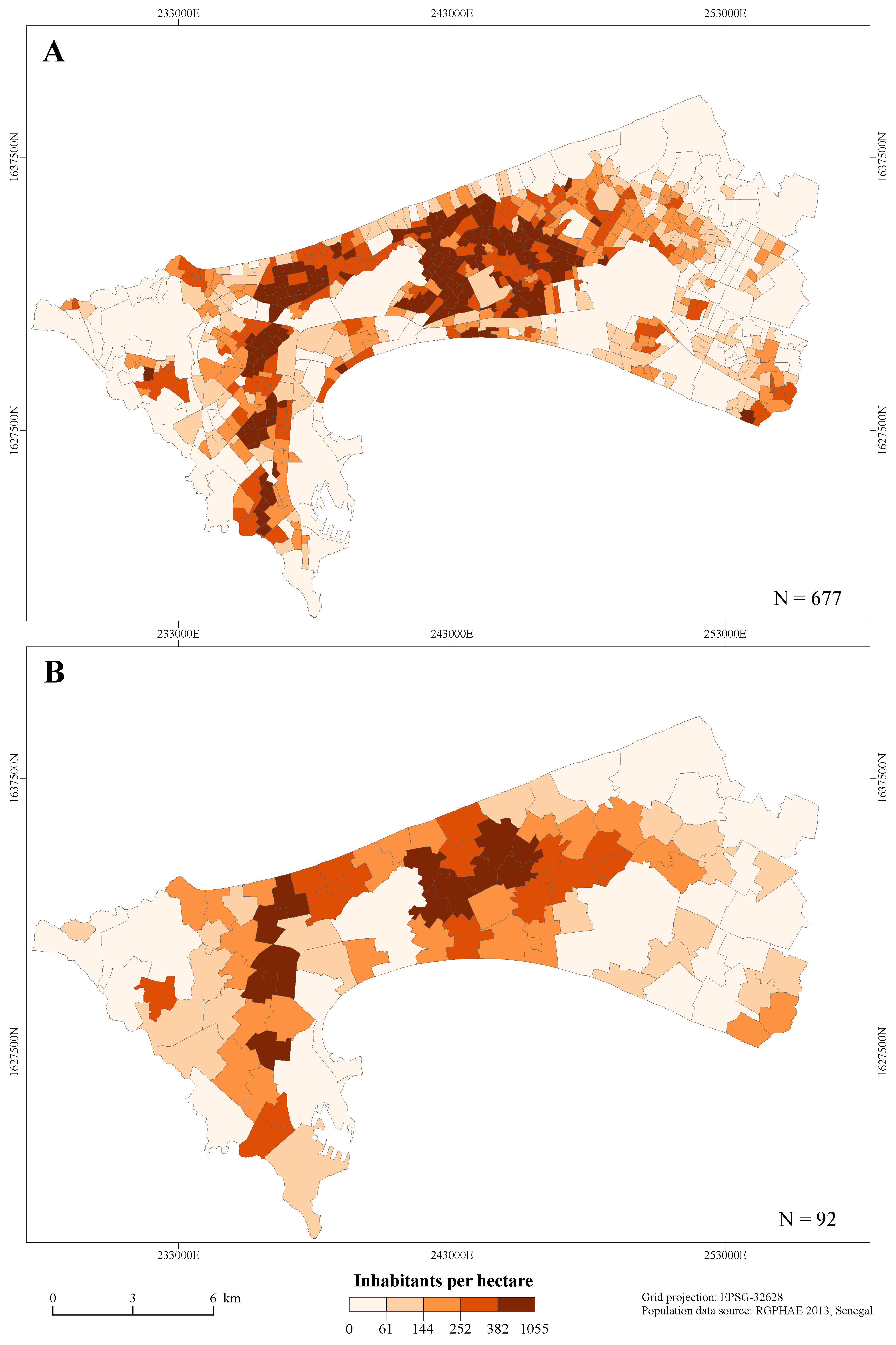
| Level | Area (ha.) | Population Density (inhab./ha.) | ||
|---|---|---|---|---|
| Mean | Minimum | Median | Maximum | |
| Level 1 (677 units) | 16.49 | 0.81 | 184.59 | 1047.23 |
| Level 0 (92 units) | 167.42 | 5.89 | 164.04 | 541.99 |
| Test | Weights Creation | MR-BU | VHR-BU | VHR-3BU | VHR-LC | VHR-LU |
|---|---|---|---|---|---|---|
| A | Simple proportion | X | ||||
| B | Simple proportion | X | ||||
| C | RF-derived weights | X | ||||
| D | RF-derived weights | X | ||||
| E | RF-derived weights | X | ||||
| F | RF-derived weights | X | X | |||
| G | RF-derived weights | X | X | |||
| H | RF-derived weights | X | X | |||
| I | RF-derived weights | X | X | |||
| J | RF-derived weights | X | X | X |
| Test | Input Data | RF Internal OOB Score | External Validation | ||
|---|---|---|---|---|---|
| Level 0 | Level 1 | %RMSE | RTAE | ||
| A | MR-BU | NA | NA | 61.00 | 36.7 |
| B | VHR-BU | NA | NA | 54.54 | 31.7 |
| C | VHR-3BU | 0.767 | 0.715 | 52.22 | 33.9 |
| D | VHR-LC | 0.759 | 0.759 | 49.31 | 30.8 |
| E | VHR-LU | 0.789 | 0.757 | 54.37 | 33.5 |
| F | MR-BU, VHR-LU | 0.808 | 0.766 | 47.59 | 29.7 |
| G | VHR-BU, VHR-LU | 0.842 | 0.768 | 46.21 | 28.2 |
| H | VHR-3BU, VHR-LU | 0.850 | 0.802 | 45.22 | 28.8 |
| I | VHR-LC, VHR-LU | 0.833 | 0.815 | 45.24 | 28.4 |
| J | MR-BU, VHR-LC, VHR-LU | 0.836 | 0.813 | 44.40 | 27.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grippa, T.; Linard, C.; Lennert, M.; Georganos, S.; Mboga, N.; Vanhuysse, S.; Gadiaga, A.; Wolff, E. Improving Urban Population Distribution Models with Very-High Resolution Satellite Information. Data 2019, 4, 13. https://doi.org/10.3390/data4010013
Grippa T, Linard C, Lennert M, Georganos S, Mboga N, Vanhuysse S, Gadiaga A, Wolff E. Improving Urban Population Distribution Models with Very-High Resolution Satellite Information. Data. 2019; 4(1):13. https://doi.org/10.3390/data4010013
Chicago/Turabian StyleGrippa, Taïs, Catherine Linard, Moritz Lennert, Stefanos Georganos, Nicholus Mboga, Sabine Vanhuysse, Assane Gadiaga, and Eléonore Wolff. 2019. "Improving Urban Population Distribution Models with Very-High Resolution Satellite Information" Data 4, no. 1: 13. https://doi.org/10.3390/data4010013
APA StyleGrippa, T., Linard, C., Lennert, M., Georganos, S., Mboga, N., Vanhuysse, S., Gadiaga, A., & Wolff, E. (2019). Improving Urban Population Distribution Models with Very-High Resolution Satellite Information. Data, 4(1), 13. https://doi.org/10.3390/data4010013






