Investigating the Evolution of Linkage Dynamics among Equity Markets Using Network Models and Measures: The Case of Asian Equity Market Integration
Abstract
1. Introduction
2. Related Works
2.1. Dependencies in Financial Time Series
2.2. Existing Methodologies
2.3. Existing Results
3. Materials and Methods
3.1. Data
3.2. Steps in Building Asian Indices Weighted Network Model
3.2.1. The Rolling Window Approach
3.2.2. Computation of Weights of Edges in the Asian Indices Network
3.2.3. Weighted Network Model Building
3.3. Computation of Network Metrics
3.3.1. Centrality Measures
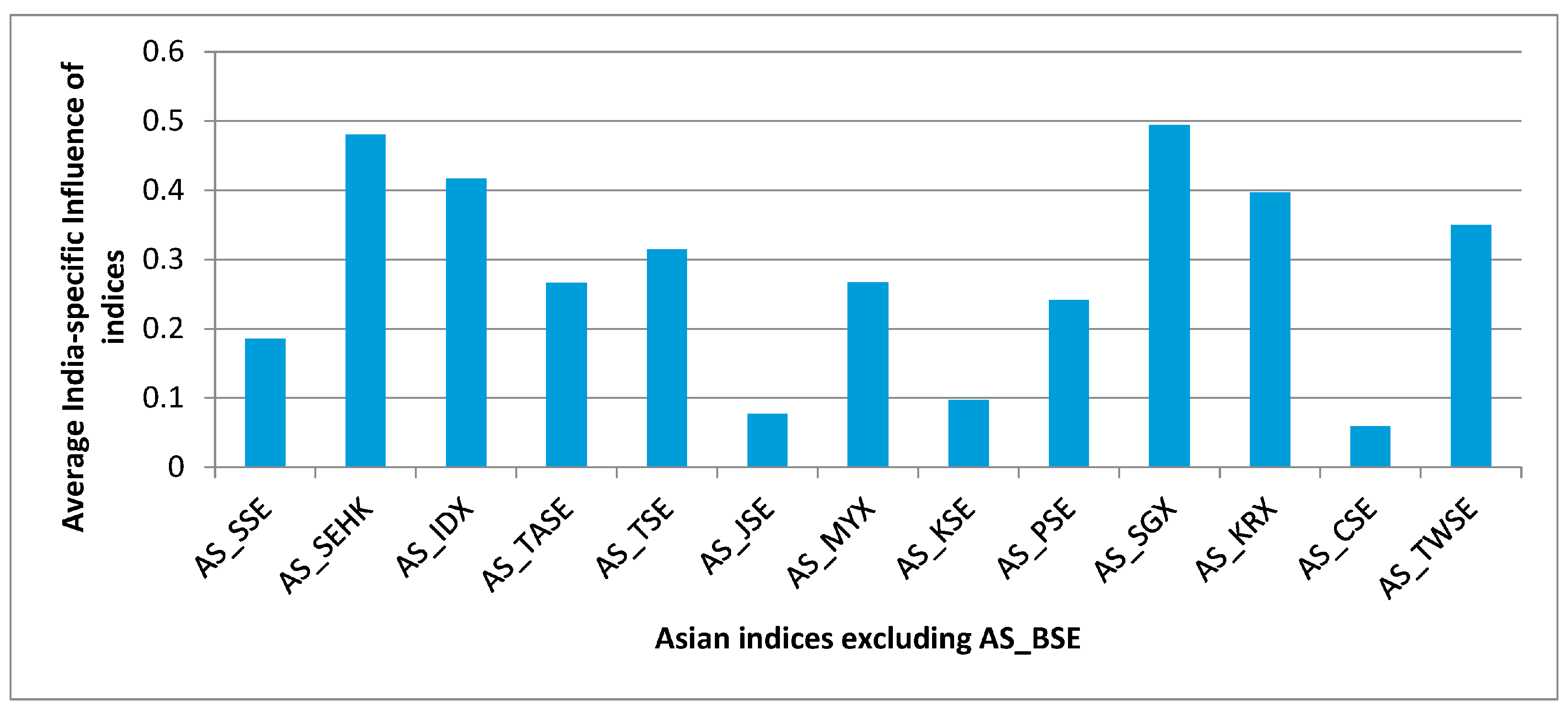
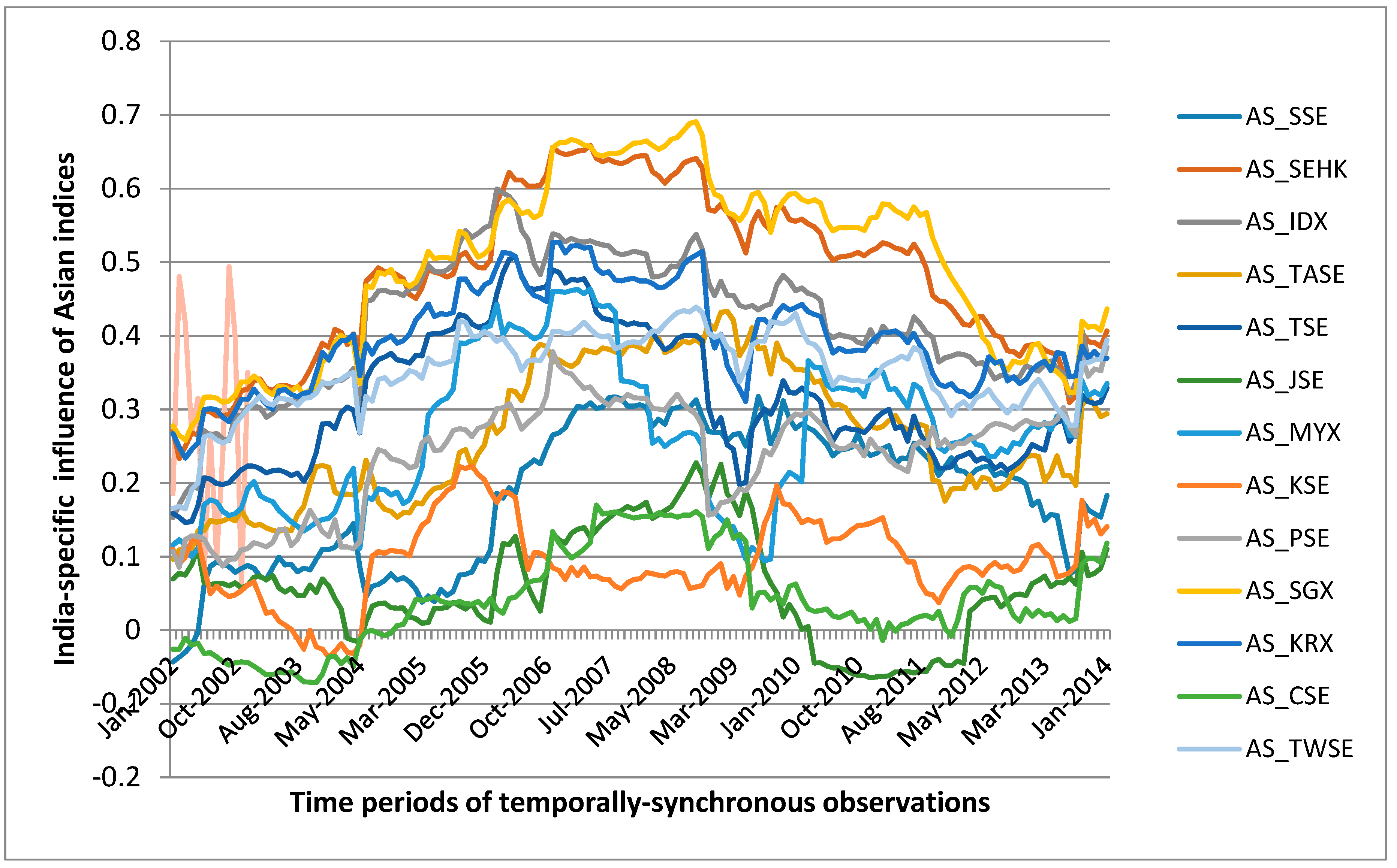
3.3.2. Influence Strength Measures
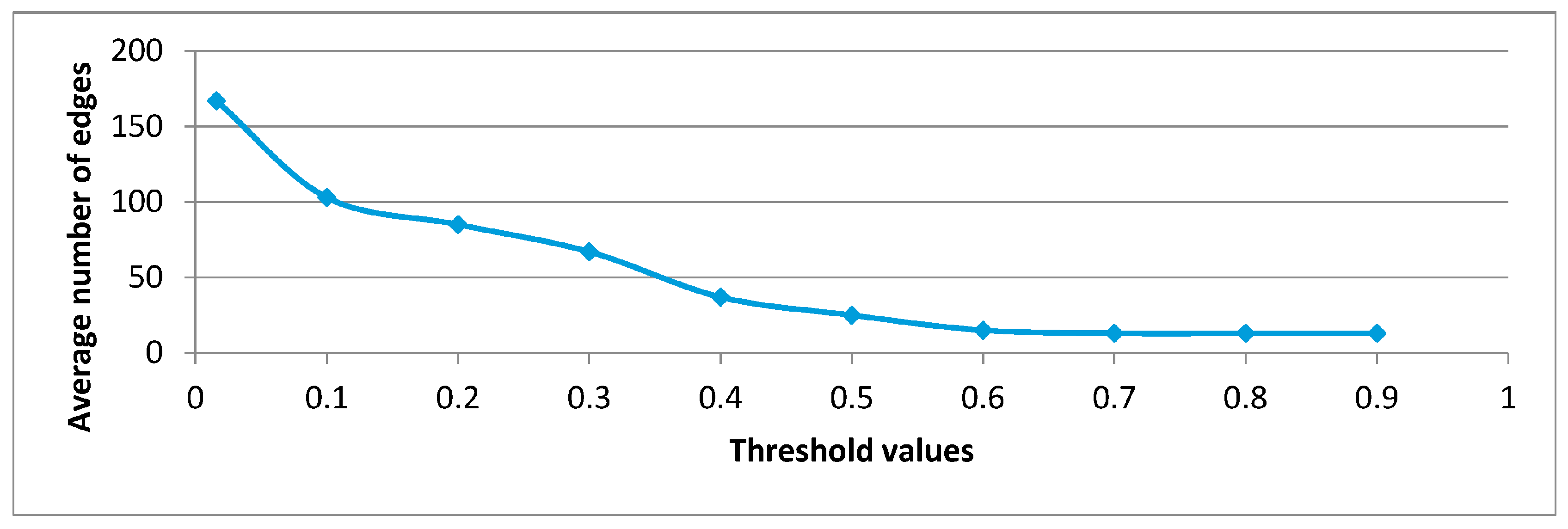
3.4. Threshold Filtering
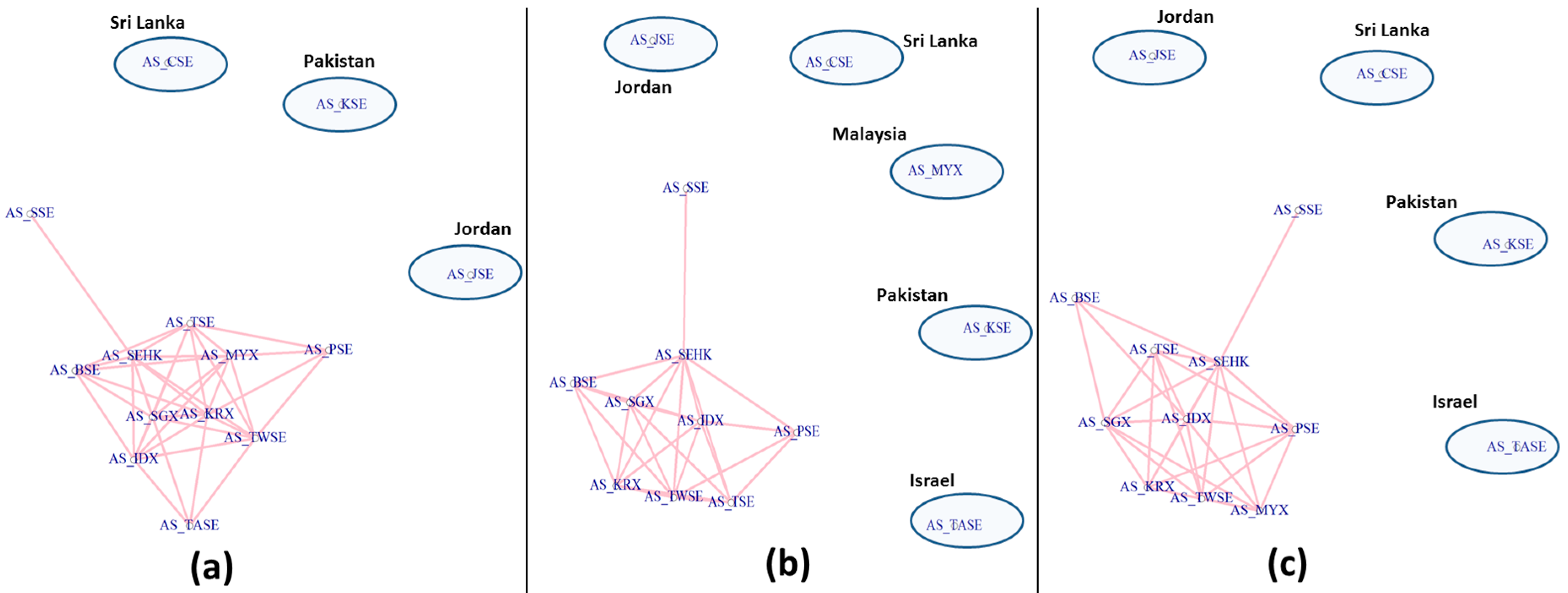
3.5. Segmentation Structure of Filtered Networks during the 2008 Crisis
4. Results
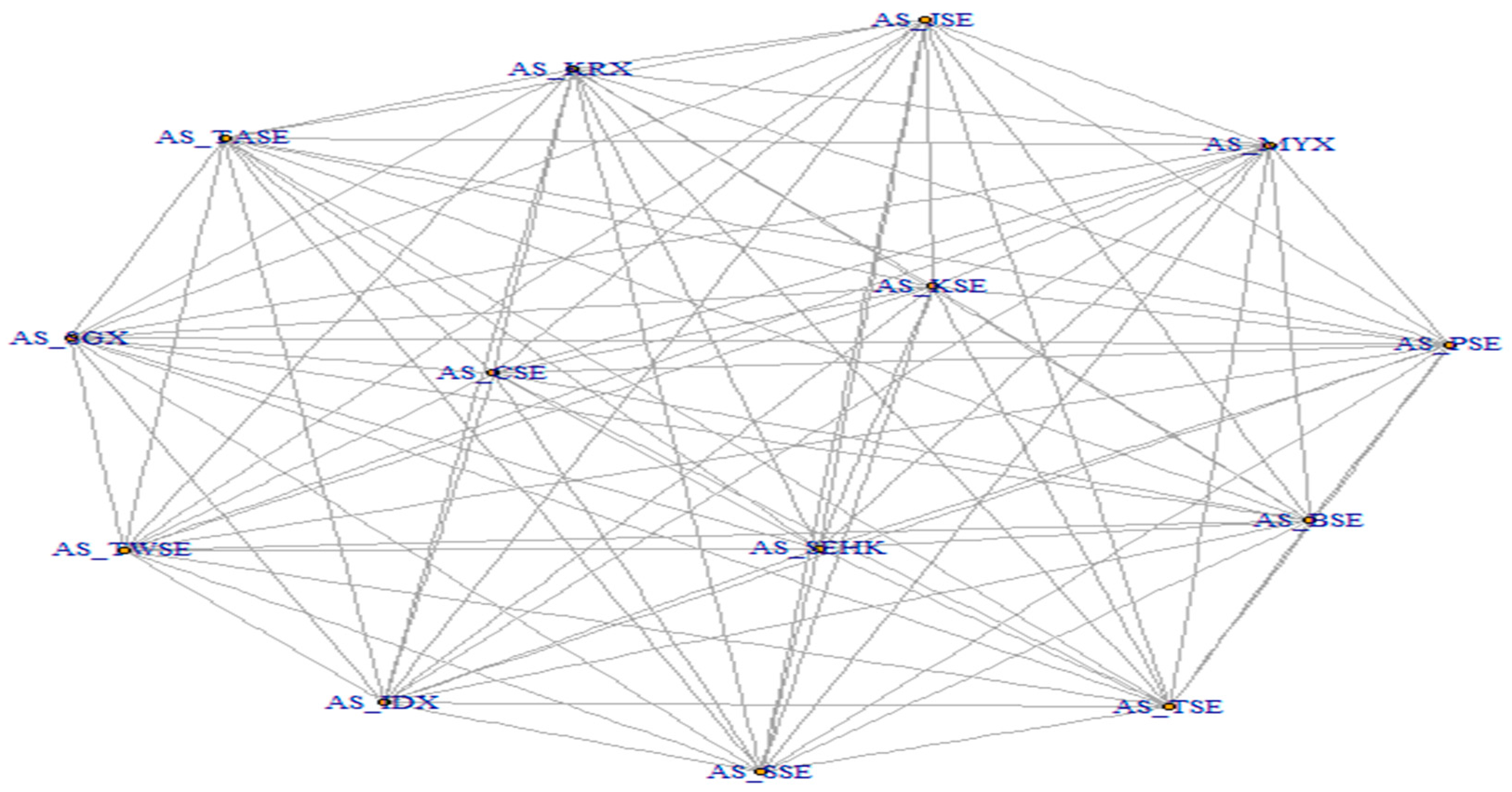
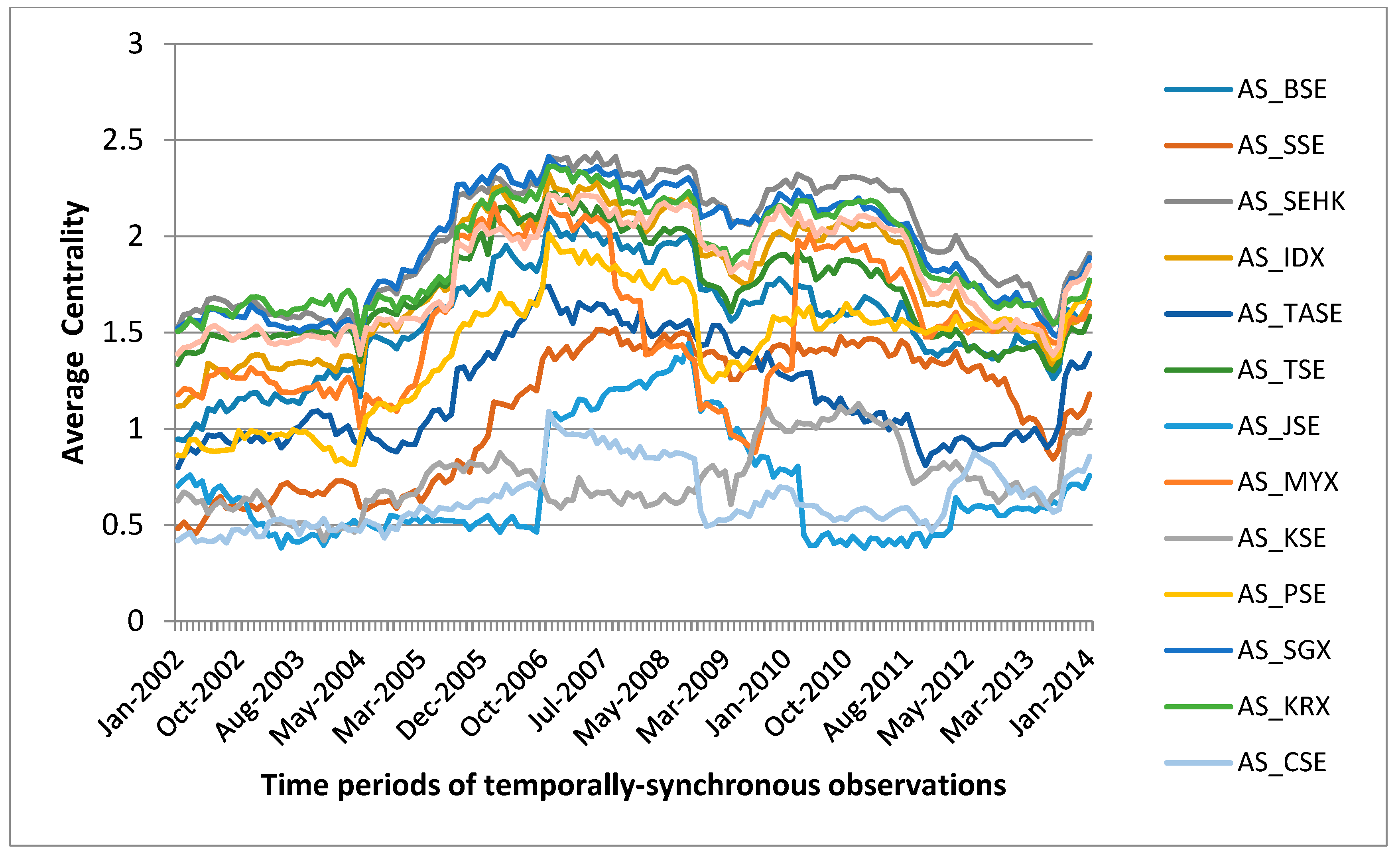
4.1. Topological Properties of the Asian Indices Network
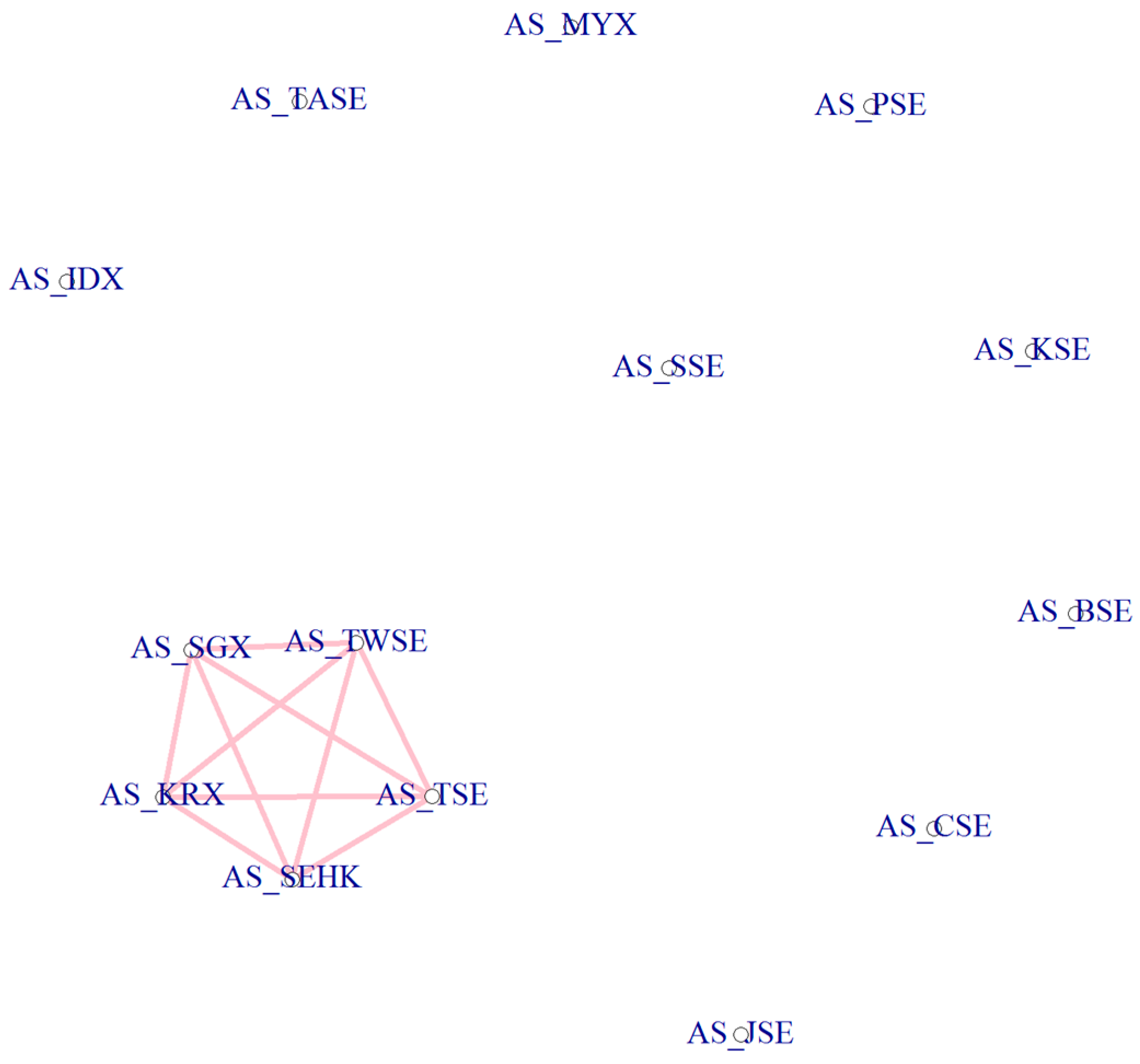
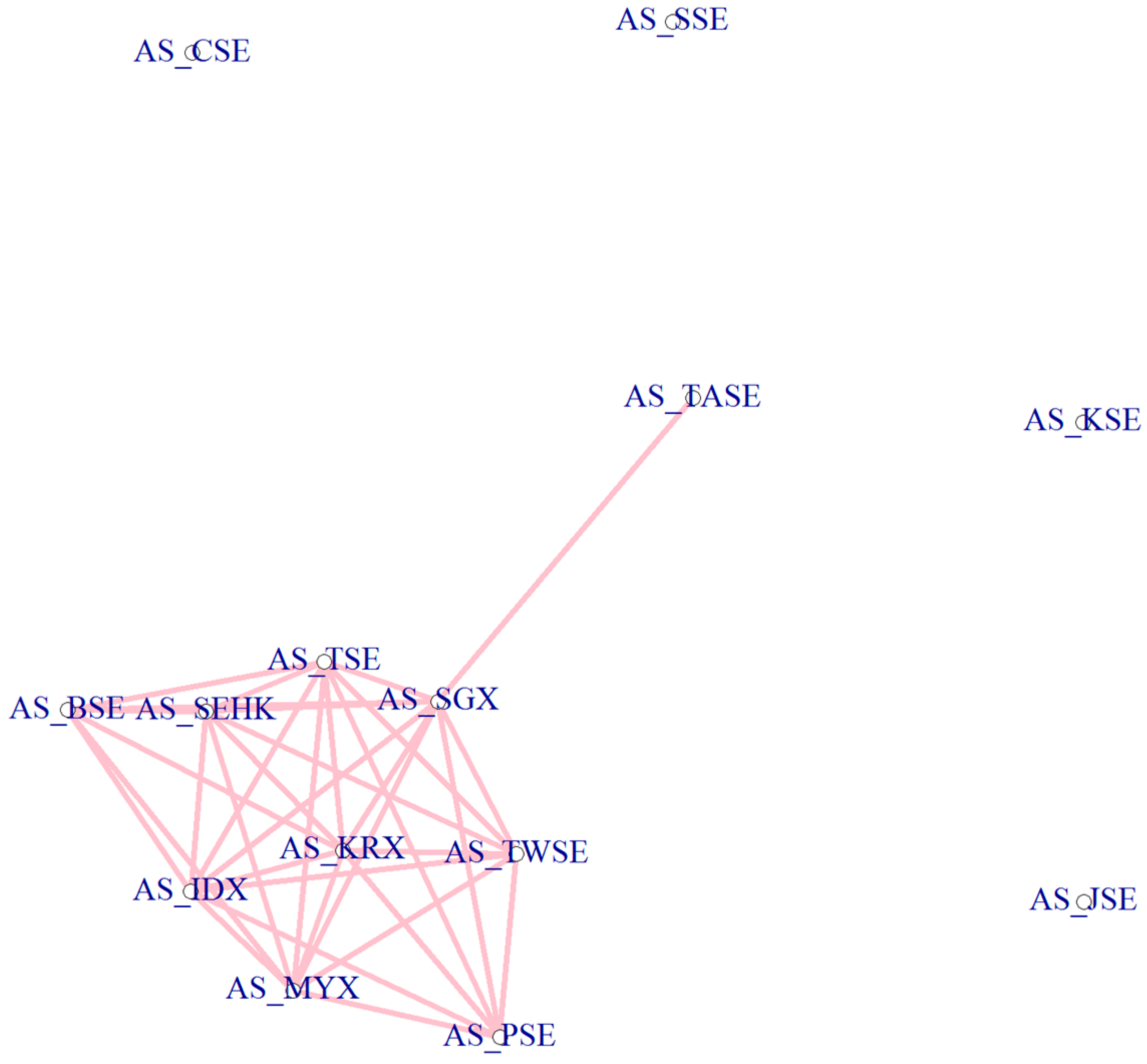
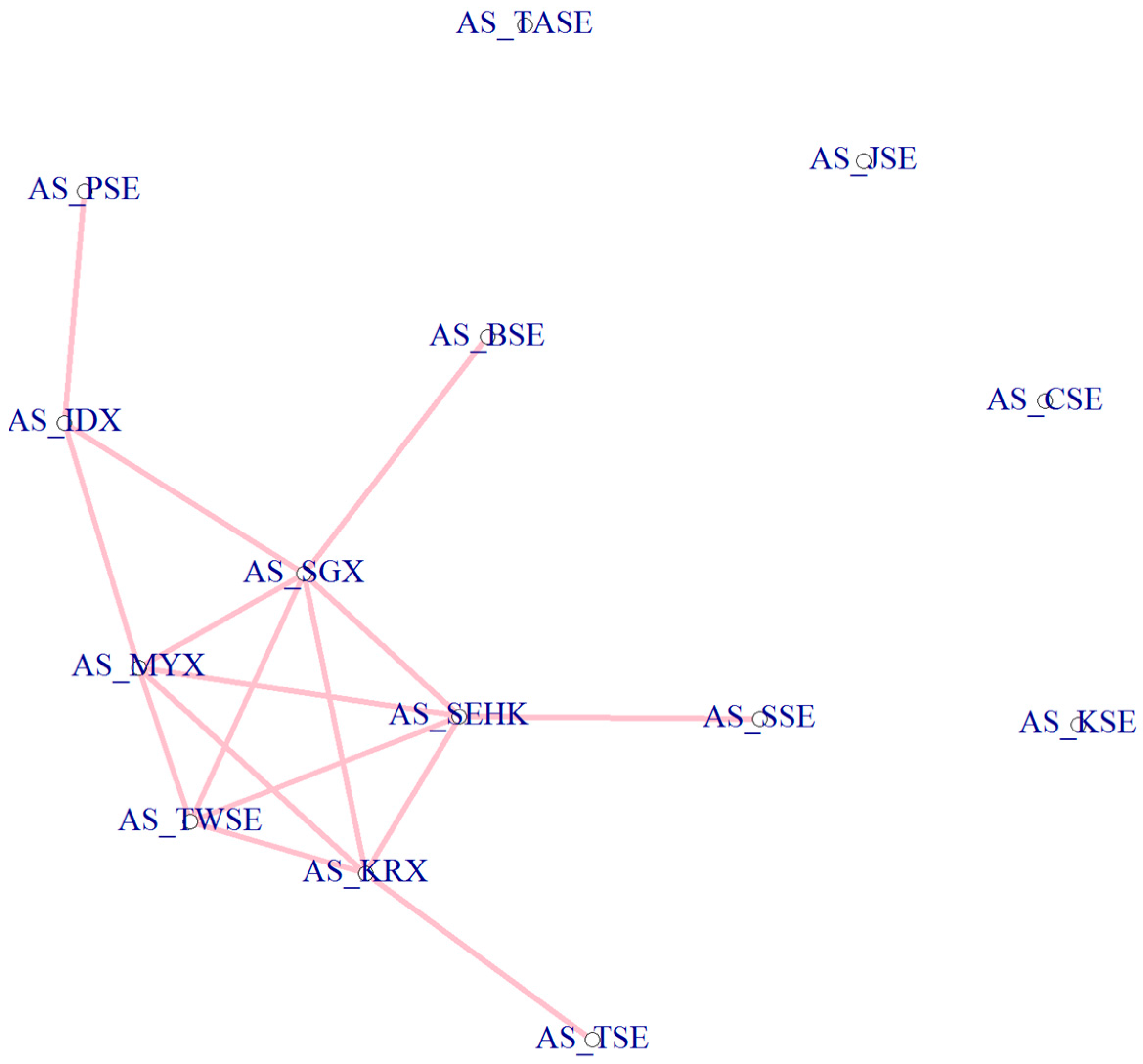
4.2. Reduced Network Visualization
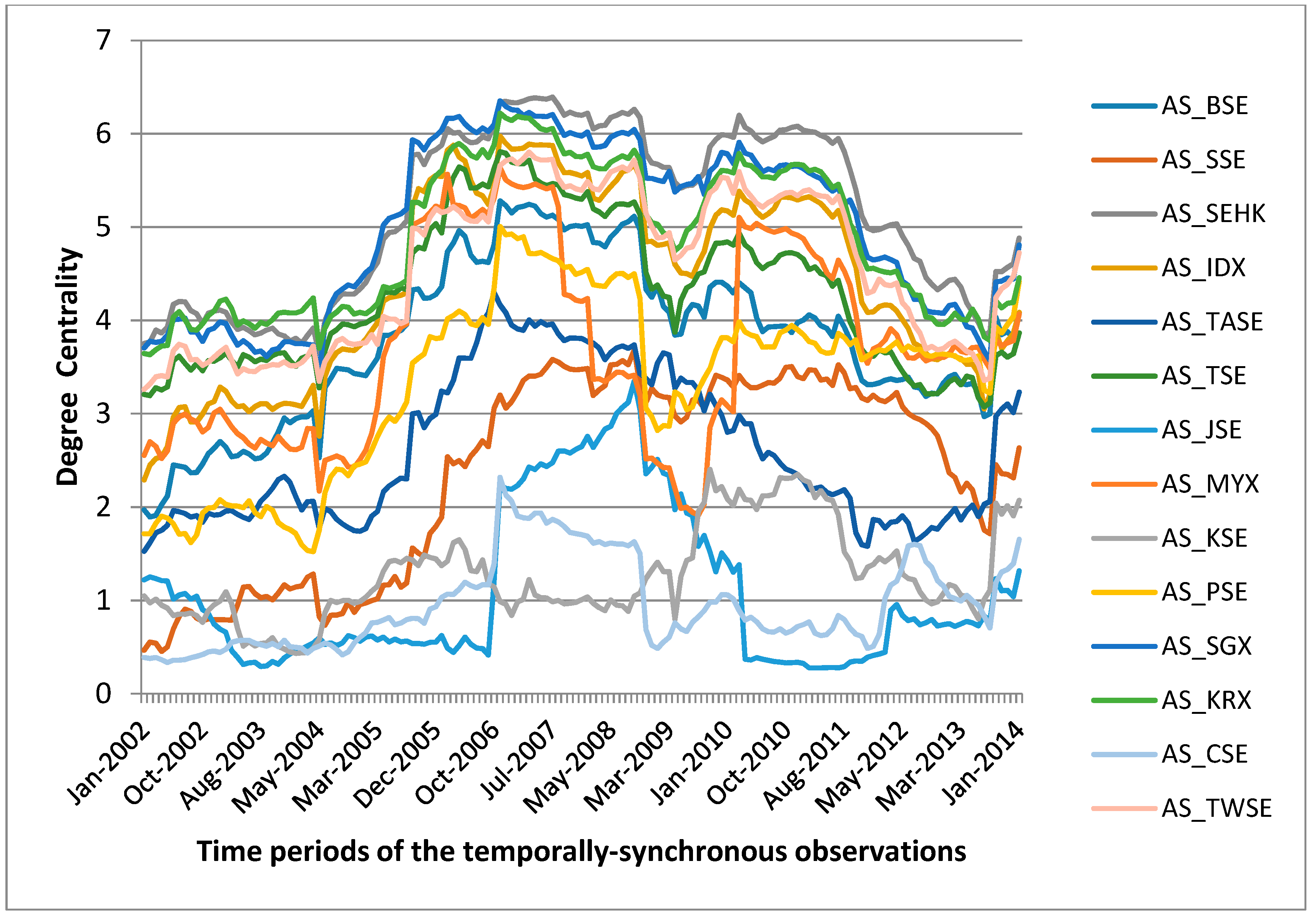
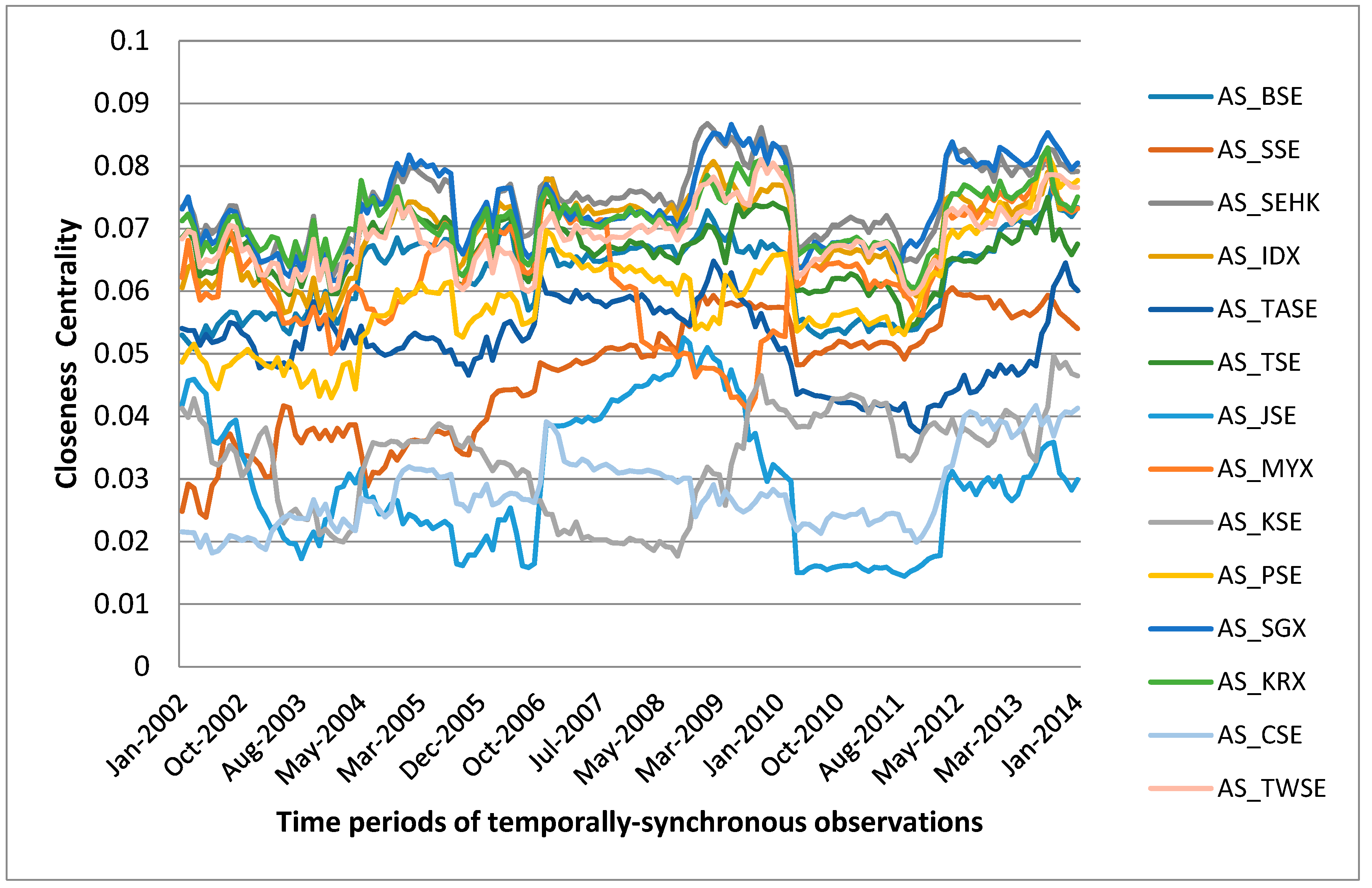
4.3. Pre-Crisis, Crisis and Post-Crisis Period Analysis
5. Discussions
6. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Setiawan, K. An alternative perspective on the stock markets integration: Multilateral measure of the degree of integration. In Proceedings of the 3rd EMG Conference on Emerging Markets Finance, London, UK, 5–6 May 2011; CASS Business School—City University London: London, UK, 2011; pp. 1–33. [Google Scholar]
- Bekaert, G.; Harvey, C. Time-varying world market integration. J. Financ. 1995, 50, 403–444. [Google Scholar] [CrossRef]
- Chan, K.C.; Gup, B.E.; Pan, M.-S. An empirical analysis of stock prices in Major Asian markets and the United States. Financ. Rev. 1992, 27, 289–307. [Google Scholar] [CrossRef]
- Hung, B.W.-S.; Cheung, Y.-L. Interdependence of Asian emerging equity markets. J. Bus. Financ. Account. 1995, 22, 281–288. [Google Scholar] [CrossRef]
- Defusco, R.A.; Geppert, J.M.; Tsetsekos, G.P. Long-run diversification potential in emerging stock markets. Financ. Rev. 1996, 31, 343–363. [Google Scholar] [CrossRef]
- Masih, R.; Masih, A.M. Long and short term dynamic causal transmission amongst international stock markets. J. Int. Money Financ. 2001, 20, 563–587. [Google Scholar] [CrossRef]
- Chung, P.J.; Liu, D.J. Common stochastic trends in Pacific Rim stock markets. Q. Rev. Econ. Financ. 1994, 34, 241–259. [Google Scholar] [CrossRef]
- Arshanapalli, B.; Doukas, J.; Lang, L.H. Pre and post-October 1987 stock market linkages between U.S. and Asian markets. Pac. Basin Financ. J. 1995, 3, 57–73. [Google Scholar] [CrossRef]
- Cheung, D.W. Pacific rim stock market integration under different federal funds rate regimes. J. Bus. Financ. Account. 1997, 24, 1343–1351. [Google Scholar] [CrossRef]
- Janakiramanan, S.; Lamba, A.S. An empirical examination of linkages between Pacific-Basin stock markets. J. Int. Financ. Mark. Inst. Money 1998, 8, 155–173. [Google Scholar] [CrossRef]
- Dekker, A.; Sen, K.; Young, M.R. Equity market linkages in the Asia Pacific region. Glob. Financ. J. 2001, 12, 1–33. [Google Scholar] [CrossRef]
- Mantegna, R. Hierarchical structure in financial markets. Eur. Phys. J. B 1999, 11, 193–197. [Google Scholar] [CrossRef]
- Onnela, J.-P.; Chakraborti, A.; Kaski, K.; Kertész, J. Dynamic asset trees and Black Monday. Phys. A Stat. Mech. Appl. 2003, 324, 247–252. [Google Scholar] [CrossRef]
- Tumminello, M.; Lillo, F.; Mantegna, R.N. Correlation, hierarchies, and networks in financial markets. J. Econ. Behav. Organ. 2010, 75, 40–58. [Google Scholar] [CrossRef]
- Plerou, V.; Gopikrishnan, P.; Rosenow, B.; Amaral, L.A.N.; Guhr, T.; Stanley, H.E. Random matrix approach to cross correlations in financial data. Phys. Rev. E 2002, 65, 066126. [Google Scholar] [CrossRef] [PubMed]
- Boginski, V.; Butenko, S.; Pardalos, P.M. Statistical analysis of financial networks. Comput. Stat. Data Anal. 2005, 48, 431–443. [Google Scholar] [CrossRef]
- Huang, W.-Q.; Zhuang, X.-T.; Yao, S. A network analysis of the Chinese stock market. Phys. A Stat. Mech. Appl. 2009, 388, 2956–2964. [Google Scholar] [CrossRef]
- Sinha, S.; Pan, R.K. Uncovering the internal structure of the Indian financial market: Large Cross-correlation behavior in the NSE. In Econophysics of Markets and Business Networks: Proceedings of the Econophys-Kolkata III; Chatterjee, A., Chatterjee, B.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 3–19. [Google Scholar]
- Namaki, A.; Shirazi, A.; Raei, R.; Jafari, G. Network analysis of a financial market based on genuine correlation and threshold method. Phys. A Stat. Mech. Appl. 2011, 390, 3835–3841. [Google Scholar] [CrossRef]
- Bonanno, G.; Caldarelli, G.; Lillo, F.; Miccichè, S.; Vandewalle, N.; Mantegna, R.N. Networks of equities in financial markets. Eur. Phys. J. B Condens. Matter 2004, 38, 363–371. [Google Scholar] [CrossRef]
- Tumminello, M.; Matteo, T.D.; Aste, T.; Mantegna, R.N. Correlation based networks of equity returns sampled at different time horizons. Eur. Phys. J. B 2007, 55, 209–217. [Google Scholar] [CrossRef]
- Tumminello, M.; Aste, T.; Matteo, T.D.; Mantegna, R.N. A tool for filtering information in complex systems. Proc. Natl. Acad. Sci. USA 2005, 102, 10421–10426. [Google Scholar] [CrossRef] [PubMed]
- Aste, T.; Shaw, W.; Matteo, T.D. Correlation structure and dynamics in volatile markets. New J. Phys. 2010, 12, 085009. [Google Scholar] [CrossRef]
- Aste, T.; Matteo, T.D. Dynamical networks from correlations. Phys. A Stat. Mech. Appl. 2006, 370, 156–161. [Google Scholar] [CrossRef]
- Matteo, T.D.; Pozzi, F.; Aste, T. The use of dynamical networks to detect the hierarchical organization of financial market sectors. Eur. Phys. J. B 2009, 73, 3–11. [Google Scholar] [CrossRef]
- Şensoy, A.; Tabak, B. Dynamic Spanning Tree Approach—The Case of Asia-Pacific Stock Markets; Working Paper Series No. 15; Research Department of Borsa İstanbul: İstanbul, Turkey, 2014. [Google Scholar]
- Pukthuanthong, K.; Roll, R. Global market integration: An alternative measure and its application. J. Financ. Econ. 2009, 94, 214–232. [Google Scholar] [CrossRef]
- Volosovych, V. Measuring financial market integration over the long run: Is there a U-Shape? J. Int. Money Financ. 2011, 30, 1535–1561. [Google Scholar] [CrossRef]
- Billio, M.; Donadelli, M.; Paradiso, A.; Riedel, M. Which market integration measure? J. Bank. Financ. 2017, 76, 150–174. [Google Scholar] [CrossRef]
- Bhattacharjee, B.; Shafi, M.; Acharjee, A. Investigating the influence relationship models for stocks in Indian Equity Market: A weighted network modelling study. PLoS ONE 2016, 11, e0166087. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.-J.; Lee, Y.; Kahng, B.; Kim, I.-M. Weighted scale-free network in financial correlations. J. Phys. Soc. Jpn. 2002, 71, 2133–2136. [Google Scholar] [CrossRef]
- Kim, H.J.; Kim, I.M.; Lee, Y.; Kahng, B. Scale-free network in stock market. J. Korean Phys. Soc. 2002, 40, 1105–1108. [Google Scholar]
- Hsieh, D.A. Chaos and nonlinear dynamics: Application to financial markets. J. Financ. 1991, 46, 1839–1877. [Google Scholar] [CrossRef]
- Scheinkman, J.A.; Lebaron, B. Nonlinear dynamics and stock returns. J. Bus. 1989, 62, 311–337. [Google Scholar] [CrossRef]
- Campbell, J.Y.; Lo, A.W.; MacKinlay, A.C. The Econometrics of Financial Markets; New Age International (P) Ltd.: New Dehli, India, 2011. [Google Scholar]
- Bampinas, G.; Panagiotidis, T. On the relationship between oil and gold before and after financial crisis: Linear, nonlinear and time-varying causality testing. Stud. Nonlinear Dyn. Econom. 2015, 19, 657–668. [Google Scholar] [CrossRef]
- Bampinas, G.; Panagiotidis, T. Oil and stock markets before and after financial crises: A local Gaussian correlation approach. J. Futures Mark. 2017, 37, 1179–1204. [Google Scholar] [CrossRef]
- Goetzmann, W.; Li, L.; Rouwenhorst, K.G. Long-term global market correlations. J. Bus. 2005, 78, 1–38. [Google Scholar] [CrossRef]
- Quinn, D.P.; Voth, H.-J. A century of global equity market correlations. Am. Econ. Rev. 2008, 98, 535–540. [Google Scholar] [CrossRef]
- Yu, C. Evaluating international financial integration in a center-periphery economy. J. Int. Econ. 2015, 95, 129–144. [Google Scholar] [CrossRef]
- Volosovych, V. Learning about financial market integration from principal components analysis. CESifo Econ. Stud. 2012, 59, 360–391. [Google Scholar] [CrossRef]
- Ball, C.A.; Torous, W.N. Contagion in the presence of stochastic interdependence. SSRN Electron. J. 2006. [Google Scholar] [CrossRef]
- Chiang, T.C.; Jeon, B.N.; Li, H. Dynamic correlation analysis of financial contagion: Evidence from Asian markets. J. Int. Money Financ. 2007, 26, 1206–1228. [Google Scholar] [CrossRef]
- Wang, P.; Moore, T. Stock market integration for the transition economies: Time-varying conditional correlation approach. Manch. Sch. 2008, 76, 116–133. [Google Scholar] [CrossRef]
- Égert, B.C.A.; Kočenda, E. Time-varying synchronization of European stock markets. Empir. Econ. 2010, 40, 393–407. [Google Scholar] [CrossRef]
- Caporale, G.M.; Spagnolo, N. Stock market integration between three CEECs, Russia, and the UK. Rev. Int. Econ. 2011, 19, 158–169. [Google Scholar] [CrossRef]
- Bekiros, S.D. Contagion, decoupling and the spillover effects of the US financial crisis: Evidence from the BRIC markets. Int. Rev. Financ. Anal. 2014, 33, 58–69. [Google Scholar] [CrossRef]
- Choudhry, T.; Jayasekera, R. Level of efficiency in the UK equity market: empirical study of the effects of the global financial crisis. Rev. Quant. Financ. Account. 2013, 44, 213–242. [Google Scholar] [CrossRef]
- Jayasinghe, P.; Tsui, A.K.; Zhang, Z. New estimates of time-varying currency betas: A trivariate BEKK approach. Econ. Model. 2014, 42, 128–139. [Google Scholar] [CrossRef]
- Huyghebaert, N.; Wang, L. The co-movement of stock markets in East Asia Did the 1997–1998 Asian financial crisis really strengthen stock market integration? China Econ. Rev. 2010, 21, 98–112. [Google Scholar] [CrossRef]
- Chelley-Steeley, P. Equity market integration in the Asia-Pacific region: A smooth transition analysis. Int. Rev. Financ. Anal. 2004, 13, 621–632. [Google Scholar] [CrossRef]
- Donadelli, M.; Paradiso, A. Is there heterogeneity in financial integration dynamics? Evidence from country and industry emerging market equity indexes. J. Int. Financ. Mark. Inst. Money 2014, 32, 184–218. [Google Scholar] [CrossRef]
- Yu, I.-W.; Fung, K.-P.; Tam, C.-S. Assessing financial market integration in Asia—Equity markets. J. Bank. Financ. 2010, 34, 2874–2885. [Google Scholar] [CrossRef]
- Click, R.W.; Plummer, M.G. Stock market integration in ASEAN after the Asian financial crisis. J. Asian Econ. 2005, 16, 5–28. [Google Scholar] [CrossRef]
- Leong, S.C.; Felmingham, B. The interdependence of share markets in the developed economies of East Asia. Pac. Basin Financ. J. 2003, 11, 219–237. [Google Scholar] [CrossRef]
- Voronkova, S. Equity market integration in Central European emerging markets: A cointegration analysis with shifting regimes. Int. Rev. Financ. Anal. 2004, 13, 633–647. [Google Scholar] [CrossRef]
- Hassan, M.; Naka, A. Short-run and long-run dynamic linkages among international stock markets. Int. Rev. Econ. Financ. 1996, 5, 387–405. [Google Scholar] [CrossRef]
- Junior, L.S. Cluster formation and evolution in networks of financial market indices. Algorithmic Financ. 2013, 2, 3–43. [Google Scholar]
- Mantegna, R.N.; Bulsara, A. Degree of correlation inside a financial market. In Applied Nonlinear Dynamics and Stochastic Systems near the Millennium; Kadtke, J.B., Ed.; American Institute of Physics: New York, NY, USA, 1997; pp. 197–202. [Google Scholar]
- Csardi, G.; Nepusz, T. The igraph software package for complex network research. InterJournal Complex Syst. 2006, 1695, 1–9. [Google Scholar]
- Freeman, L.C. Centrality in social networks. Soc. Netw. 1978, 1, 215–239. [Google Scholar] [CrossRef]
- Freeman, L.C. The Development of Social Network Analysis a Study in the Sociology of Science; Empirical Press: Vancouver, BC, Canada, 2004. [Google Scholar]
- McPherson, J.M.; Smith-Lovin, L.; Cook, J.M. Birds of a feather: Homophily in social networks. Annu. Rev. Sociol. 2001, 27, 415–444. [Google Scholar] [CrossRef]
- Wasserman, S.; Faust, K. Social Network Analysis: Methods and Applications; Cambridge University Press: New York, NY, USA, 1994. [Google Scholar]
- Barrat, A.; Barthelemy, M.; Pastor-Satorras, R.; Vespignani, A. The architecture of complex weighted networks. Proc. Natl. Acad. Sci. USA 2004, 101, 3747–3752. [Google Scholar] [CrossRef] [PubMed]
- Opsahl, T.; Colizza, V.; Panzarasa, P.; Ramasco, J.J. Prominence and Control: The weighted rich-club effect. Phys. Rev. Lett. 2008, 101, 168702. [Google Scholar] [CrossRef] [PubMed]
- Sabidussi, G. The centrality index of a graph. Psychometrika 1966, 31, 581–603. [Google Scholar] [CrossRef] [PubMed]
- Newman, M. The mathematics of networks. New Palgrave Dict. Econ. 2008, 2, 465–470. [Google Scholar]
- Brin, S.; Page, L. The anatomy of a large-scale hypertextual Web search engine. Comput. Netw. ISDN Syst. 1998, 30, 107–117. [Google Scholar] [CrossRef]
- Soh, H.; Lim, S.; Zhang, T.; Fu, X.; Lee, G.K.K.; Hung, T.G.G.; Di, P.; Prakasam, S.; Wong, L. Weighted complex network analysis of travel routes on the Singapore public transportation system. Phys. A Stat. Mech. Appl. 2010, 389, 5852–5863. [Google Scholar] [CrossRef]
- Barthélemy, M.; Barrat, A.; Pastor-Satorras, R.; Vespignani, A. Characterization and modeling of weighted networks. Phys. A Stat. Mech. Appl. 2005, 346, 34–43. [Google Scholar] [CrossRef]
- Yang, C.; Chen, Y.; Niu, L.; Li, Q. Cointegration analysis and influence rank—A network approach to global stock markets. Phys. A Stat. Mech. Appl. 2014, 400, 168–185. [Google Scholar] [CrossRef]
- Qiao, H.; Xia, Y.; Li, Y. Can network linkage effects determine return? Evidence from Chinese stock market. PLoS ONE 2016, 11, e0156784. [Google Scholar] [CrossRef] [PubMed]
- Abdul-Khaliq, S. The impact of stock market liquidity on economic growth in Jordan. Eur. J. Bus. Manag. 2013, 5, 154–158. [Google Scholar]
- Petri, M.; Saadi-Sedik, T. The Jordanian stock market: Should you invest in it for risk diversification or performance? IMF Work. Pap. 2006, 6, 1. [Google Scholar] [CrossRef]
- Junior, L.S.; Franca, I.D.P. Correlation of financial markets in times of crisis. Phys. A Stat. Mech. Appl. 2012, 391, 187–208. [Google Scholar]
- International Monetary Fund. Regional Economic Outlook: Asia and Pacific Building a Sustained Recovery; IMF: Washington, DC, USA, 2009. [Google Scholar]
- Yoshida, Y. Is this time different for Asia? Evidence from stock Markets. Discuss. Pap. Kyushu Sangyo Univ. 2010, 4, 1–35. [Google Scholar]
- Ren, F.; Lu, Y.-N.; Li, S.-P.; Jiang, X.-F.; Zhong, L.-X.; Qiu, T. Dynamic portfolio strategy using clustering approach. PLoS ONE 2017, 12, e0169299. [Google Scholar] [CrossRef] [PubMed]
- Fung, L.K.; Tam, C.; Yu, I. Assessing the integration of Asia’s equity and bond markets. In Proceedings of the First Workshop of the Asian Research Network for Financial Markets and Institutions, Hong Kong, 21 January 2008; pp. 1–37. [Google Scholar]
- Bracker, K.; Docking, D.S.; Koch, P.D. Economic determinants of evolution in international stock market integration. J. Empir. Financ. 1999, 6, 1–27. [Google Scholar] [CrossRef]
- Yang, S.-Y. Inter-day return and volatility dynamics between Japanese ADRs and their underlying securities. Appl. Financ. Econ. 2007, 17, 837–853. [Google Scholar] [CrossRef]

| Cross-Market Integration Measure(s) | Method of Computation | Studies Using the Measure for Cross-Market Integration |
|---|---|---|
| Simple correlation |
| Ref. [38,39] |
| R2 |
| Ref. [27,40] |
| 1st Principal component |
| Ref. [28,41] |
| ASI-adjusted Simple correlations |
| Ref. [42] |
| Dynamic Cross-country Correlations -GARCH |
| Ref. [43,44,45] |
| Baba Engle Kraft Kroner -GARCH |
| Ref. [46,47] |
| Conditional Beta |
| Ref. [48,49] |
| ASI-adjusted R2 |
| Ref. [29] |
| ASI-adjusted 1st Principal component |
| Ref. [29] |
| Forbes–Rigobon Correlation |
| Ref. [29] |
| Author (s) | Asian Indices Studied | Study Periods | Methodologies | Findings about Cross-Market Integration in Asia |
|---|---|---|---|---|
| Huyghebaert and Wang [50] | China (Shanghai and Shenzhen), Hong Kong, Taiwan, Singapore, South Korea and Japan | 1 July 1992–30 June 2003 | Granger causality tests, multivariate Granger causality tests based on the VAR model and impulse response analysis |
|
| Chelley-Steeley [51] | Korea, Thailand, Singapore and Taiwan | 3 January 1990–30 January 2002 | Smooth transition analysis |
|
| Donadelli and Paradiso [52] | China, India, Malaysia, Pakistan, The Philippines, Sri Lanka and Thailand Ten sector equity indexes of these countries | January 1994–July 2012 | Principal component analysis |
|
| Yu et al. [53] | Japan, Mainland China, Hong Kong SAR, Taiwan, South Korea, Singapore, Malaysia, Thailand, Indonesia and The Philippines | 16 March 1994–19 December 2008 | Cross-market return dispersion, Haldane and Hall Kalman filter method, dynamic cointegration analysis, common component approach, market cycle synchronization, dynamic conditional correlation |
|
| Click and Plummer [54] | Indonesia, Malaysia, The Philippines, Singapore and Thailand | 1 July 1998–31 December 2002 | Cointegration analysis |
|
| Symbol Used | Country | Stock Exchange | Benchmark Indices |
|---|---|---|---|
| AS_BSE | India | Bombay Stock Exchange | S&P BSE 500 Index |
| AS_SSE | China | Shanghai Stock Exchange | SSE Composite Index |
| AS_SEHK | Hong Kong | Stock Exchange of Hong Kong | Hang Seng Index |
| AS_IDX | Indonesia | Jakarta Stock Exchange | Jakarta Composite Index |
| AS_TASE | Israel | Tel Aviv Stock Exchange | TA 25 Index |
| AS_TSE | Japan | Tokyo Stock Exchange | NIKKEI 255 Index |
| AS_JSE | Jordan | Amman Stock Exchange | Amman SE AllShare Index |
| AS_MYX | Malaysia | Bursa Malaysia | FTSE KLCI Index |
| AS_KSE | Pakistan | Karachi Stock Exchange | KSE 100 Index |
| AS_PSE | Philippines | Philippine Stock Exchange | PSEi Index |
| AS_SGX | Singapore | Singapore Exchange limited | FTSE Singapore Index |
| AS_KRX | South Korea | Korea Exchange | KOSPI Composite Index |
| AS_CSE | Sri Lanka | Colombo Stock Exchange | COLOMBO IND ALL SHS Index |
| AS_TWSE | Taiwan | Taiwan Stock Exchange Corporation | TSEC weighted Index |
| Asian Index | Country | Average Closeness Centrality | Average Degree Centrality | Average Eigen Vector Centrality | Average Overall Influence Strength |
|---|---|---|---|---|---|
| AS_BSE | India | 0.0626340 | 3.7996830 | 0.8367462 | 3.6467550 |
| AS_SSE | China | 0.0466227 | 2.3656632 | 0.8803288 | 2.2372871 |
| AS_SEHK | Hong Kong | 0.0743654 | 5.1585482 | 0.7705337 | 5.0086470 |
| AS_IDX | Indonesia | 0.0691288 | 4.4158373 | 0.8158331 | 4.2644586 |
| AS_TASE | Israel | 0.0516557 | 2.6301378 | 0.8792498 | 2.4811778 |
| AS_TSE | Japan | 0.0662967 | 4.2850194 | 0.7993428 | 4.1356420 |
| AS_JSE | Jordan | 0.0294119 | 1.0910145 | 0.9293138 | 1.0000833 |
| AS_MYX | Malaysia | 0.0623657 | 3.7289809 | 0.8276162 | 3.5344467 |
| AS_KSE | Pakistan | 0.0330786 | 1.2714288 | 0.9234724 | 1.1284232 |
| AS_PSE | Philippines | 0.0591636 | 3.3492958 | 0.8603158 | 3.1989751 |
| AS_SGX | Singapore | 0.0735244 | 5.0011671 | 0.7805234 | 4.8415159 |
| AS_KRX | South Korea | 0.0712248 | 4.8687434 | 0.7856946 | 4.7235433 |
| AS_CSE | Sri Lanka | 0.0281424 | 0.9488094 | 0.9377192 | 0.8151270 |
| AS_TWSE | Taiwan | 0.0688079 | 4.5569932 | 0.7973869 | 4.4096110 |
| CENTRAL NODES | PERIPHERAL NODES | ||
|---|---|---|---|
| Market Indices | Average Centrality | Market Indices | Average Centrality |
| AS_SEHK (Hong Kong) | 1.91086705 | AS_JSE (Jordan) | 0.755388297 |
| AS_SGX (Singapore) | 1.889665576 | AS_CSE (Sri Lanka) | 0.85636622 |
| AS_TWSE (Taiwan) | 1.848760205 | AS_KSE (Pakistan) | 1.039834298 |
| AS_KRX (Korea) | 1.772898169 | AS_SSE (China) | 1.179702772 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhattacharjee, B.; Shafi, M.; Acharjee, A. Investigating the Evolution of Linkage Dynamics among Equity Markets Using Network Models and Measures: The Case of Asian Equity Market Integration. Data 2017, 2, 41. https://doi.org/10.3390/data2040041
Bhattacharjee B, Shafi M, Acharjee A. Investigating the Evolution of Linkage Dynamics among Equity Markets Using Network Models and Measures: The Case of Asian Equity Market Integration. Data. 2017; 2(4):41. https://doi.org/10.3390/data2040041
Chicago/Turabian StyleBhattacharjee, Biplab, Muhammad Shafi, and Animesh Acharjee. 2017. "Investigating the Evolution of Linkage Dynamics among Equity Markets Using Network Models and Measures: The Case of Asian Equity Market Integration" Data 2, no. 4: 41. https://doi.org/10.3390/data2040041
APA StyleBhattacharjee, B., Shafi, M., & Acharjee, A. (2017). Investigating the Evolution of Linkage Dynamics among Equity Markets Using Network Models and Measures: The Case of Asian Equity Market Integration. Data, 2(4), 41. https://doi.org/10.3390/data2040041





