1. Introduction
Many quantities have relationships that can be modeled by power laws of the form
[
1], with applications ranging from tests of the Newtonian gravitational force law [
2] to the relationship between energy metabolism and body mass [
3]. When parameters are unknown but data sets are available for variables
x and
, regression analysis may be performed to determine values for
a and
b. One commonly used form of regression analysis is nonlinear least squares (NLLS) analysis, which uses repeated iterations of an algorithm to find best fit parameters for given data.
Previous studies regarding weight–length relationships in fish ([
4], and references therein) demonstrated that a power law of the form
reduced uncertainties in parameter values, which were determined with NLLS fitting using the Levenberg–Marquardt algorithm, by replacing the coefficient
a of the traditional model with the scaling parameter
L. The previous studies were limited to exponents with values close to 3, and therefore more research is needed to test the idea in a wider range of data sets.
To generalize the range of applicability for the proposed model, this study tests the proposed improved form of the power law, again using the methods of NLLS analysis with the Levenberg–Marquardt algorithm, with a wider range of exponents, varying numbers of data points, different methods of selecting values of the independent variable, varying relative errors in the dependent variable, and different values of the scaling parameter, L (or the equivalent a). Varying these conditions allows for investigation and discussion of whether the proposed improvement to the traditional power law is viable in a wider set of circumstances than those shown by the previous study.
To compare forms of the power law, 180 data sets were fit to both traditional and proposed models to test the kinds of different conditions above. Relative errors calculated from known good values of parameters and relative uncertainties were recorded, and are compared for each model and test. The hypothesis for this study was that the proposed power law would have lower relative uncertainties and lower relative errors than the traditional power law over the values of b and other conditions tested.
2. Results
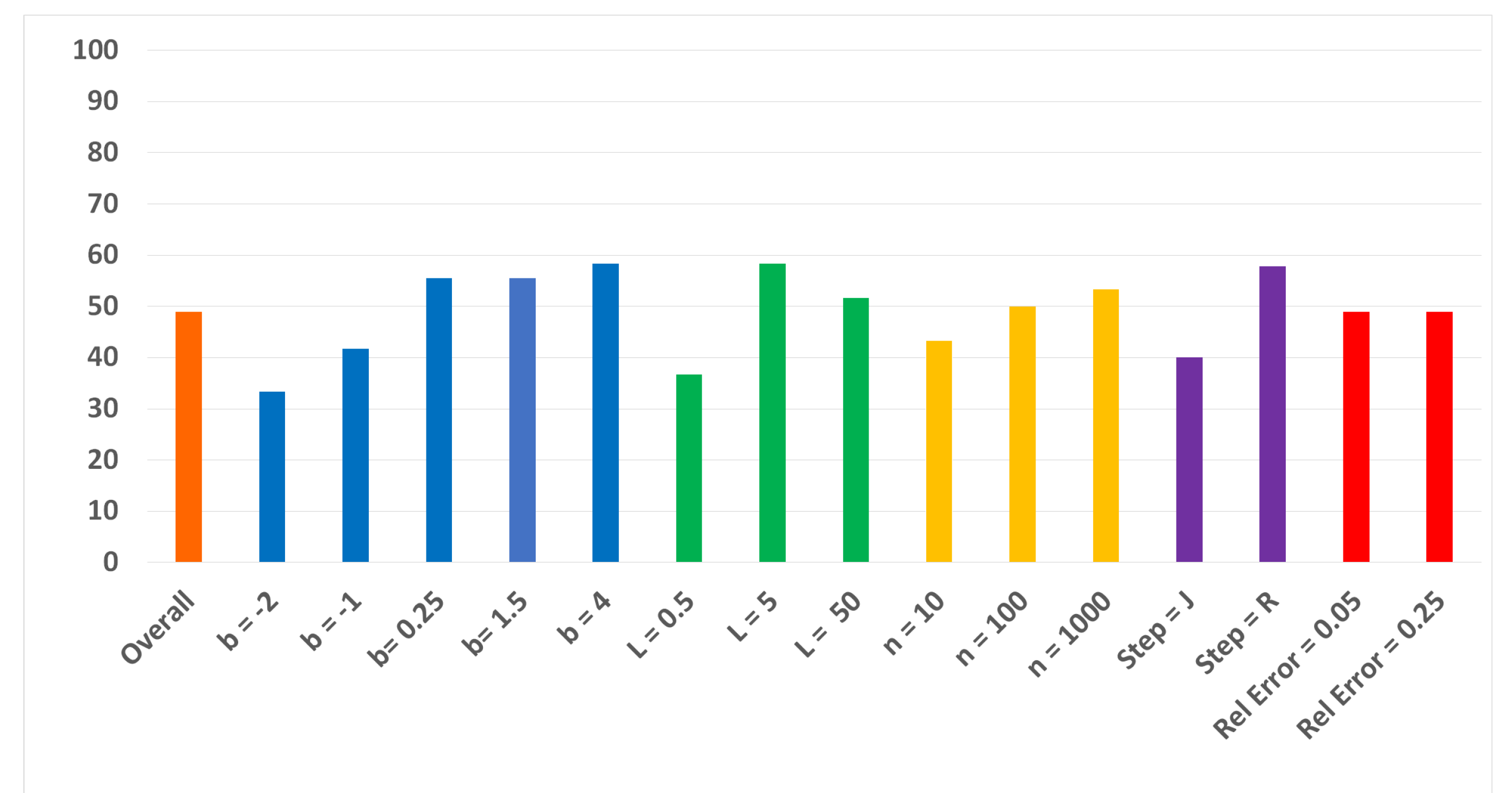
Results regarding relative errors and relative uncertainties from all trials were collected and combined for both the proposed and traditional models. In approximately 50% of all trials, the proposed law gave lower relative errors and uncertainties than the traditional law in the coefficient parameters, as seen in
Figure 1. However, the results indicate that favor is shown towards one model or the other by specific sets of conditions. For instance,
Figure 1 indicates that positive powers tended to favor the proposed power law, while negative powers tended to favor the traditional power law.
Root mean square (RMS) and mean values were also computed for the parameter errors and uncertainties for all conditions, with root mean square values seen in
Figure 2. Neither model was favored by RMS values across all conditions: the values instead depended on the particular set of conditions tested. For example,
Figure 2 indicates that the proposed model is favored with low added errors in raw data, which can be seen in the lower RMS value for an error of 5% and the higher RMS value for an error of 25% for the proposed model in comparison to the traditional model.
Thus, while the percent and RMS metrics for the total 180 trials point to an inconclusive result, favor is shown towards one model or the other by specific sets of conditions. However, in some conditions, RMS values differ from the results suggested by percent comparison. One example of this discrepancy can be seen with
. In this case, percent comparison indicates that the proposed model is more accurate, as seen in
Figure 1, while RMS values indicate that the traditional model produces lower relative errors, as seen in
Figure 2.
Despite inconsistencies between results from different comparison methods, some sets of conditions still seem to favor one model over the other when examining individual trials. As seen in
Figure 3, the set of conditions with positive exponents, relative errors of 0.05, and the scaling parameter value
L = 5 converged well for the proposed model, demonstrating that a more conclusive result may be found for certain sets of conditions.
In agreement with the previous study [
4], the relative uncertainties and errors of the exponent parameter
b were comparable for the traditional and proposed models, with each law producing very close mean and RMS values for
b, as seen in
Figure 4. Due to this, it can be seen that the difference in accuracy and precision between models is confined to the coefficient or scaling parameter.
Additionally, in 152/180 trials, the relative uncertainty and relative error values were each lower for the functional form of the power law, which implies that in 84% of all trials, these values were in agreement regarding which law was more accurate. Due to this correlation between relative errors and uncertainties, only the results for relative errors are shown.
3. Applications
The scaling power law model from the previous study [
4] has been applied to data gathered from two species of trout in a Colorado reservoir [
5], where it assisted in demonstrating that the trout were in poor health. Other potential applications of the proposed scaling version of the power law model include further ecological applications, but also have consequences in a wider array of fields, such as physics and chemistry. Three illustrative examples for potential applications were analyzed to demonstrate the implications of this study: Robert Boyle’s original dataset, two modern data sets for Kepler’s third law, and an ecological dataset for Kleiber’s law.
3.1. Robert Boyle’s Original Dataset
In his work
A Defense of the Doctrine Touching the Spring and Weight of Air [
6], Robert Boyle gave a data table from one of his experiments in support of his proposition that the volume and pressure of a gas are inversely proportional. This law, commonly known as Boyle’s Law today, takes the form of a power law, namely
.
Boyle’s data was fit with NLLS regression to both the traditional and proposed models. Known good values for
L and
a were, to the experimenter’s knowledge, unavailable for this dataset, and so relative uncertainties were the only source of comparison between the two models. The traditional model gave lower relative uncertainties for the fit, and, due to the correlation between uncertainties and errors, this means the traditional model would likely be the better choice for analysis of this dataset. The graph with Boyle’s data fit to the proposed model is shown in
Figure 5.
3.2. Kepler’s Third Law in Original and Modern Data Sets
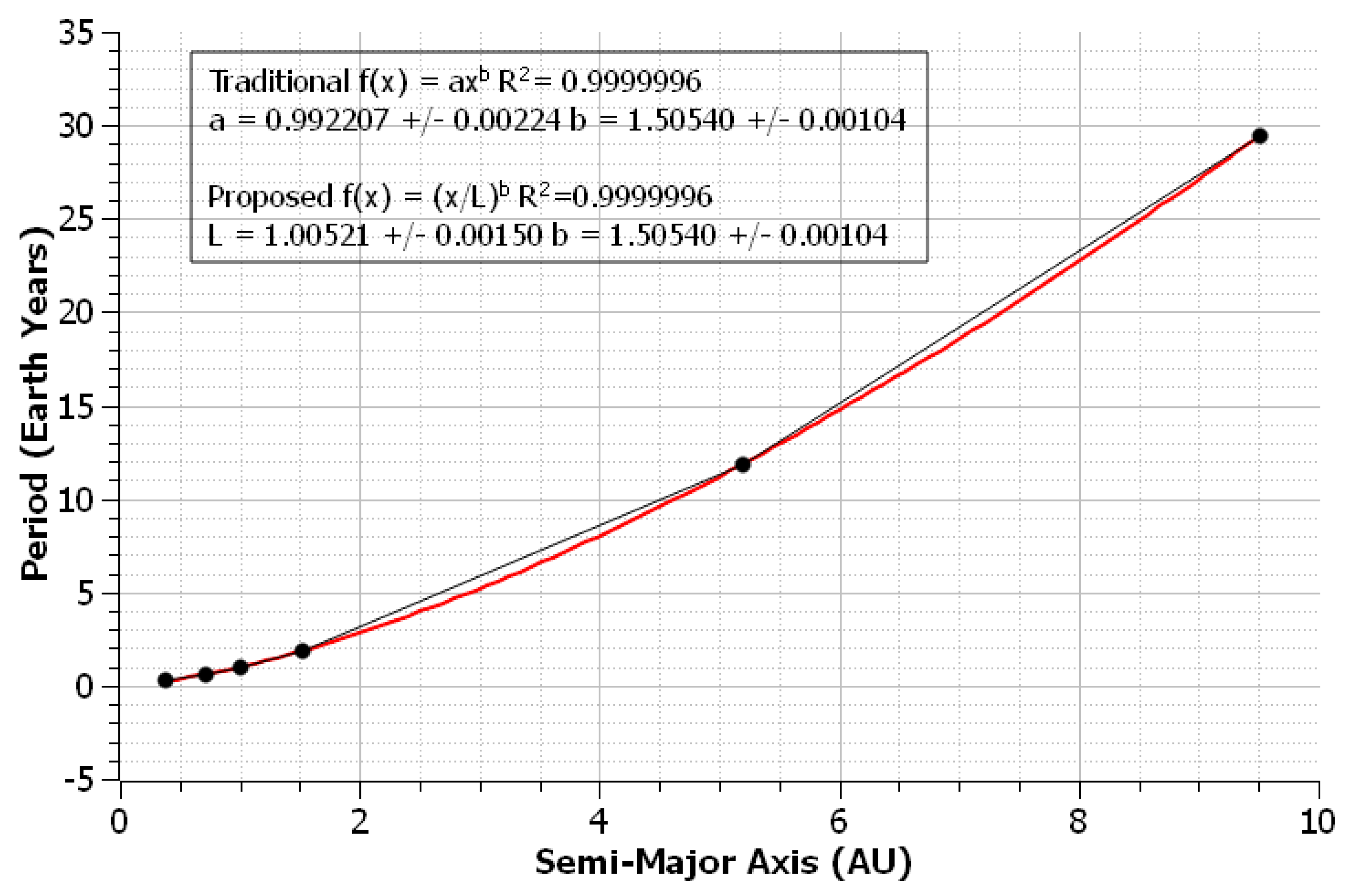
In 1619, Johannes Kepler used data gathered by Tycho Brahe to support what is now referred to as his third law. As expressed by a power relation, this law takes the form
, where
P is the period and
a is the semi-major axis of an orbit. The historical data regarded the periods and orbits of the planets in the solar system, and modern data has been gathered for the same planets. Data sets [
7] were fit with NLLS regression to both the traditional and proposed models. The known-good value for
L was determined to be 1 for planetary measurements. As seen in
Figure 6, the proposed power law produced both lower relative errors and relative uncertainties in Brahe’s dataset. For the modern dataset, which is plotted in
Figure 7, the traditional power law gave smaller relative uncertainties, while the proposed power law produced lower relative errors.
Data for the moons of Jupiter has also been gathered in recent years [
8]. This dataset was also fit with NLLS regression, with datapoints and best fit curves shown in
Figure 8. The proposed law not only produced lower relative uncertainties in both the scaling parameter and exponent for this dataset, but also output a higher
value and had a visible distinction between the curves. These differences were not typical for this study, with
values of the traditional and proposed models being comparable and the respective curves being not easily distinguishable for most data sets.
3.3. Kleiber’s Law in Avian Species
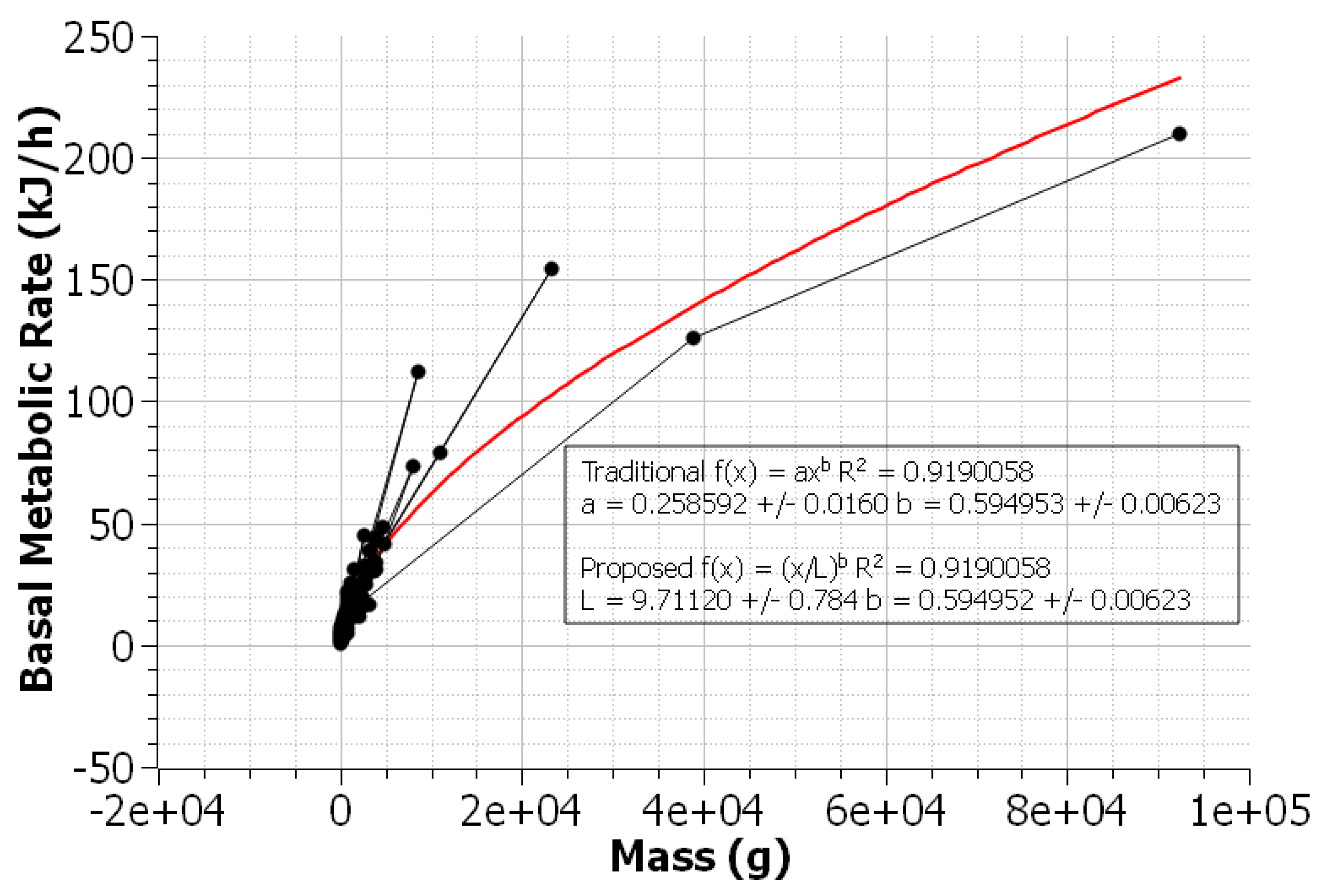
An organism’s basal metabolic rate (BMR) has been shown to be proportional to a power of its mass. This is known as Kleiber’s law and takes the form
, and has been applied to a variety of avian species [
9]. This avian dataset, with a total of 533 data points, was fit with NLLS regression to both the traditional and proposed models. Known-good values for
L (or
a) were unavailable, so relative uncertainties were the only source of comparison between the two models. As seen in
Figure 9, the proposed power law has a smaller relative uncertainty for the scaling parameter.
4. Discussion
The hypothesis that the proposed model, , would provide lower relative uncertainties and lower relative errors for all conditions compared to the traditional power law over the values of b and the other conditions tested was not supported for all data sets in the numerical experiment, with only 96/180 cases having lower errors and 88/180 cases having lower uncertainties. While uncertainty and error values were found to be different for each model in the coefficient parameters, the models provided values consistent with each other for the exponents.
Despite the lack of support for the hypothesis in all tests, this study demonstrates that the proposed law may still provide reduced uncertainties and errors in specific sets of conditions, such as non-negative exponents and certain L values. However, additional testing with an altered hypothesis must be done in order to fully determine the exact nature and impact of this set of conditions. For example, the value of L = 0.5 favored the traditional model with positive exponents and the proposed model with negative exponents, which was contrary to the results for the rest of the values of L. This apparent discrepancy indicates that further testing will be needed with a larger spectrum of values for coefficient parameters.
Due to the inconclusive nature of the results, it is recommended that an experimental approach similar to the methods described in this study be used to determine which power law model offers the least uncertainties and errors for data where accuracy is of high importance. Such an experiment could be done relatively quickly by generating imitation data sets with conditions similar to the data being fit, and then by comparing the uncertainties and errors output from each model for the artificial data sets. If the results are consistent for the data sets, then the model which the small experiment favors will most likely be the better candidate for the actual dataset. Alternatively, the raw experimental data could be fit to both models, with only the uncertainties compared. Because of the previously mentioned correlation between relative errors and relative uncertainties, such an analysis would tend to point to the better model for the data.
In addition to more specific testing with additional power law parameters, the methods of this study have the potential to be applied to a wider array of functions by replacing various coefficient parameters with scaling parameters. Polynomials might prove to be a ready next step, due to the fact that they are a sum of terms with fixed positive integer powers. Other possibilities to reduce fitting uncertainties by replacing lead coefficients with scaling parameters include Gaussian, exponential, logarithmic, and trigonometric functions. Extension of the methods of the study to functions such as these would not only provide a more general numerical basis for the proposed model, but could also increase the range of applicability of scaling parameter models to an even wider variety of scientific fields.
While this experiment did not support the proposed model for all cases, the results from a previous study [
4] were tested in a wider variety of conditions. This study has paved the way for more specific investigations, and also demonstrated an experimental approach to be used for determining the best model before a more conclusive set of conditions is established.
As demonstrated with the application of the original investigation to fisheries research [
5], there is potential for the proposed model in cases where it proves to provide more accurate results than the traditional model. Due to the widespread occurrence of power laws in empirical data, finding the most accurate model is an issue of importance across many fields, ranging from ecology to physics. When the conditions where one model is observed to consistently outperform the other are determined, the better model can then be chosen for most anticipated exponents and data sets, allowing for greater confidence in the parameters resulting from fitting empirical data.
5. Materials and Methods
Values for conditions that were varied are as follows: exponents took on values of b = , , 0.25, 1.5, and 4; selected values of L were 0.5, 5, and 50; the numbers of data points used were 10, 100, and 1000; methods for determining x values were a constant step size with added jitter and random values, with all values in the same interval; and relative errors in values were set to be 0.05 and 0.25.
A total of 180 data sets were analyzed to cover all parameter combinations described previously. Any given value of a condition was tested alongside all possible combinations of values for other conditions once to ensure testing of the hypothesis over a number of parameter values and conditions representative of a common range of experimental conditions. From the data collected, relative errors and uncertainties were then computed. Uncertainties in each parameter value were returned by the fitting algorithm in SciDAVis (version 1.D013), a regression analysis program vetted for accuracy in a previous study [
4], having been computed by standard methods. The operation of the SciDavis Levenberg–Marquardt NLLS code was validated by comparing a number of test cases with other versions of the same algorithm, including the one built into gnuplot and custom code written by one of the authors (MC). Relative uncertainties in the parameters are simply the ratio of uncertainty to best fit parameter value.
To compare the proposed law to the traditional model, relative uncertainties and errors were additionally computed for a parameter
, which is related to
a by the equation
. The relative error for
is determined by the formula
due to error propagation [
10], and a similar formula is used to determine relative uncertainty. The resulting values were then recorded. After these computations, relative uncertainties and errors of
for the traditional model were compared with relative uncertainties and errors of
L from the proposed model.
Most data sets—with the exception of a few case studies gathered from experimental data—were produced using a Microsoft Excel 2013 spreadsheet, which accepted inputs for values of L, b, relative error in , relative jitter in x values, a value for the step amount for a constant step size, a minimum value for x, and maximum values for x. The last four inputs were held constant throughout all trials, with the former three holding values of 0.1 and the last having a value of 100.
Two additional columns were created before establishing the data set values. A column of random noise (Each time random noise is used in this study, it was an approximation to a true random number generated with the RAND() spreadsheet call.) was generated with a call to NORMSINV(RAND()) for each data point. This call generated noise with a mean of zero and a standard deviation of 1. Additionally, a column of only whole numbers counting from 0 to 1001 was created, which served as a row number index for the x, , and values.
After all inputs are established, the spreadsheet computed values for each x for either a constant step size, constant step size with jitter, or a random value in an interval, depending on the sheet being used. Only the constant step size with jitter and random x value in an interval were used for experimentation. The constant step size tab computed each x value by taking the minimum x value and adding the step amount multiplied by the x value’s corresponding row number index. The constant step size with jitter tab used the same method as the constant step size except with the addition of a jitter term, which was determined by multiplying the corresponding noise value with the step amount and the relative jitter value. The random x value in an interval tab computed each value of x by taking the minimum x value and adding a random number from 0 to 1 multiplied by the maximum x value.
The spreadsheet then calculated values for and by first evaluating at every value of x. To produce a relative error in each data point with a root mean square value equal to the desired relative error, the corresponding noise value was multiplied by the desired relative error and before being added to the to produce the for the data set.
The spreadsheet-generated data sets were then copied into SciDAVis. Data was then analyzed via the Levenberg–Marquardt non-linear least squares algorithm to determine best fit parameters for each model. Both parameter values and uncertainties were recorded in a separate spreadsheet for further analysis.