Corneal Adhesion Possesses the Characteristics of Solid and Membrane
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material Preparation
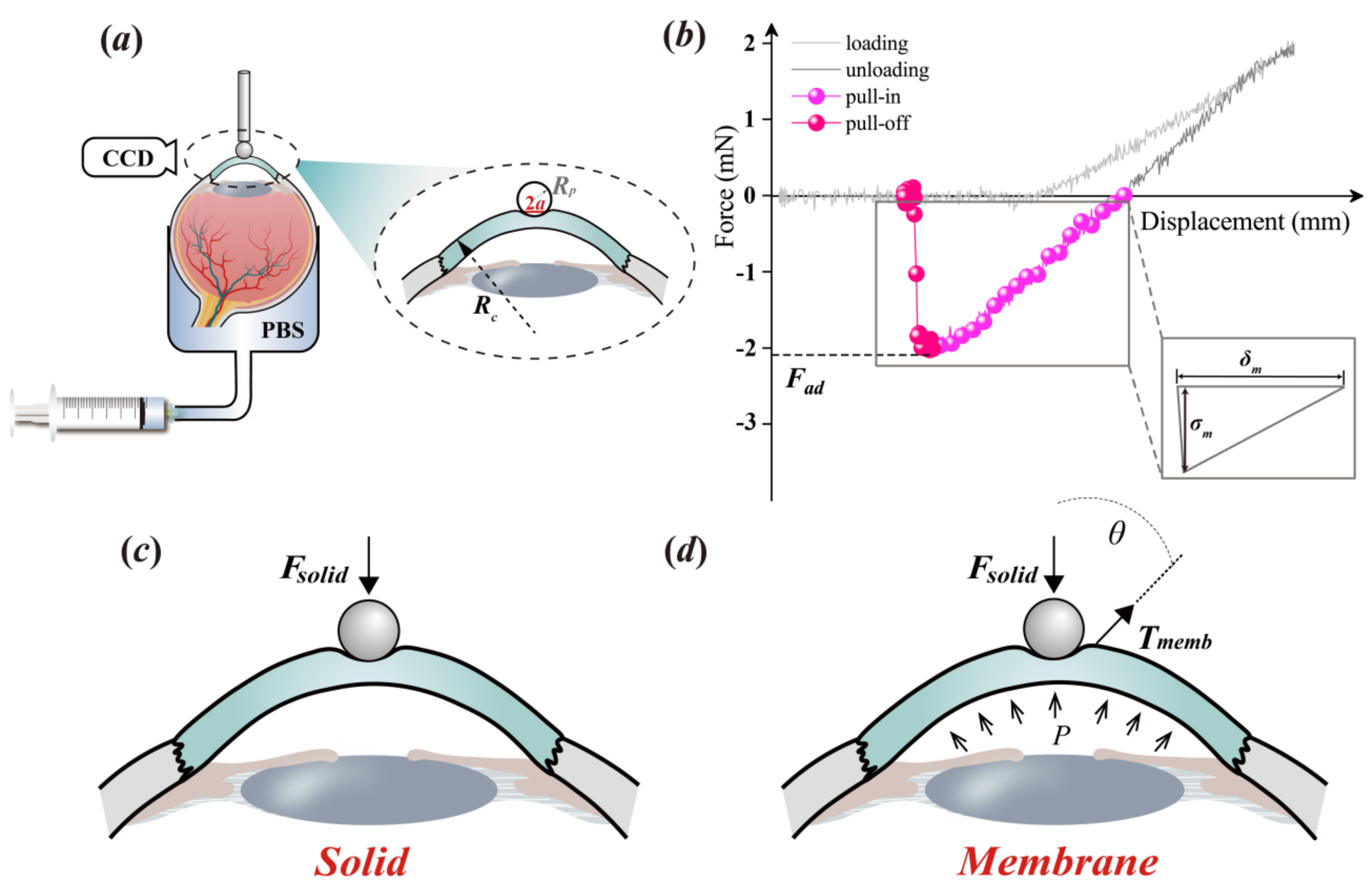
2.2. Experimental Protocol
2.3. Theoretical Analysis
2.4. Data Analysis
3. Results
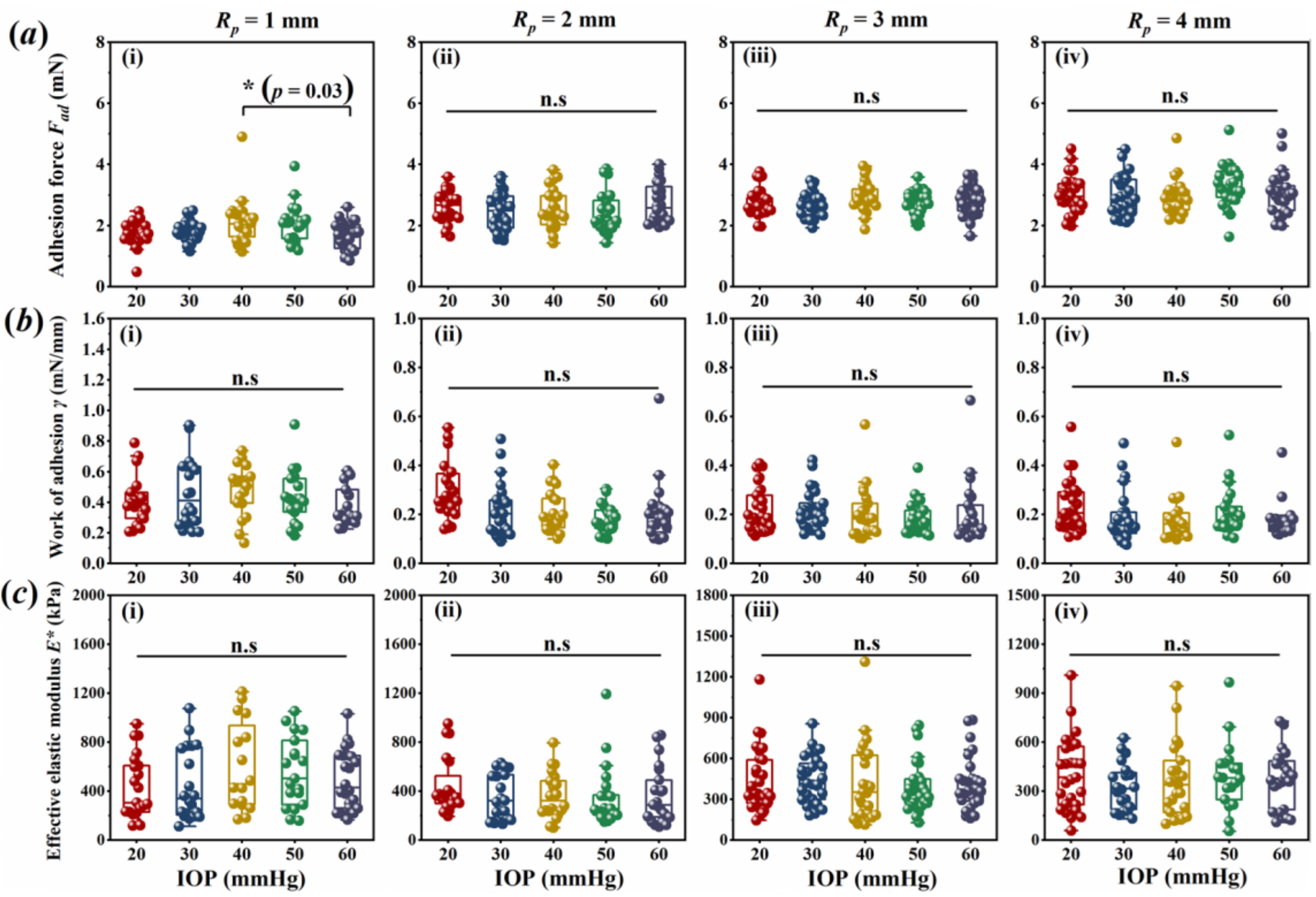
3.1. Corneal Adhesion Was Not Affected by IOP
3.2. Scale Effect of Corneal Adhesion
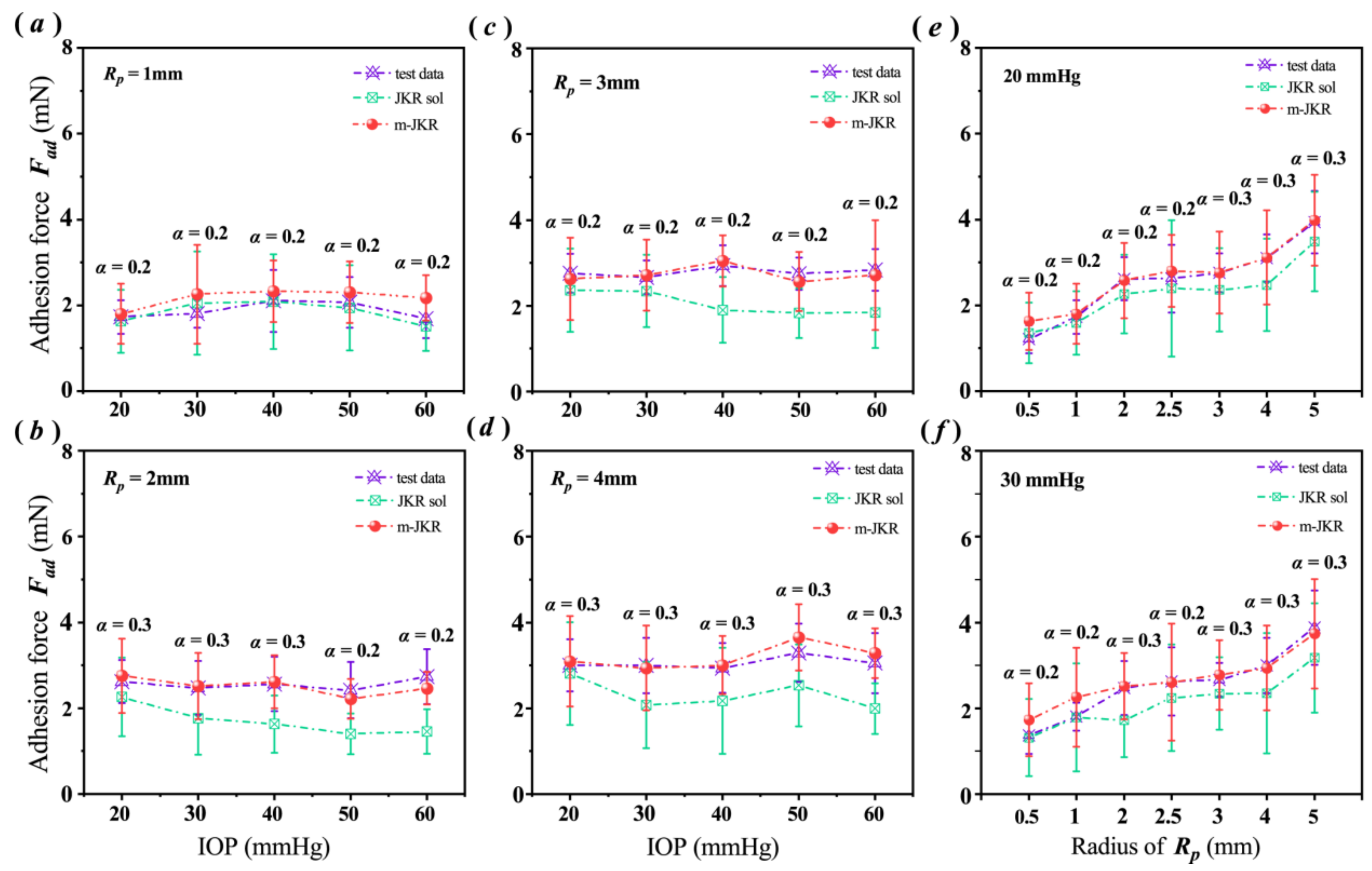
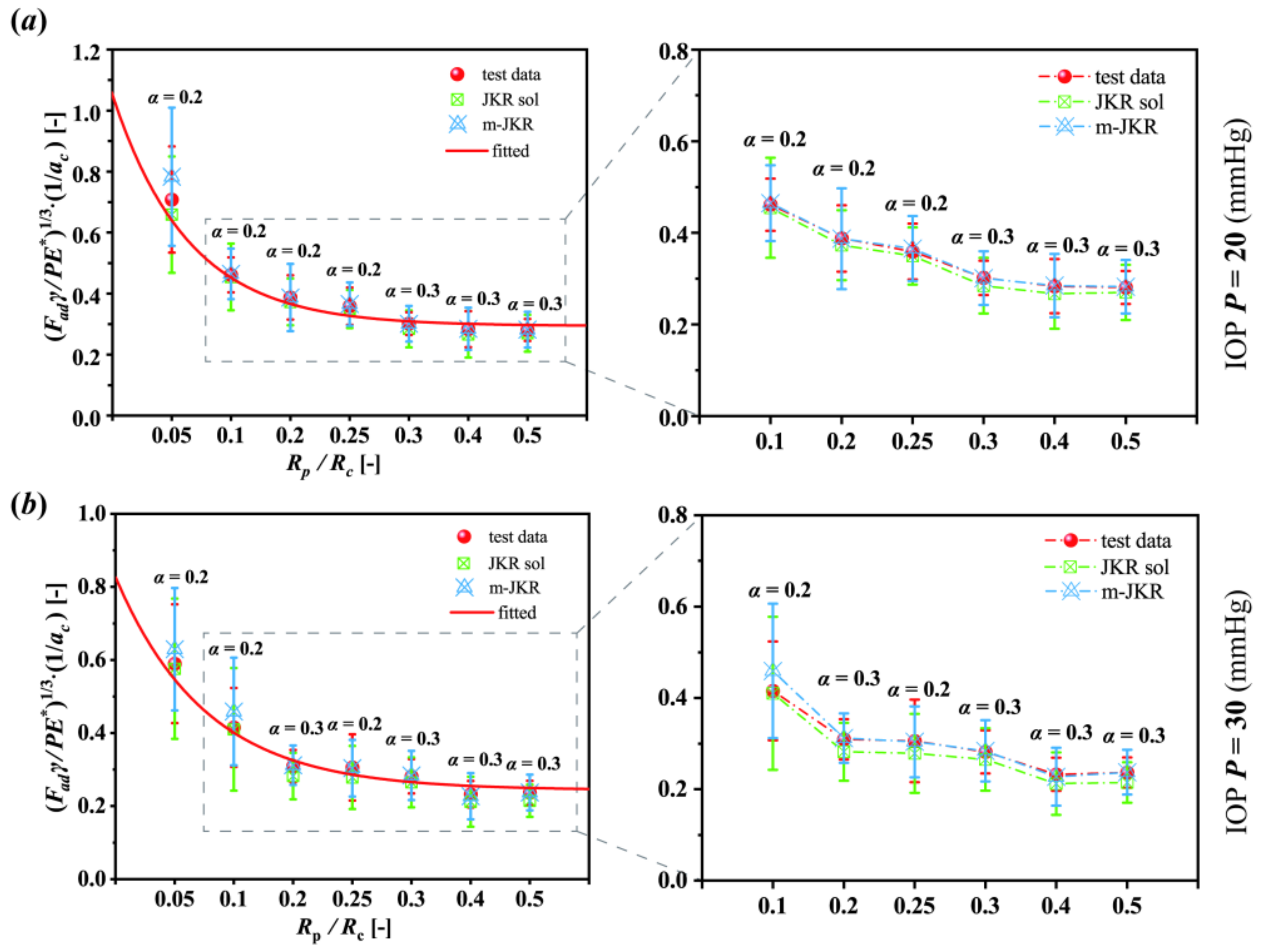
3.3. Analysis Employing the JKR Models
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Riau, A.K.; Liu, Y.C.; Yam, G.H.; Mehta, J.S. Stromal keratophakia: Corneal inlay implantation. Prog. Retin. Eye Res. 2020, 75, 100780. [Google Scholar] [CrossRef]
- Yu, Y.; Hsu, K.H.; Gharami, S.; Butler, J.E.; Hazra, S.; Chauhan, A. Interfacial polymerization of a thin film on contact lenses for improving lubricity. J. Colloid Interface Sci. 2020, 571, 356–367. [Google Scholar] [CrossRef]
- Zhu, D.; Liu, Y.; Gilbert, J.L. Micromechanical measurement of adhesion of dehydrating silicone hydrogel contact lenses to corneal tissue. Acta Biomater. 2021, 127, 242–251. [Google Scholar] [CrossRef]
- Khamar, P.; Shetty, R.; Vaishnav, R.; Francis, M.; Nuijts, R.M.; Sinha Roy, A. Biomechanics of LASIK flap and SMILE cap: A prospective, clinical study. J. Refract. Surg. 2019, 35, 324–332. [Google Scholar] [CrossRef] [PubMed]
- Sharifi, R.; Mahmoudzadeh, S.; Islam, M.M.; Koza, D.; Dohlman, C.H.; Chodosh, J.; Gonzalez-Andrades, M. Covalent Functionalization of PMMA Surface with L-3, 4-Dihydroxyphenylalanine (L-DOPA) to Enhance its Biocompatibility and Adhesion to Corneal Tissue. Adv. Mater. Interfaces 2020, 7, 1900767. [Google Scholar] [CrossRef]
- Johnson, K.L.; Kendall, K.; Roberts, A.D. Surface energy and the contact of elastic solids. Proc. Math. Phys. Eng. Sci. 1971, 324, 301–313. [Google Scholar]
- Cho, H.; Wu, G.; Christopher Jolly, J.; Fortoul, N.; He, Z.; Gao, Y.; Yang, S. Intrinsically reversible superglues via shape adaptation inspired by snail epiphragm. Proc. Natl. Acad. Sci. USA 2019, 116, 13774–13779. [Google Scholar] [CrossRef]
- Jiang, Y.; Grierson, D.S.; Turner, K.T. Flat punch adhesion: Transition from fracture-based to strength-limited pull-off. J. Phys. D Appl. Phys. 2014, 47, 325301. [Google Scholar] [CrossRef]
- Peng, B.; Feng, X.Q.; Li, Q. Decohesion of a rigid flat punch from an elastic layer of finite thickness. J. Mech. Phys. Solids 2020, 139, 103937. [Google Scholar] [CrossRef]
- Ren, Q.; Chen, J.; Li, X.; Lv, Y.; Niu, X.; Chen, W.; Gao, Z. Effective elastic modulus of an intact cornea related to indentation behavior: A comparison between the Hertz model and Johnson-Kendall-Roberts model. Exp. Eye Res. 2021, 209, 108670. [Google Scholar] [CrossRef]
- Johnson, K.L.; Greenwood, J.A. An adhesion map for the contact of elastic spheres. J. Colloid Interface Sci. 1997, 192, 326–333. [Google Scholar] [CrossRef]
- Derjaguin, B.V.; Muller, V.M.; Toporov, Y.P. Effect of contact deformations on the adhesion of particles. J. Colloid Interface Sci. 1975, 53, 314–326. [Google Scholar] [CrossRef]
- Tang, T.; Hui, C.Y. Decohesion of a rigid punch from an elastic layer: Transition from “flaw sensitive” to “flaw insensitive” regime. J. Polym. Sci. Pol. Phys. 2005, 43, 3628–3637. [Google Scholar] [CrossRef]
- Ciavarella, M.; Joe, J.; Papangelo, A.; Barber, J.R. The role of adhesion in contact mechanics. J. R. Soc. Interface 2019, 16, 20180738. [Google Scholar] [CrossRef]
- Xia, G.; Huang, Y.; Su, Y.; Chen, W. Exact axisymmetric adhesive contact analysis for a pre-deformed soft electroactive half-space. Int. J. Solids Struct. 2020, 207, 206–229. [Google Scholar] [CrossRef]
- Kuhar, K.; Jesbeer, M.; Ghatak, A. Soft Gel-Filled Composite Adhesive for Dry and Wet Adhesion. ACS Appl. Polym. Mater. 2021, 3, 3755–3765. [Google Scholar] [CrossRef]
- Hu, J.; Youssefian, S.; Obayemi, J.; Malatesta, K.; Rahbar, N.; Soboyejo, W. Investigation of adhesive interactions in the specific targeting of Triptorelin-conjugated PEG-coated magnetite nanoparticles to breast cancer cells. Acta Biomater. 2018, 71, 363–378. [Google Scholar] [CrossRef]
- Wu, G.; Gotthardt, M.; Gollasch, M. Assessment of nanoindentation in stiffness measurement of soft biomaterials: Kidney, liver, spleen, and uterus. Sci. Rep. 2020, 10, 18784. [Google Scholar] [CrossRef]
- Lai, Y.; He, D.; Hu, Y. Indentation adhesion of hydrogels over a wide range of length and time scales. Extreme Mech. Lett. 2019, 31, 100540. [Google Scholar] [CrossRef]
- Li, Y.; Huang, S.; Wei, C.; Wu, C.; Mochalin, V.N. Adhesion of two-dimensional titanium carbides (MXenes) and graphene to silicon. Nat. Commun. 2019, 10, 3014. [Google Scholar] [CrossRef]
- Deng, W.; Kesari, H. Effect of machine stiffness on interpreting contact force–indentation depth curves in adhesive elastic contact experiments. J. Mech. Phys. Solids 2019, 131, 404–423. [Google Scholar] [CrossRef]
- Hertz, H. Miscellaneous Papers; Macmillan: London, UK, 1896. [Google Scholar]
- Sneddon, I.N. The relation between load and penetration in the axisymmetric Boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 1965, 3, 47–57. [Google Scholar] [CrossRef]
- Fung, Y. Biomechanics: Mechanical Properties of Living Tissues; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Dai, A.N.; He, W.; Wang, S.B.; Chen, W.J.; Li, C.W.; Wang, Z.Y.; Li, L.A. In vivo adhesive behavior of human facial skin by a modified indentation test. J. Mech. Behav. Biomed. Mater. 2019, 92, 172–178. [Google Scholar] [CrossRef]
- Morales-Hurtado, M.; de Vries, E.G.; Peppelman, M.; Zeng, X.; Van Erp, P.E.J.; van der Heide, E. On the role of adhesive forces in the tribo-mechanical performance of ex vivo human skin. Tribol. Int. 2017, 107, 25–32. [Google Scholar] [CrossRef]
- Kendall, K. The adhesion and surface energy of elastic solids. J. Phys. D Appl. Phys. 1971, 4, 1186. [Google Scholar] [CrossRef]
- Yang, W.; Meyers, M.A.; Ritchie, R.O. Structural architectures with toughening mechanisms in Nature: A review of the materials science of Type-I collagenous materials. Prog. Mater. Sci. 2019, 103, 425–483. [Google Scholar] [CrossRef]
- Qian, J.; Gao, H. Scaling effects of wet adhesion in biological attachment systems. Acta Biomater. 2006, 2, 51–58. [Google Scholar] [CrossRef]
- Busin, M.; Leon, P.; Nahum, Y.; Scorcia, V. Large (9 mm) deep anterior lamellar keratoplasty with clearance of a 6-mm optical zone optimizes outcomes of keratoconus surgery. Ophthalmology 2017, 124, 1072–1080. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.H.; Wang, S.R.; He, Y.X.; Yao, B.Y.; Zhang, Y. The best optical zone for small-incision lenticule extraction in high myopic patients. J. Cataract. Ref. Sur. 2020, 46, 1302–1307. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zhou, H.; Huang, C.; Sun, J.; Qu, X.; Lu, Y. A novel corneal adhesive based on functionally coupled PEG-lysozyme hydrogel for wound closure after surgical eye surgery. Chin. Chem. Lett. 2022, 33, 4321–4325. [Google Scholar] [CrossRef]
- Sharifi, S.; Sharifi, H.; Guild, C.; Islam, M.M.; Tran, K.D.; Patzer, C.; Chodosh, J. Toward electron-beam sterilization of a pre-assembled Boston keratoprosthesis. Ocul. Surf. 2021, 20, 176–184. [Google Scholar] [CrossRef]
- Afferrante, L.; Violano, G. On the effective surface energy in viscoelastic Hertzian contacts. J. Mech. Phys. Solids 2022, 158, 104669. [Google Scholar] [CrossRef]
- Lyashenko, I.A.; Popov, V.L. The effect of contact duration and indentation depth on adhesion strength: Experiment and numerical simulation. Tech. Phys. 2020, 65, 1695–1707. [Google Scholar] [CrossRef]
- Pailler-Mattei, C.; Zahouani, H. Analysis of adhesive behaviour of human skin in vivo by an indentation test. Tribol. Int. 2006, 39, 12–21. [Google Scholar] [CrossRef]
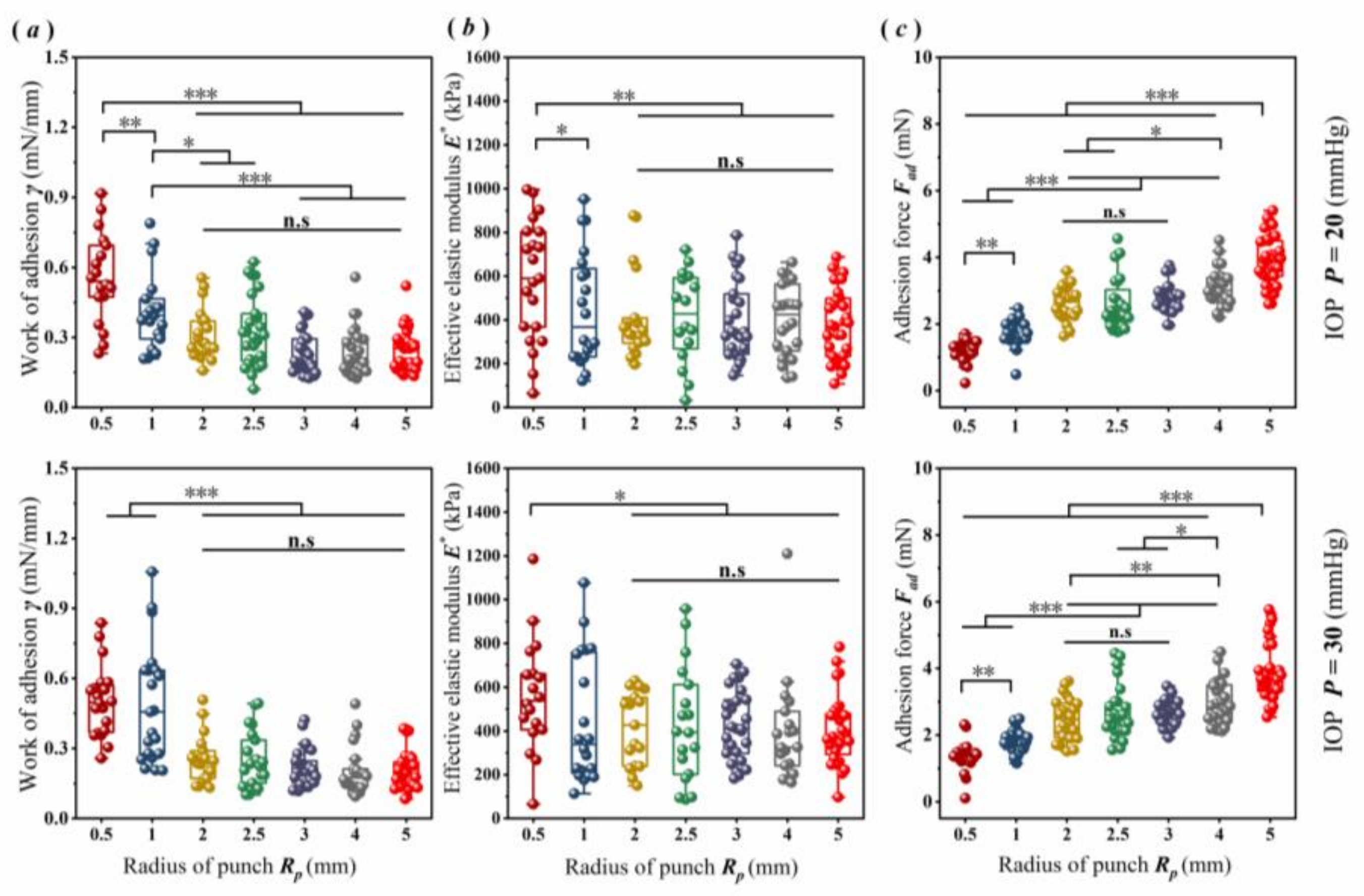
| Radius of Punch RP (mm) | ||||||||
|---|---|---|---|---|---|---|---|---|
| IOP P (mmHg) | 0.5 | 1 | 2 | 2.5 | 3 | 4 | 5 | |
| γ (mN/mm) | 20 | 0.56 ± 0.19 | 0.41 ± 0.16 | 0.29 ± 0.12 | 0.33 ± 0.15 | 0.22 ± 0.09 | 0.23 ± 0.11 | 0.24 ± 0.09 |
| 30 | 0.50 ± 0.15 | 0.46 ± 0.22 | 0.22 ± 0.11 | 0.27 ± 0.15 | 0.22 ± 0.08 | 0.19 ± 0.11 | 0.21 ± 0.08 | |
| 40 | 0.47 ± 0.17 | 0.21 ± 0.08 | 0.20 ± 0.10 | 0.18 ±0.09 | ||||
| 50 | 0.43 ± 0.17 | 0.18 ± 0.06 | 0.18 ± 0.06 | 0.21 ± 0.10 | ||||
| 60 | 0.37 ± 0.13 | 0.21 ± 0.12 | 0.20 ± 0.13 | 0.18 ± 0.08 | ||||
| E* (kPa) | 20 | 581.52 ± 275.10 | 434.18 ± 260.89 | 437.73 ± 231.14 | 777.24 ± 500.72 | 434.92 ± 235.09 | 407.72 ± 224.77 | 381.59 ± 161.94 |
| 30 | 560.80 ± 255.80 | 449.18 ± 292.02 | 361.16 ± 184.86 | 713.89 ± 382.38 | 441.29 ± 174.80 | 328.57 ± 145.96 | 403.92 ± 160.92 | |
| 40 | 601.36 ± 365.53 | 360.25 ± 182.63 | 422.27 ± 285.37 | 363.36 ± 224.58 | ||||
| 50 | 558.01 ± 282.76 | 357.27 ± 247.15 | 393.64 ± 185.03 | 395.25 ± 205.55 | ||||
| 60 | 492.78 ± 243.71 | 366.89 ± 237.06 | 418.69 ± 200.53 | 377.33 ± 177.10 | ||||
| Fad (mN) | 20 | 1.25 ± 0.25 | 1.73 ± 0.39 | 2.62 ± 0.50 | 2.62 ± 0.79 | 2.76 ± 0.46 | 3.00 ± 0.61 | 3.94 ± 0.73 |
| 30 | 1.37 ± 0.43 | 1.81 ± 0.32 | 2.47 ± 0.62 | 2.62 ± 0.79 | 2.66 ± 0.39 | 3.00 ± 0.64 | 3.88 ± 0.87 | |
| 40 | 2.10 ± 0.73 | 2.56 ± 0.64 | 2.94 ± 0.47 | 2.94 ± 0.58 | ||||
| 50 | 2.07 ± 0.59 | 2.42 ± 0.66 | 2.75 ± 0.38 | 3.29 ± 0.68 | ||||
| 60 | 1.69 ± 0.45 | 2.74 ± 0.64 | 2.84 ± 0.49 | 3.05 ± 0.70 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Ren, Q.; Zhao, D.; Gao, Z.; Li, X.; He, R.; Chen, W. Corneal Adhesion Possesses the Characteristics of Solid and Membrane. Bioengineering 2022, 9, 394. https://doi.org/10.3390/bioengineering9080394
Yang J, Ren Q, Zhao D, Gao Z, Li X, He R, Chen W. Corneal Adhesion Possesses the Characteristics of Solid and Membrane. Bioengineering. 2022; 9(8):394. https://doi.org/10.3390/bioengineering9080394
Chicago/Turabian StyleYang, Jiajin, Qiaomei Ren, Dong Zhao, Zhipeng Gao, Xiaona Li, Rui He, and Weiyi Chen. 2022. "Corneal Adhesion Possesses the Characteristics of Solid and Membrane" Bioengineering 9, no. 8: 394. https://doi.org/10.3390/bioengineering9080394
APA StyleYang, J., Ren, Q., Zhao, D., Gao, Z., Li, X., He, R., & Chen, W. (2022). Corneal Adhesion Possesses the Characteristics of Solid and Membrane. Bioengineering, 9(8), 394. https://doi.org/10.3390/bioengineering9080394






