Hybrid Zero Dynamics Control for Gait Guidance of a Novel Adjustable Pediatric Lower-Limb Exoskeleton
Abstract
:1. Introduction
2. CSU Pediatric Exoskeleton Actuator
2.1. Target Patients and Anthropometrics
2.2. Joint Actuator
2.3. Adjustable Frame Components
2.3.1. Hip Cradle Subassembly
2.3.2. Thigh Subassembly
2.3.3. Shank Subassembly
3. Reference Gait and Spatiotemporal Parameters
4. Patient-Exoskeleton Hybrid Model
4.1. Model Parameters
4.2. Equations of Motion
5. Hybrid Zero Dynamics Control
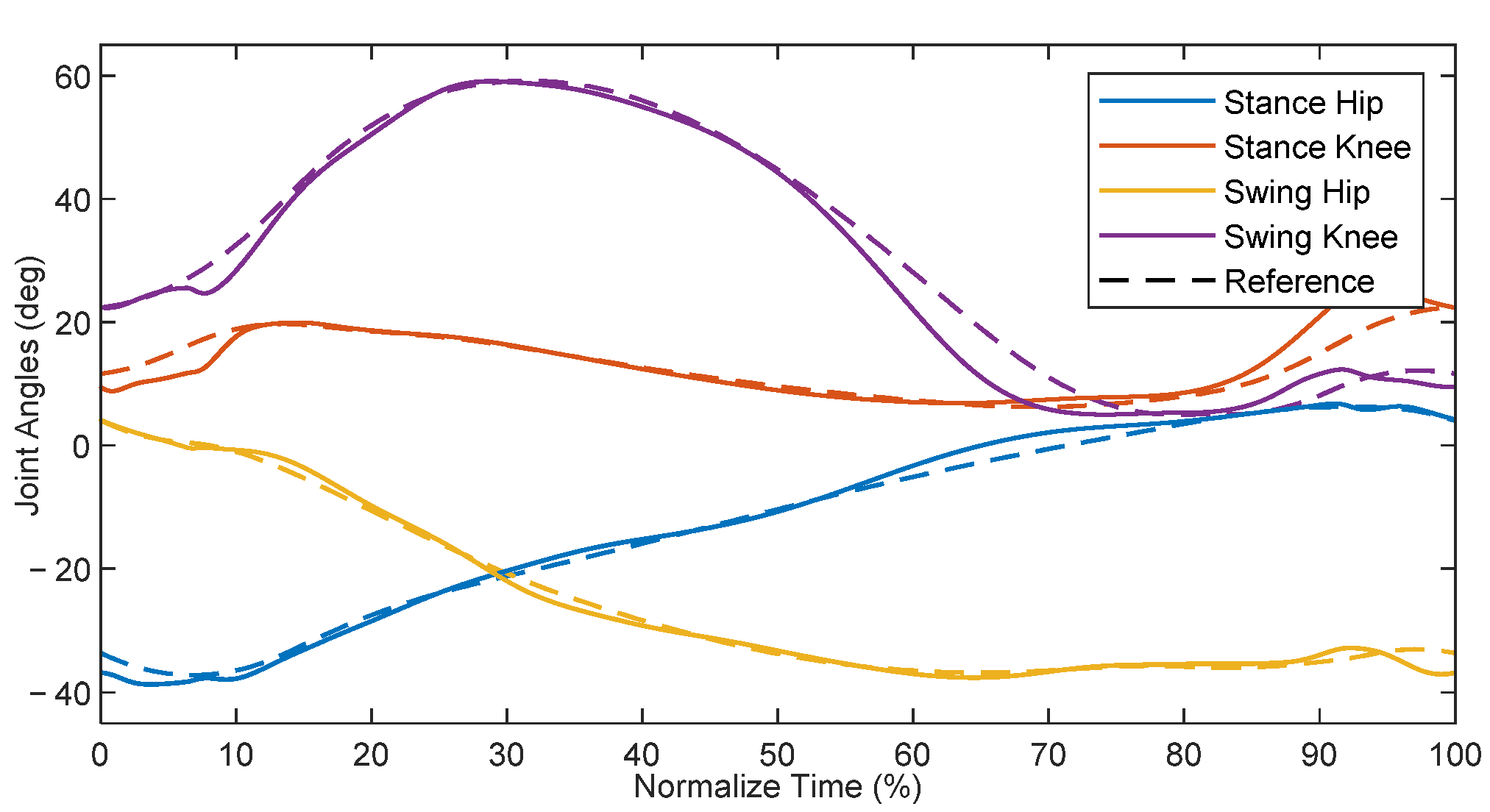
6. Simulation Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Alexander, M.A.; Matthews, D.J.; Murphy, K.P. Pediatric Rehabilitation: Principles and Practice, 5th ed.; Demos Medical Publishing: New York, NY, USA, 2015; ISBN 978-1-62070-061-7. [Google Scholar]
- Damiano, D.L.; DeJong, S.L. A Systematic Review of the Effectiveness of Treadmill Training and Body Weight Support in Pediatric Rehabilitation. J. Neurol. Phys. Ther. 2009, 33, 27–44. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Westlake, K.P.; Patten, C. Pilot Study of Lokomat versus Manual-Assisted Treadmill Training for Locomotor Recovery Post-Stroke. J. NeuroEng. Rehabil. 2009, 6, 18. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Volpini, M.; Bartenbach, V.; Pinotti, M.; Riener, R. Clinical Evaluation of a Low-Cost Robot for Use in Physiotherapy and Gait Training. J. Rehabil. Assist. Technol. Eng. 2017, 4, 2055668316688410. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Viteckova, S.; Kutilek, P.; Jirina, M. Wearable Lower Limb Robotics: A Review. Biocybern. Biomed. Eng. 2013, 33, 96–105. [Google Scholar] [CrossRef]
- Young, A.; Ferris, D. State-of-the-Art and Future Directions for Robotic Lower Limb Exoskeletons. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 171–182. [Google Scholar] [CrossRef]
- Gonzalez, A.; Garcia, L.; Kilby, J.; McNair, P. Robotic Devices for Paediatric Rehabilitation: A Review of Design Features. Biomed. Eng. OnLine 2021, 20, 89. [Google Scholar] [CrossRef]
- Eguren, D.; Contreras-Vidal, J.L. Navigating the FDA Medical Device Regulatory Pathways for Pediatric Lower Limb Exoskeleton Devices. IEEE Syst. J. 2021, 15, 2361–2368. [Google Scholar] [CrossRef]
- Copilusi, C.; Margine, A.; Dumitru, N. Case Study Regarding a New Knee Orthosis for Children with Locomotion Disabilities. Mech. Transm. Appl. 2015, 31, 147–155. [Google Scholar]
- Lerner, Z.F.; Damiano, D.L.; Bulea, T.C. The Effects of Exoskeleton Assisted Knee Extension on Lower-Extremity Gait Kinematics, Kinetics, and Muscle Activity in Children with Cerebral Palsy. Sci. Rep. 2017, 7, 13512. [Google Scholar] [CrossRef] [Green Version]
- Sancho-Pérez, J.; Pérez, M.; García, E.; Sanz-Merodio, D.; Plaza, A.; Cestari, M. Mechanical Description of ATLAS 2020, a 10-DOF Paediatric Exoskeleton. In Proceedings of the 19th International Conference on CLAWAR, London, UK, 12–14 September 2016; pp. 814–822. [Google Scholar]
- Eguren, D.; Cestari, M.; Luu, T.P.; Kilicarslan, A.; Steele, A.; Contreras-Vidal, J.L. Design of a Customizable, Modular Pediatric Exoskeleton for Rehabilitation and Mobility. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics, SMC 2019, Bari, Italy, 6–9 October 2019; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2019; pp. 2411–2416. [Google Scholar]
- Yan, T.; Cempini, M.; Oddo, C.M.; Vitiello, N. Review of Assistive Strategies in Powered Lower-Limb Orthoses and Exoskeletons. Robot. Auton. Syst. 2015, 64, 120–136. [Google Scholar] [CrossRef]
- Winter, D.A. The Biomechanics and Motor Control of Human Gait: Normal, Elderly and Pathological, 2nd ed.; University of Waterloo Press: Waterloo, ON, Canada, 1991; ISBN 978-0-88898-105-9. [Google Scholar]
- Schwartz, M.H.; Rozumalski, A.; Trost, J.P. The Effect of Walking Speed on the Gait of Typically Developing Children. J. Biomech. 2008, 41, 1639–1650. [Google Scholar] [CrossRef] [PubMed]
- Tucker, M.R.; Olivier, J.; Pagel, A.; Bleuler, H.; Bouri, M.; Lambercy, O.; Millán, J.R.; Riener, R.; Vallery, H.; Gassert, R. Control Strategies for Active Lower Extremity Prosthetics and Orthotics: A Review. J. NeuroEng. Rehabil. 2015, 12, 1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Westervelt, E.R.; Grizzle, J.W.; Chevallereau, C.; Choi, J.H.; Morris, B. Feedback Control of Dynamic Bipedal Robot Locomotion, 1st ed.; CRC Press: Boca Raton, FL, USA, 2018; ISBN 978-1-315-21942-4. [Google Scholar]
- Mummolo, C.; Mangialardi, L.; Kim, J.H. Quantifying Dynamic Characteristics of Human Walking for Comprehensive Gait Cycle. J. Biomech. Eng. 2013, 135, 091006. [Google Scholar] [CrossRef] [PubMed]
- Sreenath, K.; Park, H.-W.; Poulakakis, I.; Grizzle, J.W. A Compliant Hybrid Zero Dynamics Controller for Stable, Efficient and Fast Bipedal Walking on MABEL. Int. J. Rob. Res. 2011, 30, 1170–1193. [Google Scholar] [CrossRef] [Green Version]
- Hereid, A.; Cousineau, E.A.; Hubicki, C.M.; Ames, A.D. 3D Dynamic Walking with Underactuated Humanoid Robots: A Direct Collocation Framework for Optimizing Hybrid Zero Dynamics. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1447–1454. [Google Scholar]
- Gurriet, T.; Finet, S.; Boeris, G.; Duburcq, A.; Hereid, A.; Harib, O.; Masselin, M.; Grizzle, J.; Ames, A.D. Towards Restoring Locomotion for Paraplegics: Realizing Dynamically Stable Walking on Exoskeletons. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 2804–2811. [Google Scholar]
- Agrawal, A.; Harib, O.; Hereid, A.; Finet, S.; Masselin, M.; Praly, L.; Ames, A.D.; Sreenath, K.; Grizzle, J.W. First Steps towards Translating HZD Control of Bipedal Robots to Decentralized Control of Exoskeletons. IEEE Access 2017, 5, 9919–9934. [Google Scholar] [CrossRef] [Green Version]
- Goo, A.; Laubscher, C.A.; Sawicki, J.T. Hybrid Zero Dynamics-Based Control of an Underactuated Lower-Limb Exoskeleton for Gait Guidance. J. Dyn. Syst. Meas. 2022, 144, 061008. [Google Scholar] [CrossRef]
- Laubscher, C.A.; Goo, A.; Sawicki, J.T. Adaptive Zero Dynamics Control with Optimal State-Dependent Phase on a Lower-Limb Exoskeleton in Able-Bodied Walking. IEEE Trans. Robot. 2022; Under Review. [Google Scholar]
- Goo, A.; Laubscher, C.A.; Farris, R.J.; Sawicki, J.T. Design and Evaluation of a Pediatric Lower-Limb Exoskeleton Joint Actuator. Actuators 2020, 9, 138. [Google Scholar] [CrossRef]
- Laubscher, C.A.; Farris, R.J.; Sawicki, J.T. Design and Preliminary Evaluation of a Powered Pediatric Lower Limb Orthosis. In Proceedings of the ASME 2017 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference, Cleveland, OH, USA, 6 August 2017. [Google Scholar]
- Laubscher, C.A. Design and Development of a Powered Pediatric Lower-Limb Orthosis. PhD Thesis, Cleveland State University, Cleveland, OH, USA, 2020. [Google Scholar]
- Fryar, C.D.; Carroll, M.D.; Gu, Q.; Afful, J.; Ogden, C.L. Anthropometric Reference Data for Children and Adult: United States, 2015–2018; National Center for Health Statistics: Washington, DC, USA, 2021; Volume 46.
- Winter, D.A. Biomechanics and Motor Control of Human Movement, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009; ISBN 978-0-470-39818-0. [Google Scholar]
- Sawicki, J.T.; Laubscher, C.A.; Farris, R.J.; Etheridge, S.J.-S. Actuating Device for Powered Orthosis. U.S. Patent 11,207,234, 28 December 2021. [Google Scholar]
- Laubscher, C.A.; Farris, R.J.; van den Bogert, A.J.; Sawicki, J.T. An Anthropometrically Parametrized Assistive Lower Limb Exoskeleton. J. Biomech. Eng. 2021, 143, 105001. [Google Scholar] [CrossRef]
- Nandor, M.J.; Heebner, M.; Quinn, R.; Triolo, R.J.; Makowski, N.S. Transmission Comparison for Cooperative Robotic applications. Actuators 2021, 10, 203. [Google Scholar] [CrossRef]
- Westervelt, E.R.; Grizzle, J.W.; Koditschek, D.E. Hybrid Zero Dynamics of Planar Biped Walkers. IEEE Trans. Autom. Control 2003, 48, 42–56. [Google Scholar] [CrossRef] [Green Version]
- Fevre, M.; Wensing, P.M.; Schmiedeler, J.P. Rapid Bipedal Gait Optimization in CasADi. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020; pp. 3672–3678. [Google Scholar]
- Ames, A.D. Human-Inspired Control of Bipedal Walking Robots. IEEE Trans. Autom. Control 2014, 59, 1115–1130. [Google Scholar] [CrossRef]
- Chevallereau, C.; Abba, G.; Aoustin, Y.; Plestan, F.; Westervelt, E. RABBIT: A Testbed for Advanced Control Theory. IEEE Control Syst. Mag. 2003, 23, 57–79. [Google Scholar]
- Kolathya, S. Local Stability of PD Controlled Bipedal Walking Robots. Automatica 2020, 114, 108841. [Google Scholar] [CrossRef] [Green Version]
- Laubscher, C.A.; Goo, A.; Farris, R.J.; Sawicki, J.T. Hybrid Impedance-Sliding Mode Switching Control of the Indego Explorer Lower-Limb Exoskeleton in Able-Bodied Walking. J. Intell. Robot. Syst. 2022, 104, 76. [Google Scholar] [CrossRef]






| Age (yr) | Weight (kg) | Height (cm) |
|---|---|---|
| 6 | 23.9 ± 5.2 | 118.8 ± 6.2 |
| 8 | 31.6 ± 9.3 | 132.1 ± 8.7 |
| 11 | 46.5 ± 20.5 | 149.3 ± 11.2 |
| HAT | Thigh | Shank | |
|---|---|---|---|
| Length (m) | 0.621 | 0.324 | 0.377 |
| Mass (kg) | 21.42 | 3.16 | 1.93 |
| CoM (m) | 0.389 | 0.140 | 0.228 |
| Inertia (kg·m2) | 2.0318 | 0.0345 | 0.0473 |
| Hip Width (Min-Max cm) | Thigh Length (Min-Max cm) | Shank Length (Min cm) | |
|---|---|---|---|
| Anthropometric Range | 20.3–25.8 | 29.4–36.8 | 29.5 |
| Adjustability Range | 20.7–27.0 | 27.8–41.8 | 17.2 |
| Hip Cradle All Ages | Thigh 6 Years Old | Thigh 8 Years Old | Thigh 11 Years Old | Shank All Ages | |
|---|---|---|---|---|---|
| Mass (kg) | 0.775 | 1.244 | 1.244 | 1.244 | 0.138 |
| CoM (m) | 0.097 | 0.150 | 0.167 | 0.188 | 0.115 |
| Inertia (kg·m2) | 0.0020 | 0.0127 | 0.0159 | 0.0208 | 0.0003 |
| Age (yr) | Speed (m/s) | Step Length (m) | Step Period (s) |
|---|---|---|---|
| 6 | 1.067 ± 0.064 | 0.478 ± 0.028 | 0.449 ± 0.030 |
| 8 | 1.125 ± 0.068 | 0.532 ± 0.031 | 0.473 ± 0.031 |
| 11 | 1.196 ± 0.072 | 0.601 ± 0.035 | 0.503 ± 0.033 |
| Upper Body | Thigh | Shank | |
|---|---|---|---|
| Length (m) | 0.621 | 0.324 | 0.377 |
| Mass (kg) | 22.20 | 4.60 | 2.07 |
| CoM (m) | 0.379 | 0.148 | 0.221 |
| Inertia (kg·m2) | 2.0973 | 0.0511 | 0.0492 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goo, A.; Laubscher, C.A.; Wiebrecht, J.J.; Farris, R.J.; Sawicki, J.T. Hybrid Zero Dynamics Control for Gait Guidance of a Novel Adjustable Pediatric Lower-Limb Exoskeleton. Bioengineering 2022, 9, 208. https://doi.org/10.3390/bioengineering9050208
Goo A, Laubscher CA, Wiebrecht JJ, Farris RJ, Sawicki JT. Hybrid Zero Dynamics Control for Gait Guidance of a Novel Adjustable Pediatric Lower-Limb Exoskeleton. Bioengineering. 2022; 9(5):208. https://doi.org/10.3390/bioengineering9050208
Chicago/Turabian StyleGoo, Anthony, Curt A. Laubscher, Jason J. Wiebrecht, Ryan J. Farris, and Jerzy T. Sawicki. 2022. "Hybrid Zero Dynamics Control for Gait Guidance of a Novel Adjustable Pediatric Lower-Limb Exoskeleton" Bioengineering 9, no. 5: 208. https://doi.org/10.3390/bioengineering9050208
APA StyleGoo, A., Laubscher, C. A., Wiebrecht, J. J., Farris, R. J., & Sawicki, J. T. (2022). Hybrid Zero Dynamics Control for Gait Guidance of a Novel Adjustable Pediatric Lower-Limb Exoskeleton. Bioengineering, 9(5), 208. https://doi.org/10.3390/bioengineering9050208






