Nanopower Integrated Gaussian Mixture Model Classifier for Epileptic Seizure Prediction
Abstract
:1. Introduction
2. Motivation and Background
2.1. Epileptic Seizure Prediction
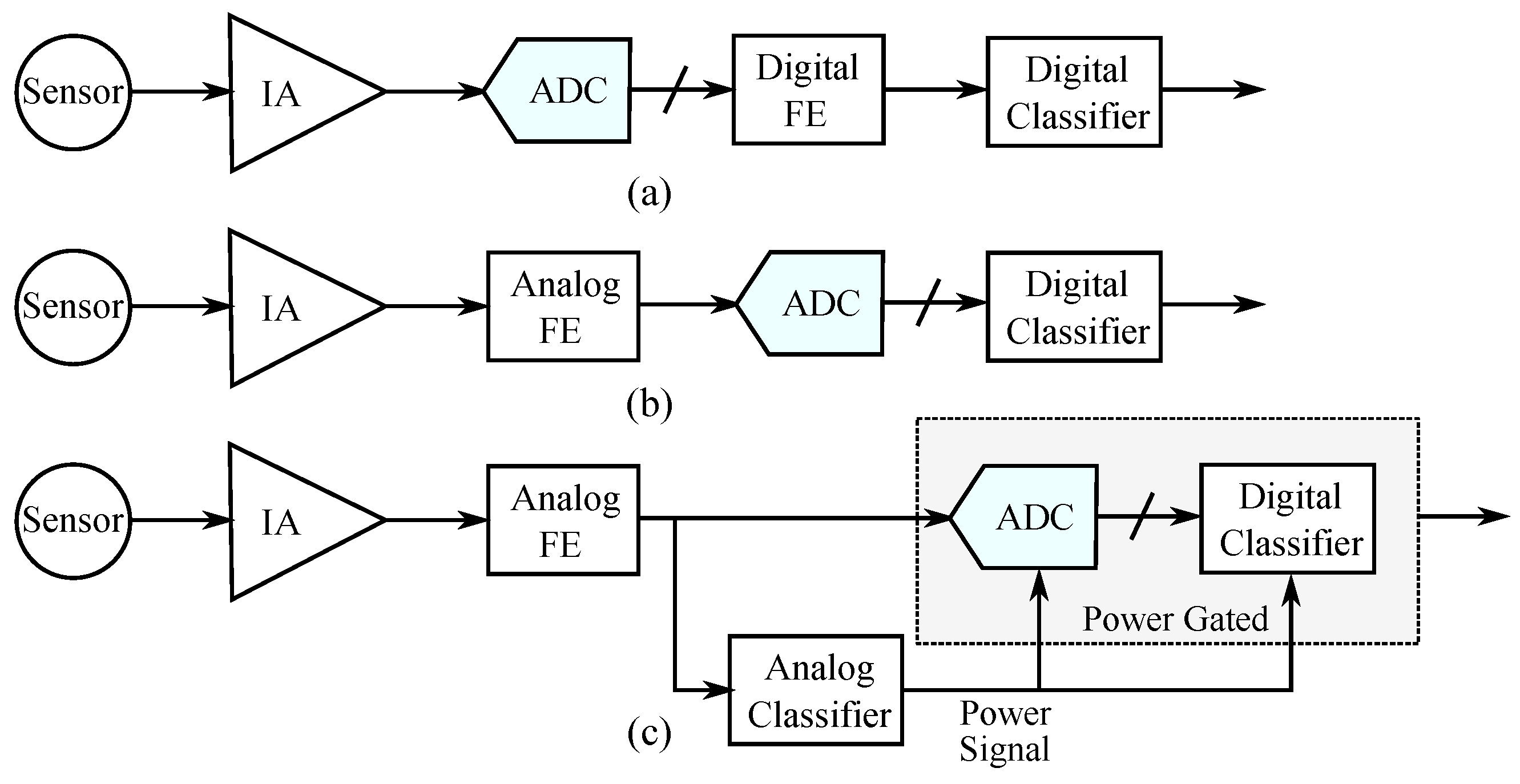
2.2. Analog Classifiers
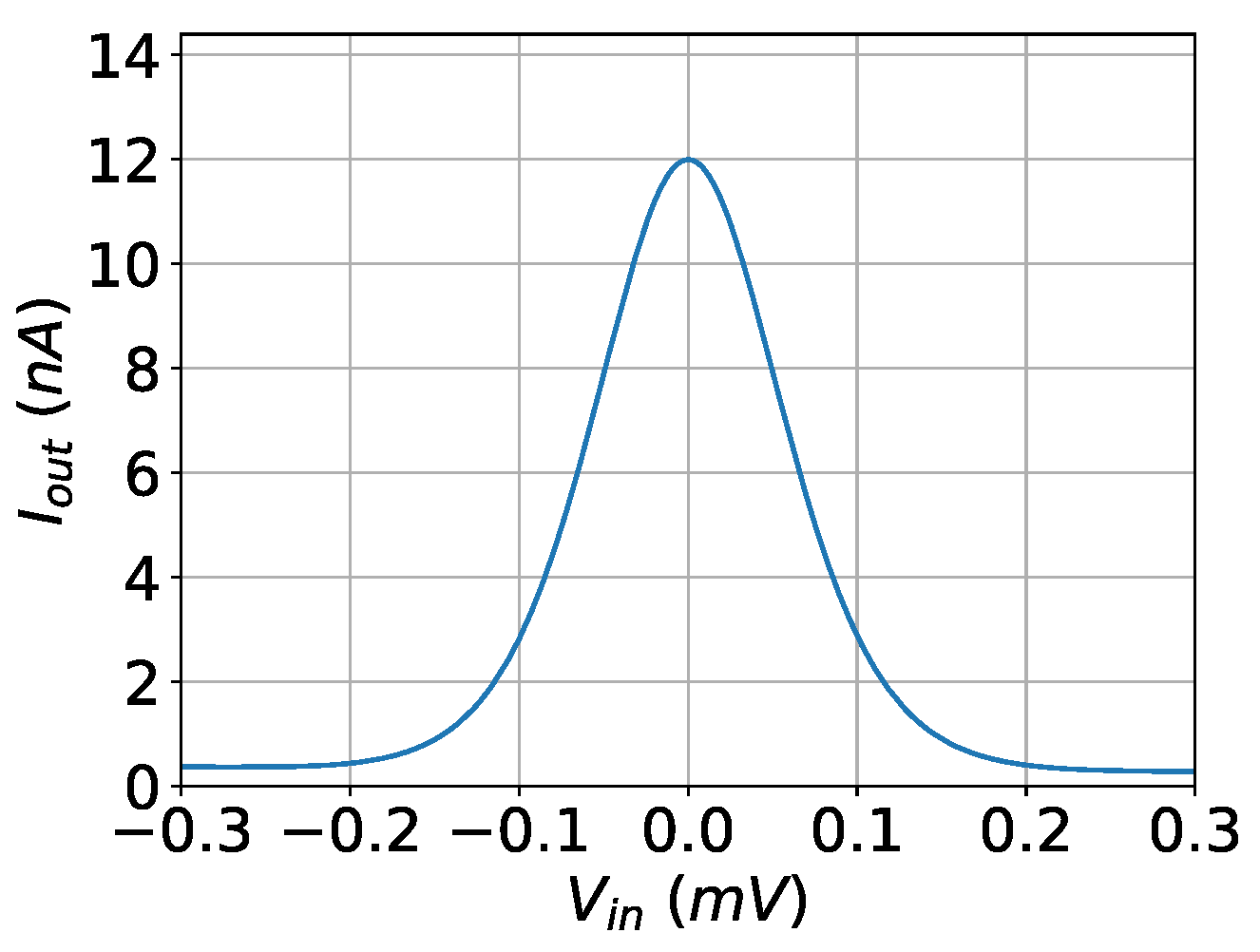
3. Gaussian Mixture Model
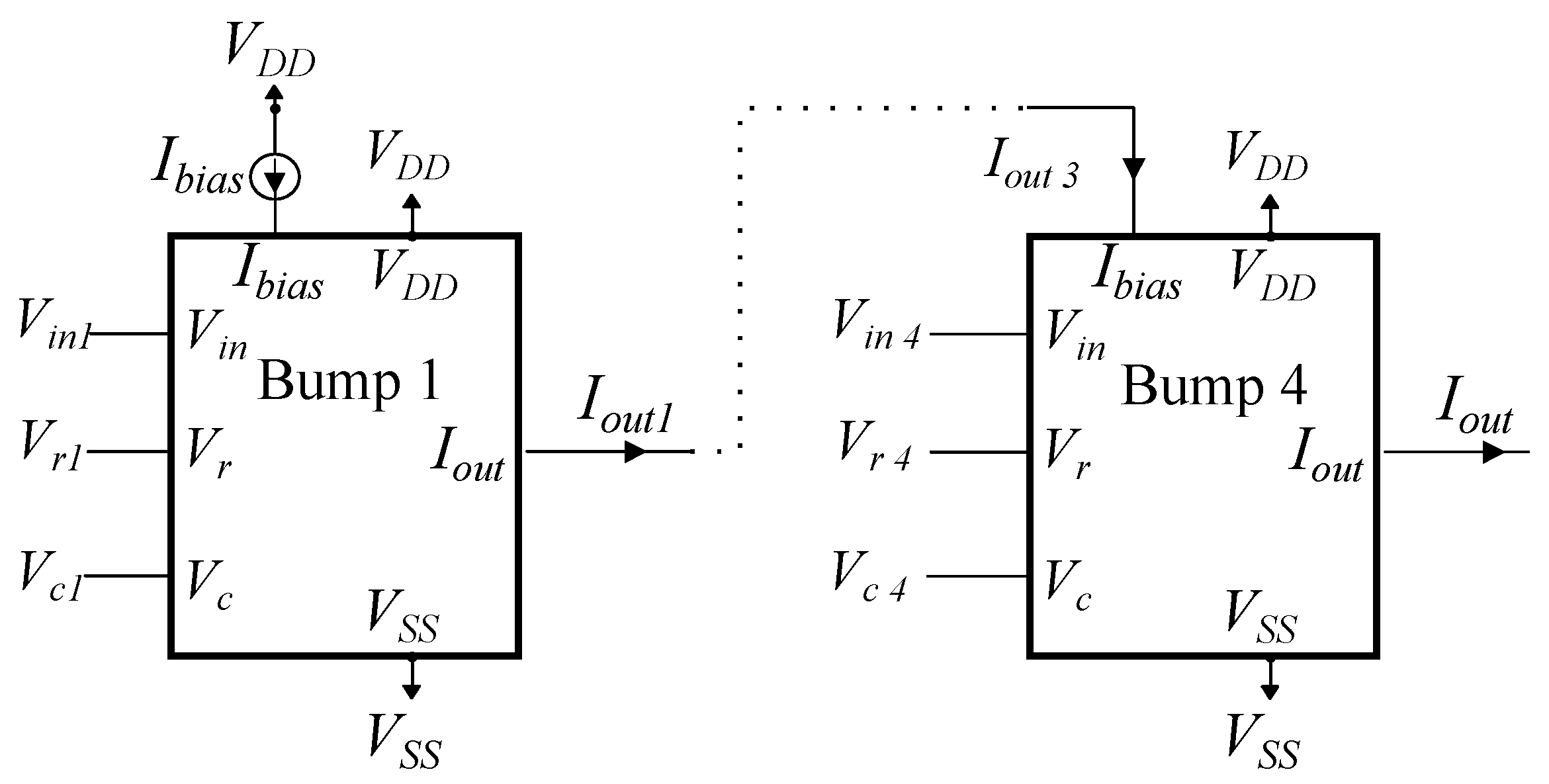
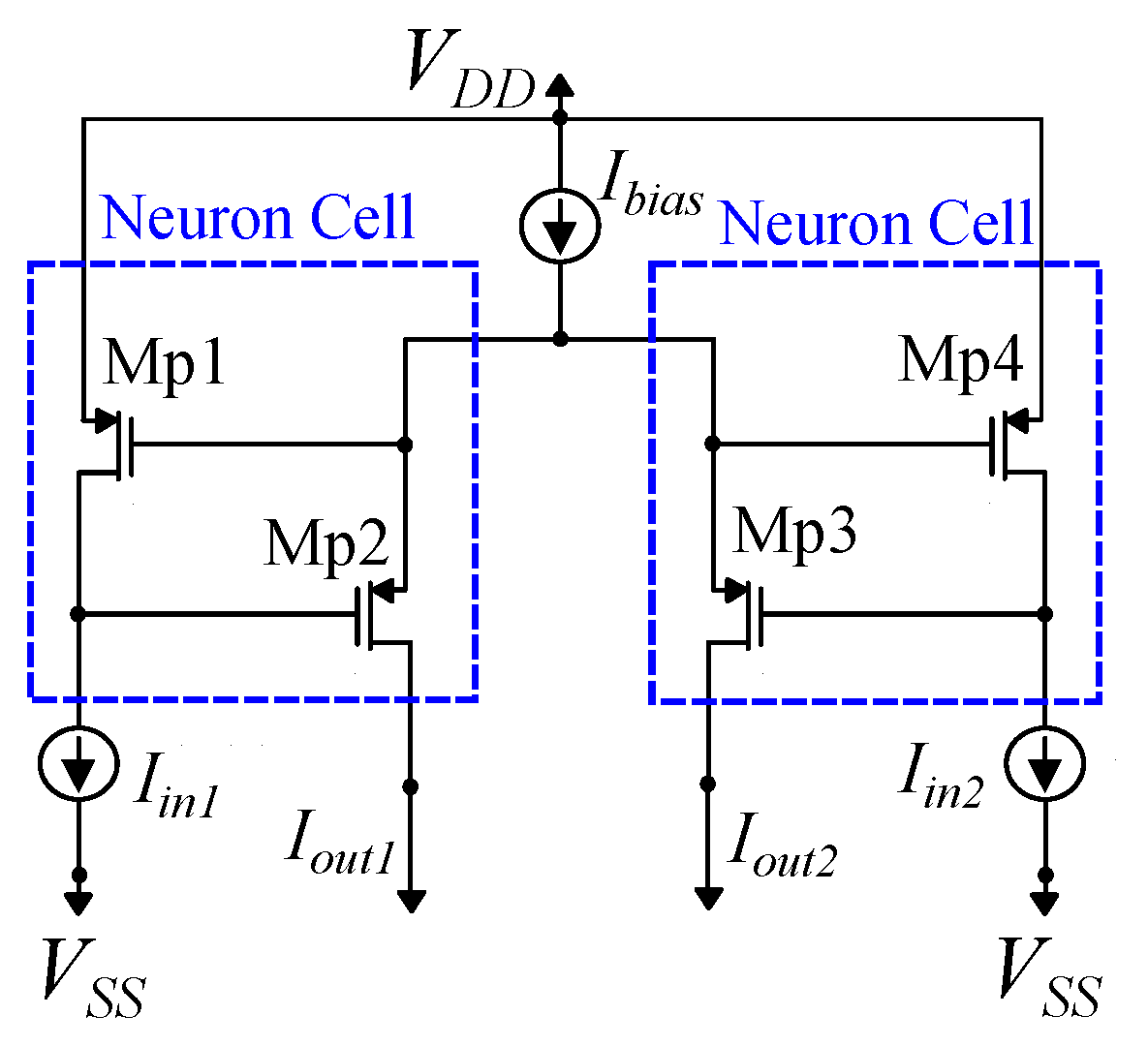
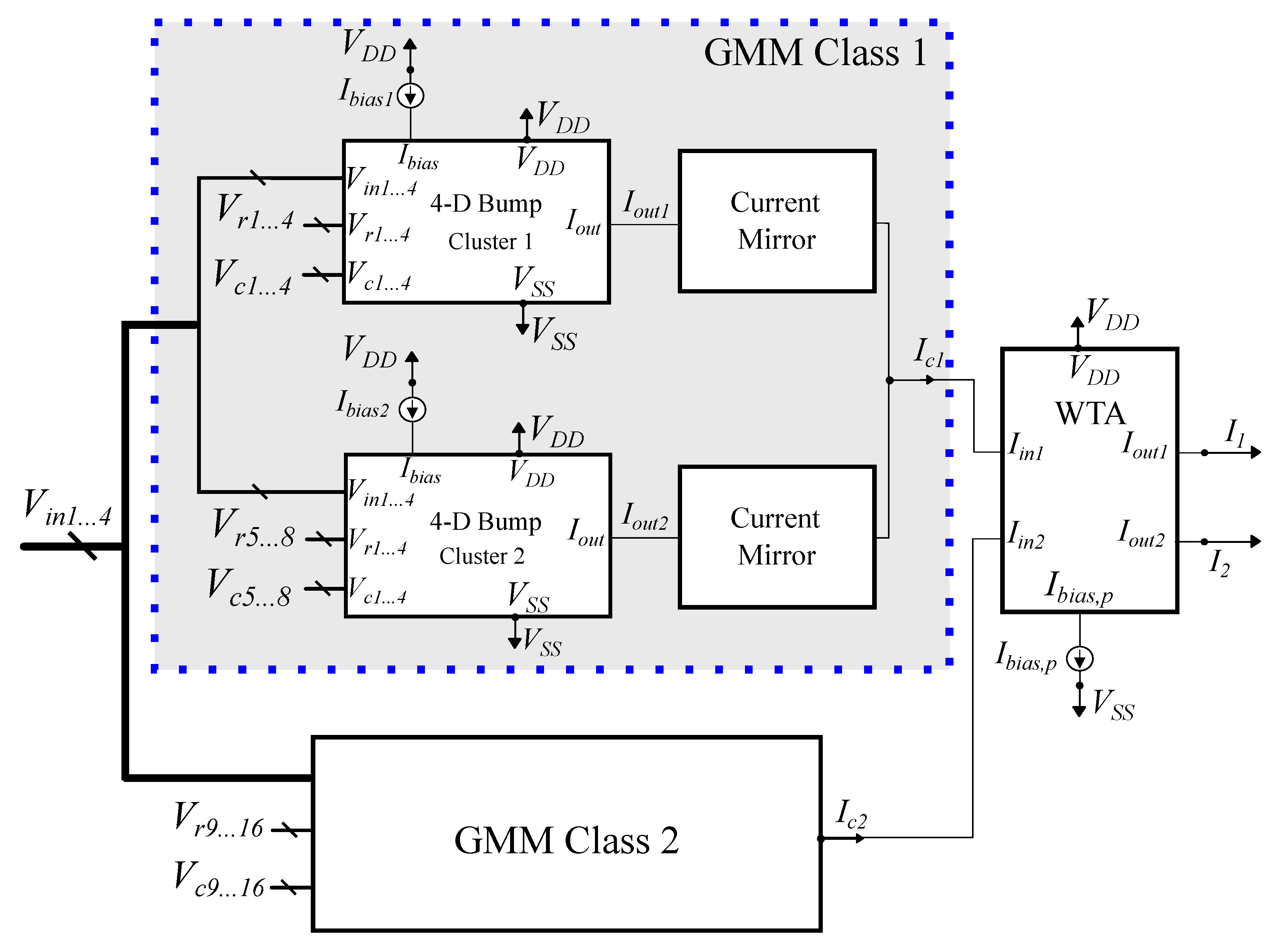
4. Proposed Architecture
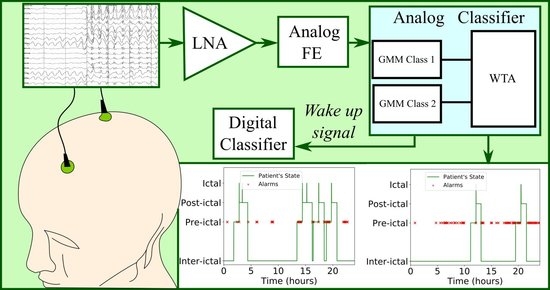
5. Epileptic Seizure Prediction Application
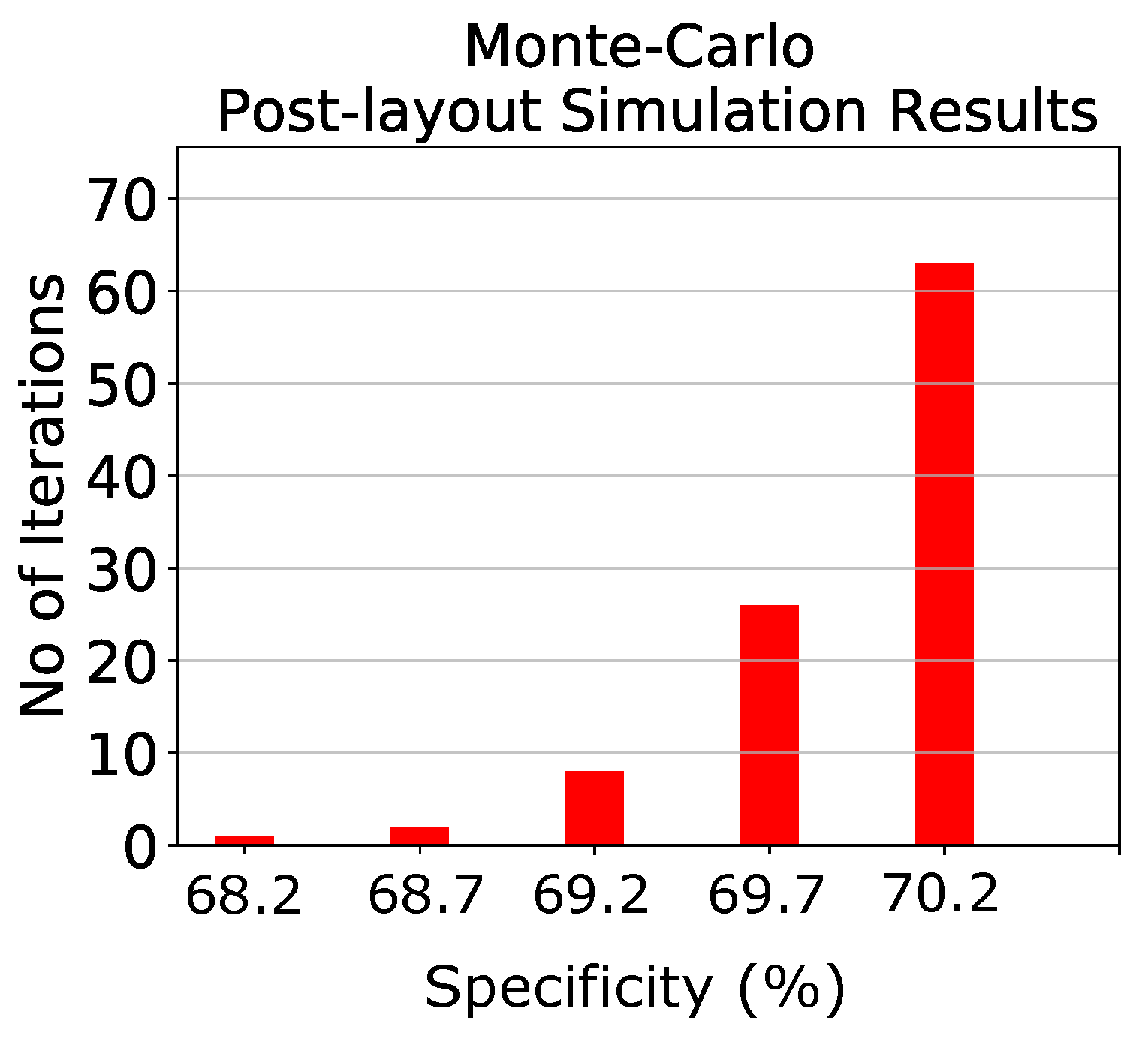
6. Discussion and Comparison
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ishtiaq, A.; Khan, M.U.; Ali, S.Z.; Habib, K.; Samer, S.; Hafeez, E. A Review of System on Chip (SOC) Applications in Internet of Things (IOT) and Medical. In Proceedings of the International Conference on Advances in Mechanical Engineering, ICAME21, Islamabad, Pakistan, 27–28 January 2021; pp. 1–10. [Google Scholar]
- Tsai, C.H.; Yu, W.J.; Wong, W.H.; Lee, C.Y. A 41.3/26.7 pJ per neuron weight RBM processor supporting on-chip learning/inference for IoT applications. IEEE J. Solid-State Circuits 2017, 52, 2601–2612. [Google Scholar] [CrossRef]
- Casson, A.J.; Yates, D.C.; Smith, S.J.; Duncan, J.S.; Rodriguez-Villegas, E. Wearable electroencephalography. IEEE Eng. Med. Biol. Mag. 2010, 29, 44–56. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- CHB-MIT Scalp EEG Database. Available online: https://physionet.org/content/chbmit/1.0.0/ (accessed on 21 March 2022).
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, 215–220. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Subasi, A.; Kevric, J.; Abdullah Canbaz, M. Epileptic seizure detection using hybrid machine learning methods. Neural Comput. Appl. 2019, 31, 317–325. [Google Scholar] [CrossRef]
- Gómez, C.; Arbeláez, P.; Navarrete, M.; Alvarado-Rojas, C.; Le Van Quyen, M.; Valderrama, M. Automatic seizure detection based on imaged-EEG signals through fully convolutional networks. Sci. Rep. 2020, 10, 21833. [Google Scholar] [CrossRef]
- Priya, S.; Inman, D.J. Energy Harvesting Technologies; Springer: New York, NY, USA, 2009; Volume 21, p. 2. [Google Scholar]
- Goetschalckx, K.; Moons, B.; Lauwereins, S.; Andraud, M.; Verhelst, M. Optimized hierarchical cascaded processing. IEEE J. Emerg. Sel. Top. Circuits Syst. 2020, 8, 884–894. [Google Scholar] [CrossRef]
- Hubara, I.; Courbariaux, M.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Quantized neural networks: Training neural networks with low precision weights and activations. J. Mach. Learn. Res. 2017, 18, 6869–6898. [Google Scholar]
- Zhang, K.; Ying, H.; Dai, H.N.; Li, L.; Peng, Y.; Guo, K.; Yu, H. Compacting Deep Neural Networks for Internet of Things: Methods and Applications. IEEE Internet Things J. 2021, 8, 11935–11959. [Google Scholar] [CrossRef]
- Villamizar, D.A.; Muratore, D.G.; Wieser, J.B.; Murmann, B. An 800 nW Switched-Capacitor Feature Extraction Filterbank for Sound Classification. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 1578–1588. [Google Scholar] [CrossRef]
- Zhang, Y.; Mirchandani, N.; Onabajo, M.; Shrivastava, A. RSSI Amplifier Design for a Feature Extraction Technique to Detect Seizures with Analog Computing. In Proceedings of the 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 12–14 October 2020; pp. 1–5. [Google Scholar]
- Yang, M.; Liu, H.; Shan, W.; Zhang, J.; Kiselev, I.; Kim, S.J.; Enz, C.; Seok, M. Nanowatt acoustic inference sensing exploiting nonlinear analog feature extraction. IEEE J. Solid-State Circuits 2021, 56, 3123–3133. [Google Scholar] [CrossRef]
- Yoo, J.; Yan, L.; El-Damak, D.; Altaf, M.A.B.; Shoeb, A.H.; Chandrakasan, A.P. An 8-cannel scalable EEG acquisition SoC with patient-specific seizure classification and recording processor. IEEE J. Solid-State Circuits 2012, 48, 214–228. [Google Scholar] [CrossRef]
- De Vita, A.; Pau, D.; Parrella, C.; Di Benedetto, L.; Rubino, A.; Licciardo, G.D. Low-power HWAccelerator for AI edge-computing in human activity recognition systems. In Proceedings of the 2020 2nd IEEE International Conference on Artificial Intelligence Circuits and Systems (AICAS), Genova, Italy, 31 August–2 September 2020; pp. 291–295. [Google Scholar]
- Yip, M.; Bohorquez, J.L.; Chandrakasan, A.P. A 0.6 V 2.9 μW mixed-signal front-end for ECG monitoring. In Proceedings of the 2012 Symposium on VLSI Circuits (VLSIC), Honolulu, HI, USA, 13–15 June 2012; pp. 66–67. [Google Scholar]
- Karoly, P.J.; Rao, V.R.; Gregg, N.M.; Worrell, G.A.; Bernard, C.; Cook, M.J.; Baud, M.O. Cycles in epilepsy. Nat. Rev. Neurol. 2021, 17, 267–284. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization; Global Campaign against Epilepsy; Programme for Neurological Diseases; Neuroscience (World Health Organization); International Bureau for Epilepsy; World Health Organization, Department of Mental Health; International League against Epilepsy. Atlas: Epilepsy Care in the World; World Health Organization: Geneva, Switzerland, 2005. [Google Scholar]
- Tsiouris, K.M.; Pezoulas, V.C.; Zervakis, M.; Konitsiotis, S.; Koutsouris, D.D.; Fotiadis, D.I. A long short-term memory deep learning network for the prediction of epileptic seizures using EEG signals. Comput. Biol. Med. 2018, 99, 24–37. [Google Scholar] [CrossRef] [PubMed]
- Shoaib, M.; Jha, N.K.; Verma, N. A compressed-domain processor for seizure detection to simultaneously reduce computation and communication energy. In Proceedings of the IEEE 2012 Custom Integrated Circuits Conference, San Jose, CA, USA, 9–12 September 2012; pp. 1–4. [Google Scholar]
- Zhang, J.; Huang, L.; Wang, Z.; Verma, N. A seizure-detection IC employing machine learning to overcome data-conversion and analog-processing non-idealities. In Proceedings of the 2015 IEEE Custom Integrated Circuits Conference (CICC), San Jose, CA, USA, 28–30 September 2015; pp. 1–4. [Google Scholar]
- Lin, S.K.; Wang, L.C.; Lin, C.Y.; Chiueh, H. An ultra-low power smart headband for real-time epileptic seizure detection. IEEE J. Transl. Eng. Health Med. 2018, 6, 1–10. [Google Scholar] [CrossRef]
- Abdelhameed, A.M.; Bayoumi, M. An Efficient Deep Learning System for Epileptic Seizure Prediction. In Proceedings of the 2021 IEEE International Symposium on Circuits and Systems (ISCAS), Daegu, Korea, 22–28 May 2021; pp. 1–5. [Google Scholar]
- O’Shea, A.; Lightbody, G.; Boylan, G.; Temko, A. Neonatal seizure detection from raw multi-channel EEG using a fully convolutional architecture. Neural Netw. 2020, 123, 12–25. [Google Scholar] [CrossRef]
- Shoeb, A.H.; Guttag, J.V. Application of machine learning to epileptic seizure detection. In Proceedings of the ICML, Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Lasefr, Z.; Reddy, R.R.; Elleithy, K. Smart phone application development for monitoring epilepsy seizure detection based on EEG signal classification. In Proceedings of the 2017 IEEE 8th Annual Ubiquitous Computing, Electronics and Mobile Communication Conference (UEMCON), New York, NY, USA, 19–21 October 2017; pp. 83–87. [Google Scholar]
- Tzallas, A.T.; Tsipouras, M.G.; Fotiadis, D.I. Epileptic seizure detection in EEGs using time–frequency analysis. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 703–710. [Google Scholar] [CrossRef]
- Chen, H.; Gu, X.; Mei, Z.; Xu, K.; Yan, K.; Lu, C.; Wang, L.; Shu, F.; Xu, Q.; Oetomo, S.B.; et al. A wearable sensor system for neonatal seizure monitoring. In Proceedings of the 2017 IEEE 14th International Conference on Wearable and Implantable Body Sensor Networks (BSN), Eindhoven, The Netherlands, 9–12 May 2017; pp. 27–30. [Google Scholar]
- Gheryani, M.; Salem, O.; Mehaoua, A. An effective approach for epileptic seizures detection from multi-sensors integrated in an Armband. In Proceedings of the 2017 IEEE 19th International Conference on e-Health Networking, Applications and Services (Healthcom), Dalian, China, 12–15 October 2017; pp. 1–6. [Google Scholar]
- Ramirez-Alaminos, J.M.; Sendra, S.; Lloret, J.; Navarro-Ortiz, J. Low-cost wearable bluetooth sensor for epileptic episodes detection. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Marquez, A.; Dunn, M.; Ciriaco, J.; Farahmand, F. iSeiz: A low-cost real-time seizure detection system utilizing cloud computing. In Proceedings of the 2017 IEEE Global Humanitarian Technology Conference (GHTC), San Jose, CA, USA, 19–22 October 2017; pp. 1–7. [Google Scholar]
- Iranmanesh, S.; Rodriguez-Villegas, E. A 950 nW analog-based data reduction chip for wearable EEG systems in epilepsy. IEEE J. Solid-State Circuits 2017, 52, 2362–2373. [Google Scholar] [CrossRef] [Green Version]
- Iranmanesh, S.; Raikos, G.; Imtiaz, S.A.; Rodriguez-Villegas, E. A seizure-based power reduction SoC for wearable EEG in epilepsy. IEEE Access 2019, 7, 151682–151691. [Google Scholar] [CrossRef]
- Imtiaz, S.A.; Iranmanesh, S.; Rodriguez-Villegas, E. A low power system with EEG data reduction for long-term epileptic seizures monitoring. IEEE Access 2019, 7, 71195–71208. [Google Scholar] [CrossRef]
- Liu, S.C.; Kramer, J.; Indiveri, G.; Delbrück, T.; Douglas, R. Analog VLSI: Circuits and Principles; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Chakrabartty, S.; Cauwenberghs, G. Sub-microwatt analog VLSI trainable pattern classifier. IEEE J. Solid-State Circuits 2007, 42, 1169–1179. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Srivastava, A.; Peng, L.; Chen, Q. Long short-term memory network design for analog computing. ACM J. Emerg. Technol. Comput. Syst. (JETC) 2019, 15, 1–27. [Google Scholar] [CrossRef]
- Zhang, R.; Shibata, T. Fully parallel self-learning analog support vector machine employing compact gaussian generation circuits. Jpn. J. Appl. Phys. 2012, 51, 04DE10. [Google Scholar] [CrossRef]
- Zhang, R.; Shibata, T. An analog on-line-learning K-means processor employing fully parallel self-converging circuitry. Analog Integr. Circuits Signal Process. 2013, 75, 267–277. [Google Scholar] [CrossRef] [Green Version]
- Alimisis, V.; Gennis, G.; Dimas, C.; Sotiriadis, P.P. An Analog Bayesian Classifier Implementation, for Thyroid Disease Detection, based on a Low-Power, Current-Mode Gaussian Function Circuit. In Proceedings of the 2021 International Conference on Microelectronics (ICM), New Cairo City, Egypt, 19–22 December 2021; pp. 153–156. [Google Scholar]
- Kang, K.; Shibata, T. An on-chip-trainable Gaussian-kernel analog support vector machine. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 57, 1513–1524. [Google Scholar] [CrossRef]
- Peng, S.Y.; Hasler, P.E.; Anderson, D. An analog programmable multi-dimensional radial basis function based classifier. In Proceedings of the 2007 IFIP International Conference on Very Large Scale Integration, Atlanta, GA, USA, 15–17 October 2007; pp. 13–18. [Google Scholar]
- Lopez-Martin, A.J.; Carlosena, A. Current-mode multiplier/divider circuits based on the MOS translinear principle. Analog Integr. Circuits Signal Process. 2001, 28, 265–278. [Google Scholar] [CrossRef]
- Alimisis, V.; Gourdouparis, M.; Gennis, G.; Dimas, C.; Sotiriadis, P.P. Analog Gaussian Function Circuit: Architectures, Operating Principles and Applications. Electronics 2021, 10, 2530. [Google Scholar] [CrossRef]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Delbrueck, T.; Mead, C. Bump circuits. In Proceedings of the International Joint Conference on Neural Networks, Nagoya, Japan, 25–29 October 1993; Volume 1, pp. 475–479. [Google Scholar]
- Alimisis, V.; Gourdouparis, M.; Dimas, C.; Sotiriadis, P.P. A 0.6 V, 3.3 nW, Adjustable Gaussian Circuit for Tunable Kernel Functions. In Proceedings of the 2021 34th SBC/SBMicro/IEEE/ACM Symposium on Integrated Circuits and Systems Design (SBCCI), Campinas, Brazil, 23–27 August 2021; pp. 1–6. [Google Scholar]
- Lazzaro, J.; Ryckebusch, S.; Mahowald, M.A.; Mead, C.A. Winner-take-all networks of O (n) complexity. In Proceedings of the Advances in Neural Information Processing Systems 1 (NIPS 1988), Denver, CO, USA, 27–30 November 1988; Volume 1. [Google Scholar]
- Alimisis, V.; Gourdouparis, M.; Dimas, C.; Sotiriadis, P.P. Ultra-Low Power, Low-Voltage, Fully-Tunable, Bulk-Controlled Bump Circuit. In Proceedings of the 2021 10th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 5–7 July 2021; pp. 1–4. [Google Scholar]
- Chakrabartty, S.; Cauwenberghs, G. Fixed-current method for programming large floating-gate arrays. In Proceedings of the 2005 IEEE International Symposium on Circuits and Systems, Kobe, Japan, 23–26 May 2005; pp. 3934–3937. [Google Scholar]
- Chakrabartty, S.; Cauwenberghs, G. Sub-microwatt analog VLSI support vector machine for pattern classification and sequence estimation. In Proceedings of the Advances in Neural Information Processing Systems 17 (NIPS 2004), Vancouver, BC, Canada, 13–18 December 2004; Volume 17. [Google Scholar]
- Cauwenberghs, G.; Yariv, A. Fault-tolerant dynamic multilevel storage in analog VLSI. IEEE Trans. Circuits Syst. II Analog Digital Signal Process. 1994, 41, 827–829. [Google Scholar] [CrossRef]
- Hock, M.; Hartel, A.; Schemmel, J.; Meier, K. An analog dynamic memory array for neuromorphic hardware. In Proceedings of the 2013 European Conference on Circuit Theory and Design (ECCTD), Dresden, Germany, 8–12 September 2013; pp. 1–4. [Google Scholar]
- Miller, R. Theory of the normal waking EEG: From single neurones to waveforms in the alpha, beta and gamma frequency ranges. Int. J. Psychophysiol. 2007, 64, 18–23. [Google Scholar] [CrossRef]
- Chen, M.; Boric-Lubecke, O.; Lubecke, V.M. 0.5-μm CMOS Implementation of Analog Heart-Rate Extraction With a Robust Peak Detector. IEEE Trans. Instrum. Meas. 2008, 57, 690–698. [Google Scholar] [CrossRef]
- Altman, D.G.; Bland, J.M. Diagnostic tests. 1: Sensitivity and specificity. BMJ Br. Med. J. 1994, 308, 1552. [Google Scholar] [CrossRef] [Green Version]
- Grosselin, F.; Navarro-Sune, X.; Vozzi, A.; Pandremmenou, K.; De Vico Fallani, F.; Attal, Y.; Chavez, M. Quality assessment of single-channel EEG for wearable devices. Sensors 2019, 19, 601. [Google Scholar] [CrossRef] [PubMed] [Green Version]



| Ref. | Model | Device | Power Related Metric |
|---|---|---|---|
| [13] | SVM | hardware | μW |
| [15] | SVM | hardware | μW |
| [20] | LSTM | software | N/A |
| [21] | SVM | hardware | |
| [22] | SVM | hardware | |
| [23] | Perceptron | hardware | mW/ 25 h |
| [24] | VAE | software | N/A |
| [25] | CNN | software | N/A |
| [26] | SVM | software | N/A |
| [27] | multi-model | smartphone | N/A |
| [28] | ANN | software | N/A |
| [29] | custom | (MCU) MSP430 and Cloud | N/A |
| [30] | custom | smartphone | N/A |
| [31] | custom | arduino | N/A |
| [32] | SDA | cloud | N/A |
| [33] | filters | hardware | μW |
| [34] | filters | hardware | mW |
| [35] | filters | hardware | μW |
| Ref. | Technology | Model | Dimensions | Power Consumption | Area |
|---|---|---|---|---|---|
| [37] | m | SVM | 14 | 840.0 nW | mm |
| [38] | 180 nm | LSTM | 16 × 16 matrix | mW | mm |
| [39] | 180 nm | SVM | 64 | N/A | mm |
| [40] | 180 nm | K-means | 164 | N/A | N/A |
| [41] | 90 nm | Bayesian | 5 | 365 nW | mm |
| [42] | 180 nm | SVM | 2 | W | mm |
| [43] | m | RBF NN | 2 | N/A | 2.250 mm |
| Differential Block | W/L m/m) | Current Correlator | W/L (m/m) |
|---|---|---|---|
| , | , | ||
| , | – | ||
| – | - | - | |
| - | - |
| Method | Best | Worst | Mean | Std. |
|---|---|---|---|---|
| Software | % | % | % | % |
| Proposed | % | % | % | % |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alimisis, V.; Gennis, G.; Touloupas, K.; Dimas, C.; Uzunoglu, N.; Sotiriadis, P.P. Nanopower Integrated Gaussian Mixture Model Classifier for Epileptic Seizure Prediction. Bioengineering 2022, 9, 160. https://doi.org/10.3390/bioengineering9040160
Alimisis V, Gennis G, Touloupas K, Dimas C, Uzunoglu N, Sotiriadis PP. Nanopower Integrated Gaussian Mixture Model Classifier for Epileptic Seizure Prediction. Bioengineering. 2022; 9(4):160. https://doi.org/10.3390/bioengineering9040160
Chicago/Turabian StyleAlimisis, Vassilis, Georgios Gennis, Konstantinos Touloupas, Christos Dimas, Nikolaos Uzunoglu, and Paul P. Sotiriadis. 2022. "Nanopower Integrated Gaussian Mixture Model Classifier for Epileptic Seizure Prediction" Bioengineering 9, no. 4: 160. https://doi.org/10.3390/bioengineering9040160
APA StyleAlimisis, V., Gennis, G., Touloupas, K., Dimas, C., Uzunoglu, N., & Sotiriadis, P. P. (2022). Nanopower Integrated Gaussian Mixture Model Classifier for Epileptic Seizure Prediction. Bioengineering, 9(4), 160. https://doi.org/10.3390/bioengineering9040160