Predicting the Effect of Localized ACL Damage on Neighbor Ligament Mechanics via Finite Element Modeling
Abstract
:1. Introduction
2. Materials and Methods
2.1. Damage Modeling Procedure
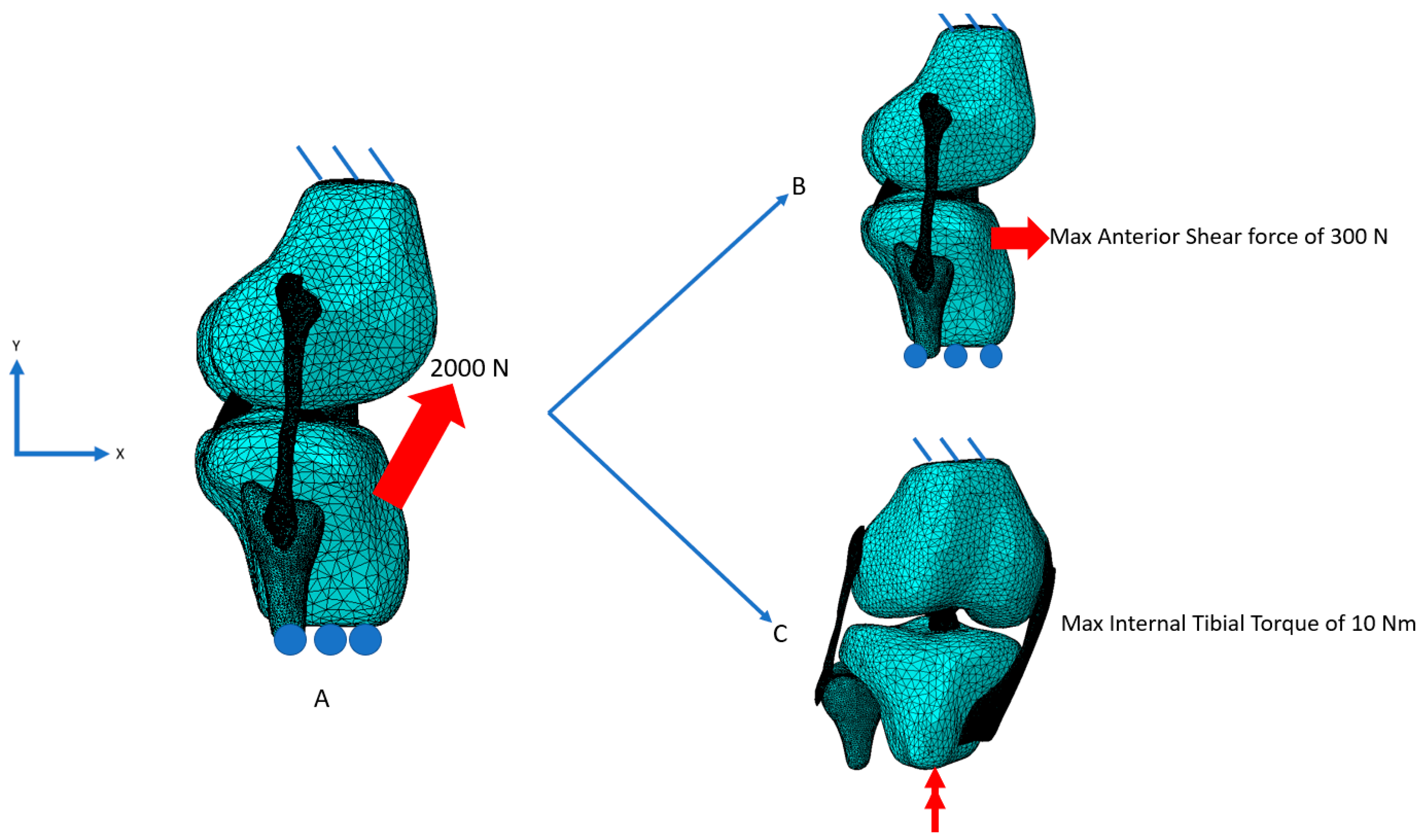
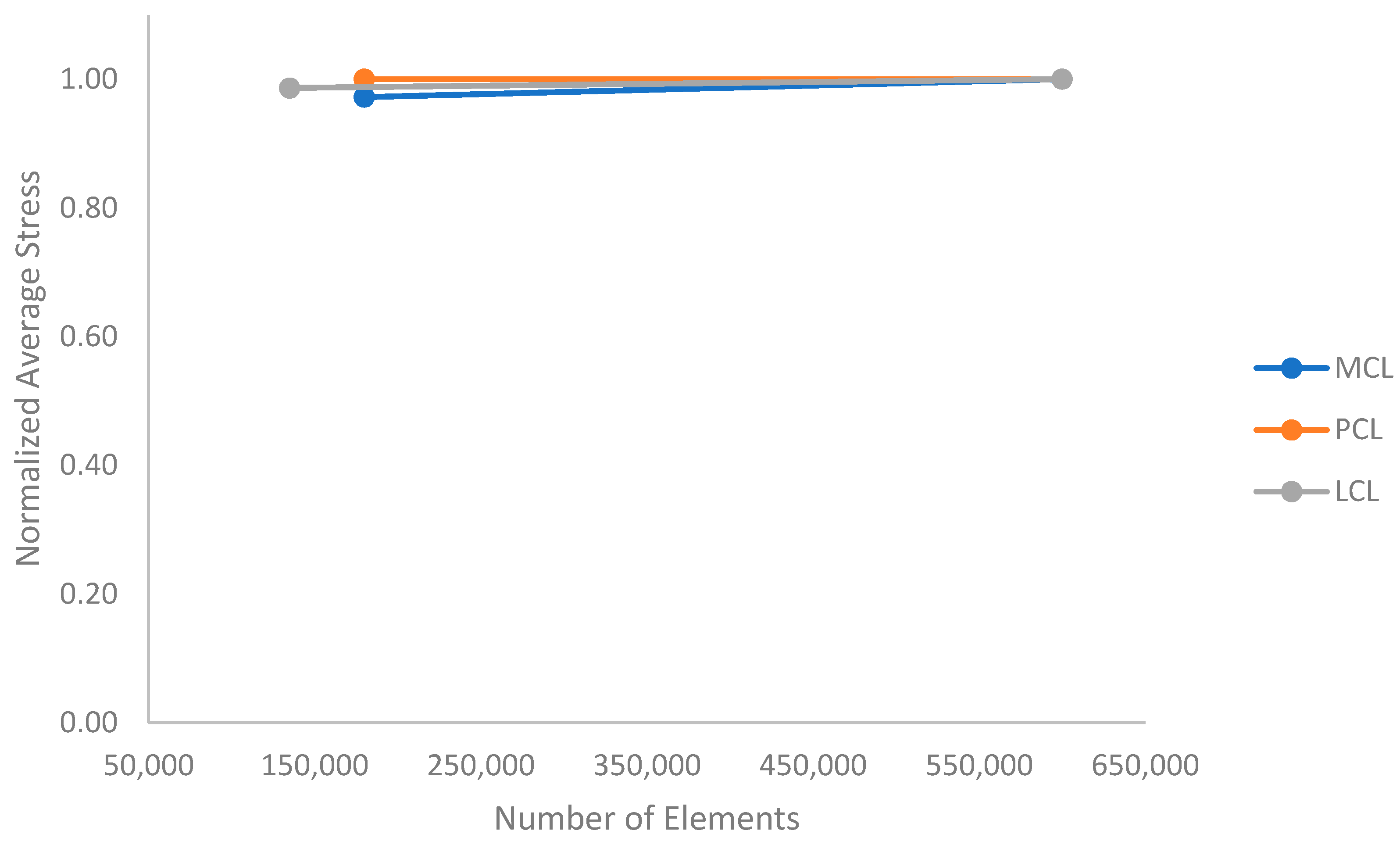
2.2. Model Setup
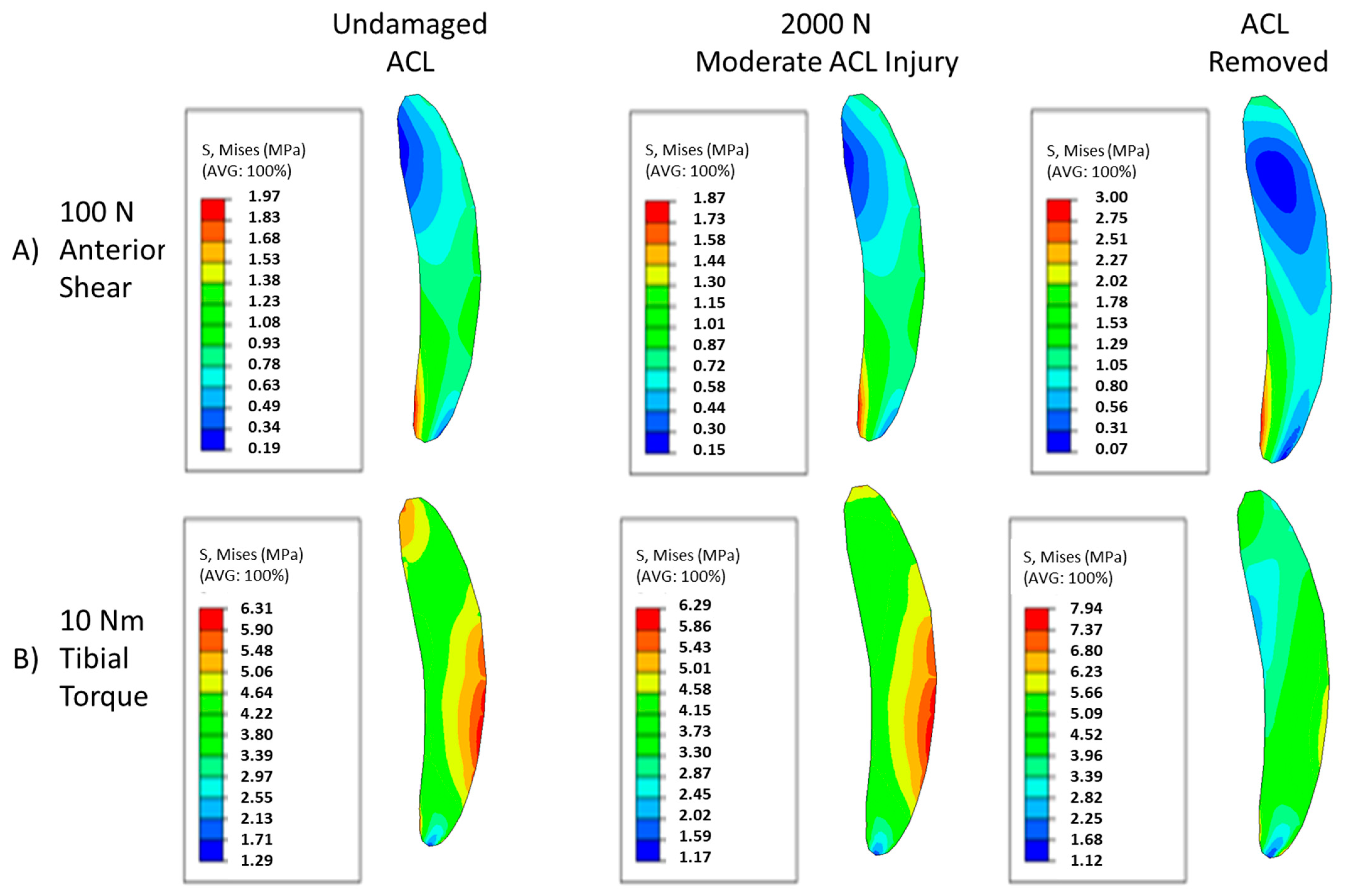
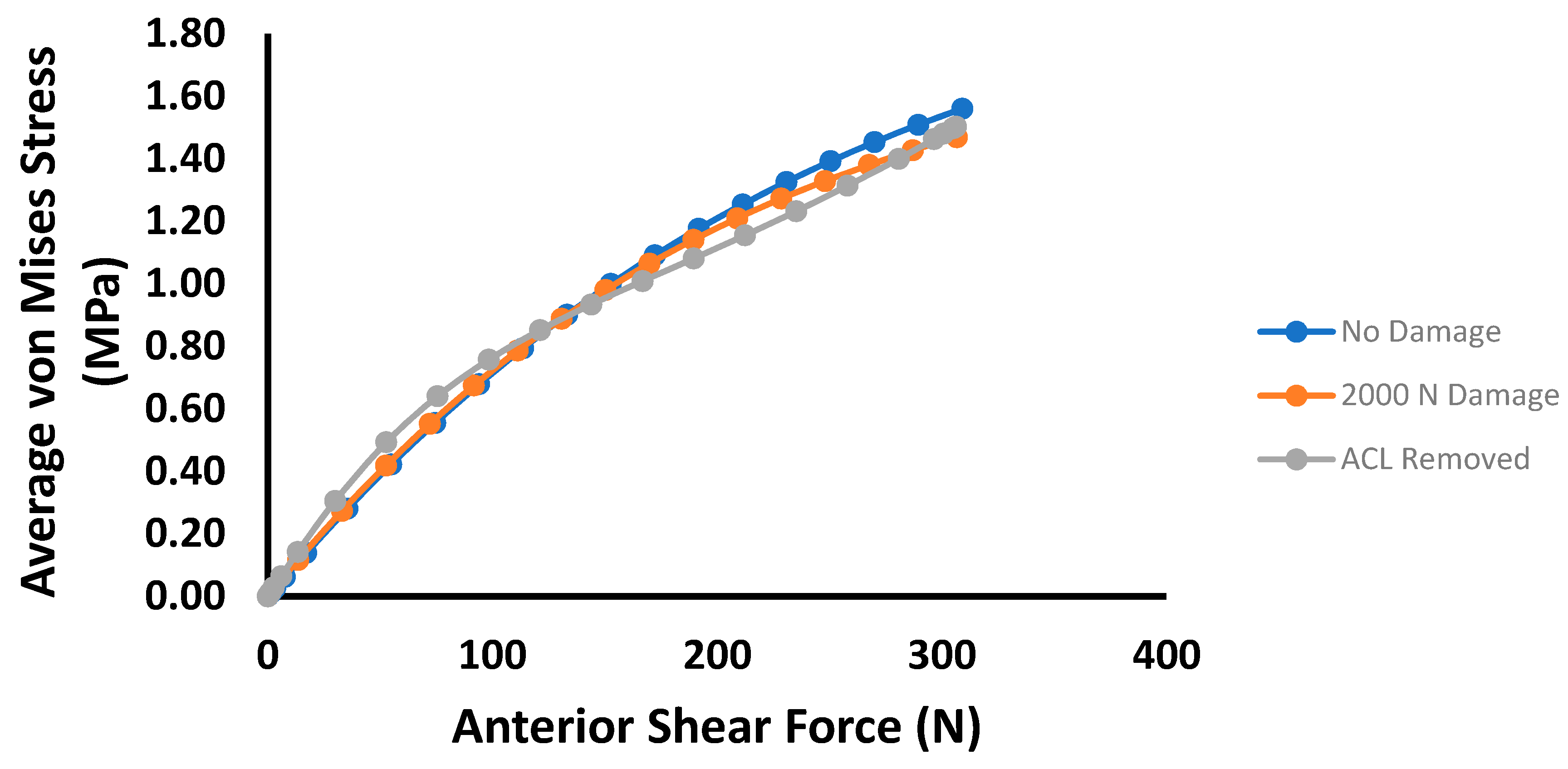
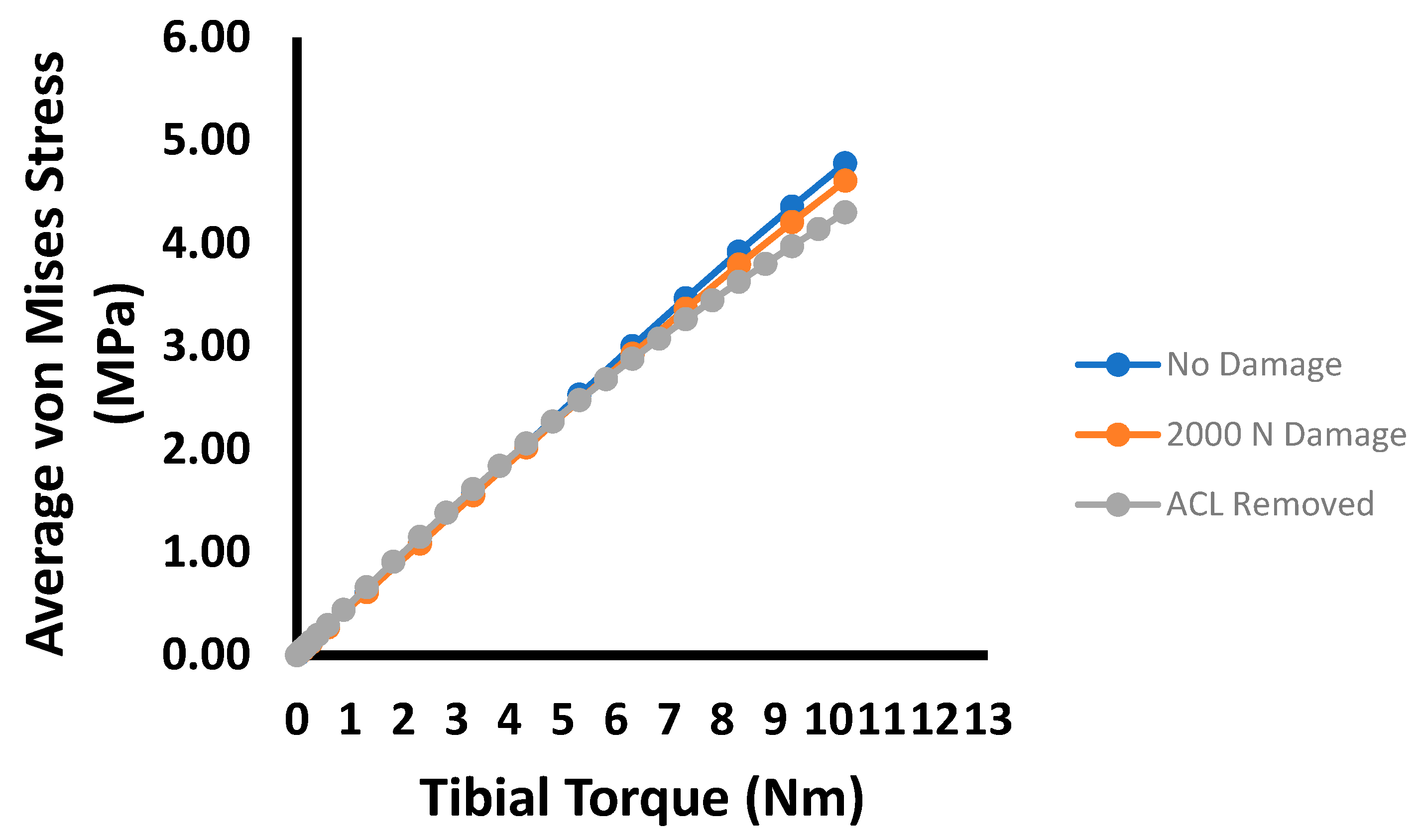
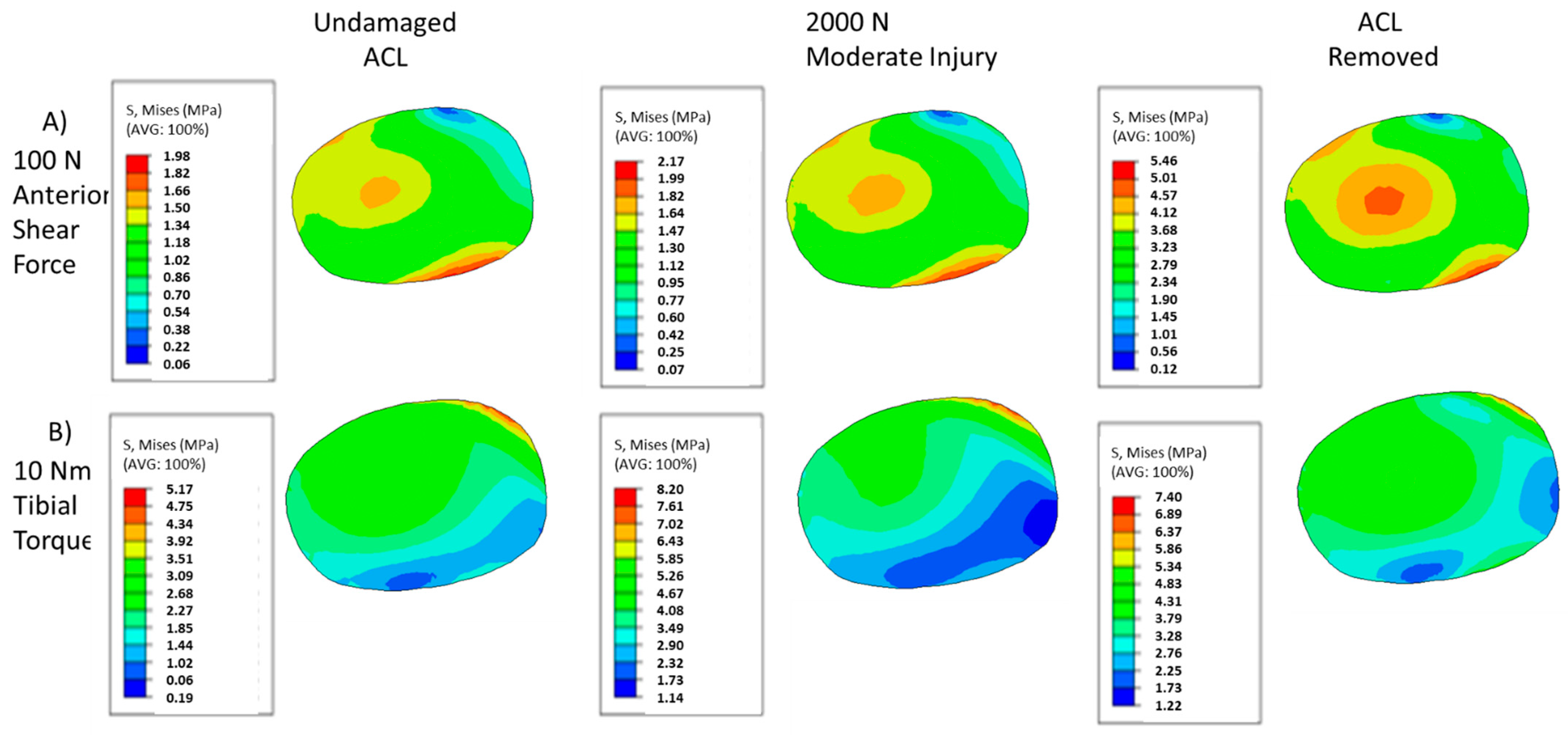
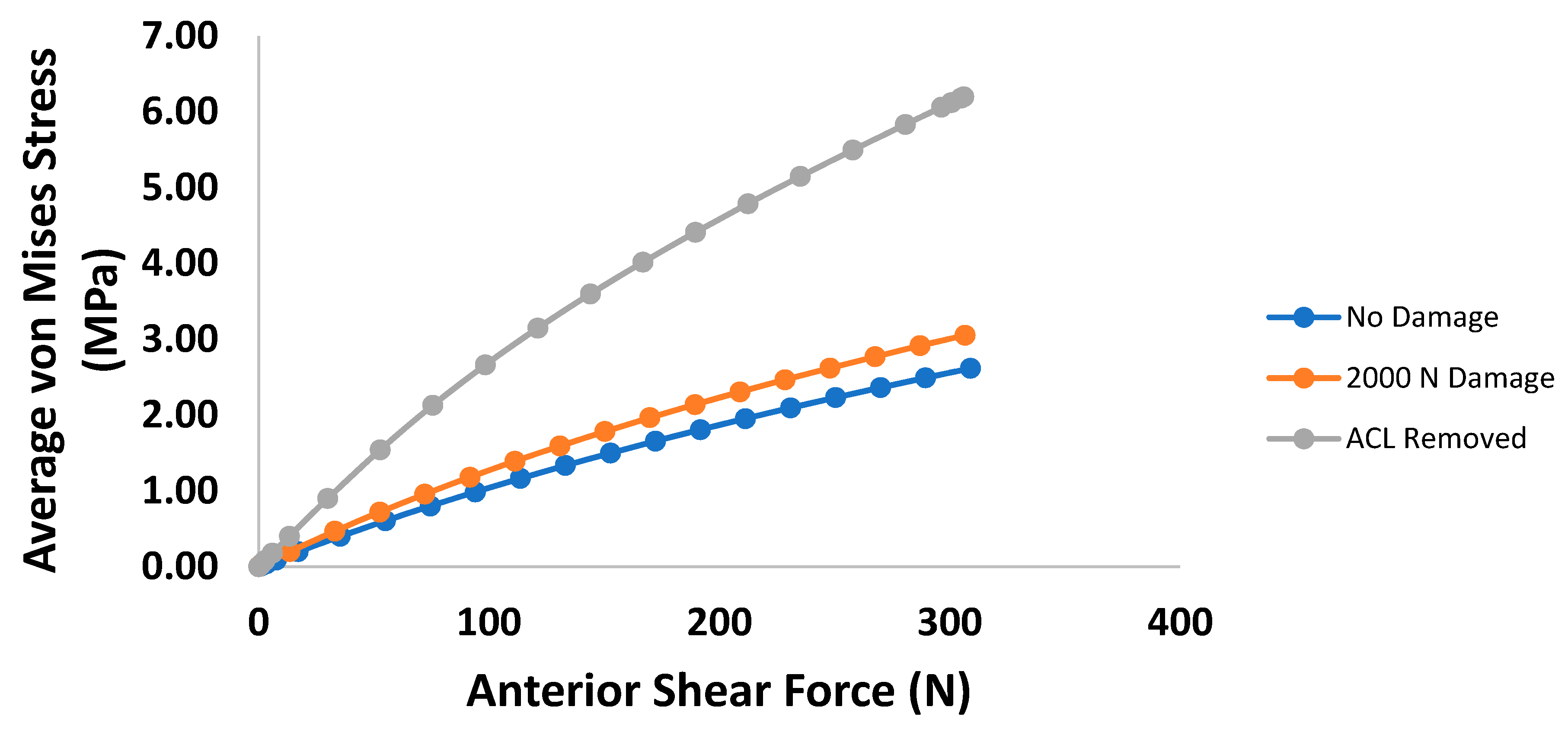
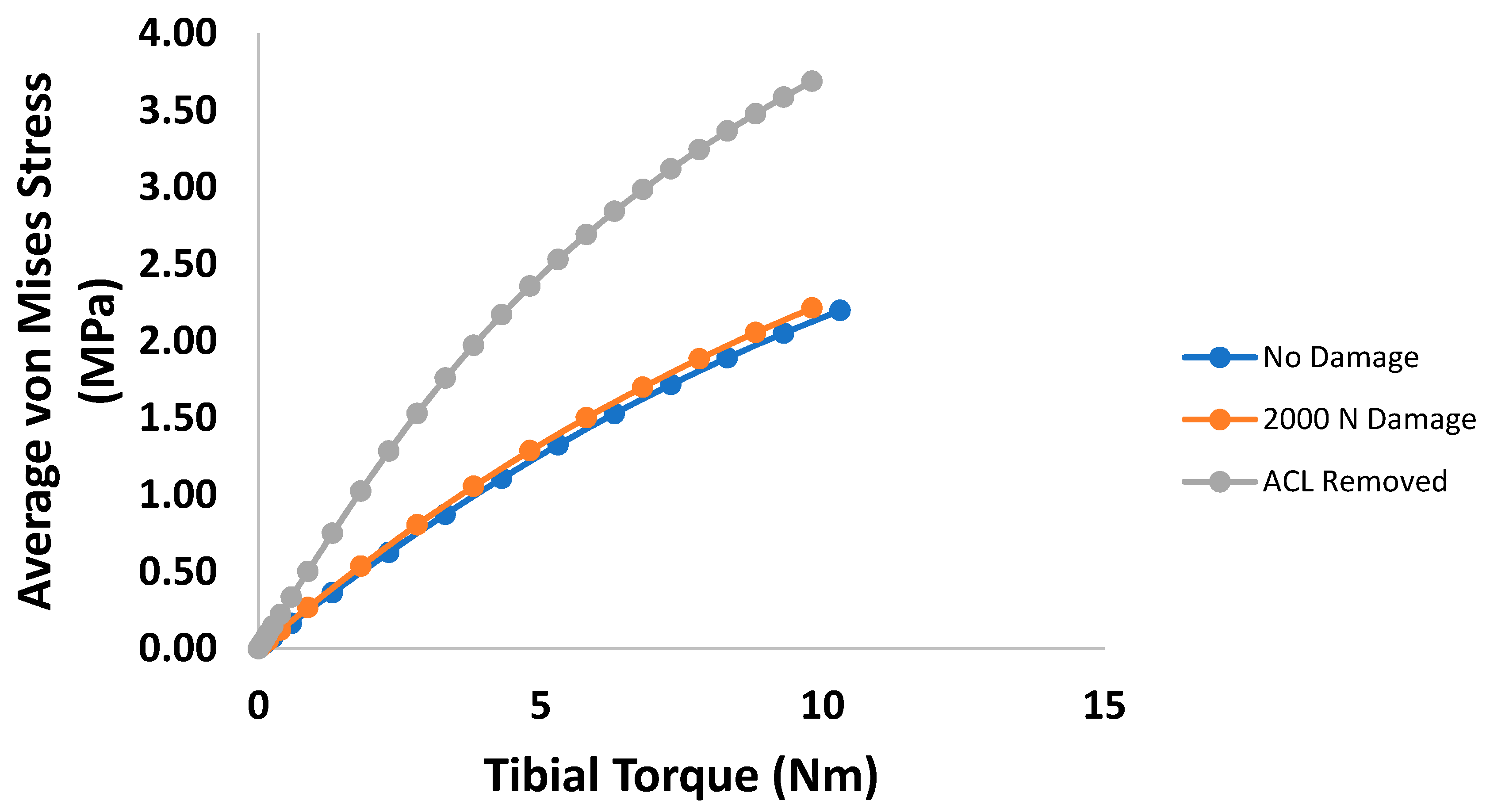
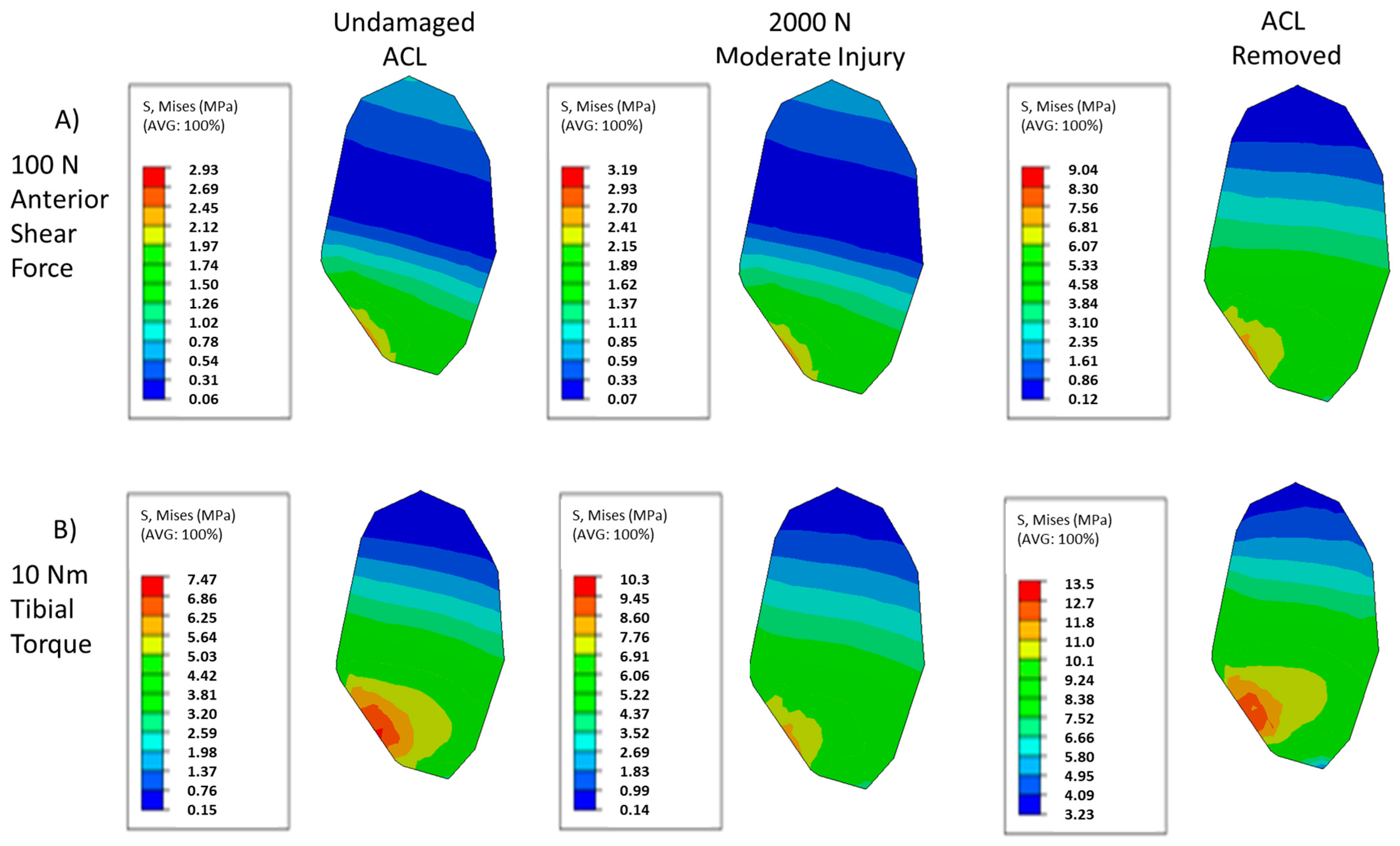
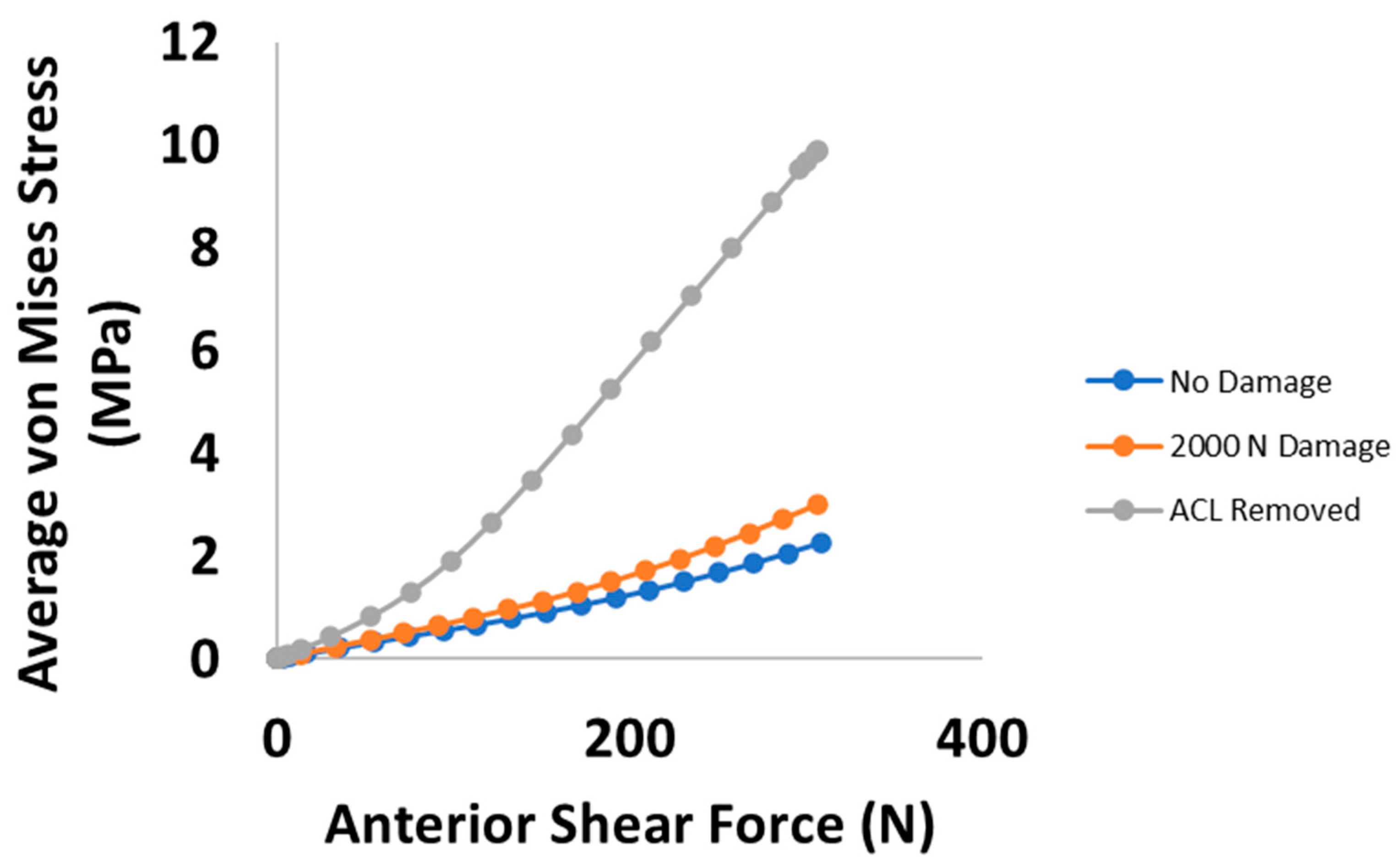
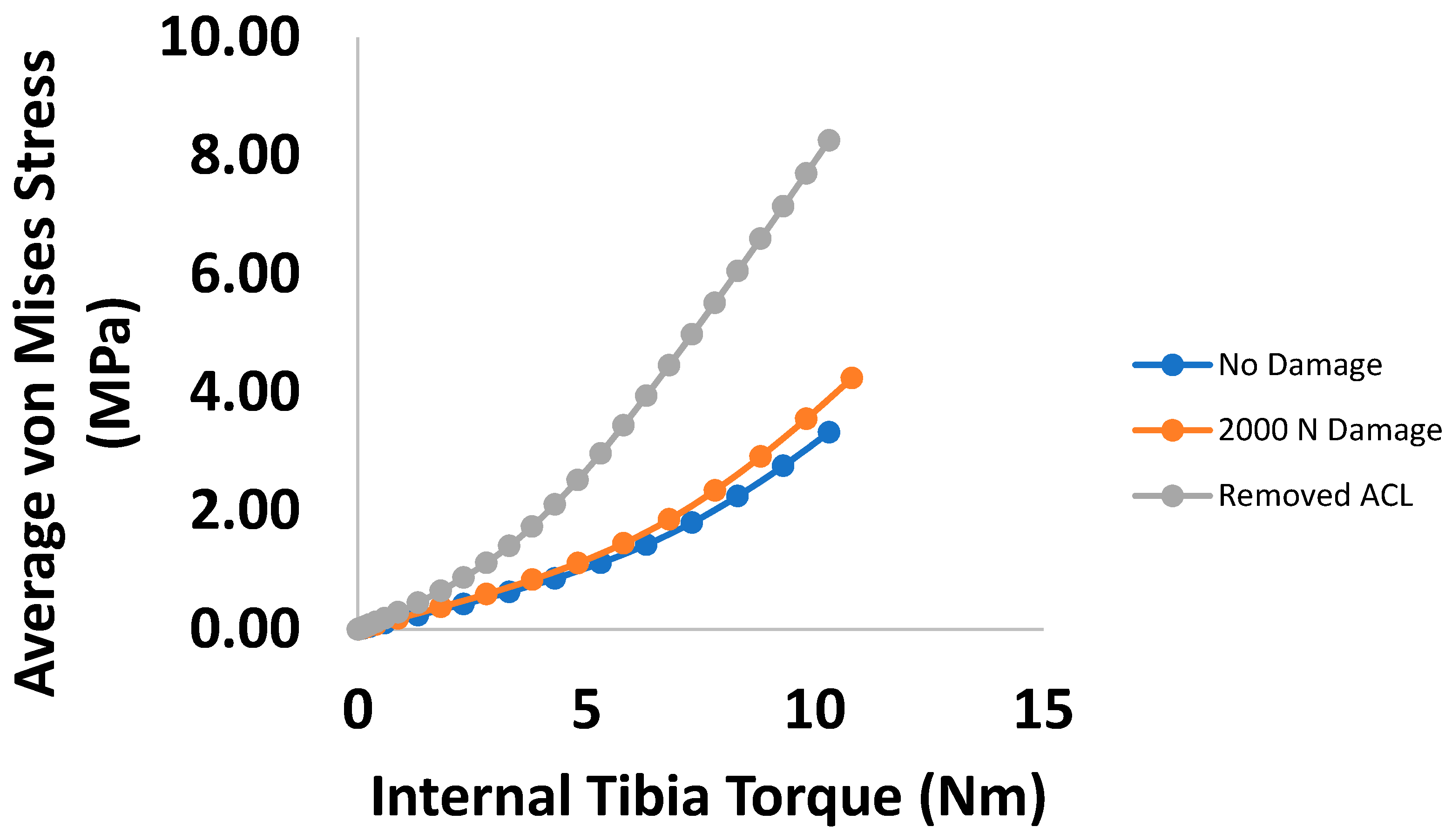
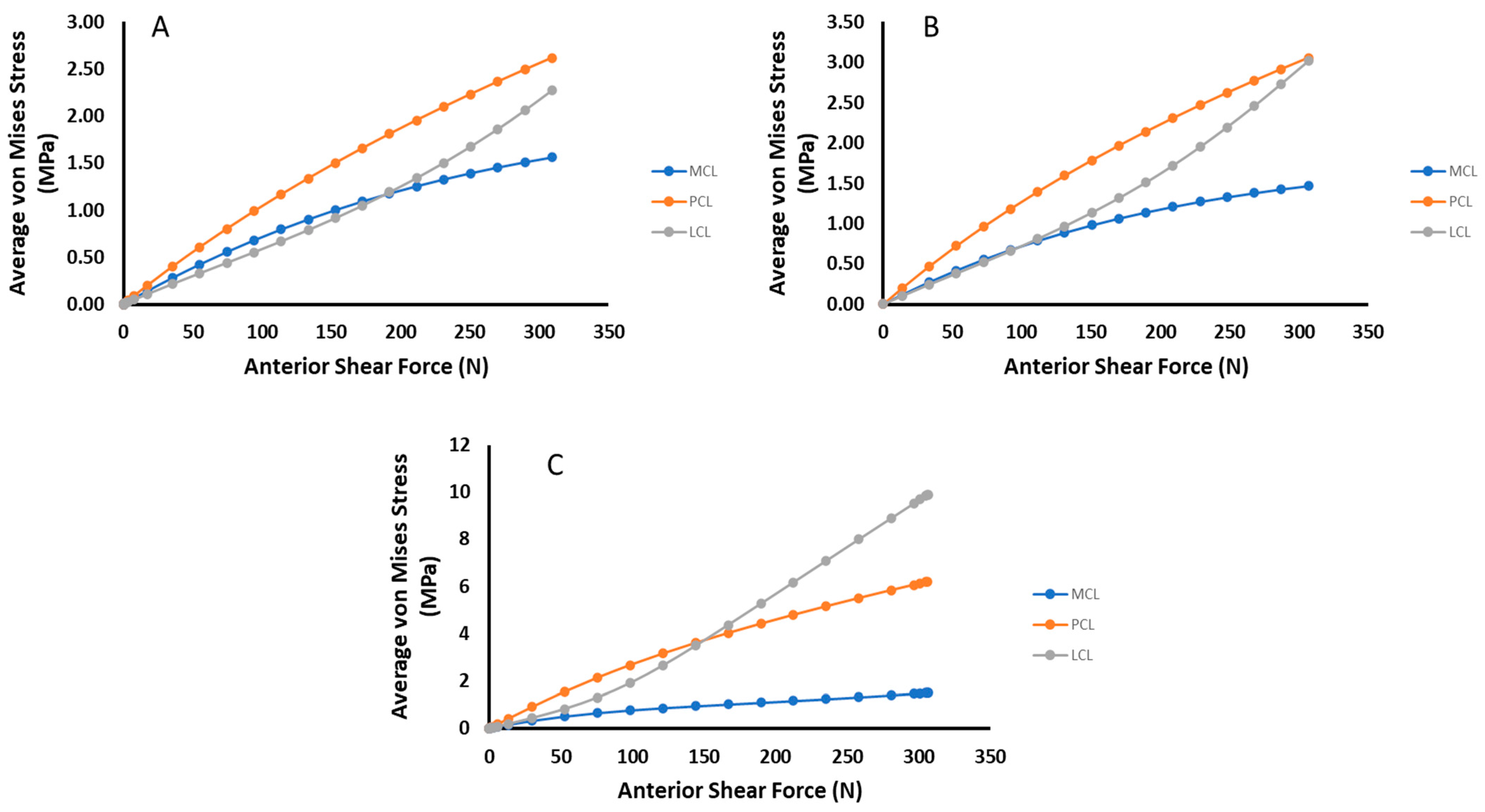
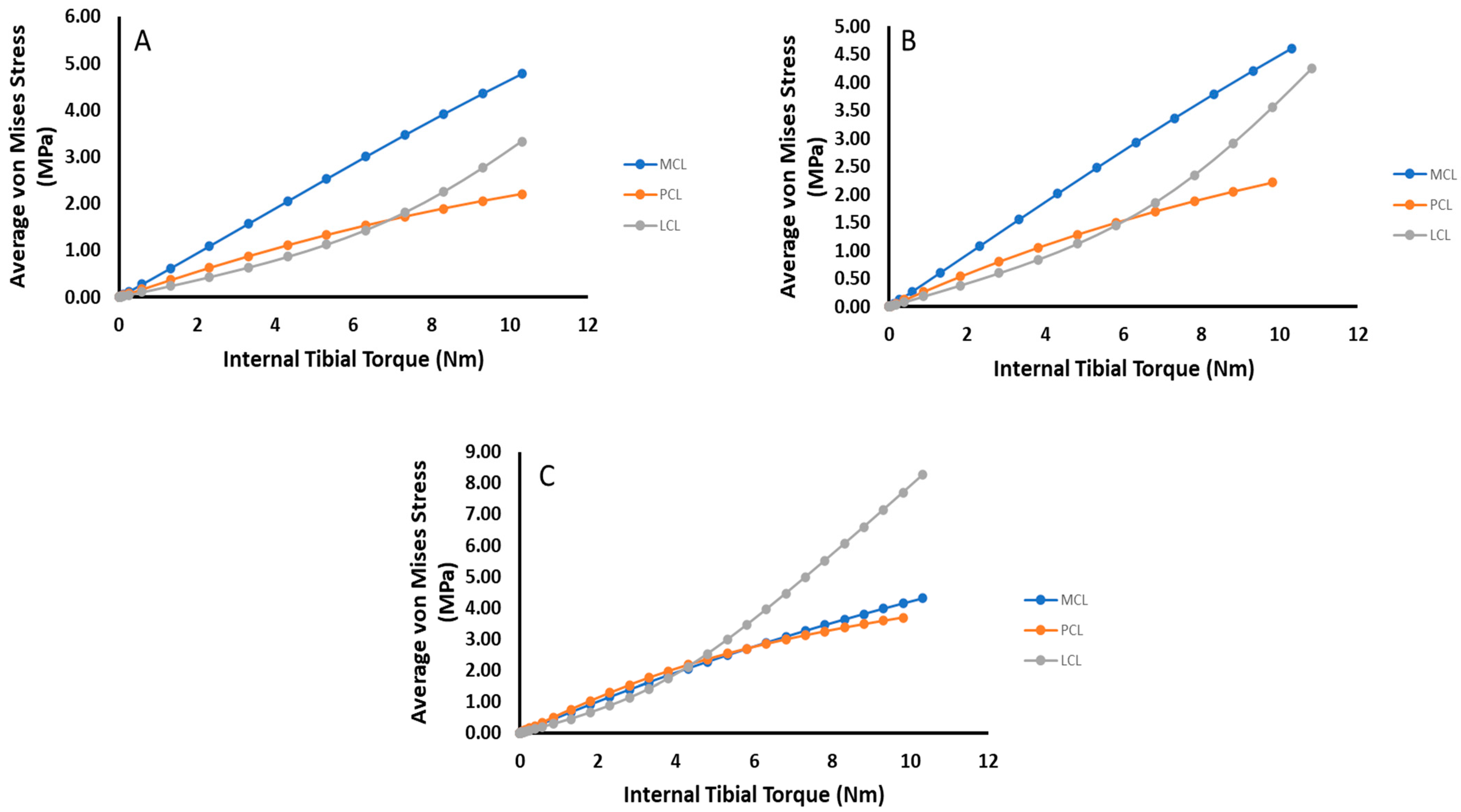
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mclean, S.G.; Mallett, K.F.; Arruda, E.M. Deconstructing the Anterior Cruciate Ligament: What We Know and Do Not Know About Function, Material Properties, and Injury Mechanics. J. Biomech. Eng. 2015, 137, 020906. [Google Scholar] [CrossRef] [PubMed]
- Rao, Z.; Zhou, C.; Kernkamp, W.A.; Foster, T.E.; Bedair, H.S.; Li, G. In Vivo Kinematics and Ligamentous Function of the Knee during Weight-Bearing Flexion: An Investigation on Mid-Range Flexion of the Knee. Knee Surg. Sports Traumatol. Arthrosc. 2020, 28, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Bendjaballah, M.; Shirazi-Adl, A.; Zukor, D. Finite Element Analysis of Human Knee Joint in Varus-Valgus. Clin. Biomech. 1997, 12, 139–148. [Google Scholar] [CrossRef]
- Bendjaballah, M.Z.; Shirazi-Adl, A.; Zukor, D.J. Biomechanical Response of the Passive Human Knee Joint under Anterior-Posterior Forces. Clin. Biomech. 1998, 13, 625–633. [Google Scholar] [CrossRef]
- Benjaminse, A.; Gokeler, A.; van der Schans, C.P. Clinical Diagnosis of an Anterior Cruciate Ligament Rupture: A Meta-Analysis. J. Orthop. Sports Phys. Ther. 2006, 36, 267–288. [Google Scholar] [CrossRef] [PubMed]
- LaBella, C.R.; Hennrikus, W.; Hewett, T.E.; Brenner, J.S.; Brooks, A.; Demorest, R.A.; Halstead, M.E.; Weiss Kelly, A.K.; Koutures, C.G.; LaBotz, M.; et al. Anterior Cruciate Ligament Injuries: Diagnosis, Treatment, and Prevention. Pediatrics 2014, 133, e1437–e1450. [Google Scholar] [CrossRef] [Green Version]
- Allen, C.R.; Livesay, G.A.; Wong, E.K.; Woo, S.L. Injury and Reconstruction of the Anterior Cruciate Ligament and Knee Osteoarthritis. Osteoarthr. Cartil. 1999, 7, 110–121. [Google Scholar] [CrossRef] [Green Version]
- Simon, D.; Mascarenhas, R.; Saltzman, B.M.; Rollins, M.; Bach, B.R.; MacDonald, P. The Relationship between Anterior Cruciate Ligament Injury and Osteoarthritis of the Knee. Adv. Orthop. 2015, 2015, 928301. [Google Scholar] [CrossRef]
- Shekarforoush, M.; Beveridge, J.E.; Hart, D.A.; Frank, C.B.; Shrive, N.G. Correlation between Translational and Rotational Kinematic Abnormalities and Osteoarthritis-like Damage in Two in Vivo Sheep Injury Models. J. Biomech. 2018, 75, 67–76. [Google Scholar] [CrossRef]
- Kwon, O.S.; Purevsuren, T.; Kim, K.; Park, W.M.; Kwon, T.K.; Kim, Y.H. Influence of Bundle Diameter and Attachment Point on Kinematic Behavior in Double Bundle Anterior Cruciate Ligament Reconstruction Using Computational Model. Comput. Math. Methods Med. 2014, 2014, 948292. [Google Scholar] [CrossRef]
- DeMorat, G.; Weinhold, P.; Blackburn, T.; Chudik, S.; Garrett, W. Aggressive Quadriceps Loading Can Induce Noncontact Anterior Cruciate Ligament Injury. Am. J. Sports Med. 2004, 32, 477–483. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Suggs, J.; Gill, T. The Effect of Anterior Cruciate Ligament Injury on Knee Joint Function under a Simulated Muscle Load: A Three-Dimensional Computational Simulation. Ann. Biomed. Eng. 2002, 30, 713–720. [Google Scholar] [CrossRef] [PubMed]
- Rahemi, H.; Farahmand, F.; Rezaeian, T.; Parnianpour, M. Computer simulation of knee arthrometry to study the effects of partial ACL injury and tibiofemoral contact. In Proceedings of the 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS’08—Personalized Healthcare through Technology, Vancouver, BC, Canada, 20–24 August 2008; pp. 895–898. [Google Scholar] [CrossRef]
- Ochi, M.; Murao, T.; Sumen, Y.; Kobayashi, K.; Adachi, N. Isolated Posterior Cruciate Ligament Insufficiency Induces Morphological Changes of Anterior Cruciate Ligament Collagen Fibrils. Arthroscopy 1999, 15, 292–296. [Google Scholar] [CrossRef]
- Moglo, K.E.; Shirazi-Adl, A. On the Coupling between Anterior and Posterior Cruciate Ligaments, and Knee Joint Response under Anterior Femoral Drawer in Flexion: A Finite Element Study. Clin. Biomech. 2003, 18, 751–759. [Google Scholar] [CrossRef]
- Lujan, T.J.; Dalton, M.S.; Thompson, B.M.; Ellis, B.J.; Weiss, J.A.; Lujan, A. Effect of ACL Deficiency on MCL Strains and Joint Kinematics. J. Biomech. Eng. 2006, in press. Available online: https://www.sci.utah.edu/publications/lujan06/lujan_jbme_2007.pdf (accessed on 15 May 2019). [CrossRef]
- Noyes, F.; Torvik, P. Biomechanics of Anterior Cruciate Ligament Failure: An Analysis of Strain-Rate Sensitivity and Mechanisms of Failure in Primates. J. Bone Jt. Surg. Am. 1974, 56, 236–253. [Google Scholar] [CrossRef]
- Panjabi, M.M.; Yoldas, E.; Oxland, T.R.; Crisco, J.J. Subfailure Injury of the Rabbit Anterior Cruciate Ligament. Orthop. Res. Soc. 1996, 14, 216–222. [Google Scholar] [CrossRef]
- Provenzano, P.P.; Heisey, D.; Hayashi, K.; Lakes, R.; Vanderby, R. Subfailure Damage in Ligament: A Structural and Cellular Evaluation. J. Appl. Physiol. 2002, 92, 362–371. [Google Scholar] [CrossRef] [Green Version]
- Quinn, K.P.; Winkelstein, B.A. Altered Collagen Fiber Kinematics Define the Onset of Localized Ligament Damage during Loading. J. Appl. Physiol. 2008, 105, 1881–1888. [Google Scholar] [CrossRef]
- Gasser, T.C.; Ogden, R.W.; Holzapfel, G.A. Hyperelastic Modelling of Arterial Layers with Distributed Collagen Fibre Orientations. J. R. Soc. Interface 2006, 3, 15–35. [Google Scholar] [CrossRef]
- McLean, J.P.; Gan, Y.; Lye, T.H.; Qu, D.; Lu, H.H.; Hendon, C.P. High-Speed Collagen Fiber Modeling and Orientation Quantification for Optical Coherence Tomography Imaging. Opt. Express 2019, 27, 14457. [Google Scholar] [CrossRef] [PubMed]
- Natali, A.; Pavan, P.; Dorow, C. A Transversally Isotropic Elasto-Damage Constitutive Model for the Periodontal Ligament. Comput. Methods Biomech. Biomed. Eng. 2003, 6, 329–336. [Google Scholar] [CrossRef] [PubMed]
- Natali, A.N.; Pavan, P.G.; Carniel, E.L.; Lucisano, M.E.; Taglialavoro, G. Anisotropic Elasto-Damage Constitutive Model for the Biomechanical Analysis of Tendons. Med. Eng. Phys. 2005, 27, 209–214. [Google Scholar] [CrossRef] [PubMed]
- Ristaniemi, A.; Stenroth, L.; Mikkonen, S.; Korhonen, R.K. Comparison of Elastic, Viscoelastic and Failure Tensile Material Properties of Knee Ligaments and Patellar Tendon. J. Biomech. 2018, 79, 31–38. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- SIMULIA, 2019; Abaqus/CAE: Palo Alto, CA, USA, 2021.
- Rupin, F.; Saied, A.; Dalmas, D.; Peyrin, F.; Haupert, S.; Barthel, E.; Boivin, G.; Laugier, P. Experimental Determination of Young Modulus and Poisson Ratio in Cortical Bone Tissue Using High Resolution Scanning Acoustic Microscopy and Nanoindentation. J. Acoust. Soc. Am. 2008, 123, 3785. [Google Scholar] [CrossRef]
- NIH. U.S. National Library of Medicine National Institutes of Health. Available online: https://www.nlm.nih.gov/research/visible/visible_human.html (accessed on 15 May 2019).
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An Open-Source Platform for Biological-Image Analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wan, C.; Hao, Z.; Wen, S. The Joint Biomechanics Change by Different Anterior Cruciate Ligament Constitutive Models Under Axial Torque Load. Int. Mech. Eng. Congr. Expo. 2012, 45189, 423–428. [Google Scholar] [CrossRef]
- Wan, C.; Hao, Z.; Wen, S. The Effect of the Variation in ACL Constitutive Model on Joint Kinematics and Biomechanics Under Different Loads: A Finite Element Study. J. Biomech. Eng. 2013, 135, 0410021–0410029. [Google Scholar] [CrossRef]
- Ellis, B.J.; Lujan, T.J.; Dalton, M.S.; Weiss, J.A. Medial Collateral Ligament Insertion Site and Contact Forces in the ACL-Deficient Knee. J. Orthop. Res. 2006, 24, 800–810. [Google Scholar] [CrossRef]
- Engebretsen, L.; Lew, W.D.; Lewis, J.L.; Hunter, R.E. Knee Mechanics after Repair of the Anterior Cruciate Ligament a Cadaver Study of Ligament Augmentation. Acta Orthop. 1989, 60, 703–709. [Google Scholar] [CrossRef] [Green Version]
- Gobbi, A.; Herman, K.; Grabowski, R.; Szwedowski, D. Primary Anterior Cruciate Ligament Repair With Hyaluronic Scaffold and Autogenous Bone Marrow Aspirate Augmentation in Adolescents With Open Physes. Arthrosc. Tech. 2019, 8, e1561–e1568. [Google Scholar] [CrossRef] [PubMed]
- Pailhé, R.; Cavaignac, E.; Murgier, J.; Laffosse, J.-M.; Swider, P. Biomechanical Study of ACL Reconstruction Grafts. J. Orthop. Res. 2015, 33, 1188–1196. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Richardson, M.W.; Tsouris, N.D.; Hassan, C.R.; Elbayar, J.H.; Qin, Y.-X.; Komatsu, D.E.; Rizzi, A.V.; Paci, J.M. A Biomechanical Comparison of Alternative Graft Preparations for All-Inside Anterior Cruciate Ligament Reconstruction. Arthrosc. J. Arthrosc. Relat. Surg. 2019, 35, 1547–1554. [Google Scholar] [CrossRef] [PubMed]
- Yaru, N.C.; Daniel, D.M.; Penner, D. The Effect of Tibial Attachment Site on Graft Impingement in an Anterior Cruciate Ligament Reconstruction. Am. J. Sports Med. 1992, 20, 217–220. [Google Scholar] [CrossRef] [PubMed]
| C1 (Pa) | D | K1 (Pa) | K2 | k | λ0 | λc | β |
|---|---|---|---|---|---|---|---|
| 5,000,000 | 1 × 10–9 | 20,600,000 | 0.201 | 0 | 1.183 | 1.35 | 0.00019 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Knapp, A.; Williams, L.N. Predicting the Effect of Localized ACL Damage on Neighbor Ligament Mechanics via Finite Element Modeling. Bioengineering 2022, 9, 54. https://doi.org/10.3390/bioengineering9020054
Knapp A, Williams LN. Predicting the Effect of Localized ACL Damage on Neighbor Ligament Mechanics via Finite Element Modeling. Bioengineering. 2022; 9(2):54. https://doi.org/10.3390/bioengineering9020054
Chicago/Turabian StyleKnapp, Alexander, and Lakiesha N. Williams. 2022. "Predicting the Effect of Localized ACL Damage on Neighbor Ligament Mechanics via Finite Element Modeling" Bioengineering 9, no. 2: 54. https://doi.org/10.3390/bioengineering9020054
APA StyleKnapp, A., & Williams, L. N. (2022). Predicting the Effect of Localized ACL Damage on Neighbor Ligament Mechanics via Finite Element Modeling. Bioengineering, 9(2), 54. https://doi.org/10.3390/bioengineering9020054





