Investigation on the Modeling and Reconstruction of Head Injury Accident Using ABAQUS/Explicit
Abstract
1. Introduction
2. Methodology
2.1. FE Human Head Model
2.2. Material Properties
2.3. Numerical Algorithm
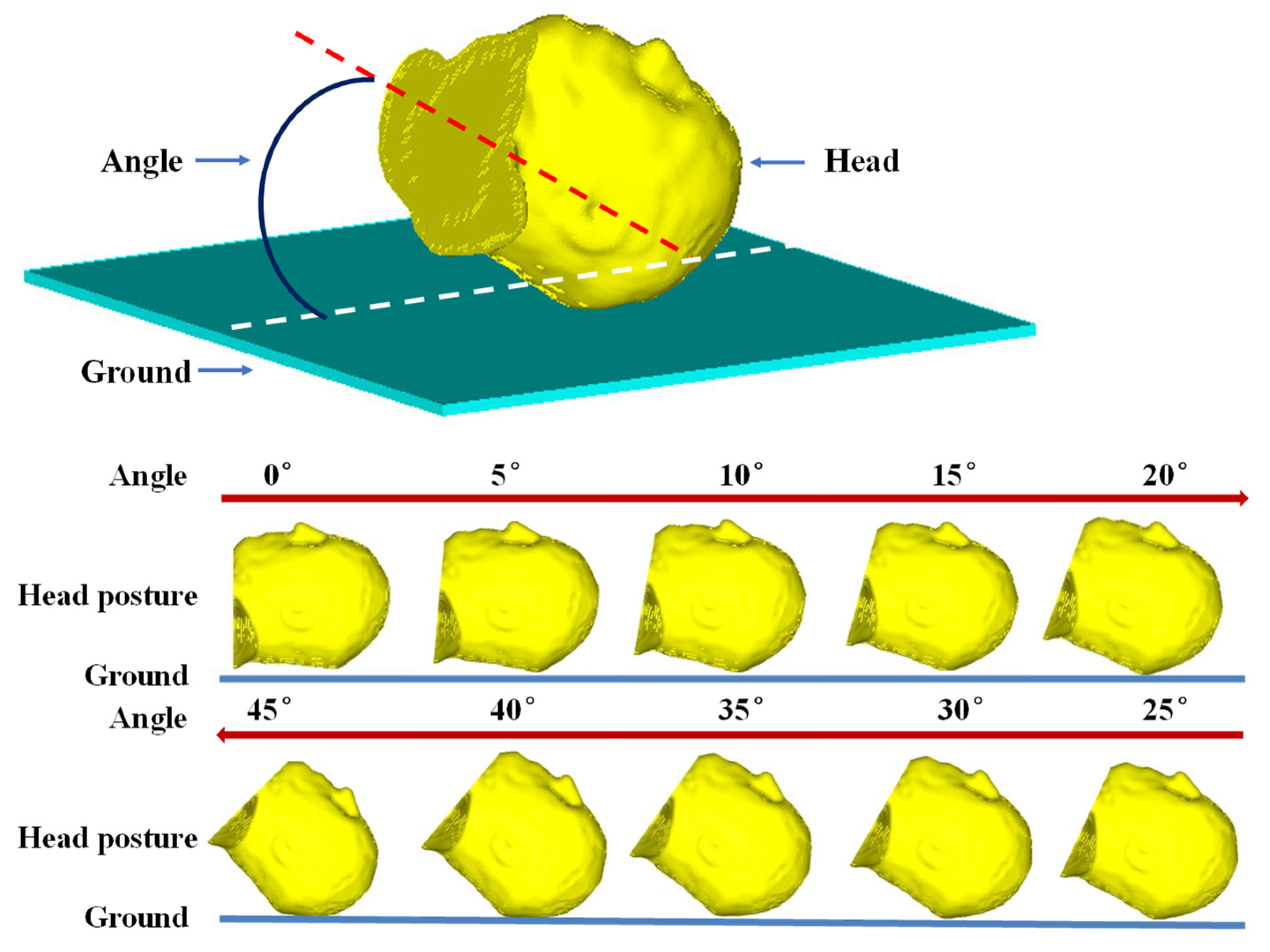
2.4. Head–Ground Impact Simulations
2.5. Head Injury Threshold Criteria
3. Results
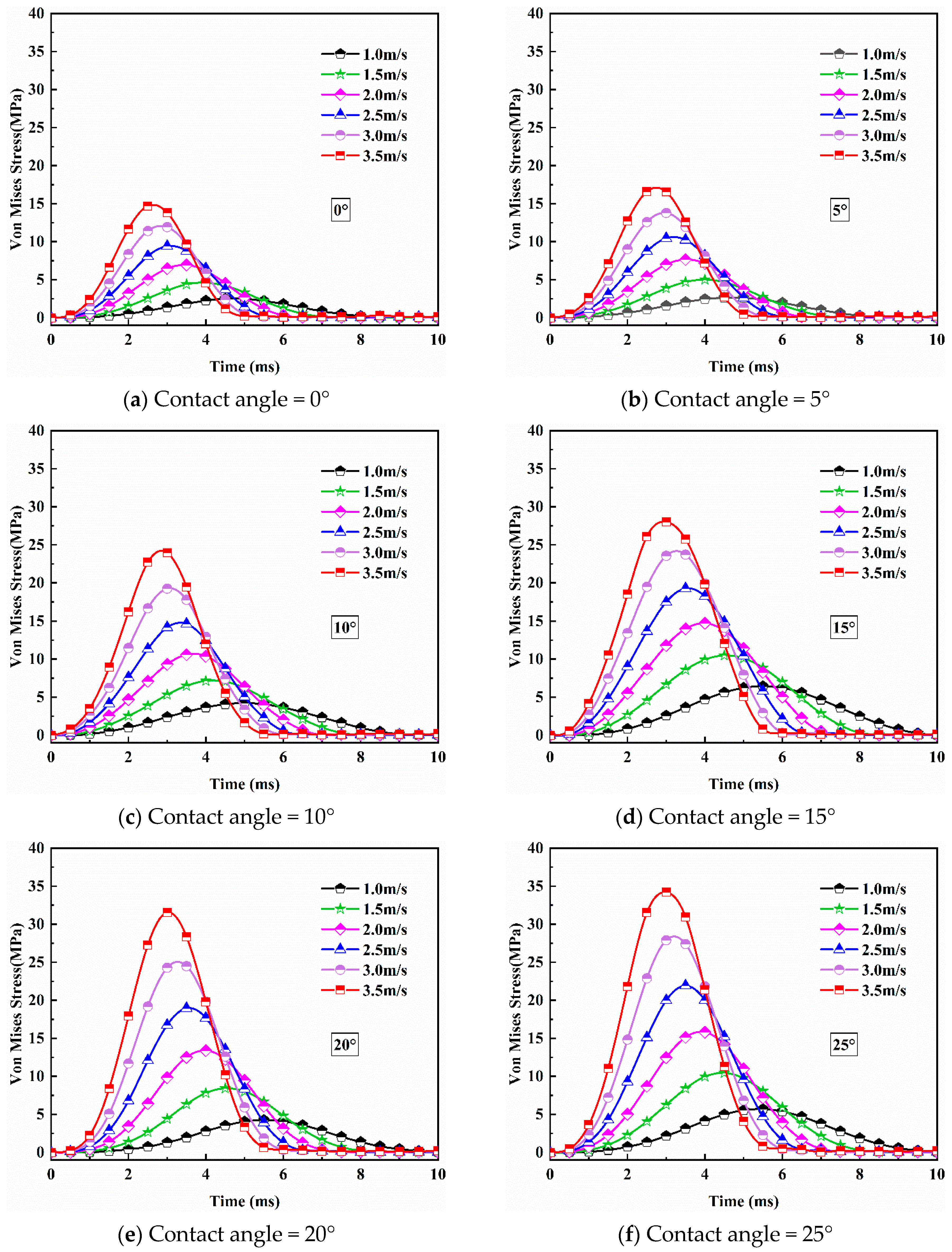
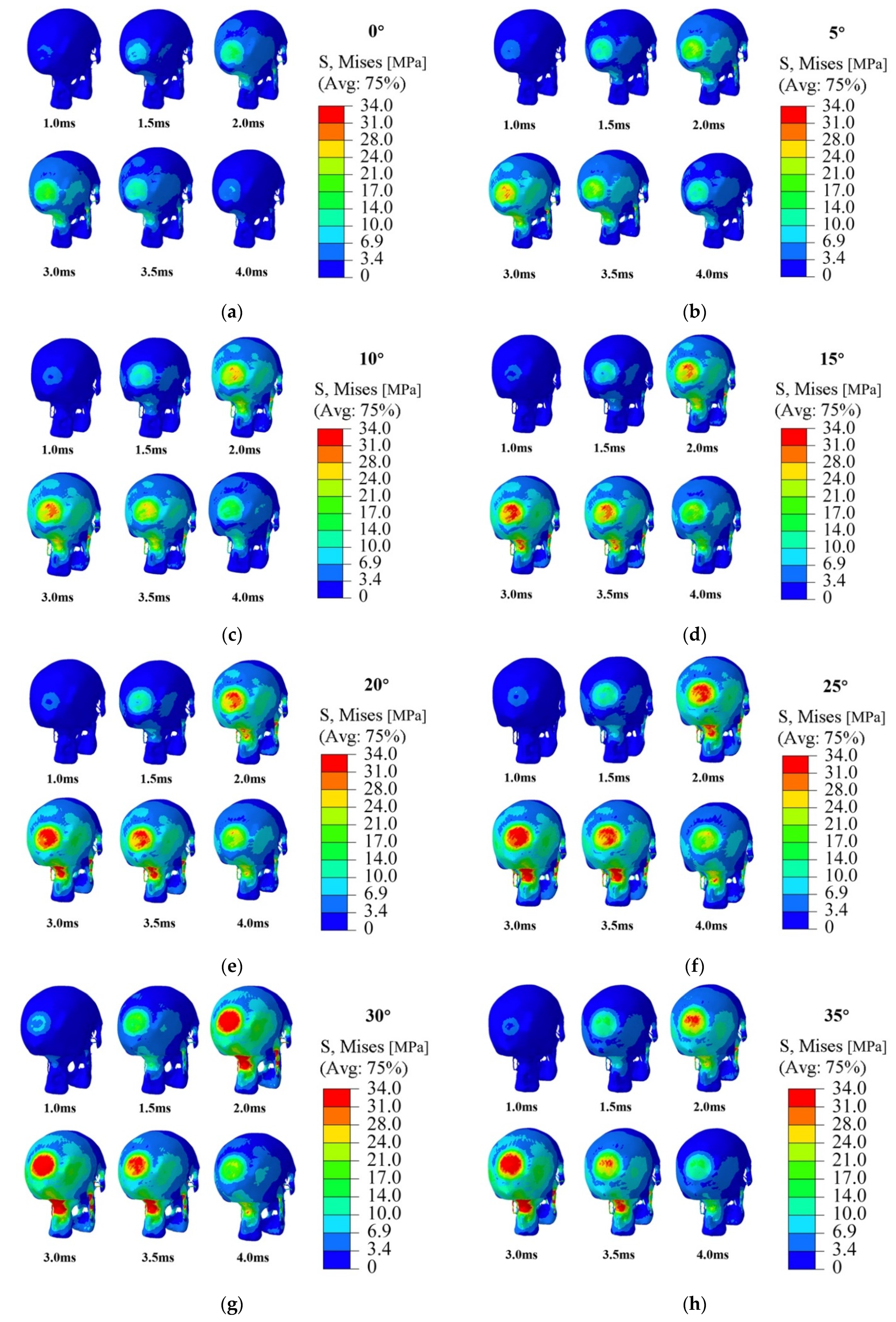
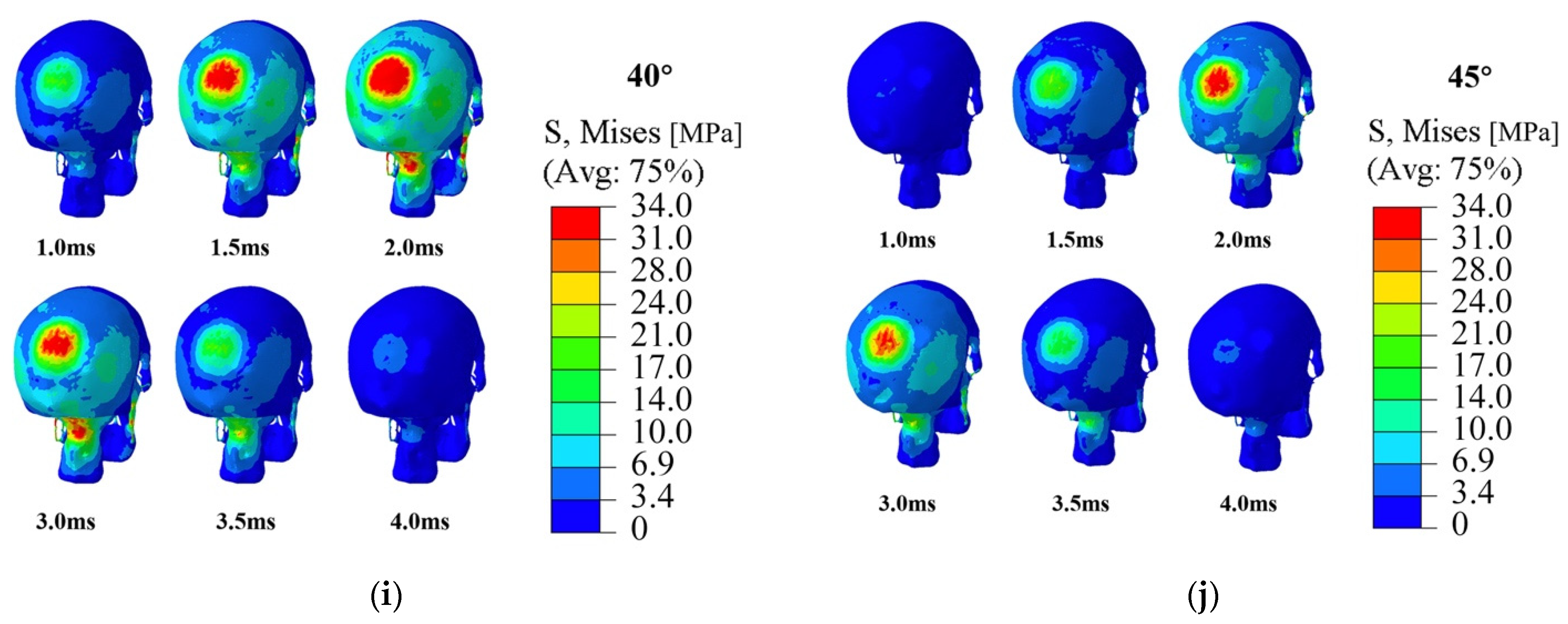
3.1. Skull Injury under Different Impact Conditions
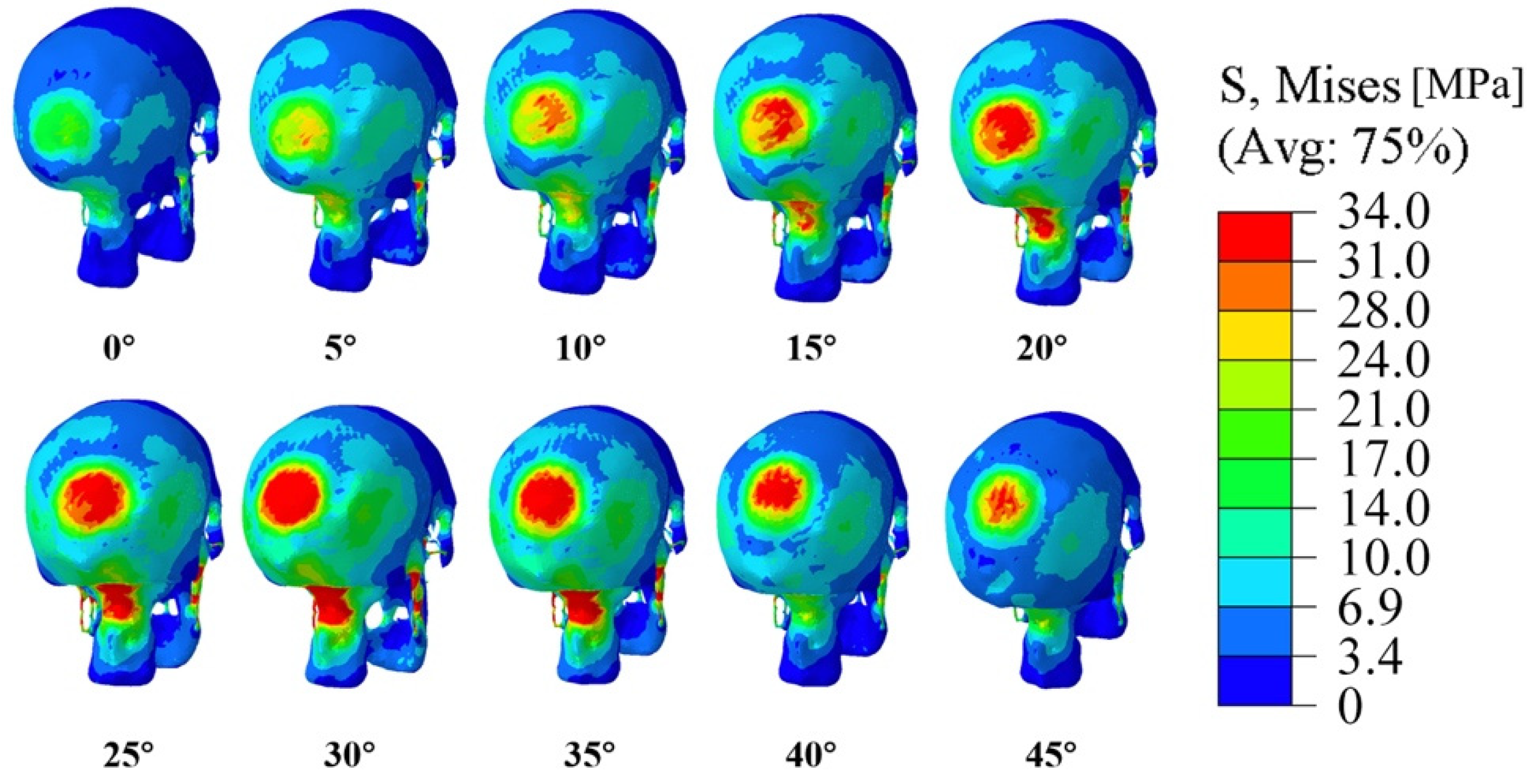
3.2. Effects of Impact Angle on Peak Stress Value of the Skull
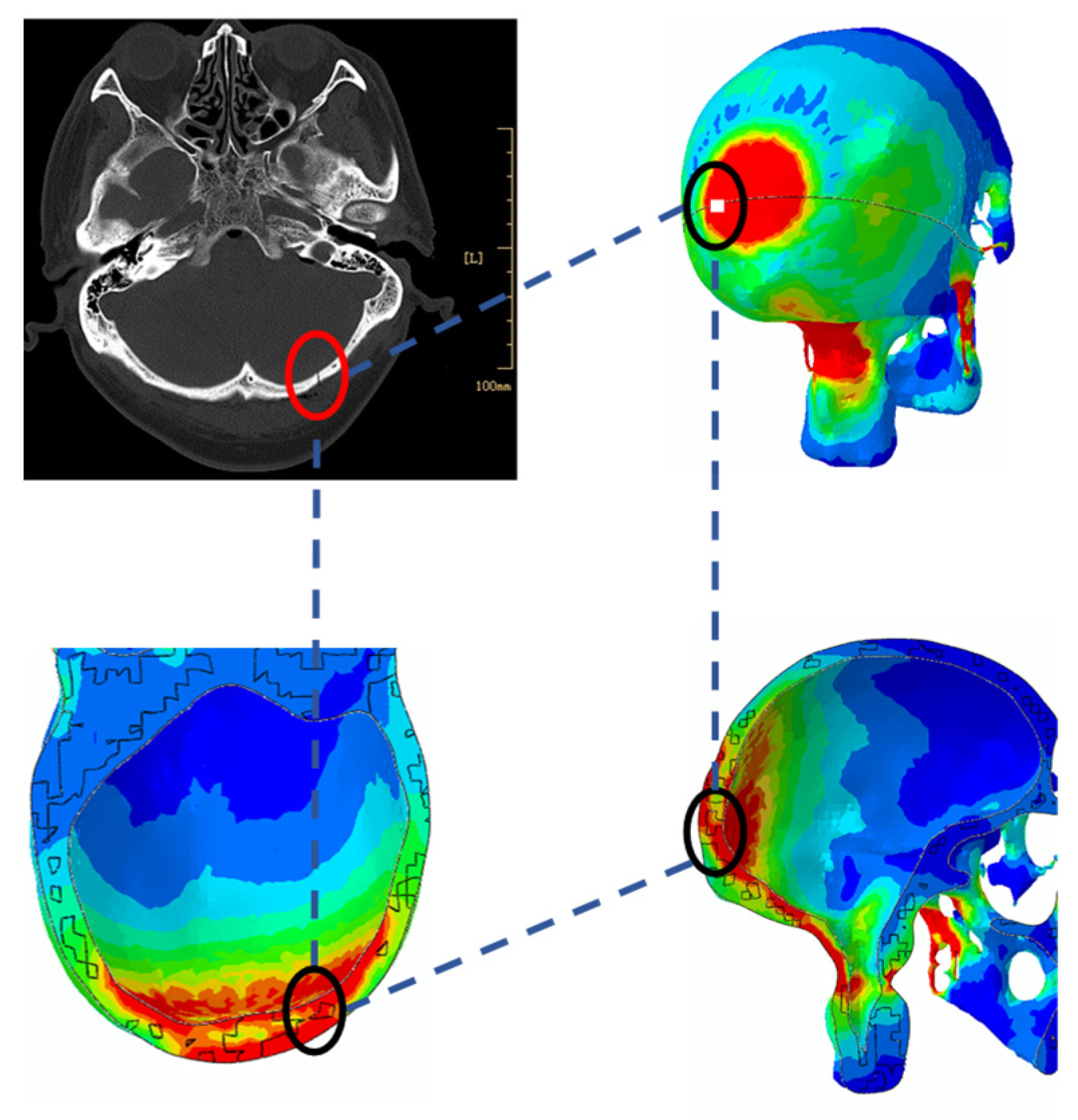
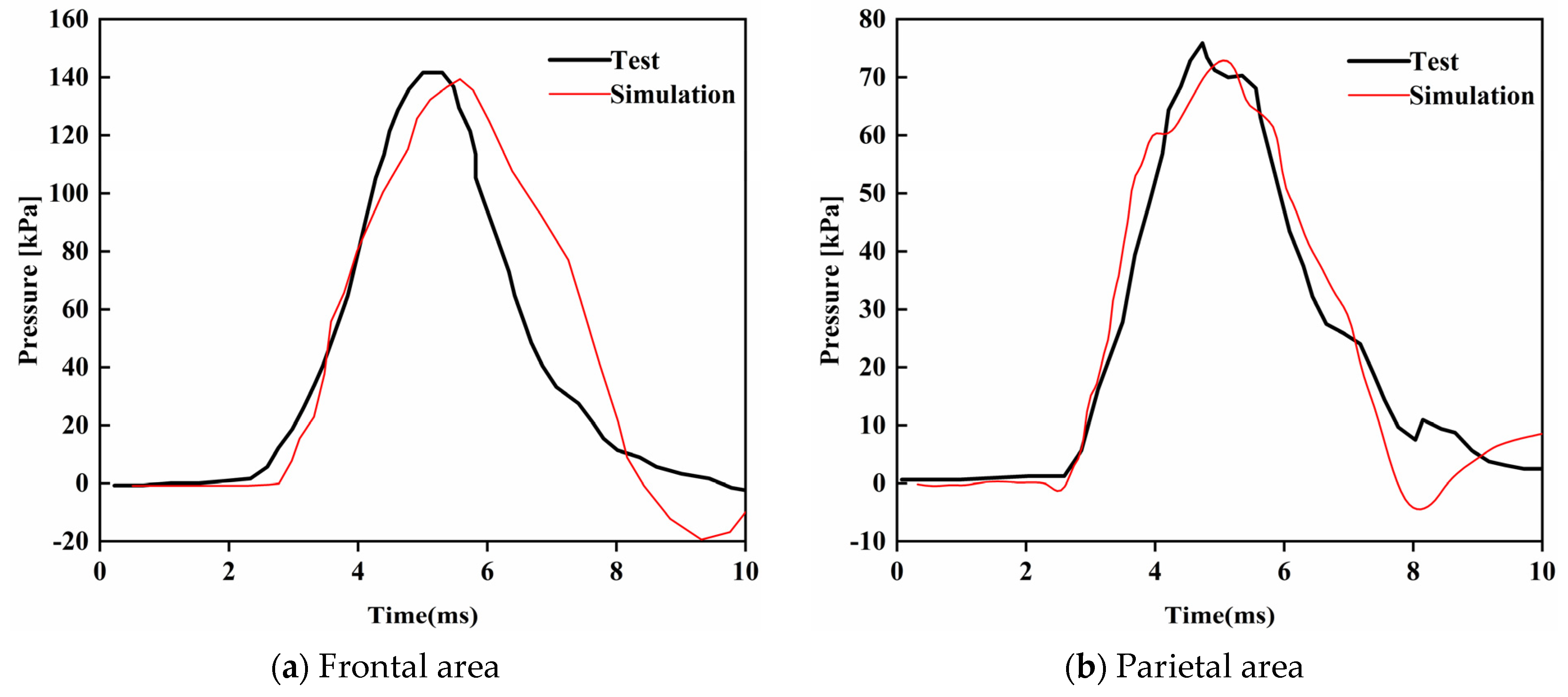
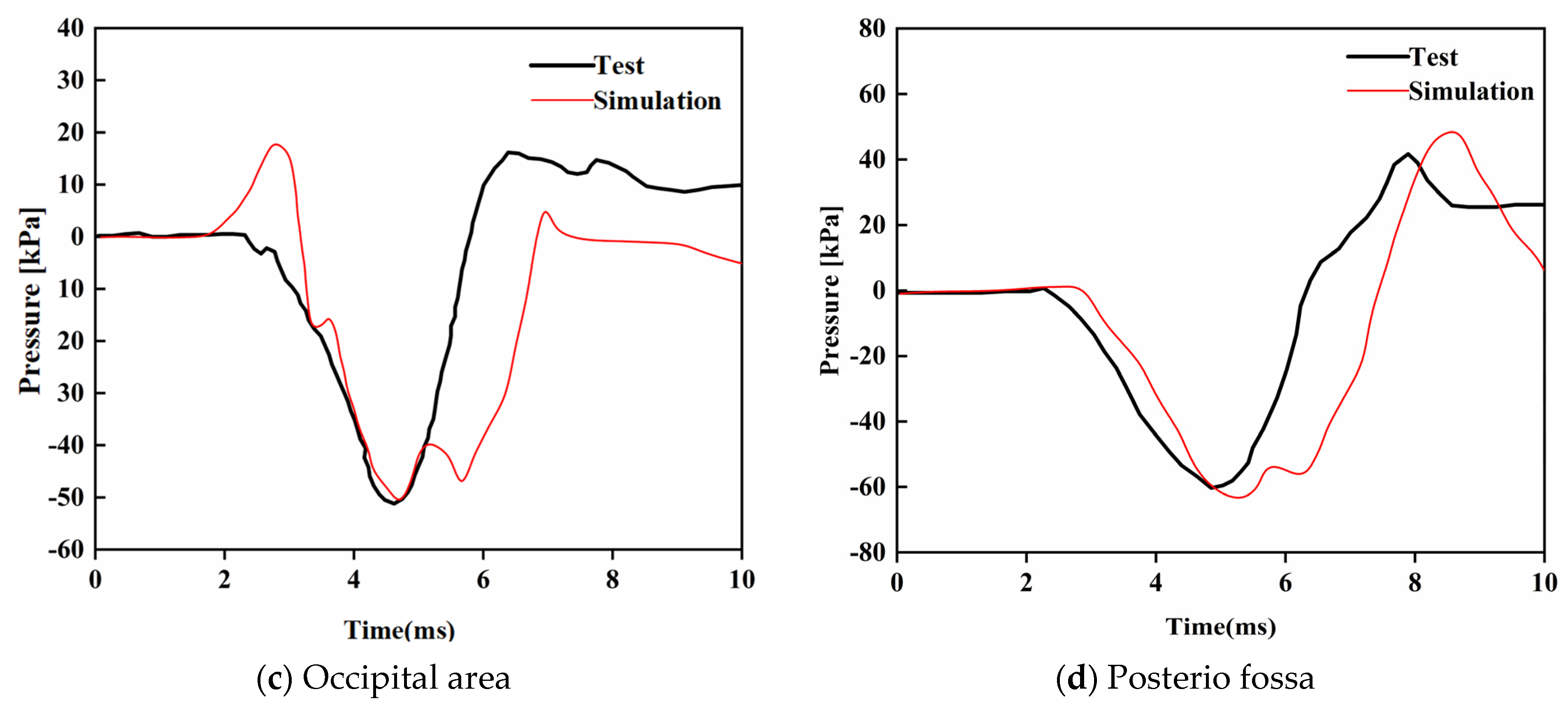
4. Validation
5. Discussion
6. Conclusions
- (1)
- At the same impact speed, the maximum peak von Mises stress is reached when the contact angle is 30°.
- (2)
- The maximum peak stress increases as the impact speed increases and when the impact speed is 3.5 m/s at the contact angle of 30°, the peak stress generated at the impact exceeds the threshold value and would cause the skull to fracture.
- (3)
- FE methods are a powerful tool for reconstructing scenes of traffic crashes and reproducing impact processes in a time- and cost-effective manner. The combination of the FE methods and experimental data can reveal valuable insights into traffic crashes and assist forensic analysts in identifying the responsibilities of involved parties and revealing the courses of accidents.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Health Organization. Global Status Report on Road Safety 2018; World Health Organization: Geneva, Switzerland, 2018. [Google Scholar]
- Cory, C.Z.; Jones, M.D.; James, D.S.; Leadbeatter, S.; Nokes, L.D.M. The potential and limitations of utilising head impact injury models to assess the likelihood of significant head injury in infants after a fall. Forensic Sci. Int. 2001, 123, 89–106. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Peng, Y.; Yang, J.; Otte, D.; Wang, B. A study on correlation of pedestrian head injuries with physical parameters using in-depth traffic accident data and mathematical models. Accid. Anal. Prev. 2018, 119, 91–103. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.H.; Mao, H. Modeling of the Brain for Injury Simulation and Prevention. In Biomechanics of the Brain; Springer: Berlin/Heidelberg, Germany, 2011; pp. 91–110. [Google Scholar]
- Li, S.-Q.; Peng, Y.-L.; Xiao, L.-Y.; Meng, S.-M.; Wang, P.; Xu, J.-P. Analysis of the mechanism of the road traffic accidents in-situ and the future research trends. J. Saf. Environ. 2014, 14, 14–19. [Google Scholar]
- Deng, X.-Q.; Potula, S.; Grewal, H.; Solanki, K.N.; Tschopp, M.A.; Horstemeyer, M.F. Finite element analysis of occupant head injuries: Parametric effects of the side curtain airbag deployment interaction with a dummy head in a side impact crash. Accid. Anal. Prev. 2013, 55, 232–241. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.-H.; Jin, X.-L.; Zhang, X.-Y.; Hou, X.-Y. Scene reconstruction and process reappearance of car-pedestrian collision traffic accidents. J. Syst. Simul. 2010, 22, 1288–1291. [Google Scholar]
- Berthelson, P.R.; Ghassemi, P.; Wood, J.W.; Liu, Y.-C.; Al-Graitti, A.J.; Jones, M.D.; Chowdhury, S.; Prabhu, R.K. Evaluation of occupant neck injury response to varied impact conditions using a finite element-mathematical surrogate modeling approach. Int. J. Crashworthiness, 2020; in press. [Google Scholar]
- Cui, P.; An, M.; Zhang, X.; Guo, Y. Dynamic response and damage analysis of human head and neck in automobile rear impact. J. Med. Biomech. 2020, 35, 83–89. [Google Scholar]
- He, G.; Fang, L.; Liu, Y.-C. Mesoscale simulation-based parametric study of damage potential in brain tissue using hyperelastic and internal state variable models. J. Biomech. Eng. 2022, 144, 071005. [Google Scholar] [CrossRef]
- Liu, Y.-C. Development and evaluation of a finite element truck chassis crash model. Int. J. Crashworthiness 2010, 15, 107–113. [Google Scholar] [CrossRef]
- Liu, Y.-C. Development of simplified truck chassis model for crash analysis in different impact scenarios. Int. J. Crashworthiness 2010, 15, 457–467. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Day, M.L. Experimental analysis and computer simulation of automotive bumper system under impact conditions. Int. J. Comput. Methods Eng. Sci. Mech. 2008, 9, 51–59. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Day, M.L. Simplified truck chassis modeling and crashworthiness analysis. Int. J. Heavy Veh. Syst. 2008, 15, 237–254. [Google Scholar] [CrossRef]
- Liu, Y.-C. Crashworthiness design of thin-walled curved beams with box and channel cross sections. Int. J. Crashworthiness 2010, 15, 413–423. [Google Scholar] [CrossRef]
- Liu, Y.-C. Thin-walled curved hexagonal beams in crashes—FEA and design. Int. J. Crashworthiness 2010, 15, 151–159. [Google Scholar] [CrossRef]
- Feyzi, M.; Fallahnezhad, K.; Taylor, M.; Hashemi, R. The mechanics of head-neck taper junctions: What do we know from finite element analysis? J. Mech. Behav. Biomed. Mater. 2021, 116, 104338. [Google Scholar] [CrossRef] [PubMed]
- Mao, H.; Zhang, L.; Jiang, B.; Genthikatti, V.V.; Jin, X.; Zhu, F.; Makwana, R.; Gill, A.; Jandir, G.; Singh, A.; et al. Development of a finite element human head model partially validated with thirty five experimental cases. J. Biomech. Eng. 2013, 135, 111002. [Google Scholar] [CrossRef]
- Raul, J.S.; Deck, C.; Willinger, R.; Ludes, B. Finite-element models of the human head and their applications in forensic practice. Int. J. Leg. Med. 2008, 122, 359–366. [Google Scholar] [CrossRef] [PubMed]
- Ruan, J.S.; Khalil, T.; King, A.I. Dynamic response of the human head to impact by three-dimensional finite element analysis. J. Biomech. Eng. 1994, 116, 44–50. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; Khalil, C.T.B.; King, A.I. A new model comparing impact responses of the homogeneous and inhomogeneous human brain. SAE Pap. 1995, 104, 2999–3015. [Google Scholar]
- Zhang, L.; Yang, K.H.; Dwarampudi, R.; Omori, K.; Li, T.; Chang, K.; Hardy, W.N.; Khalil, T.B.; King, A.I. Recent advances in brain injury research: A new human head model development and validation. SAE Pap. 2001, 45, 1–25. [Google Scholar]
- Kleiven, S.; Hardy, W.N. Correlation of an FE model of the human head with local brain motion. SAE Pap. 2002, 46, 123–144. [Google Scholar]
- Horgan, T.J.; Gilchrist, M.D. The creation of three-dimensional finite element models for simulating head impact biomechanics. Int. J. Crashworthiness 2003, 8, 353–366. [Google Scholar] [CrossRef]
- Sahoo, D.; Deck, C.; Yoganandan, N.; Willinger, R. Development of skull fracture criterion based on real-world head trauma simulations using finite element head model. J. Mech. Behav. Biomed. Mater. 2016, 57, 24–41. [Google Scholar] [CrossRef] [PubMed]
- Cotton, R.T.; Pearce, C.W.; Young, P.G.; Kota, N.; Leung, A.C.; Bagchi, A.; Qidwai, S.M. Development of a geometrically accurate and adaptable finite element head model for impact simulation: The Naval Research Laboratory-Simpleware Head Model. Comput. Methods Biomech. Biomed. Eng. 2016, 19, 101–113. [Google Scholar] [CrossRef] [PubMed]
- Trotta, A.; Clark, J.M.; McGoldrick, A.; Gilchrist, M.D.; Annaidh, A.N. Biofidelic finite element modelling of brain trauma: Importance of the scalp in simulating head impact. Int. J. Mech. Sci. 2020, 173, 105448. [Google Scholar] [CrossRef]
- Han, Y.; He, W.; Shi, L.; Wu, H.; Pan, D.; Huang, H. Helmet protective performance via reconstruction of electric two-wheeler rider’s head-to-ground impact accidents. Int. J. Crashworthiness 2020, 25, 493–504. [Google Scholar] [CrossRef]
- Deng, X.-Q.; Chen, S.-A.; Prabhu, R.; Jiang, Y.-Y.; Mao, Y.; Horstemeyer, M.F. Finite element analysis of the human head under side car crash impacts at different speeds. J. Mech. Med. Biol. 2014, 14, 1440002. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Glass, G.A. Choose the best element size to yield accurate FEA results while reduce FE model’s complexity. Br. J. Eng. Technol. 2013, 1, 13–28. [Google Scholar]
- Liu, Y.-C.; Day, M.L. ANSYS and LS-DYNA used for structural analysis. Int. J. Comput. Aided Eng. Technol. 2008, 1, 31–44. [Google Scholar] [CrossRef]
- Shi, L.-L.; Han, Y.; Huang, H.-W.; Davidson, J.; Thomson, R. Evaluation of injury thresholds for predicting severe head injuries in vulnerable road users resulting from ground impact via detailed accident reconstructions. Biomech. Model. Mechanobiol. 2020, 19, 1845–1863. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.; Poplin, G.; Bollapragada, V.; Daniel, T.; Crandall, J. Monte Carlo method for estimating whole-body injury metrics from pedestrian impact simulation results. Accid. Anal. Prev. 2020, 147, 105761. [Google Scholar] [CrossRef]
- McElhaney, J.H.; Fogle, J.L.; Melvin, J.W.; Haynes, R.R.; Roberts, V.L.; Alem, N.M. Mechanical properties on cranial bone. J. Biomech. 1970, 3, 495–511. [Google Scholar] [CrossRef] [PubMed]
- Nahum, A.M. Intracranial pressure dynamics during head impact. SAE Tech. Pap. 1977. [Google Scholar] [CrossRef]
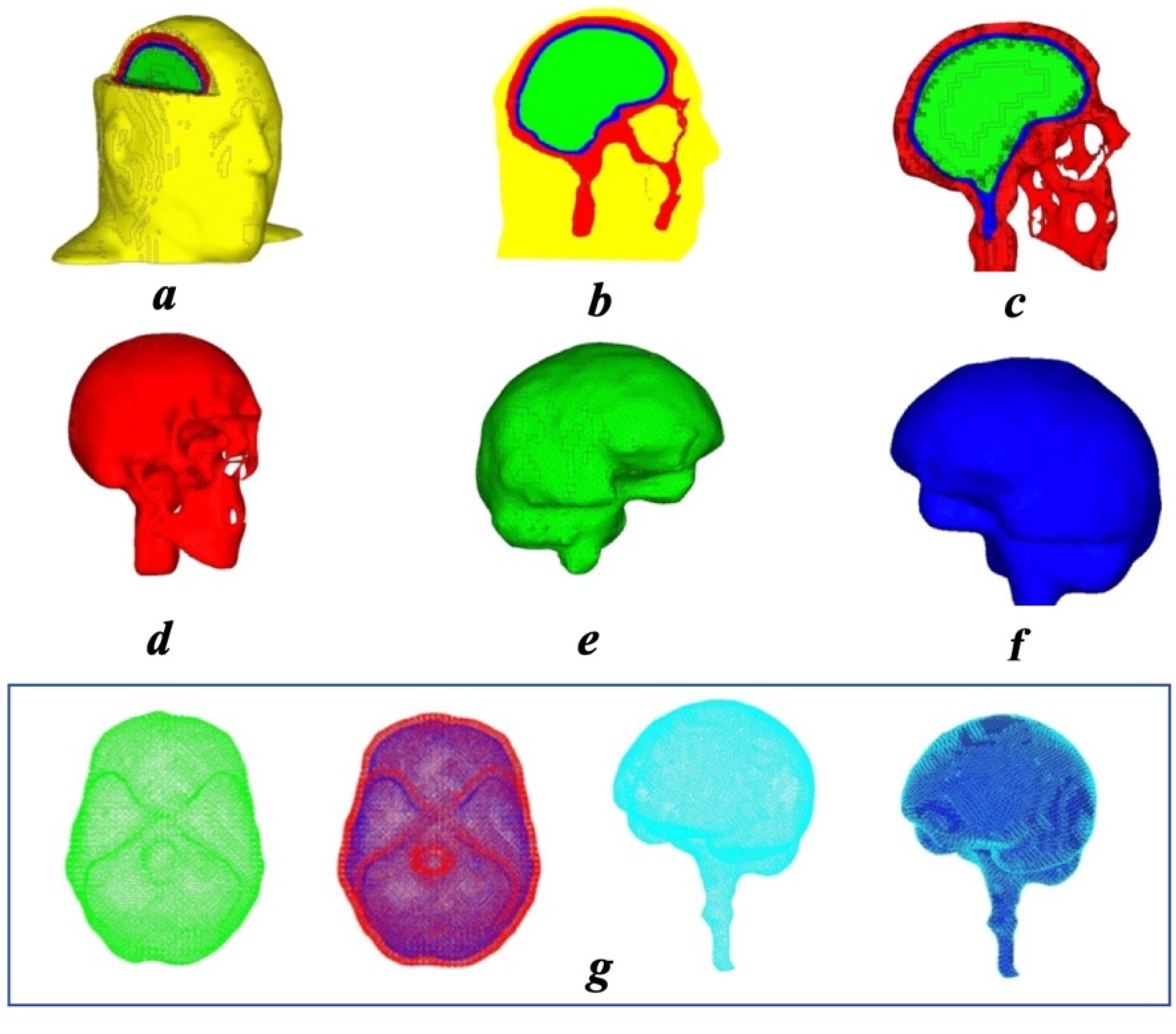
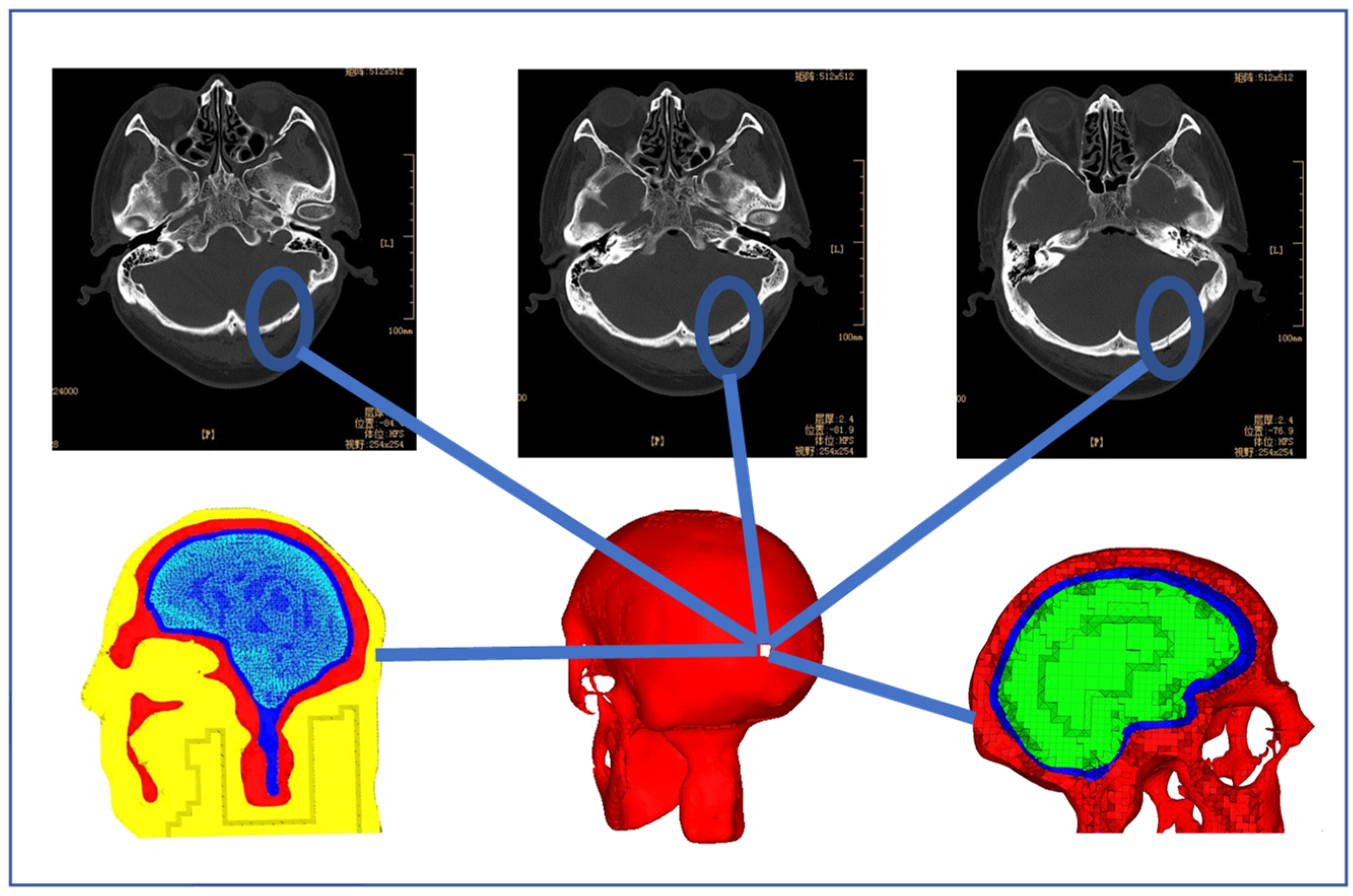


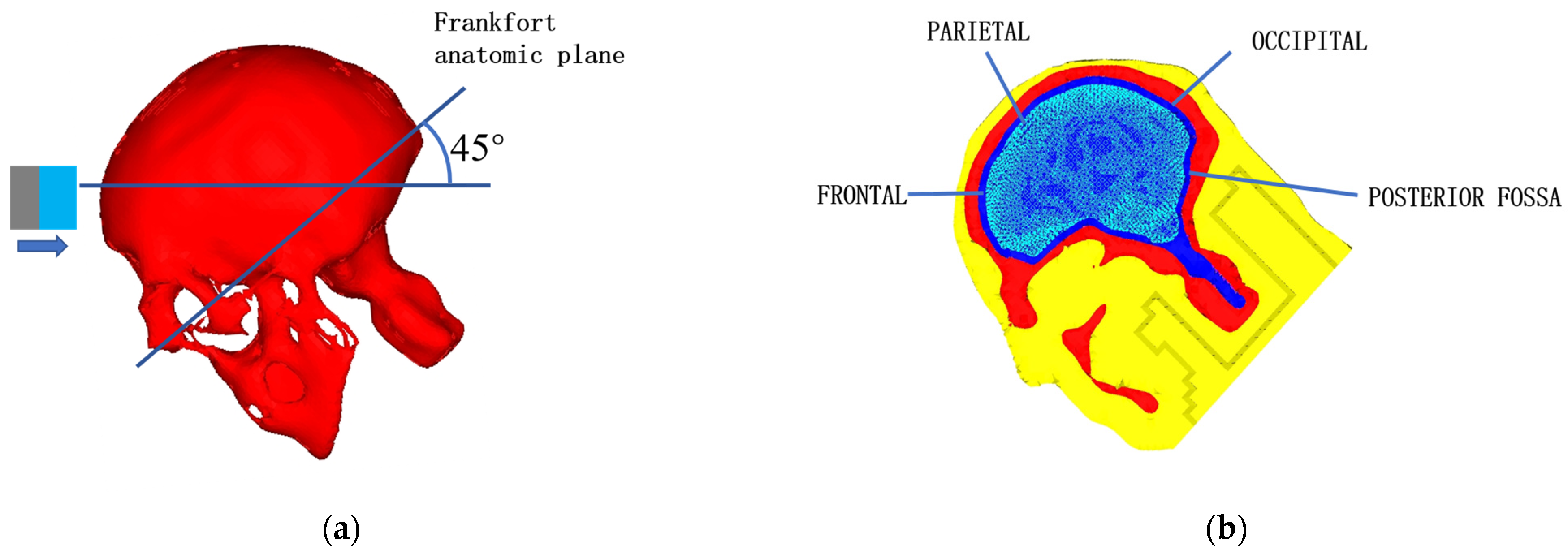
| Component | Skull | Brain | Cerebrospinal Fluid | Scalp and Skin |
|---|---|---|---|---|
| No. of elements | 229,176 | 52,636 | 113,083 | 242,885 |
| Component | Density (kg/m3) | Young’s Modulus | Poisson’s Ratio |
|---|---|---|---|
| Skull | 2.0 × 103 | 20.1 GPa | 0.28 |
| CSF | 1.0 × 103 | 1.20 MPa | 0.49 |
| Scalp, Skin, etc. | 1.2 × 103 | 16.70 MPa | 0.42 |
| Ground | 7.8 × 103 | 210 GPa | 0.30 |
| Component | Density (kg/m3) | Young’s Modulus | Short-Time Shear Modulus | Long-Time Shear Modulus | Decay Constant |
|---|---|---|---|---|---|
| Brain | 1.04 × 103 | 2.19 GPa | 0.528 MPa | 0.168 MPa | 80 |
| Form of Injury | Parameters | Threshold |
|---|---|---|
| Brain damage | ICP | Damage (>235 KPa) Small or non-injury (<173 KPa) |
| Cut stress | Severe injuries (11~16.5 KPa). | |
| Von Mises stress | Bruising (7~8.6 KPa). Mild traumatic brain injury (>20 KPa) Concussion (15~20 KPa) Shaft rope damage (>26 KPa) | |
| Skull fracture | Von Mises stress | Skull fracture (>34.47 MPa) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, X.; Du, Z.; Feng, H.; Wang, S.; Luo, H.; Liu, Y. Investigation on the Modeling and Reconstruction of Head Injury Accident Using ABAQUS/Explicit. Bioengineering 2022, 9, 723. https://doi.org/10.3390/bioengineering9120723
Deng X, Du Z, Feng H, Wang S, Luo H, Liu Y. Investigation on the Modeling and Reconstruction of Head Injury Accident Using ABAQUS/Explicit. Bioengineering. 2022; 9(12):723. https://doi.org/10.3390/bioengineering9120723
Chicago/Turabian StyleDeng, Xingqiao, Zhifei Du, Huiling Feng, Shisong Wang, Heng Luo, and Yucheng Liu. 2022. "Investigation on the Modeling and Reconstruction of Head Injury Accident Using ABAQUS/Explicit" Bioengineering 9, no. 12: 723. https://doi.org/10.3390/bioengineering9120723
APA StyleDeng, X., Du, Z., Feng, H., Wang, S., Luo, H., & Liu, Y. (2022). Investigation on the Modeling and Reconstruction of Head Injury Accident Using ABAQUS/Explicit. Bioengineering, 9(12), 723. https://doi.org/10.3390/bioengineering9120723








