Effective Capacitance from Equivalent Electrical Circuit as a Tool for Monitoring Non-Adherent Cell Suspensions at Low Frequencies
Abstract
1. Introduction
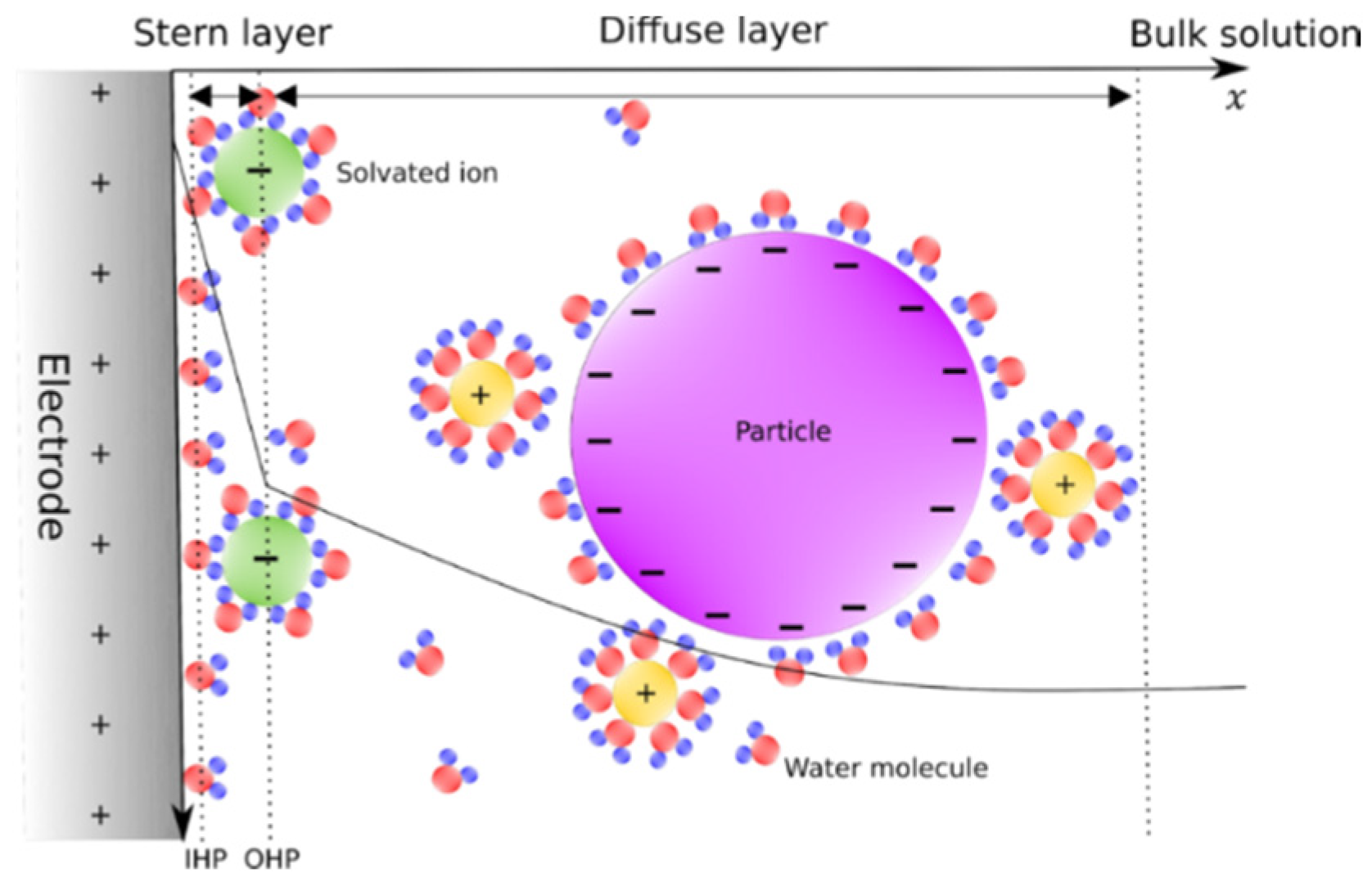
2. Theoretical Framework
3. Materials and Methods
3.1. PMMA Particle Suspensions (Biological Phantom) Preparation
3.2. Non-Adherent Cell Suspensions Preparation
3.3. Numerical Simulations
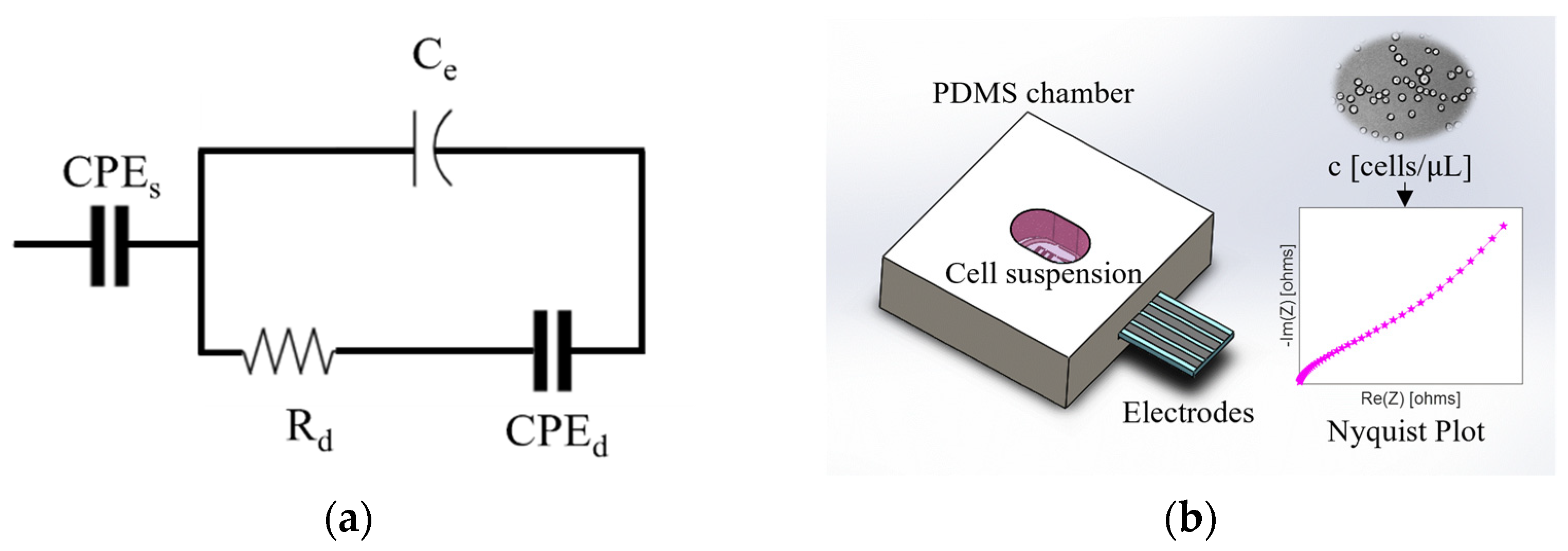
3.4. EIS Measurements and Analysis
4. Results and Discussion
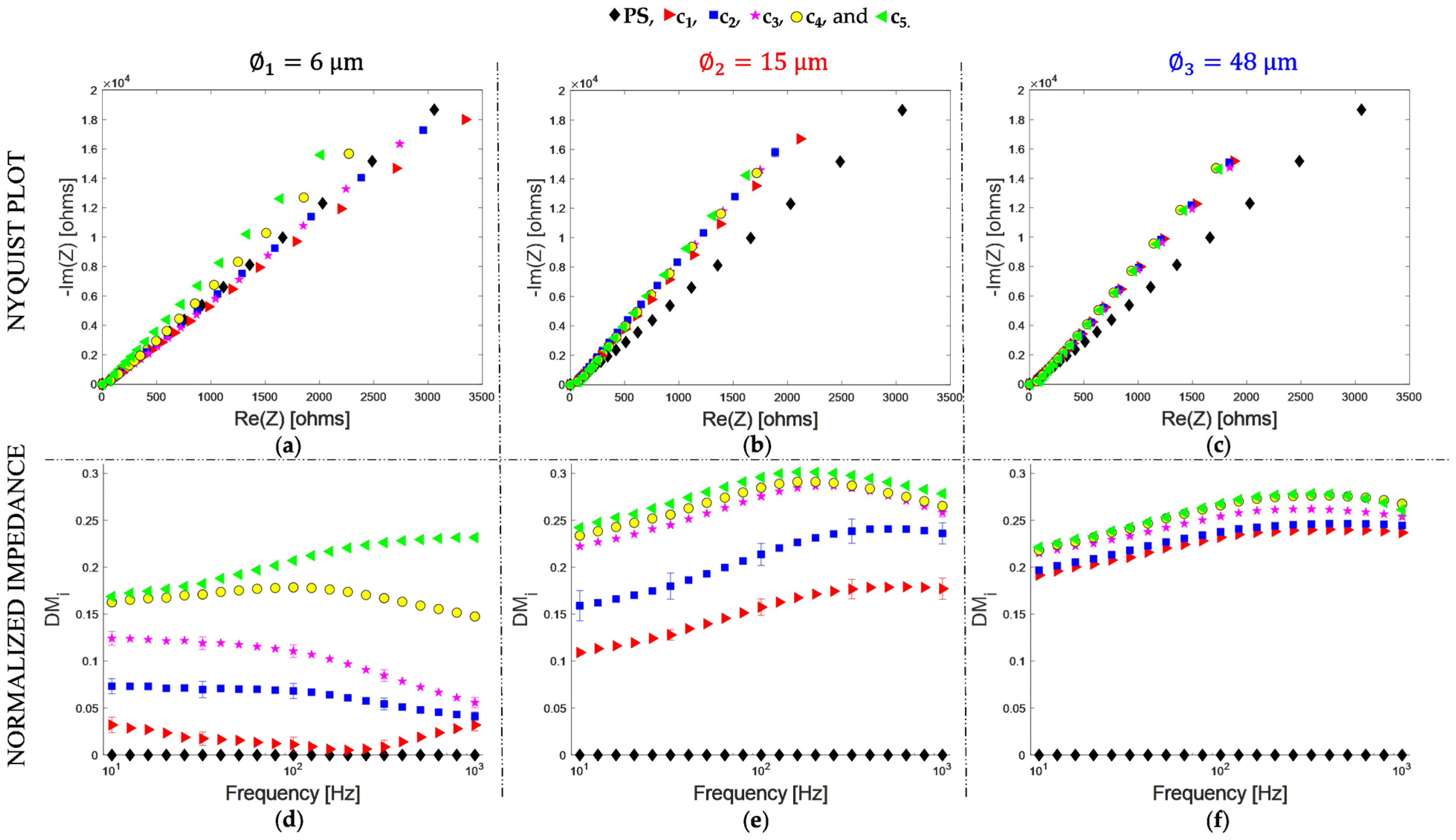
4.1. Numerical Simulations
4.2. EIS Analysis for PMMA Particle Suspensions (Biological Phantom)
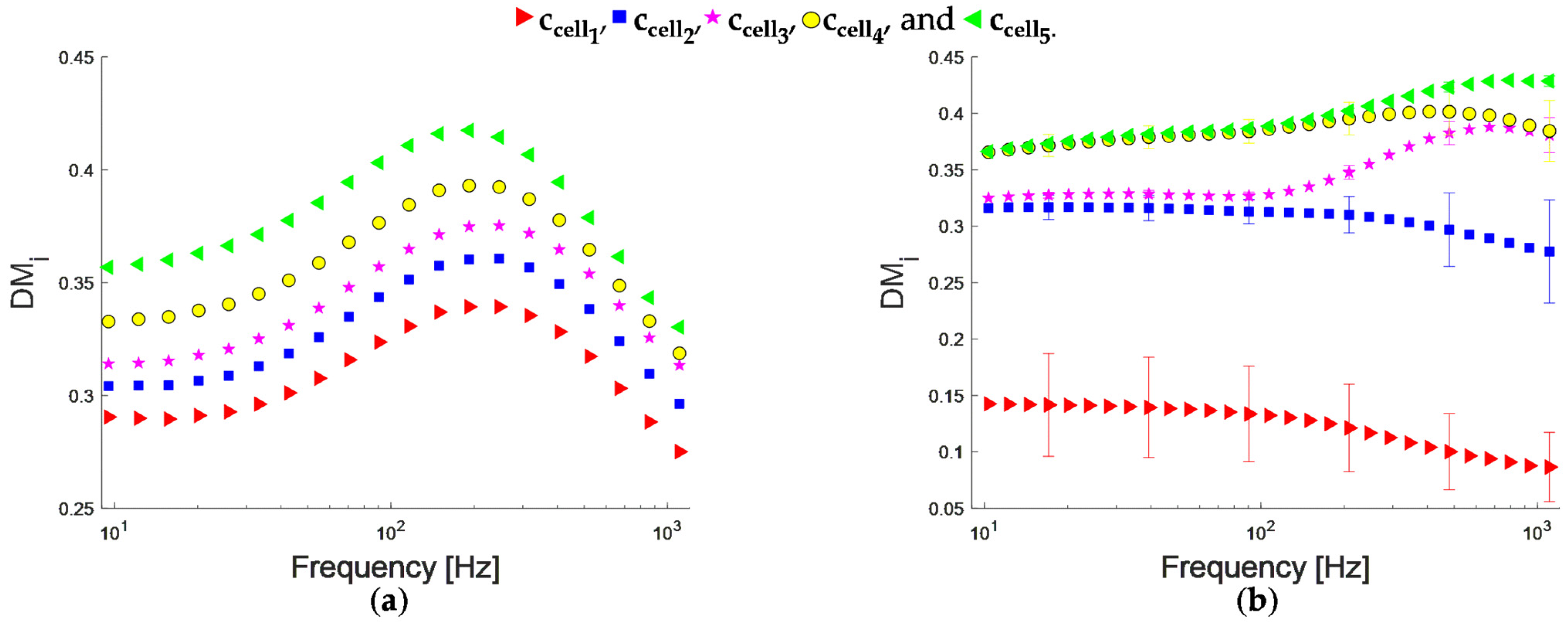
4.3. EIS Analysis for Non-Adherent Cell Suspensions
5. Conclusions
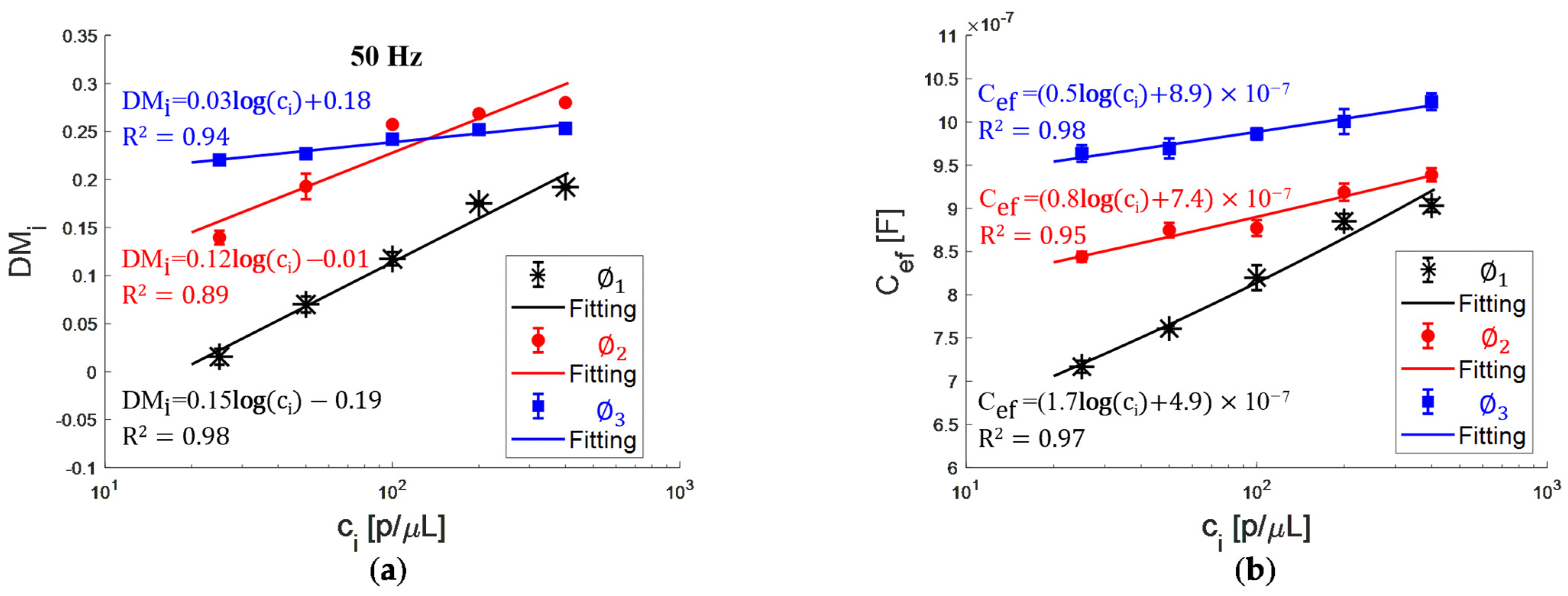
- The normalized impedance is a function of particle concentration and size for diameters of 6 and 15 μm, showing limitations for particles of 48 μm, starting with a volume fraction of 58 × 10−4. The sensitivity of the curve decreases with the particle size;
- The effective capacitance is a function of particle concentration and size for diameters of 6, 15, and 48 μm, evaluated in a volume fraction of 0.03 × 10−4 to 230 × 10−4. The sensitivity of the curve also decreases with the particle size;
- For non-adherent cell suspensions, the normalized impedance is not significantly different for K-562 cells and leukocytes. In contrast, the effective capacitance has a well distinguishable curve depending on concentration for each cell type, evaluated in a range of 25 cells/μL to 400 cells/μL with 100 μL of volume sample;
- The normalized impedance is a simple approach that only requires arithmetic treatment of the data, having limitations for analyzing changes in the sample size, which could be a drawback for a biological assay. On the other hand, effective capacitance is a more robust approach, which requires an optimization algorithm to determine the values of electrical circuit components. Nonetheless, it shows a better result for the sample size analysis.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Strubbe, F.; Beunis, F.; Marescaux, M.; Neyts, K. Charging mechanism in colloidal particles leading to a linear relation between charge and size. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2007, 75, 031405. [Google Scholar] [CrossRef] [PubMed]
- Ohshima, H. (Ed.) Chapter 1—Electrical double layer around a charged colloidal particle in an electrolyte solution. In Interface Science and Technology; Elsevier: Amsterdam, The Netherlands, 2006; Volume 12, pp. 1–38. [Google Scholar] [CrossRef]
- Maximova, N.; Dahl, O. Environmental implications of aggregation phenomena: Current understanding. Curr. Opin. Colloid Interface Sci. 2006, 11, 246–266. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, M.; Yao, J. Characterization of Colloidal Particles Using Electrical Impedance Spectroscopy in Two-electrode System with Carbon Probe. Procedia Eng. 2015, 102, 322–328. [Google Scholar] [CrossRef]
- Kuang, W.; Nelson, S.O. Low-Frequency Dielectric Dispersion from Ion Permeability of Membranes. J. Colloid Interface Sci. 1997, 193, 242–249. [Google Scholar] [CrossRef] [PubMed]
- Asami, K. Radiofrequency Dielectric Properties of Cell Suspensions. In Dielectric Relaxation in Biological Systems: Physical Principles, Methods, and Applications; Raicu, V., Feldman, Y., Eds.; Oxford University Press: Oxford, UK, 2015. [Google Scholar] [CrossRef]
- Chassagne, C.; Dubois, E.; Jiménez, M.L.; van der Ploeg, J.P.M.; van Turnhout, J. Compensating for Electrode Polarization in Dielectric Spectroscopy Studies of Colloidal Suspensions: Theoretical Assessment of Existing Methods. Front. Chem. 2016, 4, 30. [Google Scholar] [CrossRef] [PubMed]
- Awasthi, P.; Das, S. Reduced electrode polarization at electrode and analyte interface in impedance spectroscopy using carbon paste and paper. Rev. Sci. Instrum. 2019, 90, 124103. [Google Scholar] [CrossRef]
- Jiménez, M.L.; Arroyo, F.J.; van Turnhout, J.; Delgado, A.V. Analysis of the Dielectric Permittivity of Suspensions by Means of the Logarithmic Derivative of Its Real Part. J. Colloid Interface Sci. 2002, 249, 327–335. [Google Scholar] [CrossRef]
- Khademi, M.; Barz, D.P.J. Dielectric relaxation spectroscopy of aqueous micellar electrolyte solutions: A novel application to infer Dukhin number and zeta potential of a micelle. Electrophoresis 2019, 40, 710–719. [Google Scholar] [CrossRef]
- Paivana, G.; Barmpakos, D.; Mavrikou, S.; Kallergis, A.; Tsakiridis, O.; Kaltsas, G.; Kintzios, S. Evaluation of Cancer Cell Lines by Four-Point Probe Technique, by Impedance Measurements in Various Frequencies. Biosensors 2021, 11, 345. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, M. Experimental study on dielectric relaxation of SiO2 nano-particle suspensions for developing a particle characterization method based on electrical impedance spectroscopy. Powder Technol. 2015, 281, 200–213. [Google Scholar] [CrossRef]
- Yao, J.; Sapkota, A.; Konno, H.; Obara, H.; Sugawara, M.; Takei, M. Noninvasive online measurement of particle size and concentration in liquid–particle mixture by estimating equivalent circuit of electrical double layer. Part. Sci. Technol. 2016, 34, 517–525. [Google Scholar] [CrossRef]
- Ramírez-Chavarría, R.G.; Sánchez-Pérez, C.; Romero-Ornelas, L.; Ramón-Gallegos, E. Time-Constant-Domain Spectroscopy: An Impedance-Based Method for Sensing Biological Cells in Suspension. IEEE Sens. J. 2021, 21, 185–192. [Google Scholar] [CrossRef]
- Lockett, V.; Horne, M.; Sedev, R.; Rodopoulos, T.; Ralston, J. Differential capacitance of the double layer at the electrode/ionic liquids interface. Phys. Chem. Chem. Phys. 2010, 12, 12499–12512. [Google Scholar] [CrossRef]
- Kang, J.; Wen, J.; Jayaram, S.H.; Yu, A.; Wang, X. Development of an equivalent circuit model for electrochemical double layer capacitors (EDLCs) with distinct electrolytes. Electrochim. Acta 2014, 115, 587–598. [Google Scholar] [CrossRef]
- Khademi, M.; Barz, D.P.J. Structure of the Electrical Double Layer Revisited: Electrode Capacitance in Aqueous Solutions. Langmuir 2020, 36, 4250–4260. [Google Scholar] [CrossRef] [PubMed]
- Schwan, H.P. Electrical properties of tissues and cell suspensions: Mechanisms and models. In Proceedings of the 16th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Baltimore, MD, USA, 3–6 November 1994; Volume 1, pp. A70–A71. [Google Scholar] [CrossRef]
- Heileman, K.; Daoud, J.; Tabrizian, M. Dielectric spectroscopy as a viable biosensing tool for cell and tissue characterization and analysis. Biosens. Bioelectron. 2013, 49, 348–359. [Google Scholar] [CrossRef] [PubMed]
- Morgan, H.; Sun, T.; Holmes, D.; Gawad, S.; Green, N.G. Single cell dielectric spectroscopy. J. Phys. Appl. Phys. 2006, 40, 61–70. [Google Scholar] [CrossRef]
- Asami, K. Characterization of biological cells by dielectric spectroscopy. J. Non-Cryst. Solids 2002, 305, 268–277. [Google Scholar] [CrossRef]
- Sun, T.; Tsuda, S.; Zauner, K.-P.; Morgan, H. On-chip electrical impedance tomography for imaging biological cells. Biosens. Bioelectron. 2010, 25, 1109–1115. [Google Scholar] [CrossRef]
- Shamoon, D.; Lasquellec, S.; Brosseau, C. Perspective: Towards understanding the multiscale description of cells and tissues by electromechanobiology. J. Appl. Phys. 2018, 123, 240902. [Google Scholar] [CrossRef]
- Wang, L.; Hu, S.; Liu, K.; Chen, B.; Wu, H.; Jia, J.; Yao, J. A hybrid Genetic Algorithm and Levenberg–Marquardt (GA–LM) method for cell suspension measurement with electrical impedance spectroscopy. Rev. Sci. Instrum. 2020, 91, 124104. [Google Scholar] [CrossRef] [PubMed]
- Xia, S.; Zhu, P.; Pi, F.; Zhang, Y.; Li, Y.; Wang, J.; Sun, X. Development of a simple and convenient cell-based electrochemical biosensor for evaluating the individual and combined toxicity of DON, ZEN, and AFB1. Biosens. Bioelectron. 2017, 97, 345–351. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Li, F.; Nordin, A.N.; Tarbell, J.; Voiculescu, I. Toxicity studies using mammalian cells and impedance spectroscopy method. Sens. Bio-Sens. Res. 2015, 3, 112–121. [Google Scholar] [CrossRef]
- Tran, T.B.; Baek, C.; Min, J. Electric Cell-Substrate Impedance Sensing (ECIS) with Microelectrode Arrays for Investigation of Cancer Cell–Fibroblasts Interaction. PLoS ONE 2016, 11, e0153813. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Zhang, Y.; Zheng, L.; Zhan, Y.; He, L. Graphene oxide/poly-l-lysine assembled layer for adhesion and electrochemical impedance detection of leukemia K562 cancercells. Biosens. Bioelectron. 2013, 42, 112–118. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Du, D.; Yan, F.; Ju, H.X.; Lian, H.Z. Electrochemical Antitumor Drug Sensitivity Test for Leukemia K562 Cells at a Carbon-Nanotube-Modified Electrode. Chem.-Eur. J. 2005, 11, 1467–1472. [Google Scholar] [CrossRef] [PubMed]
- Huerta-Nuñez, L.F.E.; Gutierrez-Iglesias, G.; Martinez-Cuazitl, A.; Mata-Miranda, M.M.; Alvarez-Jiménez, V.D.; Sánchez-Monroy, V.; Golberg, A.; González-Díaz, C.A. A biosensor capable of identifying low quantities of breast cancer cells by electrical impedance spectroscopy. Sci. Rep. 2019, 9, 6419. [Google Scholar] [CrossRef]
- Pretini, V.; Koenen, M.H.; Kaestner, L.; Fens, M.H.A.M.; Schiffelers, R.M.; Bartels, M.; Van Wijk, R. Red Blood Cells: Chasing Interactions. Front. Physiol. 2019, 10, 945. [Google Scholar] [CrossRef]
- Randviir, E.P.; Banks, C.E. Electrochemical impedance spectroscopy: An overview of bioanalytical applications. Anal. Methods 2013, 5, 1098–1115. [Google Scholar] [CrossRef]
- de León-Hernández, A.; Sánchez-Pérez, C.; Ramírez-Chavarría, R.G. An equivalent electric circuit as a tool for monitoring micron sized-particles in suspension from electrical impedance measurements. J. Phys. Conf. Ser. 2021, 1723, 012045. [Google Scholar] [CrossRef]
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods: Fundamentals and Applications, 2nd ed.; John Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Kilic, M.S.; Bazant, M.Z.; Ajdari, A. Steric effects in the dynamics of electrolytes at large applied voltages. I. Double-layer charging. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2007, 75, 021502. [Google Scholar] [CrossRef] [PubMed]
- Córdoba-Torres, P.; Mesquita, T.J.; Nogueira, R.P. Relationship between the Origin of Constant-Phase Element Behavior in Electrochemical Impedance Spectroscopy and Electrode Surface Structure. J. Phys. Chem. C 2015, 119, 4136–4147. [Google Scholar] [CrossRef]
- Huang, V.; Vivier, V.; Orazem, M.E.; Pebere, N.; Tribollet, B. The Apparent CPE Behavior of a Disk Electrode with Faradaic Reactions: A Global and Local Impedance Analysis. ECS Trans. 2007, 3, 567–585. [Google Scholar] [CrossRef]
- Orazem, M.E.; Frateur, I.; Tribollet, B.; Vivier, V.; Marcelin, S.; Pébère, N.; Bunge, A.L.; White, E.A.; Riemer, D.P.; Musiani, M. Dielectric Properties of Materials Showing Constant-Phase-Element (CPE) Impedance Response. J. Electrochem. Soc. 2013, 160, C215. [Google Scholar] [CrossRef]
- Kakaei, M.N.; Neshati, J.; Rezaierod, A.R. On the Extraction of the Effective Capacitance from Constant Phase Element Parameters. Prot. Met. Phys. Chem. Surf. 2018, 54, 548–556. [Google Scholar] [CrossRef]
- Hirschorn, B.; Orazem, M.E.; Tribollet, B.; Vivier, V.; Frateur, I.; Musiani, M. Determination of effective capacitance and film thickness from constant-phase-element parameters. IMPEDANCE Spectrosc. Transf. Funct. 2010, 55, 6218–6227. [Google Scholar] [CrossRef]
- Jović, V.D.; Jović, B.M. EIS and differential capacitance measurements onto single crystal faces in different solutions: Part I: Ag(111) in 0.01 M NaCl. J. Electroanal. Chem. 2003, 541, 1–11. [Google Scholar] [CrossRef]
- Brug, G.J.; van den Eeden, A.L.G.; Sluyters-Rehbach, M.; Sluyters, J.H. The analysis of electrode impedances complicated by the presence of a constant phase element. J. Electroanal. Chem. Interfacial Electrochem. 1984, 176, 275–295. [Google Scholar] [CrossRef]
- Slouka, C.; Wurm, D.J.; Brunauer, G.; Welzl-Wachter, A.; Spadiut, O.; Fleig, J.; Herwig, C. A Novel Application for Low Frequency Electrochemical Impedance Spectroscopy as an Online Process Monitoring Tool for Viable Cell Concentrations. Sensors 2016, 16, 1900. [Google Scholar] [CrossRef]
- Schmid-Schönbein, G.W.; Shih, Y.Y.; Chien, S. Morphometry of Human Leukocytes. Blood 1980, 56, 866–875. [Google Scholar] [CrossRef]
- Tan, H.; Wang, M.; Zhang, Y.; Huang, X.; Chen, D.; Wu, M.-H.; Wang, J.; Chen, J. Classification of White Blood Cells Based on Cell Diameter, Specific Membrane Capacitance and Cytoplasmic Conductivity Leveraging Microfluidic Constriction Channel. In Proceedings of the 2021 21st International Conference on Solid-State Sensors, Actuators and Microsystems (Transducers), Orlando, FL, USA, 20–24 June 2021; pp. 1028–1031. [Google Scholar] [CrossRef]
- Henslee, B.E.; Morss, A.; Hu, X.; Lafyatis, G.P.; Lee, L.J. Electroporation Dependence on Cell Size: Optical Tweezers Study. Anal. Chem. 2011, 83, 3998–4003. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Li, H.; Xie, J.; Zhao, P.; Gore, J.C.; Xu, J. Quantification of cell size using temporal diffusion spectroscopy. Magn. Reson. Med. 2016, 75, 1076–1085. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Liu, L.; Xi, N.; Wang, Y.; Dong, Z.; Xiao, X.; Zhang, W. Atomic force microscopy imaging and mechanical properties measurement of red blood cells and aggressive cancer cells. Sci. China Life Sci. 2012, 55, 968–973. [Google Scholar] [CrossRef] [PubMed]
- Kho, D.; MacDonald, C.; Johnson, R.; Unsworth, C.P.; O’Carroll, S.J.; Mez, E.D.; Angel, C.E.; Graham, E.S. Application of xCELLigence RTCA Biosensor Technology for Revealing the Profile and Window of Drug Responsiveness in Real Time. Biosensors 2015, 5, 199–222. [Google Scholar] [CrossRef]
- van Kralingen, C.; Kho, D.T.; Costa, J.; Angel, C.E.; Graham, E.S. Exposure to inflammatory cytokines IL-1β and TNFα induces compromise and death of astrocytes; implications for chronic neuroinflammation. PLoS ONE 2013, 8, e84269. [Google Scholar] [CrossRef]


| Case | |||
|---|---|---|---|
| a | 1 | 0.7 | 1.1 |
| b | 1 | 0.8 | 1.3 |
| c | 1 | 0.9 | 1.6 |
| d | 2 | 0.9 | 2.6 |
| e | 4 | 0.9 | 4.6 |
| ci [p/μL] | Diameter | × 10−3 | [μF] | [Ω] | × 10−7 | ||
|---|---|---|---|---|---|---|---|
| c1 | 0.86 | 0.31 | 0.57 | 3815 | 9.9 | 0.73 | |
| 1.86 | 0.24 | 0.74 | 6412 | 7.1 | 0.74 | ||
| 0.62 | 0.36 | 0.84 | 7284 | 6.9 | 0.75 | ||
| c2 | 1.54 | 0.26 | 0.62 | 3868 | 9.4 | 0.75 | |
| 1.43 | 0.26 | 0.82 | 3570 | 6.9 | 0.71 | ||
| 0.54 | 0.37 | 0.85 | 6753 | 6.7 | 0.75 | ||
| c3 | 0.89 | 0.31 | 0.66 | 3863 | 9.3 | 0.76 | |
| 8.50 | 0.44 | 0.72 | 1186 | 8.6 | 0.8 | ||
| 1.05 | 0.3 | 0.86 | 7078 | 7.2 | 0.75 | ||
| c4 | 1.44 | 0.27 | 0.71 | 4561 | 8.2 | 0.78 | |
| 5.18 | 0.15 | 0.76 | 1741 | 8.3 | 0.8 | ||
| 0.16 | 0.29 | 0.88 | 7875 | 7.7 | 0.76 | ||
| c5 | 3.32 | 0.19 | 0.76 | 5049 | 8 | 0.75 | |
| 6.63 | 0.12 | 0.77 | 1827 | 8 | 0.81 | ||
| 0.97 | 0.28 | 0.90 | 10692 | 6.6 | 0.74 |
| Vf × 10−4 | |||
|---|---|---|---|
| Sample | |||
| c1 | 0.03 | 0.4 | 14 |
| c2 | 0.06 | 0.9 | 29 |
| c3 | 0.1 | 2 | 58 |
| c4 | 0.2 | 4 | 120 |
| c5 | 0.5 | 7 | 230 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De León-Hernández, A.; Romero-Ornelas, L.; Ramírez-Chavarría, R.G.; Ramón-Gallegos, E.; Sánchez-Pérez, C. Effective Capacitance from Equivalent Electrical Circuit as a Tool for Monitoring Non-Adherent Cell Suspensions at Low Frequencies. Bioengineering 2022, 9, 697. https://doi.org/10.3390/bioengineering9110697
De León-Hernández A, Romero-Ornelas L, Ramírez-Chavarría RG, Ramón-Gallegos E, Sánchez-Pérez C. Effective Capacitance from Equivalent Electrical Circuit as a Tool for Monitoring Non-Adherent Cell Suspensions at Low Frequencies. Bioengineering. 2022; 9(11):697. https://doi.org/10.3390/bioengineering9110697
Chicago/Turabian StyleDe León-Hernández, Alma, Luisa Romero-Ornelas, Roberto G. Ramírez-Chavarría, Eva Ramón-Gallegos, and Celia Sánchez-Pérez. 2022. "Effective Capacitance from Equivalent Electrical Circuit as a Tool for Monitoring Non-Adherent Cell Suspensions at Low Frequencies" Bioengineering 9, no. 11: 697. https://doi.org/10.3390/bioengineering9110697
APA StyleDe León-Hernández, A., Romero-Ornelas, L., Ramírez-Chavarría, R. G., Ramón-Gallegos, E., & Sánchez-Pérez, C. (2022). Effective Capacitance from Equivalent Electrical Circuit as a Tool for Monitoring Non-Adherent Cell Suspensions at Low Frequencies. Bioengineering, 9(11), 697. https://doi.org/10.3390/bioengineering9110697






