Sensitivity Analysis of Cardiac Alternans and Tachyarrhythmia to Ion Channel Conductance Using Population Modeling
Abstract
1. Introduction
2. Materials and Methods
2.1. In Silico Electrophysiological Model
2.2. Simulation Protocols
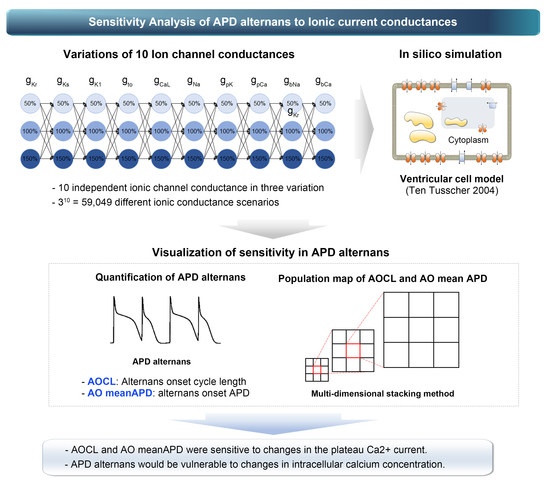
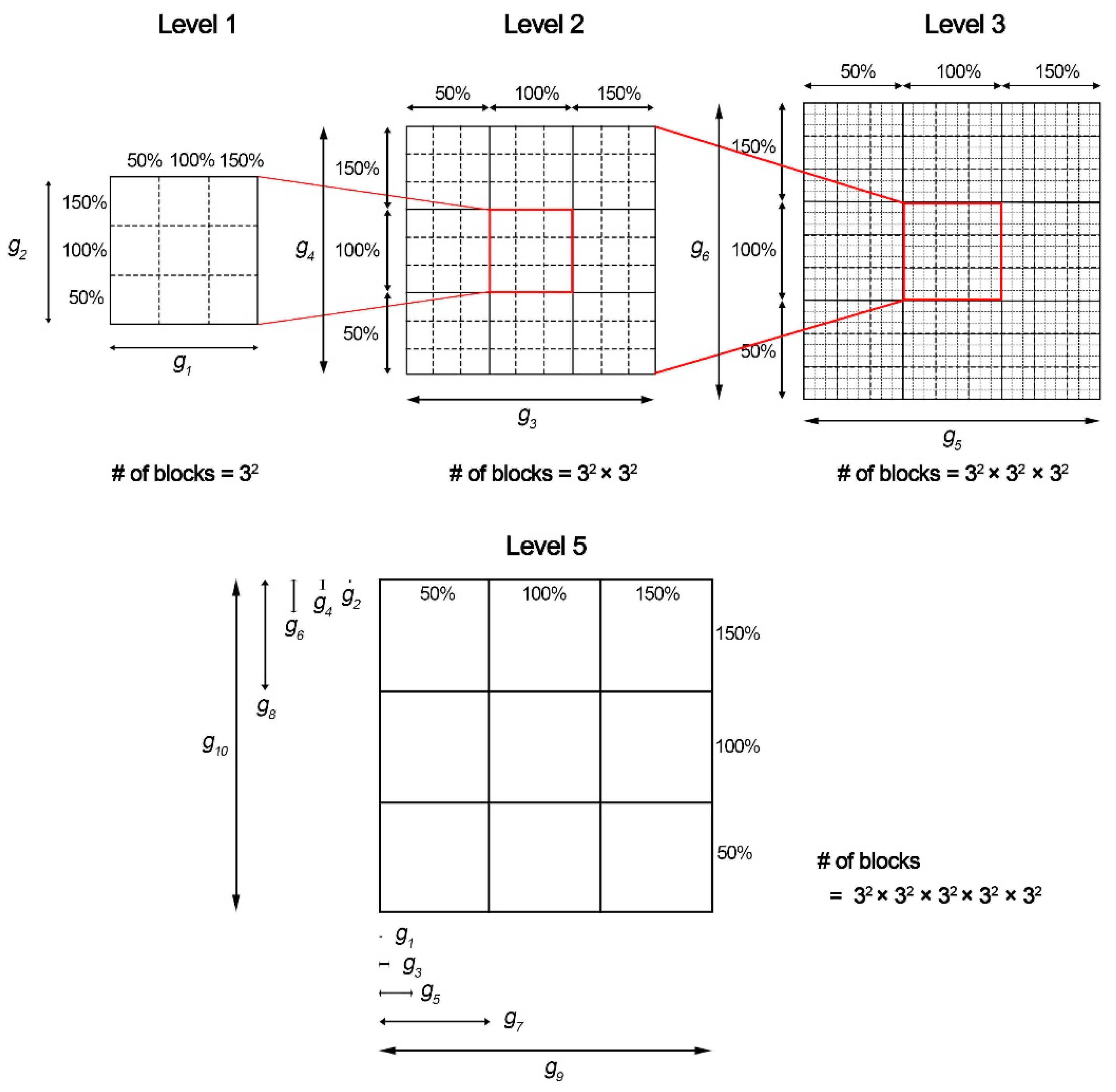
2.3. Population Modeling
3. Results
3.1. The Most Influential Ion Channels to AOCL and AO MeanAPD
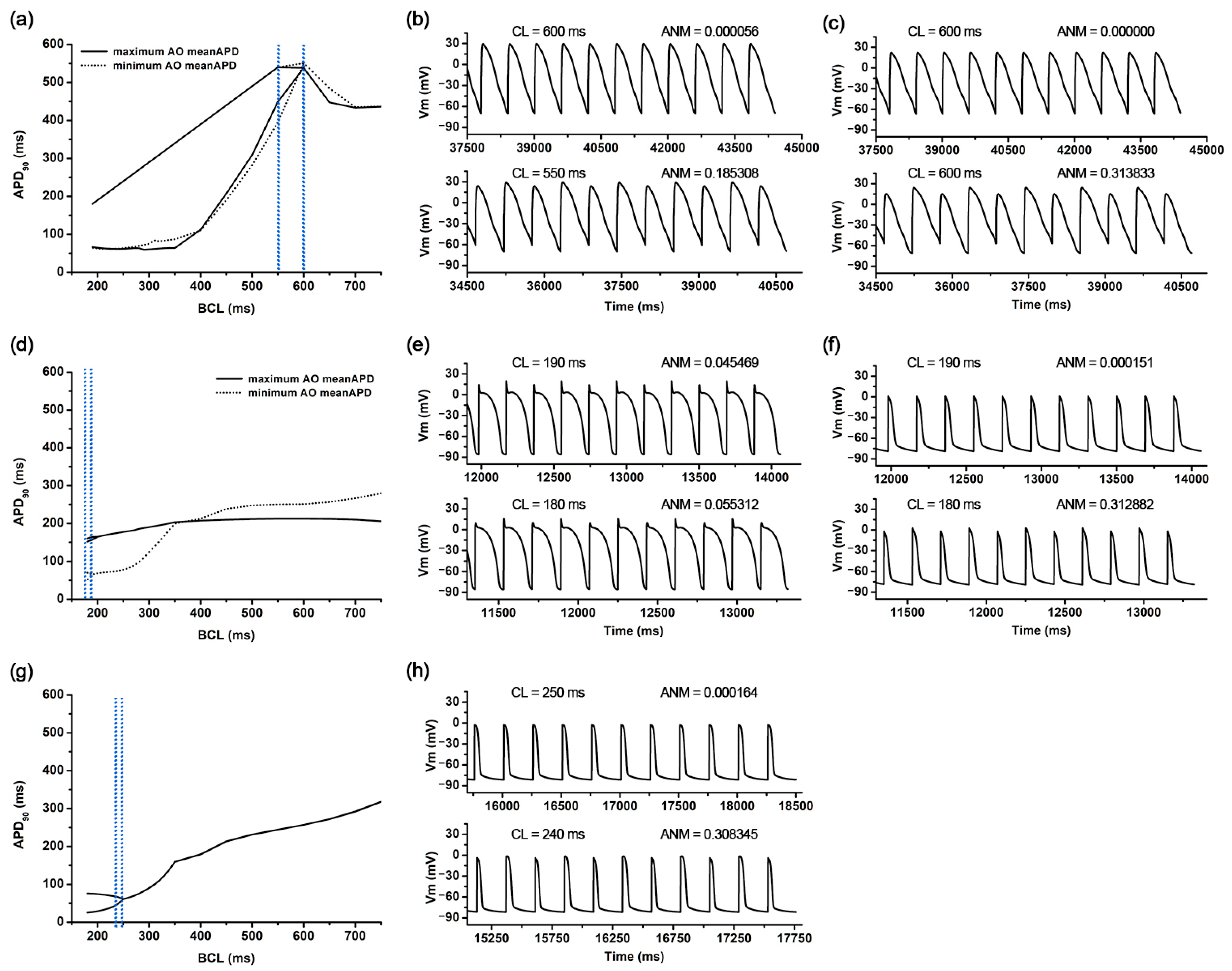
3.2. Ion Channel Variation Scenarios at the Maximal and Minimal AOCL
3.3. Ion Channel Variation Scenarios at the Minimal AO meanAPD
3.4. Non Alternans Scenarios
4. Discussion
- AOCL and AO meanAPD were sensitive to changes in the plateau Ca2+ current (gpCa). Accordingly, it was expected that APD alternans would be vulnerable to changes in intracellular calcium concentration.
- When APD alternans occurred, AOCL and AO meanAPD were proportional correlations (correlation 0.958, p-value < 0.01), similar to the cardiomyocytes without APD alternans; it is well-known that APD decreases as the cycle length shortens in normal cardiomyocytes.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chang, K.C.; Trayanova, N.A. Mechanisms of arrhythmogenesis related to calcium-driven alternans in a model of human atrial fibrillation. Sci. Rep. 2016, 6, 36395. [Google Scholar] [CrossRef] [PubMed]
- Tse, G.; Wong, S.T.; Tse, V.; Lee, Y.T.; Lin, H.Y.; Yeo, J.M. Cardiac dynamics: Alternans and arrhythmogenesis. J. Arrhythm. 2016, 32, 411–417. [Google Scholar] [CrossRef] [PubMed]
- Nolasco, J.B.; Dahlen, R.W. A graphic method for the study of alternation in cardiac action potentials. J. Appl. Physiol. 1968, 25, 191–196. [Google Scholar] [CrossRef] [PubMed]
- Ten Tusscher, K.H.W.J.; Panfilov, A.V. Alternans and spiral breakup in a human ventricular tissue model. Am. J. Physiol. Circ. Physiol. 2006, 291, H1088–H1100. [Google Scholar] [CrossRef] [PubMed]
- Chang, K.C.; Bayer, J.D.; Trayanova, N.A. Disrupted Calcium Release as a Mechanism for Atrial Alternans Associated with Human Atrial Fibrillation. PLoS Comput. Biol. 2014, 10, 12. [Google Scholar] [CrossRef]
- Narayan, S.M.; Franz, M.R.; Clopton, P.; Pruvot, E.J.; Krummen, D.E. Repolarization alternans reveals vulnerability to human atrial fibrillation. Circulation 2011, 123, 2922–2930. [Google Scholar] [CrossRef]
- Narayan, S.M.; Bode, F.; Karasik, P.L.; Franz, M.R. Alternans of atrial action potentials during atrial flutter as a precursor to atrial fibrillation. Circulation 2002, 106, 1968–1973. [Google Scholar] [CrossRef]
- Grandi, E.; Pandit, S.V.; Voigt, N.; Workman, A.J.; Dobrev, D.; Jalife, J.; Bers, D.M. Human atrial action potential and Ca 2+ model: Sinus rhythm and chronic atrial fibrillation. Circ. Res. 2011, 109, 1055–1066. [Google Scholar] [CrossRef]
- Fox, J.J.; McHarg, J.L.; Gilmour, R.F. Ionic mechanism of electrical alternans. Am. J. Physiol. Heart Circ. Physiol. 2002, 282, 516–530. [Google Scholar] [CrossRef]
- Sobie, E.A. Parameter sensitivity analysis in electrophysiological models using multivariable regression. Biophys. J. Biophys. Soc. 2009, 96, 1264–1274. [Google Scholar] [CrossRef]
- Kurata, Y.; Hisatome, I.; Matsuda, H.; Shibamoto, T. Dynamical mechanisms of pacemaker generation in IK1- downregulated human ventricular myocytes: Insights from bifurcation analyses of a mathematical model. Biophys. J. 2005, 89, 2865–2887. [Google Scholar] [CrossRef]
- Ten Tusscher, K.H.; Noble, D.; Noble, P.J.; Panfilov, A.V. A model for human ventricular tissue. AJP Heart Circ. Physiol. 2004, 286, H1573–H1589. [Google Scholar] [CrossRef]
- Kharche, S.; Adeniran, I.; Stott, J.; Law, P.; Boyett, M.R.; Hancox, J.C.; Zhang, H. Pro-arrhythmogenic effects of the S140G KCNQ1 mutation in human atrial fibrillation—Insights from modelling. J. Physiol. 2012, 590, 4501–4514. [Google Scholar] [CrossRef]
- Giudicessi, J.R.; Ye, D.; Tester, D.J.; Crotti, L.; Mugione, A.; Nesterenko, V.V.; Albertson, R.M.; Antzelevitch, C.; Schwartz, P.J.; Ackerman, M.J. Transient outward current (I to) gain-of-function mutations in the KCND3-encoded Kv4.3 potassium channel and Brugada syndrome. Heart Rhythm 2011, 8, 1024–1032. [Google Scholar] [CrossRef]
- Gemmell, P.; Burrage, K.; Rodriguez, B.; Quinn, T.A. Population of computational rabbit-specific ventricular action potential models for investigating sources of variability in cellular repolarisation. PLoS ONE 2014, 9, 15–19. [Google Scholar] [CrossRef][Green Version]
- Peng, W. Clutter-Based Dimension Reordering in Multi-Dimensional Data Visualization. Ph.D. Thesis, Worcester Polytechnic Institute, Worcester, MA, USA, 2005. [Google Scholar]
- Peng, W.; Ward, M.O.; Rundensteiner, E.A. Clutter reduction in multi-dimensional data visualization using dimension reordering. In Proceedings of the IEEE Symposium on Information Visualization, INFO VIS, Austin, TX, USA, 10–12 October 2004. [Google Scholar]
- Cherry, E.M.; Fenton, F.H. Suppression of alternans and conduction blocks despite steep APD restitution: Electrotonic, memory, and conduction velocity restitution effects. Am. J. Physiol. Circ. Physiol. Am. Physiol. Soc. 2004, 286, H2332–H2341. [Google Scholar] [CrossRef]
- Panfilov, A.V. Spiral waves in excitable media with negative restitution. Phys. Rev. E 2001, 63, 1–4. [Google Scholar]
- Panfilov, A.V.; Zemlin, C.W. Wave propagation in an excitable medium with a negatively sloped restitution curve. Chaos 2002, 12, 800–806. [Google Scholar] [CrossRef]
- Narayan, S.M.; Bayer, J.D.; Lalani, G.; Trayanova, N.A. Action Potential Dynamics Explain Arrhythmic Vulnerability in Human Heart Failure. A Clinical and Modeling Study Implicating Abnormal Calcium Handling. J. Am. Coll. Cardiol. 2008, 52, 1782–1792. [Google Scholar] [CrossRef]
- Bayer, J.D.; Narayan, S.M.; Lalani, G.G.; Trayanova, N.A. Rate-dependent action potential alternans in human heart failure implicates abnormal intracellular calcium handling. Heart Rhythm 2010, 7, 1093–1101. [Google Scholar] [CrossRef] [PubMed]
- Shih, H.-T. Anatomy of the Action Potential in the Heart. Texas Heart Inst. J. 1994, 21, 30–41. [Google Scholar]
- Ravens, U.; Cerbai, E. Role of potassium currents in cardiac arrhythmias. Europace 2008, 10, 1133–1137. [Google Scholar] [CrossRef] [PubMed]
- Surawicz, B. Role of potassium channels in cycle length dependent regulation of action potential duration in mammalian cardiac purkinje and ventricular muscle fiber. Cardiovasc. Res. 1992, 26, 1021–1029. [Google Scholar] [CrossRef] [PubMed]
- Taylor, A.L.; Hickey, T.J.; Prinz, A.A.; Marder, E. Structure and visualization of high-dimensional conductance spaces. J. Neurophysiol. 2006, 96, 891–905. [Google Scholar] [CrossRef] [PubMed]
- Muszkiewicz, A.; Britton, O.J.; Gemmell, P.; Passini, E.; Sánchez, C.; Zhou, X.; Carusi, A.; Quinn, T.A.; Burrage, K.; Bueno-Orovio, A.; et al. Variability in cardiac electrophysiology: Using experimentally-calibrated populations of models to move beyond the single virtual physiological human paradigm. Prog. Biophys. Mol. Biol. 2016, 120, 115–127. [Google Scholar] [CrossRef]
- Britton, O.J.; Bueno-Orovio, A.; Van Ammel, K.; Lu, H.R.; Towart, R.; Gallacher, D.J.; Rodriguez, B. Experimentally calibrated population of models predicts and explains intersubject variability in cardiac cellular electrophysiology. Proc. Natl. Acad. Sci. USA 2013, 110, E2098–E2105. [Google Scholar] [CrossRef]
- Song, E.; Lee, Y.-S. Interpretable machine learning of action potential duration restitution kinetics in single-cell models of atrial cardiomyocytes. J. Electrocardiol. 2022, 74, 137–145. [Google Scholar] [CrossRef]
- Llopis-Lorente, J.; Trenor, B.; Saiz, J. Considering population variability of electrophysiological models improves the in silico assessment of drug-induced torsadogenic risk. Comput. Methods Programs Biomed. 2022, 221, 106934. [Google Scholar] [CrossRef]
- Gizzi, A.; Cherry, E.M.; Gilmour, R.F.; Luther, S.; Filippi, S.; Fenton, F.H. Effects of pacing site and stimulation history on alternans dynamics and the development of complex spatiotemporal patterns in cardiac tissue. Front. Physiol. 2013, 4, 71. [Google Scholar] [CrossRef]
- Cusimano, N.; Gerardo-Giorda, L.; Gizzi, A. A space-fractional bidomain framework for cardiac electrophysiology: 1D alternans dynamics. Chaos 2021, 31, 7. [Google Scholar] [CrossRef]
- Hurtado, D.E.; Castro, S.; Gizzi, A. Computational modeling of non-linear diffusion in cardiac electrophysiology: A novel porous-medium approach. Comput. Methods Appl. Mech. Eng. 2016, 300, 70–83. [Google Scholar] [CrossRef]

| Abbreviation | Description | Conductance (nS/pF) |
|---|---|---|
| GKs | Conductance of slow delayed rectifier K+ current | 0.245 |
| GKr | Conductance of rapid delayed rectifier K+ current | 0.096 |
| GK1 | Conductance of maximal inward K+ current | 5.405 |
| GNa | Conductance of maximal Na+ current | 14.838 |
| GbNa | Conductance of maximal background Na+ current | 0.00029 |
| GCaL | Conductance of maximal L-type Ca2+ current | 0.0000398 |
| GbCa | Conductance of maximal background Ca2+ current | 0.000592 |
| Gto | Conductance of transient output K+ current | 0.294 |
| GpCa | Conductance of maximal plateau Ca2+ current | 0.025 |
| GpK | Conductance of maximal plateau K+ current | 0.0146 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, D.U.; Marcellinus, A.; Lim, K.M. Sensitivity Analysis of Cardiac Alternans and Tachyarrhythmia to Ion Channel Conductance Using Population Modeling. Bioengineering 2022, 9, 628. https://doi.org/10.3390/bioengineering9110628
Jeong DU, Marcellinus A, Lim KM. Sensitivity Analysis of Cardiac Alternans and Tachyarrhythmia to Ion Channel Conductance Using Population Modeling. Bioengineering. 2022; 9(11):628. https://doi.org/10.3390/bioengineering9110628
Chicago/Turabian StyleJeong, Da Un, Aroli Marcellinus, and Ki Moo Lim. 2022. "Sensitivity Analysis of Cardiac Alternans and Tachyarrhythmia to Ion Channel Conductance Using Population Modeling" Bioengineering 9, no. 11: 628. https://doi.org/10.3390/bioengineering9110628
APA StyleJeong, D. U., Marcellinus, A., & Lim, K. M. (2022). Sensitivity Analysis of Cardiac Alternans and Tachyarrhythmia to Ion Channel Conductance Using Population Modeling. Bioengineering, 9(11), 628. https://doi.org/10.3390/bioengineering9110628