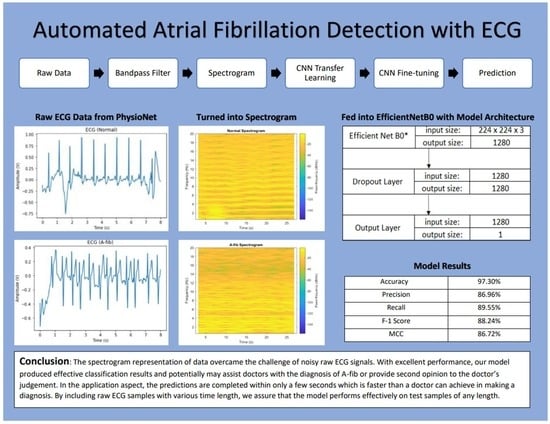
Automated Atrial Fibrillation Detection with ECG
Abstract
1. Introduction
2. Materials and Methods
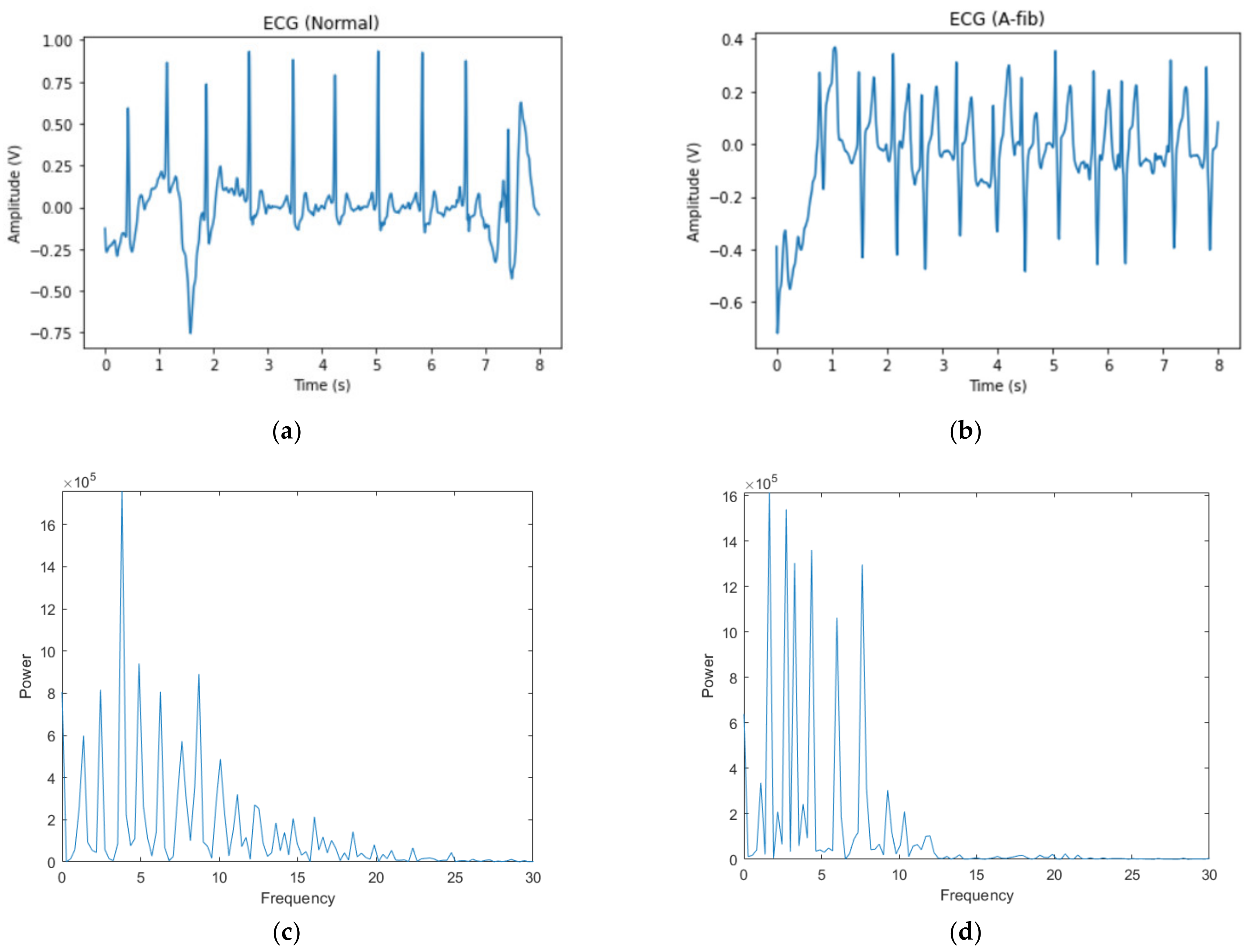
2.1. Data
2.2. Methods
2.2.1. Bandpass Filter
2.2.2. Spectrogram
2.2.3. Data Augmentation
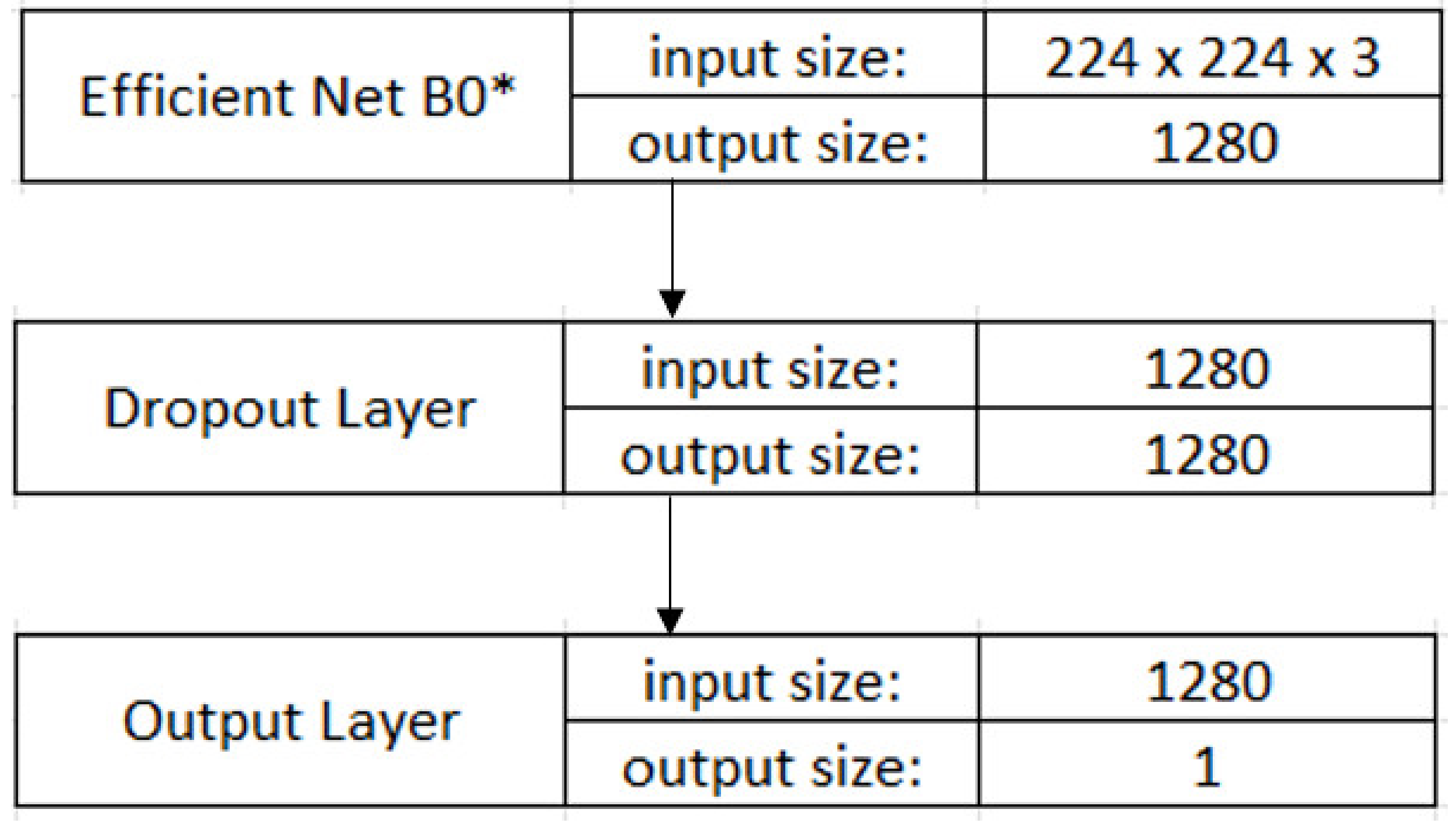
2.2.4. CNN Model
2.2.5. Transfer Learning and Fine-Tuning
3. Results
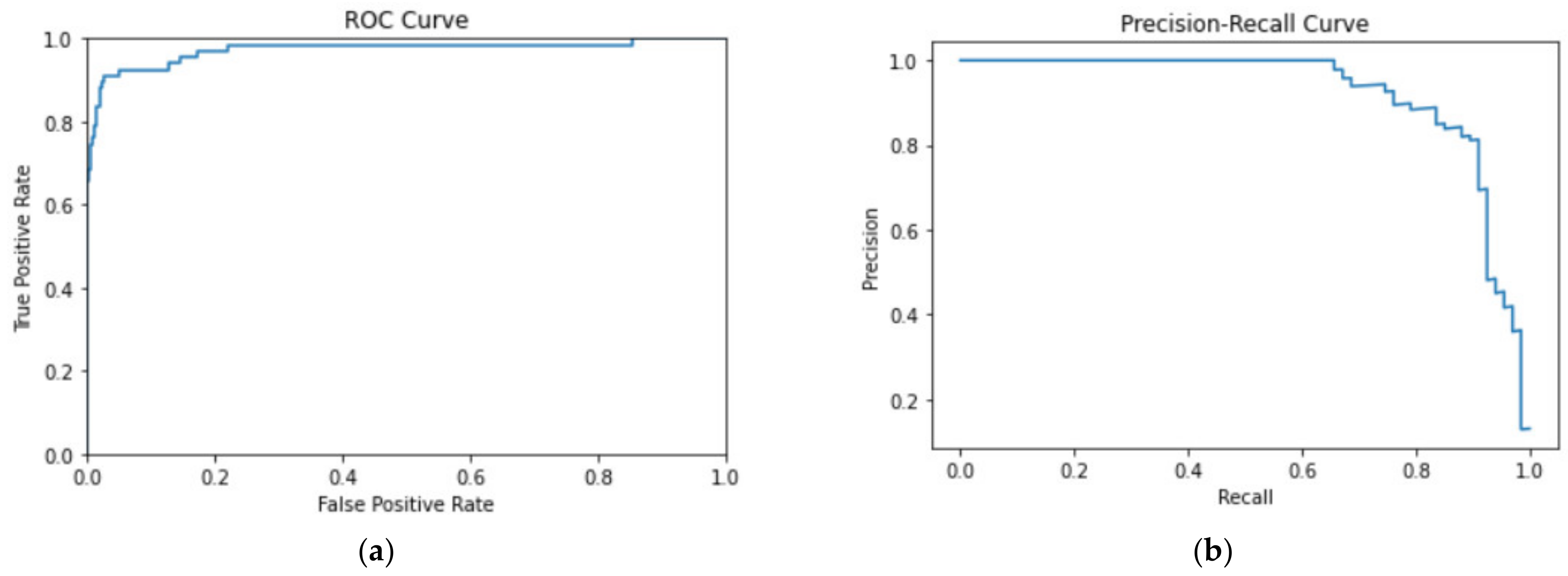
3.1. Evaluation Metrics
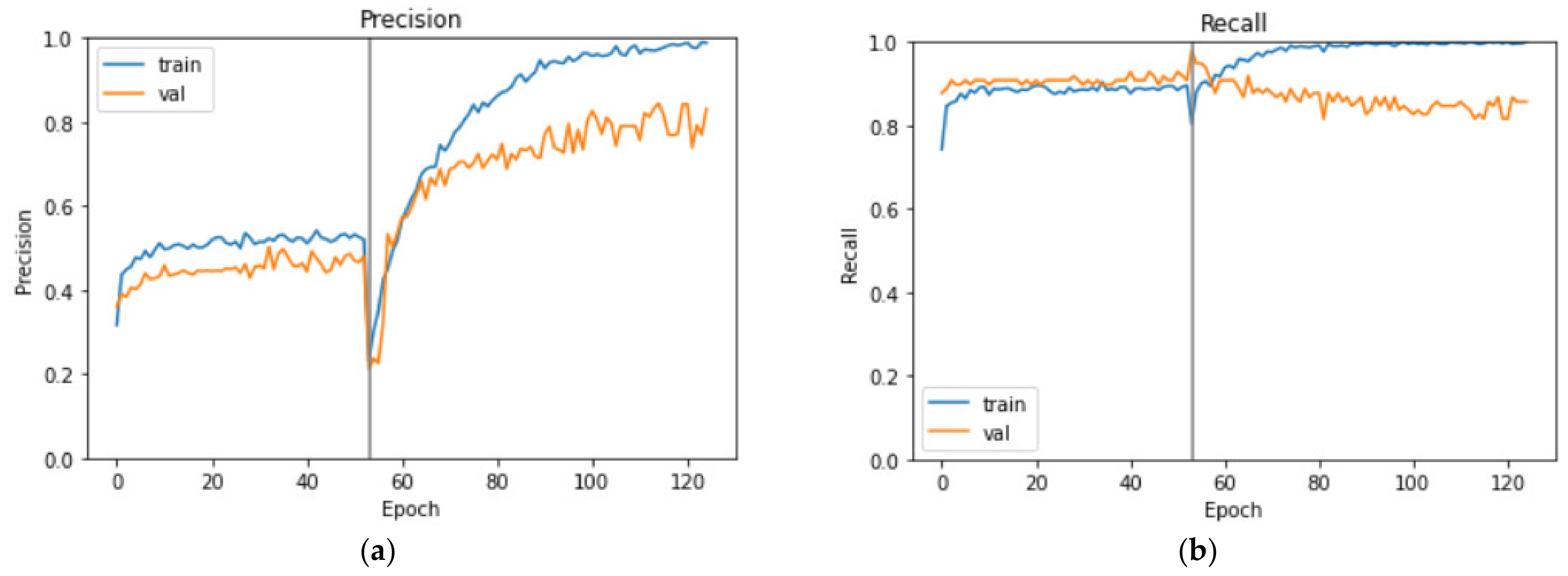
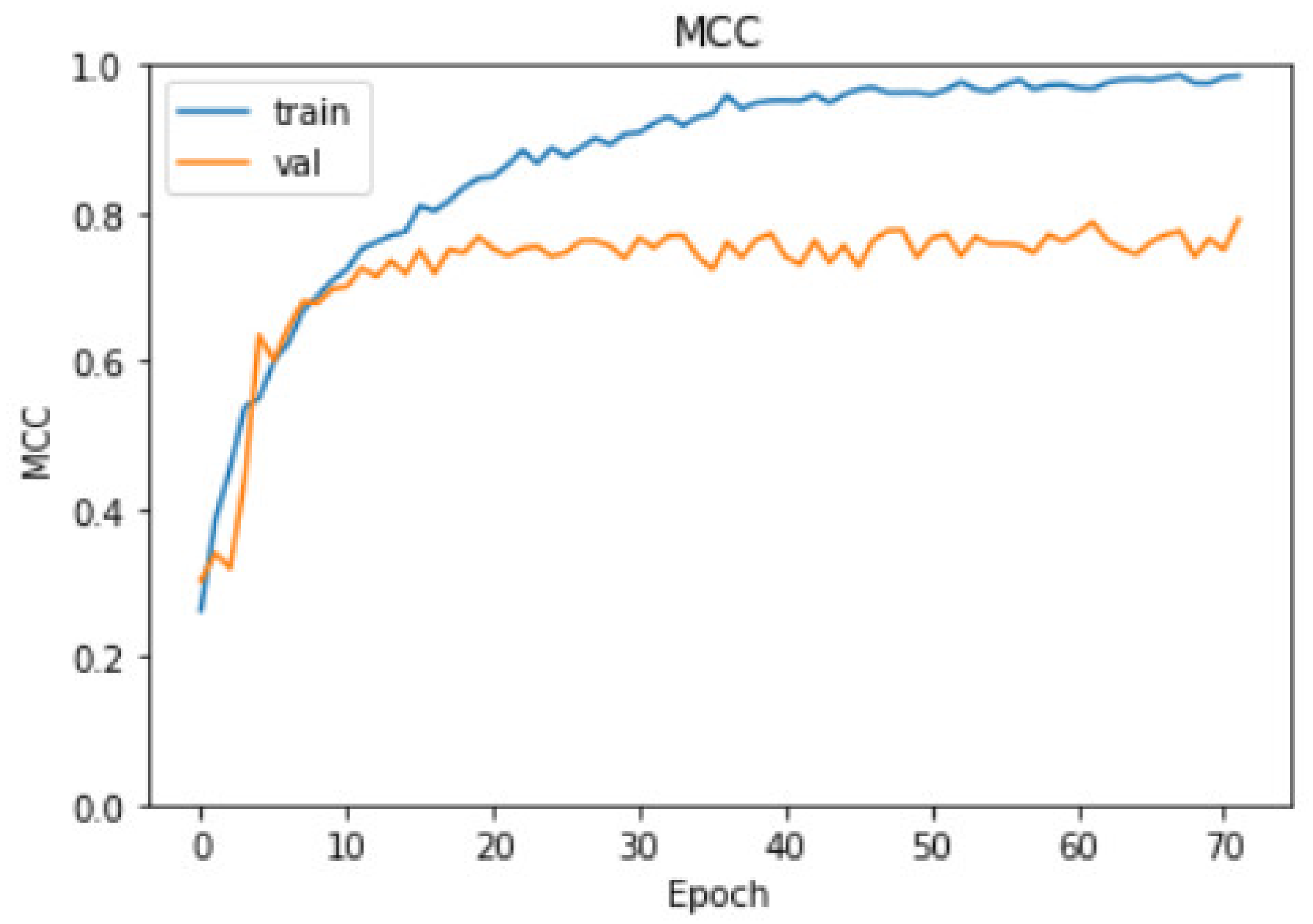
3.2. Evaluation Results
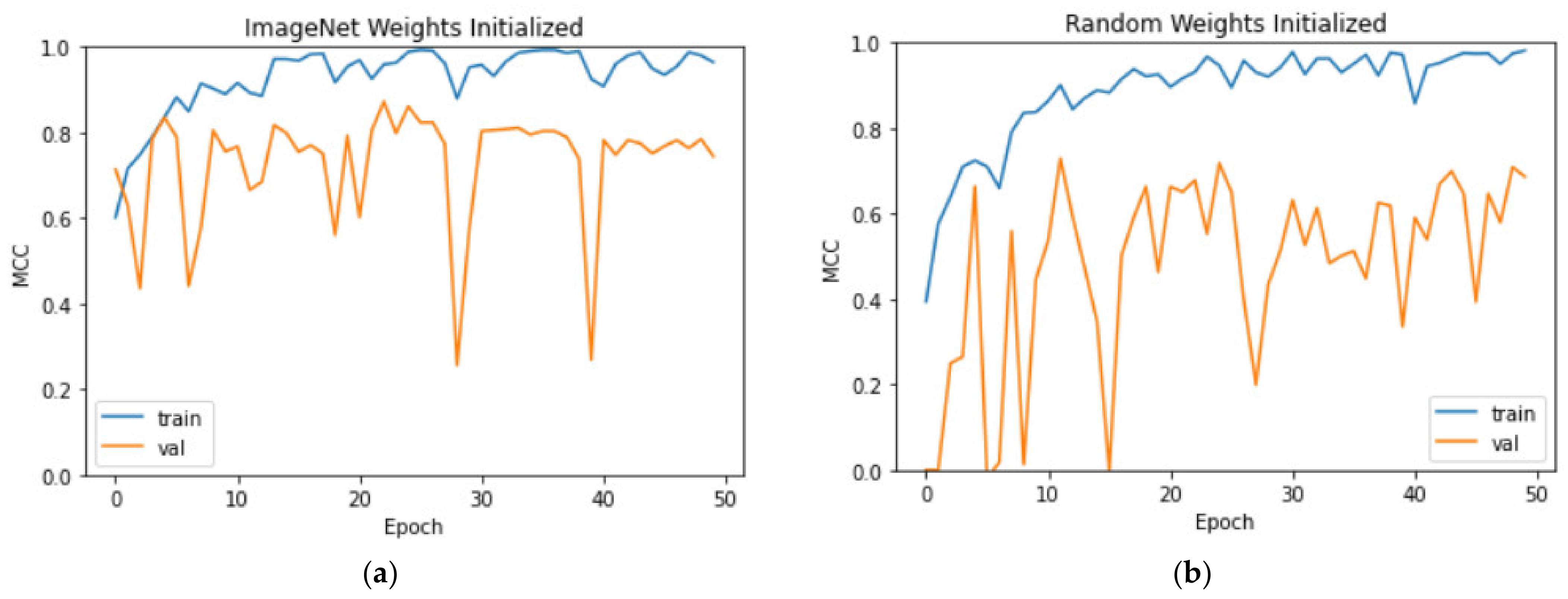
3.3. Comparison of the Training Methods
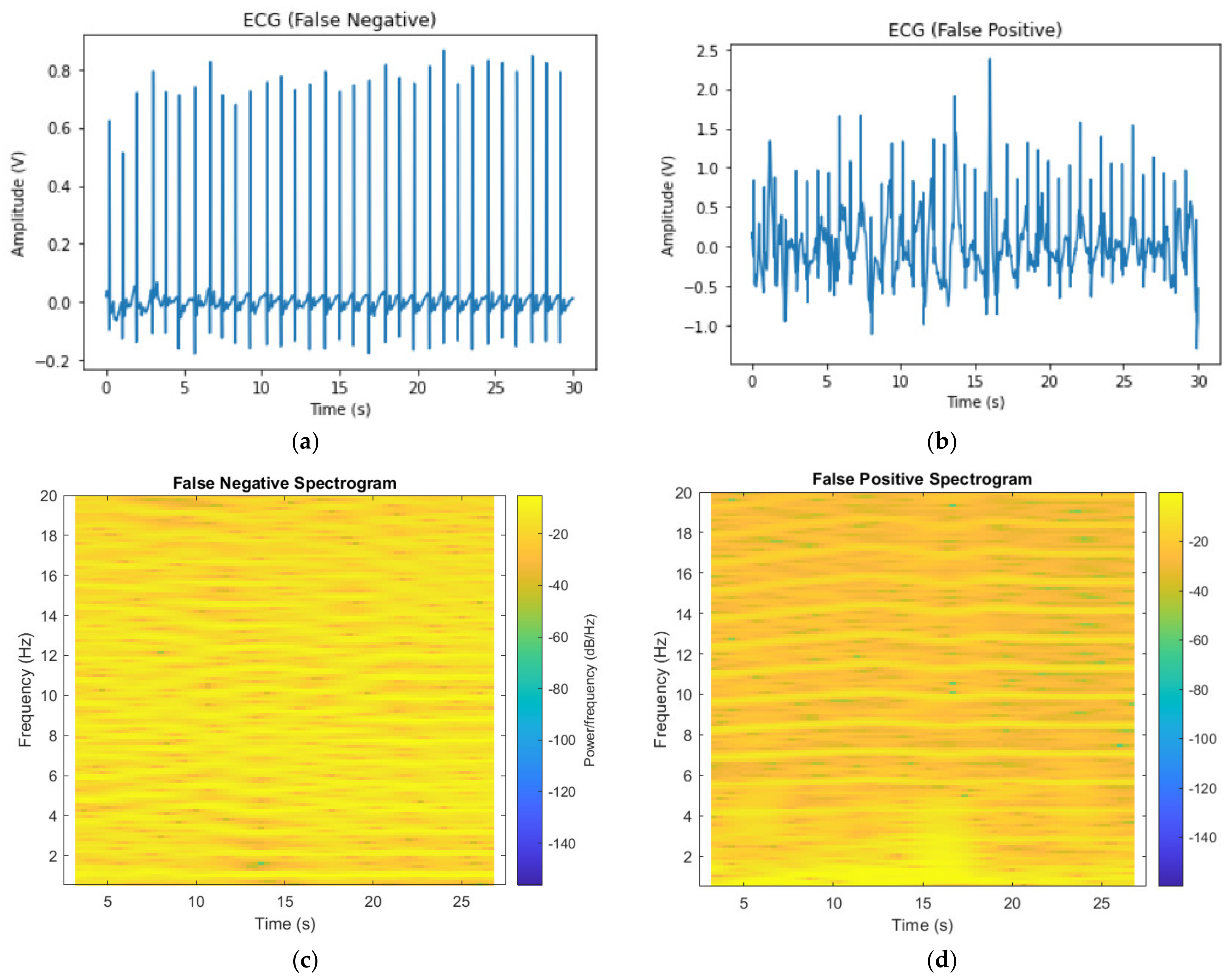
3.4. Examples of Incorrect Predictions
3.5. Dropout Rate Changes
3.6. Result Comparison with Related Works
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alzubaidi, L.; Al-Amidie, M.; Al-Asadi, A.; Humaidi, A.J.; Al-Shamma, O.; Fadhel, M.A.; Zhang, J.; Santamaría, J.; Duan, Y. Novel Transfer Learning Approach for Medical Imaging with Limited Labeled Data. Cancers 2021, 13, 1590. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Pandey, S.K.; Pawar, U.; Janghel, R.R. Classification of ECG Arrhythmia using Recurrent Neural Networks. Procedia Comput. Sci. 2018, 132, 1290–1297. [Google Scholar] [CrossRef]
- Faust, O.; Shenfield, A.; Kareem, M.; San, T.R.; Fujita, H.; Acharya, U.R. Automated detection of atrial fibrillation using long short-term memory network with RR interval signals. Comput. Biol. Med. 2018, 102, 327–335. [Google Scholar] [CrossRef] [PubMed]
- January, C.T.; Wann, L.S.; Alpert, J.S.; Calkins, F.H.; Cigarroa, J.E.; Cleveland, J.C.; Conti, J.B.; Ellinor, P.; Ezekowitz, M.D.; Field, M.E.; et al. 2014 AHA/ACC/HRS guideline for the management of patients with atrial fibrillation: A report of the American College of Cardiology/American Heart Association Task Force on practice guidelines and the Heart Rhythm Society. J. Am. Coll. Cardiol. 2014, 6, 2071–2104. [Google Scholar] [CrossRef]
- Kannel, W.; Wolf, P.; Benjamin, E.; Levy, D. Prevalence, incidence, prognosis, and predisposing conditions for atrial fibrillation: Population-based estimates. Am. J. Cardiol. 1998, 82, 2N–9N. [Google Scholar] [CrossRef]
- Stewart, S.; Hart, C.L.; Hole, D.J.; McMurray, J.J. A population-based study of the long-term risks associated with atrial fibrillation: 20-year follow-up of the Renfrew/Paisley study. Am. J. Med. 2002, 113, 359–364. [Google Scholar] [CrossRef]
- Gajewski, J.; Singer, R.B. Mortality in an Insured Population With Atrial Fibrillation. JAMA 1981, 245, 1540–1544. [Google Scholar] [CrossRef]
- Wolf, P.A.; Abbott, R.D.; Kannel, W.B. Atrial fibrillation as an independent risk factor for stroke: The Framingham Study. Stroke 1991, 22, 983–988. [Google Scholar] [CrossRef]
- Benjamin, E.J.; Virani, S.S.; Callaway, C.W.; Chamberlain, A.M.; Chang, A.R.; Cheng, S.; Chiuve, S.E.; Cushman, M.; Delling, F.N.; Deo, R.; et al. Heart Disease and Stroke Statistics-2018 Update: A Report From the American Heart Association. Circulation 2018, 137, e67–e492. [Google Scholar] [CrossRef] [PubMed]
- Healey, J.S.; Connolly, S.J.; Gold, M.R.; Israel, C.W.; Van Gelder, I.C.; Capucci, A.; Lau, C.; Fain, E.; Yang, S.; Bailleul, C.; et al. Subclinical Atrial Fibrillation and the Risk of Stroke. N. Engl. J. Med. 2012, 366, 120–129. [Google Scholar] [CrossRef] [PubMed]
- Verberk, W.J.; Omboni, S.; Kollias, A.; Stergiou, G.S. Screening for atrial fibrillation with automated blood pressure measurement: Research evidence and practice recommendations. Int. J. Cardiol. 2016, 203, 465–473. [Google Scholar] [CrossRef] [PubMed]
- Rincón, F.; Grassi, P.R.; Khaled, N.; Atienza, D.; Sciuto, D. Automated real-time atrial fibrillation detection on a wearable wireless sensor platform. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; pp. 2472–2475. [Google Scholar] [CrossRef]
- Hong, S.; Wu, M.; Zhou, Y.; Wang, Q.; Shang, J.; Li, H.; Xie, J. ENCASE: An ENsemble ClASsifiEr for ECG Classification Using Expert Features and Deep Neural Networks. In Proceedings of the 2017 Computing in Cardiology (CinC), Rennes, France, 24–27 September 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Ribeiro, A.L.P.; Ribeiro, M.H.; Paixão, G.M.M.; Oliveira, D.M.; Gomes, P.R.; Canazart, J.A.; Ferreira, M.P.S.; Andersson, C.R.; Macfarlane, P.W.; Meira, W.; et al. Automatic diagnosis of the 12-lead ECG using a deep neural network. Nat. Commun. 2020, 11, 1760. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimi, Z.; Loni, M.; Daneshtalab, M.; Gharehbaghi, A. A review on deep learning methods for ECG arrhythmia classification. Expert Syst. Appl. X 2020, 7, 100033. [Google Scholar] [CrossRef]
- Plesinger, F.; Nejedly, P.; Viscor, I.; Halamek, J.; Jurak, P. Automatic detection of atrial fibrillation and other arrhythmias in holter ECG recordings using rhythm features and neural networks. In Proceedings of the 2017 Computing in Cardiology (CinC), Rennes, France, 24–27 September 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Kamaleswaran, R.; Mahajan, R.; Akbilgic, O. A robust deep convolutional neural network for the classification of abnormal cardiac rhythm using single lead electrocardiograms of variable length. Physiol. Meas. 2018, 39, 035006. [Google Scholar] [CrossRef]
- Andreotti, F.; Carr, O.; Pimentel, M.A.F.; Mahdi, A.; De Vos, M. Comparing Feature Based Classifiers and Convolutional Neural Networks to Detect Arrhythmia from Short Segments of ECG. In Proceedings of the 2017 Computing in Cardiology Conference, Rennes, France, 24–27 September 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Fan, X.; Yao, Q.; Cai, Y.; Miao, F.; Sun, F.; Li, Y. Multiscaled Fusion of Deep Convolutional Neural Networks for Screening Atrial Fibrillation From Single Lead Short ECG Recordings. IEEE J. Biomed. Health Inform. 2018, 22, 1744–1753. [Google Scholar] [CrossRef]
- Xiong, Z.; Stiles, M.; Zhao, J. Robust ECG Signal Classification for the Detection of Atrial Fibrillation Using Novel Neural Networks. In Proceedings of the 2017 Computing in Cardiology (CinC), Rennes, France, 24–27 September 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Maknickas, V.; Maknickas, A. Atrial Fibrillation Classification Using QRS Complex Features and LSTM. In Proceedings of the 2017 Computing in Cardiology (CinC), Rennes, France, 24–27 September 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International conference on machine learning, Long Beach, CA, USA, 9 June–15 September 2019; pp. 6105–6114. [Google Scholar] [CrossRef]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 6. [Google Scholar] [CrossRef] [PubMed]
- Lever, J.; Krzywinski, M.; Altman, N. Classification evaluation. Nat. Methods 2016, 13, 603–604. [Google Scholar] [CrossRef]
- Clifford, G.D.; Liu, C.; Moody, B.; Lehman, L.H.; Silva, I.; Li, Q.; Johnson, A.E.; Mark, R.G. AF classification from a short single lead ECG recording: The PhysioNet/Computing in Cardiology Challenge 2017. In Proceedings of the 2017 Computing in Cardiology (CinC), Rennes, France, 24–27 September 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.-K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A Comprehensive Survey on Transfer Learning. Proc. IEEE 2020, 109, 43–76. [Google Scholar] [CrossRef]



| Type | # of Samples | Mean | Median | Max | Min | SD |
|---|---|---|---|---|---|---|
| Normal | 5154 | 31.9 | 30 | 61 | 9 | 10.0 |
| A-fib | 771 | 31.6 | 30 | 60 | 10 | 12.5 |
| Predicted | Positive | Negative | |
|---|---|---|---|
| Actual | |||
| Positive | 59 | 8 | |
| Negative | 11 | 514 | |
| Our B0 Model | Our B0 Model with Data Augmentation | |
|---|---|---|
| Accuracy | 96.79% | 95.86% |
| Precision | 84.29% | 84.94% |
| Recall | 88.06% | 85.45% |
| F1 Score | 86.13% | 85.19% |
| MCC | 84.34% | 82.79% |
| AUC | 95.34% | 96.94% |
| AUC-PR | 92.21% | 92.65% |
| (i) TL-FT | (ii) TL-WI | (iii) RWI | |
|---|---|---|---|
| TP | 59 | 55 | 58 |
| FP | 11 | 7 | 31 |
| TN | 514 | 518 | 494 |
| FN | 8 | 12 | 9 |
| Accuracy | 96.79% | 96.79% | 93.24% |
| Precision | 84.29% | 88.71% | 65.17% |
| Recall | 88.06% | 82.09% | 86.57% |
| F1 Score | 86.13% | 85.27% | 74.36% |
| MCC | 84.34% | 83.55% | 71.50% |
| AUC | 95.34% | 96.24% | 96.64% |
| AUC-PR | 92.21% | 92.42% | 85.45% |
| Dropout Rate | Accuracy | Precision | Recall | F1 Score | MCC |
|---|---|---|---|---|---|
| 0.95 | 96.62% | 86.15% | 83.58% | 84.85% | 82.96% |
| 0.9 | 97.13% | 85.71% | 89.55% | 87.59% | 85.99% |
| 0.8 | 97.30% | 86.96% | 89.55% | 88.24% | 86.72% |
| 0.7 | 96.79% | 83.33% | 89.55% | 86.33% | 84.59% |
| 0.5 | 96.79% | 84.29% | 88.06% | 86.13% | 84.34% |
| 0 | 96.96% | 90.16% | 82.09% | 85.94% | 84.35% |
| Works | Model Type | Data Input | Addressed Data Imbalance? |
|---|---|---|---|
| Plesinger et al. [18] | CNN, NN, and BT | Raw signal | No |
| Kamaleswaran et al. [19] | 13-layer 1D CNN | Repeating segments or zero-padding until 18,286 samples | No |
| Andreotti et al. [20] | ResNet | Truncated to the first minute | Yes |
| Fan et al. [21] | Multiscaled Fusion of CNN | Padded or cropped to fixed lengths | Yes |
| Xiong et al. [22] | 16-layer 1D CNN | 5-sec segments | No |
| Maknickas et al. [23] | LSTM | Divided into 46-timestep segments; padded shorter ones | No |
| Our work | EfficientNet B0 | Raw signal | Yes |
| Works | Classification Type | Precision, Recall | F1 Scores * | F1 Score (Avg.) | MCC |
|---|---|---|---|---|---|
| Ref. [18] | 4-class | - | 91%, 80%, 74% | 81% | - |
| Ref. [19] | 4-class | - | 91%, 82%, 75% | 83% | - |
| Ref. [20] | 4-class | - | 93%, 78%, 78% | 83% | - |
| Ref. [21] | 2-class | 85.43, 92.41% (padded/cropped to 5 s) 91.78%, 93.77% (padded/cropped to 20 s) | - | 88.78% 92.76% | - |
| Ref. [22] | 4-class | - | 90%, 82%, 75% | 82% | - |
| Ref. [23] | 4-class | - | 90%, 75%, 69% | 78% | - |
| Our work | 2-class | 86.96%, 89.55% | - | 88.24% | 86.72% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, T.-R.; Lu, S.; Yan, Y. Automated Atrial Fibrillation Detection with ECG. Bioengineering 2022, 9, 523. https://doi.org/10.3390/bioengineering9100523
Wei T-R, Lu S, Yan Y. Automated Atrial Fibrillation Detection with ECG. Bioengineering. 2022; 9(10):523. https://doi.org/10.3390/bioengineering9100523
Chicago/Turabian StyleWei, Ting-Ruen, Senbao Lu, and Yuling Yan. 2022. "Automated Atrial Fibrillation Detection with ECG" Bioengineering 9, no. 10: 523. https://doi.org/10.3390/bioengineering9100523
APA StyleWei, T.-R., Lu, S., & Yan, Y. (2022). Automated Atrial Fibrillation Detection with ECG. Bioengineering, 9(10), 523. https://doi.org/10.3390/bioengineering9100523