Prediction of the Ibuprofen Loading Capacity of MOFs by Machine Learning
Abstract
:1. Introduction
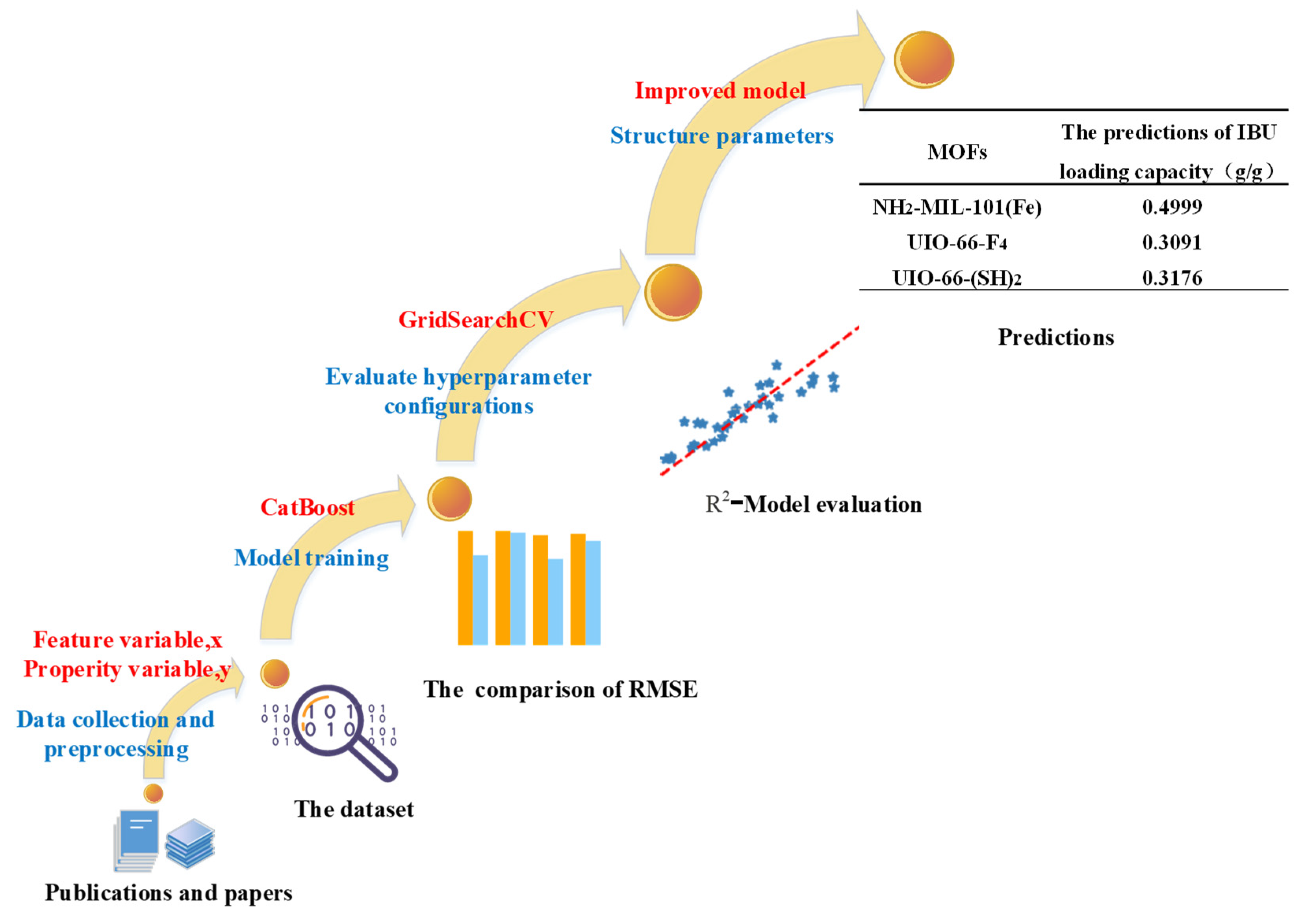
2. Materials and Methods
2.1. Data Acquisition
2.2. Data Processing
2.3. Methodology
2.4. Computational Modeling
3. Results and Discussion
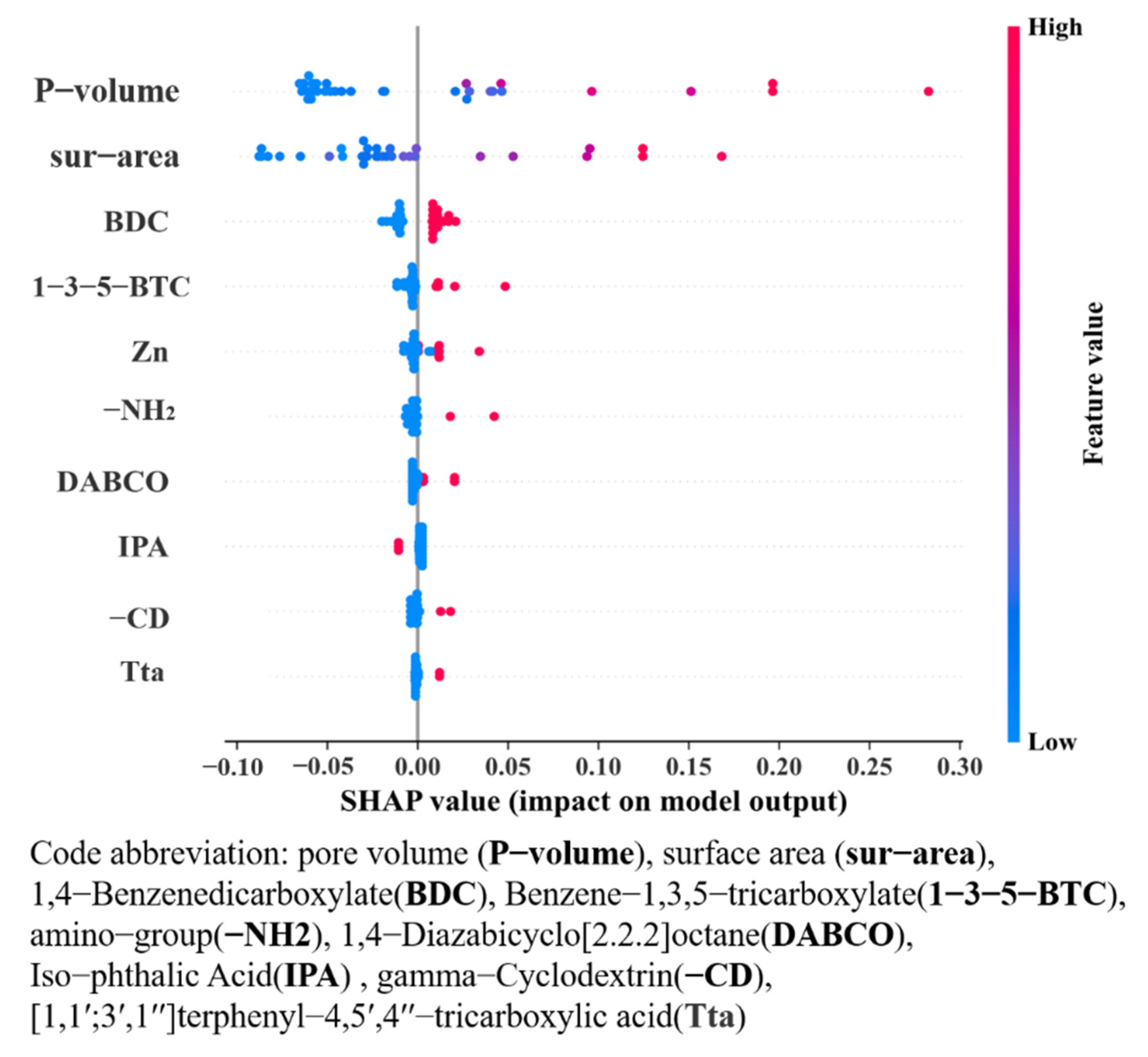
3.1. The Screening of Correlation Parameters
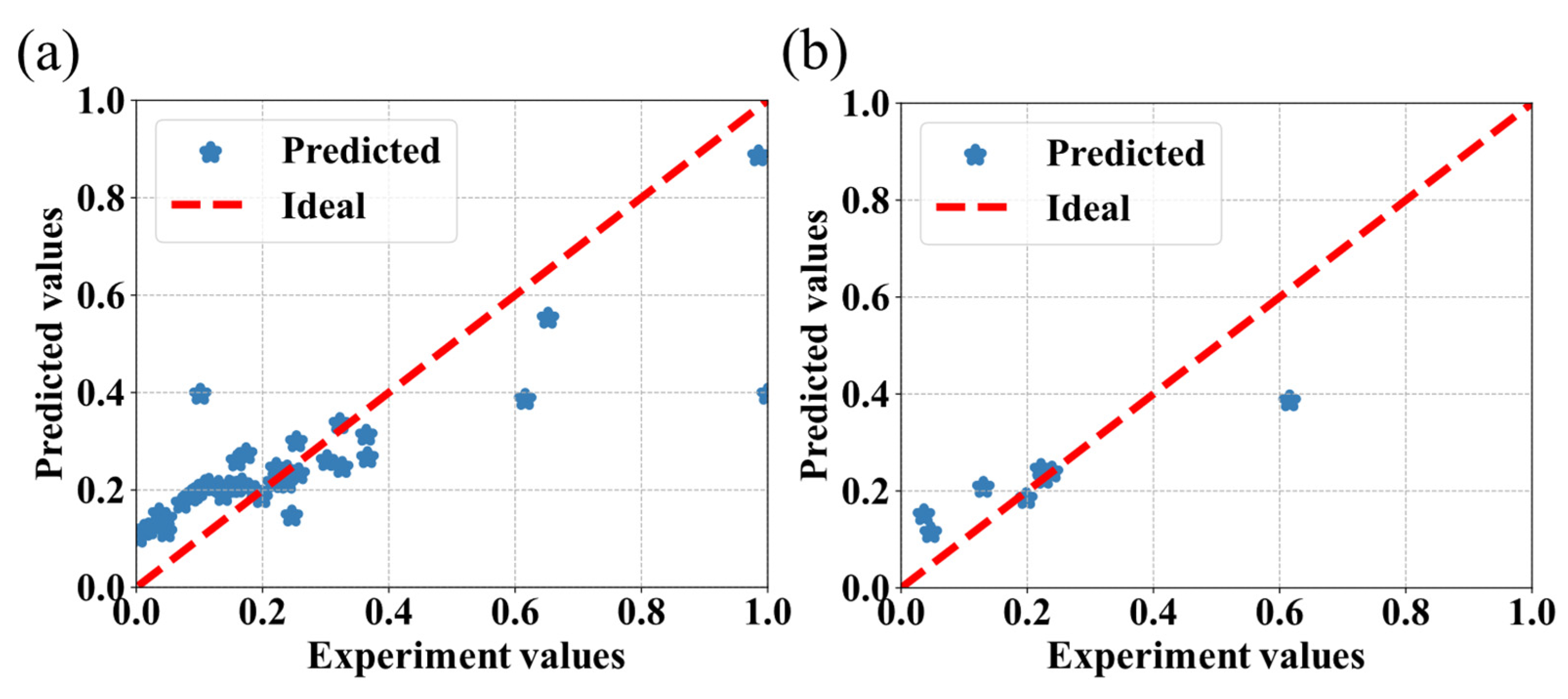
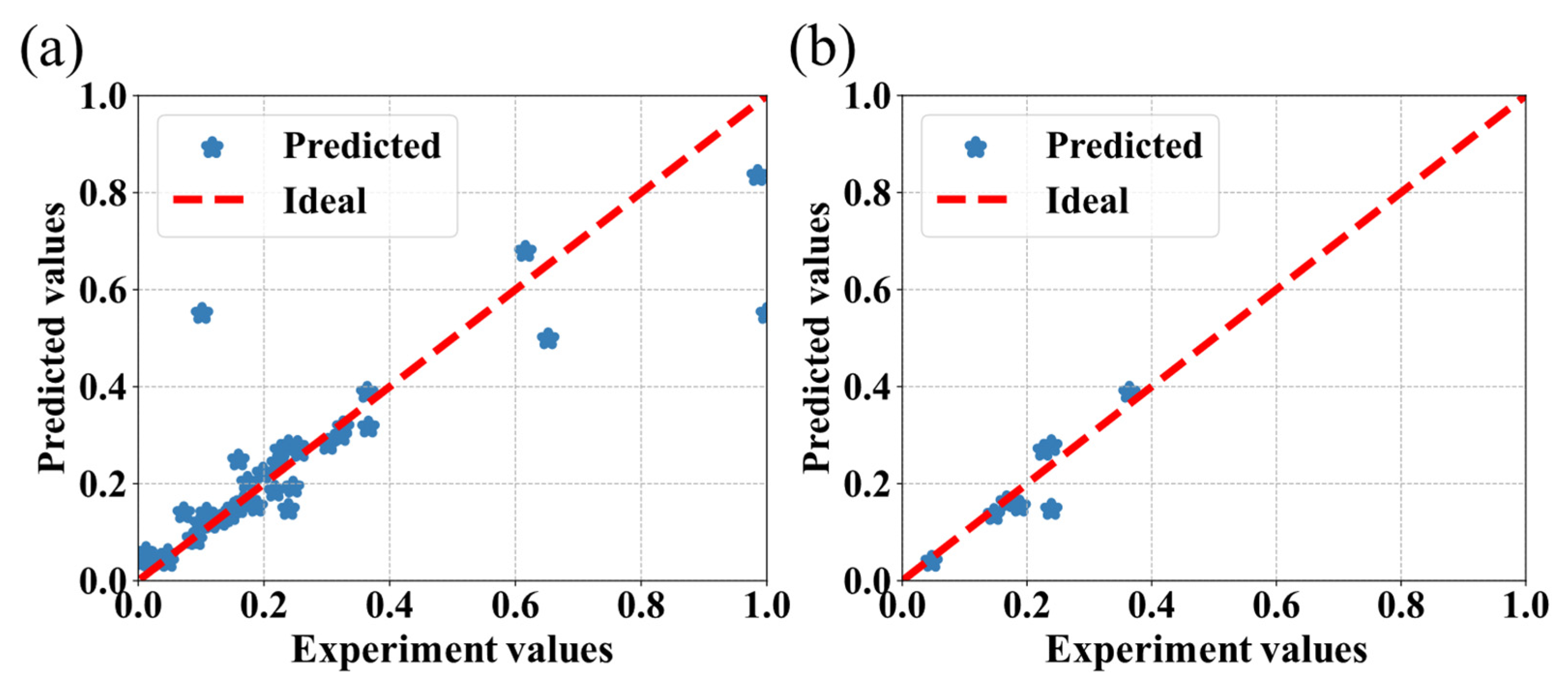
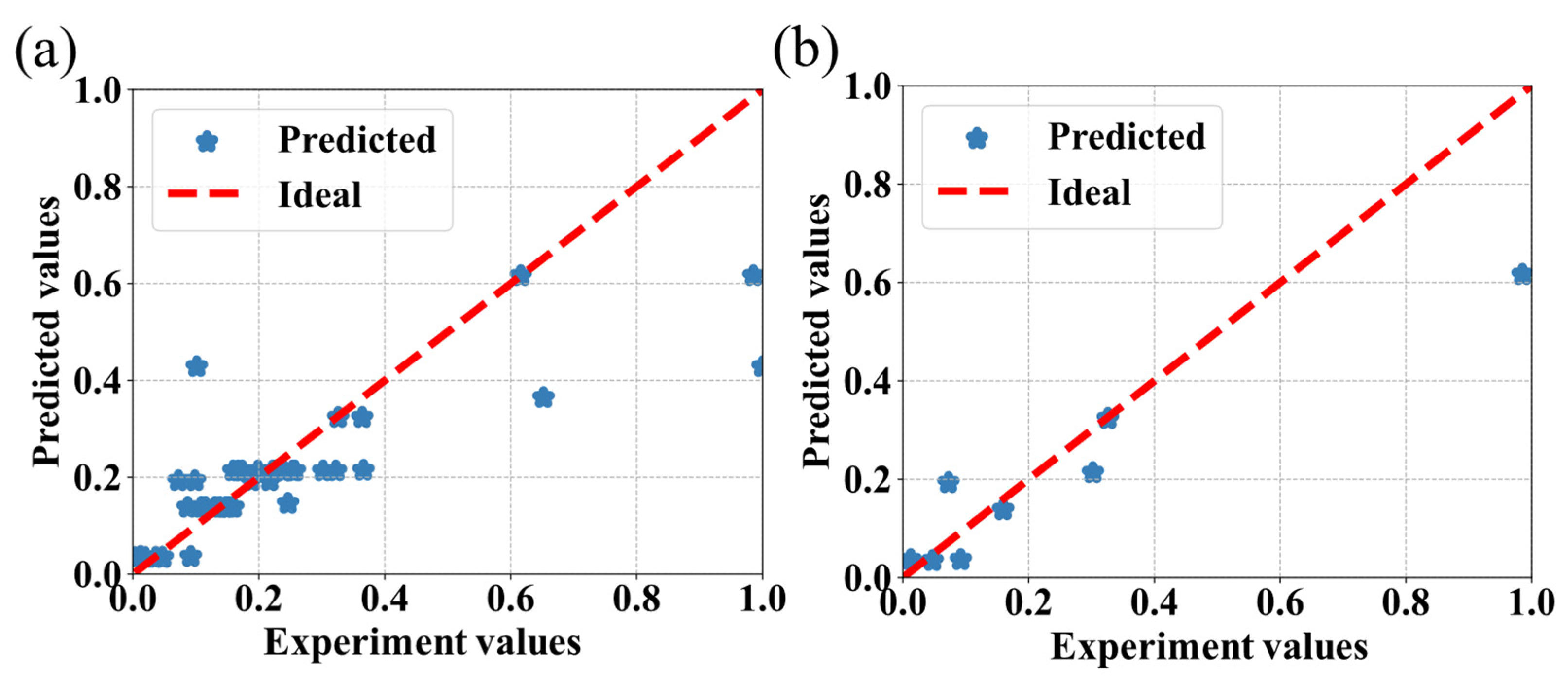
3.2. The Comparison of Different Machine Learning Algorithms
3.3. Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lestari, W.W.; Arvinawati, M.; Martien, R.; Kusumaningsih, T. Green and facile synthesis of MOF and nano MOF containing zinc(II) and benzen 1,3,5-tri carboxylate and its study in ibuprofen slow-release. Mater. Chem. Phys. 2018, 204, 141–146. [Google Scholar] [CrossRef]
- Jiang, K.; Ni, W.; Cao, X.; Zhang, L.; Lin, S. A nanosized anionic MOF with rich thiadiazole groups for controlled oral drug delivery. Mater. Today Bio 2022, 13, 100180. [Google Scholar] [CrossRef] [PubMed]
- Ma, P.; Zhang, J.; Liu, P.; Wang, Q.; Zhang, Y.; Song, K.; Li, R.; Shen, L. Computer-assisted design for stable and porous metal-organic framework (MOF) as a carrier for curcumin delivery. LWT 2020, 120, 108949. [Google Scholar] [CrossRef]
- Phatharapeetranun, N.; Ksapabutr, B.; Marani, D.; Bowen, J.R.; Esposito, V. 3D-printed barium titanate/poly-(vinylidene fluoride) nano-hybrids with anisotropic dielectric properties. J. Mater. Chem. C 2017, 5, 12430–12440. [Google Scholar] [CrossRef]
- Wang, G.; Huang, X.; Jiang, P. Tailoring Dielectric Properties and Energy Density of Ferroelectric Polymer Nanocomposites by High-k Nanowires. ACS Appl. Mater. Interface 2015, 7, 18017–18027. [Google Scholar] [CrossRef]
- Yang, Y.; Li, L.; Lin, R.; Ye, Y.; Yao, Z.; Yang, L.; Xiang, F.; Chen, S.; Zhang, Z.; Xiang, S.; et al. Ethylene/ethane separation in a stable hydrogen-bonded organic framework through a gating mechanism. Nat. Chem. 2021, 13, 933–939. [Google Scholar] [CrossRef]
- Zhang, L.; Li, L.; Hu, E.; Yang, L.; Shao, K.; Yao, L.; Jiang, K.; Cui, Y.; Yang, Y.; Li, B.; et al. Boosting Ethylene/Ethane Separation within Copper(I)-Chelated Metal–Organic Frameworks through Tailor-Made Aperture and Specific π-Complexation. Adv. Sci. 2020, 7, 1901918. [Google Scholar] [CrossRef]
- Cui, Y.; Zhang, J.; He, H.; Qian, G. Photonic functional metal-organic frameworks. Chem. Soc. Rev. 2018, 47, 5740–5785. [Google Scholar] [CrossRef]
- Dhakshinamoorthy, A.; Asiri, A.M.; Garcia, H. 2D Metal–Organic Frameworks as Multifunctional Materials in Heterogeneous Catalysis and Electro/Photocatalysis. Adv. Mater. 2019, 31, 1900617. [Google Scholar] [CrossRef]
- Rivera-Torrente, M.; Mandemaker, L.D.B.; Filez, M.; Delen, G.; Seoane, B.; Meirer, F.; Weckhuysen, B.M. Spectroscopy, microscopy, diffraction and scattering of archetypal MOFs: Formation, metal sites in catalysis and thin films. Chem. Soc. Rev. 2020, 49, 6694–6732. [Google Scholar] [CrossRef]
- Liu, G.; Cadiau, A.; Liu, Y.; Adil, K.; Chernikova, V.; Carja, I.; Belmabkhout, Y.; Karunakaran, M.; Shekhah, O.; Zhang, C.; et al. Enabling Fluorinated MOF-Based Membranes for Simultaneous Removal of H2S and CO2 from Natural Gas. Angew. Chem. Int. Ed. 2018, 57, 14811–14816. [Google Scholar] [CrossRef] [PubMed]
- Robison, L.; Zhang, L.; Drout, R.J.; Li, P.; Haney, C.R.; Brikha, A.; Noh, H.; Mehdi, B.L.; Browning, N.D.; Dravid, V.P.; et al. A Bismuth Metal–Organic Framework as a Contrast Agent for X-ray Computed Tomography. ACS Appl. Bio Mater. 2019, 2, 1197–1203. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Chen, Y.; Wang, S.; Li, P.; Mirkin, C.A.; Farha, O.K. DNA-Functionalized Metal–Organic Framework Nanoparticles for Intracellular Delivery of Proteins. J. Am. Chem. Soc. 2019, 141, 2215–2219. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Hou, S.; Zhao, X.; Liu, D. Adsorption and pH-Responsive Release of Tinidazole on Metal–Organic Framework CAU-1. J. Chem. Eng. Data 2019, 64, 1851–1858. [Google Scholar] [CrossRef]
- Baino, F.; Kargozar, S. Regulation of the Ocular Cell/Tissue Response by Implantable Biomaterials and Drug Delivery Systems. Bioengineering 2020, 7, 65. [Google Scholar] [CrossRef]
- Horcajada, P.; Serre, C.; Vallet-Regí, M.; Sebban, M.; Taulelle, F.; Férey, G. Metal–Organic Frameworks as Efficient Materials for Drug Delivery. Angew. Chem. Int. Ed. 2006, 45, 5974–5978. [Google Scholar] [CrossRef]
- Suwardi, A.; Wang, F.; Xue, K.; Han, M.Y.; Teo, P.; Wang, P.; Wang, S.; Liu, Y.; Ye, E.; Li, Z.; et al. Machine Learning-Driven Biomaterials Evolution. Adv. Mater. 2022, 34, 2102703. [Google Scholar] [CrossRef]
- Wang, Y.; Yan, J.; Wen, N.; Xiong, H.; Cai, S.; He, Q.; Hu, Y.; Peng, D.; Liu, Z.; Liu, Y. Metal-organic frameworks for stimuli-responsive drug delivery. Biomaterials 2020, 230, 119619. [Google Scholar] [CrossRef]
- Wu, M.; Yang, Y. Metal-Organic Framework (MOF)-Based Drug/Cargo Delivery and Cancer Therapy. Adv. Mater. 2017, 29, 1606134. [Google Scholar] [CrossRef]
- Ye, Q.; Wang, Y.; Shen, S.; Xu, C.; Wang, J. Biomaterials-Based Delivery of Therapeutic Antibodies for Cancer Therapy. Adv. Healthc. Mater. 2021, 10, 2002139. [Google Scholar] [CrossRef]
- Ashrafizadeh, M.; Hushmandi, K.; Rahmani Moghadam, E.; Zarrin, V.; Hosseinzadeh Kashani, S.; Bokaie, S.; Najafi, M.; Tavakol, S.; Mohammadinejad, R.; Nabavi, N.; et al. Progress in Delivery of siRNA-Based Therapeutics Employing Nano-Vehicles for Treatment of Prostate Cancer. Bioengineering 2020, 7, 91. [Google Scholar] [CrossRef] [PubMed]
- Bjerk, T.R.; Severino, P.; Jain, S.; Marques, C.; Silva, A.M.; Pashirova, T.; Souto, E.B. Biosurfactants: Properties and Applications in Drug Delivery, Biotechnology and Ecotoxicology. Bioengineering 2021, 8, 115. [Google Scholar] [CrossRef] [PubMed]
- Medina-Franco, J.L.; López-López, E.; Andrade, E.; Ruiz-Azuara, L.; Frei, A.; Guan, D.; Zuegg, J.; Blaskovich, M.A.T. Bridging informatics and medicinal inorganic chemistry: Toward a database of metallodrugs and metallodrug candidates. Drug Discov. Today 2022, 27, 1420–1430. [Google Scholar] [CrossRef] [PubMed]
- Sikander, R.; Wang, Y.; Ghulam, A.; Wu, X. Identification of Enzymes-specific Protein Domain Based on DDE, and Convolutional Neural Network. Front. Genet. 2021, 12, 759384. [Google Scholar] [CrossRef] [PubMed]
- Abdi, J.; Hadipoor, M.; Hadavimoghaddam, F.; Hemmati-Sarapardeh, A. Estimation of tetracycline antibiotic photodegradation from wastewater by heterogeneous metal-organic frameworks photocatalysts. Chemosphere 2022, 287, 132135. [Google Scholar] [CrossRef] [PubMed]
- Javanbakht, S.; Pooresmaeil, M.; Namazi, H.; Heydari, A. Facile synthesis of Zn-based metal-organic framework in the presence of carboxymethyl cellulose: A safe carrier for ibuprofen. Int. J. Biol. Macromol. 2021, 191, 531–539. [Google Scholar] [CrossRef]
- Pardakhti, M.; Moharreri, E.; Wanik, D.; Suib, S.L.; Srivastava, R. Machine Learning Using Combined Structural and Chemical Descriptors for Prediction of Methane Adsorption Performance of Metal Organic Frameworks (MOFs). ACS Comb. Sci. 2017, 19, 640–645. [Google Scholar] [CrossRef] [PubMed]
- Gurnani, R.; Yu, Z.; Kim, C.; Sholl, D.S.; Ramprasad, R. Interpretable Machine Learning-Based Predictions of Methane Uptake Isotherms in Metal–Organic Frameworks. Chem. Mater. 2021, 33, 3543–3552. [Google Scholar] [CrossRef]
- Suyetin, M. The application of machine learning for predicting the methane uptake and working capacity of MOFs. Faraday Discuss. 2021, 231, 224–234. [Google Scholar] [CrossRef]
- Batra, R.; Chen, C.; Evans, T.G.; Walton, K.S.; Ramprasad, R. Prediction of water stability of metal–organic frameworks using machine learning. Nat. Mach. Intell. 2020, 2, 704–710. [Google Scholar] [CrossRef]
- Gul, G.; Yildirim, R.; Ileri-Ercan, N. Cytotoxicity analysis of nanoparticles by association rule mining. Environ. Sci. Nano 2021, 8, 937–949. [Google Scholar] [CrossRef]
- Ji, Z.; Guo, W.; Wood, E.L.; Liu, J.; Sakkiah, S.; Xu, X.; Patterson, T.A.; Hong, H. Machine Learning Models for Predicting Cytotoxicity of Nanomaterials. Chem. Res. Toxicol. 2022, 35, 125–139. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, A.; Siegel, D.J. Predicting hydrogen storage in MOFs via machine learning. Patterns 2021, 2, 100291. [Google Scholar] [CrossRef]
- Giappa, R.M.; Tylianakis, E.; Di Gennaro, M.; Gkagkas, K.; Froudakis, G.E. A combination of multi-scale calculations with machine learning for investigating hydrogen storage in metal organic frameworks. Int. J. Hydrogen Energy 2021, 46, 27612–27621. [Google Scholar] [CrossRef]
- Bucior, B.J.; Bobbitt, N.S.; Islamoglu, T.; Goswami, S.; Gopalan, A.; Yildirim, T.; Farha, O.K.; Bagheri, N.; Snurr, R.Q. Energy-based descriptors to rapidly predict hydrogen storage in metal–organic frameworks. Mol. Syst. Des. Eng. 2019, 4, 162–174. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS 2018), Montreal, QC, Canada, 3–8 December 2018; Volume 31. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hastie, T.; Rosset, S.; Zhu, J.; Zou, H. Multi-class adaboost. Stat. Interface 2009, 2, 349–360. [Google Scholar] [CrossRef]
- Horcajada, P.; Serre, C.; Maurin, G.; Ramsahye, N.A.; Balas, F.; Vallet-Regí, M.; Sebban, M.; Taulelle, F.; Férey, G. Flexible Porous Metal-Organic Frameworks for a Controlled Drug Delivery. J. Am. Chem. Soc. 2008, 130, 6774–6780. [Google Scholar] [CrossRef]
- Babarao, R.; Jiang, J. Unraveling the Energetics and Dynamics of Ibuprofen in Mesoporous Metal−Organic Frameworks. J. Phys. Chem. C 2009, 113, 18287–18291. [Google Scholar] [CrossRef]
- Horcajada, P.; Chalati, T.; Serre, C.; Gillet, B.; Sebrie, C.; Baati, T.; Eubank, J.F.; Heurtaux, D.; Clayette, P.; Kreuz, C.; et al. Porous metal–organic-framework nanoscale carriers as a potential platform for drug delivery and imaging. Nat. Mater. 2010, 9, 172–178. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, M.O.; de Paula, M.V.; Wanderley, K.A.; Vasconcelos, I.B.; Alves, S., Jr.; Soares, T.A. Metal organic frameworks for drug delivery and environmental remediation: A molecular docking approach. Int. J. Quantum Chem. 2012, 112, 3346–3355. [Google Scholar] [CrossRef]
- Bernini, M.C.; Fairen-Jimenez, D.; Pasinetti, M.; Ramirez-Pastor, A.J.; Snurr, R.Q. Screening of bio-compatible metal–organic frameworks as potential drug carriers using Monte Carlo simulations. J. Mater. Chem. B 2014, 2, 766–774. [Google Scholar] [CrossRef] [PubMed]
- Bueno-Perez, R.; Martin-Calvo, A.; Gómez-Álvarez, P.; Gutiérrez-Sevillano, J.J.; Merkling, P.J.; Vlugt, T.J.H.; van Erp, T.S.; Dubbeldam, D.; Calero, S. Enantioselective adsorption of ibuprofen and lysine in metal–organic frameworks. Chem. Commun. 2014, 50, 10849–10852. [Google Scholar] [CrossRef]
- Borboudakis, G.; Stergiannakos, T.; Frysali, M.; Klontzas, E.; Tsamardinos, I.; Froudakis, G.E. Chemically intuited, large-scale screening of MOFs by machine learning techniques. npj Comput. Mater. 2017, 3, 40. [Google Scholar] [CrossRef]
- Mohammadi, M.; Hadavimoghaddam, F.; Pourmahdi, M.; Atashrouz, S.; Munir, M.T.; Hemmati-Sarapardeh, A.; Mosavi, A.H.; Mohaddespour, A. Modeling hydrogen solubility in hydrocarbons using extreme gradient boosting and equations of state. Sci. Rep. 2021, 11, 17911. [Google Scholar] [CrossRef]
- Choi, J.; Trinh, T.X.; Yoon, T.; Kim, J.; Byun, H. Quasi-QSAR for predicting the cell viability of human lung and skin cells exposed to different metal oxide nanomaterials. Chemosphere 2019, 217, 243–249. [Google Scholar] [CrossRef]
- Shen, Z.; Wang, S.; Shen, Z.; Tang, Y.; Xu, J.; Lin, C.; Chen, X.; Huang, Q. Deciphering controversial results of cell proliferation on TiO2 nanotubes using machine learning. Regen. Biomater. 2021, 8. [Google Scholar] [CrossRef]
- Abdi, J.; Hadavimoghaddam, F.; Hadipoor, M.; Hemmati-Sarapardeh, A. Modeling of CO2 adsorption capacity by porous metal organic frameworks using advanced decision tree-based models. Sci. Rep. 2021, 11, 24468. [Google Scholar] [CrossRef]
- Bauder, R.; Khoshgoftaar, T. Medicare Fraud Detection using CatBoost. In Proceedings of the 2020 IEEE 21st International Conference on Information Reuse and Integration for Data Science (IRI), Las Vegas, NV, USA, 11–13 August 2020; pp. 97–103. [Google Scholar] [CrossRef]
- Cao, Y.; Karimi, M.; Kamrani, E.; Nourani, P.; Mohammadi Manesh, A.; Momenieskandari, H.; Anqi, A.E. Machine learning methods help accurate estimation of the hydrogen solubility in biomaterials. Int. J. Hydrogen Energy 2022, 47, 3611–3624. [Google Scholar] [CrossRef]
- Santana, R.; Zuluaga, R.; Gañán, P.; Arrasate, S.; Onieva, E.; González-Díaz, H. Predicting coated-nanoparticle drug release systems with perturbation-theory machine learning (PTML) models. Nanoscale 2020, 12, 13471–13483. [Google Scholar] [CrossRef] [PubMed]
- Hancock, J.T.; Khoshgoftaar, T.M. CatBoost for big data: An interdisciplinary review. J. Big Data 2020, 7, 94. [Google Scholar] [CrossRef] [PubMed]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]




| MOFs | Metal Ions | Organic Linkers | Surface Area m2/g | Pore Volume cm3/g | IBU Loading Capacity g/g | Reference |
|---|---|---|---|---|---|---|
| MIL-100 | Cr | BDC | 3340 | 1.160 | 0.350 | [16] |
| MIL-101 | Cr | BDC | 5510 | 2.020 | 0.140 | [16] |
| MIL-53(Cr) | Cr | BDC | 1500 | 1.600 | 0.220 | [40] |
| UMCM-1 | Zn | BDC, BTC | 4764 | 2.280 | 1.360 | [41] |
| MIL-100(Fe) | Fe | BDC | 1900 | 0.590 | 0.330 | [42] |
| [Zn(BDC)(H2O)2]n | Zn | BDC, DABCO | 1545 | 0.669 | 0.445 | [43] |
| MIL-53 | Fe | BDC | 954 | 0.479 | 0.231 | [44] |
| … | … | … | ... | ... | ... | … |
| CD-MOF-1 | K | γ-CD | 1220 | 0.493 | 0.274 | [44] |
| MIL-47 | V | BDC | 729 | 0.270 | 0.120 | [45] |
| MIL-53 | Cr | BDC | 864 | 0.290 | 0.190 | [45] |
| Algorithm | R2 | RMSE (%) |
|---|---|---|
| AdaBoost | 0.66 | 12.10 |
| SVR | 0.70 | 10.53 |
| RF | 0.72 | 9.62 |
| CatBoost | 0.76 | 9.81 |
| MOFs | Metal Ions | Organic Linkers | The Predictions of IBU Loading Capacity (g/g) |
|---|---|---|---|
| NH2-MIL-101(Fe) | Fe | BDC | 0.4999 |
| UIO-66-F4 | Zr | BDC | 0.3091 |
| UIO-66-(SH)2 | Zr | BDC | 0.3176 |
| NO2-UIO-66 | Zr | BDC | 0.3361 |
| MOF-74(Ni) | Ni | BDC | 0.3160 |
| NH2-MIL-101(Cr) | Cr | BDC | 0.4965 |
| MIL-101(Cr) | Cr | BDC | 0.5408 |
| UIO-66 | Ni | BDC | 0.3285 |
| NH2-UIO-66 | Ni | BDC | 0.3197 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Wang, Y.; Yuan, J.; Li, X.; Wu, S.; Bao, Y.; Feng, Z.; Ou, F.; He, Y. Prediction of the Ibuprofen Loading Capacity of MOFs by Machine Learning. Bioengineering 2022, 9, 517. https://doi.org/10.3390/bioengineering9100517
Liu X, Wang Y, Yuan J, Li X, Wu S, Bao Y, Feng Z, Ou F, He Y. Prediction of the Ibuprofen Loading Capacity of MOFs by Machine Learning. Bioengineering. 2022; 9(10):517. https://doi.org/10.3390/bioengineering9100517
Chicago/Turabian StyleLiu, Xujie, Yang Wang, Jiongpeng Yuan, Xiaojing Li, Siwei Wu, Ying Bao, Zhenzhen Feng, Feilong Ou, and Yan He. 2022. "Prediction of the Ibuprofen Loading Capacity of MOFs by Machine Learning" Bioengineering 9, no. 10: 517. https://doi.org/10.3390/bioengineering9100517
APA StyleLiu, X., Wang, Y., Yuan, J., Li, X., Wu, S., Bao, Y., Feng, Z., Ou, F., & He, Y. (2022). Prediction of the Ibuprofen Loading Capacity of MOFs by Machine Learning. Bioengineering, 9(10), 517. https://doi.org/10.3390/bioengineering9100517






