Multiscale Entropy Analysis of Heart Rate Variability in Neonatal Patients with and without Seizures
Abstract
:1. Introduction
2. Materials and Methods
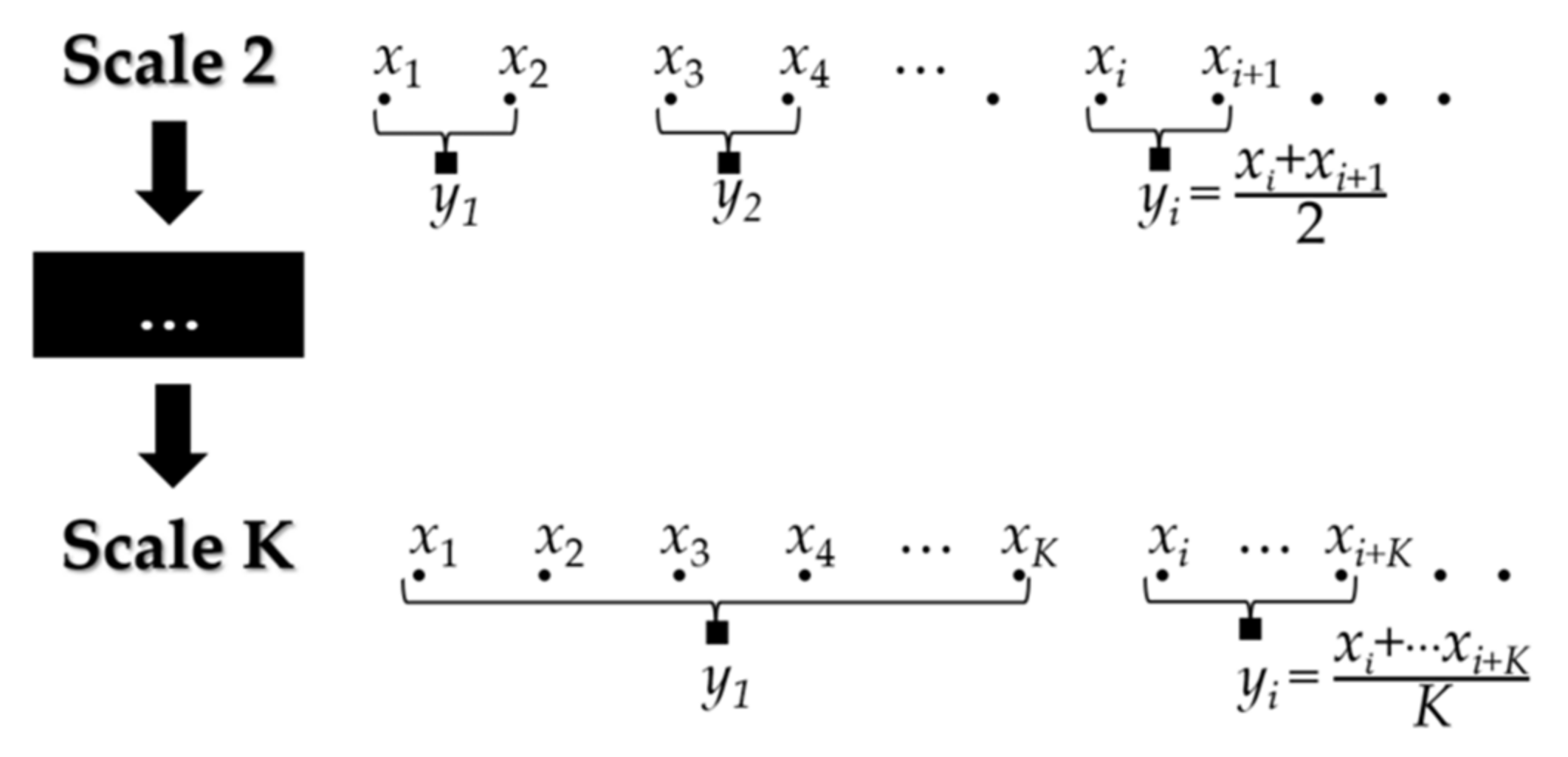
2.1. Multiscale Analysis
2.2. Approximate Entropy, Sample Entropy, and Generalized Sample Entropy
2.3. Fuzzy Entropy
2.4. Permutation Entropy
2.5. Distribution Entropy
2.6. Statistical Analysis
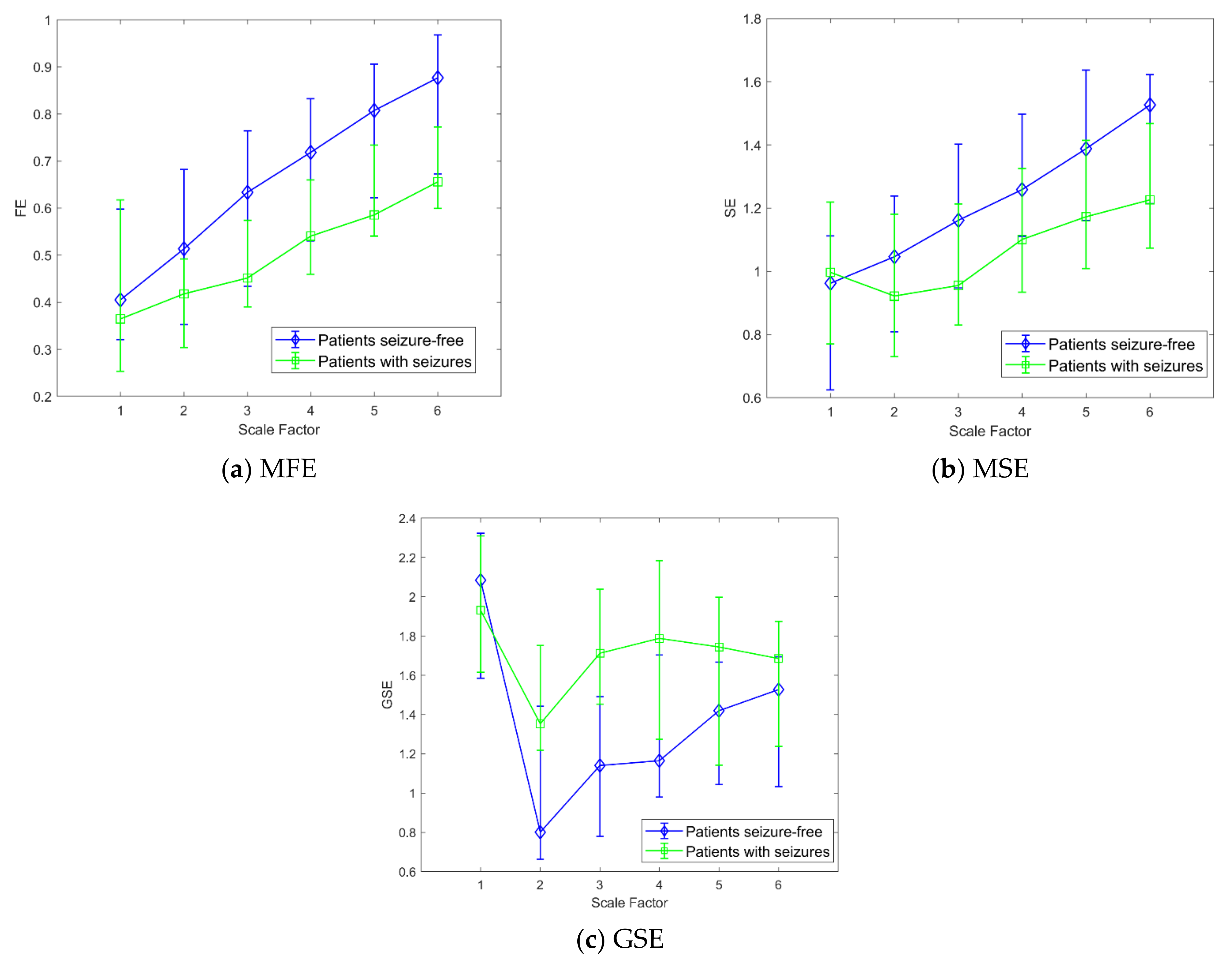
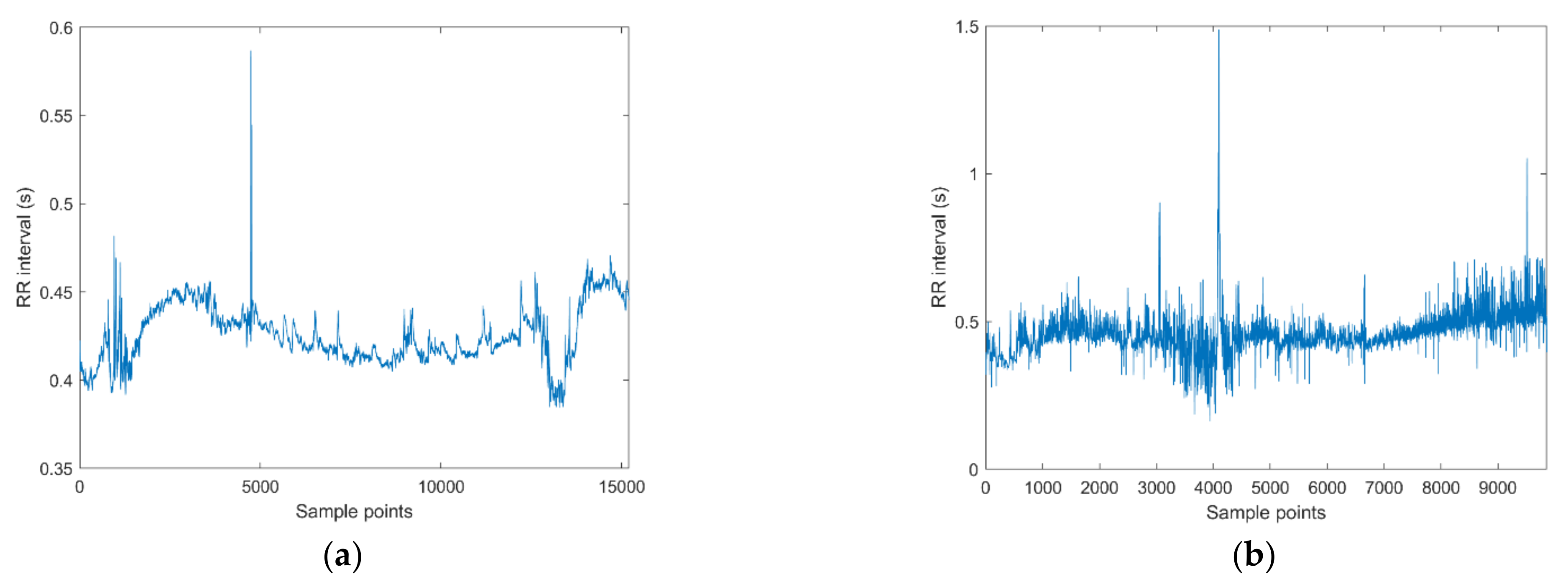
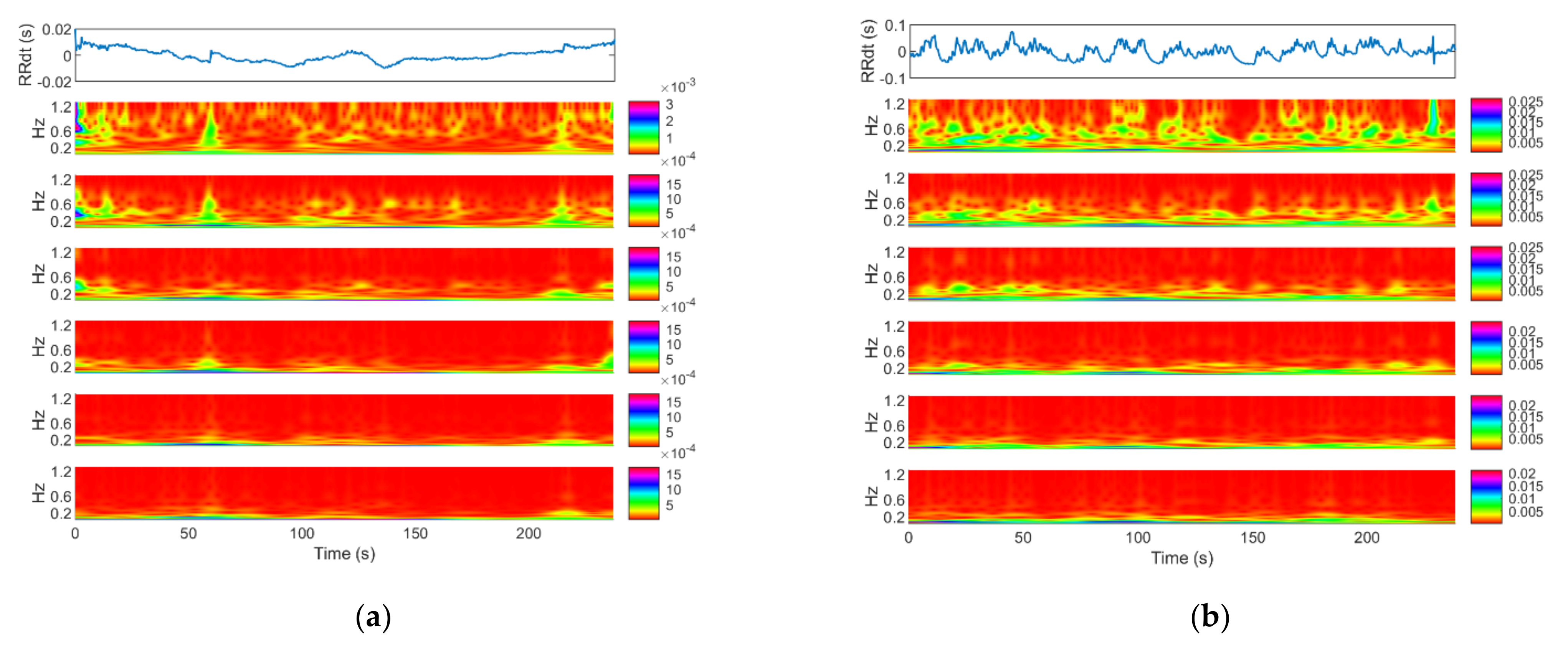
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pressler, R.M.; Cilio, M.R.; Mizrahi, E.M.; Moshé, S.L.; Nunes, M.L.; Plouin, P.; Vanhatalo, S.; Yozawitz, E.; de Vries, L.S.; Vinayan, K.P.; et al. The ILAE classification of seizures and the epilepsies: Modification for seizures in the neonate. Position paper by the ILAE Task Force on Neonatal Seizures. Epilepsia 2021, 62, 615–628. [Google Scholar] [CrossRef] [PubMed]
- Kang, S.K.; Kadam, S.D. Neonatal Seizures: Impact on Neurodevelopmental Outcomes. Front. Pediatr. 2015, 3, 101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pisani, F.; Spagnoli, C.; Falsaperla, R.; Nagarajan, L.; Ramantani, G. Seizures in the neonate: A review of etiologies and outcomes. Seizure 2021, 85, 48–56. [Google Scholar] [CrossRef] [PubMed]
- Thibeault-Eybalin, M.-P.; Lortie, A.; Carmant, L. Neonatal Seizures: Do They Damage the Brain? Pediatr. Neurol. 2009, 40, 175–180. [Google Scholar] [CrossRef]
- Pavel, A.M.; Rennie, J.M.; de Vries, L.S.; Blennow, M.; Foran, A.; Shah, D.K.; Pressler, R.M.; Kapellou, O.; Dempsey, E.M.; Mathieson, S.R.; et al. A machine-learning algorithm for neonatal seizure recognition: A multicentre, randomised, controlled trial. Lancet Child Adolesc. Health 2020, 4, 740–749. [Google Scholar] [CrossRef]
- Hellström-Westas, L. Amplitude-integrated electroencephalography for seizure detection in newborn infants. Semin. Fetal Neonatal Med. 2018, 23, 175–182. [Google Scholar] [CrossRef]
- Shellhaas, R.A.; Soaita, A.I.; Clancy, R.R. Sensitivity of Amplitude-Integrated Electroencephalography for Neonatal Seizure Detection. Pediatrics 2007, 120, 770–777. [Google Scholar] [CrossRef]
- Temko, A.; Lightbody, G. Detecting Neonatal Seizures with Computer Algorithms. J. Clin. Neurophysiol. 2016, 33, 394–402. [Google Scholar] [CrossRef]
- O’Shea, A.; Lightbody, G.; Boylan, G.; Temko, A. Neonatal seizure detection from raw multi-channel EEG using a fully convolutional architecture. Neural Netw. 2020, 123, 12–25. [Google Scholar] [CrossRef]
- Frassineti, L.; Ermini, D.; Fabbri, R.; Manfredi, C. Neonatal Seizures Detection using Stationary Wavelet Transform and Deep Neural Networks: Preliminary Results. In Proceedings of the 2020 IEEE 20th Mediterranean Electrotechnical Conference (MELECON), Palermo, Italy, 16–18 June 2020; pp. 344–349. [Google Scholar] [CrossRef]
- Greene, B.R.; De Chazal, P.; Boylan, G.B.; Connolly, S.; Reilly, R.B. Electrocardiogram Based Neonatal Seizure Detection. IEEE Trans. Biomed. Eng. 2007, 54, 673–682. [Google Scholar] [CrossRef] [Green Version]
- Cabon, S.; Poree, F.; Simon, A.; Rosec, O.; Pladys, P.; Carrault, G. Video and audio processing in paediatrics: A review. Physiol. Meas. 2019, 40, 02TR02. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, A.; Domoki, F.; Bari, F. Seizure-Induced Alterations in Cerebrovascular Function in the Neonate. Dev. Neurosci. 2008, 30, 293–305. [Google Scholar] [CrossRef]
- Bersani, I.; Piersigilli, F.; Gazzolo, D.; Campi, F.; Savarese, I.; Dotta, A.; Tamborrino, P.P.; Auriti, C.; Di Mambro, C. Heart rate variability as possible marker of brain damage in neonates with hypoxic ischemic encephalopathy: A systematic review. Eur. J. Nucl. Med. Mol. Imaging 2021, 180, 1335–1345. [Google Scholar] [CrossRef]
- Lucchini, M.; Fifer, W.P.; Sahni, R.; Signorini, M.G. Novel heart rate parameters for the assessment of autonomic nervous system function in premature infants. Physiol. Meas. 2016, 37, 1436–1446. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Statello, R.; Carnevali, L.; Alinovi, D.; Pisani, F.; Sgoifo, A. Heart rate variability in neonatal patients with seizures. Clin. Neurophysiol. 2018, 129, 2534–2540. [Google Scholar] [CrossRef] [PubMed]
- Humeau-Heurtier, A. Entropy Analysis in Health Informatics. In Signal Processing Techniques for Computational Health Informatics; Ahad, M.A.R., Ahmed, M.U., Eds.; Springer: Cham, Switzerland, 2020; Volume 192, pp. 123–143. [Google Scholar] [CrossRef]
- Valenza, G.; Nardelli, M.; Bertschy, G.; Lanata, A.; Scilingo, E.P. Mood states modulate complexity in heartbeat dynamics: A multiscale entropy analysis. EPL Europhys. Lett. 2014, 107, 18003. [Google Scholar] [CrossRef]
- Nardelli, M.; Lanata, A.; Bertschy, G.; Scilingo, E.P.; Valenza, G. Heartbeat Complexity Modulation in Bipolar Disorder during Daytime and Nighttime. Sci. Rep. 2017, 7, 17920. [Google Scholar] [CrossRef] [Green Version]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef] [Green Version]
- Vanhatalo, S.; Kaila, K. Development of neonatal EEG activity: From phenomenology to physiology. Semin. Fetal Neonatal Med. 2006, 11, 471–478. [Google Scholar] [CrossRef]
- Frassineti, L.; Parente, A.; Manfredi, C. Multiparametric EEG analysis of brain network dynamics during neonatal seizures. J. Neurosci. Methods 2021, 348, 109003. [Google Scholar] [CrossRef]
- Stevenson, N.J.; Tapani, K.; Lauronen, L.; Vanhatalo, S. A dataset of neonatal EEG recordings with seizure annotations. Sci. Data 2019, 6, 190039. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tarvainen, M.P.; Niskanen, J.-P.; Lipponen, J.; Ranta-Aho, P.O.; Karjalainen, P. Kubios HRV—Heart rate variability analysis software. Comput. Methods Programs Biomed. 2014, 113, 210–220. [Google Scholar] [CrossRef]
- The MathWorks, Inc. MATLAB and Statistics and Machine Learning Toolbox Release; The MathWorks, Inc.: Natick, MA, USA, 2020. [Google Scholar]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [Green Version]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [Green Version]
- Costa, M.D.; Goldberger, A.L. Generalized Multiscale Entropy Analysis: Application to Quantifying the Complex Volatility of Human Heartbeat Time Series. Entropy 2015, 17, 1197–1203. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of Surface EMG Signal Based on Fuzzy Entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation Entropy: A Natural Complexity Measure for Time Series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Li, P.; Liu, C.; Li, K.; Zheng, D.; Liu, C.; Hou, Y. Assessing the complexity of short-term heartbeat interval series by distribution entropy. Med. Biol. Eng. Comput. 2014, 53, 77–87. [Google Scholar] [CrossRef]
- Camm, A.J.; Malik, M.; Bigger, J.T.; Breithardt, G.; Cerutti, S.; Cohen, R.J.; Coumel, P.; Fallen, E.L.; Kennedy, H.L.; Kleiger, R.E. Heart rate variability: Standards of measurement, physiological interpretation and clinical use. Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology. Circulation 1996, 93, 1043–1065. [Google Scholar]
- Doyle, O.; Temko, A.; Marnane, W.; Lightbody, G.; Boylan, G. Heart rate based automatic seizure detection in the newborn. Med. Eng. Phys. 2010, 32, 829–839. [Google Scholar] [CrossRef] [PubMed]
- Yentes, J.; Hunt, N.; Schmid, K.K.; Kaipust, J.P.; McGrath, D.; Stergiou, N. The Appropriate Use of Approximate Entropy and Sample Entropy with Short Data Sets. Ann. Biomed. Eng. 2013, 41, 349–365. [Google Scholar] [CrossRef] [PubMed]
- Humeau-Heurtier, A. The Multiscale Entropy Algorithm and Its Variants: A Review. Entropy 2015, 17, 3110–3123. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.-D.; Wu, C.-W.; Lee, K.-Y.; Lin, S.-G. Modified multiscale entropy for short-term time series analysis. Phys. A Stat. Mech. Appl. 2013, 392, 5865–5873. [Google Scholar] [CrossRef]
- Upadhyay, R.; Padhy, P.; Kankar, P. A comparative study of feature ranking techniques for epileptic seizure detection using wavelet transform. Comput. Electr. Eng. 2016, 53, 163–176. [Google Scholar] [CrossRef]
- Liao, F.Y.; Jan, Y.-K. Assessing skin blood flow dynamics in older adults using a modified sample entropy approach. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2014, 2014, 722–725. [Google Scholar] [CrossRef]
- Valencia, J.F.; Porta, A.; Vallverdu, M.; Clariá, F.; Baranowski, R.; Orlowska-Baranowska, E.; Caminal, P. Refined Multiscale Entropy: Application to 24-h Holter Recordings of Heart Period Variability in Healthy and Aortic Stenosis Subjects. IEEE Trans. Biomed. Eng. 2009, 56, 2202–2213. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.-D.; Wu, C.-W.; Lin, S.-G.; Wang, C.-C.; Lee, K.-Y. Time Series Analysis Using Composite Multiscale Entropy. Entropy 2013, 15, 1069–1084. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.-D.; Wu, C.-W.; Lin, S.-G.; Lee, K.-Y.; Peng, C.-K. Analysis of complex time series using refined composite multiscale entropy. Phys. Lett. A 2014, 378, 1369–1374. [Google Scholar] [CrossRef]
- Amoud, H.; Snoussi, H.; Hewson, D.; Doussot, M.; Duchene, J. Intrinsic Mode Entropy for Nonlinear Discriminant Analysis. IEEE Signal Process. Lett. 2007, 14, 297–300. [Google Scholar] [CrossRef]
- Jiang, Y.; Peng, C.-K.; Xu, Y. Hierarchical entropy analysis for biological signals. J. Comput. Appl. Math. 2011, 236, 728–742. [Google Scholar] [CrossRef] [Green Version]
- Hu, M.; Liang, H. Adaptive Multiscale Entropy Analysis of Multivariate Neural Data. IEEE Trans. Biomed. Eng. 2012, 59, 12–15. [Google Scholar] [CrossRef] [PubMed]
- Borin, A.M.S.; Silva, L.E.V.; Murta, L.O. Modified multiscale fuzzy entropy: A robust method for short-term physiologic signals. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 083135. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Yao, W.; Wu, M.; Shi, Z.; Wang, J.; Ning, X. Multiscale permutation entropy analysis of electrocardiogram. Phys. A Stat. Mech. Its Appl. 2017, 471, 492–498. [Google Scholar] [CrossRef]
- Lee, D.-Y.; Choi, Y.-S. Multiscale Distribution Entropy Analysis of Short-Term Heart Rate Variability. Entropy 2018, 20, 952. [Google Scholar] [CrossRef] [Green Version]
- Costa, M.; Ghiran, I.; Peng, C.-K.; Nicholson-Weller, A.; Goldberger, A.L. Complex dynamics of human red blood cell flickering: Alterations within vivo aging. Phys. Rev. E 2008, 78, 020901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frassineti, L.; Barba, C.; Melani, F.; Piras, F.; Guerrini, R.; Manfredi, C. Automatic detection and sonification of nonmotor generalized onset epileptic seizures: Preliminary results. Brain Res. 2019, 1721, 146341. [Google Scholar] [CrossRef]
- Lake, D.E.; Richman, J.S.; Griffin, M.P.; Moorman, J.R. Sample entropy analysis of neonatal heart rate variability. Am. J. Physiol. Integr. Comp. Physiol. 2002, 283, R789–R797. [Google Scholar] [CrossRef] [Green Version]
- Borin, A.M.S., Jr.; Humeau-Heurtier, A.; Murta, L.O., Jr.; Silva, L.E.V. Multiscale Entropy Analysis of Short Signals: The Robustness of Fuzzy Entropy-Based Variants, preprint (version 1) available at Research Square; 2021; Available online: https://doi.org/10.21203/rs.3.rs-361154/v1 (accessed on 1 September 2021).
- Porta, A.; Bari, V.; Marchi, A.; De Maria, B.; Castiglioni, P.; Di Rienzo, M.; Guzzetti, S.; Cividjian, A.; Quintin, L. Limits of permutation-based entropies in assessing complexity of short heart period variability. Physiol. Meas. 2015, 36, 755–765. [Google Scholar] [CrossRef] [Green Version]
- Buchanan, G.F. Impaired CO2-Induced Arousal in SIDS and SUDEP. Trends Neurosci. 2019, 42, 242–250. [Google Scholar] [CrossRef] [PubMed]
- Karmakar, C.; Udhayakumar, R.; Palaniswami, M. Entropy Profiling: A Reduced—Parametric Measure of Kolmogorov—Sinai Entropy from Short-Term HRV Signal. Entropy 2020, 22, 1396. [Google Scholar] [CrossRef] [PubMed]
- Valenza, G.; Garcia, R.G.; Citi, L.; Scilingo, E.P.; A Tomaz, C.; Barbieri, R. Nonlinear digital signal processing in mental health: Characterization of major depression using instantaneous entropy measures of heartbeat dynamics. Front. Physiol. 2015, 6, 74. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Michniewicz, B.; Szpecht, D.; Sowińska, A.; Sibiak, R.; Szymankiewicz, M.; Gadzinowski, J. Biomarkers in newborns with hypoxic-ischemic encephalopathy treated with therapeutic hypothermia. Child’s Nerv. Syst. 2020, 36, 2981–2988. [Google Scholar] [CrossRef] [PubMed]
- Locatelli, A.; Lambicchi, L.; Incerti, M.; Bonati, F.; Ferdico, M.; Malguzzi, S.; Torcasio, F.; Calzi, P.; Varisco, T.; Paterlini, G. Is perinatal asphyxia predictable? BMC Pregnancy Childbirth 2020, 20, 186–188. [Google Scholar] [CrossRef] [PubMed]




| MAE Scale Factor | 0 vs. 1 KW-Test p-Value | int vs. 1 KW-Test p-Value | MW-Test p-Value | STATS 0 MEDIAN (IQR) | STATS 1 MEDIAN (IQR) | STATS INT MEDIAN (IQR) |
|---|---|---|---|---|---|---|
| 1 | 0.4756 | 0.1252 | 0.8048 | 1.01 (0.82–1.07) | 0.92 (0.66–1.04) | 1.01 (0.77–1.16) |
| 2 | 0.0809 | 0.2318 | 0.2312 | 0.88 (0.83–0.97) | 0.83 (0.72–0.90) | 0.89 (0.77–0.95) |
| 3 | 0.0129 * | 0.2160 | 0.0549 | 0.83 (0.77–0.88) | 0.73 (0.67–0.81) | 0.80 (0.73–0.84) |
| 4 | 0.0937 | 0.7387 | 0.2872 | 0.74 (0.69–0.78) | 0.68 (0.65–0.74) | 0.71 (0.66–0.77) |
| 5 | 0.7395 | 1 | 0.5686 | 0.67 (0.64–0.71) | 0.66 (0.58–0.69) | 0.64 (0.62–0.71) |
| 6 | 1 | 1 | 0.6620 | 0.61 (0.56–0.64) | 0.59 (0.56–0.65) | 0.59 (0.56–0.64) |
| MSE Scale Factor | 0 vs. 1 KW-Test p-Value | int vs. 1 KW-Test p-Value | MW-Test p-Value | STATS 0 MEDIAN (IQR) | STATS 1 MEDIAN (IQR) | STATS INT MEDIAN (IQR) |
|---|---|---|---|---|---|---|
| 1 | 1 | 0.1742 | 0.6213 | 0.96 (0.62–1.11) | 0.85 (0.52–1.15) | 1.05 (0.74–1.24) |
| 2 | 0.1642 | 0.1733 | 0.3420 | 1.04 (0.80–1.23) | 0.87 (0.63–1.06) | 1.01 (0.79–1.25) |
| 3 | 0.0054 * | 0.0786 | 0.0503 | 1.16 (0.94–1.40) | 0.88 (0.67–1.11) | 1.02 (0.90–1.24) |
| 4 | 0.0022 * | 0.0990 | 0.0275 * | 1.25 (1.11–1.49) | 0.94 (0.76–1.24) | 1.13 (0.98–1.34) |
| 5 | 0.0022 * | 0.0455 * | 0.0318 * | 1.38 (1.16–1.63) | 0.97 (0.86–1.20) | 1.23 (1.06–1.42) |
| 6 | 0.0064 * | 0.2387 | 0.0440 * | 1.52 (1.21–1.62) | 1.15 (0.94–1.32) | 1.28 (1.07–1.46) |
| GSE Scale Factor | 0 vs. 1 KW-Test p-Value | int vs. 1 KW-Test p-Value | MW-Test p-Value | STATS 0 MEDIAN (IQR) | STATS 1 MEDIAN (IQR) | STATS INT MEDIAN (IQR) |
|---|---|---|---|---|---|---|
| 1 | 1 | 0.4084 | 0.9092 | 2.08 (1.58–2.32) | 1.87 (1.47–2.31) | 2.09 (1.66–2.41) |
| 2 | 0.5154 | 1.0000 | 0.0574 | 0.80 (0.66–1.44) | 1.44 (0.72–1.69) | 1.33 (0.86–1.83) |
| 3 | 0.2617 | 1.0000 | 0.0166 * | 1.14 (0.77–1.49) | 1.61 (0.86–2.17) | 1.66 (0.85–2.08) |
| 4 | 0.9657 | 1.0000 | 0.0681 | 1.16 (0.97–1.70) | 1.56 (0.72–2.45) | 1.55 (0.92–2.15) |
| 5 | 1 | 1.0000 | 0.0908 | 1.41 (1.04–1.66) | 1.50 (0.93–2.00) | 1.33 (0.84–2.04) |
| 6 | 1 | 1.0000 | 0.1434 | 1.52 (1.03–1.69) | 1.62 (0.82–1.93) | 1.51 (0.97–1.85) |
| MFE Scale Factor | 0 vs. 1 KW-Test p-Value | int vs. 1 KW-Test p-Value | MW-Test p-Value | STATS 0 MEDIAN (IQR) | STATS 1 MEDIAN (IQR) | STATS INT MEDIAN (IQR) |
|---|---|---|---|---|---|---|
| 1 | 0.9564 | 0.2411 | 0.8344 | 0.40 (0.32–0.59) | 0.35 (0.19–0.52) | 0.41 (0.25–0.64) |
| 2 | 0.0316 * | 0.3318 | 0.0526 | 0.51 (0.35–0.68) | 0.36 (0.25–0.46) | 0.43 (0.32–0.57) |
| 3 | 0.0052 * | 0.2207 | 0.0150 * | 0.63 (0.43–0.76) | 0.42 (0.31–0.50) | 0.47 (0.41–0.58) |
| 4 | 0.0031 * | 0.1444 | 0.0204 * | 0.71 (0.53–0.83) | 0.47 (0.41–0.59) | 0.57 (0.47–0.68) |
| 5 | 0.0013 * | 0.0469 * | 0.0194 * | 0.80 (0.62–0.90) | 0.53 (0.46–0.65) | 0.64 (0.56–0.75) |
| 6 | 0.0011 * | 0.0864 | 0.0083* | 0.87 (0.67–0.96) | 0.59 (0.52–0.73) | 0.70 (0.59–0.80) |
| MPE Scale Factor | 0 vs. 1 KW-Test p-Value | int vs. 1 KW-Test p-Value | MW-Test p-Value | STATS 0 MEDIAN (IQR) | STATS 1 MEDIAN (IQR) | STATS INT MEDIAN (IQR) |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0.7323 | 0.6912 (0.6895–0.6921) | 0.6913 (0.6882–0.6925) | 0.6913 (0.6869–0.6925) |
| 2 | 0.5050 | 0.9519 | 0.3769 | 0.6913 (0.6898–0.6918) | 0.6919 (0.6899–0.6924) | 0.6911 (0.6889–0.6923) |
| 3 | 1 | 0.3827 | 0.7467 | 0.6915 (0.6896–0.6922) | 0.6917 (0.6890–0.6925) | 0.6902 (0.6890–0.6916) |
| 4 | 1 | 1 | 0.8792 | 0.6914 (0.6893–0.6918) | 0.6911 (0.6889–0.6916) | 0.6909 (0.6896–0.6921) |
| 5 | 1 | 1 | 0.4529 | 0.6911 (0.6903–0.6918) | 0.6908 (0.6870–0.6914) | 0.6911 (0.6888–0.6918) |
| 6 | 1 | 1 | 0.4359 | 0.6909 (0.6897–0.6920) | 0.6905 (0.6880–0.6917) | 0.6901 (0.6888–0.6917) |
| MDE Scale Factor | 0 vs. 1 KW-Test p-Value | int vs. 1 KW-Test p-Value | MW-Test p-Value | STATS 0 MEDIAN (IQR) | STATS 1 MEDIAN (IQR) | STATS INT MEDIAN (IQR) |
|---|---|---|---|---|---|---|
| 1 | 0.3664 | 0.2952 | 0.2312 | 0.8931 (0.8681–0.9062) | 0.9057 (0.8859–0.9167) | 0.8932 (0.8706–0.9083) |
| 2 | 0.8091 | 0.5365 | 0.7323 | 0.9064 (0.9019–0.9168) | 0.9176 (0.8998–0.9269) | 0.9075 (0.8919–0.9211) |
| 3 | 1 | 0.6727 | 1.0000 | 0.9178 (0.9128–0.9253) | 0.9228 (0.9026–0.9328) | 0.9169 (0.9094–0.9261) |
| 4 | 1 | 0.2114 | 0.7756 | 0.9200 (0.9149–0.9283) | 0.9269 (0.9125–0.9351) | 0.9183 (0.9114–0.9250) |
| 5 | 1 | 0.7985 | 0.8942 | 0.9177 (0.9104–0.9300) | 0.9272 (0.9134–0.9347) | 0.9198 (0.9100–0.9263) |
| 6 | 1 | 0.3935 | 0.9697 | 0.9205 (0.9154–0.9233) | 0.9240 (0.9100–0.9336) | 0.9164 (0.9069–0.9249) |
| Multiscale Entropy Index | CI—Median (iqr) Class “0” | CI—Median (iqr) Class “1” | CI—Median (iqr) Class “INT” |
|---|---|---|---|
| MAE | −3.9 (−4.2: −3.7) | −3.6 (−3.9: −3.1) | −3.8 (−4.0: −3.4) |
| MSE * | 6.3 (5.1: 7.2) | 4.2 (2.6: 5.6) | 5.0 (3.3: 6.2) |
| MFE * | 3.1 (2.3: 3.7) | 2.3 (1.7: 2.7) | 2.6 (1.6: 3.1) |
| GSE | −5.9 (−8.1: −3.1) | −2.1 (−7.0: 9.4) | −5.7 (−8.2: −1.3) |
| MPE | −3.4 (−3.5: 3.5) | −3.4 (−3.5: 3.4) | −3.4 (−3.5: 3.4) |
| MDE | 4.6 (4.5: 4.6) | 4.6 (4.0: 4.6) | 4.6 (4.5: 4.6) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frassineti, L.; Lanatà, A.; Olmi, B.; Manfredi, C. Multiscale Entropy Analysis of Heart Rate Variability in Neonatal Patients with and without Seizures. Bioengineering 2021, 8, 122. https://doi.org/10.3390/bioengineering8090122
Frassineti L, Lanatà A, Olmi B, Manfredi C. Multiscale Entropy Analysis of Heart Rate Variability in Neonatal Patients with and without Seizures. Bioengineering. 2021; 8(9):122. https://doi.org/10.3390/bioengineering8090122
Chicago/Turabian StyleFrassineti, Lorenzo, Antonio Lanatà, Benedetta Olmi, and Claudia Manfredi. 2021. "Multiscale Entropy Analysis of Heart Rate Variability in Neonatal Patients with and without Seizures" Bioengineering 8, no. 9: 122. https://doi.org/10.3390/bioengineering8090122
APA StyleFrassineti, L., Lanatà, A., Olmi, B., & Manfredi, C. (2021). Multiscale Entropy Analysis of Heart Rate Variability in Neonatal Patients with and without Seizures. Bioengineering, 8(9), 122. https://doi.org/10.3390/bioengineering8090122








