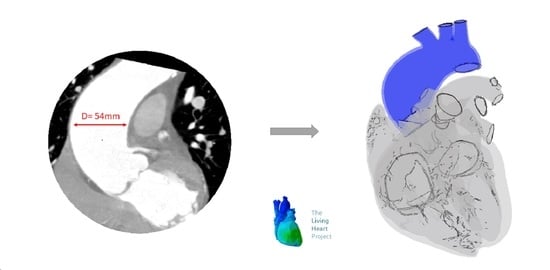
Patient-Specific Analysis of Ascending Thoracic Aortic Aneurysm with the Living Heart Human Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Patient Study Case
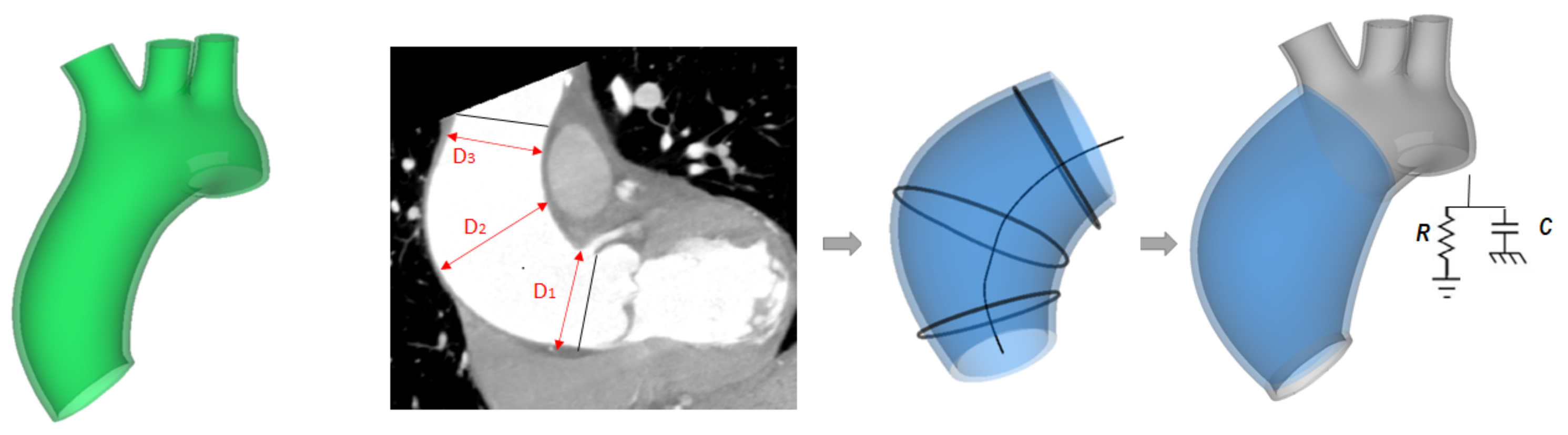
2.2. ATAA Reconstruction
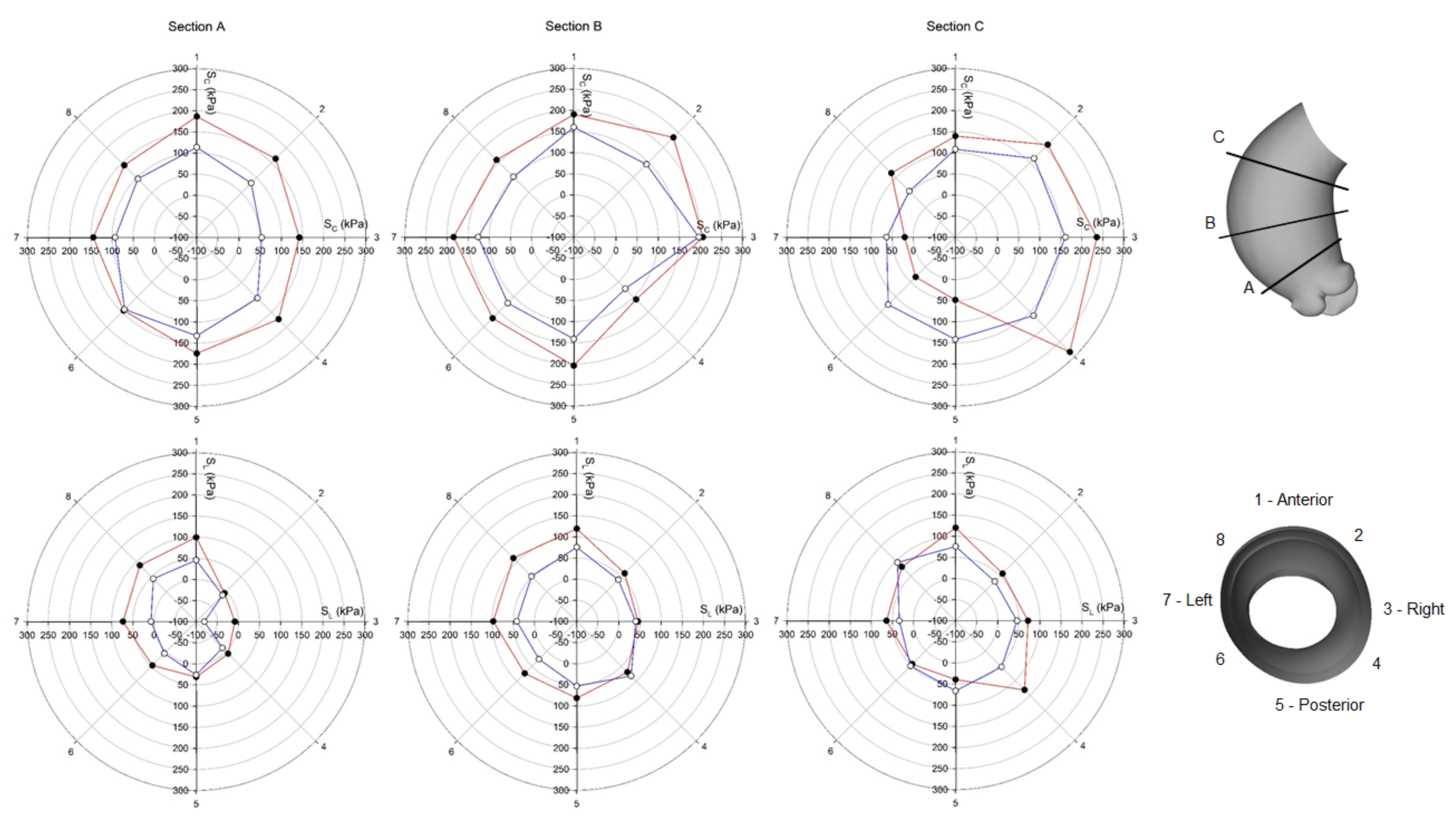
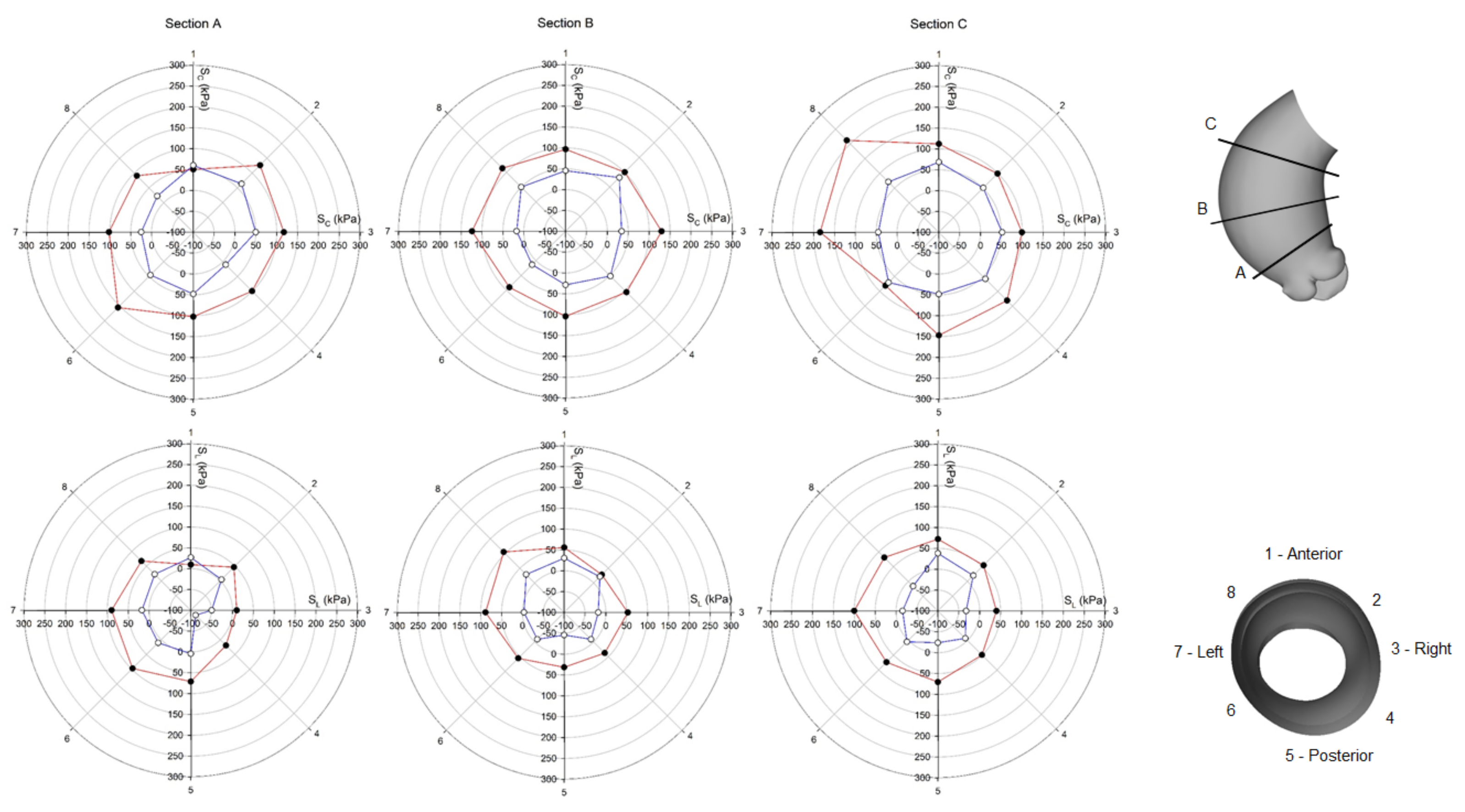
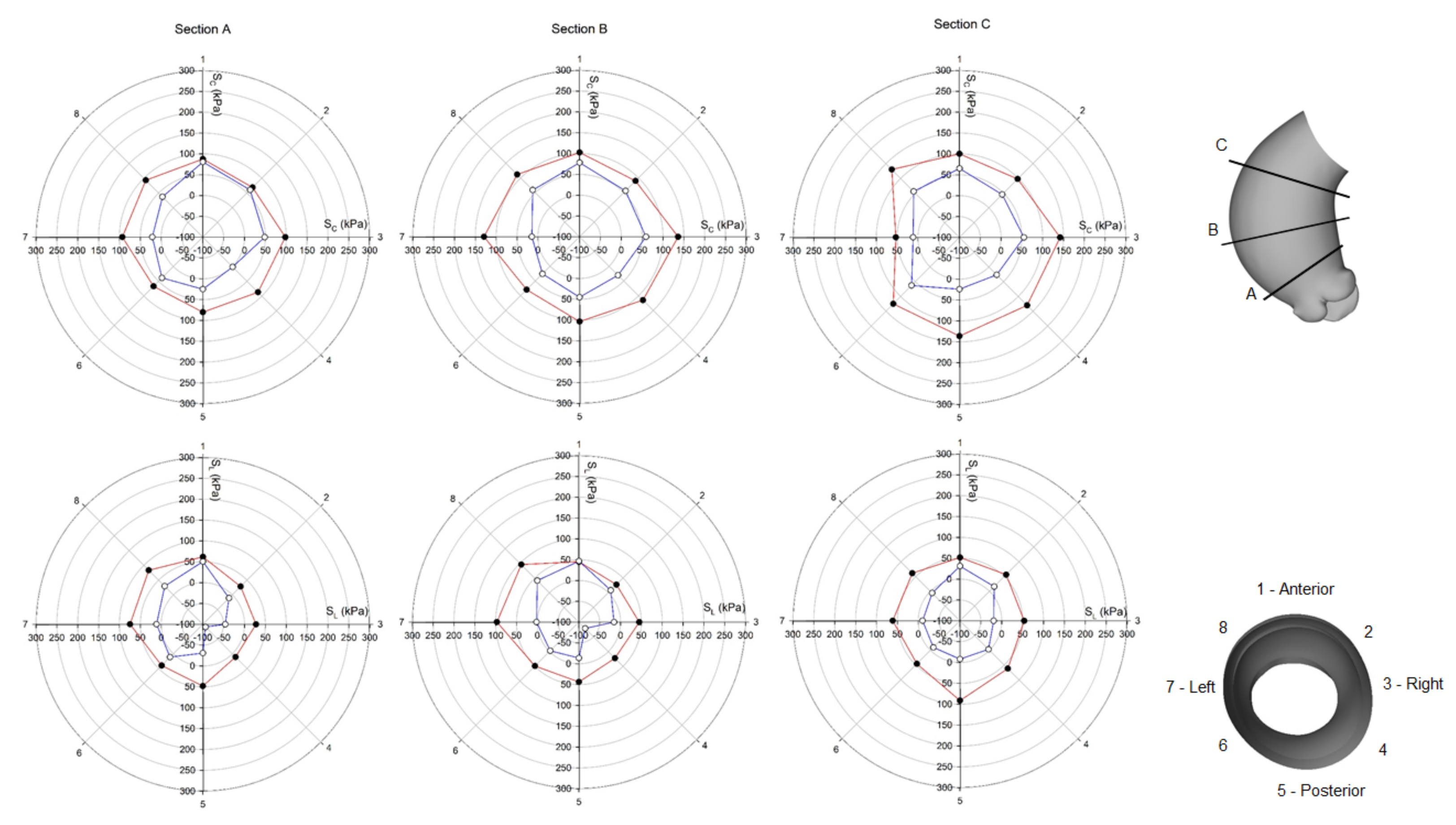
2.3. Biaxial Testing
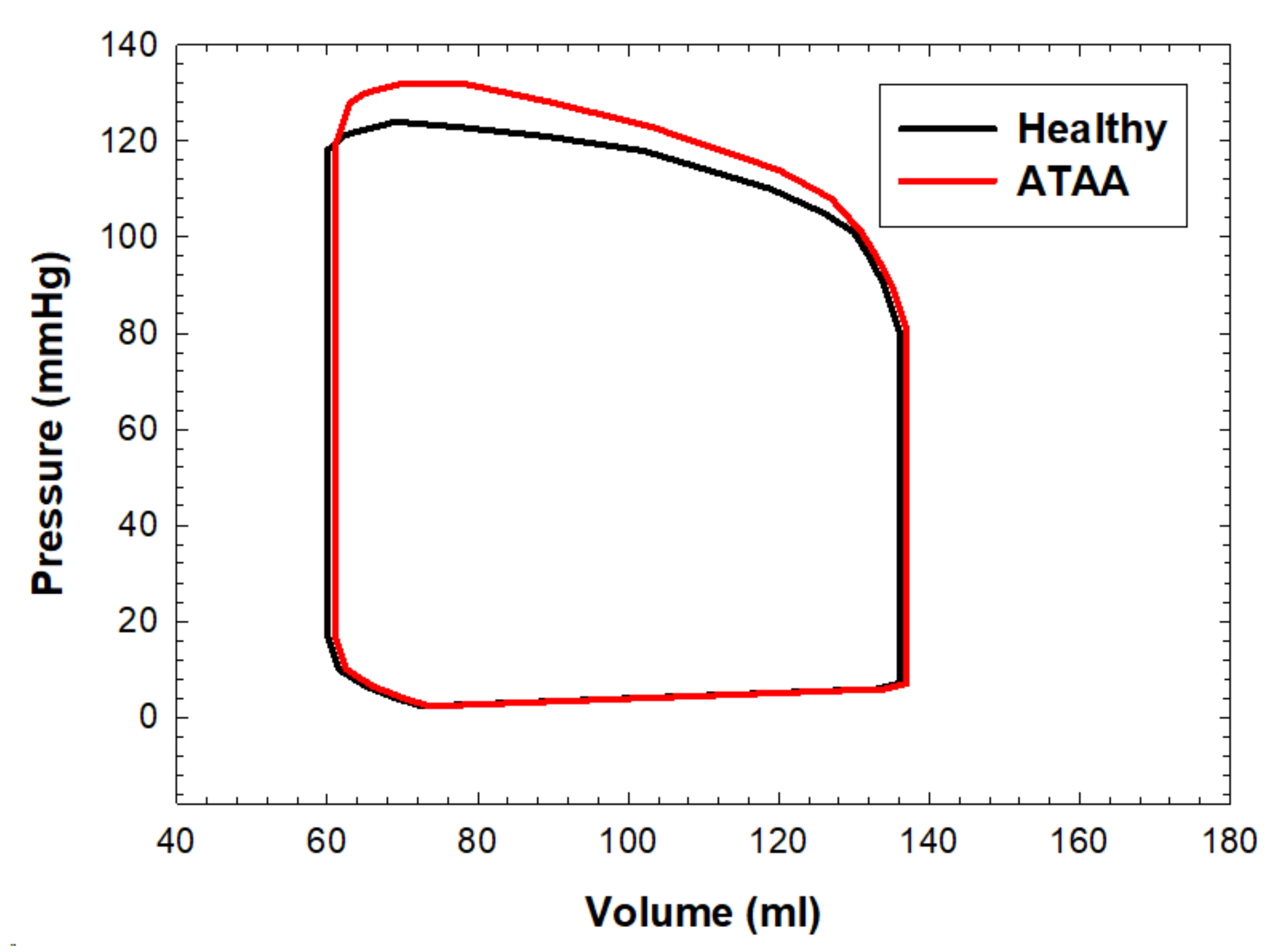
2.4. LHHM Model and Adaption to ATAA
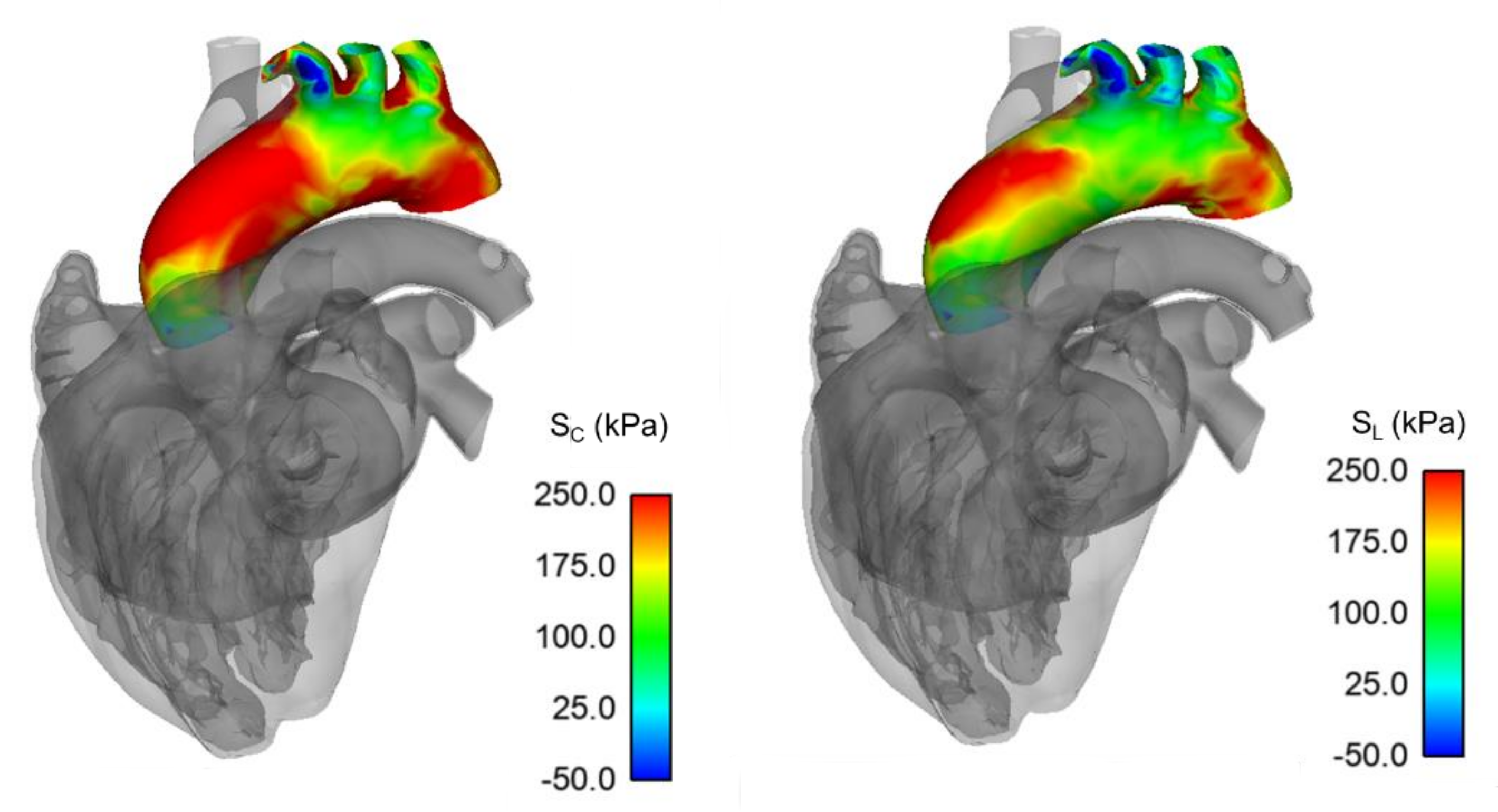
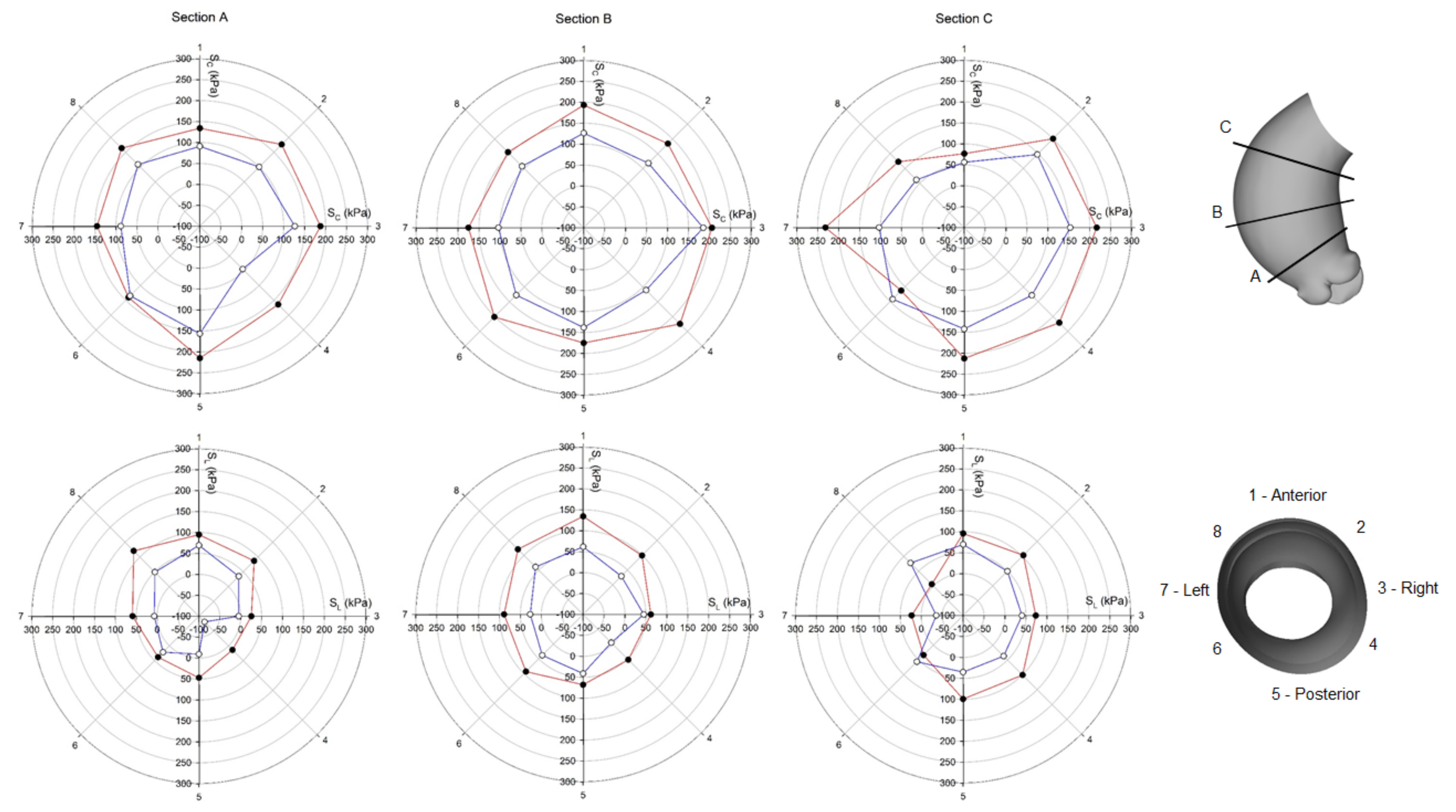
3. Results
4. Discussion
Study Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Chau, K.H.; Elefteriades, J.A. Natural history of thoracic aortic aneurysms: Size matters, plus moving beyond size. Prog. Cardiovasc. Dis. 2013, 56, 74–80. [Google Scholar] [CrossRef]
- Elefteriades, J.A. Thoracic aortic aneurysm: Reading the enemy’s playbook. Curr. Probl. Cardiol. 2008, 33, 203–277. [Google Scholar] [CrossRef] [PubMed]
- Coady, M.A.; Rizzo, J.A.; Hammond, G.L.; Mandapati, D.; Darr, U.; Kopf, G.S.; Elefteriades, J.A.; Isom, O.W.; Robicsek, F.; Griepp, R.B. What is the appropriate size criterion for resection of thoracic aortic aneurysms? J. Thorac. Cardiovasc. Surg. 1997, 113, 476–491. [Google Scholar] [CrossRef] [Green Version]
- Pape, L.A.; Tsai, T.T.; Isselbacher, E.M.; Oh, J.K.; O’Gara, P.T.; Evangelista, A.; Fattori, R.; Meinhardt, G.; Trimarchi, S.; Bossone, E.; et al. Aortic diameter >= 5.5 cm is not a good predictor of type A aortic dissection—Observations from the international registry of acute aortic dissection (IRAD). Circulation 2007, 116, 1120–1127. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paruchuri, V.; Salhab, K.F.; Kuzmik, G.; Gubernikoff, G.; Fang, H.; Rizzo, J.A.; Ziganshin, B.A.; Elefteriades, J.A. Aortic Size Distribution in the General Population: Explaining the Size Paradox in Aortic Dissection. Cardiology 2015, 131, 265–272. [Google Scholar] [CrossRef] [PubMed]
- Della Corte, A.; Body, S.C.; Booher, A.M.; Schaefers, H.J.; Milewski, R.K.; Michelena, H.I.; Evangelista, A.; Pibarot, P.; Mathieu, P.; Limongelli, G.; et al. Surgical treatment of bicuspid aortic valve disease: Knowledge gaps and research perspectives. J. Thorac. Cardiovasc. Surg. 2014, 147, 1749–1757. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Della Corte, A.; Michelena, H.I.; Citarella, A.; Votta, E.; Piatti, F.; Lo Presti, F.; Ashurov, R.; Cipollaro, M.; Forte, A. Risk Stratification in Bicuspid Aortic Valve Aortopathy: Emerging Evidence and Future Perspectives. Curr. Probl. Cardiol. 2021, 46, 100428. [Google Scholar] [CrossRef]
- Della Corte, A.; Bancone, C.; Dialetto, G.; Covino, F.E.; Manduca, S.; Montibello, M.V.; De Feo, M.; Buonocore, M.; Nappi, G. The ascending aorta with bicuspid aortic valve: A phenotypic classification with potential prognostic significance. Eur. J. Cardiothorac. Surg. 2014, 46, 240–247, discussion 247. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mahadevia, R.; Barker, A.J.; Schnell, S.; Entezari, P.; Kansal, P.; Fedak, P.W.; Malaisrie, S.C.; McCarthy, P.; Collins, J.; Carr, J.; et al. Bicuspid aortic cusp fusion morphology alters aortic three-dimensional outflow patterns, wall shear stress, and expression of aortopathy. Circulation 2014, 129, 673–682. [Google Scholar] [CrossRef] [Green Version]
- Barker, A.J.; Lanning, C.; Shandas, R. Quantification of hemodynamic wall shear stress in patients with bicuspid aortic valve using phase-contrast MRI. Ann. Biomed. Eng. 2010, 38, 788–800. [Google Scholar] [CrossRef] [Green Version]
- Martin, C.; Sun, W.; Pham, T.; Elefteriades, J. Predictive biomechanical analysis of ascending aortic aneurysm rupture potential. Acta Biomater. 2013, 9, 9392–9400. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Trabelsi, O.; Davis, F.M.; Rodriguez-Matas, J.F.; Duprey, A.; Avril, S. Patient specific stress and rupture analysis of ascending thoracic aneurysms. J. Biomech. 2015, 48, 1836–1843. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhong, Y.; Gu, C. Deformable Models for Surgical Simulation: A Survey. IEEE Rev. Biomed. Eng. 2018, 11, 143–164. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.N. A direct Jacobian total Lagrangian explicit dynamics finite element algorithm for real-time simulation of hyperelastic materials. Int. J. Numer. Methods Eng. 2021, 122, 5744–5772. [Google Scholar] [CrossRef]
- Joldes, G.R.; Miller, K.; Wittek, A.; Doyle, B. A simple, effective and clinically applicable method to compute abdominal aortic aneurysm wall stress. J. Mech. Behav. Biomed. Mater. 2016, 58, 139–148. [Google Scholar] [CrossRef] [Green Version]
- Gallo, A.; Agnese, V.; Coronnello, C.; Raffa, G.M.; Bellavia, D.; Conaldi, P.G.; Pilato, M.; Pasta, S. On the prospect of serum exosomal miRNA profiling and protein biomarkers for the diagnosis of ascending aortic dilatation in patients with bicuspid and tricuspid aortic valve. Int. J. Cardiol. 2018, 273, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Micaelo, N.; Beltran-Debon, R.; Baiges, I.; Faiges, M.; Alegret, J.M. Specific circulating microRNA signature of bicuspid aortic valve disease. J. Transl. Med. 2017, 15, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Forte, A.; Bancone, C.; Cobellis, G.; Buonocore, M.; Santarpino, G.; Fischlein, T.J.M.; Cipollaro, M.; De Feo, M.; Della Corte, A. A possible early biomarker for bicuspid aortopathy: Circulating transforming growth factor beta-1 to soluble endoglin ratio. Circ. Res. 2017, 120, 1800–1811. [Google Scholar] [CrossRef]
- Nathan, D.P.; Xu, C.; Gorman, J.H., III; Fairman, R.M.; Bavaria, J.E.; Gorman, R.C.; Chandran, K.B.; Jackson, B.M. Pathogenesis of acute aortic dissection: A finite element stress analysis. Ann. Thorac. Surg. 2011, 91, 458–463. [Google Scholar] [CrossRef]
- Krishnan, K.; Ge, L.; Haraldsson, H.; Hope, M.D.; Saloner, D.A.; Guccione, J.M.; Tseng, E.E. Ascending thoracic aortic aneurysm wall stress analysis using patient-specific finite element modeling of in vivo magnetic resonance imaging. Interact. Cardiovasc. Thorac. Surg. 2015, 21, 471–480. [Google Scholar] [CrossRef] [Green Version]
- Pasta, S.; Gentile, G.; Raffa, G.M.; Bellavia, D.; Chiarello, G.; Liotta, R.; Luca, A.; Scardulla, C.; Pilato, M. In silico shear and intramural stresses are linked to aortic valve morphology in dilated ascending aorta. Eur. J. Vasc. Endovasc. Surg. 2017, S1078-5884, 30331–30333. [Google Scholar] [CrossRef]
- Pasta, S.; Gentile, G.; Raffa, G.M.; Scardulla, F.; Bellavia, D.; Luca, A.; Pilato, M.; Scardulla, C. Three-dimensional parametric modeling of bicuspid aortopathy and comparison with computational flow predictions. Artif. Organs 2017, 41, E92–E102. [Google Scholar] [CrossRef]
- Pasta, S.; Rinaudo, A.; Luca, A.; Pilato, M.; Scardulla, C.; Gleason, T.G.; Vorp, D.A. Difference in hemodynamic and wall stress of ascending thoracic aortic aneurysms with bicuspid and tricuspid aortic valve. J. Biomech. 2013, 46, 1729–1738. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Campobasso, R.; Condemi, F.; Viallon, M.; Croisille, P.; Campisi, S.; Avril, S. Evaluation of peak wall stress in an ascending thoracic aortic aneurysm using fsi simulations: Effects of aortic stiffness and peripheral resistance. Cardiovasc. Eng. Technol. 2018, 9, 707–722. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Flores, N.; Lum, M.; Wisneski, A.D.; Xuan, Y.; Inman, J.; Hope, M.D.; Saloner, D.A.; Guccione, J.M.; Ge, L.; et al. Wall stress analyses in patients with >/=5 cm versus <5 cm ascending thoracic aortic aneurysm. J. Thorac. Cardiovasc. Surg. 2021, 162, 1452–1459. [Google Scholar] [PubMed]
- Mendez, V.; Di Giuseppe, M.; Pasta, S. Comparison of hemodynamic and structural indices of ascending thoracic aortic aneurysm as predicted by 2-way FSI, CFD rigid wall simulation and patient-specific displacement-based FEA. Comput. Biol. Med. 2018, 100, 221–229. [Google Scholar] [CrossRef] [PubMed]
- Rinaudo, A.; Raffa, G.M.; Scardulla, F.; Pilato, M.; Scardulla, C.; Pasta, S. Biomechanical implications of excessive endograft protrusion into the aortic arch after thoracic endovascular repair. Comput. Biol. Med. 2015, 66, 235–241. [Google Scholar] [CrossRef] [PubMed]
- Beller, C.J.; Labrosse, M.R.; Thubrikar, M.J.; Robicsek, F. Role of aortic root motion in the pathogenesis of aortic dissection. Circulation 2004, 109, 763–769. [Google Scholar] [CrossRef] [Green Version]
- The Living Heart Project—A Translational Research Initiative to Revolutionize Cardiovascular Science through Realistic Simulation. Available online: https://www.3ds.com/products-services/simulia/solutions/life-sciences-healthcare/the-living-heart-project/ (accessed on 26 October 2021).
- Pasta, S.; Agnese, V.; Di Giuseppe, M.; Gentile, G.; Raffa, G.M.; Bellavia, D.; Pilato, M. In vivo strain analysis of dilated ascending thoracic aorta by ECG-gated CT angiographic imaging. Ann. Biomed. Eng. 2017, 45, 2911–2920. [Google Scholar] [CrossRef] [PubMed]
- Scardulla, F.; Pasta, S.; D’Acquisto, L.; Sciacca, S.; Agnese, V.; Vergara, C.; Quarteroni, A.; Clemenza, F.; Bellavia, D.; Pilato, M. Shear stress alterations in the celiac trunk of patients with a continuous-flow left ventricular assist device as shown by in-silico and in-vitro flow analyses. J. Heart Lung Transplant. Off. Publ. Int. Soc. Heart Transplant. 2017, 36, 906–913. [Google Scholar] [CrossRef] [PubMed]
- Di Giuseppe, M.; Alotta, G.; Agnese, V.; Bellavia, D.; Raffa, G.M.; Vetri, V.; Zingales, M.; Pasta, S.; Pilato, M. Identification of circumferential regional heterogeneity of ascending thoracic aneurysmal aorta by biaxial mechanical testing. J. Mol. Cell. Cardiol. 2019, 130, 205–215. [Google Scholar] [CrossRef] [PubMed]
- Baillargeon, B.; Rebelo, N.; Fox, D.D.; Taylor, R.L.; Kuhl, E. The living heart project: A robust and integrative simulator for human heart function. Eur. J. Mech. A Solids 2014, 48, 38–47. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hurtado, D.E.; Kuhl, E. Computational modelling of electrocardiograms: Repolarisation and T-wave polarity in the human heart. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 986–996. [Google Scholar] [CrossRef] [Green Version]
- Dabiri, Y.; Sack, K.L.; Shaul, S.; Sengupta, P.P.; Guccione, J.M. Relationship of transmural variations in myofiber contractility to left ventricular ejection fraction: Implications for modeling heart failure phenotype with preserved ejection fraction. Front. Physiol. 2018, 9, 1003. [Google Scholar] [CrossRef] [Green Version]
- Pasta, S.; Phillippi, J.A.; Tsamis, A.; D’Amore, A.; Raffa, G.M.; Pilato, M.; Scardulla, C.; Watkins, S.C.; Wagner, W.R.; Gleason, T.G.; et al. Constitutive modeling of ascending thoracic aortic aneurysms using microstructural parameters. Med. Eng. Phys. 2016, 38, 121–130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Walker, J.C.; Ratcliffe, M.B.; Zhang, P.; Wallace, A.W.; Hsu, E.W.; Saloner, D.A.; Guccione, J.M. Magnetic resonance imaging-based finite element stress analysis after linear repair of left ventricular aneurysm. J. Thorac. Cardiovasc. Surg. 2008, 135, 1094–1102. [Google Scholar] [CrossRef] [Green Version]
- Holzapfel, G.A.; Ogden, R.W. Constitutive modelling of passive myocardium: A structurally based framework for material characterization. Philos. Trans. A Math. Phys. Eng. Sci. 2009, 367, 3445–3475. [Google Scholar] [CrossRef]
- Wisneski, A.D.; Wang, Y.; Deuse, T.; Hill, A.C.; Pasta, S.; Sack, K.L.; Yao, J.; Guccione, J.M. Impact of aortic stenosis on myofiber stress: Translational application of left ventricle-aortic coupling simulation. Front. Physiol. 2020, 11, 574211. [Google Scholar] [CrossRef]
- Kozerke, S.; Scheidegger, M.B.; Pedersen, E.M.; Boesiger, P. Heart motion adapted cine phase-contrast flow measurements through the aortic valve. Magn. Reson. Med. 1999, 42, 970–978. [Google Scholar] [CrossRef]
- Plonek, T.; Zak, M.; Burzynska, K.; Rylski, B.; Gozdzik, A.; Kustrzycki, W.; Beyersdorf, F.; Jasinski, M.; Filipiak, J. The combined impact of mechanical factors on the wall stress of the human ascending aorta—A finite elements study. BMC Cardiovasc. Disord. 2017, 17, 297. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Emerel, L.; Thunes, J.; Kickliter, T.; Billaud, M.; Phillippi, J.A.; Vorp, D.A.; Maiti, S.; Gleason, T.G. Predissection-derived geometric and distensibility indices reveal increased peak longitudinal stress and stiffness in patients sustaining acute type A aortic dissection: Implications for predicting dissection. J. Thorac. Cardiovasc. Surg. 2019, 158, 355–363. [Google Scholar] [CrossRef]
- Gomez, A.; Wang, Z.; Xuan, Y.; Wisneski, A.D.; Hope, M.D.; Saloner, D.A.; Guccione, J.M.; Ge, L.; Tseng, E.E. Wall stress distribution in bicuspid aortic valve-associated ascending thoracic aortic aneurysms. Ann. Thorac. Surg. 2020, 110, 807–814. [Google Scholar] [CrossRef]
- Wu, J.; Zafar, M.A.; Li, Y.; Saeyeldin, A.; Huang, Y.; Zhao, R.; Qiu, J.; Tanweer, M.; Abdelbaky, M.; Gryaznov, A.; et al. Ascending aortic length and risk of aortic adverse events: The neglected dimension. J. Am. Coll. Cardiol. 2019, 74, 1883–1894. [Google Scholar] [CrossRef]
- Pasta, S.; Agnese, V.; Gallo, A.; Cosentino, F.; Di Giuseppe, M.; Gentile, G.; Raffa, G.M.; Maalouf, J.F.; Michelena, H.I.; Bellavia, D.; et al. Shear Stress and Aortic Strain Associations with Biomarkers of Ascending Thoracic Aortic Aneurysm. Ann. Thorac. Surg. 2020, 110, 1595–1604. [Google Scholar] [CrossRef] [PubMed]
- Sahli Costabal, F.; Yao, J.; Kuhl, E. Predicting the cardiac toxicity of drugs using a novel multiscale exposure-response simulator. Comput. Methods Biomech. Biomed. Engin. 2018, 21, 232–246. [Google Scholar] [CrossRef] [Green Version]
- Genet, M.; Lee, L.C.; Baillargeon, B.; Guccione, J.M.; Kuhl, E. Modeling pathologies of diastolic and systolic heart failure. Ann. Biomed. Eng. 2016, 44, 112–127. [Google Scholar] [CrossRef] [PubMed]
- Sack, K.L.; Dabiri, Y.; Franz, T.; Solomon, S.D.; Burkhoff, D.; Guccione, J.M. Investigating the role of interventricular interdependence in development of right heart dysfunction during lvad support: A patient-specific methods-based approach. Front. Physiol. 2018, 9, 520. [Google Scholar] [CrossRef]
- Baillargeon, B.; Costa, I.; Leach, J.R.; Lee, L.C.; Genet, M.; Toutain, A.; Wenk, J.F.; Rausch, M.K.; Rebelo, N.; Acevedo-Bolton, G.; et al. Human cardiac function simulator for the optimal design of a novel annuloplasty ring with a sub-valvular element for correction of ischemic mitral regurgitation. Cardiovasc. Eng. Technol. 2015, 6, 105–116. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, R.P.; Marom, G.; Bianchi, M.; D’Souza, K.; Zietak, W.; Bluestein, D. Numerical evaluation of transcatheter aortic valve performance during heart beating and its post-deployment fluid-structure interaction analysis. Biomech. Model. Mechanobiol. 2020, 19, 1725–1740. [Google Scholar] [CrossRef] [PubMed]
- Morany, A.; Lavon, K.; Bluestein, D.; Hamdan, A.; Haj-Ali, R. Structural responses of integrated parametric aortic valve in an electro-mechanical full heart model. Ann. Biomed. Eng. 2021, 49, 441–454. [Google Scholar] [CrossRef] [PubMed]
- Cosentino, F.; Agnese, V.; Raffa, G.M.; Gentile, G.; Bellavia, D.; Zingales, M.; Pilato, M.; Pasta, S. On the role of material properties in ascending thoracic aortic aneurysms. Comput. Biol. Med. 2019, 109, 70–78. [Google Scholar] [CrossRef] [PubMed]
- Sassani, S.G.; Tsangaris, S.; Sokolis, D.P. Layer- and region-specific material characterization of ascending thoracic aortic aneurysms by microstructure-based models. J. Biomech. 2015, 48, 3757–3765. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cutugno, S.; Agnese, V.; Gentile, G.; Raffa, G.M.; Wisneski, A.D.; Guccione, J.M.; Pilato, M.; Pasta, S. Patient-Specific Analysis of Ascending Thoracic Aortic Aneurysm with the Living Heart Human Model. Bioengineering 2021, 8, 175. https://doi.org/10.3390/bioengineering8110175
Cutugno S, Agnese V, Gentile G, Raffa GM, Wisneski AD, Guccione JM, Pilato M, Pasta S. Patient-Specific Analysis of Ascending Thoracic Aortic Aneurysm with the Living Heart Human Model. Bioengineering. 2021; 8(11):175. https://doi.org/10.3390/bioengineering8110175
Chicago/Turabian StyleCutugno, Salvatore, Valentina Agnese, Giovanni Gentile, Giuseppe M. Raffa, Andrew D. Wisneski, Julius M. Guccione, Michele Pilato, and Salvatore Pasta. 2021. "Patient-Specific Analysis of Ascending Thoracic Aortic Aneurysm with the Living Heart Human Model" Bioengineering 8, no. 11: 175. https://doi.org/10.3390/bioengineering8110175
APA StyleCutugno, S., Agnese, V., Gentile, G., Raffa, G. M., Wisneski, A. D., Guccione, J. M., Pilato, M., & Pasta, S. (2021). Patient-Specific Analysis of Ascending Thoracic Aortic Aneurysm with the Living Heart Human Model. Bioengineering, 8(11), 175. https://doi.org/10.3390/bioengineering8110175